2019-2020年中考数学复习 考点跟踪突破8 一次函数

2019-2020 年九年级放学期中考复习数学试题：一次函数一、玩转重庆七年中考真题命题点 1正比率函数分析式确实定1、（ 2013重庆中考 B 卷）已知正比率函数y=kx( k0 )的图象经过点（1，-2），则正比率函数的分析式为A. y 2x y2x y 1 x y 1 xB. C.2 D.2命题点 2一次函数的图像与性质（ 2 次）2、（ 2014 重庆中考 B 卷）若点（ 3， 1）在一次函数ykx2( k0)的图象上，则 k 的值是（）A、5B、4C、3D、1二、重难点打破命题点 1求一次函数的分析式例 1、（ 2014 牡丹江）已知一次函数的图像与y 轴交点的纵坐标为 -2 ，当 x=2 时， y=1, ，则此函数的分析式为。

（解题四步：设、代、求、写）变式改编：1、（2014?宜宾）如图，过 A 点的一次函数的图象与正比率函数y=2x 的图象订交于点 B，则这个一次函数的分析式是（）A． y=2x+3B． y=x﹣ 3C． y=2x﹣ 3D． y=﹣ x+32 、（ 2015 一中）已知一次函数ykx b k 0（1）若一次函数图象经过点A 2, 1 , B1,8 ,C t, 4，求一次函数的分析式，以及的值。

5,0（ 2 ）若一次函数图象过点2且函数图象与坐标轴围成的三角形面积为254 ，求一次函数的分析式。

命题点 2 一次函数的图像和性质例 2 、（2015一中）已知y kx k 0 图象过第二、四象限，则一次函数y 2kx k 的图象大概是（）A.B.C.D．变式改编：1、（2015一中）如图为直线l : y mx n（m,n是常数）的图象，化简n2n m.。

2、2014?张家界）已知一次函数y=（ 1﹣ m） x+m﹣ 2，当 m时， y 随 x 的增大而增大．命题点 3 一次函数的交点问题例 3、函数 y=2x与 y=x+1 的图像的交点坐标是。

变式改编： 1、不论 m为什么实数，直线y x 2m 与 y x 4的交点不行能在（）A．第一象限． B. 第二象限． C.第三象限． D.第四象限．2、（2014?永州）如图，已知直线l1 ：y=k1x+4 与直线 l2 ：y=k2x ﹣5 交于点 A，它们与 y 轴的交点分别为点 B， C，点 E，F 分别为线段 AB、AC的中点，则线段EF 的长度为。

2020年中考数学复习《一次函数》高频考点突破与提升复习资料一.本章知识梳理1.一般的若y kx b =+（k ，b 是常数，且0k ≠），那么y 叫做x 的一次函数，当b=0时，一次函数y=kx 也叫正比例函数。

2.正比例函数kx y =（0k ≠）是一次函数的特殊形式,当x=0时，y=0,故正比例函数图像过原点（0,0).3.一次函数的图像和性质：y 随的增大而增大 y 随的增大而减小说明： （1）与坐标轴交点（0，b ）和（-kb ，0）, b 的几何意义：_____________________ （2）增减性： k>0，y 随x 的增大而增大；k<0，y 随x 增大而减小.（3）倾斜度：|k|越大，图象越接近于y 轴；|k|越小，图象越接近于x 轴。

（4）图像的平移：当b>0时，将直线y=kx 的图象向上平移b 个单位可得y=kx+b 的图像； 当b<0时，将直线y=kx 的图象向下平移b 个单位可得y=kx+b 的图像.4.直线b 1=k 1x+b 1与直线y 2=k 2x+b 2（k 1≠0 ，k 2≠0）的位置关系．①k 1≠k 2⇔y 1与y 2相交；②⎩⎨⎧=≠2121b b k k ⇔y 1与y 2相交于y 轴上同一点（0，b 1）或（0，b 2）； ③⎩⎨⎧≠=2121,b b k k ⇔y 1与y 2平行； ④⎩⎨⎧==2121,b b k k ⇔y 1与y 2重合.5.一次函数解析式的确定，主要有三种方法：(1)由已知函数推导或推证(2)由实际问题列出二元方程，再转化为函数解析式。

(3)用待定系数法求函数解析式。

二．高频考点解析题型一：一次函数的概念例1.已知函数y=(m-2)32-m x +3,当m 为何值时，y 是x 的一次函数？解析：根据一次函数的定义，x 的次数必须为1，系数不为0，即可求出m 的值.变式练习：1.已知函数y=(m-1)x+m 是一次函数，求m 的范围.2.已知函数y=(k-1)x+k 2-1,当k____________时，它是一次函数，当k__________时，它是正比例函数.答案：1.m ≠1 2. ≠1, -1题型二：一次函数的图像与性质例2.对于一次函数y=﹣2x+4，下列结论错误的是（ ）A ． 函数值随自变量的增大而减小B ． 函数的图象不经过第三象限C ． 函数的图象向下平移4个单位长度得y=﹣2x 的图象D ． 函数的图象与x 轴的交点坐标是（0，4）解析：这是探究型题目，考查一次函数的性质；一次函数图象与几何变换。

一次函数1．（ 2019?通辽）如图，直线 y＝ kx+b（ k≠ 0）经过点（﹣ 1，3），则不等式kx+b≥ 3 的解集为（）A ．x＞﹣ 1 B． x＜﹣ 1C． x≥ 3 D． x≥﹣ 12．（ 2019?梧州）直线 y＝ 3x+1 向下平移 2 个单位，所得直线的分析式是（）A ．y＝ 3x+3 B． y＝ 3x﹣ 2 C． y＝ 3x+2 D． y＝ 3x﹣ 13．（ 2019?邵阳）一次函数 y1＝ k1x+b1的图象 l 1以下图，将直线 l1向下平移若干个单位后得直线 l 2， l 2的函数表达式为y2＝ k2x+b2．以下说法中错误的选项是（）A ．k1＝ k2 B． b1＜ b2C． b1＞ b2 D．当 x＝ 5 时， y1＞y24．（ 2019?广元）如图，过点 A0（ 0 ，1）作 y 轴的垂线交直线 l： y＝x 于点 A1，过点 A1 作直线 l 的垂线，交 y 轴于点 A2，过点 A2作 y 轴的垂线交直线 l 于点 A3，，这样挨次下去，获得△ A0A1A2，△ A2A3A4，△ A4A5A6，，其面积分别记为S1，S2， S3，，则S100为（）A ．（） 100 B．（ 3 ） 100C． 3 ×4199 D． 3 ×23955．（2019?东营）甲、乙两队参加了“端午情，龙舟韵”赛龙舟竞赛，两队在竞赛时的行程s（米）与时间t（秒）之间的函数图象以下图，请你依据图象判断，以下说法正确的选项是（）A．乙队抢先抵达终点B．甲队比乙队多走了 126 米C．在 47.8 秒时，两队所走行程相等D ．从出发到13.7 秒的时间段内，乙队的速度慢6．（ 2019?聊城）某快递企业每日上午9： 00﹣ 10： 00 为集中揽件和派件时段，甲库房用来揽收快件，乙库房用来派发快件，该时段内甲、乙两库房的快件数目y（件）与时间 x（分）之间的函数图象以下图，那么当两库房快递件数同样时，现在的时间为（）A ．9： 15 B． 9： 20C． 9： 25 D． 9： 307．（ 2019?苏州）若一次函数y＝ kx+b（ k， b 为常数，且k≠ 0）的图象经过点A（ 0，﹣ 1），B（ 1， 1），则不等式kx+b＞ 1 的解为（）A ．x＜ 0 C． x＜ 1 B． x＞ 0 D． x＞ 18．（ 2019?杭州）已知一次函数y1＝ ax+b 和 y2＝ bx+a（ a≠b），函数y1和y2的图象可能是（）A．B．C．D．9．（ 2019?绍兴）若三点（ 1， 4），（ 2， 7），（ a， 10）在同向来线上，则 a 的值等于（）A．﹣1 B．0.C． 3 D． 410．（ 2019?枣庄）如图，向来线与两坐标轴的正半轴分别交于A B两点，P是线段AB上，随意一点（不包含端点），过点 P 分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为8，则该直线的函数表达式是（）A ．y＝﹣ x+4 C． y＝ x+8 B． y＝ x+4 D． y＝﹣ x+811．（ 2019?徐州）函数y＝ x+1 的图象与x 轴、 y 轴分别交于A、B 两点，点 C 在x 轴上．若△ ABC 为等腰三角形，则知足条件的点 C 共有个．12．（ 2019?贵阳）在平面直角坐标系内，一次函数y＝k1x+b1与 y＝ k2x+b2的图象以下图，则对于 x， y 的方程组的解是．13．（ 2019?东营）如图，在平面直角坐标系中，函数y＝x 和 y＝﹣x 的图象分别为直线 l 1， l2，过l 1上的点A1（ 1，）作x 轴的垂线交l 2于点A2，过点A2作y 轴的垂线交 l 1于点 A3，过点 A3作 x 轴的垂线交 l 2于点 A4，挨次进行下去，则点 A2019的横坐标为．14．（ 2019?烟台）如图，直线 y＝ x+2 与直线 y＝ ax+ c 订交于点P（ m，3），则对于 x 的不等式 x+2≤ax+c 的解为．15．（ 2019?郴州）某商铺今年 6 月初销售纯净水的数目以下表所示：日期 1 2 3 4数目（瓶）120 125 130 135察看此表，利用所学函数知识展望今年 6 月 7 日该商铺销售纯净水的数目约为瓶．16．（ 2019?雅安）某商场计划购进甲、乙两种商品，两种商品的进价、售价以下表：商品甲乙进价（元 / 件）x+60 x售价（元 / 件）200 100若用 360 元购进甲种商品的件数与用180 元购进乙种商品的件数同样．（ 1）求甲、乙两种商品的进价是多少元？（ 2）若商场销售甲、乙两种商品共50 件，此中销售甲种商品为 a 件（ a≥ 30），设销售完50 件甲、乙两种商品的总收益为w 元，求w 与a 之间的函数关系式，并求出w 的最小值．17 2019 11km之内，每高升1km 6℃；又知在．（?陕西）依据记录，从地面向上，气温降低距离地面 11km 以上高空，气温几乎不变．若地面气温为m（℃），设距地面的高度为 x （km）处的气温为 y（℃）（1）写出距地面的高度在 11km 之内的 y 与 x 之间的函数表达式；（2）上周日，小敏在乘飞机从上海飞回西安途中，某一时辰，她从机舱内屏幕显示的相关数据得悉，飞机外气温为﹣26℃时，飞机距离地面的高度为7km，求当时这架飞机下方地面的气温；小敏想，若是飞机当时在距离地面12km 的高空，飞机外的气温是多少度呢？恳求出若是当时飞机距离地面12km 时，飞机外的气温．18 2019活动小组对学校400米的跑道进行规划设计，跑道．（?宁夏）在综合与实践活动中，由两段直道和两头是半圆弧的跑道构成．此中400 米跑道最内圈为400 米，两头半圆弧的半径为36 米．（π取）．（1）求 400 米跑道中一段直道的长度；（2）在活动中发现跑道周长（单位：米）随跑道宽度（距最内圈的距离，单位：米）的变化而变化．请达成下表：跑道宽度 /米0 1 2 3 4 5跑道周长 /米400若设 x 表示跑道宽度（单位：米），y 表示该跑道周长（单位：米），试写出 y 与 x 的函数关系式：（ 3）将 446 米的跑道周长作为米）形成的地区最多能铺设道宽为400 米跑道场所的最外沿，那么它与最内圈（跑道周长1.2 米的跑道多少条？40019．（ 2019?齐齐哈尔）甲、乙两地间的直线公路长为400 千米．一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行，货车比轿车早出发 1 小时，途中轿车出现了故障，停下维修，货车仍持续行驶． 1 小时后轿车故障被清除，此时接到通知，轿车马上掉头按原路原速返回甲地（接到通知及掉头时间不计）．最后两车同时抵达甲地，已知两车距各自出发地的距离y（千米）与轿车所用的时间x（小时）的关系以下图，请联合图象解答以下问题：（ 1）货车的速度是千米/小时；轿车的速度是千米/小时；t值为．（2）求轿车距其出发地的距离 y（千米）与所用时间 x（小时）之间的函数关系式并写出自变量 x 的取值范围；（ 3）请直接写出货车出发多长时间两车相距90 千米．20．（ 2019?镇江）学校数学兴趣小组利用机器人展开数学活动．在相距 150 个单位长度的直线跑道AB 上，机器人甲从端点 A 出发，匀速来回于端点A、B 之间，机器人乙同时从端点 B 出发，以大于甲的速度匀速来回于端点B、A 之间．他们抵达端点后马上转身折返，用时忽视不计．兴趣小构成员研究这两个机器人迎面相遇的状况，这里的” 迎面相遇“包含当面相遇、在端点处相遇这两种．【察看】①察看图 1，若这两个机器人第一次迎面相遇时，相遇地址与点 A 之间的距离为 30 个单位长度，则他们第二次迎面相遇时，相遇地址与点 A 之间的距离为个单位长度；② 若这两个机器人第一次迎面相遇时，相遇地址与点 A 之间的距离为40 个单位长度，则他们第二次迎面相遇时，相遇地址与点 A 之间的距离为个单位长度；【发现】设这两个机器人第一次迎面相遇时，相遇地址与点 A 之间的距离为 x 个单位长度，他们第二次迎面相遇时，相遇地址与点 A 之间的距离为y 个单位长度．兴趣小构成员发现了y 与 x 的函数关系，并画出了部分函数图象（线段OP，不包含点 O，如图 2 所示）．① a＝；② 分别求出各部分图象对应的函数表达式，并在图 2 中补全函数图象；【拓展】设这两个机器人第一次迎面相遇时，相遇地址与点 A 之间的距离为 x 个单位长度，他们第三次迎面相遇时，相遇地址与点 A 之间的距离为y 个单位长度．若这两个机器人第三次迎面相遇时，相遇地址与点 A 之间的距离 y 不超出 60 个单位长度，则他们第一次迎面相遇时，相遇地址与点 A 之间的距离 x 的取值范围是．（直接写出结果）。

2020年数学一轮复习之针对训练：一次函数的突破1．如图所示，将长方形纸片OABC放入直角坐标系xoy中，使OA、OC分别落在x、y轴的正半轴上，连接AC，且AC＝4，．（1）求A、C两点的坐标；（2）求AC两点所在直线的解析式；2．一列快车从甲地匀速驶往乙地，一列慢车从乙地匀速驶往甲地．两车行驶的时间为xh，两车之间的距离为ykm，图中的折线表示y与x之间的函数关系，根据图象解决以下问题：（1）甲、乙两地的距离为720 km；（2）慢车的速度为80 km/h，快车的速度为120 km/h；（3）求当x为多少时，两车之间的距离为500km，请通过计算求出x的值．3．如图，一次函数y＝kx+b的图象与直线交于点A（4，3），与y轴交于点B，且OA ＝OB．（1）求一次函数的表达式；（2）求两直线与y轴围成的三角形的面积．（3）在x轴上是否存在点C，使△AOC是以OA为腰的等腰三角形？若存在，直接写出C 的坐标；若不存在，说明理由．4．如图，一次函数的图象过A（3，0），B（0，3）两点．（1）求直线AB的函数表达式；（2）直线y＝﹣3x﹣3交x轴于点C，E为直线AB上一动点．①求CE的最小值；②D是直线y＝﹣3x﹣3上任意一点，F为直线AB上另一动点，若△DEF是以2为直角边长的等腰直角三角形，求D点的坐标．5．如图，已知过点B （1，0）的直线l 1与直线l 2：y ＝2x +4相交于点P （﹣1，a ），l 1与y 轴交于点C ，l 2与x 轴交于点A ．（1）求a 的值及直线l 1的解析式．（2）求四边形PAOC 的面积．（3）在x 轴上方有一动直线平行于x 轴，分别与l 1，l 2交于点M ，N ，且点M 在点N 的右侧，x 轴上是否存在点Q ，使△MNQ 为等腰直角三角形？若存在，请直接写出满足条件的点Q 的坐标；若不存在，请说明理由．6．如图，函数y ＝x +b 的图象与x 轴、y 轴分别交于点A 、B ，与函数y ＝x 的图象交于点M ，点M 的横坐标为3．（1）求点A 的坐标；（2）在x 轴上有一动点P （a ，0）．①若三角形ABP 是以AB 为底边的等腰三角形，求a 的值；②过点P 作x 轴的垂线，分别交函数y ＝﹣x +b 和y ＝x 的图象于点C 、D ，若DC ＝2CP ，求a 的值．7．如图，平面直角坐标系中，直线AB：y＝kx+3（k≠0）交x轴于点A（4，0），交y轴正半轴于点B，过点C（0，2）作y轴的垂线CD交AB于点E，点P从E出发，沿着射线ED 向右运动，设PE＝n．（1）求直线AB的表达式；（2）当△ABP为等腰三角形时，求n的值；（3）若以点P为直角顶点，PB为直角边在直线CD的上方作等腰Rt△BPM，试问随着点P 的运动，点M是否也在直线上运动？如果在直线上运动，求出该直线的解析式；如果不在直线上运动，请说明理由．8．如图，直线y＝kx+b与x轴、y轴分别交于点A，B，且OA，OB的长（OA＞OB）是方程x2﹣10x+24＝0的两个根，P（m，n）是第一象限内直线y＝kx+b上的一个动点（点P不与点A，B重合）．（1）求直线AB的解析式．（2）C是x轴上一点，且OC＝2，求△ACP的面积S与m之间的函数关系式；（3）在x轴上是否有在点Q，使以A，B，Q为顶点的三角形是等腰三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．9．如图，A，B是直线y＝x+4与坐标轴的交点，直线y＝﹣2x+b过点B，与x轴交于点C．（1）求A，B，C三点的坐标；（2）当点D是AB的中点时，在x轴上找一点E，使ED+EB的和最小，画出点E的位置，并求E点的坐标．（3）若点D是折线A﹣B﹣C上一动点，是否存在点D，使△ACD为直角三角形，若存在，直接写出D点的坐标；若不存在，请说明理由．10．如图，在平面直角坐标系xOy中，已知正比例函数y＝x与一次函数y＝﹣x+7的图象交于点A，x轴上有一点P（a，0）．（1）求点A的坐标；（2）若△OAP为等腰三角形，则a＝±5或8或；（3）过点P作x轴的垂线（垂线位于点A的右侧）、分别交y＝x和y＝﹣x+7的图象于点B、C，连接OC．若BC＝OA，求△OBC的面积．11．【模型建立】（1）如图1，等腰直角三角形ABC 中，∠ACB ＝90°，CB ＝CA ，直线ED 经过点C ，过A 作AD ⊥ED 于点D ，过B 作BE ⊥ED 于点E ．求证：△BEC ≌△CDA ；【模型应用】（2）①已知直线l 1：y ＝x +8与坐标轴交于点A 、B ，将直线l 1绕点A 逆时针旋转45°至直线l 2，如图2，求直线l 2的函数表达式；②如图3，长方形ABCO ，O 为坐标原点，点B 的坐标为（8，﹣6），点A 、C 分别在坐标轴上，点P 是线段BC 上的动点，点D 是直线y ＝﹣3x +6上的动点且在y 轴的右侧．若△APD 是以点D 为直角顶点的等腰直角三角形，请直接写出点D 的坐标．12．在平面直角坐标系xOy 中，对于任意两点M （x 1，y 1），N （x 2，y 2），若点P （x ，y ）满足x ＝3（x 1+x 2），y ＝3（y 1+y 2），则称点P 为点M ，N 的衍生点．（1）求点M （2，1），N （﹣1，﹣）的衍生点；（2）如图，已知B 是直线y 1＝x +上的一点，A （4，0），点P （x ，y ）是A ，B 的衍生点．①求y 与x 的函数关系式；②若直线BP 与x 轴交于点Q ，是否存在以AQ 为直角边的Rt △APQ ，若存在，求出所有满足条件的B 点坐标；若不存在，说明理由．13．如图，已知直线y＝2x+b交x轴于点A（﹣2，0），交y轴于点B，直线y＝2交AB于点C，交y轴于点D，P是直线y＝2上一动点，设P（m，2）．（1）求直线AB的解析式和点B，点C的坐标；（2）直接写出m为何值时，△ABP是等腰三角形；（3）求△ABP的面积（用含m的代数式表示）．14．如图，四边形ABCD为平行四边形纸片．把纸片ABCD折叠，使点B恰好落在CD边上，折痕为AF．且AB＝10cm、AD＝8cm、DE＝6cm．（1）求证：平行四边形ABCD是矩形；（2）如图，以点B为坐标原点，水平方向、竖直方向为x轴、y轴建立平面直角坐标系，求直线AF的解析式；（3）在（2）中的坐标系内是否存在这样的点P，使得以点P、A、E、F为顶点的四边形是平行四边形？若不存在，请说明理由；若存在，直接写出点P的坐标．15．如图1，已知一次函数y＝kx﹣6的图象与x轴交于点A（﹣8，0），与y轴交于B点，BE平分∠ABO交x轴于点E．（1）求k的值及直线BE的表达式；（2）过点A作AF⊥BE，垂足为F，连接OF，求△AFO的面积及点F的坐标；（3）如图2，点B关于x轴的对称点为点C，过A作AD∥y轴交直线BE于点D，点M是线段AD上一动点，已知点P是直线BE上的一动点，当点P在第二象限，且△CPM是不以C为直角顶点的等腰直角三角形，求出点P的坐标．答案与解析1．如图所示，将长方形纸片OABC放入直角坐标系xoy中，使OA、OC分别落在x、y轴的正半轴上，连接AC，且AC＝4，．（1）求A、C两点的坐标；（2）求AC两点所在直线的解析式；解：（1）∵，∴设CO＝x，则AO＝2x，∵AC＝4，∴x2+（2x）2＝（4）2，解得：x＝4，∴A（8，0），C（0，4）；（2）设AC两点所在直线的解析式为y＝kx+b，∵图象过A（8，0），C（0，4），∴，解得：，∴AC两点所在直线的解析式为y＝﹣x+4．2．一列快车从甲地匀速驶往乙地，一列慢车从乙地匀速驶往甲地．两车行驶的时间为xh，两车之间的距离为ykm，图中的折线表示y与x之间的函数关系，根据图象解决以下问题：（1）甲、乙两地的距离为720 km；（2）慢车的速度为80 km/h，快车的速度为120 km/h；（3）求当x为多少时，两车之间的距离为500km，请通过计算求出x的值．解：（1）甲、乙两地的距离为720km，故答案为：720；（2）设慢车的速度为akm/h，快车的速度为bkm/h，根据题意，得，解得，故答案为80，120；（3）由题意，可知两车行驶的过程中有2次两车之间的距离为500km．即相遇前：（80+120）x＝720﹣500，解得x＝1.1，相遇后：∵点C（6，480），∴慢车行驶20km两车之间的距离为500km，∵慢车行驶20km需要的时间是＝0.25（h），∴x＝6+0.25＝6.25（h），故x＝1.1 h或6.25 h，两车之间的距离为500km．3．如图，一次函数y＝kx+b的图象与直线交于点A（4，3），与y轴交于点B，且OA ＝OB．（1）求一次函数的表达式；（2）求两直线与y轴围成的三角形的面积．（3）在x轴上是否存在点C，使△AOC是以OA为腰的等腰三角形？若存在，直接写出C 的坐标；若不存在，说明理由．解：（1）A（4，3），则OA＝5＝OB，则一次函数y＝kx+b表达式为：y＝kx﹣5，将点A的坐标代入上式并解得：k＝2，故一次函数的表达式为：y＝2x﹣5；＝×OB×x A＝5×4＝10；（2）S△AOB（3）设点C坐标为：（m，0），则OA2＝25，AC2＝（m﹣4）2+9，CO2＝m2，①当OA＝CO时，即m2＝25，解得：m＝±5；②当AO＝AC时，同理可得：m＝0（舍去）或8，故点C的坐标为：（5，0）或（﹣5，0）或（8，0）．4．如图，一次函数的图象过A（3，0），B（0，3）两点．（1）求直线AB的函数表达式；（2）直线y＝﹣3x﹣3交x轴于点C，E为直线AB上一动点．①求CE的最小值；②D是直线y＝﹣3x﹣3上任意一点，F为直线AB上另一动点，若△DEF是以2为直角边长的等腰直角三角形，求D点的坐标．解：（1）设直线AB的函数表达式为：y＝kx+b，由题意可得：解得：∴直线AB的函数表达式为：y＝﹣x+3；（2）①如图1，当CE⊥AB时，CE有最小值，∵直线y＝﹣3x﹣3交x轴于点C，∴点C（﹣1，0），且A（3，0），B（0，3）∴AC＝4，OA＝OB＝3，∴∠BAO＝45°，且CE⊥AB，∴AC＝CE，∴CE＝＝2，∴CE的最小值为2；②设直线AB与直线y＝﹣3x﹣3交于点H，∴解得：∴点H（﹣3，6）如图2，若点E是直角顶点时，∵△DEF是以2为直角边长的等腰直角三角形，∴DE＝2，DE⊥AB，当点D在点B下方时，由①可知点D与点C重合时，△DEF是等腰直角三角形，∴点D（﹣1，0）当点D在点B上方时，∵DE＝D'E'＝2，∠DHE＝∠D'HE'，且∠D'E'H＝∠DEH，∴△DEH≌△D'E'H（AAS）∴D'H＝DH，且点H（﹣3，6），点D（﹣1，0）∴点D'（﹣5，12）如图3，若点D是直角顶点，则DE＝2，DE∥AC，设点D坐标（a，﹣3a﹣3）∴点E（a﹣2，﹣3a﹣3）或（a+2，﹣3a﹣3），且点E在直线y＝﹣x+3上，∴﹣3a﹣3＝﹣a+2+3，或﹣3a﹣3＝﹣a﹣2+3∴a＝﹣﹣3，或a＝﹣3，∴点D 坐标（﹣﹣3，3+6）或（﹣3，﹣3+6） 综上所述：点D 坐标为：（﹣﹣3，3+6）或（﹣3，﹣3+6）或（﹣1，0）或（﹣5，12）．5．如图，已知过点B （1，0）的直线l 1与直线l 2：y ＝2x +4相交于点P （﹣1，a ），l 1与y 轴交于点C ，l 2与x 轴交于点A ．（1）求a 的值及直线l 1的解析式．（2）求四边形PAOC 的面积．（3）在x 轴上方有一动直线平行于x 轴，分别与l 1，l 2交于点M ，N ，且点M 在点N 的右侧，x 轴上是否存在点Q ，使△MNQ 为等腰直角三角形？若存在，请直接写出满足条件的点Q 的坐标；若不存在，请说明理由．解：（1）∵y ＝2x +4过点P （﹣1，a ），∴a ＝2，∵直线l 1过点B （1，0）和点P （﹣1，2），设线段BP 所表示的函数表达式y ＝kx +b 并解得：函数的表达式y ＝﹣x +1；（2）过点P 作PE ⊥OA 于点E ，作PF ⊥y 轴交y 轴于点F ，则；（3）如图，M（1﹣a， a），点N，∵MN＝NQ，则，①当MN＝NQ时，②当MN＝MQ时，③当MQ＝NQ时，，∴，∴．综上，点Q的坐标为：（﹣，0）或（﹣，0）或（﹣，0）．6．如图，函数y＝x+b的图象与x轴、y轴分别交于点A、B，与函数y＝x的图象交于点M，点M的横坐标为3．（1）求点A的坐标；（2）在x轴上有一动点P（a，0）．①若三角形ABP是以AB为底边的等腰三角形，求a的值；②过点P作x轴的垂线，分别交函数y＝﹣x+b和y＝x的图象于点C、D，若DC＝2CP，求a的值．解：（1）函数y＝x的图象交于点M，点M的横坐标为3，则点M（3，3），将点M的坐标代入函数y＝x+b并解得：b＝4，故点A的坐标为：（12，0）；（2）①如图1，连接PB，ABP是以AB为底边的等腰三角形，则BP是AB的中垂线，OP＝a，则AP＝12﹣a＝BP，OB＝4，由勾股定理得：（12﹣a）2＝16+a2，解得：a＝；②P（a，0），则点C、D的坐标分别为：（a，﹣a+4）、（a，a）；DC＝2CP，即|﹣a+4﹣a|＝2（﹣a+4），解得：a＝±6．7．如图，平面直角坐标系中，直线AB：y＝kx+3（k≠0）交x轴于点A（4，0），交y轴正半轴于点B，过点C（0，2）作y轴的垂线CD交AB于点E，点P从E出发，沿着射线ED 向右运动，设PE＝n．（1）求直线AB的表达式；（2）当△ABP为等腰三角形时，求n的值；（3）若以点P为直角顶点，PB为直角边在直线CD的上方作等腰Rt△BPM，试问随着点P的运动，点M是否也在直线上运动？如果在直线上运动，求出该直线的解析式；如果不在直线上运动，请说明理由．解：将点A的坐标代入直线AB：y＝kx+3并解得：k＝﹣，故AB的表达式为：y＝﹣x+3；（2）当y＝2时，x＝，故点E（，2），则点P（n+，2），而点A、B坐标分别为：（4，0）、（0，3），则AP2＝（+n﹣4）2+4；BP2＝（n+）2+1，AB2＝25，当AP＝BP时，（ +n﹣4）2+4＝（n+）2+1，解得：n＝；当AP＝AB时，同理可得：n＝+（不合题意值已舍去）；当AB＝BP时，同理可得：n＝﹣+2；故n＝或+或﹣+2；（3）在直线上，理由：如图，过点M作MD⊥CD于点H，∵∠BPC+∠PBC＝90°，∠BPC+∠MPH＝90°，∴∠CPB＝∠MPH，BP＝PM，∠MHP＝∠PCB＝90°∴MHP△≌△PCB（AAS），则CP＝MH＝n+，BC＝1＝PH，故点M（n+，n+），故点M在直线y＝x+1上．8．如图，直线y＝kx+b与x轴、y轴分别交于点A，B，且OA，OB的长（OA＞OB）是方程x2﹣10x+24＝0的两个根，P（m，n）是第一象限内直线y＝kx+b上的一个动点（点P不与点A，B重合）．（1）求直线AB的解析式．（2）C是x轴上一点，且OC＝2，求△ACP的面积S与m之间的函数关系式；（3）在x轴上是否有在点Q，使以A，B，Q为顶点的三角形是等腰三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．解：（1）x2﹣10x+24＝0，解得：x＝4或6，故点A、B的坐标分别为：（6，0）、（0，4），把点A、B的坐标代入一次函数表达式：y＝kx+b得：，解得：，故直线AB的表达式为：y＝﹣x+4；（2）设点P（m，﹣m+4），当点C在x正半轴时，OC＝2，AC＝4，S＝×4×（﹣m+4）＝﹣m+8；当点C在x轴负半轴时，同理可得：S＝﹣m+16，故S＝﹣m+16或S＝﹣m+8（0＜m＜6）；（3）设点Q（s，0），则AB2＝52，AQ2＝（6﹣s）2，BQ2＝s2+16，①当AB＝AQ时，52＝（6﹣s）2，解得：s＝6±2；②当AB＝BQ时，同理可得：s＝±6（舍去6）；③当AQ＝BQ时，同理可得：s＝，综上，点Q的坐标为：（6，0）或（6﹣2，0）或（﹣6，0）或（，0）．9．如图，A，B是直线y＝x+4与坐标轴的交点，直线y＝﹣2x+b过点B，与x轴交于点C．（1）求A，B，C三点的坐标；（2）当点D是AB的中点时，在x轴上找一点E，使ED+EB的和最小，画出点E的位置，并求E点的坐标．（3）若点D是折线A﹣B﹣C上一动点，是否存在点D，使△ACD为直角三角形，若存在，直接写出D点的坐标；若不存在，请说明理由．解：（1）在y＝x+4中，令x＝0，得y＝4，令y＝0，得x＝﹣4，∴A（﹣4，0），B（0，4）．把B（0，4）代入，y＝﹣2x+b，得b＝4∴直线BC为：y＝﹣2x+4．在y＝﹣2x+4中，令y＝0，得x＝2，∴C点的坐标为（2，0）；（2）如图点E为所求点D是AB的中点，A（﹣4，0），B（0，4）．∴D（﹣2，2）．的坐标为（0，﹣4）．点B关于x轴的对称点B1设直线DB的解析式为y＝kx+b．1（0，﹣4）代入一次函数表达式并解得：把D（﹣2，2），B1故该直线方程为：y＝﹣3x﹣4．令y＝0，得E点的坐标为（﹣，0）．（3）存在，D点的坐标为（﹣1，3）或．①当点D在AB上时，由OA＝OB＝4得到：∠BAC＝45°，由等腰直角三角形求得D点的坐标为（﹣1， 3）；②当点D在BC上时，如图，设AD交y轴于点F．在△AOF与△BOC中，∠FAO＝∠CBO，∠AOF＝∠BOD，AO＝BO，∴△AOF≌△BOC（ASA）．∴OF＝OC＝2，∴点F的坐标为（0，2），易得直线AD的解析式为，与y＝﹣2x+4组成方程组并解得：x＝，∴交点D的坐标为．10．如图，在平面直角坐标系xOy中，已知正比例函数y＝x与一次函数y＝﹣x+7的图象交于点A，x轴上有一点P（a，0）．（1）求点A的坐标；（2）若△OAP为等腰三角形，则a＝±5或8或；（3）过点P作x轴的垂线（垂线位于点A的右侧）、分别交y＝x和y＝﹣x+7的图象于点B、C，连接OC．若BC＝OA，求△OBC的面积．解：（1）联立y＝x与一次函数y＝﹣x+7并解得：x＝4，故点A（4，3）；（2）点A（4，3），则OA＝5，①当OA＝PO时，OA＝5＝PO，即a＝±5②当OA＝AP时，则点P（8，0），即a＝8；③当AP＝OP时，如图所示，连接AP，过点A作AH⊥x轴于点H，AP ＝PO ＝a ，则PH ＝4﹣a ，则（4﹣a ）2+9＝a 2， 解得：a ＝；综上，a ＝±5或8或；故答案为：±5或8或；（3）∵P （a ，0），则点B 、C 的坐标分别为：（a ， a ）、（a ，﹣a +7），∴BC ＝a +a ﹣7＝×5＝7，解得：a ＝8，故点P （8，0），即OP ＝8；△OBC 的面积＝×BC ×OP ＝×7×8＝28．11．【模型建立】（1）如图1，等腰直角三角形ABC 中，∠ACB ＝90°，CB ＝CA ，直线ED 经过点C ，过A 作AD ⊥ED 于点D ，过B 作BE ⊥ED 于点E ．求证：△BEC ≌△CDA ；【模型应用】（2）①已知直线l 1：y ＝x +8与坐标轴交于点A 、B ，将直线l 1绕点A 逆时针旋转45°至直线l 2，如图2，求直线l 2的函数表达式；②如图3，长方形ABCO ，O 为坐标原点，点B 的坐标为（8，﹣6），点A 、C 分别在坐标轴上，点P 是线段BC 上的动点，点D 是直线y ＝﹣3x +6上的动点且在y 轴的右侧．若△APD 是以点D 为直角顶点的等腰直角三角形，请直接写出点D 的坐标．解：（1）∵∠EBC+∠ECB＝90°，∠ECB+∠ACD＝90°，∴∠ACD＝∠BCE，∠ADC＝∠BEC＝90°，CB＝CA，∴△BEC≌△CDA（AAS）；：y＝x+8与坐标轴交于点A、B，则点A、B的坐标分别为：（﹣6，0）、（2）①直线l1（0，8），则AO＝6，OB＝8，于点C，过点C作CH⊥y轴于点H，如图2，过点B作CB⊥AB交l2由（1）知：△CHB≌△BOA（AAS），∴CH＝OB＝8，HB＝OA，故点C（﹣8，14），将点A、C的坐标代入一次函数表达式：y＝kx+b并解得：l的表达式为：y＝﹣7x﹣42；2②点D在y＝﹣3x+6上，设点D（m，﹣3m+6），过点D作x轴的平行线交y轴于点M，交CB的延长线于点N，则△DMA ≌△PND （AAS ），∴AM ＝PN ，即8﹣m ＝|﹣6+3m ﹣6|，解得：m ＝2或5；故点P 的坐标为：（2，0）或（5，﹣9）．12．在平面直角坐标系xOy 中，对于任意两点M （x 1，y 1），N （x 2，y 2），若点P （x ，y ）满足x ＝3（x 1+x 2），y ＝3（y 1+y 2），则称点P 为点M ，N 的衍生点．（1）求点M （2，1），N （﹣1，﹣）的衍生点；（2）如图，已知B 是直线y 1＝x +上的一点，A （4，0），点P （x ，y ）是A ，B 的衍生点．①求y 与x 的函数关系式；②若直线BP 与x 轴交于点Q ，是否存在以AQ 为直角边的Rt △APQ ，若存在，求出所有满足条件的B 点坐标；若不存在，说明理由．解：（1）x ＝3×（2﹣1）＝3；y ＝3×（1﹣）＝1；∴点M 、N 的衍生点是（3，﹣1）；（2）①由题意设：点B （t ， t +），∵点P （x ，y ）是点A 、B 的衍生点，∴x＝3（4+t），y＝3（0+t+）＝t+5；则t＝x﹣4，∴y＝（x﹣4）＝x﹣1；②当∠AQP＝90°时，如图1所示，设P（m， m﹣1），则点B（m， m+），由点P是点A、B的衍生点得：m＝3（4+m）或m﹣1＝3（﹣m++0），解得：m＝﹣6，即点B（﹣6，﹣），当∠PAQ＝90°时，如图2所示，则点P（4，1），由点P是点A、B的衍生点得：点B（﹣，）；综上所述，存在以AQ为直角边的Rt△APQ，此时满足条件的点B坐标是（﹣6，﹣）或（﹣，）．13．如图，已知直线y＝2x+b交x轴于点A（﹣2，0），交y轴于点B，直线y＝2交AB于点C，交y轴于点D，P是直线y＝2上一动点，设P（m，2）．（1）求直线AB的解析式和点B，点C的坐标；（2）直接写出m为何值时，△ABP是等腰三角形；（3）求△ABP的面积（用含m的代数式表示）．解：（1）将点A的坐标代入y＝2x+b得：0＝2×（﹣2）+b，解得：b＝4，故直线AB的表达式为：y＝2x+4，则点B（0，4），当y＝2时，x＝﹣1，即点C（﹣1，2）；（2）点A（﹣2，0）、点B（0，4），点P（m，2），则AB2＝20，AP2＝（m+2）2+4，PB2＝m2+4，①当AB＝AP时，即20＝（m+2）2+4，解得：m＝2或﹣6，②当AB＝BP时，同理可得：m＝4或﹣4，③当AP＝BP时，同理可得：m＝﹣1，综上，m＝﹣4或﹣6或2或4或﹣1；（3）如图所示，点C（﹣1，2），则PC＝|m+1|，△ABP的面积S＝PC×OB＝2|m+1|．当m≥﹣1时，S＝2m+2，当m＜﹣1时，S＝﹣2m﹣2，即△ABP的面积S＝．14．如图，四边形ABCD为平行四边形纸片．把纸片ABCD折叠，使点B恰好落在CD边上，折痕为AF．且AB＝10cm、AD＝8cm、DE＝6cm．（1）求证：平行四边形ABCD是矩形；（2）如图，以点B为坐标原点，水平方向、竖直方向为x轴、y轴建立平面直角坐标系，求直线AF的解析式；（3）在（2）中的坐标系内是否存在这样的点P，使得以点P、A、E、F为顶点的四边形是平行四边形？若不存在，请说明理由；若存在，直接写出点P的坐标．解：（1）证明：∵把纸片ABCD折叠，使点B恰好落在CD边上，∴AE＝AB＝10，AE2＝102＝100，又∵AD2+DE2＝82+62＝100，∴AD2+DE2＝AE2，∴△ADE是直角三角形，且∠D＝90°，又∵四边形ABCD为平行四边形，∴平行四边形ABCD是矩形（有一个角是直角的平行四边形是矩形）；（2）设BF＝x，则EF＝BF＝x，EC＝CD﹣DE＝10﹣6＝4cm，FC＝BC﹣BF＝8﹣x，在Rt△EFC中，EC2+FC2＝EF2，即42+（8﹣x）2＝x2，解得：x＝5，故BF＝5cm，则点E（8，4），则点F（5，0）、而点A（0，10），将点A、F的坐标代入一次函数表达式：y＝kx+b并解得：直线AF的表达式为：y＝﹣2x+10；（3）存在，理由：设点P（a，b），点A、F、E的坐标分别为：（0，10）、（5，0）、（8，4），①当AF是平行四边形的一条边时，点A向下平移10个单位向右平移5个单位得到F，同样点E（P）向下平移10个单位向右平移5个单位得到P（E），即：8﹣10＝a，4+5＝b或8+10＝a，4﹣5＝b，解得：a＝﹣2，b＝9或a＝18，b＝﹣1，②当AF是平行四边形的对角线时，由中点公式得：0+5＝a+8，10+0＝4+b，解得：a＝﹣3，b＝6；综上点P的坐标为：（﹣2，9）或（18，﹣1）或（﹣3，6）．15．如图1，已知一次函数y＝kx﹣6的图象与x轴交于点A（﹣8，0），与y轴交于B点，BE平分∠ABO交x轴于点E．（1）求k的值及直线BE的表达式；（2）过点A作AF⊥BE，垂足为F，连接OF，求△AFO的面积及点F的坐标；（3）如图2，点B关于x轴的对称点为点C，过A作AD∥y轴交直线BE于点D，点M是线段AD上一动点，已知点P是直线BE上的一动点，当点P在第二象限，且△CPM是不以C为直角顶点的等腰直角三角形，求出点P的坐标．解：（1）将点A的坐标代入一次函数表达式并解得：k＝﹣，过点E作EH⊥AB于点H，OA＝8，OB＝6，则AB＝10，设：OE＝x，则EH＝OE＝x，AE＝8﹣x，AH＝10﹣6＝4，在Rt△AEH中，（8﹣x）2＝16+x2，解得：x＝3，故点E（﹣3，0）；由点B、E的坐标得直线BE的表达式为：y＝﹣2x﹣6…①；（2）AF⊥BE，则直线AF的表达式为：y＝x+4…②，联立①②并解得：x＝﹣4，故点F（﹣4，2）；△AFO的面积＝8×2＝8；（3）设点P（m，﹣2m﹣6），点M（﹣8，n），①当∠PMC＝90°时，如图2左侧图，分别过点P、C作直线AD的垂线交于点R、H，∵∠CMH+∠HCM＝90°，∠HMC+∠PMR＝90°，∴∠HCM＝∠RMP，PM＝CM，∴△CHM≌△MRP，∴CH＝MR，HM＝PR，即8＝n+2m+6，6﹣n＝m+8，解得：m＝4，n＝﹣6（与点M是线段AD上一动点不符，舍去）；②当∠MPC＝90°时，同理可得：△CHP≌△PGM，∴CH＝GP，即|6+2m+6|＝|﹣8﹣m|，解得：m＝﹣4或﹣，故点P的坐标为：（﹣4，2）或（﹣，）．。

2020年中考数学复习突破与提升专题练习（知识点解析+练习反馈）一．一次函数的定义1．一次函数的定义：函数y= kx+b (k、b为常数，k≠0，自变量x的次数是1次)叫做一次函数。

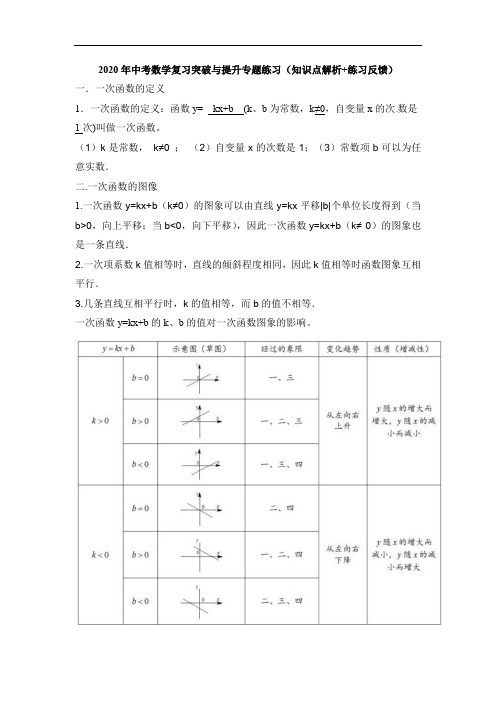
（1）k是常数，k≠0 ；（2）自变量x的次数是1；（3）常数项b可以为任意实数．二.一次函数的图像1.一次函数y=kx+b（k≠0）的图象可以由直线y=kx平移|b|个单位长度得到（当b>0，向上平移；当b<0，向下平移），因此一次函数y=kx+b（k≠ 0）的图象也是一条直线．2.一次项系数k值相等时，直线的倾斜程度相同，因此k值相等时函数图象互相平行．3.几条直线互相平行时，k的值相等，而b的值不相等．一次函数y=kx+b的k、b的值对一次函数图象的影响。

4.（1）k的符号决定一次函数的增减性①当k>0时，图象一定经过第一、第三象限，图象从左向右上升，y随x的增大而增大；②当k<0时，图象一定经过第二、第四象限，图象从左向右下降，y随x的增大而减小．（2）b的符号决定一次函数与y轴的交点位置①当b>0时，图象与y轴的交点在x轴上方，图象一定经过第一、第二象限；②当b<0时，图象与y轴的交点在x轴下方，图象一定经过第三、第四象限；③当b=0时，函数图象一定经过原点．（3）k、b的符号共同决定一次函数所在的象限①已知k，b的符号判断一次函数经过的象限．②可由一次函数y=kx+b图象的位置确定其系数k、b的符号．【技巧总结】一次函数的性质可简记为“正奇负偶，正前负后”，一般来说讨论一次函数图象的性质可以遵从“先k后b”的顺序，然后依据若k的值为正数时，图象经过奇数（第一、第三）象限；k的值为负数时，图象经过偶数（第二、第四）象限；b的值为正数时（图象上移），图象经过前两个象限；b的值为负数时（图象下移），图象经过后两个象限．三.一次函数的解析式四.一次函数解析式与一次函数图象我们可以由函数图象的意义知，对于满足函数关系式y=kx+b的点(x ，y)在其对应的图象上，这个图象就是一条直线l，反之，对于直线l上的点的坐标(x ，y)满足y=kx+b，也就是说，直线l与y=kx+b是一一对应的，故而我们通常把一次函数y=kx+b的图象叫做直线l：y=kx+b，有时直接称为直线y=kx+b．但是需要特别注意对于一次函数来说要始终保证k≠0这个条件.五.待定系数法求一次函数解析式六．练习反馈1. 下列各曲线中不能表示y是x的函数的是 ( ),③y=8,④y=-8x2+6,⑤y=-0.5x-1中,一次函数有2.下列函数:①y=-8x,②y=-8x( )A.1个B.2个C.3个D.4个3. 一次函数y=kx+b满足kb>0,且y随x的增大而减小,则此函数的图象不经过( )A.第一象限B.第二象限C.第三象限D.第四象限4. 下列图形中,表示一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn ≠0)的图象的是 ( )5. 关于直线l:y=kx+k(k≠0),下列说法不正确的是 ( )A.点(0,k)在l上B.l经过定点(-1,0)C.当k>0时,y随x的增大而增大D.l经过第一、二、三象限6. 小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部.则下面可以近似地刻画出容器最高水位h与注水时间t 之间的变化情况的是 ( )7.若正比例函数y=kx(k是常数,k≠0)的图象经过第二、四象限,则k的值可以是__ __(写出一个即可).8. 若点A(2,y1),B(-1,y2)都在直线y=-2x上,则y1与y2的大小关系是__ _.9.已知函数y=(k-1)x+k2-1,当k__ __时,它是一次函数,当k=__ __时,它是正比例函数.10. 直线y=2x-1沿y轴平移3个单位,则平移后直线与y轴的交点坐标为__ __.11. 放学后,李明骑车回家,他经过的路程s(千米)与所用时间t(分钟)的函数关系如图所示,则李明的骑车速度是__ _千米/分钟.12. 王明从家到图书馆看报然后返回,他离家的距离y与离家时间x之间的对应关系如图所示.如果王明在图书馆看报30 min,那么他离家50 min时离家的距离为__ __km.13. 一次函数y=kx+b经过点(-1,1)和点(2,7).(1)求这个一次函数的解析式.(2)将所得函数图象平移,使它经过点(2,-1),求平移后直线的解析式.14. 已知一次函数y=2x-3.(1)请在平面直角坐标系中画出此函数的图象.(2)求出此函数与坐标轴围成的三角形的面积.15. 已知:一次函数y=kx+b的图象经过M(0,2),N(1,3)两点.(1)求k,b的值.(2)若一次函数y=kx+b的图象与x轴交点为A(a,0),求a的值.16. 某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准.该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.(1)若某月用水量为18立方米,则应交水费多少元?(2)求当x>18时,y关于x的函数表达式.若李敏家某月交水费81元,则这个月用水量为多少立方米?。

2019-2020年中考数学总复习全程考点训练10一次函数（含解析）一、选择题1．若正比例函数y ＝kx 的图象经过点(1，2)，则k 的值为(D ) A ．－12 B ．－2C.12D ．2 【解析】 ∵正比例函数y ＝kx 的图象经过点(1，2)，∴2＝k ，即k ＝2.故选D. 2．一次函数y ＝－x ＋1的图象是(C )【解析】 直线y ＝－x ＋1经过点(0，1)，(1，0)，故选C.3．将直线y ＝2x 向右平移1个单位后所得图象对应的函数表达式为(B ) A ．y ＝2x －1 B ．y ＝2x －2 C ．y ＝2x ＋1 D ．y ＝2x ＋2【解析】 直线平移“上加下减，左加右减”，故y ＝2(x －1)．也可选一个特殊点，如(0，0)向右平移后即为(1，0)，得y ＝2x ＋b 过(1，0)，即可求出b ＝－2.4．如果一次函数y ＝kx ＋b 的函数值y 随x 的增大而减小，且图象与y 轴的负半轴相交，那么下列对k 和b 的符号的判断正确的是(D )A ．k >0，b >0B ．k >0，b <0C ．k <0，b >0D ．k <0，b <0【解析】 y 随x 的增大而减小，故k <0；与y 轴交于负半轴，故b <0.故选D.5．在平面直角坐标系中，点P 在直线x ＋y －4＝0上，O 为原点，则||OP 的最小值为(B ) A ．－2 B ．2 2C. 6D.10【解析】 如解图所示．(第5题解)令x ＝0，则y ＝4； 令y ＝0，则x ＝4. ∴A (0，4)，B (4，0)． ∴OA ＝4，OB ＝4.∴AB ＝4 2.当OP ⊥AB 时，OP 最小．此时OP ＝12AB ＝2 2.(第6题)6．甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500 m ，先到终点的人原地休息．已知甲先出发2 s ，在跑步过程中，甲、乙两人的距离y (m)与乙出发的时间t (s)之间的关系如图所示，给出下列结论：①a ＝8；②b ＝92；③c ＝123.其中正确的是(A )A ．①②③B ．①②C ．①③D ．②③【解析】 ∵乙出发时甲行了2 s ，相距8 m ， ∴甲的速度为8÷2＝4(m/s)． ∵100 s 时乙开始休息，∴乙的速度是500÷100＝5(m/s)． ∵a (s)后甲、乙相遇，∴a ＝8÷(5－4)＝8(s)，故①正确；∵100 s 时乙到达终点，甲走了4×(100＋2)＝408(m)，∴b ＝500－408＝92(m)，故②正确； ∵甲到达终点一共耗时500÷4＝125(s)， ∴c ＝125－2＝123(s)，故③正确． 综上所述，①②③皆正确．(第7题)7．如图，点A ，B ，C 在一次函数y ＝－2x ＋m 的图象上，它们的横坐标依次为－1，1，2，分别过这些点作x 轴与y 轴的垂线，则图中阴影部分的面积之和是(B )A ．1B ．3C ．3(m －1) D.32(m －2) 【解析】 易得点A (－1，m ＋2)，B (1，m －2)，C (2，m －4)，∴S ＝12×1×(m ＋2－m ＋4)＝3.二、填空题8．一次函数y ＝－43x －4的图象与x 轴的交点坐标是(－3，0)，与y 轴的交点坐标是(0，－4)．(第9题)9．如图，一次函数y ＝(m －1)x －3的图象分别与x 轴，y 轴的负半轴交于A ，B 两点，则m 的取值范围是m ＜1．【解析】 ∵函数图象经过第二、四象限， ∴m －1＜0，∴m ＜1.(第10题)10．某市出租车计费方法如图所示，x (km)表示行驶里程，y (元)表示车费，请根据图象回答下列问题：(1)出租车的起步价是__8__元，当x >3时，y 关于x 的函数表达式为y ＝2x ＋2． (2)若某乘客有一次乘出租车的车费为32元，则这位乘客乘车的里程为__15__km. 【解析】 (1)由图象，得出租车的起步价是8元，设当x ＞3时，y 关于x 的函数表达式为y ＝kx ＋b ，由函数图象，得⎩⎪⎨⎪⎧8＝3k ＋b ，12＝5k ＋b ，解得⎩⎪⎨⎪⎧k ＝2，b ＝2.故y 关于x 的函数表达式为y ＝2x ＋2. (2)当y ＝32时，32＝2x ＋2，解得x ＝15.(第11题)11．如图，直线y 1＝kx ＋b 经过点A (0，2)，且与直线y 2＝mx 交于点P (1，m )，则不等式组mx >kx ＋b >mx －2的解是1＜x ＜2．【解析】 由已知，得b ＝2，k ＋2＝m ，∴k ＝m －2. ∴mx >kx ＋b >mx －2可化为mx >(m －2)x ＋2>mx －2， 即0>－2x ＋2>－2，解得1<x <2.(第12题)12．已知直线y 1＝x ，y 2＝13x ＋1，y 3＝－45x ＋5的图象如图所示，若无论x 取何值，y 总取y 1，y 2，y 3中的最小值，则y 的最大值为3717．【解析】 y 的最大值为y 2和y 3的交点的函数值，联立⎩⎪⎨⎪⎧y 2＝13x ＋1，y 3＝－45x ＋5，得y 2和y3的交点为⎝ ⎛⎭⎪⎫6017，3717. 三、解答题(第13题)13．在平面直角坐标系中，一次函数的图象与坐标轴围成的三角形，叫做此一次函数的坐标三角形．如图，若某个一次函数的图象与x 轴，y 轴分别交于点A ，B ，则△OAB 为此函数的坐标三角形．(1)求函数y ＝－34x ＋3的坐标三角形的三条边长．(2)若函数y ＝－34x ＋b (b 为常数)的坐标三角形的周长为16，求此三角形的面积．【解析】 (1)函数y ＝－34x ＋3的图象与x 轴的交点为(4，0)，与y 轴的交点为(0，3)，∴坐标三角形的三条边长分别为3，4，5.(2)函数y ＝－34x ＋b 的图象与y 轴的交点为(0，b )，与x 轴的交点为⎝ ⎛⎭⎪⎫43b ，0， ∴坐标三角形的斜边长为⎪⎪⎪⎪⎪⎪53b .∵坐标三角形的周长为16，∴|b |＋⎪⎪⎪⎪⎪⎪43b ＋⎪⎪⎪⎪⎪⎪53b ＝16， ∴|b |＝4.∴S △＝12·|b |·⎪⎪⎪⎪⎪⎪43b ＝323.(第14题)14．如图，一次函数y ＝－23x ＋2的图象分别与x 轴，y 轴交于点A ，B ，以线段AB 为边在第一象限内作等腰直角三角形ABC ，且∠BAC ＝90°.求过B ，C 两点的直线的表达式．【解析】 对于y ＝－23x ＋2，令x ＝0，则y ＝2，令y ＝0，则x ＝3，∴点B (0，2)，A (3，0)．过点C 作CD ⊥OA 交x 轴于点D .∵△ABC 为等腰Rt△，∴∠BAC ＝90°，AB ＝AC ， ∴∠BAO ＋∠DAC ＝90°. ∵∠BOA ＝∠ADC ＝90°， ∴∠OBA ＋∠BAO ＝90°. ∴∠OBA ＝∠DAC . ∴△ACD ≌△BAO (AAS )， ∴AD ＝BO ＝2，CD ＝AO ＝3， ∴OD ＝3＋2＝5，∴点C (5，3)．设过B ，C 两点的表达式为y ＝kx ＋b ，则⎩⎪⎨⎪⎧b ＝2，5k ＋b ＝3，解得⎩⎪⎨⎪⎧k ＝15，b ＝2.∴直线BC 的表达式为y ＝15x ＋2.15．游泳池常需换水清洗，图中的折线表示游泳池换水清洗过程“排水—清洗—灌水”中水量y (m 3)与时间t (min)之间的函数表达式．(1)根据图中提供的信息，求整个换水清洗过程水量y (m 3)与时间t (min)之间的函数表达式； (2)排水、清洗、灌水各花了多少时间？(第15题)【解析】 (1)排水阶段：设函数表达式为y ＝kt ＋b ，图象经过点(0，1500)，(25，1000)，则⎩⎪⎨⎪⎧b ＝1500，25k ＋b ＝1000.解得⎩⎪⎨⎪⎧k ＝－20，b ＝1500.故排水阶段的函数表达式为y ＝－20t ＋1500； 清洗阶段：y ＝0；灌水阶段：设函数表达式为y ＝at ＋c ，图象经过点(195，1000)，(95，0)，则⎩⎪⎨⎪⎧195a ＋c ＝1000，95a ＋c ＝0，解得⎩⎪⎨⎪⎧a ＝10，c ＝－950.∴灌水阶段的函数表达式为y ＝10t －950. (2)∵排水阶段的函数表达式为y ＝－20t ＋1500， ∴当y ＝0时，0＝－20t ＋1500，解得t ＝75.则排水时间为75 min ，清洗时间为95－75＝20(min)． ∵根据图象可以得出游泳池的蓄水量为1500 m 3， ∴1500＝10t －950，解得t ＝245， 故灌水所用时间为245－95＝150(min)．16．某景区的三个景点A ，B ，C 在同一线路上，甲、乙两名游客从景点A 出发，甲步行到景点C ，乙乘景区观光车先到景点B ，在B 处停留一段时间后，再步行到景点C .甲、乙两人离开景点A 后的路程s (m)关于时间t (min)的函数图象如图所示．根据以上信息回答下列问题：(1)乙出发后多长时间与甲相遇？(2)要使甲到达景点C 时，乙与景点C 的路程不超过400 m ，则乙从景点B 步行到景点C 的速度至少为多少(结果精确到0.1 m/min)?(第16题)【解析】 (1)设s 甲＝kt ，将点(90，5400)的坐标代入，得5400＝90k ，解得k ＝60， ∴s 甲＝60t .当20≤t ≤30时，设s 乙＝at ＋b ，将点(20，0)，(30，3000)的坐标代入，得⎩⎪⎨⎪⎧20a ＋b ＝0，30a ＋b ＝3000，解得⎩⎪⎨⎪⎧a ＝300，b ＝－6000. ∴当20≤t ≤30时，s 乙＝300t －6000.当y 甲＝y 乙时，60t ＝300t －6000，解得t ＝25， ∴乙出发5 min 后与甲相遇．(2)由题意可得，当甲到达景点C ，乙距离景点C 400 m 时，乙需要步行的距离为5400－3000－400＝2000(m)，乙所用的时间为30 min ， 故乙从景点B 步行到景点C 的速度至少为200030≈66.7(m/min)．答：乙从景点B 步行到景点C 的速度至少为66.7 m/min.。

2020年中考数学复习突破与提升专题练习（知识点解析+练习反馈）一．一次函数的定义1．一次函数的定义：函数y= kx+b (k、b为常数，k≠0，自变量x的次数是1次)叫做一次函数。

（1）k是常数，k≠0 ；（2）自变量x的次数是1；（3）常数项b可以为任意实数．二.一次函数的图像1.一次函数y=kx+b（k≠0）的图象可以由直线y=kx平移|b|个单位长度得到（当b>0，向上平移；当b<0，向下平移），因此一次函数y=kx+b（k≠ 0）的图象也是一条直线．2.一次项系数k值相等时，直线的倾斜程度相同，因此k值相等时函数图象互相平行．3.几条直线互相平行时，k的值相等，而b的值不相等．一次函数y=kx+b的k、b的值对一次函数图象的影响。

4.（1）k的符号决定一次函数的增减性①当k>0时，图象一定经过第一、第三象限，图象从左向右上升，y随x的增大而增大；②当k<0时，图象一定经过第二、第四象限，图象从左向右下降，y随x的增大而减小．（2）b的符号决定一次函数与y轴的交点位置①当b>0时，图象与y轴的交点在x轴上方，图象一定经过第一、第二象限；②当b<0时，图象与y轴的交点在x轴下方，图象一定经过第三、第四象限；③当b=0时，函数图象一定经过原点．（3）k、b的符号共同决定一次函数所在的象限①已知k，b的符号判断一次函数经过的象限．②可由一次函数y=kx+b图象的位置确定其系数k、b的符号．【技巧总结】一次函数的性质可简记为“正奇负偶，正前负后”，一般来说讨论一次函数图象的性质可以遵从“先k后b”的顺序，然后依据若k的值为正数时，图象经过奇数（第一、第三）象限；k的值为负数时，图象经过偶数（第二、第四）象限；b的值为正数时（图象上移），图象经过前两个象限；b的值为负数时（图象下移），图象经过后两个象限．三.一次函数的解析式四.一次函数解析式与一次函数图象我们可以由函数图象的意义知，对于满足函数关系式y=kx+b的点(x ，y)在其对应的图象上，这个图象就是一条直线l，反之，对于直线l上的点的坐标(x ，y)满足y=kx+b，也就是说，直线l与y=kx+b是一一对应的，故而我们通常把一次函数y=kx+b的图象叫做直线l：y=kx+b，有时直接称为直线y=kx+b．但是需要特别注意对于一次函数来说要始终保证k≠0这个条件.五.待定系数法求一次函数解析式六．练习反馈1.下列各曲线中不能表示y是x的函数的是 ( ),③y=8,④y=-8x2+6,⑤y=-0.5x-1中,一次函数有2.下列函数:①y=-8x,②y=-8x( )A.1个B.2个C.3个D.4个3.一次函数y=kx+b满足kb>0,且y随x的增大而减小,则此函数的图象不经过( )A.第一象限B.第二象限C.第三象限D.第四象限4. 下列图形中,表示一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn ≠0)的图象的是 ( )5. 关于直线l:y=kx+k(k≠0),下列说法不正确的是 ( )A.点(0,k)在l上B.l经过定点(-1,0)C.当k>0时,y随x的增大而增大D.l经过第一、二、三象限6. 小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部.则下面可以近似地刻画出容器最高水位h与注水时间t 之间的变化情况的是 ( )7.若正比例函数y=kx(k是常数,k≠0)的图象经过第二、四象限,则k的值可以是__ __(写出一个即可).8. 若点A(2,y1),B(-1,y2)都在直线y=-2x上,则y1与y2的大小关系是__ _.9.已知函数y=(k-1)x+k2-1,当k__ __时,它是一次函数,当k=__ __时,它是正比例函数.10. 直线y=2x-1沿y轴平移3个单位,则平移后直线与y轴的交点坐标为__ __.11. 放学后,李明骑车回家,他经过的路程s(千米)与所用时间t(分钟)的函数关系如图所示,则李明的骑车速度是__ _千米/分钟.12. 王明从家到图书馆看报然后返回,他离家的距离y与离家时间x之间的对应关系如图所示.如果王明在图书馆看报30 min,那么他离家50 min时离家的距离为__ __km.13. 一次函数y=kx+b经过点(-1,1)和点(2,7).(1)求这个一次函数的解析式.(2)将所得函数图象平移,使它经过点(2,-1),求平移后直线的解析式.14.已知一次函数y=2x-3.(1)请在平面直角坐标系中画出此函数的图象.(2)求出此函数与坐标轴围成的三角形的面积.15.已知:一次函数y=kx+b的图象经过M(0,2),N(1,3)两点.(1)求k,b的值.(2)若一次函数y=kx+b的图象与x轴交点为A(a,0),求a的值.16.某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准.该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.(1)若某月用水量为18立方米,则应交水费多少元?(2)求当x>18时,y关于x的函数表达式.若李敏家某月交水费81元,则这个月用水量为多少立方米?。

知识像烛光，能照亮一个人，也能照亮无数的人。

--培根一次函数知识点总结与常见题型基本概念1、变量：在一个变化过程中可以取不同数值的量。

常量：在一个变化过程中只能取同一数值的量。

例题：在匀速运动公式vt s =中,v 表示速度,t 表示时间,s 表示在时间t 内所走的路程,则变量是________,常量是_______。

在圆的周长公式C =2πr 中，变量是________，常量是_________.2、函数：一般的，在一个变化过程中，如果有两个变量x 和y ，并且对于x 的每一个确定的值，y 都有唯一确定的值与其对应，那么我们就把x 称为自变量，把y 称为因变量，y 是x 的函数。

*判断Y 是否为X 的函数，只要看X 取值确定的时候，Y 是否有唯一确定的值与之对应例题：下列函数（1）y =πx (2)y =2x －1 (3)y =1x (4)y =21－3x (5)y =x 2－1中，是一次函数的有（ ）（A ）4个 （B ）3个 （C ）2个 （D ）1个3、定义域：一般的，一个函数的自变量允许取值的范围，叫做这个函数的定义域。

4、确定函数定义域的方法：（1）关系式为整式时，函数定义域为全体实数；（2）关系式含有分式时，分式的分母不等于零；（3）关系式含有二次根式时，被开放方数大于等于零；（4）关系式中含有指数为零的式子时，底数不等于零； （5）实际问题中，函数定义域还要和实际情况相符合，使之有意义。

例题：下列函数中，自变量x 的取值范围是x ≥2的是（ ）A ．yB ．yC ．yD ．y函数y =x 的取值范围是___________. 已知函数221+-=x y ，当11≤<-x 时，y 的取值范围是 （ ）A .2325≤<-yB .2523<<yC .2523<≤yD .2523≤<y5、函数的图像一般来说，对于一个函数，如果把自变量与函数的每对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图象．6、函数解析式：用含有表示自变量的字母的代数式表示因变量的式子叫做解析式。