简单的平移作图
- 格式:doc
- 大小:80.50 KB
- 文档页数:2



图形在坐标中的平移(基础)知识讲解【学习目标】1. 能在直角坐标系中用坐标的方法研究图形的平移变换,掌握图形在平移过程中各点的变化规律,理解图形在平面直角坐标系上的平移实质是点坐标的对应变换.2. 运用点的坐标的变化规律来进行简单的平移作图.【要点梳理】要点一、点在坐标中的平移在平面直角坐标系中,将点(x,y)向右或向左平移a个单位长度,可以得到对应点(x+a,y)或(x-a,y);将点(x,y)向上或向下平移b个单位长度,可以得到对应点(x,y+b)或(x,y-b).要点诠释:(1)在坐标系内,左右平移的点的坐标规律:右加左减;(2)在坐标系内,上下平移的点的坐标规律:上加下减;(3)在坐标系内,平移的点的坐标规律:沿x轴平移纵坐标不变,沿y轴平移横坐标不变.要点二、图形在坐标中的平移在平面直角坐标系内,如果把一个图形各个点的横坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.要点诠释:(1)平移是图形的整体位置的移动,图形上各点都发生相同性质的变化,因此图形的平移问题可以转化为点的平移问题来解决.(2)平移只改变图形的位置,图形的大小和形状不发生变化.【典型例题】类型一、点在坐标中的平移1.写出下列各点平移后的点的坐标:(1)将A(-3,2)向右平移3个单位;(2)将B(1,-2)向左平移3个单位;(3)将C(4,7)向上平移2个单位;(4)将D(-1,2)向下平移1个单位.(5)将E(2,-3)先向右平移1个单位,再向下平移1个单位.【思路点拨】根据平移中点的变化规律:横坐标右移加,左移减;纵坐标上移加,下移减.即可得出平移后点的坐标.【答案与解析】解:由题意可得:(1)平移后点的坐标为:(0,2);(2)平移后点的坐标为:(-2,-2);(3)平移后点的坐标为:(4,9);(4)平移后点的坐标为:(-1,1);(6)平移后点的坐标为:(3,-4).【总结升华】本题考查了点的平移及平移特征,掌握平移中点的变化规律是关键.2.(荆门)将点P向左平移2个单位,再向上平移1个单位得到P′(-1,3),则点P 的坐标是.【思路点拨】在平面直角坐标系中,图形的平移与图形上某点的平移相同,本题需注意的是已知新点的坐标,求原来点的坐标,注意平移的顺序的反过来的运用.【答案】(1,2).【解析】新点P′的横坐标是-1,纵坐标是3,点P′向右平移2个单位,再向下平移1个单位得到原来的点P,即点P的横坐标是-1+2=1,纵坐标为3-1=2.则点P的坐标是(1,2).【总结升华】左右平移的单位数是平移后点的横坐标减去平移前对应点的横坐标,上下平移的单位数是平移后点的纵坐标减去对应平移前点的纵坐标.举一反三:【高清课堂:第二讲平面直角坐标系2 369935 练习4 】【变式1】已知:两点A(-4,2)、B(-2,-6),(1)线段AB的中点C坐标是;(2)若将线段AB沿x轴向右平移5个单位,得到线段A1B1,则A1点的坐标是 ,B1点的坐标是.(3)若将线段AB沿y轴向下平移3个单位,得到线段A2B2,则A2点的坐标是 ,B2点的坐标是.【答案】(1)(-3, -2); (2)(1,2),(3,-6); (3)(-4,-1),(-2,-9).【变式2】(2015•海安县校级二模)在平面直角坐标系中,将点A(﹣2,3)向右平移2个单位长度,再向下平移6个单位长度得点B,则点B的坐标是.【答案】(0,﹣3).解:∵将点A(﹣2,3)向右平移2个单位长度,再向下平移6个单位长度得点B,∴点B的坐标是(﹣2+2,3﹣6),即(0,﹣3).类型二、图形在坐标中的平移3.(2015春•邵阳县期末)在平面直角坐标系中,已知线段AB的两个端点分别是A(﹣3,1),B(1,3).把线段AB平移后得到线段A′B′,A与A′对应,B与B′对应.若点A′的坐标是(﹣1,﹣1),则点B′的坐标为.【思路点拨】各对应点之间的关系是横坐标加2,纵坐标减2,那么让点B的横坐标加2,纵坐标减2即为点B′的坐标.【答案】(3,1).【解析】解:由A(﹣3,1)的对应点A′的坐标为(﹣1,﹣1 ),坐标的变化规律可知:各对应点之间的关系是横坐标加2,纵坐标减2,∴点B′的横坐标为1+2=3;纵坐标为3﹣2=1;即所求点B′的坐标为(3,1).故答案为(3,1).【总结升华】此题主要考查了坐标与图形的变化﹣平移,解决本题的关键是根据已知对应点找到各对应点之间的变化规律.举一反三:【变式】按要求平移下面的图形.(1)将图形①先向右平移3个格,再向下平移5个格.(2)将图形②先向左平移2个格,再向上平移3个格.【答案】解:作图如下:4. 如图所示的直角坐标系中,△ABC的顶点坐标分别是A(0,0),B(6,0),C(5,5).(1)求△ABC的面积;(2)如果将△ABC向上平移1个单位长度,得△A1B1C1,再向右平移2个单位长度,得到△A2B2C2,试求A2、B2、C2的坐标;(3)△A2B2C2与△ABC的大小、形状有什么关系.【思路点拨】 (1)已知AB=6,故只要求得C到x轴距离即可.(2)在平面直角坐标系中,将图形向右(或左)平移a个单位长度,那么图形的点(x,y)向右(或向左)平移a个单位长度,可得对应点(x+a,y)或(x-a,y),将图形向上(或向下)平移b个单位长度,可得到对应点(x,y+b)或(x,y-b).(3)可根据平移的性质进行分析和判断.【答案与解析】解:(1)点C到x轴的距离为5,所以11651522ABCS AB h==⨯⨯=△;(2)根据题意求出三角形A2B2C2各顶点的坐标为A2(2,1),B2(8,1),C2(7,6);(3)连接A2B2C2三点可以看出△A2B2C2与△ABC的大小、形状相等或相同.【总结升华】平移只改变图形的位置,不改变图形的形状和大小.举一反三:【变式】如图,三角形DEF经过平移后得到三角形ABC,则点D坐标为,点E的坐标为.【答案】D(2,2),E(3,-2).。


图形的平移和旋转【图形的平移】(1)平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移,平移不改变图形的形状和大小.注意:①平移是运动的一种形式,是图形变换的一种,本讲的平移是指平面图形在同一平面内的变换.②图形的平移有两个要素:一是图形平移的方向,二是图形平移的距离,这两个要素是图形平移的依据.③图形的平移是指图形整体的平移,经过平移后的图形,与原图形相比,只改变了位置,而不改变图形的大小,这个特征是得出图形平移的基本性质的依据.(2)平移的基本性质:由平移的基本概念知,经过平移,图形上的每一个点都沿同一个方向移动相同的距离,平移不改变图形的形状和大小,因此平移具有下列性质:经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.注意:①要正确找出“对应线段,对应角”,从而正确表达基本性质的特征.②“对应点所连的线段平行且相等”,这个基本性质既可作为平移图形之间的性质,又可作为平移作图的依据.(3)简单的平移作图平移作图:确定一个图形平移后的位置所需条件为:①图形原来的位置;②平移的方向;③平移的距离.例1.如图,△ABC 绕C 点旋转后,顶点A 的对应点为点D ,试确定顶点B•对应点的位置,以及旋转后的三角形.分析:绕C 点旋转,A 点的对应点是D 点,那么旋转角就是∠ACD ,根据对应点与旋转中心所连线段的夹角等于旋转角,即∠BCB ′=ACD ,•又由对应点到旋转中心的距离相等,即CB=CB ′,就可确定B ′的位置,如图所示. 解:(1)连结CD(2)以CB 为一边作∠BCE ,使得∠BCE=∠ACD (3)在射线CE 上截取CB ′=CB 则B ′即为所求的B 的对应点. (4)连结DB ′则△DB ′C 就是△ABC 绕C 点旋转后的图形.例2.如图,四边形ABCD 是边长为1的正方形,且DE=14,△ABF 是△ADE 的旋转图形. (1)旋转中心是哪一点? (2)旋转了多少度? (3)AF 的长度是多少?(4)如果连结EF ,那么△AEF 是怎样的三角形?分析:由△ABF 是△ADE 的旋转图形,可直接得出旋转中心和旋转角,要求AF•的长度,根据旋转前后的对应线段相等,只要求AE 的长度,由勾股定理很容易得到.•△ABF 与△ADE 是完全重合的,所以它是直角三角形. 解:(1)旋转中心是A 点. (2)∵△ABF 是由△ADE 旋转而成的 ∴B 是D 的对应点 ∴∠DAB=90°就是旋转角 (3)∵AD=1,DE=14∴=4∵对应点到旋转中心的距离相等且F是E的对应点∴AF=4(4)∵∠EAF=90°(与旋转角相等)且AF=AE ∴△EAF是等腰直角三角形.【图形的旋转】(1)旋转的概念:图形绕着某一点(固定)转动的过程,称为旋转,这一固定点叫做旋转中心。
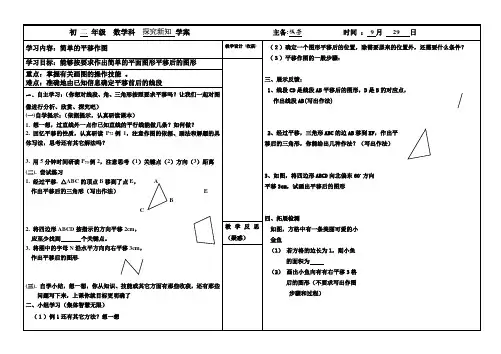


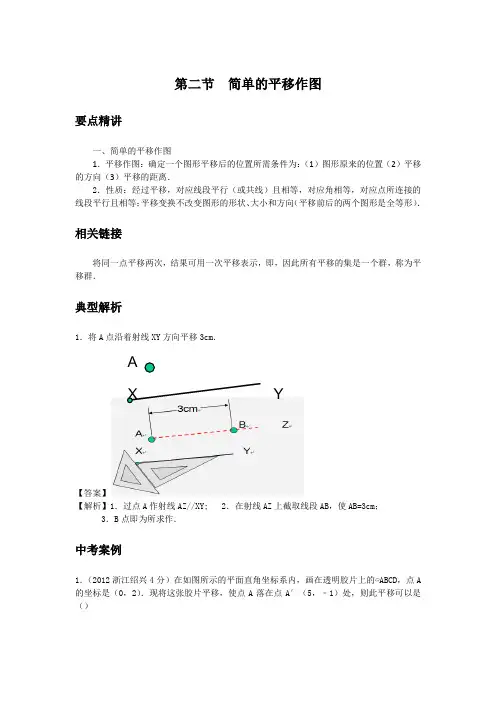
第二节 简单的平移作图要点精讲一、简单的平移作图1.平移作图:确定一个图形平移后的位置所需条件为:(1)图形原来的位置(2)平移的方向(3)平移的距离.2.性质:经过平移,对应线段平行(或共线)且相等,对应角相等,对应点所连接的线段平行且相等;平移变换不改变图形的形状、大小和方向(平移前后的两个图形是全等形). 相关链接将同一点平移两次,结果可用一次平移表示,即,因此所有平移的集是一个群,称为平移群.典型解析1.将A 点沿着射线XY 方向平移3cm .【答案】【解析】1.过点A 作射线AZ//XY; 2.在射线AZ 上截取线段AB ,使AB=3cm ;3.B 点即为所求作.中考案例1.(2012浙江绍兴4分)在如图所示的平面直角坐标系内,画在透明胶片上的▱ABCD ,点A 的坐标是(0,2).现将这张胶片平移,使点A 落在点A′(5,﹣1)处,则此平移可以是()A YA.先向右平移5个单位,再向下平移1个单位B.先向右平移5个单位,再向下平移3个单位C.先向右平移4个单位,再向下平移1个单位D.先向右平移4个单位,再向下平移3个单位【答案】B.【解析】根据坐标的平移变化的规律,左右平移只改变点的横坐标,左减右加.上下平移只改变点的纵坐标,下减上加.因此,根据A的坐标是(0,2),横坐标加5,纵坐标减3得到点A′(5,﹣1),故先向右平移5个单位,再向下平移3个单位.故选B.针对训练1.如图,将四边形ABCD先向左平移3个单位,再向上平移2个单位,那么点A的对应点A1的坐标是()A.(6,1)B.(0,1)C.(0,-3)D.(6,-3)2.在平面直角坐标系中,将点M(1,2)向左平移2个长度单位后得到点N,则点N的坐标是()A.(-1,2)B.(3,2)C.(1,4)D.(1,0)3.下列说法正确的是()A.由平移得到的两个图形的对应点连线长度不一定相等B.我们可以把“火车在一段笔直的铁轨上行驶了一段距离”看作“火车沿着铁轨方向的平移”C.小明第一次乘观光电梯,随着电梯向上升,他高兴地对同伴说:“太棒了,我现在比大楼还高呢,我长高了!”D.在图形平移过程中,图形上可能会有不动点4.在平面直角坐标系中,一青蛙从点A(-1,0)处向右跳2个单位长度,再向上跳2个单位长度到点A′处,则点A′的坐标为 ____________ .5.如图,在平面直角坐标系中,△ABC经过平移后点A的对应点为点A′,则平移后点B的对应点B′的坐标为 ____________ .6.在平面直角坐标系中,将点P(﹣1,4)向右平移2个单位长度后,再向下平移3个单位长度,得到点P1,则点P1的坐标为____________ .7.如图,A.B的坐标分别为(1,0)、(0,2),若将线段AB平移到至A1B1,A1、B1的坐标分别为(2,a)、(b,3),则a+b=____________ .8.在平面直角坐标系中,△ABC 的三个顶点的坐标分别是A(-2,3),B(-4,-1),C(2,0),将△ABC平移至△A1B1C1 的位置,点A、B、C 的对应点分别是A1B1C1,若点A1 的坐标为(3,1).则点C1 的坐标为____________ .参考答案1.【答案】B【解析】∵四边形ABCD先向左平移3个单位,再向上平移2个单位,∴点A也先向左平移3个单位,再向上平移2个单位,∴由A(3,-1)可知,A′坐标为(0,1).故选B.2.【答案】A【解析】根据坐标的平移变化的规律,左右平移只改变点的横坐标,左减右加.上下平移只改变点的纵坐标,下减上加.因此,将点M(1,2)向左平移2个长度单位后得到点N的坐标是(1-2,2),即(-1,2).故选A.3.【答案】B【解析】根据平移性质判断4.【答案】(1,2)【解析】根据坐标的平移变化的规律,左右平移只改变点的横坐标,左减右加.上下平移只改变点的纵坐标,下减上加.因此,一青蛙从点A(-1,0)处向右跳2个单位长度,再向上跳2个单位长度到点A′处,则点A′的坐标为(-1+2,0+2),即(1,2).5.【答案】(﹣2,1)【解析】根据坐标的平移变化的规律,左右平移只改变点的横坐标,左减右加.上下平移只改变点的纵坐标,下减上加.因此,由图可得,点A(1,﹣1),A′(﹣3,3),∴平移的规律是:向左平移4个单位,再向上平移4个单位.∵点B的坐标为(2,﹣3),∴B′的坐标为(﹣2,1).6.【答案】(1,1)【解析】根据坐标的平移变化的规律,左右平移只改变点的横坐标,左减右加.上下平移只改变点的纵坐标,下减上加.因此,∵点P(﹣1,4)向右平移2个单位长度,向下平移3个单位长度,∴﹣1+2=1,4﹣3=1.∴点P1的坐标为(1,1).7.【答案】2【解析】∵A(1,0)转化为A1(2,a)横坐标增加了1,B(0,2)转化为B1(b,3)纵坐标增加了1,∴a=0+1=1,b=0+1=1.∴a+b=1+1=2.8.【答案】(7,-2)【解析】根据A点平移后的坐标变化,确定三角形的平移方法,得到C点的平移方法:由A(-2,3)平移后点A1的坐标为(3,1),可得A点横坐标加5,纵坐标减2,则点C的坐标变化与A点的变化相同,故C1(2+5,0-2),即(7,-2).扩展知识线段的平移作法作法1:将线段两端点分别平移,然后将两个平移后的点连成线段,即为原线段平移后的线段;作法2:将线段一端点平移,然后过平移后的点作原线段的平行线,在该平行线适当方向截取长度为指定线段长度,则所得线段为所求.。

图形的平移与旋转(1)知识概述1、生活中的平移.在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.2、简单的平移作图.二、重点知识归纳及讲解1、图形的平移是日常生活中比较常见的几何图形变换形式,属全等变化的一种情况.平移不改变图形的大小和形状,经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.2、对于简单的平移作图,要注意选好一个“基本图形”,把基本图形中的每一个点都沿着相同的方向平行移动相同的距离,再连结相应线段,就可得到平移后的图形.三、难点知识剖析1、如图(1),将△ABC在图中平移,(平移时△ABC的三个顶点一定落在图中两线交点上),最多能平移几次?分析:抓住将三角形ABC平移,就是将顶点A、B、C向同一方向平移相同的单位.解答:能平移三次,具体做法见图(2).将△ABC先向下移一个单位得到△AˊBˊCˊ,再沿AˊCˊ向左上方平移到△A"B"C"处,然后向下平移到△位置.2、如图,经过平移,四边形的顶点A移到了点E,作出平移后的四边形EFGH.分析:根据平移的对应线为平行且相等的性质作图.解答:分别过B、C、D三点向右方作AE的平行线,并依次截取BH=AE,CG=AE,DF=AE,再连接成四边形EFGH,即为平移后的四边形.一、选择题1、如图,A、B、C、D是视力表中一行图案,可以通过平移图形①得到的是()A.B.C.D.2、下列各商标图案是利用平移来设计的个数是()A.1个B.2个C.3个D.4个3、在图中,由△ABC平移而得到的三角形共有()个A.2个B.3个C.4个D.5个4、下面A、B、C、D四个图案,那么平移图案(1),得到图案()A.B.C.D.5、如图,下列哪一项的右边图形是由左边图形平移而得()A.B.C.D.6、如图的图案中,可由一个“基本图案”平移而成的是()A.B.C.D.7、如图,△ABE沿射线XY的方向平移一定距离后成为△CDF,那么下面结论:①△CDF≌ABE;②AC∥EF;③∠AEB=∠CFD;④BD=EF,其中正确的有()A.1个B.2个C.3个D.4个B 卷二、解答题1、将图中的图案的一个顶点A移到了点F,请作出平移后的图案.2、将图中的正方形ABCD平移,顶点A移到了点E,作出平移后的正方形.3、如图,能由△AOB平移而得的图形是哪个?4、如图在正方体ABCD——AˊBˊCˊDˊ中,哪些线段可看做是由C ˊDˊ平移得到的?哪些线段可看做是由B Bˊ平移得到的?AˊDˊ是否也可由CˊDˊ或B Bˊ平移得到?5、如图,图中由△ABC平移而得的三角形共有多少个?如果照这个图沿AB、AC方向延伸平移下去,第n排有多少个平移而得的三角形?6、观察下面两幅图案,分析这两个图案是通过怎样的“基本图案”变化而成.答案:1、略2、向左边的方向,过B、C、D点分别作AE的平行线,依次截取与AE等长的线段为BF、CG、DH,则正方形EFGH是平移后的正方形.3、△EOF和△COD4、AB、AˊBˊ,CD可以看作是由CˊDˊ平移得到的,AAˊ,CC ˊ,DDˊ可以看作是由BBˊ平移得到的,AˊDˊ无法由CˊDˊ或BB ˊ平移得到5、9个,n个6、如图(1)(2)中的阴影部分分别向上、下、左、右平移就可以得到整个图案.图形的平移与旋转(2)知识概述1、生活中的旋转在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角称为旋转角.2、简单的旋转作图3、简单的图案设计二、重点知识归纳及讲解1、旋转之后得到的图形与原来的图形全等,即旋转不改变图形的大小和形状.2、画旋转后的图形时,首先必须明确旋转中心,其次要注意对应点到旋转中心的距离相等,还要注意,在同一个图形中的旋转角相等.3、在认识图形变化时,要根据我们已掌握的对称的性质,平移和旋转的特征去仔细观察、分析,同时要注意“基本图案”是经过怎样的变化形成美观的图案.4、学习简单的图案设计,学会利用平移、旋转的知识,画出精美的几何图案,培养创新意识,创意美丽作品。
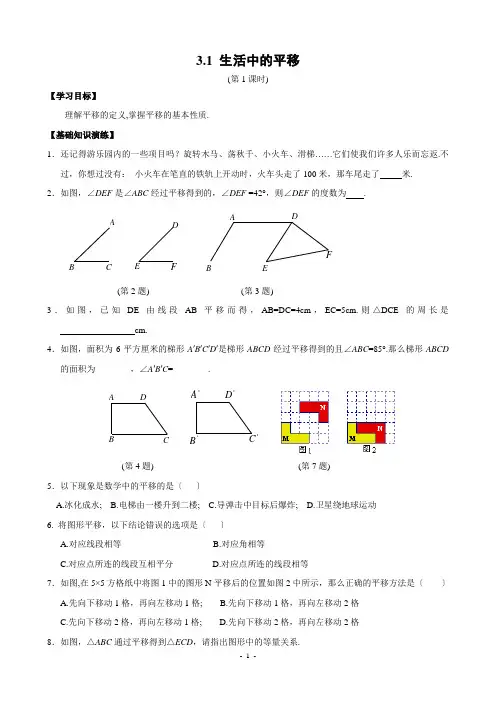
3.1 生活中的平移(第1课时)【学习目标】理解平移的定义,掌握平移的基本性质. 【基础知识演练】1.还记得游乐园内的一些项目吗?旋转木马、荡秋千、小火车、滑梯……它们使我们许多人乐而忘返.不过,你想过没有: 小火车在笔直的铁轨上开动时,火车头走了100米,那车尾走了 米. 2.如图,∠DEF 是∠ABC 经过平移得到的,∠DEF =42°,则∠DEF 的度数为 .EDCBAFEDB AF(第2题) (第3题)3.如图,已知DE 由线段AB 平移而得,AB=DC=4cm ,EC=5cm.则△DCE 的周长是 _________________cm.4.如图,面积为6平方厘米的梯形A ′B ′C ′D ′是梯形ABCD 经过平移得到的且∠ABC =85°.那么梯形ABCD 的面积为________,∠A ′B ′C =________.D 'DCB AA 'B 'C '(第4题) (第7题) 5.以下现象是数学中的平移的是〔 〕A.冰化成水;B.电梯由一楼升到二楼;C.导弹击中目标后爆炸;D.卫星绕地球运动 6. 将图形平移,以下结论错误的选项是〔 〕A.对应线段相等B.对应角相等C.对应点所连的线段互相平分D.对应点所连的线段相等7.如图,在5×5方格纸中将图1中的图形N 平移后的位置如图2中所示,那么正确的平移方法是〔 〕 A.先向下移动1格,再向左移动1格; B.先向下移动1格,再向左移动2格 C.先向下移动2格,再向左移动1格; D.先向下移动2格,再向左移动2格 8.如图,△ABC 通过平移得到△ECD ,请指出图形中的等量关系.9.举3个生活中常见的平移的例子.【思维技能整合】10. 甲图向上平移2个单位得到乙图,乙图向左平移2个单位得到丙图,丙图向下平移2个单位得到丁图,那么丁图向______平移______个单位可以得到甲图.11. 如图,将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形,至少需要移动〔〕A.8格B.9格C.11格D.12格AC DE F【发散创新尝试】12.如下图有两个村庄A和B被一条河隔开,现要架一座桥〔桥与河岸垂直〕,请你设计一种方案,使由A到B的路程最短.【回忆体会联想】13.问:什么叫平移?答: 在平面内,将一个图形沿移动一定的距离,这样的图形运动称为平移.问:平移的基本性质是什么?答: 经过平移,对应线段,对应角分别;对应点所连的线段.参考答案1. 100 2. 42° 3. 13 4. 6平方厘米 ∠A ′B ′C ′=85° 5.B 6. C 7.C8.AB =EC ,AC =ED ,BC =CD ,∠A =∠E ,∠B =∠ECD ,∠ACB =∠D ,∠A =∠ACE 9.略 10.右,2 11.B 12.略 13.某个方向,相等,平行且相等.参考答案1.A 2~9.略 10. 〔1〕略;〔2〕作A ’与点A 关于直线L 成轴对称,连接A ’B 交直线L 于点P ,则点P 为所求 11.乙公司提供的有用面积为900002m ,比甲单位提供的895002m 多,应购买乙公司的土地 12.位置,方向,距离参考答案1.B 2.C 3.B 4.不是,因为汽车的整体形状发生了变化 5.〔1〕不是.〔2〕不是 6.略7.(1)其特点可以看成由一个“基本图形”经过平移而得到另一个图形(2)(1)~(5)均可以看成前一个图形是后一个图形向前平移一定距离后得到的.(6)中的下面图形可以看成是上面图形向下平移一段距离再向右平移一段距离后得到的.〔3〕略 8. B9. 连结AB ,作AB 的垂直平分线,交射线BO 于点C ,则点C 即为机器人截住小球的位置.机器人平移的方向为从点A 到点C 的方向. 10.如图11.平移3.2 简单的平移作图【学习目标】会按要求作出简单平面图形平移后的图形.了解确定一个图形平移后的位置的条件.【基础知识演练】1.确定一个图形平移后的位置,除需要原来的位置外,还需要什么条件?下面来进行体会:将△ABC平移到△DEF,不能确定△DEF位置的是〔〕A.已知平移的方向B.已知点A的对应点D的位置C.已知边AB的对应边DE的位置D.已知∠A的对应角∠D的位置2.经过平移,△ABC的边AB移到了MN,作出平移后的三角形,你能给出几种作法?3.如图,将字母N按箭头所指的方向平移2cm,作出平移后的图形.4.已知图中的每个小正方形的边长都是1个单位.将图中的格点△ABC,先向右平移3个单位,再向上平移2个单位,得到△A1B1C1,请你在图中画出△A1B1C1.CA B5.请将图中的“小鱼”向左平移6格.6.如图,正方形ABCD的对角线交点O移到了O′的位置,请作出此正方形平移后的图形.7.如图,经过平移五角星的顶点A移到了点B,作出平移后的图形.8. 作线段AB和CD,且AB和CD互相垂直平分,交点为O,AB=2C D.分别取OA、OB、OC、OD的中点A′、B′、C′、D′,连结CA′、DA′、CB′、DB′、AC′、AD′、BC′、BD′得到一个四角星图案.将此四角星沿水平方向向右平移2厘米,作出平移前后的图形.【思维技能整合】9. 如图,经过平移,扇形上的点A移到了F,作出平移后的扇形.10. 如图,有一条小船.〔1〕假设把小船平移,使点A平移到点B,请你在图中画出平移后的小船;〔2〕假设该小船先从点A航行到达岸边L的点P处补给后,再航行到点B,但要求航程最短,试在图中画出点P的位置.【发散创新尝试】11面积大的为购买对象.【回忆体会联想】12.师:生: (1)3.2 简单的平移作图(2)【学习目标】了解图形之间的平移关系.了解平移在现实生活中的应用.【基础知识演练】1.生活中经常见到一些美丽的图案,这些图案有许多是由基本图形平移组成的,如:以下图形中只能用其中一部分平移而得到的是〔〕A B C D2.如图图案中可以看作由图案自身的一部分经过平移后而得到的是〔〕3.如图的图案中,可以看出由图案自身的部分经过平移而得到的是〔〕4.汽车在笔直的公路上行驶,我们可以把它看成是汽车沿着公路的方向移动了一定的距离,这就是平移,想一想,如果汽车在盘山公路上行驶,这也是数学上的平移吗?为什么?5.如图,由图形A变化到图形B,是不是平移得到的?为什么?6.如图,第2个图形是第1个图形平移得到的,请你仿照这种方法,在格点处画出平移后的第3和第4个图形.7.小明和婷婷在一起做拼图游戏,他们用“○○、△△、=”构思出了独特而有意义的图形并根据图形还用简洁的语言进行了表述:〔1〕请分析这些图案的构成特点;〔2〕分析这些图案的平移现象;〔3〕仿照他们的方法自己设计两个有意义的图案.【思维技能整合】8. 如图,把边长为2的正方形的局部进行图①~图④的变换,拼成图⑤,则图⑤的面积是〔〕A.18B.16C.12D.89.如图,一机器人在点A处发现一个小球自B点处沿着射线BO方向匀速滚去,机器人立即从A处出发匀速直线前进去拦截小球,假设小球滚动速度与机器人行走速度相等,请在图中标出机器人的平移方向及最快能截住小球的位置C.〔此题中的机器人行走、小球滚动均视为点的平移〕OA B【发散创新尝试】10.如图,有一个由火柴搭成的图形.移走其中的4根火柴,使之留下5个正方形且留下的每一根都是正方形的边或边的一部分.请你将符合条件的图形画出来.【回忆体会联想】11.一些复合图案,它的许多部分可以通过而相互得到,可见平移在现实生活中有着广泛的应用,也可利用平移来解决一些有趣的问题.如图,10根火柴可以拼成向下飞的编幅形状,你能只平移3根火柴就使它向上飞吗?请你试有试.3.3 生活中的旋转【学习目标】了解旋转的定义.理解旋转的基本性质. 【基础知识演练】1.日常生活中,我们经常见到以下情景:①钟表指针的转动;②汽车方向盘的转动;③打气筒打气时,活塞的运动;④传送带上瓶装饮料的移动.其中属于旋转的是 .2.在字母“X”、“V”、“Z”、“H”中绕某点旋转〔旋转度数不超过180〕后能与原字母重合的是____ .3.如图,△BCD 是由△ABD 旋转而成的,其中AB=CD ,AD=BC ,则旋转中心是点 ,旋转角是 度.A BCOD EF(第3题) (第4题) (第6题)4.如图中的图形,是由基本图案多边形ABCDE 旋转而成的,它的旋转角为〔 〕 A .30°B .60°C .90°D .150° 5.以下说法不正确的选项是〔 〕 A .旋转中心在旋转过程中是不动的;B .旋转形成的图形是由旋转中心和旋转角共同决定的;C .旋转不改变图形的形状和大小;D .旋转改变图形的形状但不改变大小6.如图,如果把钟表的指针看做四边形AOBC ,它绕O 点旋转得到四边形DOEF ,在这个旋转过程中: (1)旋转中心是什么?旋转角是什么?(2)经过旋转,点A 、B 分别移动到什么位置? (3)AO 与DO 的长有什么关系?BO 与EO 呢?(4)∠AOD 与∠BOE 有什么大小关系?7.观察以下图形,它可以看作是什么“基本图形”通过怎样的旋转而得到的?【思维技能整合】8. 同学们曾玩过万花筒,它是由三块等宽等长的玻璃围成的,如图是看到的万花筒的一个图案,图中所有的小三角形均是全等的等边三角形,其中的菱形AEFG可以看成是把菱形ABCD以点A为中心〔〕A.顺时针旋转60°得到B.顺时针旋转120°得到C.逆时针旋转60°得到D.逆时针旋转120°得到9. 如下图的五角星绕中心旋转,最少旋转________度后才能与自身重合.10. 钟表的分针匀速旋转一周需要60分钟,那么:〔1〕它的旋转中心是什么?〔2〕分针旋转一周,时针旋转多少度?〔3〕下午3点半时,时针和分针的夹角是多少度?【发散创新尝试】11.分析图中的旋转现象.【回忆体会联想】12.问:旋转的基本性质有哪些?答:旋转不改变图形的和,但图形上的每个点同时都按相同的方式转动相同的 .旋转前后两个图形对应点到旋转中心的距离,对应点与旋转中心的连线所成的角彼此 .参考答案1.①②2.X,Z,H 3.BD的中点,180 4.B 5.D6.(1)旋转中心是O点,旋转角是∠AOD. ∠BOE.(2)点A旋转到点D的位置,点B旋转到点E的位置.(3) OA与OD是相等的.OB与OE是相等的.(4)∠AOD与∠BOE是相等的7.图形(1)是通过一条线段绕点O旋转360°而得到的;图形(2)可以看作是“一个Rt△ABC”绕线段AC旋转360°而得到的;图形(3)将矩形ABCD绕AD旋转一周而得到的8. D 9. 72 10. (1)时针和分针的交点;(2)30°;(3)75°11。
图形的平移与旋转【知识点梳理】一、平移定义和规律1.平移的定义:在平面,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.注意:〔1〕平移不改变图形的形状和大小〔也不会改变图形的方向,但改变图形的位置〕;〔2〕图形平移的要素:平移方向、平移距离.2.平移的规律〔性质〕:经过平移,对应点所连的线段平行且相等,对应线段平行且相等、对应角相等.注意:平移后,原图形与平移后的图形全等.3.简单的平移作图平移作图,就是把整个图案的每一个特征点按一定方向和一定的距离平行移动.平移作图要注意:①方向;②距离.二、旋转的定义和规律1.旋转的定义:在平面,将一个图形饶一个定点沿某个方向转动一个角度,这样的图形运动称为旋转.这个定点称为旋转中心,转动的角称为旋转角.关键:〔1〕旋转不改变图形的形状和大小〔但会改变图形的方向,也改变图形的位置〕;〔2〕图形旋转的要素:旋转中心、旋转方向、旋转角.2.旋转的规律〔性质〕:经过旋转,图形上的每一个点都绕旋转中心沿一样方向转动了一样的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.〔旋转前后两个图形的对应线段相等、对应角相等.)注意:旋转后,原图形与旋转后的图形全等.3.简单的旋转作图:旋转作图,就是把整个图案的每一个特征点绕旋转中心按一定的旋转方向和一定的旋转角度旋转移动.旋转作图要注意:①旋转方向;②旋转角度.【典题例题】【例1】、在以下实例中,不属于平移过程的有〔〕①时针运行的过程;②火箭升空的过程;③地球自转的过程;④飞机从起跑到离开地面的过程。
A、1个B、2个C、3个D、4个【例2】、如下图的每个图形中的两个三角形是经过平移得到的是〔〕【例3】、以下图形经过平移后恰好可以与原图形组合成一个长方形的是〔 〕A 、三角形B 、正方形C 、梯形D 、都有可能【例4】、在图形平移的过程中,以下说法中错误的选项是〔 〕A 、图形上任意点移动的方向一样B 、图形上任意点移动的距离一样C 、图形上可能存在不动的点D 、图形上任意两点连线的长度不变【例5】、有关图形旋转的说法中错误的选项是〔 〕A 、图形上每一点到旋转中心的距离相等B 、图形上每一点移动的角度一样C 、图形上可能存在不动点D 、图形上任意两点连线的长度与旋转其对应两点连线的长度相等。
一、教学目标:
1、知识目标:能熟练掌握简单图形的移动规律,能按要求作出简单平面图形平移后的图形,能够探索图形之间的平移关系;
2、能力目标:①在实践操作过程中,逐步探索图形之间的平移关系;②对组合图形要找到一个或者几个“基本图案”,并能通过对“基本图案”的平移,复制所求的图形;
3、情感目标:经历对图形进行观察、分析、欣赏和动手操作、画图等过程,发展初步的审美能力,增强对图形欣赏的意识。
二、重点与难点:
重点:图形连续变化的特点;
难点:图形的划分。
三、教学方法:
讲练结合
四、自学过程:
1、观察下面的图案:
(1)这个图案有什么特点?
(2)它可以通过什么“基本图案”经过怎样的平移而形成?(3)在平移过程中,“基本图案”的大小、形状、位置是否发生了
2、分析下图:由其中一对兔子和乌龟怎样得到下面漂亮图案?
3、请观察下列图案,并分析图案形成过程。
二、练习
1、利用平移分析下图的形成过程。
2、请你为班级“学习专栏”设计报头图案,并用文字说明图案的
含义,如图①。
(要求是由“基本图形”经过平移而形成,要有创意!
学教反思:。