第八章 时间序列分析教学资料
- 格式:doc
- 大小:1.07 MB
- 文档页数:18

第⼋章时间序列分析第⼋章时间序列分析与预测【课时】6学时【本章内容】§ 时间序列的描述性分析时间序列的含义、时间序列的图形描述、时间序列的速度分析§ 时间序列及其构成分析时间序列的构成因素、时间序列构成因素的组合模型§ 时间序列趋势变动分析移动平均法、指数平滑法、模型法§ 时间序列季节变动分析[原始资料平均法、趋势-循环剔除法、季节变动的调整§ 时间序列循环变动分析循环变动及其测定⽬的、测定⽅法本章⼩结【教学⽬标与要求】1.掌握时间序列的四种速度分析2.掌握时间序列的四种构成因素3.掌握时间序列构成因素的两种常⽤模型4.掌握测定长期趋势的移动平均法5.了解测定长期趋势的指数平滑法6.;7.掌握测定长期趋势的线性趋势模型法8.了解测定长期趋势的⾮线性趋势模型法9.掌握分析季节变动的原始资料平均法10.掌握分析季节变动的循环剔出法11.掌握测定循环变动的直接法和剩余法【教学重点与难点】1.对统计数据进⾏趋势变动分析,利⽤移动平均法、指数平滑法、线性模型法求得数据的长期趋势;2.对统计数据进⾏季节变动分析,利⽤原始资料平均法、趋势-循环剔除法求得数据的季节变动;3.对统计数据进⾏循环变动分析,利⽤直接法、剩余法求得循环变动。
【导⼊】;很多社会经济现象总是随着时间的推移不断发展变化,为了探索现象随时间⽽发展变化的规律,不仅要从静态上分析现象的特征、内部结构以及相互关联的数量关系,⽽且应着眼于现象随时间演变的过程,从动态上去研究其发展变动的过程和规律。
这时需要⼀些专门研究按照时间顺序观测的序列数据的统计分析⽅法,这就是统计学中的时间序列分析。
通过介绍⼀些时间序列分析的例⼦,让同学们了解时间序列的应⽤,并激发学⽣学习本章知识的兴趣。
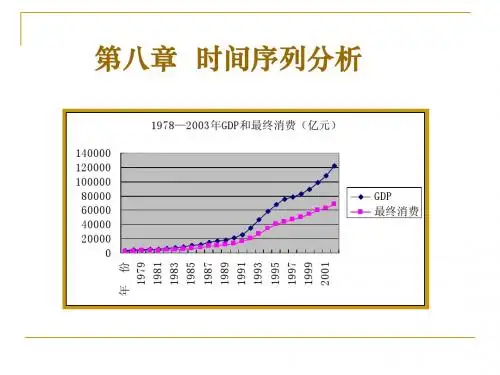
1.为了表现中国经济的发展状况,把中国经济发展的数据按年度顺序排列起来,据此来研究。
2.公司对未来的销售量作出预测。
这种预测对公司的⽣产进度安排、原材料采购、存货策略、资⾦计划等都⾄关重要。








时间序列分析教材本教材将介绍时间序列分析的基本概念、常用方法和应用示例,帮助读者了解和掌握时间序列分析的基本原理和操作方法。
一、时间序列分析的基本概念1、时间序列的特点:时间序列数据具有趋势性、季节性和周期性等特点,可以通过分析这些特征来预测未来的数据变化。
2、平稳时间序列:平稳时间序列是指时间序列数据的统计特性在时间上保持恒定,如均值、方差和自相关系数等。
平稳时间序列可以使用各种统计方法进行分析和预测。
3、非平稳时间序列:非平稳时间序列是指时间序列数据的统计特性在时间上发生变化,如趋势变化、季节变化和周期变化等。
非平稳时间序列需要进行差分或转化处理,使其变为平稳时间序列再进行分析。
二、时间序列分析的基本方法1、时间序列的图形表示:通过绘制时间序列的折线图、散点图和自相关图等,可以观察数据的分布、趋势和季节性等特征。
2、时间序列的分解:时间序列的分解是将时间序列数据分解为趋势、季节和随机成分三个部分,以便更好地对数据进行分析和预测。
3、时间序列的平滑方法:平滑方法包括移动平均法和指数平滑法,可以减少数据的随机波动,更好地揭示数据的趋势性。
4、时间序列的预测方法:预测方法包括线性回归模型、ARIMA模型和季节性ARIMA模型等,可以基于历史数据对未来数据进行预测。
5、时间序列的评估方法:评估方法包括残差分析、均方误差和平均绝对误差等,可以评估预测模型的准确性和可靠性。
三、时间序列分析的应用示例1、经济学中的时间序列分析:时间序列分析可以应用于宏观经济指标的预测和监测,如国内生产总值、通货膨胀率和失业率等。
2、金融学中的时间序列分析:时间序列分析可以应用于股票价格、汇率和利率等金融数据的分析和预测,帮助投资者进行投资决策。
3、气象学中的时间序列分析:时间序列分析可以应用于气象数据的分析和预测,如气温、降雨量和风速等,帮助预测天气变化和灾害风险。
四、时间序列分析的实际案例1、某股票价格的时间序列分析:通过对某只股票价格的时间序列数据进行分析,预测未来股票价格的走势,指导投资决策。
第八章时间序列分析第八章时间序列分析与预测【课时】6学时【本章内容】§8.1 时间序列的描述性分析时间序列的含义、时间序列的图形描述、时间序列的速度分析§8.2 时间序列及其构成分析时间序列的构成因素、时间序列构成因素的组合模型§ 8.3 时间序列趋势变动分析移动平均法、指数平滑法、模型法§8.4 时间序列季节变动分析原始资料平均法、趋势-循环剔除法、季节变动的调整§8.5 时间序列循环变动分析循环变动及其测定目的、测定方法本章小结【教学目标与要求】1.掌握时间序列的四种速度分析2.掌握时间序列的四种构成因素3.掌握时间序列构成因素的两种常用模型4.掌握测定长期趋势的移动平均法5.了解测定长期趋势的指数平滑法6.掌握测定长期趋势的线性趋势模型法7.了解测定长期趋势的非线性趋势模型法8.掌握分析季节变动的原始资料平均法9.掌握分析季节变动的循环剔出法10.掌握测定循环变动的直接法和剩余法【教学重点与难点】1.对统计数据进行趋势变动分析,利用移动平均法、指数平滑法、线性模型法求得数据的长期趋势;2.对统计数据进行季节变动分析,利用原始资料平均法、趋势-循环剔除法求得数据的季节变动;3.对统计数据进行循环变动分析,利用直接法、剩余法求得循环变动。
【导入】很多社会经济现象总是随着时间的推移不断发展变化,为了探索现象随时间而发展变化的规律,不仅要从静态上分析现象的特征、内部结构以及相互关联的数量关系,而且应着眼于现象随时间演变的过程,从动态上去研究其发展变动的过程和规律。
这时需要一些专门研究按照时间顺序观测的序列数据的统计分析方法,这就是统计学中的时间序列分析。
通过介绍一些时间序列分析的例子,让同学们了解时间序列的应用,并激发学生学习本章知识的兴趣。
1.为了表现中国经济的发展状况,把中国经济发展的数据按年度顺序排列起来,据此来研究。
2.公司对未来的销售量作出预测。
这种预测对公司的生产进度安排、原材料采购、存货策略、资金计划等都至关重要。
3.车站对未来节日客流量的预测。
4.投资者对股票、基金未来走势的预测。
【教学内容】第八章时间序列分析与预测时间序列包括确定型时间序列和随机型时间序列。
确定型时间序列是指事物的发展与确定的变化规律,序列的变化过程可以用时间t的确定函数来描述;随机型时间序列是指事物的变化没有必然的变化规律,需要把时间序列作为一个随机过程来描述和研究。
本章只讨论确定型时间序列分析和预测方法。
§8.1时间序列的描述性分析一、时间序列的含义☞一个变量在一定连续时点或一定连续时期上测量的观测值的集合称为时间序列。
➢时间序列的基本要素:1)是被研究现象所属的时间范围。
2)是反映该现象在一定时间条件下数量特征的值,即在不同时间上的统计数据时间可以是年份、季度、月份或其他任何时间形式。
本书用t表示所观察的时间、Y表示观察值,则),,2,1(niYi为时间it上的观察值。
➢时间序列分析的分类:1. 平稳序列与非平稳序列平稳序列是基本上不存在趋势的序列。
这类序列中的各观察值基本上在某个固定的水平上波动,虽然在不同的时间段波动的程度不同,但并不存在某种规律,而其波动可以看出是随机的。
非平稳序列是包含趋势性、季节性或周期性的序列。
可能只包含其中的一种成分,也可能是几种成分的组合,因此非平稳时间序列又可以分为有趋势的序列,有趋势、季节性和周期性的序列,即复合型序列。
2. 绝对数时间序列、相对数时间序列和平均数时间序列(1)绝对数时间序列:由一系列绝对数按时间顺序排列而成的序列。
它是时间序列中最基本的表现形式,用于反映现象在不同时间上所达到的绝对水平。
根据观察值所属的时间状况不同,分为:时期序列和时点序列。
如国内生产总值序列就是时期序列,时期序列中的观察值反映现象在一段时期内的活动总量,并且各观察值可以直接相加,用于反映现象在更长一段时期内的活动总量;如年末总人口属于时点序列,时点序列中的观察值反映现象在某一瞬间时点上的总量,它是在某一时点上统计得到的,序列中的各观察值通常不能相加。
(2)相对数时间序列:由一系列相对数按时间顺序排列而成的序列。
如人口自然增长率序列。
(3)平均数时间序列:由一系列平均数按时间顺序排列而成的序列。
如居民平均消费水平序列。
➢发展水平时间序列中每一项数据反映了现象在各个时间上达到的规模或水平,也称为相应时间上的发展水平。
➢ 基期与基期水平在对各时间的发展水平进行比较时,把作为比较基础的那个时期称为基期,相对应的发展水平称为基期水平。
➢ 报告期与报告期水平把所研究考察的那个时期成为报告期,相对应的发展水平称为报告期水平。
在时间序列中,用i t 表示现象所属的时间,i Y 表示现象在不同时间上的观察值。
i Y 也称为现象在时间i t 上的发展水平,它表示现象在某一时间上所达到的一种数量状态。
若观察的时间范围为n t t t ,,,21 ,相应的观察值表示为n Y Y Y ,,,21 ,其中1Y 称为最初发展水平,n Y 为最末发展水平。
若将整个观察时期内的各观察值与某个特定时期0t 做比较时,时间可表示为n t t t t ,,,,210 ,相应的观察值表示为n Y Y Y Y ,,,,210 ,其中0Y 称为基期水平,n Y 为报告期水平。
➢ 时间序列分析的目的二、 时间序列的图形描述可以用图形描述时间序列的变化模式和变动趋势,分析观察数据随时间变化的形态。
图形可以直观、简明地表现某种现象随时间变化的模式和趋势,但较为粗糙。
见书中P256图8.2和图8.3三、 时间序列的速度分析为了研究时间序列随时间而变化的速率,经常需要分析其发展速度和增长速度。
1. 发展速度发展速度是报告期发展水平与基期发展水平之比,用于描述现象在观察期内相对的发展变化程度。
有环比发展速度和定期发展速度之分:环比发展速度:),,2,1(1n i Y Y R i i i ==- 定基发展速度:),,2,1(0n i Y Y R ii ==环比发展速度与定基发展速度之间的关系是:统计分析的目的 分析过去认识规律(1)观察期内各环比发展速度的连乘积等于最末期的定基发展速度:∏∏=-为连乘符号01Y Y Y Y n i i(2)两个相邻的定基发展速度,用后者除以前者,等于相应的环比发展速度:1010--=÷i i i i Y Y Y Y Y Y 2. 增长速度 “增长率”是增长量与基期水平之比,用于描述现象的相对增长程度。
它可以根据增长量求得,也可以根据发展速度求得,计算公式为:1-=-==发展速度基期水平基期水平报告期水平基期水平增长量增长速度 由于采用的基期不同,增长速度也可以分为环比增长速度和定基增长速度。
环比增长速度:),,2,1(1111n i Y Y Y Y Y G i i i i i i =-=-=--- 定基增长速度:),,2,1(1000n i Y Y Y Y Y G i i i =-=-=环比增长速度与定基增长速度之间没有直接的换算关系。
在由环比增长速度推算定基增长速度时,可先将各环比增长速度加1后连乘,再将结果减1,即得定基增长速度。
(二)平均发展速度与平均增长速度平均发展速度是各个时期环比发展速度的平均数,用于描述现象在整个观测期内平均发展变化的程度。
平均增长速度(平均增长率)则是用于描述现象在整个观察期内平均增长变化的程度,通常用平均发展速度减1求得。
计算平均发展速度的常用方法是水平法,又称为几何平均法,是根据各期的环比发展速度采用几何平均法计算出来的:),,2,1(0111201n i Y Y Y Y Y Y Y Y Y Y R n n n i i n n n ===⨯⨯⨯=∏-- 平均增长速度1-=R G▲ 不能直接对环比增长速度进行几何平均数的运算来寻找平均增长速度计算平均发展速度应用几何法的特点:1. 用几何平均法计算平均发展速度的特点是着眼于期末水平,不论中间水平变化过程怎样,只要期末水平确定,对平均发展速度的计算结果没有影响。
2. 几何平均法计算平均发展速度隐含着一个假定:从时间序列的最初水平出发,以计算的平均发展速度代替各期的环比发展速度,计算出的期末水平与实际的期末水平一致。
3. 平均发展速度表明的是在基期水平基础上的发展状况,在运用平均发展速度的时候应注意与基期水平联系起来分析4. 由于平均发展速度是各期环比发展速度的序时平均,可能会掩盖各期特殊发展的情况,所以应当把平均发展速度与各环比发展速度结合起来进行分析。
§8.2 时间序列及其构成因素一、 时间序列的构成因素T 趋势:指时间序列在长时间内呈现出某种持续向上或持续向下的状态或律,包括线性趋势和非线性趋势。
长期趋势可能呈现不断增长的态势,也可能呈现为不断降低的趋势,或者还可能呈现为不变的水平趋势。
长期趋势是受某种长期起根本性作用的因素影响的结果例:社会进步、经济发展、人口总量S 季节性(季节变动):不是仅指随一年中四季而变动,而是泛指一年内有规律的、按一定周期(年、季、月、周、日)重复出现的变化。
季节变动的原因通常与自然条件有关,同时也可能由于生产条件、节假日、风俗习惯等社会经济因素所致。
例:产品的销售淡季、旅游淡季等C 周期性(循环波动):是时间序列中呈现出来的围绕长期趋势的一种波浪型或振荡式变动。
它不同于趋势变动,不是朝着单一方向的持续运动,而是涨落相间的交替波动;它也不同于季节变动,季节变动有比较固定的规律,且变动周期大多为一年,而循环波动则无固定规律,变动周期多在一年以上,且周期长短不一。
1.001.201.401357911131517192123252729313335系数月份I 不规则波动(随机性):除去趋势、周期性和季节性之后的偶然性波动。
0.511.5123456789101112系数月份二、组合模型乘法模型: Yt = Tt·St·Ct·It➢假定四个成分对现象发展的影响是相互的➢长期趋势成分取与时间序列原始指标数值Y相同计量单位的绝对量;以长期趋势为基础,其余成分则均以比率(相对量)表示➢一般来说,在时间序列中,长期趋势是经常存在的,季节变动因素和循环变动因素则不一定存在。
当季节变动或循环变动成分不存在时,乘法模型中的S或C取值为1加法模型: Yt = Tt + St+ Ct + It➢假定四个因素的影响是独立的,➢每个成分均以与时间序列原始指标数值Y相同计量单位的绝对量来表示。
➢一般来说,在时间序列中,长期趋势是经常存在的,季节变动因素和循环变动因素则不一定存在。
当季节变动或循环变动成分不存在时,在加法模型中的S或C取值为0。
§8.3 时间序列趋势变动分析时间序列的长期趋势是就一个较长的时期而言,一般来说,分析长期趋势的时期越长越好。