1.晶体结构讲解

第2章晶体结构为了便于对材料进行研究，常常将材料进行分类。

如果按材料的状态进行分类，可以将材料分成晶态材料，非晶材料及准晶材料。

因所有的晶态材料有其共同的规律，近代晶体学知识就是为研究这些共同规律而必备的基础。

同时为了研究非晶材料与准晶材料及准晶材料也必须以晶体学理论做为基础。

在一般的教材中对晶体学的基础知识已经有了不同深度的阐述，作为辅导教材，对教科书上已经有较多阐述的内容，本章中就简要的进行说明，而重点在于用动画形式，将在教材中难以用文字表达清楚的内容进行较多的阐述，加深对教材内容的理解记忆2.1晶体学基础2.1.1 空间点阵和晶胞具有代表性的基本单元（最小平行六面体）作为点阵的组成单元，称为晶胞。

将晶胞作三维的重复堆砌就构成了空间点阵。

为了便于分析研究晶体中质点的排列规律性，可先将实际晶体结构看成完整无缺的理想晶体并简化，将其中每个质点抽象为规则排列于空间的几何点，称之为阵点。

这些阵点在空间呈周期性规则排列并具有完全相同的周围环境，这种由它们在三维空间规则排列的阵列称为空间点阵，简称点阵。

同一空间点阵可因选取方式不同而得到不相同的晶胞<晶胞、晶轴和点阵矢量>根据6个点阵参数间的相互关系，可将全部空间点阵归属于7种类型，即7个晶系。

按照"每个阵点的周围环境相同"的要求，布拉菲（Bravais A．）用数学方法推导出能够反映空间点阵全部特征的单位平面六面体只有14种，这14种空间点阵也称布拉菲点阵。

空间点阵是晶体中质点排列的几何学抽象。

1 空间点阵最初人们认为凡是具有规则外形的天然矿物均为晶体。

但现在人们认识到晶体的规则的几何外形是内部结构规律的外在反映. 近代的科学研究表明了下面的两个基本事实:1）如果说某一种材料是晶体，其基本的特征是：组成该材料的内部的微观粒子(原子,分子,离子等)在三微的空间做有规则的周期性的排列。

2）这种排列的规律决定了材料的性能。

根据这样的事实我们可以抽象出个的重要概念即空间点阵。

晶体的常识(全套教案)第一章：引言教学目标：1. 让学生了解晶体的基本概念和特点。

2. 培养学生对晶体研究的兴趣。

教学内容：1. 晶体的定义：晶体是由原子、分子或离子按照一定的规律排列形成的固体物质。

教学活动：1. 引入话题：通过展示晶体的图片，引导学生思考为什么晶体具有规则的形状。

2. 讲解晶体定义和特点：通过PPT或板书，详细讲解晶体的定义和特点。

3. 讨论：让学生举例说明生活中常见的晶体，并分析其特点。

教学评价：1. 检查学生对晶体定义和特点的理解程度。

2. 观察学生在讨论中的参与情况和思考能力。

第二章：晶体的结构教学目标：1. 让学生了解晶体结构的基本类型。

2. 培养学生对晶体结构的理解和分析能力。

教学内容：1. 晶体结构的基本类型：立方晶系、六方晶系、四方晶系、正交晶系和单斜晶系。

2. 晶体结构的表示方法：晶胞、晶格和空间群。

教学活动：1. 讲解晶体结构的基本类型：通过PPT或板书，讲解各种晶体结构的特点和实例。

2. 展示晶体结构的图片和模型：让学生直观地了解晶体结构的形状和结构特点。

3. 练习：让学生分析给出的晶体结构图，判断其属于哪种基本类型。

教学评价：1. 检查学生对晶体结构的基本类型的理解和记忆。

2. 观察学生在练习中的操作情况和分析能力。

第三章：晶体的生长教学目标：1. 让学生了解晶体生长的原理和过程。

2. 培养学生对晶体生长的理解和观察能力。

教学内容：1. 晶体生长的原理：溶液蒸发、熔体冷却、离子注入等。

2. 晶体生长过程：成核、生长和成熟阶段。

教学活动：1. 讲解晶体生长的原理：通过PPT或板书，讲解晶体生长的原理和过程。

2. 演示晶体生长实验：进行晶体生长实验，让学生观察和记录晶体生长的过程。

3. 讨论：让学生分析晶体生长的速度和形状受到哪些因素的影响。

教学评价：1. 检查学生对晶体生长的原理和过程的理解程度。

2. 观察学生在实验中的观察和记录能力。

第四章：晶体的性质教学目标：1. 让学生了解晶体的一些基本性质。

117晶体结构一、基本概念（The Basic Concepts ）： 1．晶体（Crystals ）：(1)物质的质点（分子、离子或原子）在空间有规则地排列而成的、具有整齐外形的、以多面体出现的固体物质，称为晶体。

(2) 晶体有同质多象性 由同样的分子（或原子）可以以不同的方式堆积成不同的晶体，这种现象叫做同质多象性。

但同一种物质的气态、液态只存在一种结构。

(3) 晶体的几何度量和物理效应常随方向不同而表现出量上的差异，这种性质称为各向异性。

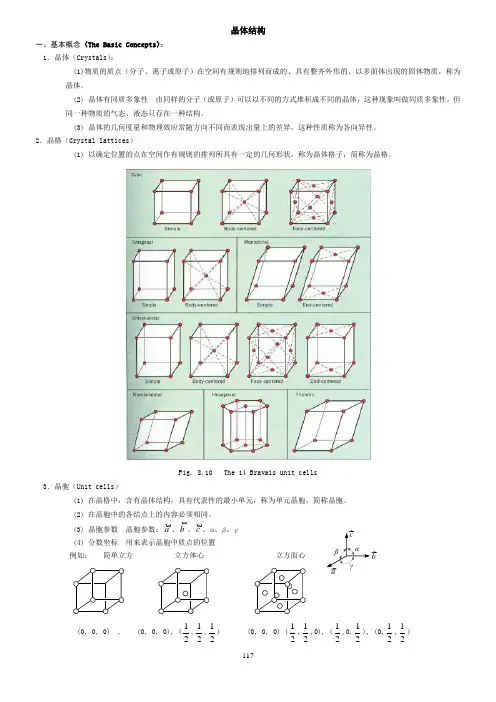
2．晶格（Crystal lattices ）(1) 以确定位置的点在空间作有规则的排列所具有一定的几何形状，称为晶体格子，简称为晶格。

Fig. 8.10 The 14 Bravais unit cells3．晶胞（Unit cells ）(1) 在晶格中，含有晶体结构，具有代表性的最小单元，称为单元晶胞，简称晶胞。

(2) 在晶胞中的各结点上的内容必须相同。

(3) 晶胞参数 晶胞参数：a、b、c、α、β、γ (4) 分数坐标 用来表示晶胞中质点的位置例如： 简单立方 立方体心 立方面心(0, 0, 0) , (0, 0, 0), (21,21,21) (0, 0, 0) (21,21,0), (21,0,21), (0,21,21) αβγbc a118在分数坐标中，绝对不能出现1，因为1即0。

这说明晶胞是可以前后、左右、上下平移的。

等价点只需要一个坐标来表示即可，上述三个晶胞中所含的质点分别为1、2、4，所以分数坐标分别为1组、2组和4组。

(5) 晶面指数 晶面在三维空间坐标上的截距的倒数（h 、k 、l ）来表示晶体中的晶面，称为晶面指数，如立方晶系中(100),(110),(111)面分别为(100) (110)(111)lFig. 8.12 Selected planes and their Miller indices for cubic system用X-ray 的衍射可以测量晶体中的面间距，2d ·sin θ = n ·λ。

第一章晶体结构1-1. 试述晶态、非晶态、准晶、多晶和单晶的特征性质。

解：晶态固体材料中的原子有规律的周期性排列，或称为长程有序。

非晶态固体材料中的原子不是长程有序地排列，但在几个原子的范围内保持着有序性，或称为短程有序。

准晶态是介于晶态和非晶态之间的固体材料，其特点是原子有序排列，但不具有平移周期性。

另外，晶体又分为单晶体和多晶体：整块晶体内原子排列的规律完全一致的晶体称为单晶体；而多晶体则是由许多取向不同的单晶体颗粒无规则堆积而成的。

1-2. 晶格点阵与实际晶体有何区别和联系？解：晶体点阵是一种数学抽象，其中的格点代表基元中某个原子的位置或基元质心的位置，也可以是基元中任意一个等价的点。

当晶格点阵中的格点被具体的基元代替后才形成实际的晶体结构。

晶格点阵与实际晶体结构的关系可总结为：晶格点阵＋基元＝晶体结构1-3. 晶体结构可分为Bravais格子和复式格子吗？解：晶体结构可以分为Bravais格子和复式格子，当基元只含一个原子时，每个原子的周围情况完全相同，格点就代表该原子，这种晶体结构就称为简单格子或Bravais格子；当基元包含2个或2个以上的原子时，各基元中相应的原子组成与格点相同的网格，这些格子相互错开一定距离套构在一起，这类晶体结构叫做复式格子。

心四方解：（a）“面心＋体心”立方不是布喇菲格子。

从“面心＋体心”立方体的任一顶角上的格点看，与它最邻近的有12个格点；从面心任一点看来，与它最邻近的也是12个格点；但是从体心那点来看，与它最邻近的有6个格点，所以顶角、面心的格点与体心的格点所处的几何环境不同，即不满足所有格点完全等价的条件，因此不是布喇菲格子，而是复式格子，此复式格子属于简立方布喇菲格子。

（b）“边心”立方不是布喇菲格子。

从“边心”立方体竖直边心任一点来看，与它最邻近的点子有8个；从“边心”立方体水平边心任一点来看，与它最邻近的点子也有8个。

虽然两者最邻近的点数相同，距离相等，但他们各自具有不同的排列。

第一章 晶体结构本章首先从晶体结构的周期性出发，来阐述完整晶体中离子、原子或分子的排列规律。

然后，简略的阐述一下晶体的对称性与晶面指数的特征，介绍一下倒格子的概念。

§1.1晶体的周期性一、晶体结构的周期性1．周期性的定义从X 射线研究的结果，我们知道晶体是由离子、原子或分子（统称为粒子）有规律地排列而成的。

晶体中微粒的排列按照一定的方式不断的做周期性重复，这样的性质成为晶体结构的周期性。

周期性：晶体中微粒的排列按照一定的方式不断的做周期性重复，这样的性质成为晶体结构的周期性。

晶体结构的周期性可由X-Ray 衍射直接证实，这种性质是晶体最基本或最本质的特征。

（非晶态固体不具备结构的周期性。

非晶态的定义等略），在其后的学习中可发现，这种基本性质对固体物理的学习具有重要的意义或是后续学习的重要基础。

2．晶格 格点和点阵晶格：晶体中微粒重心，做周期性的排列所组成的骨架，微粒重心所处的位置称为晶格的格点（或结点）。

格点的总体称为点阵。

整个晶体的结构，可看成是由格点沿空间三个不同方向， 各自按一定距离周期性平移而构成。

每个平移的距离称为周期。

在某一特定方向上有一定周期，在不同方向上周期不一定相同。

晶体通常被认为具有周期性和对称性，其中周期性最为本质。

对称性其实质是来源于周期性。

故周期性是最为基本的对称性，即“平移对称性”（当然，有更为复杂或多样的对称性，但周期性或平移对称性是共同的）。

3．平移矢量和晶胞据上所述，基本晶体的周期性，我们可以在晶体中选取一定的单元，只要将其不断地重复平移，其每次的位移为a 1，a 2，a 3，就可以得到整个晶格。

则→1a ，→2a ，→3a 就代表重复单元的三个棱边之长及其取向的矢量，称为平移矢量，这种重复单元称为晶胞，其基本特性为：⑴晶胞平行堆积在一起，可以充满整个晶体⑵任何两个晶胞的对应点上，晶体的物理性质相同，即：()⎪⎭⎫⎝⎛+++=→→→332211anananrQrQ其中→r为晶胞中任一点的位置矢量。