光学第5章习题及答案

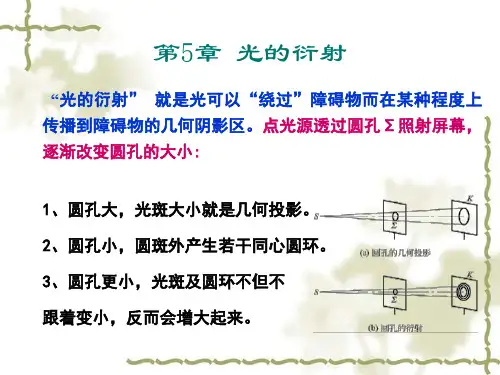
第5章透镜及其应用一．选择题（共21小题）1．小元同学让太阳光通过透明的镜片照射到白墙上，其现象如图所示。

从图中现象可看出（）A．这是一块凸透镜，和近视眼镜的镜片一样B．这是一块凸透镜，和老花眼镜的镜片一样C．这是一块凹透镜，和近视眼镜的镜片一样D．这是一块凹透镜，和老花眼镜的镜片一样2．有两个直径都为d的透镜，为辨别两个透镜的种类，现将它们正对太阳光，在纸上分别得到大小不同两个光斑，分别为甲、乙，透镜与光斑的大小如图所示（d1＜d＜d2），根据这两个光斑（）A．甲、乙能被准确判断透镜的种类B．甲能被准确判断透镜的种类而乙不能C．乙能被准确判断透镜的种类而甲不能D．甲、乙均不能被准确判断透镜的种类3．下列说法中正确的是（）A．凸透镜只对平行光有会聚作用B．反射光线与入射光线有时可以不在同一平面内C．近视眼镜片，对光线有发散作用D．人离平面镜越远，人在平面镜中所成的像就越小4．如图所示，一束平行光经过中间为“空气凹透镜”的玻璃砖后将会（）A．还是平行光B．发散C．会聚D．以上都有可能5．如图所示的四个情景中，成实像的是（）A．水面飞鸟的“倒影”B．照相机胶片上的像C．船上人看到水里的鱼D．通过放大镜看到的字6．下列是小华学习了“凸透镜成像”和“平面镜成像”后，总结出的关于实像和虚像的一些特点，其中错误的是（）A．虚像不可以用光屏承接B．光屏能承接到的一定是实像C．凸透镜所成的虚像始终是正立的D．平面镜成虚像时，像和物位于镜面的同侧7．我校教师运用了人脸识别系统签到，老师们站在机器前0.5m～1.2m处时，安装在墙上的人脸识别系统的摄像机就可以对其面部特征进行快速核对。

由此判断，人脸识别系统的摄像机的镜头（）A．相当于凸透镜，焦距可能为0.4 mB．相当于凸透镜，焦距可能为0.1 mC．相当于凹透镜，焦距可能为0.4 mD．相当于凹透镜，焦距可能为0.1 m8．购物支付已进入“刷脸”时代，如图所示，消费者结账时只需面对摄像头（相当于一个凸透镜），经系统自动拍照、扫描等，确认相关信息后，即可迅速完成交易。

应用光学试题第五章光度学和色度学基础一、填空题（建议每空1分）I级I级1空（建议每空1分）1、在国际单位制中，光学量的单位是__________ 。

发光强度2、朗伯辐射体又称为___________辐射体。

余弓玄3、点光源在某一方向在单位立体角内发出的光通量称为_______ 。

发光强度4、点周围全部立体角的大小为__________ o4兀5、单位受照面积所接收的光通量被称为光______ -照度6、光源投射到某方向上单位面积、单位立体角内的光通量称为发光______ o亮度7、光源每瓦功率发出的光通量，称为该光源的________ o发光效率8、若1 itf面积接收的光通量是31m,则该受照面积上的光照度值是___ 勒克斯。

39、正常人眼能承受的光亮度约为________ c d/m\1000010、正常情况下，读书时所需要的光照度大约为_______ 1X05011、在暗视觉的情况下，人眼最敏感的光的波长要比明视觉时要_______ O长12、在明视觉时，相同功率的蓝光与黄光，人会感觉_______ 的功率更大。

黄光13、透射光学材料主要分为三大类，即光学晶体、光学塑料和光学_______ 。

玻璃14、无色光学玻璃可以分为冕牌玻璃和______ -火石玻璃15＞表达式v=（n D-l）/ （（nF-nc）描述的是光学玻璃在可见光波段的常数。

阿贝16、阿贝常数通常被用来表示光学材料的_______ 特性。

色散17、在表示可见光波段的F、D、C谱线中，用来校正单色光像差的谱线是光。

D18、通常情况下，冕牌玻璃的阿贝常数要____ （高/低）于火石玻璃的阿贝常数。

高19、朗伯辐射体是指在各方向的发光______ 相同的辐射体。

亮度20.平方反比定律表面，当用点光源垂直照明时，受光面的光照度与光源的发光强度成_______ O正比21、探照灯可以使沿轴线方向的发光______ 得以成千倍的增加，从而提高照明效果。

显微镜和望远镜练习题一、填空题1、望远镜的物镜是_______，但它可以会聚更多的光，从而使所成的像变得更亮；现代天文望远镜都力求把物镜的口径____________（选填“缩小”或“加大”），以便观测到更暗的星。

2、显微镜的物镜形成的是___________像，目镜形成的是__________像。

3、天文爱好者可以使用望远镜观察远处的物体，当被观察物体在物镜的两倍焦距以外时，物体成一个__________的__________像，这个像位于目镜的一倍焦距以内，物体通过目镜成一个____ ______的__________像（填“放大”或“缩小”、“实”或“虚”），观察者就能看清楚远处的物体，这就是望远镜的原理.4、观察细胞等微小物体，要用；观察较远处的物体和天体的运动要用。

5、如图所示为一种光学显微镜，其中目镜和物镜都是由________制成的，在光线较弱的情况下，反光镜可以选用________（选填：“平面镜”、“凹面镜”）。

6、用一个凹透镜和一个凸透镜可制成一架镜，用两个焦距不同的凸透镜可以制成镜，也可以制成镜。

若用来观察细小的物体，必须用焦距的作为物镜，用焦距的作为目镜。

7、显微镜有____个凸透镜，靠近眼睛的叫____，它的作用____．靠近物体的叫____．要想看清太空中的星星要用____，它有____个凸透镜，靠近眼睛的叫____，靠近物体的叫____．它能使物体成____、____的____像．二、选择题8、显微镜可以观察微小的生物，是因为显微镜放大倍数较大，被观察的物体经过了（）A 一次放大作用B 二次放大作用C 三次放大作用D 四次放大作用9、下列关于显微镜和望远镜的说法中最贴切的是（）A．物体经显微镜和望远镜都成放大倒立的像B．显微镜和望远镜的目镜亦可作物镜使用因为它们都只是普通的并无规格的凸透镜C．显微镜和望远镜的目镜都相当于一个放大镜工作D．物体经过显微镜和望远镜所成的像都比实际物体大了很多倍10、望远镜能对远处的物体进行视角放大,它利用两个焦距不同的凸透镜分别作为物镜和目镜,则物镜和目镜对被观察物体所成的像是( )A.物镜和目镜都成虚像B.物镜和目镜都成实像C.物镜成倒立放大的实像D.目镜成正立放大的虚像11、显微镜由目镜和物镜等元件构成，下列关于显微镜的说法正确的是（）A．目镜的焦距很短B．通过目镜看到放大的实像C．物镜的焦距很短D．显微镜的放大倍数等于物镜和目镜放大倍数之和12、显微镜的结构如图所示，则下列说法正确的是( ）。

新人教版第五章《透镜及其应用》章末测试题及答案满分：100分时间：45分钟班级：姓名：一、选择题（每题3分，共30分）1.如图所示，下列透镜属于凸透镜的是（）2.关于透镜对光线的作用，下列叙述不正确的是（）A.凸透镜对光线有会聚作用B.点光源发光经凸透镜后的光线一定是发散的C.凹透镜对光线有发散作用D.点光源发光经凹透镜后的光线一定是发散的3.下图中各图分别表示经过透镜后的光路图，其中正确的是（）4．关于透镜，下列说法中不正确的是（）A．照相机的镜头相当于一个凸透镜B．用凸透镜可以看清物体的细小之处C．凸透镜和凹透镜都有两个焦点D．光线通过凸透镜后会聚到主轴上的点一定是焦点5．如图所示，图甲是小艳利用某透镜观察到的小明眼睛的像；图乙是小亮利用某眼镜观察到的课本上“物理”字的像。

关于上述两种情况中所观察到的像或用到的光学仪器，下列说法正确的是（）A．甲图中的像一定是虚像，像的位置可能在小艳的眼睛和透镜之间B．甲图中的像可能是实像，像的位置可能在小明的眼睛和透镜之间C．乙图中的像一定是虚像，该眼镜是近视镜D．乙图中的像可能是实像，该眼镜是老花镜6．一束平行光正对凸透镜照射时，在离透镜15cm处的光屏上得到一个亮点，那么当物体位于透镜前35cm处时，在透镜的另一侧可得到 ( )A．倒立、缩小的实像 B.倒立、放大的实像C．正立、放大的虚像 D.正立、缩小的虚像7．如图所示，a、b、c、d是距凸透镜不同距离的四个点，F为焦点。

下列几种光学仪器的成像原理与物体在不同点时的成像情况相对应，下列说法正确的是（）A．幻灯机是根据物体放在c点时的成像特点制成的B．照相机是根据物体放在d点时的成像特点制成的C ．使用放大镜时的成像情况与物体放在a 点时的成像情况相似D ．人眼看物体时的成像情况与物体放在F 点时的成像情况相似8．烛焰通过凸透镜恰好在光屏上得到一个放大的像，若保持凸透镜位置不变，把烛焰和光屏位置对调一下，则 ( )A ．光屏上仍能成一个放大的像 B. 光屏上能成一个缩小的像C ．光屏上不能成像，但通过透镜能看到 D. 以上说法都不对9．来自于物体的光经过晶状体等会聚在视网膜上，形成物体的像。

A1 Acos30sin10
或
( A1 )2 0.0933
A2
5.8 平面偏振光垂直于射到一块光轴平行于表面 的方解石晶片上，光的振动面和晶片的主截面成300。 （a）试问透射出来的两束平面偏振光的相对强度为 多少；（b）用钠光时，如要产生900的位相差，晶 片的厚度应为多少？（ 5890A ）
kz


x

sint

kz


y
当 A A A时，有
1
2


E


E左

E右

2 A cost

kz


x
此即为线偏振光。
5.15 设一方解石晶片沿平行于光轴切出，其 厚度为0.0343mm，放在两个正交的尼科耳棱镜间。 平行光束经过第一尼科耳棱镜后，垂直地射到波片 上，对于钠光（589.3nm）而言，晶体的折射率为 n0 1.658, ne 1.486 。问通过第二个尼科耳棱镜后 光束发生的干涉是加强还是减弱？如果两个尼科耳 棱镜的主截面是互相平行的，结果又如何？


A' s1

0.5

0.5A0.5故：I r

A0 ' s1

0.5I i
A' 0.5 s1
0.56A.25故 ：Ir 6
0
I
i
I
r

5.6 如图所示，一块折射率n=1.50的平面玻璃浸 在n =1.33水中，已知一束光入射到水面上时反射光 是完全偏振光，若要使玻璃表面的反射光也是完全 偏振光，则玻璃表面与水平面的夹角θ 应是多大?
无吸收，试问N3和N1主截面的夹角为何值时，通过系 统的光强最大？设入射光强为I0，求此时所能通过 的最大光强。

1 1 0 1 1 1 = 2 − 1 2 0 − j− j
这正是一个偏振方向与 x 轴成 − 45 角的线偏振光， 它能够通过透光轴与 x 轴成 − 45 角的偏 振器。
2
tan θ o no = tan θ e n e
5-3（1）一右旋圆偏振光在通过 1/2 波片以后变成一个左旋圆偏振光，求此 1/2 波片的ቤተ መጻሕፍቲ ባይዱ 斯矩阵表示。
（2）快轴沿 x 方向的 1/4 波片，其琼斯矩阵为 1 0 ，一线偏振光的偏振方向与 x 轴的 0 j
交角为 45 ，求此线偏振光经过上述 1/4 波片后的偏振态。若入射至上述 1/4 波片的光 是一左旋圆偏振光，结果又如何？ （3） 用快轴沿 y 轴的 1/4 波片和透光轴与 x 轴成-45 角的偏振器组合在一起, 就构成了 一个只让入射的右旋圆偏振光通过的装置，试证明这一结论。 解： （1）由讲义第一章中表 1-2，入射的右旋圆偏振光电矢量的列矩阵为 E i =
2016高等光学第5次作业答案
解： （5.2 节）
解：D 与 E 之间的夹角等于 S 与 k 之间的夹角。推导参考 5.2.4 节
最后的结果为
解：
证明：参考 5.4.2 节 o 光折射满足折射定律
n o sin θ o = n1 sin θ1 (θ1为入射角) tan θ o = n1 / no sin θ1 1 − ( n1 / no sin θ1 )
因此有
1 1 1 J 11 = 2 J 21 2 j
1 0 J = 0 − 1
它是一个快轴沿 x 轴或 y 轴的 1 2 波片。
E tx 1 1 0 1 1 1 （2） = = 2 0 j 1 2 j E ty

丝，问其通过球面的共轭像在何处？当入射高度
h=10mm，实际光线的像方截距为多少？与高斯像面的距离
为多少？
解：
8、一球面镜半径 r=-100mm, 求 ＝ 0 ， -0.1 ， -0.2 ， -1 ，1 ， 5， 10，∝时的物距像距。
第 4 页 共 29 页
解：（ 1）
东北石油大学测控 09 级工程光学期末复习资料
解：
100mm，则所得像与物
6．希望得到一个对无限远成像的长焦距物镜，焦距 系统最后一面到像平面的距离 （工作距） 为 并画出光路图。
解：
=1200mm，由物镜顶点到像面的距离 L=700 mm，由 ，按最简单结构的薄透镜系统考虑， 求系统结构，
7．一短焦距物镜，已知其焦距为 系统结构。
35 mm，筒长 L=65 mm，工作距 , 按最简单结构的薄透镜系统考虑，求
3．一光学系统由一透镜和平面镜组成，如图
3-29 所示，平面镜 MM与透镜光轴垂直交于 D 点，透镜前方
离平面镜 600 mm有一物体 AB，经透镜和平面镜后，所成虚像
至平面镜的距离为 150 mm，且像高为
物高的一半，试分析透镜焦距的正负，确定透镜的位置和焦距，并画出光路图。
解：平面镜成 β =1 的像，且分别在镜子两侧，物像虚实相反 级工程光学期末复习资料
第六章习题
1．如果一个光学系统的初级子午彗差等于焦宽（），则
应等于多少？
解：
2．如果一个光学系统的初级球差等于焦深
（），则
应为多少？ 解：
3． 设计一双胶合消色差望远物镜，
和火石玻璃 F2（
，
面的曲率半径。
解：
，采用冕牌玻璃 K9 （
解：设一个气泡在中心处，另一个在第二面和中心之间。

e ikr ~ ~ E P C E Q K d r （1）c 没有具体形式。
（2） K ( )
的出现没有理论依据。
既然 d是次波源,发出球面波, 以
d
为中心的 =1 因 该 成
任意方向上波动的性质是相同的.亦即, K ( )
立,但实验证明
K ( ) 1,这就需要找到它的具体形式。
e ikr e ikr ~ ~ ~ E P C E Q K d C E Q K d 1 2 r r ~ ~ ~ E P E1 P E 2 P
互补屏单独产生的衍射场复振幅之和，等于没有屏时的复
振幅。
在复振幅为0的点，互补屏分别产生的场位相差为，强度

e
ikz1
e
ik 2 2 x y 2z
i z



E , e
ik 2 2 2z
e
ik 2 x1 2 y 2 z1
d d
衍射图：
x, y 2 E x, y E * x, y L x, y E
涉影响显著。
1 1 cos ~ E P ir 2


~ E Q e ikr d
三、巴俾涅(Babinet)原理 互补屏原理： 1、开圆孔的无穷大不透明屏； 2、大小与圆孔相同的不透明屏； ~ ~ E1 ( P ) E 2 ( P ) 互补屏单独放置时p点的复振幅。 ~ E ( P ) 没有屏时，p点的复振幅。
§5-2 基尔霍夫衍射理论
一、亥姆霍兹-基尔霍夫积分定理： 2~ 2~ Ek E 0 光波电磁场复振幅： 标量场的衍射理论：

第五章 部分相干光理论5.1 证明解析信号的实部u 和虚部u 之间互为希尔伯特变换，即它们之间有下面的关系()t u t r ()()t i ()()⎰∞∞--=ξξξπd )(P.V.1)()()(t u t u r i ， ⎰∞∞---=ξξξπd )(.P.V 1)()()(tu t u i r证明：（1）由(5-10)式，解析函数的实部()()0()2Re ()exp(2)d r r u t j t νπνν∞⎡=-⎢⎣⎦⎰U ⎤⎥t （5.1-11）而，比较以上两式，可见有关系式)](Re[)()(t t u r u = （5.1-13）⎰∞-=0)(d )2exp()(2)(νπννt j t r U u 上式可表示为 （5.1-18）⎰∞∞--+=νπνννd )2exp()()sgn 1()()(t j t r U u 又因为 ()()exp(2)d t j νπνν∞-∞=-⎰u U所以有 ()()(1sgn )()r νν=+U νU )r （5.1-19）对上式两边取傅里叶逆变换11()1()()11((){()}{()}{(sgn )()}(){sgn )}{()}r r r t u t ννννν-----==+=+*u U U U U F F F F F ν上式中 1{sgn }jtνπ-=-F 再利用卷积定义⎰⎰∞∞---=*=*ηξηξηξd d ),(),(y x f g f g g f 令 t j f π-= ， )()(t j t f -=-ξπξ ， ， )()(t u g r =)()()(ξξr u g =所以 ⎰∞∞--+=ξξξπd )(..)()()()(t u V P jt ut r r u （5.1-22）可见 ⎰∞∞--=ξξξπd )(..1)()()(t u V P t ur i（2）参考教材中（5.1-10）式的推导过程，对于解析函数的虚部有下式成立（P5.1-1）⎥⎥⎦⎤⎢⎢⎣⎡-=⎰∞)()(d )2exp()(Re 2)(νπννt j t ui i U)](Re[)()(t j t u i u -= （P5.1-2）比较（P5.1-1）和（P5.1-2）式，得到⎰∞-=-0)(d )2exp()(2)(νπννt j t j i U u所以⎰∞-=0)(d )2exp()(2)(νπννt j j t i U u )()sgn 1()()(νννi j U U +=对上式两边取傅里叶逆变换得)}(){sgn )}({)}({)()(1)(11ννννi i j j t U U U u ---+==F F F)()}({}{sgn )()(11t ju j i i +*=--ννU F F )(d )(..1)()(t ju tu V P i i +--=⎰∞∞-ξξξπ所以 ⎰∞∞---=ξξξπd )(..1)()()(t u V P t ui r5.2 考察用宽带光作杨氏干涉实验(1) 证明观察屏上的入射光场可表示为⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=c r t P t c r t P t t Q 222111,d d ,d d ),(u K u K u 其中 iii i i i i i cr A s cr πθπθ2)(d 2)(k k K ≅=⎰⎰个针孔第 2,1=i 而为第个针孔的面积。

1. 试确定下面两列光波
E1=A0[excos（wt-kz）+eycos（wt-kz-π/2）]
E2=A0[exsin（wt-kz）+eysin（wt-kz-π/2）]
的偏振态。 解 ：E1 =A0[excos(wt-kz)+eycos(wt-kz-π/2)]
=A0[excos(wt-kz)+eysin(wt-kz)] 为左旋圆偏振光 E2 =A0[exsin(wt-kz)+eysin(wt-kz-π/2)]
=930nm =860nm =716.9nm =614.3nm =537.5nm =477.8nm =430nm =390nm
18. 把一块切成长方体的 KDP 晶体放在两个正交的偏振片之间组成一个普克尔斯效应的装
m 置。已知电光常数 γ=1.06*10-11 v ，寻常光在该晶体中的折射率,n o = 1.51，若入射光 0 的
2
这说明光路上任一点振动的 x 分量和 y 分量对时间有相同的依赖关系，它们都决定于
cos(t ) 因此它们是同相位的，这说明它们合成的是线偏振光。
14. 设一方解石波片沿平行光轴方向切出，其厚度为 0.0343mm，放在两个正交的尼科耳棱 镜间。平行光束经过第一尼科耳棱镜后，垂直地射到波片上，对于钠光（589.3nm）而言。
0.093
I2o
Io1 cos2 100
1 4
I1
cos2
100
②当入射光振动面与尼科耳主截面分居晶体主截面两侧时
I e1
I1
cos2
300
3 4
I1
Io2
I1 cos2
600
1 4
I1
I2e
I1e

光学教程（叶玉堂著）课后答案下载《光学教程》是清华大学出版社xx年出版图书，作者是叶玉堂，饶建珍，肖峻等。

以下是为大家的光学教程（叶玉堂著），仅供大家参考!点击此处下载???光学教程（叶玉堂著）课后答案???本教程以物理光学和应用光学为主体内容。

第1章到第3章为应用光学部分，介绍了几何光学基础知识和光在光学系统中的传播和成像特性，注意介绍了激光系统和红外系统。

第4～8章为物理光学部分，讨论了光在各向同性介质、各向异性介质中的传播规律，光的干涉、衍射、偏振特性及光与物质的相互作用，并结合介绍了DWDM、双光子吸收、Raman放大、光学孤子等相关领域的应用和进展;第9章则专门介绍航天光学遥感、自适应光学、红外与微光成像、瞬态光学、光学信息处理、微光学、单片光电集成等光学新技术。

第一篇应用光学第1章几何光学基础1.1几何光学的基本定律1.2物像基本概念1.3球面和球面系统1.4平面与平面系统1.5光学材料例题习题第2章理想光学系统2.1理想光学系统的基本特性、基点和基面 2.2理想光学系统的物像关系2.3理想光学系统的放大率2.4理想光学系统的组合2.5单透镜2.6光学系统中的光束限制2.7像差概述2.8波像差2.9矩阵运算在几何光学中的应用例题习题第3章光学仪器的基本原理3.1眼睛3.2放大镜3.3显微镜3.4望远镜3.5摄影系统3.6现代光学系统习题第二篇物理光学第4章光的电磁理论4.1电磁波谱电磁场基本方程4.2光波在各向同性介质中的传播 4.3光波的偏振特性4.4光波在介质界面上的反射和折射 4.5光波场的频率谱4.6球面光波和柱面光波例题习题第5章光的干涉5.1光干涉的条件5.2双光束干涉5.3多光束干涉5.4光学薄膜5.5典型的干涉仪及其应用5.6光的相干性例题习题第6章光的衍射6.1光的衍射现象6.2衍射的基本原理6.3夫琅禾费衍射6.4光学成像系统的衍射和分辨本领 6.5夫琅禾费多缝衍射6.6衍射光栅6.7菲涅耳衍射6.8全息术例题习题第7章晶体光学7.1介电张量7.2单色平面波在晶体中的传播7.3单轴晶体和双轴晶体的光学性质 7.4晶体光学性质的图形表示7.5平面波在晶体表面的反射和折射 7.6偏振器和补偿器7.7偏振光和偏振器件的琼斯矩阵 7.8偏振光的干涉7.9电光效应7.10声光效应7.11旋光现象7.12磁致旋光效应例题习题第8章光的吸收、色散和散射8.1光与物质相互作用的经典理论8.2光的吸收8.3光的色散8.4光的散射例题习题第9章现代光学技术简介9.1航天光学遥感9.2自适应光学9.3红外与微光成像9.4瞬态光学9.5光学信息处理9.6微光学9.7单片光电集成习题答案参考文献主题索引1.阳光大学生网课后答案下载合集2.光学教程叶玉堂饶建珍课后答案清华大学出版社3.光学教程第三版姚启钧著课后习题答案高等教育出版社4.光学教程郭永康鲍培谛课后答案四川大学出版社。

南开考研光学专业习题与解答第五章第五章光在介质界⾯上的反射和折射例题5.1 试计算如计算题5.1图所⽰的全反射棱镜（n=1.6），在实现光路转折过程中的光能损失百分之多少？假定介质是⽆吸收.解光经过棱镜过程中，三次发⽣反射，其中第⼆次全反射，⽆能量损失，仅在玻璃和空⽓界⾯上通过时有反射能量损失，每次因反射损失的百分数为%3.5)0.16.10.16.1()(221212=+-=+-=n n n n R ，故总的能量损失为%37.10053.0)053.01(053.0=?-+．5.2 由于⼀般光学玻璃在红外线波段不透光，所以在此波段要⽤锗板（n=4）作为红外线仪器的窗⼝。

试问光经过由锗板作的窗⽚时，光能损失多少？解光在锗板表⾯的能流反射率为36.0).10.40.10.4().10.1(22=--=--=n n R ，两次总能流的反射损失为%5959.036.0)36.01(36.0==-+．5.3 ⼀复合物镜由两个透镜组成，其中⼀个的折射率52.11=n ，另⼀个的折射率60.12=n ，将这两个透镜⽤54.10=n 的树胶粘在⼀起．设光在透镜上的⼊射⾓都很⼩，试求光在透过此物镜时由于反射⽽造成的损失．将此损失与两透镜不粘在⼀起⽽使其间留⼀空⽓薄隙时的损失相⽐较．解（１）⽤54.1=n 的加拿⼤树胶粘合时，共有４次反射损失，各次能流反射率为 %26.4)152.1152.1(21=+-=R ，522103.4)52.154.152.154.1(-?=+-=R ，423106.3)54.160.154.160.1(-?=+-=R ，%33.5).160.10.160.1(24=+-=R ．总的透过能流为%64.90)1)(1)(1)(1(4321=----R R R R ．n 计算题5.1图（２）未⽤树胶粘合时，可求出%26.421==R R ，%33.543==R R ，总能流透过率为82.2％.5.4 如计算题5.5图所⽰，已知⼀束⾃然光光⼊射到 3/4=n 的⽔⾯上时，反射光是完全偏振的．⼀块折射率0n 2/3=的平⾯玻璃浸没在⽔⾯下，欲使玻璃表⾯的反射光p 也是完全偏振的，问玻璃表⾯与⽔平⾯的夹⾓θ应该是多少？解如计算题5.４解图所⽰，光束⼊射到⽔⾯上Ａ点，反射光是完全偏振光，⼊射⾓必然是布儒斯特⾓．015333.1==-tg i p ，折射⾓为0002375390=-=i ．⼜因光线p 是线偏振光，所以在⽔中玻璃表⾯的Ｂ点，光线的⼊射⾓也为布儒斯特⾓，14.48)4323(=?i p ．由图中的⼏何关系可计算得玻璃表⾯与⽔⾯的夹⾓004.11)4.4890(3790180=----=θ5.5 已知红宝⽯的折射率为1.76，线偏振态的激光通过红宝⽯棒，光束在棒内沿棒轴线⽅向传播,欲使光在棒的端⾯上没有反射损失．试问光束的⼊射⾓i 应为多⼤？棒端⾯对棒轴倾⾓应取何值？⼊射光的振动⽅向如何？解欲使⼊射线偏振光在红宝⽯棒的端⾯⽆反射损失，光线应以布儒斯特⾓⼊射，且线偏振光的振动⾯要平⾏与⼊射⾯．因此0 11.6076.1==-tg i ，由⼏何关系，棒端⾯与棒轴线的夹⾓应为09.291.6090=-．5.6 已知5.11=n ，0.12=n ，015.54=i ，⼊射的是8.6320=λ纳⽶的氦氖激光，计算题5.5图计算题 5.４图计算题5.４解图试求穿透深度．解氦氖激光由光密媒质进⼊光疏媒质，临界⾓0142)5.1/1(sin ==-c i ，⼊射⾓⼤于临界⾓，发⽣全内反射．穿透深度为（毫⽶）．322612010173.242sin 5.54sin 12108.632sinsin12--?=-?=-=ππλci i d问答题5.1 试举⼀透射光强⼤于⼊射光强的具体例⼦．答：当内反射时，折射光束横截⾯⽐⼊射光束横截⾯⼩，因此在透射光能流⼩于⼊射光流时，可能有透射光光强⼤于⼊射光光强的情况．例如，5.11=n ，0.12=n ，0130=i ，026.48=i ，代⼊菲涅⽿公式，得325.1=s t ，398.1=p t ，171.1=s T ，303.1=p T ．光强透射⽐⼤于１．5.2 在平静⽔⾯湖边洗脸时，我们很难看到⾃⼰对⽔⾯的反射像．但是站在平静⽔⾯的湖边看湖对岸的⼭、树以及建筑物的⽔中倒影却⼗分明亮，试解释之．答：因为在湖边洗脸时，观察的是垂直⼊射、外反射的光，在空⽓与⽔界⾯上，由菲⽿公式可知，这种情况下反射光能量很⼩，因此看不到⾃⼰的像．⽽观察湖对岸的⼭、树以及建筑物，是观察外反射、掠⼊射的光，此时光能量⼏乎全部反射到⼈眼中来，看到的景物清晰明亮．5.3 如何测量⼀块形状不规则的，外表⾯⽑糙的固体光学介质对于某种准单⾊可见光的折射率？答：将待测光学介质放⼊某种折射率可调的液体中，⽤单⾊光光源照明.若光学介质的折射率与透明液体的折率相同，则界⾯没有光能量反射，因此我们⽆法看到介质的存在．设法调透明液体的折射率，直⾄界⾯消失为⽌，⽤Ａbbe 折射仪测得液体的折射率，即为固体光学介质的折射率．假如⽤⽩光照射会看到什么情景呢？⾸先要说明的是世界上不存在对可见光有相同⾊散曲线（即折射率n 随波长λ变化的曲线）的不同介质，所以固体和液体对某⼀波长可以有相同的折射率，但对其他波长却不可能再有相同的折射率．这样对⽩光中的其他波长能流就会有些反射，使⼈们见到与某⼀波长互补颜⾊的固体块．5.4 光束由空⽓射向玻璃，什么情况下光能全部透射？什么情况下光能全部反射？答：当⼊射光束是线偏振光，振动⾯与⼊射⾯平⾏，并且以布儒斯特⾓⼊射时，光能全部透过；当⼊射光以接近900的⾓⼊射，即掠⼊射时，光能量全部反射． 5.5 在实验室⾥，偏振⽚的透振⽅向常常没有标出，⽤什么简单⽅法可以将它鉴别出来？答：在实验室中，选择⼀光亮的桌⼦⾯（或玻璃板），拿来偏振⽚放在眼前，迎着⼊射光观看桌⼦表⾯的反射光，并不断地改变反射⾓，同时不停地旋转偏振⽚，直⾄看到＂两明两零＂（即旋转偏振⽚⼀周，看到两次最⼤光强，两次零光强）的现象为⽌．此时，偏振⽚的透振⽅向恰于⼊射⾯垂直，此时光线的⼊射⾓恰为布儒斯特⾓．5.6 ⼊射的线偏光通过外反射⼊能否变为椭圆偏振光？通过内反射能不能？通过全反射能不能？答：⼊射的线偏振光通过外反射及⼩于临界⾓内反射时，相移⾮零即π，故反射光不会是椭圆偏振光．但通过全内反射则可以成为椭圆偏振光．5.7 ⼊射的椭圆偏振光通过外反射能否变为线偏振光？通过内反射能不能？通过全反射能不能？答：以布儒斯特⾓⼊射的椭圆偏振光外反射和内反射都可以得到振动⾯垂直于⼊射⾯的线偏振光．在⼤于临界⾓⼊射的全反射情况下，若（s pδδ-）值恰能将⼊射椭圆偏振光已有的δ补偿为零或π，则反射的是线偏振光． 5.8 ⼊射的线偏振光通过单次全内反射后能否成为圆偏振光？答：不能．因为要成为圆偏振光应有两个条件，⼀是分解的s 分量和p 分量振幅相等，这容易作到．第⼆个条件是分解的s 分量和p 分量应有π/2的相位差,这在单次全内反射的情况下，不能实现．5.9 虚波⽮的物理意义是什么？振幅反射⽐为复数代表什么物理意义？答：虚透射波⽮说明光疏介质中有倏逝波存在．r 为复数说明反射光振动与⼊射光振动不是同时达到最⼤值．5.10 光强反射率R=(R s + R p )/2公式对于怎样偏振态的⼊射光才能成⽴．答：当⼊射光的s 分量和p 分量相等时，例如⾃然光，圆偏振光，总的光强反射率才有)(21])2()2[(120200p s p s R R r I r I I R +=+=．5.11 ⼀束右旋圆偏振光由空⽓中垂直⼊射到玻璃上，试分析反射光的偏振态．答：如问答题5.11图(a)建⽴坐标系．由于观察者对于⼊射光是顺着光传播⽅向＂看＂，所以⼊射右旋圆偏振光在所建⽴的xy 平⾯内（图b ），电⽮量的端点是随时间左旋的．光振动⽅程可以表⽰为)2sin(πω+=t A E x ，)sin(t A E y ω=．根据菲涅⽿公式，光在空⽓玻璃界⾯上反射时应分解为s 分量和p 分量，在本题中就是振动⾯沿x ⽅向和y ⽅向的线偏振光．这两个⽅向的振动在垂直⼊射外反射情况下，⼊射光相对于反射光有π的相位变化，且两线偏振光振幅等⽐例地减⼩，因此反射光光振动⽅程为)2sin(ππω++'=t A E x ，)sin(πω+'=t A E y．这显然是⼀左旋圆偏振光的⽅程．反射光仍然是圆偏振光，不过右旋变为左旋（图c ），同时能量变⼩．因此，对于观察者来说，⼀个电⽮量向左旋转⼊射于｛｛玻璃表⾯的圆偏振光，反射光电⽮量仍然向左旋转着反射回来．就是说，右旋填空题5.1 折射率为4/3的⽔和折射率为3/2的玻璃界⾯,⽔中的偏化⾓为____，玻璃中的偏化⾓⽚偏化⾓为______．5.2 ⾃然光仅在______的情况下，反射的光才是⾃然光．5.3 ⼀束光由空⽓中以600的⼊射⾓进⼊各向同性透明介质，此时光光能量没有反射损失．这种介质的折射率为，⼊射光的偏振态为___________．5.4 线偏振光通过外反射______（能，不能）变为椭圆偏振光；圆偏振光通过外反射__ __（能，不能）变为线偏振光．5.5 ⼀束⾃然光以布儒斯特⾓通过折射率为1.5的玻璃⽚堆，当玻璃⽚的数⽬为___________时，透射光的偏振度为90%(忽略玻璃的吸收).5.6 布儒斯特定律提供了⼀种测定不透明电解质折射率的⽅法，今测得某⼀电解质的起偏振⾓为580，则这种电解质的折射率为_ _ ___.选择题：5.1 指出下列各种说法的正误：（1）偏化⾓i p 可能⽐临界⾓c i ⼤，（2）同⼀个介质中偏化⾓i p 总⽐临界⾓i c ⼩，（3）临界⾓只能在光密介质中存在，偏化⾓只能在光疏介质中存在，（4）只要存在两种介质的界⾯，则两种介质都有⾃⼰的偏化⾓值，且⼆者之和等于900. 5.2 下列各种说法正确的是：（1）除全内反射情况外，线偏振光单次经介质表⾯反射，永远得不到椭圆偏振光，（2）光波在不同介质界⾯上反射可能存在光能量毫不反射的情况，（3）光波在不同介质界⾯上反射，有可能存在⼊射能流全部反射的情况，（4）对于⼊射⾓固定的外反射情况下，两种介质折射率差别越⼤，则界⾯反射出更多的光能量．5.3 光在两各向同性介质界⾯上反射，下⾯哪⼀种说法是对的：（1）⾃然光⼊射，能得到部分偏振光的反射，（2）⾃然光⼊射，得不到反射的⾃然光，（3）⾃然光⼊射，不可能反射出线偏振光，（a ）（b ）（c ）反射光在xy 平⾯内也左旋问答题5.12图（4）线偏振光⼊射，反射出的不可能是⾃然光．5.4下列各种说法，哪种是对的？（1）光波从空⽓⼊射到透明介质表⾯，透⼊介质的能流总⽐返回空⽓的能流要强，（2）外反射和内反射情况下，对于⾃然光来说，反射的S能流⼀般总⽐P能流⼤，（3）在外反射情况下，随着⼊射⾓的增⼤，反射能流也越来越⼤，（4）光波⼊射到透明介质截⾯上，⼊射光能流与反射光、透射光能流符合能量守恒定律．。

工程光学第二版习题答案（李湘宁-贾志宏）汇总重点第一章习题1、已知真空中的光速c＝3m/，求光在水（n=1.333）、冕牌玻璃（n=1.51）、火石玻璃（n=1.65）、加拿大树胶（n=1.526）、金刚石（n=2.417）等介质中的光速。

解：则当光在水中，n=1.333时，v=2.25m/,当光在冕牌玻璃中，n=1.51时，v=1.99m/,当光在火石玻璃中，n＝1.65时，v=1.82m/，当光在加拿大树胶中，n=1.526时，v=1.97m/，当光在金刚石中，n=2.417时，v=1.24m/。

2、一物体经针孔相机在屏上成一60mm大小的像，若将屏拉远50mm，则像的大小变为70mm,求屏到针孔的初始距离。

解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为某，则可以根据三角形相似得出：所以某=300mm即屏到针孔的初始距离为300mm。

3、一厚度为200mm的平行平板玻璃（设n=1.5），下面放一直径为1mm的金属片。

若在玻璃板上盖一圆形纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片最小直径应为多少？解：令纸片最小半径为某,则根据全反射原理，光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射，而这里正是由于这个原因导致在玻璃板上方看不到金属片。

而全反射临界角求取方法为：其中n2=1,n1=1.5,同时根据几何关系，利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为：(2)联立（1）式和（2）式可以求出纸片最小直径某=179.385mm，所以纸片最小直径为358.77mm。

4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0，求光纤的数值孔径（即n0inI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角）。

解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律则有：n0inI1=n2inI2(1)而当光束由光纤芯入射到包层的时候满足全反射，使得光束可以在光纤内传播，则有：(2)由（1）式和（2）式联立得到n0inI1.5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上，求其会聚点的位置。

第五章 光的干涉5－1 波长为589.3nm 的钠光照射在一双缝上，在距双缝200cm 的观察屏上测量20个条纹共宽3cm ，试计算双缝之间的距离。

解：由题意，条纹间距为：cm e 15.0203==∴双缝间距为：m e D d 391079.015.0103.589200--⨯≈⨯⨯==λ5－2 在杨氏干涉实验中，两小孔的距离为1.5mm ，观察屏离小孔的垂直距离为1m ，若所用光源发出波长1λ＝650nm 和2λ＝532nm 的两种光波，试求两光波分别形成的条纹间距以及两组条纹的第8级亮纹之间的距离。

解：对于1λ＝650nm 的光波，条纹间距为：m d D e 339111043.0105.1106501---⨯≈⨯⨯⨯==λ 对于2λ＝532nm 的光波，条纹间距为：m d D e 339221035.0105.1105321---⨯≈⨯⨯⨯==λ ∴两组条纹的第8级条纹之间的距离为： m e e x 3211064.0)(8-⨯=-=∆5－3 一个长40mm 的充以空气的气室置于杨氏装置中的一个小孔前，在观察屏上观察到稳定的干涉条纹系，继后抽去气室中的空气，注入某种气体，发现条纹系移动了30个条纹。

已知照射光波波长为656.28nm ，空气折射率为1.000276，试求注入气体的折射率n g 。

解：气室充入空气和充气体前后，光程的变化为： D n g )000276.1(-=∆δ 而这一光程变化对应于30个波长： λδ30=∆∴λ30)1(=-D n g000768.1000276.110401028.6563039=+⨯⨯⨯=--g n5－4 在菲涅耳双面镜干涉实验中，光波长为600nm ，光源和观察屏到双面镜交线的距离分别为0.6m 和1.8m ，双面镜夹角为10－3rad ，求：（1）观察屏上的条纹间距；（2）屏上最多能看到多少亮条纹？解：如图所示，S 1S 2的距离为：αsin 2l d =∴条纹间距为：αλλsin 2)(l q l d D e +== ∵α角很小∴mmm l q l e 2.1102.1106.0210600)8.16.0(2)(339=⨯=⨯⨯⨯⨯+=+≈---αλ屏上能产生条纹的范围，如图阴影所示mmmq qtg y 6.3108.12223=⨯⨯=≈=-αα∴最多能看到的亮条纹数为：32.16.3===e y n5－5 在如图所示的洛埃镜实验中，光源S 1到观察屏的距离为2m ，光源到洛埃镜面的垂直距离为2.5mm 。

乱
是各个振动
的无规混杂
光的振动方向应始终与光的传播方向垂直, 在垂直于光 的传播方向的平面内, 光矢量具有不同的振动状态，叫 做光波的偏振态. 光的偏振现象
光波按偏振态来划分，可分为三大类： (1)自然光； (2)完全偏振光； 线偏振光，圆偏振光，椭圆偏振光 (3)部分偏振光。
2 自然光与偏振光
当 i1 i2 900 时, 分母无穷大,rp 0,
因此任何偏振态的光,若以满足 i1 i2 900
的入射角入射时,反射光中只有 s 分量,没有p分量, p 分量全部透射. 此时的入射角称为布布儒儒斯斯特特角角(也叫偏
i . 化角),记为 p
由费涅耳公式知当
n1
ip
π/2
ip
i2
2
n2
天然晶体中，电气石（六角 形片状）具有最强的二向色 性
自然光 入射
线偏振 光出射
E∥光轴：
吸收很少 通过较多
E⊥光轴： 吸收较多 通过很少
1mm厚的电气石晶体可把垂直于光轴振动的光矢量全部吸收！
二、人造偏振片：
透明聚乙烯醇片，强烈吸收某一方向上的光振动，透射光成 为线偏振光。
透振方向：允许通过光矢量振动的方向。 透振方向
横波
纵波 横波----振动方向垂直于传播方向；如水波。有偏振性 纵波----振动方向平行于传播方向；如声波。无偏振性
透振方向 腰横别扁担进不了城门！
Maxwell电磁波理论和实验表明，光波是横波。
电 磁 波 的 振 动 方 式 光除了有干涉和衍射现象外还有偏振现象
在干涉和衍射里，光波的振动是以标量形式来处理的， 即未考虑振动的方向，只研究光振动的大小和强度分布。而研究光的偏振现象， 光波必须用矢量来描述。

I0 I1 = 2
2
I0 2 I 2 = I1 cos θ = cos θ 2
2
I0 I = I 2 cos ( − θ ) = cos 2 θ sin 2 θ 2 2 I0 I0 2 = sin 2θ = (1 − cos 4θ ) 8 16
π
θ = ωt
I0 I = (1 − cos 4ωt ) 16
5.10 （1）线偏振光垂直入射到一个表面和光轴 ） 平行的波片上。透射后， 平行的波片上。透射后，原来在波片中的寻常光及 非常光产生了π的位相差 问波片的厚度为多少？ 的位相差。 非常光产生了 的位相差。问波片的厚度为多少？已 ；（2） 知： ne = 1.5442, no = 1.5533 λ = 500nm ）问这块波 ；（ 片应怎样放置才能使透射出来的光是线偏振光。 片应怎样放置才能使透射出来的光是线偏振光。而 它的振动面和入射光的振动面成90 它的振动面和入射光的振动面成 0角。 解：（1）波片的厚度应为 ）
A sin (i − i ： =− A sin (i + i
' s1 1 s1 1
2
2
) )
sin (60 − 30 =− sin (60 + 30
r 0
) )
= −0.5
∴ A = −0.5 × 0.5 A
' s1
I 故： = 6.25 I
i
5.6 如图所示，一块折射率n=1.50的平面玻璃浸 如图所示，一块折射率 的平面玻璃浸 水中， 在n =1.33水中，已知一束光入射到水面上时反射光 水中 是完全偏振光， 是完全偏振光，若要使玻璃表面的反射光也是完全 偏振光，则玻璃表面与水平面的夹角 应是多大? 偏振光，则玻璃表面与水平面的夹角θ 应是多大

高等光学第4-5章习题答案第四章标量衍射理论基础4.1证明（4-21）式所示的索末菲辐射条件成立。

证明：球面2S是中心位于1S面上的发散球面波的波面，假定2S面上的光场分布表示为rjkr)exp(=U式中r表示产生发散球面波的点光源到球面2S上任意一点的距离。

1exp()cos()cos(,)r jkrjkn r n r r r∂∂∂∂===−∂∂∂∂U U Un,r n r当∞→R时，有∞→r，所以这时有1),cos(≈rn2)exp()exp(1rjkrjkrjkrrjkjkn−≅−−=−∂∂UUU当∞→R时，上式分母中的r可用R来代替，于是2exp()1lim lim lim(cos sin)R R RjkrR jk R kr j krn R R→∞→∞→∞∂−=−=−+∂UUlim0jkrReR→∞=−=4.2 参考图4-8，考虑在瑞利—索末菲理论中采用下式所表示的格林函数，即010110101exp()exp()()jkr jkrPr r+=+G(1)证明+G的法线方向的导数在孔径平面上为零。

(2)利用这个格林函数，求出用孔径上的任意扰动来表示()pU的表达式，要得到这个结果必须用什么样的边界条件。

(3)利用(2)的结果，求出当孔径被从2P点发散的球面波照明时()pU的表达式证明: 下面是教材中图4-8（1）)(1P +G 由两项迭加而成，它们分别表示从互为镜像的点0P 和0~P 发出的两个初相位相同的单位振幅的球面波。

孔径平面1S 上任一点1P 的+G 值为010101011~)~exp()exp()(r r jk r jkr P +=+G （P4.2-1） 1()P +G 的法向导数为0101010101010101~)~exp(~1)~,cos()exp(1),cos(r r r r n r n G jk jk r jkr r jk n −+ −=∂∂+ （P4.2-2） 对于互为镜像点的0P 和0~P 来说，有)~,cos(),cos(0101r n r n −= 0101~r r = （P4.2-3）将以上关系式代入（P4.2-2）式，得到0n+∂=∂G （P4.2-4） （2）根据（4-22）式，观察点0P 的光扰动可以用整个平面1S 上的光扰动U 和它的法向导数来表示∫∫∂∂−∂∂=1d 41)(0S s n n P G U G U U π（P4.2-5） 由0101~r r =，得01011)exp(2)(r jkr P =+G （P4.2-6）将上式和（P4.2-4）式一同代入（P4.2-5）式，得到∫∫∫∫∂∂=∂∂=+11d )exp(21d 41)(01010S S s r jkr ns G n P U U U ππ（P4.2-7）为了将上式所表示的结果进一步简化，根据孔径Σ上的场去计算0P 点的复振幅分布)(0P U ，只需要规定如下两个边界条件：（a ）在孔径Σ上，场分布的法向导数n U ∂∂与不存在衍射屏时的值完全相同。