有价值的数学

《数学课程标准》提出了：“人人学有价值的数学，人人都能获得必需的数学，不同的人在数学上得到不同的发展”等新课程理念。

但在现实的课堂教学中往往还是“一刀切”的现象，对学生提出共同的要求，采取相同的手段，致使学生疲于应付、生吞活剥，从而导致教学效果两级分化，出现差生“晕车”、优生“陪读”等不理想的现象。

这种忽略学生差异的教学思想与新课程理念是格格不入的。

在小学数学教学中，努力做到，让“学困生吃得了”、“中等生吃得好”、“优生吃得饱”。

由此可见学习新课程标准、改变教育观念的重要性。

我有以下几点体会：一、教学目标分层要求。

在制订教学目标时，教师既要重视教学中的统一标准，突出教学要求的一致性，又要注意学生的个性差异，突出教学目标的层次性，做到统一性与层次性相结合。

一方面根据课程标准的学习目标和班级学生的实际情况，着眼面向全体学生进行分类设计，使全体学生达到一定的要求，就是“下要保底”的教学目标。

另一方面要考虑到“上不封顶”的目的，在目标设计时要有弹性，提出的目标要有层次性，以保证不同学生求知需要能得到满足。

二、教学内容分层渐进。

在设计教学内容时，要考虑到层次性，由浅入深、分层渐进，根据学生的实际学习起点，采取因人而异的措施。

起点较低的同学教学指导要有所倾斜，设计问题采取“小步子、慢速度”的教育原则；对优生设计的教学问题要灵活一些，而且要有一定的难度，同时鼓励学生自己提出问题，通过讨论解决问题。

在练习题的设计上更要有一定的梯度，由基本题到变式题再到发展题，还要设计一些机动题，根据课堂上的具体情况来取舍。

主要是应注意分层提问和分层练习。

三、教学形式分层实施。

在教学过程中，教师在组织形式上要改变传统的固定方式，根据教学的实际需要临时进行分层组织。

当需要全班进行交流时，就采取“全班式”的组织形式；当需要进行小组合作学习时，就采取“小组式”的组织形式；当教学中根据需要进行重新组织时，就采取“自由式”的组织形式，让同一层次或同一兴趣的学生组合到一起去。

生活当中有价值的数学问题1.为什么瓦屋是三角形呢2.桌子问题：一张方桌，砍掉一个角还剩下几个角；3.切豆腐问题：一块豆腐切三刀，最多能切成几块；4.切西瓜问题：一个西瓜用三刀切七份，吃完剩下八块皮，如何做到；5.竹竿问题：5米长的竹竿能不能通过一米高的门；6.纸盒问题：边长一米的方盒子能不能容下一米五的木棍；7.时钟问题：经过12小时，时钟和分针重复多少次；8.折纸问题：一张1毫米厚的纸，对折1000次，厚度有多高；9.烙饼问题：烙一张饼用两分钟，烙正、反面各用一分钟，锅里最多同时放两张饼，那么烙三张饼最少用几分钟。

10.早在封建社会的中国历法把一昼夜分成一百刻再分十二时，每时八刻三十三秒三十三微三十三纤，永无尽数。

而西方国家则把九十六刻分成十二时则无余数，方便计算。

11.旧中国的瓦房，房顶从正中央向房子前后两侧向下倾斜切都是呈现三角形状，三角形具有稳定性被运用在房屋的建设中；现在各种道路建筑桥梁等的建设更是离不开数学。

12.市内里的红绿灯，每隔多久红灯亮一次？一辆车在这段路上行驶时速多少，撞上红灯亮的次数才是最少？最节省时间？一层楼有多高？10米是多长？比你高的人是谁？比你矮的人是谁？和你差不多的是谁？古今中外出现的很多关于数学与生活的故事，数学涉及的领域实在是太广了。

13.在经济学的应用：银行利率、股票的上涨与下跌、衣服打折等等。

14.银行存款分：整存整取、零存整取、定期存款、活期、国债这些存款形式各种各样，利率也有大有小，平时我们是这样计算利率的：本金×利率×时间=所得利息，然后还要从利息里扣除20%来上税（除国债外）之后剩下的80%的利息就是你自己应得的利息了。

15.工程师使用比例尺，为了让人们更好的了解这件东西；商农使用的四则计算，是为了更简单、准确的计算出该商品价值；制作各类统计表，是为了更好的统计资料，使人一看一目了然；使用百分数，是为了更好的计算出商品打折后的价钱及折扣率；16.计算容积或体积而使用去尾法，是为了确保无误的让物品存放而不溢出；同一类单位换算，是为了方便我们的计算；使用代数代表运算定律和计算公式,是为了更方便地为研究和解决问题。

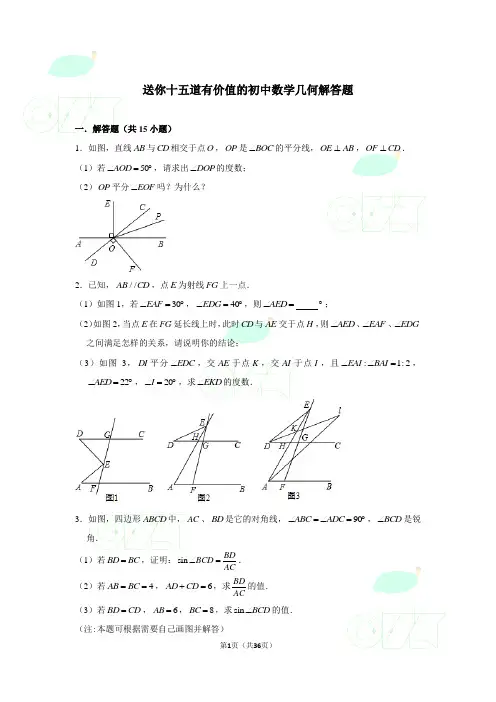
送你十五道有价值的初中数学几何解答题一．解答题（共15小题）1．如图，直线AB与CD相交于点O，OP是BOC∠的平分线，OE AB⊥，OF CD⊥．（1）若50AOD∠=︒，请求出DOP∠的度数；（2）OP平分EOF∠吗？为什么？2．已知，//AB CD，点E为射线FG上一点．（1）如图1，若30EAF∠=︒，40EDG∠=︒，则AED∠=︒；（2）如图2，当点E在FG延长线上时，此时CD与AE交于点H，则AED∠、EAF∠、EDG∠之间满足怎样的关系，请说明你的结论；（3）如图3，DI平分EDC∠，交AE于点K，交AI于点I，且:1:2EAI BAI∠∠=，22AED∠=︒，20I∠=︒，求EKD∠的度数．3．如图，四边形ABCD中，AC、BD是它的对角线，90ABC ADC∠=∠=︒，BCD∠是锐角．（1）若BD BC=，证明：sinBD BCDAC∠=．（2）若4AB BC==，6AD CD+=，求BDAC的值．（3）若BD CD=，6AB=，8BC=，求sin BCD∠的值．（注:本题可根据需要自己画图并解答）4．如图，90BAD CAE ∠=∠=︒，AB AD =，AE AC =，AF CB ⊥，垂足为F ． （1）求证：ABC ADE ∆≅∆； （2）求FAE ∠的度数； （3）求证：2CD BF DE =+．5．如图，已知正方形ABCD 的边长为2，连接AC 、BD 交于点O ，CE 平分ACD ∠交BD 于点E ， （1）求DE 的长；（2）过点EF 作EF CE ⊥，交AB 于点F ，求BF 的长； （3）过点E 作EG CE ⊥，交CD 于点G ，求DG 的长．6．（1）一个多边形每个内角都相等，且每个外角等于一个内角的23，求这个多边形的边数；（2）两个多边形边数之比为3:4，内角和之比为2:3，求这两个多边形的边数．7．如图所示，在直角坐标系中，第一次将OAB ∆变换成△11OA B 第二次将△11OA B 变换成△22OA B ，第三次将△22OA B 变换成△33OA B ，已知(1,3)A ，1(2,3)A ，2(4,3)A ，3(8,3)A ，(2,0)B ，1(4,0)B ，2(8,0)B ，3(16,0)B ．（1）求OAB ∆的面积；（2）写出△44OA B 的各个顶点的坐标；（3）按此图形变化规律，你能写出△n n OA B 的面积与OAB ∆的面积的大小关系吗？ 8．如图，在ABC ∆中，AB AC =，以AB 为直径作圆O ，分别交BC 于点D ，交CA 的延长线于点E ，过点D 作DH AC ⊥于点H ，连接DE 交线段OA 于点F ． （1）求证：DH 是圆O 的切线； （2）若32FD EF =，求证；A 为EH 的中点． （3）若1EA EF ==，求圆O 的半径．9．如图，点O 为Rt ABC ∆斜边AB 上的一点，以OA 为半径的O e 与BC 切于点D ，与AC 交于点E ，连接AD ． （1）求证：AD 平分BAC ∠；（2）若60BAC ∠=︒，2OA =，求阴影部分的面积（结果保留)π．10．如图，AH 是圆O 的直径，AE 平分FAH ∠，交O e 于点E ，过点E 的直线FG AF ⊥，垂足为F，B为直径OH上一点，点E、F分别在矩形ABCD的边BC和CD上．（1）求证：直线FG是Oe的切线；（2）若8e的直径．EB=，求OAD=，511．如图，AB是圆O的弦，D为半径OA的中点，过D作CD OA⊥交弦AB于点E，交圆=．O于点F，且CE CB（1）求证：BC是Oe的切线；（2）连接AF，BF，求ABF∠的度数；（3）如果3g的值．OA=，求AE AB12．如图，以ABC∆的BC边上一点O为圆心，经过A、C两点且与BC边交于点E，点D 为CE的下半弧的中点，连接AD交线段EO于点F，若AB BF=．（1）求CAD∠的度数；（2）求证：AB是Oe的切线；（3）若8DF=，求线段AB的长．CF=，21013．已知AB是半圆O的直径，M，N是半圆不与A，B重合的两点，且点N在弧BM 上．（1）如图1，6MA =，8MB =，60NOB ∠=︒，求NB 的长；（2）如图2，过点M 作MC AB ⊥于点C ，点P 是MN 的中点，连接MB 、NA 、PC ，试探究MCP ∠、NAB ∠、MBA ∠之间的数量关系，并证明．14．如图，AB 是圆O 的直径，O 为圆心，AD 、BD 是半圆的弦，且PDA PBD ∠=∠．延长PD 交圆的切线BE 于点E（1）判断直线PD 是否为O e 的切线，并说明理由； （2）如果60BED ∠=︒，3PD =，求PA 的长．（3）将线段PD 以直线AD 为对称轴作对称线段DF ，点F 正好在圆O 上，如图2，求证：四边形DFBE 为菱形．15．如图，AB 是O e 的直径，点C 是BA 延长线上一点，CD 切O e 于点D ，1CA =，CD 是O e 3 ． （1） 求O e 的半径R ；（2） 如图 1 ，弦//DE CB ，动点Q 从A 出发沿直径AB 向B 运动的过程中， 图中阴影部分的面积是否发生变化， 若发生变化， 请你说明理由；若不发生变化， 请你求出阴影部分的面积；（3） 如图 2 ，动点M 从A 出发， 在O e 上按逆时针方向向B 运动 ． 连接DM ，过D作DM的垂线，与MB的延长线交于点N，当点M运动到什么位置时，DN取到最大值？求此时动点M所经过的弧长．参考答案与试题解析一．解答题（共15小题）1．如图，直线AB 与CD 相交于点O ，OP 是BOC ∠的平分线，OE AB ⊥，OF CD ⊥． （1）若50AOD ∠=︒，请求出DOP ∠的度数； （2）OP 平分EOF ∠吗？为什么？【思路】（1）根据对顶角相等、角平分线的性质求得1252COP BOC ∠=∠=︒；然后由平角的定义推知180COD ∠=︒，则DOP COD COP ∠=∠-∠； （2）根据垂直的定义、角平分线的定义求得EOP FOP ∠=∠． 【解析】（1）Q 直线AB 与CD 相交于点O ， 50BOC AOD ∴∠=∠=︒， OP Q 是BOC ∠的平分线，11502522COP BOC ∴∠=∠=⨯︒=︒，18025155DOP COD COP ∴∠=∠-∠=︒-︒=︒；（2）OP 平分EOF ∠，理由如下：OE AB ⊥Q ，OF CD ⊥， 90EOB COF ∴∠=∠=︒， OP Q 是BOC ∠的平分线， POC POB ∴∠=∠，EOB POB COF POC ∴∠-∠=∠-∠，即EOP FOP ∠=∠， OP ∴平分EOF ∠．【考点】本题考查了垂直的定义，对顶角、邻补角以及角平分线的定义．解题时一定要数形结合．2．已知，//AB CD ，点E 为射线FG 上一点．（1）如图1，若30EAF ∠=︒，40EDG ∠=︒，则AED ∠= 70 ︒；（2）如图2，当点E 在FG 延长线上时，此时CD 与AE 交于点H ，则AED ∠、EAF ∠、EDG ∠之间满足怎样的关系，请说明你的结论；（3）如图3，DI 平分EDC ∠，交AE 于点K ，交AI 于点I ，且:1:2EAI BAI ∠∠=，22AED ∠=︒，20I ∠=︒，求EKD ∠的度数．【思路】（1）延长DE 交AB 于H ，依据平行线的性质，可得40D AHE ∠=∠=︒，再根据AED ∠是AEH ∆的外角，即可得到304070AED A AHE ∠=∠+∠=︒+︒=︒；（2）依据//AB CD ，可得EAF EHC ∠=∠，再根据EHC ∠是DEH ∆的外角，即可得到EHG AED EDG ∠=∠+∠，即EAF AED EDG ∠=∠+∠；（3）设EAI α∠=，则3BAE α∠=，进而得出2EDK α∠=-︒，依据EHC EAF AED EDG ∠=∠=∠+∠，可得32224αα=︒+-︒，求得16EDK ∠=︒，即可得出EKD ∠的度数．【解析】（1）如图，延长DE 交AB 于H ， //AB CD Q ， 40D AHE ∴∠=∠=︒，AED ∠Q 是AEH ∆的外角，304070AED A AHE ∴∠=∠+∠=︒+︒=︒，故答案为：70；（2）EAF AED EDG ∠=∠+∠． 理由：//AB CD Q ， EAF EHC ∴∠=∠， EHC ∠Q 是DEH ∆的外角， EHG AED EDG ∴∠=∠+∠， EAF AED EDG ∴∠=∠+∠；（3）:1:2EAI BAI ∠∠=Q ，∴设EAI α∠=，则3BAE α∠=，22AED ∠=︒Q ，20I ∠=︒，DKE AKI ∠=∠，又180EDK DKE DEK ∠+∠+∠=︒Q ，180KAI KIA AKI ∠+∠+∠=︒， 2EDK α∴∠=-︒，DI Q 平分EDC ∠，224CDE EDK α∴∠=∠=-︒， //AB CD Q ，EHC EAF AED EDG ∴∠=∠=∠+∠，即32224αα=︒+-︒， 解得18α=︒， 16EDK ∴∠=︒，∴在DKE ∆中，1801622142EKD ∠=︒-︒-︒=︒．【考点】本题主要考查了平行线的性质，三角形外角性质以及三角形内角和定理的综合应用，解决问题的关键是作辅助线构造内错角，运用三角形外角性质进行计算求解．解题时注意：三角形的一个外角等于和它不相邻的两个内角的和．3．如图，四边形ABCD 中，AC 、BD 是它的对角线，90ABC ADC ∠=∠=︒，BCD ∠是锐角．（1）若BD BC =，证明：sin BDBCD AC∠=． （2）若4AB BC ==，6AD CD +=，求BDAC的值． （3）若BD CD =，6AB =，8BC =，求sin BCD ∠的值． （注:本题可根据需要自己画图并解答）【思路】（1）如图1中，过点B 作AD 的垂线BE 交DA 的延长线于点E ，只要证明BED ABC ∆∆∽，即可解决问题．（2）如图2中，过点B 作BF BD ⊥交DC 的延长线于F ．只要证明DAB CBF ∆≅∆，推出6DF AD CD =+=，求出BD 、AC 即可．（3）当BD CD =时，如图3中，过点B 作//MN DC ，过点C 作CN MN ⊥，垂足为NM 延长BA 交MN 于点N ，则四边形DCNM 是矩形，ABM BCN ∆∆∽，所以68AM MB AB BN CN BC ===，设6AM y =，8BN y =，6BM x =，8CN x =，通过BD DC =，列出方程求出x 、y 的关系，求出AB ，即可解决问题．【解析】（1）如图1中，过点B 作AD 的垂线BE 交DA 的延长线于点E ，90ABC ADC ∠=∠=︒Q ， 180ADC ABC ∴∠+∠=︒，∴四边形ABCD 四点共圆，BDE ACB ∴∠=∠，EAB BCD ∠=∠， 90BED ABC ∠=∠=︒Q ， BED ABC ∴∆∆∽，∴sin sin BD BEEAB BCD AC AB==∠=∠；（2）如图2中，过点B 作BF BD ⊥交DC 的延长线于F ．90ABC DBF ∠=∠=︒Q ，360BAD BCD ABC ADC ∠+∠+∠+∠=︒，180ABC ADC ∠+∠=︒， 180BAD BCD BCF ∴∠=︒-∠=∠， BCF BAD ∠=∠Q ，BC BA =， DAB CBF ∴∆≅∆，BD BF ∴=，AD CF =，90DBF ∠=︒Q ，BDF ∴∆是等腰直角三角形，122BD DF ∴=， 6AD CD +=Q ， 6CF CD DF ∴+==，32BD ∴=，2242AC AB BC =+=，∴323442BD AC ==．（3）当BD CD =时，如图3中，过点B 作//MN DC ，过点C 作CN MN ⊥，垂足为N ，延长DA 交MN 于点M ，则四边形DCNM 是矩形，ABM BCN ∆∆∽，∴68AM BM AB BN NC BC ===， 设6AM y =，8BN y =，6BM x =，8CN x =，在Rt BDM ∆中，2210BD BMDM x =+=， BD DC =Q ，1068x x y ∴=+， 2x y ∴=，在Rt ABM ∆中，22(6)(12)65AB y y y =+=， 2sin sin 5565BM BCD MAB AB y ∴∠=∠===． 【考点】本题属于四边形综合题，主要考查了全等三角形的判定和性质、相似三角形的判定和性质、勾股定理，矩形的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形或相似三角形，学会利用参数解决问题．4．如图，90BAD CAE ∠=∠=︒，AB AD =，AE AC =，AF CB ⊥，垂足为F ． （1）求证：ABC ADE ∆≅∆； （2）求FAE ∠的度数； （3）求证：2CD BF DE =+．【思路】（1）根据题意和题目中的条件可以找出ABC ADE ∆≅∆的条件； （2）根据（1）中的结论和等腰直角三角形的定义可以得到FAE ∠的度数； （3）根据题意和三角形全等的知识，作出合适的辅助线即可证明结论成立． 【解析】证明：（1）90BAD CAE ∠=∠=︒Q ， 90BAC CAD ∴∠+∠=︒，90CAD DAE ∠+∠=︒， BAC DAE ∴∠=∠，在BAC ∆和DAE ∆中， AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩，()BAC DAE SAS ∴∆≅∆；（2）90CAE ∠=︒Q ，AC AE =， 45E ∴∠=︒，由（1）知BAC DAE ∆≅∆， 45BCA E ∴∠=∠=︒， AF BC ⊥Q ， 90CFA ∴∠=︒， 45CAF ∴∠=︒，4590135FAE FAC CAE ∴∠=∠+∠=︒+︒=︒；（3）延长BF 到G ，使得FG FB =， AF BG ⊥Q ，90AFG AFB ∴∠=∠=︒，在AFB ∆和AFG ∆中， BF GF AFB AFG AF AF =⎧⎪∠=∠⎨⎪=⎩， ()AFB AFG SAS ∴∆≅∆， AB AG ∴=，ABF G ∠=∠， BAC DAE ∆≅∆Q ，AB AD ∴=，CBA EDA ∠=∠，CB ED =，AG AD ∴=，ABF CDA ∠=∠， G CDA ∴∠=∠， 45GCA DCA ∠=∠=︒Q ，在CGA ∆和CDA ∆中， GCA DCA CGA CDA AG AD ∠=∠⎧⎪∠=∠⎨⎪=⎩， CG CD ∴=，22CG CB BF FG CB BF DE BF =++=+=+Q ， 2CD BF DE ∴=+．【考点】本题考查全等三角形的判定与性质，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．5．如图，已知正方形ABCD的边长为2，连接AC、BD交于点O，CE平分ACD∠交BD 于点E，（1）求DE的长；（2）过点EF作EF CE⊥，交AB于点F，求BF的长；（3）过点E作EG CE⊥，交CD于点G，求DG的长．【思路】（1）求出BC BE=，根据勾股定理求出BD，即可求出DE；（2）求出FEB ECD=即可；∆≅∆，根据全等三角形的性质得出BF DE（3）延长GE交AB于F，证GDE FBE∽，得出比例式，代入即可求出答案．∆∆【解析】（1）Q四边形ABCD是正方形，∴∠=∠=︒，ABC ADC90DBC BCA ACD∠=∠=∠=︒，45∠，CEQ平分DCA122.52ACE DCE ACD ∴∠=∠=∠=︒，4522.567.5BCE BCA ACE ∴∠=∠+∠=︒+︒=︒， 45DBC ∠=︒Q ，18067.54567.5BEC BCE ∴∠=︒-︒-︒=︒=∠， 2BE BC ∴==，在Rt ACD ∆中，由勾股定理得：22(2)(2)2BD =+=， 22DE BD BE ∴=-=-；（2）FE CE ⊥Q ，90CEF ∴∠=︒，9067.522.5FEB CEF CEB DCE ∴∠=∠-∠=︒-︒=︒=∠， 45FBE CDE ∠=∠=︒Q ，BE BC CD ==， FEB ECD ∴∆≅∆， 22BF DE ∴==-；（3）延长GE 交AB 于F ，由（2）知：22DE BF == 由（1）知：2BE BC == Q 四边形ABCD 是正方形，//AB DC∴，DGE BFE∴∆∆∽，∴DG DE BF BE=，∴22 222-=-解得：324DG=．【考点】本题考查了正方形的性质，全等三角形的性质和判定，相似三角形的性质和判定等知识点，能综合运用知识点进行推理是解此题的关键，题目比较好，难度偏大．6．（1）一个多边形每个内角都相等，且每个外角等于一个内角的23，求这个多边形的边数；（2）两个多边形边数之比为3:4，内角和之比为2:3，求这两个多边形的边数．【思路】（1）一个多边形的每个外角都等于其内角23，则内角和是外角和的1.5倍，根据多边形的外角和是360︒，即可求得多边形的内角和的度数，依据多边形的内角和公式即可求解．（2）设多边形的边数为3n，则另一个为4n，分别表示出两个多边形的内角和得到有关n的方程求解即可．【解析】（1）多边形的内角和是：360 1.5540︒⨯=︒．设多边形的边数是n，则(2)180540n-=g，解得：5n=．故这个多边形的边数是5；（2）Q两个多边形的边数之比为3:4，∴设多边形的边数为3n，则另一个为4n，Q内角和度数之比为2:3，(32):(42)2:3n n∴--=，解得：2n=，36n∴=，48n =．故这两个多边形的边数分别为6和8．【考点】本题主要考查了多边形的内角和定理以及多边形的外角和定理，注意多边形的外角和不随边数的变化而变化．（2）中正确的设出边数并表示出其内角和是解决本题的关键．7．如图所示，在直角坐标系中，第一次将OAB ∆变换成△11OA B 第二次将△11OA B 变换成△22OA B ，第三次将△22OA B 变换成△33OA B ，已知(1,3)A ，1(2,3)A ，2(4,3)A ，3(8,3)A ，(2,0)B ，1(4,0)B ，2(8,0)B ，3(16,0)B ．（1）求OAB ∆的面积；（2）写出△44OA B 的各个顶点的坐标；（3）按此图形变化规律，你能写出△n n OA B 的面积与OAB ∆的面积的大小关系吗？ 【思路】（1）根据三角形的面积公式：面积12=⨯底⨯高进行计算即可；（2）对于1A ，2n A A ⋯坐标找规律可将其写成竖列，比较从而发现n A 的横坐标为2n ，而纵坐标都是3，同理1B ，2B ，n B 也一样找规律．（3）根据三角形的底边后一个是前一个三角形的底边的2倍，先求出△n n OA B 的底边n OB 的长度，高都是3不变，然后利用三角形的面积公式分别计算出两三角形的面积，相除即可得到倍数．【解析】（1）12OAB A S OB y ∆=g12332=⨯⨯=；（2）根据图示知O 的坐标是(0,0)；已知(1,3)A ，1(2,3)A ，2(4,3)A ，3(8,3)A ，对于1A ，2n A A ⋯坐标找规律比较从而发现n A 的横坐标为2n ，而纵坐标都是3；同理1B ，2n B B ⋯也一样找规律，规律为n B 的横坐标为12n +，纵坐标为0． 由上规律可知：4A 的坐标是(16,3)，4B 的坐标是(32,0)； 综上所述，(0,0)O ，4(16,3)A ，4(32,0)B ；（3）根据规律，后一个三角形的底边是前一个三角形底边的2倍，高相等都是4，12n n OB +∴=，11233222n n n OAnBn OAB S S +∆∆=⨯⨯=⨯=即2n OAnBn OAB S S ∆∆=．【考点】本题是观察坐标规律的问题，需要分别从横坐标，纵坐标两方面观察规律，写出答案．8．如图，在ABC ∆中，AB AC =，以AB 为直径作圆O ，分别交BC 于点D ，交CA 的延长线于点E ，过点D 作DH AC ⊥于点H ，连接DE 交线段OA 于点F ． （1）求证：DH 是圆O 的切线； （2）若32FD EF =，求证；A 为EH 的中点． （3）若1EA EF ==，求圆O 的半径．【思路】（1）根据同圆的半径相等和等边对等角证明：ODB OBD ACB ∠=∠=∠，则DH OD ⊥，DH 是圆O 的切线；（2）如图2，先证明E B C ∠=∠=∠，得EDC ∆是等腰三角形，证明AEF ODF ∆∆∽，则32FD OD EF AE ==，设3OD x =，2AE x =，可得8EC x =，根据等腰三角形三线合一得：4EH CH x ==，从而得结论；（3）如图2，设O e 的半径为r ，即OD OB r ==，证明DF OD r ==，则1DE DF EF r =+=+，1BD CD DE r ===+，证明BFD EFA ∆∆∽，列比例式为：EF BFFA FD=，则列方程可求出r 的值．【解析】证明：（1）连接OD ，如图1， OB OD =Q ，ODB ∴∆是等腰三角形， OBD ODB ∠=∠①，在ABC ∆中，AB AC =Q ， ABC ACB ∴∠=∠②，由①②得：ODB OBD ACB ∠=∠=∠， //OD AC ∴， DH AC ⊥Q ， DH OD ∴⊥，DH ∴是圆O 的切线；（2）如图1，在O e 中，E B ∠=∠Q ，∴由（1）可知：E B C ∠=∠=∠，EDC ∴∆是等腰三角形， Q32FD EF =， //AE OD Q ， AEF ODF ∴∆∆∽，∴32FD OD EF AE ==， 设3OD x =，2AE x =， AO BO =Q ，//OD AC ， BD CD ∴=， 26AC OD x ∴==，268EC AE AC x x x ∴=+=+=， ED DC =Q ，DH EC ⊥， 4EH CH x ∴==，422AH EH AE x x x ∴=-=-=，AE AH ∴=， A ∴是EH 的中点；（3）如图1，设O e 的半径为r ，即OD OB r ==，EF EA =Q ， EFA EAF ∴∠=∠，//OD EC Q ， FOD EAF ∴∠=∠，则FOD EAF EFA OFD ∠=∠=∠=∠， DF OD r ∴==，1DE DF EF r ∴=+=+，1BD CD DE r ∴===+，在O e 中，BDE EAB ∠=∠Q ，BFD EFA EAB BDE ∴∠=∠=∠=∠， BF BD ∴=，BDF ∆是等腰三角形， 1BF BD r ∴==+，22(1)1AF AB BF OB BF r r r ∴=-=-=-+=-，BFD EFA ∠=∠Q ，B E ∠=∠， BFD EFA ∴∆∆∽，∴EF BFFA FD =， ∴111r r r+=-， 解得：115r +=，215r -=（舍)，综上所述，O e 的半径为15+．【考点】本题是圆的综合题，考查了等腰三角形的性质和判定、切线的性质和判定、三角形的中位线、三角形相似的性质和判定、圆周角定理，第三问设圆的半径为r ，根据等边对等角表示其它边长，利用比例列方程解决问题．9．如图，点O 为Rt ABC ∆斜边AB 上的一点，以OA 为半径的O e 与BC 切于点D ，与AC 交于点E ，连接AD ．（1）求证：AD 平分BAC ∠；（2）若60BAC ∠=︒，2OA =，求阴影部分的面积（结果保留)π．【思路】（1）由Rt ABC ∆中，90C ∠=︒，O e 切BC 于D ，易证得//AC OD ，继而证得AD 平分CAB ∠．（2）如图，连接ED ，根据（1）中//AC OD 和菱形的判定与性质得到四边形AEDO是菱形，则AEM DMO ∆≅∆，则图中阴影部分的面积=扇形EOD 的面积．【解析】（1）证明：O Q e 切BC 于D ，OD BC ∴⊥，AC BC ⊥Q ，//AC OD ∴，CAD ADO ∴∠=∠，OA OD =Q ，OAD ADO ∴∠=∠，OAD CAD ∴∠=∠，即AD 平分CAB ∠；（2）设EO 与AD 交于点M ，连接ED ．60BAC ∠=︒Q ，OA OE =，AEO ∴∆是等边三角形，AE OA ∴=，60AOE ∠=︒，AE AO OD ∴==，又由（1）知，//AC OD 即//AE OD ，∴四边形AEDO 是菱形，则AEM DMO ∆≅∆，60EOD ∠=︒，AEM DMO S S ∆∆∴=，260223603EOD S S ππ⋅⨯∴===阴影扇形．【考点】此题考查了切线的性质、等腰三角形的性质．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．10．如图，AH 是圆O 的直径，AE 平分FAH ∠，交O e 于点E ，过点E 的直线FG AF ⊥，垂足为F ，B 为直径OH 上一点，点E 、F 分别在矩形ABCD 的边BC 和CD 上．（1）求证：直线FG 是O e 的切线；（2）若8AD =，5EB =，求O e 的直径．【思路】（1）连接OE ，证明FG 是O e 的切线，只要证明90OEF ∠=︒即可；（2）先求出CE ，利用角平分线得出5EF BE ==，进而求出CF ，即可利用勾股定理求出AB ，最后用勾股定理即可得出结论．【解析】（1）如图1，连接OE ，OA OE=Q，EAO AEO∴∠=∠，AEQ平分FAH∠，EAO FAE∴∠=∠，FAE AEO∴∠=∠，//AF OE∴，180AFE OEF∴∠+∠=︒，AF GF⊥Q，90AFE OEF∴∠=∠=︒，OE GF∴⊥，Q点E在圆上，OE是半径，GF∴是Oe的切线．（2）设AB x=，Q四边形ABCD是矩形，AB CD x∴==，8BC AD==，3CE BC BE∴=-=，AEQ是BAF∠的角平分线，BE AB⊥，EF AF⊥，5EF BE∴==，在Rt CEF∆中，根据勾股定理得，4CF=，4DF CD CF x∴=-=-，在Rt ABE∆和Rt AFE∆中，EF EB AE AE=⎧⎨=⎩，Rt ABE Rt AFE(HL)∴∆≅∆，AF AB x ∴==，在Rt ADF ∆中，22(4)64x x --=，10x ∴=，10AB ∴=，设O e 的半径为r ，10OB r ∴=-，在Rt BOE ∆中，22(10)25r r --=， 254r ∴=， O ∴e 的直径为252． 【考点】本题考查的是切线的判定，勾股定理，矩形的性质，全等三角形的判定和性质，角平分线定理，解决本题的关键是要证某线是圆的切线，已知此线过圆上某点，连接圆心和这点（即为半径），再证垂直即可11．如图，AB 是圆O 的弦，D 为半径OA 的中点，过D 作CD OA ⊥交弦AB 于点E ，交圆O 于点F ，且CE CB =．（1）求证：BC 是O e 的切线；（2）连接AF ，BF ，求ABF ∠的度数；（3）如果3OA =，求AE AB g 的值．【思路】（1）连接OB ．欲证明BC 是切线，只要证明OB BC ⊥即可；（2）连接OF ．只要证明AOF ∆是等边三角形，可得1302ABF AOF ∠=∠=︒； （3）只要证明DAE BAH ∆∆∽，可得AD AE AB AH=，即可推出AE AB AD AH =g g ； 【解析】（1）证明：连接OB ．CD OA ⊥Q ，90ADE ∴∠=︒，90DAE AED ∴∠+∠=︒，OA OB =Q ，A OBA ∴∠=∠，CE CB =Q ，CBE CEB AED ∴∠=∠=∠，90ABO CBE ∴∠+∠=︒，90OBC ∴∠=︒，OB BC ∴⊥．（2）连接OF ．AD OD =Q ，FD OA ⊥，FA FO AO ∴==，AOF ∴∆是等边三角形，60AOF ∴∠=︒，1302ABF AOF ∴∠=∠=︒．（3）延长AO 交O e 于H ，连接BH ．AH Q 是直径，90ABH ADE ∴∠=∠=︒，DAE HAB ∠=∠Q ，DAE BAH ∴∆∆∽， ∴AD AEAB AH =，3692AE AB AD AH ∴==⨯=g g ． 【考点】本题考查圆综合题、切线的判定、等边三角形的判定和性质、相似三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，属于中考常考题型．12．如图，以ABC ∆的BC 边上一点O 为圆心，经过A 、C 两点且与BC 边交于点E ，点D为CE 的下半弧的中点，连接AD 交线段EO 于点F ，若AB BF =．（1）求CAD ∠的度数；（2）求证：AB 是O e 的切线；（3）若8CF =，210DF =，求线段AB 的长．【思路】（1）求出¶CD的度数是90︒，根据圆周角定理得出即可； （2）求出1809090OAD BAD ODF OFD ∠+∠=∠+∠=︒-︒=︒，根据切线的判定得出即可；（3）根据勾股定理求出半径，根据切割线定理得出2AB BE BC =⨯，代入即可求出AB ．【解析】（1）CE Q 为O e 直径，D 为¶CE的中点， ∴¶CD的度数是90︒， 190452CAD ∴∠=⨯︒=︒；（2）证明：连接OA ，0OA D =Q ，ODA OAD ∴∠=∠，OD Q 为半径，D 为¶EC 的中点， OD CE ∴⊥，90DOF ∴∠=︒，90ODA OFD ∴∠+∠=︒，BAF AFB ∠=∠Q ，AFB OFD ∠=∠，90OAF BAF ∴∠+∠=︒，即OA AB ⊥，AB ∴是O e 的切线；（3）设OE OC OD R ===，在Rt OFD ∆中，222OF OD DF +=，8CF =Q ，210DF =，222(8)(210)R R ∴-+=，解得：2R =或6，8CF =Q ，2R ∴=舍去，即6OE OD OC ===，12CE =，624EF =-=，BA Q 是O e 的切线，BEC 是O e 的割线，∴由切割线定理得：2AB BE BC =⨯，AB BF =Q ，2(4)(8)AB AB AB ∴=-⨯+，解得：8AB =．【考点】本题考查了垂径定理，切割线定理，圆周角定理，等腰三角形的性质和判定等知识点，能综合运用定理进行推理是解此题的关键．13．已知AB 是半圆O 的直径，M ，N 是半圆不与A ，B 重合的两点，且点N 在弧BM 上．（1）如图1，6MA =，8MB =，60NOB ∠=︒，求NB 的长；（2）如图2，过点M 作MC AB ⊥于点C ，点P 是MN 的中点，连接MB 、NA 、PC ，试探究MCP ∠、NAB ∠、MBA ∠之间的数量关系，并证明．【思路】（1）只要证明OBN ∆是等边三角形即可解决问题；（2）结论：90MCP MBA NAB ∠+∠+∠=︒．方法一：如图2中，画O e ，延长MC交O e 于点Q ，连接NQ ，NB ．关键是证明//CP QN ；方法二：如图21-中，连接MO ，OP ，NO ，BN ．关键是证明MCP NBM ∠=∠；【解析】（1）如图1，AB Q 是半圆O 的直径，90M ∴∠=︒，在Rt AMB ∆中，22AB MA MB =+，10AB ∴=．5OB ∴=，OB ON =Q ，又60NOB ∠=︒Q ，NOB ∴∆是等边三角形，5NB OB ∴==．（2）结论：90MCP MBA NAB ∠+∠+∠=︒．理由：方法一：如图2中，画O e ，延长MC 交O e 于点Q ，连接NQ ，NB ．MC AB ⊥Q ，又OM OQ =Q ，MC CQ ∴=，即 C 是MQ 的中点，又P Q 是MQ 的中点，CP ∴是MQN ∆的中位线，//CP QN ∴，MCP MQN ∴∠=∠，12MQN MON ∠=∠Q ，12MBN MON ∠=∠，MQN MBN ∴∠=∠，MCP MBN ∴∠=∠，AB Q 是直径，90ANB ∴∠=︒，∴在ANB ∆中，90NBA NAB ∠+∠=︒，90MBN MBA NAB ∴∠+∠+∠=︒，即90MCP MBA NAB ∠+∠+∠=︒．方法二：如图21-中，连接MO ，OP ，NO ，BN ．P Q 是MN 中点，又OM ON =Q ，OP MN ∴⊥， 且12MOP MON ∠=∠， MC AB ⊥Q ，90MCO MPO ∴∠=∠=︒，∴设OM 的中点为Q ，则 QM QO QC QP ===，∴点C ，P 在以OM 为直径的圆上， 在该圆中，12MCP MOP MQP ∠=∠=∠， 又12MOP MON ∠=∠Q ， 12MCP MON ∴∠=∠， 在半圆O 中，12NBM MON ∠=∠， MCP NBM ∴∠=∠，AB Q 是直径，90ANB ∴∠=︒，∴在ANB ∆中，90NBA NAB ∠+∠=︒，90NBM MBA NAB ∴∠+∠+∠=︒，即90MCP MBA NAB ∠+∠+∠=︒．【考点】本题考查圆周角定理、垂径定理、平行线的性质、直径的性质、三角形内角和定理等知识，解题的关键是学会添加常用辅助线，学会用转化的思想思考问题．14．如图，AB是圆O的直径，O为圆心，AD、BD是半圆的弦，且PDA PBD∠=∠．延长PD交圆的切线BE于点E（1）判断直线PD是否为Oe的切线，并说明理由；（2）如果60PD=，求PA的长．∠=︒，3BED（3）将线段PD以直线AD为对称轴作对称线段DF，点F正好在圆O上，如图2，求证：四边形DFBE为菱形．【思路】（1）连接OD，由AB是圆O的直径可得90∠+∠=︒，ADO PDA∠=︒，进而求得90ADB即可得出直线PD为Oe的切线；（2）根据BE是Oe的切线，e的切线，则90∠=︒，再由PD为OEBA∠=︒，即可求得30P得90∠=︒，根据三角函数的定义求得OD，由勾股定理得OP，即可得出PA；PDO（3）根据题意可证得ADF PDA PBD ABF∠=∠=∠=∠，由AB是圆O的直径，得90∠=︒，ADB 设PBD x∠=∠=︒+︒，2∠=︒，由圆内接四边形的DBF xDAF PAD x∠=︒，则可表示出90性质得出x的值，可得出BDE∆是等边三角形．进而证出四边形DFBE为菱形．【解析】（1）直线PD为Oe的切线证明：如图1，连接OD，ABQ是圆O的直径，90∴∠=︒ADB∴∠+∠=︒，ADO BDO90又DO BO∴∠=∠Q，BDO PBD=∠=∠Q，BDO PDAPDA PBD∴∠=∠⊥∴∠+∠=︒，即PD OD90ADO PDAQ点D在Oe的切线．e上，∴直线PD为O（2）BEQ是Oe的切线，90∴∠=︒EBAP∴∠=︒Q，3060BED∠=︒PD Q 为O e 的切线，90PDO ∴∠=︒在Rt PDO ∆中，30P ∠=︒，3PD ∴tan30OD PD︒=，解得1OD = ∴222PO PD OD =+=211PA PO AO ∴=-=-=（3）（方法一）证明：如图2，依题意得：ADF PDA ∠=∠，PAD DAF ∠=∠PDA PBD ADF ABF ∠=∠∠=∠QADF PDA PBD ABF ∴∠=∠=∠=∠AB Q 是圆O 的直径90ADB ∴∠=︒设PBD x ∠=︒，则90DAF PAD x ∠=∠=︒+︒，2DBF x ∠=︒Q 四边形AFBD 内接于O e ，180DAF DBF ∴∠+∠=︒即902180x x ︒++=︒，解得30x =︒30ADF PDA PBD ABF ∴∠=∠=∠=∠=︒BE Q 、ED 是O e 的切线，DE BE ∴=，90EBA ∠=︒60DBE ∴∠=︒，BDE ∴∆是等边三角形．BD DE BE ∴==又903060260FDB ADB ADF DBF x ∠=∠-∠=︒-︒=︒∠=︒=︒QBDF ∴∆是等边三角形．BD DF BF ∴==DE BE DF BF ∴===，∴四边形DFBE 为菱形（方法二）证明：如图3，依题意得：ADF PDA ∠=∠，APD AFD ∠=∠，PDA PBD ∠=∠Q ，ADF ABF ∠=∠，PAD DAF ∠=∠，ADF AFD BPD ABF ∴∠=∠=∠=∠AD AF ∴=，//BF PDDF PB BE ∴⊥Q 为切线BE PB ∴⊥//DF BE ∴∴四边形DFBE 为平行四边形PE Q 、BE 为切线BE DE ∴=∴四边形DFBE 为菱形【考点】本题是一道综合性的题目，考查了切线的判定和性质，圆周角定理和菱形的性质，是中档题，难度较大．15．如图，AB 是O e 的直径，点C 是BA 延长线上一点，CD 切O e 于点D ，1CA =，CD 是O e 3 ．（1） 求O e 的半径R ；（2） 如图 1 ，弦//DE CB ，动点Q 从A 出发沿直径AB 向B 运动的过程中， 图中阴影部分的面积是否发生变化， 若发生变化， 请你说明理由；若不发生变化， 请你求出阴影部分的面积；（3） 如图 2 ，动点M 从A 出发， 在O e 上按逆时针方向向B 运动 ． 连接DM ，过D 作DM 的垂线， 与MB 的延长线交于点N ，当点M 运动到什么位置时，DN 取到最大值？求此时动点M 所经过的弧长 ．【思路】（1） 由题意，CD 是O e 31CA =，在直角CDO ∆中， 根据勾股定理222CD OD CO +=，代入即可求出；（2） 由//DE CB ，可知， 动点Q 从A 出发沿直径AB 向B 运动的过程中，DEQ∆的面积不变， 则阴影部分的面积不变；当点Q 运动到O 点时， 则60DOE ∠=︒，即可求出阴影部分的面积；（3） 如图， 连接AD 、BD ，当DM 过圆心O 时，DN 取到最大值；易证ADB MDN ∆∆∽，由已知， 可求得，1AD =，3BD =所以，3DN DM =，此时，120AOM ∠=︒，即可求得·AM 的长 ． 【解析】 （1）CD Q 切O e 于点D ，∴三角形CDO 是直角三角形，1CA =Q ，CD 是O e 3∴在直角CDO ∆中，222CD OD CO +=， 则，2223)(1)R R R +=+，1R ∴=；（2）//DE CB Q ，∴动点Q 从A 出发沿直径AB 向B 运动的过程中，DEQ ∆的底DE 不变， 底DE上的高不变，DEQ ∴∆的面积不变， 则阴影部分的面积不变；由1OD =，2CO =，30C ∴∠=︒，则60COD ∠=︒，60ODE ∴∠=︒，ODE OED ∠=∠Q ，60OED ∴∠=︒60DOE ∴∠=︒，26013606S R ππ︒∴=⨯=︒阴影； （3） 如图， 连接AD 、BD ，DAB DMN ∴∠=∠，又90ADB MDN ∠=∠=︒，ADB MDN ∴∆∆∽，又1AD =，2AB =，3BD ∴=，∴3DN BD DM AD==， 3DN DM ∴=，∴当DM 为最大值， 即DM 过圆心O 时，DN 取到最大值；60AOD ∠=︒Q ，120AOM ∴∠=︒，∴·120223603AM R ππ︒=⨯=︒．【考点】本题考查了切线的性质、扇形面积的计算、弧长的计算及直角三角形的知识，作辅助线连接圆心和切点，利用垂直构造直角三角形解决是解答本题的关键．。

数学1、新课改理念：人人学（有价值）的数学；人人都能获得（必要）的数学；不同的人在数学上得到（不同的发展）。

2、学生的数学学习内容应当是（现实的），（有意义的），（富有挑战性的），这些内容要有力于学生主动的进行（观察）、（实验）、（猜测）、（验证）、（推理）与（交流）等数学活动。

3、数学活动必须建立在学生的（认知发展水平）和（已有的知识经验）基础之上。

4、学生是数学学习的主人，教师是数学学习的（组织者）、（引导者）和（合作者）。

5、数学课程将九年的学习时间具体划分为（3）个学段，即：（1---3年级）为第一学段，（4---6年级）为第二学段，（7---9年级）为第三学段。

6、数学课程标准在各个学段中，安排了四个学习领域，请你具体说明是哪四个领域？（数与代数，空间与图形，统计与概率，实践与综合应用）7、数学课程内容的学习，强调学生的数学活动，发展学生的（数感）、（符号感）、（空间观念）、（统计观念）、（应用意识）与（推理能力）。

8、数学推理能力主要表现在哪些方面？（能通过观察、实验、归纳、类比等获得数学猜想，并进一步寻求证据、给出证明或举出反例，能清晰有条理的表达自己的思考过程，做到言之有理、落笔有据，在与他人交流的过程中能运用数学语言合乎逻辑的进行讲座与质疑）9、数学课程总目标对学生“解决问题”方面的要求是什么？（初步学会从数学的角度提出问题、理解问题并能综合运用所学知识和技能解决问题，发展应用意识，形成解决问题的一些基本策略，体验解决问题策略的多样性，发展实践能力和创新精神；学会与人合作，并能与他人交流思维的过程和结果；初步形成评价与反思的意识）10、数学课标对第一学段认识图形与位置方面的具体目标是什么？（1、会用上、下、左、右、前、后描述物体的相对位置；2、在东、南、西、北和东北、西北、东南、西南中，给一个方向，辨认其余七个方向，并能运用这些词语描述物体所在的方向；会看简单的线路图）11、数学课标第一学段对“实践活动”的具体目标是什么？（1、经历观察、操作、实验、调查、推理等实践活动；在合作与交流的过程中，获得良好的情感体验；2、获得一些初步的数学实践活动经验，能够运用所学的知识和方法解决简单问题；3、感受数学在日常生活中的作用）12、数学评价的目的是什么？（评价的目的是全面了解学生的学习状况，激励学生的学习热情，促进学生的全面发展。

3年级电费有价值数学问题全文共四篇示例，供读者参考第一篇示例：3年级的小朋友在学习数学的时候，常常会感到学习的内容有些难以理解，但是如果把数学和日常生活联系起来，就会变得有趣而且容易理解许多。

今天我们就来谈谈一个关于电费的有价值数学问题。

在我们的日常生活中，用电是必不可少的。

我们在家中使用电灯、电视、电冰箱等电器，都需要消耗电能，然后我们就要支付相应的电费。

那么，我们如何计算电费呢？其实，计算电费就是一个涉及到数学知识的问题。

假设小明家里一个月的用电量为200度，电费标准是每度电0.5元，那么小明这个月需要支付多少电费呢？这是一个简单的数学问题，我们可以用乘法来解决。

首先要计算出小明这个月的用电费用为200度×0.5元/度=100元。

所以，小明这个月的电费是100元。

接下来，我们再来谈谈有关电费的有价值数学问题。

假设小红家里一个月的用电量是150度，小明家里一个月的用电量是200度，那么谁的电费更高呢？这个问题需要我们比较两个数的大小，也就是一个涉及到“大”和“小”的数学问题。

小红和小明的电费分别是150元和100元，可以看出小红的电费更高。

我们可以用小于、等于和大于的符号来表示大小关系，即150<200，所以150度的电费小于200度的电费。

这就是一个简单的大小比较数学问题，但是可以引导小朋友学会灵活运用数学知识。

我们还可以通过电费问题来学习乘法和除法。

假设小明一家一个月用电200度，为了节约用电成本，他们决定每天用电的时间缩短为2小时，那么这样一个月的电费会是多少呢？这就是一个涉及到时间和电费的乘法问题。

小明一家每天用电的时间缩短为2小时，那么一个月就是2小时×30天=60小时，也就是小明一家一个月用电的总时间变为60小时。

如果小明家里一个小时用电1度，那么一个月总共用电200度，那么一个月用电费就是60小时×1度/小时=60度，再乘以电费标准0.5元/度，得出小明一家一个月电费是60度×0.5元/度=30元。

“人人学有价值的数学，人人都能获得必需的数学”之我见《数学课程标准》提出了：“人人学有价值的数学，人人都能获得必需的数学，不同的人在数学上得到不同的发展”等新课程理念。

就这一理念我想从以下几个方面谈谈自己的想法：一、何为有价值的数学？数学内容的价值如何体现？个人认为，凡有利于学生发展，有利于促进学生形成良好的情感与价值观的数学内容就是有价值的数学。

而数学内容的价值并不完全在教材中静态呈现，它需要教师去思考、去捕捉、去开发，然后通过教学活动动态地渗透。

二、尊重教材，更应注重挖掘教材。

教师不仅是教材的使用者，更应成为教材的重组者、开发者，要能最大限度地开发并体现教材的价值。

三、“探究”学习，教师在先。

时下，以培养学生探究意识、探究能力为目标的“探究性”学习已成为教师课题研究的一个热点。

我认为，要培养学生的探究意识，教师首先要有探究意识。

至于其中的道理，由于自身欠缺思考，也就一直成为教学上的一个盲点。

试想：教师头脑中没有“为什么”，如何引导学生去意识、去探究“为什么”？因此，我们应着力加强对教学内容的整体意识、问题意识、探究意识。

教师只有具备了探究意识，才能使开发教材成为可能，只有具备了探究能力，才能充分挖掘教学内容的价值。

四、关注、开发练习的价值。

在新课程理念指导下，课堂教学改革正显蓬勃之势。

我们的新理念、新思想不是仅仅为新授课服务的，它应渗透到每一节课，每一个教学过程。

新教材为我们提供了许多具有丰富内涵的练习，因此，我们不能单一的利用练习巩固新知、训练解题技巧而忽视了它蕴含的诸如数学思想、数学方法、思维方式、学习策略、创新意识等等教学价值。

（一个练习包含其中的一个或几个方面，并不一定包含全部）。

如何开发练习的价值，如何在我们的课堂中充分体现、发挥练习的价值，是我们面临的一个新命题。

我想，当练习的价值被我们合理开发并能在课堂上充分体现时，练习课也一定精彩纷呈。

五、数学学习活动应当是一个生动活泼的、主动的和富有个性的过程。

原来数学可以更美的——新课程小学数学作业设计的策略《数学课程标准》指出新的理念：“人人学有价值的数学，人人都能获得必需的数学；不同的人在数学上得到不同的发展。

”新课程的作业已不再完全是课堂教学的附属，更而是重建与提升课程意义及人生意义的重要内容。

每一次作业都是学生成长的生长点。

学生在问题的不断生成、不断解决的探索中成长；在知识的不断运用中，在知识与能力的不断互动中，在情感、态度、价值观的不断碰撞中成长。

新课程理念下的作业是具有学生鲜明的价值追求、理想、愿望的活动。

作业成为学生课外、校外的一种生活过程和生活方式。

学生对待作业的态度也成为一种生活态度，学生在作业过程中体验幸福和快乐、苦恼和辛劳。

这样的作业已不再是强加给学生的负担，而是学生成长的一种自觉的学习需要、生活需要、人生需要。

下面我结合自己在人教版数学实验教材的教学中，谈一谈新课程数学作业设计的策略。

一、变“枯燥”为“有趣”学习兴趣是学习动机中一个最活跃的因素，没有兴趣的学习是一种消磨智慧的“苦役”。

著名心理学家布鲁纳曾说：“学习的最好刺激是对所学材料的兴趣。

”布置的作业从“写”的单一形式中走出来，将数学知识融入生动有趣的活动中，与画画、游戏、制作、参观、访问等学生喜闻乐见的形式巧妙结合，把知识、技能的训练与非智力因素的培养和智力因素的开发及活动巧妙联系，符合小学生好好生和形象思维为主的心理特点，让作业变得更“生动、有趣”。

1、游戏式作业游戏是儿童低年级学生最喜欢的活动之一。

学生在游戏中边玩边学，学中有玩，玩中有学。

游戏式作业将所学的知识蕴涵于游戏中，是学生最喜欢的数学作业。

如教学完“乘法口诀”后，可以设计“对口令”的游戏，让学生与学生玩，学生与家长玩。

再如教学《可能性》这一课后，可以设计如“猜球”、“猜硬币”等游戏作业，课后，学生相互之间玩一玩。

又如教学《生活中的大数》后，可以设计“猜数”“组数”等游戏作业。

学生在游戏中学习，不仅在学习中体验知识的魅力、成功的喜悦，而且培养了他们用数学语言与人交流合作的能力，令学生感觉到数学作业是一个游戏天地、学习的乐园。

人人学有价值的数学
没有价值的数学，即使人人能够接受也不应进入课堂。

数学教育首要的是使学生学习那些既是未来社会所需要的，又是个体发展所必须的；既对学生走向社会适应未来生活有帮助，又对学生的智力训练有价值的数学。

学生在义务教学阶段要学习的东西很多，我们不可能让学生在这样宝贵的时间内仅仅学习从属于哪一种价值（或需要）的知识，而必须设计出具有双重乃至多重价值的数学课程。

其实，即使像“测量”这样纯“实用数学”的知识，只要从量化的数学的根本观点来精心设计就可以对学生一般能力的发展、对数学素养和科学精神的培养起积极作用。

有价值的数学有显性和隐性之分，显性的数学包括重要的数学事实、基本的数学概念和原理、必要的运用数学以解决问题的技能；隐性的数学，即集中反映为具有元认知作用的各种思想意识（如函数思想、统计思想、优化思想和计算机意识、应用意识等等）；具有智能价值的数学思维能力（如主要用于分析问题的模型化能力。

主要用于解决问题的应用能力和一般智力意义上的推理能力等）以及具有人格建构作用的各种数学品质（如热爱科学、追求真理的求实、创新精神，一丝不苟、勤奋学习的科学态度等）。

设计有价值的数学问题，启发学生数学思考好的数学问题对于数学教学有着无法估量的价值。

有价值的数学问题是数学教学的有效载体，它具有恰当的探索空间，具有较好的针对性，具有一定的趣味性。

教师提问后一定要给学生留足独立思考的时空，以使问题的价值充分实现，从而，启发学生数学思考，引导学生逐步的积累数学活动经验。

苏霍姆林斯基说过：在人的心灵深处，都有一种根深蒂固的需要，这就是希望自己是一个发现者、研究者、探索者，而在儿童的精神世界中，这种需要特别强烈。

“学起于思，思源于疑”。

有价值的数学问题是学生思维的起点，是学生学习的内驱力，它能使学生的探索欲望从潜伏状态迅速转入活跃状态。

一、创设问题情境，引发有价值的数学思考。

《数学课程标准》十分重视数学与现实生活的联系，不仅要求选材必须密切联系学生生活实际，而且要求“数学教学必须从学生熟悉的生活情境和感兴趣的事物出发，为他们提供观察和操作的机会”。

情境创设是现代数学教学中的一个亮点，它使枯燥、抽象的数学知识更贴近学生的生活，符合学生的认知经验。

使学生在生动有趣的情境中获得基本的数学知识和技能、基本思想与基本的活动经验。

通过学生熟悉的、感兴趣的数学现象或数学问题，充分调动学生的学习积极性，促使他们以较高的热情参与到自主学习和自主探究中，进一步达到教与学的和谐统一，以动态生成方式引导学生有价值的数学思考。

比如，在教学可能性时，准备好一个大纸箱，里面装着十个红球和十个黄球，学生分组来摸，看是先摸球的小组摸到红球的可能性大，还是后摸球的小组摸到红球的可能性大。

学生通过分析和实践发现每次摸出红、黄球的情况会不同，理解了先摸球的小组不一定摸到红球的可能性就大，而后摸球的小组，也不一定摸到红球的可能性就小；教师精心创设问题情境，学生通过观察操作分析发现，每次摸球可能性大小的数据都会变化，发现每次摸出不同颜色的球后，再摸出红球的可能性都会变化，充分且深刻地感受了事件的随机性。

这样的问题情境不是为了教学而教学，而是以看似平常的问题激起学生的兴趣，使学生感到问题来自身边，既熟悉又奇妙，产生了积极的心理倾向，调动了参与数学活动的积极性，从而引发学生的数学思考；使学生从解决实际问题的需要出发，积极地探寻和解决问题，以此获得兴趣体验，知识理解。

五年级上册有没有很有价值的数学问题
五年级上册的数学问题有很多有价值的问题，以下是一些例子：
1. 分数和小数的互化：让学生理解分数和小数之间的关系，并能够将它们互化。

这个问题可以帮助他们更好地理解这两种数学形式。

2. 面积计算：学生需要学习如何计算不同形状的面积，例如长方形、正方形、三角形和圆形。

这个问题可以帮助他们理解形状和空间的概念。

3. 分数加减法：分数加减法是一个重要的数学问题，它需要学生理解分数的概念，并能够将它们相加或相减。

这个问题可以帮助他们解决许多实际问题。

4. 质数和合数：学生需要学习如何识别质数和合数，并了解它们的性质。

这个问题可以帮助他们更好地理解数字的概念。

5. 方程式解决：学生需要学习如何解决简单的方程式，例如 x + 3 = 7。

这个问题可以帮助他们理解数学建模的概念，并学会解决实际问题。

6. 逻辑推理：学生需要学习如何进行逻辑推理，例如通过给定的信息推断出结论或证明某个命题的真假。

这个问题可以帮助他们更好地理解逻辑和推理的概念。

这些数学问题都具有实际意义和价值，可以帮助五年级学生更好地理解数学概念，并为未来的数学学习打下坚实的基础。

1、 有4对人，任取3人，组成一个小组，不能从任意一对中取2个，问有多少种可能性？C83–C 41 C 61 先取得所有的组合数，然后减去选取了成对的情况，（C 43C 21 C 21 C 21） 2、 17个人中任取3人分别放在3个屋中，其中7个只能在某两个屋，另外10个只能在另一个屋，有多少种分法？P 72P1013、 A,B,C,D,E,F 排在1，2，3，4，5，6这六个位置，问A不在1，B 不在2，C 不在3的排列的种数？P66 -3P 55 +3P 44 -P 33(先取总数，后分别把A 放1，B 放2, C 放3,把这个数量算出，从总数中减去即可，建议用三个同样的环相互交错取总数的方法计算)4、 5辆车排成一排，1辆黄色，1两蓝色，3辆红色，且3辆红车不可分辨，问有多少种排法？P55 /P 33如果再加一个条件2辆不可分辨的白色车，同理：P77 /P33 P 225、 6个身高不同的人分成2排，每排3人，每排从左到右，由低到高，且后排的人比他身前的人高，问有多少种排法？5种。

穷举发。

2001年一月份出现。

6、 掷一个均匀硬币2N 次，求出现正面K 次的概率。

C2nk (1/2) 2n独立重复试验。

如果在一次试验中某事件发生的概率是P ，那么在n 次独立重复试验中这个事件恰好发生K 次的概率为P n （K ）＝C n k P k (1－P) n-k（一夫妇生四孩子，问生2男2女的情况之几率；每次生男女概率相同，1/2,如抛硬币问题（抛四次，2次朝上）,即C 42(1/2) 4＝3/8 7、 自然数计划S 中所有满足n 100, 问满足n(n+1)(n+2) 被6整除的n 的取值概率？ 由于3个连续自然数必包括一个偶数及一个可被3整除的数，因此100％8、 A>B （成功的概率）？（1） A 前半部分的成功概率为1％，B 前半部分成功概率为1.4%. （2） A 后半部分的成功概率为10％，B 后半部分成功概率为8.5%.C. P(A)=1%*10% P(B)=1.4%*8.5%9、 集合A 中有100个数，B 中有50个数，并且满足A 中元素于B 中元素关系a+b=10的有20对。