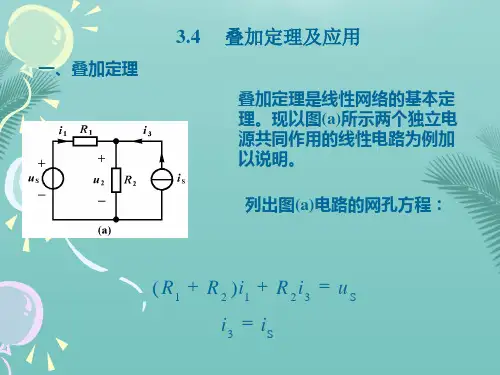
线性网络定理

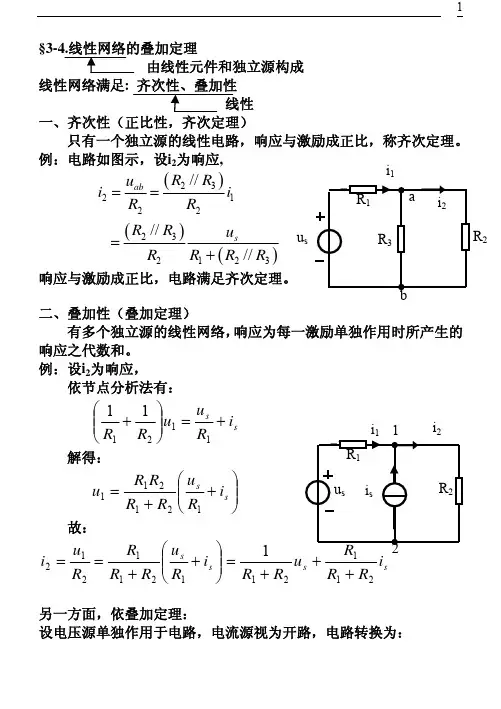
只有一个独立源的线性电路，响应与激励成正比，称齐次定理。

例：电路如图示，设i 2为响应,()()()232122232123//// //ab sR R u i i R R R R u R R R R ===+二、叠加性（叠加定理） 有多个独立源的线性网络，响应为每一激励单独作用时所产生的响应之代数和。

例：设i 2为响应，依节点分析法有：21211212⎠⎝i 2=另一方面，依叠加定理：设电压源单独作用于电路，电流源视为开路，电路转换为：2112R R u i s+=−s i R R R i 21122+=−依叠加定理，当两个独立源同时作用于电路时，有：12212212121s s R i i i u i R R R R −−=+=+++与节点电位分析法求得的结论一致。

注：在使用叠加定理时，应注意以下几点：1） 线性电容（）视为端电压随时间变化的理想电压源；c q u ∝线性电感（L i ψ∝）视为端电流随时间变化的理想电流源。

2）当某一激励源单独作用时，其它激励源视为零值（电压源视为短路；电流源视为开路）。

3）受控源不能视为激励。

4）叠加定理不适合功率计算（非线性 22Ri RuP ==∵）。

5）多个激励时，只有当所有激励都扩大k 倍时，响应才扩大k 倍。

例3-17用叠加定理求图中电压U 1及电流源的功率解：设电压源单独作用，电流源视为开路，电路为右图所示：依分压公式有： V U 102510//201010//2011=×+=−设电流源单独作用，电压源视为短路，电路为下图所示：()V U 65.110//10//2021=×=−设电压源和电流源同时作用：V U U U 1661021111=+=+=−−电流源的端电压：V U U 91625251=−=−=电流源吸收的功率（注意：电流源为关联参考方向）：9 1.513.5P U I W =×=×=例3-18用叠加定理求I x解：设电压源单独作用（受控源不能单独作用），电路如右图所示：()AI I I X X X 2010212 111=∴=−++−−−设电流源单独作用，电路为右图示：用节点分析法，有：⎪⎩⎪⎨⎧−=+=⎟⎠⎞⎜⎝⎛+−−补充212311212121X X I U I U解得：A I X 6.02−=−()A I I I X X X 4.16.0221=−+=+=−−例3-19设，利用响应与激励成比例的性质求：V U S 4−=?=IIA I 1=V U S 36=，由图可推得：解：设依齐次定理：S S S U I U I k kU I 361361=⇒==⇒=依题意： ()A I V U S 9143614−=−=⇒−=作业：3-14，3-17。

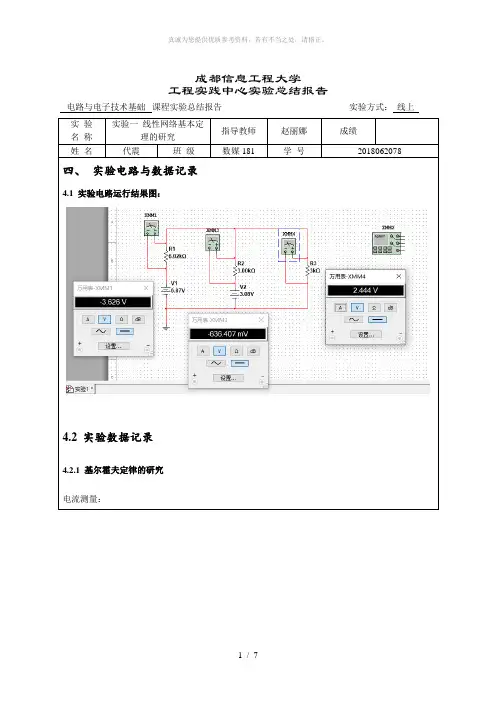
成都信息工程大学工程实践中心实验总结报告电路与电子技术基础课程实验总结报告实验方式：线上实验名称实验一线性网络基本定理的研究指导教师赵丽娜成绩姓名代震班级数媒181 学号2018062078四、实验电路与数据记录4.1 实验电路运行结果图：4.2 实验数据记录4.2.1 基尔霍夫定律的研究电流测量：4.2.2 叠加原理的研究表1.1 基尔霍夫定律、叠加原理数据记录表U R1/V U R2/V U RL/V U S1、U S2共同作用-3.63 -0.64 2.44 U S1单独作用-4.86 1.21 1.21U S2单独作用 1.23 -1.85 1.23 U S1、U S2共同作用I1= -0.60 mA I2= -0.21 mA I L= 0.81 mA4.2.3 戴维南定理的研究①开路电压U OC= 4.07 V，短路电流I SC= 2.04 mA。

②等效电阻R o = 1.9951 KΩ。

4.2.4 测定原网络的外特性表1.2 原网络外特性数据记录表R L/Ω∞3K 2K 1K 原网络U/V 4.07 2.44 2.04 1.36 戴维南等效电路U/V 4.07 2.44 2.04 1.362.5 最大功率传输定理表1.3 最大功率传输定理数据记录表R L/Ω∞3K 2K 1K 电压U/V功率P/W五、数据分析及实验结论5.1 基尔霍夫电流和电压定律的验证：（提示：①KCL验证：如何从I1、I2、I L三者电流关系角度验证KCL？②KVL验证：选取某一回路，根据该回路上各支路电压关系验证KVL。

）1.基尔霍夫电流定律的验证：选取节点a，由4.2.1中的图中数据得：I1= -0.60 mA I2= -0.21 mA I L= 0.81 mA-0.60+(-0.21)+0.81=0所以：I1+I2+IL=0符合KCL定律：在集总参数电路中，任何时刻，对任一节点，所有支路电流的代数和恒等零。

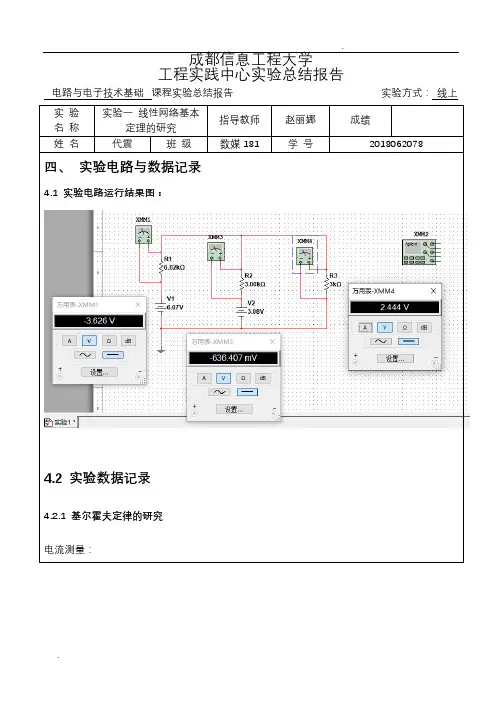
成都信息工程大学工程实践中心实验总结报告电路与电子技术基础课程实验总结报告实验方式：线上实验名称实验一线性网络基本定理的研究指导教师赵丽娜成绩姓名代震班级数媒181 学号2018062078四、实验电路与数据记录4.1 实验电路运行结果图：4.2 实验数据记录4.2.1 基尔霍夫定律的研究电流测量：4.2.2 叠加原理的研究表1.1 基尔霍夫定律、叠加原理数据记录表U R1/V U R2/V U RL/V U S1、U S2共同作用-3.63 -0.64 2.44 U S1单独作用-4.86 1.21 1.21U S2单独作用 1.23 -1.85 1.23 U S1、U S2共同作用I1= -0.60 mA I2= -0.21 mA I L= 0.81 mA4.2.3 戴维南定理的研究①开路电压U OC= 4.07 V，短路电流I SC= 2.04 mA。

②等效电阻R o = 1.9951 KΩ。

4.2.4 测定原网络的外特性表1.2 原网络外特性数据记录表R L/Ω∞3K 2K 1K 原网络U/V 4.07 2.44 2.04 1.36 戴维南等效电路U/V 4.07 2.44 2.04 1.36对于电路中的左侧网孔，按照标出的绕行方向，根据表格中各元件的吸收或放出的电压，-3.63 -0.64得出关系：Us1-Ur1+Ur2+Us2= -6-(-3.63）+(-0.64)+3= -0.01这个误差在误差范围之内，可以用来验证KVL定律：在集总参数电路中，任一时刻，沿任一回路所有支路电压的代数和恒等于零。

∑u=05.2 叠加原理的验证：（提示：从表1.1中共同作用数据与单独作用数据关系来看，如何验证叠加原理？）由表中数据可知：-3.63 = -4.86+1.23-0.64 = 1.21+(-1.85)故：Us1、Us2共同作用导致的电压Ur1和Ur2等于仅有Us1作用时以及仅有Us2作用时的各对应电压值的代数和，验证了叠加原理。

线性电路的分析方法和网络定理
线性电路的分析方法主要有两种：基尔霍夫定律分析法和等效电路法。

1. 基尔霍夫定律分析法：
基尔霍夫定律是指基尔霍夫电流定律和基尔霍夫电压定律。

根据基尔霍夫电流定律，一个节点的进入电流等于离开电流的代数和。

根据基尔霍夫电压定律，一个回路中所有电压的代数和等于零。

利用这两个定律，可以列出若干个方程来求解电路的未知量，比如电流和电压。

2. 等效电路法：
等效电路法是指通过将复杂的线性电路简化为等效电路，再进行分析。

常见的等效电路包括电阻、电容和电感等。

通过将电路中的各个元件用等效电路替代，可以用简单的电阻、电容和电感的连接方式来分析电路。

等效电路法可以大大简化复杂的电路分析过程，使得计算更加方便。

网络定理是一种用于分析线性电路的重要工具，常见的网络定理包括：欧姆定律、基尔霍夫定律、奥姆-柯西定律、叠加原理、原电流原压理论、特尔肯定理等。

这些定理可以用来简化电路分析过程，提高分析的效率和准确性。

例如，奥姆定律可以通过电压和电阻的关系来计算电流；叠加原理可以将复杂电路分解为几个简单电路进行分析；特尔肯定理可以通过等效电路简化电路分析等。

第三章线性网络的一般分析方法和网络定理线性网络的一般分析方法和网络定理是线性系统理论的基础，对于理解和分析线性网络的性质和行为具有重要意义。

本章将介绍线性系统的一般分析方法和一些常见的网络定理。

线性网络一般分析方法包括模型描述、稳态分析和频域分析等。

模型描述是指将线性系统用数学方程建模，常见的描述方法包括微分方程、差分方程和传递函数等。

稳态分析是指研究系统在长时间作用下的稳定行为，包括零输入响应和零状态响应。

频域分析是指将系统的输入和输出用频域表达，通过频率响应函数分析系统的频率特性。

线性系统的性质和行为可以利用一些重要的网络定理进行分析和描述。

常见的网络定理包括叠加原理、超级位置原理、频域定理和稳定性条件等。

叠加原理是线性系统最基本的性质之一，它表示系统输出可以分解为各个输入分量响应的叠加。

具体地说，如果一个线性系统对于输入信号x1(t)的响应为y1(t)，对于输入信号x2(t)的响应为y2(t)，那么对于输入信号x(t)=x1(t)+x2(t)，系统的响应为y(t)=y1(t)+y2(t)。

超级位置原理是叠加原理的一种推广，它描述了线性系统对于输入信号的定比例缩放响应的性质。

具体地说，如果一个线性系统对于输入信号x(t)的响应为y(t)，那么对于输入信号kx(t)（k为常数），系统的响应为ky(t)。

频域定理是指在频域上分析线性系统的性质和行为，常见的频域定理包括傅里叶变换、拉普拉斯变换和z变换等。

通过频域分析，可以得到系统的频率响应函数，从而研究系统的频率特性。

稳定性条件是指线性系统的稳定性的必要和充分条件。

对于连续时间系统，稳定性条件是系统的所有特征根（极点）的实部都小于零；对于离散时间系统，稳定性条件是系统的所有特征根（极点）的模都小于1除了以上介绍的常见网络定理外，还有一些其他重要的网络定理，如包络定理、发散定理、主值定理等，它们在具体的分析和设计问题中具有重要的应用。

总之，线性网络的一般分析方法和网络定理是理解和分析线性系统行为和性质的基础。