数值分析简明教程
- 格式:pdf
- 大小:554.63 KB
- 文档页数:13



数值分析简明教程修订版教学设计一、教学目标本教学设计旨在让学生学会使用数值分析方法处理实际问题,掌握数值解法的基本原理、基本思想和方法,具备数值分析和计算机辅助设计能力,并能够对不同数值分析方法进行综合分析,选择最佳的解法。
二、教学内容和教学方法2.1 教学内容1.方程求解与根的寻找2.一次线性方程组求解3.常微分方程数值解法4.插值与逼近5.数值积分与微积分方程求解2.2 教学方法本课程采用讲授与实例演示相结合的教学方法。
针对不同内容,采用不同的教学方法:1.方程求解与根的寻找:讲解主要理论知识,然后通过编程演示实例进行深入讲解。
2.一次线性方程组求解:通过算法推导演示求解过程,然后结合实例进行练习。
3.常微分方程数值解法:通过算法推导演示求解过程,然后通过实例让学生独立进行求解。
4.插值与逼近:通过实例演示讲解,然后通过编程让学生进行计算。
5.数值积分与微积分方程求解:通过算法推导演示求解过程,然后通过实例让学生独立进行求解。
三、教学评估与作业3.1 教学评估课程中将采用多种方式来进行教学评估,包括课堂提问、小组讨论、实验报告和期末考试等。
其中,期末考试占总评成绩的50%。
3.2 作业要求本课程将布置多种类型的作业,包括课后习题、课堂练习、编程作业和实验报告等。
作业占总评成绩的50%。
四、教学进度安排1.方程求解与根的寻找(2周)2.一次线性方程组求解(2周)3.常微分方程数值解法(4周)4.插值与逼近(2周)5.数值积分与微积分方程求解(4周)五、教学资源本课程所需的教学资源包括:1.讲义:对数值分析基本知识和方法进行全面讲解。
2.编程软件:如MATLAB、Python等。
3.实例程序:涵盖方程求解、矩阵计算、方程组求解等。
4.教学视频:教师根据课堂教学内容精心录制的视频,便于学生复习。
六、教学心得与体会本教学设计将理论讲解和实践操作相结合,使学生在实践中深入理解数值分析的思想、方法和技术,从而提高他们的计算机科学与数学水平,增强他们的迈向工程技术领域和科学研究领域的实用能力。
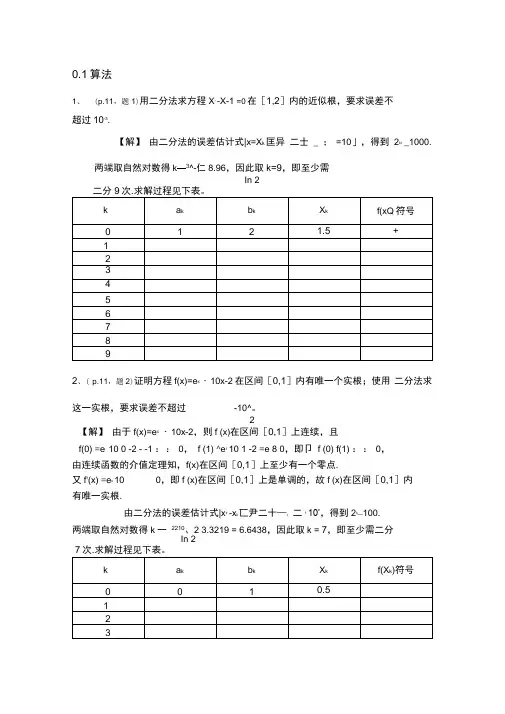
0.1算法1、(p.11,题1)用二分法求方程X’ -X-1 =0在[1,2]内的近似根,要求误差不超过10-3.【解】由二分法的误差估计式|x=X k匡异二士 _ ; =10」,得到2k1_1000.两端取自然对数得k—3^-仁8.96,因此取k=9,即至少需In 2二分9次.求解过程见下表。
2、( p.11,题2)证明方程f(x)=e X・10x-2在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过-10^。
2【解】由于f(x)=e X・10x-2,则f (x)在区间[0,1]上连续,且f(0) =e°10 0 -2 - -1 ::0,f (1) ^e110 1 -2 =e 8 0,即卩f (0) f(1) ::0,由连续函数的介值定理知,f(x)在区间[0,1]上至少有一个零点.又f'(x) =e x10 0,即f (x)在区间[0,1]上是单调的,故f (x)在区间[0,1]内有唯一实根.由二分法的误差估计式|x* -x k匸尹二十—;二110’,得到2k—100.两端取自然对数得k 一2210、2 3.3219 = 6.6438,因此取k = 7,即至少需二分In 2r3评 (1)(2) X1|e - X 2 | X 2 | e - X 3 |X 3四=1.85% ; 2.70.05 2.71-1.85% ;:::0.0005 =0.0184%。
2.718经四舍五入得到的近似数,其所有数字均为有效数字;近似数的0.2误差1- (p.〔2 ,题 8)已知 e=2.71828 …;试冋其近似值 x^ = 2 3 4 5-7 , x 2 = 2.71 , x 2=2.71 , X 3 = 2.718各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:1 1因为|e-x 1 | = 0.01828…:::0.05 10 ,所以x 1 =2.7有两位有效数字;21 』因为|e-x 2 | = 0.00828…:::0.05 10 ,所以x 2 =2.71亦有两位有效数字;2 1 3因为|e-x 3 |=0.00028…:::0.0005 10 ,所以x^2.718有四位有效数字; 22 ( p.12,题9)设捲=2.72 ; x 2 =2.71828 ; x3 =0.0718均为经过四舍五入得出的近 似值,试指明它们的绝对误差(限)与相对误差(限)。

比较详细的数值分析课后习题答案0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=- x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=- x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=- x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。


比较详细的数值分析课后习题答案0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=-K x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=-K x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=-K x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。

数值分析P97页 习题三 2 解:()()2112230.2()10.210.80.80.20.80.20.80.61440.4613n n n n n y y y x y y y y +=+--=+⨯-==+⨯--⨯==同理,7. 解:()()()22212111,0.1(2)11,0.1(2)112p n n n n n n c n n n n p n n p c y y hf x y y y x y y hf x y y y x y y y +++⎧=+=+⨯-⎪+⎪⎪=+=+⨯-⎨+⎪⎪=+⎪⎩111230.1,0.097,0.09850.1913,0.2737p c y y y y y =====同理,11. 解:()112341213243123412340.2226833830.223830.228330.21, 1.4, 1.58, 1.05,(0.2) 2.30041.0986,0.7692,0.8681,0.5780,(0.4)2.4654n n nn n n y y k k k k k y k y k k y k k y k k k k k y k k k k y +⎧=+⨯+++⎪⎪=-⎪⎪⎪=--⨯⨯⎨⎪⎪=--⨯⨯⎪⎪=--⨯⨯⎪⎩==========同理,13. 解:()()[]()[]()110.220.22321,00,(0.2)0.181(0.4)(0.2)3(0.2)10.1810.1310.18110.3267(0.6)(0.4)3(0.4)(0.2)0.32670.1310.3267(10.181)0.4468n n nn hy y y y y y y y y y y y y y y +-''=+-'=-=='=+-=+⨯⨯--=⎡⎤⎣⎦''=+-=+⨯⨯---=⎡⎤⎣⎦(0.8)0.5454,(1)0.6265y y ==同理,习题四),(,121)('sin 21)('cos 21)(.2∞-∞∈<≤-==x x xx x x ϕϕϕ证明:迭代函数 所以在均收敛。
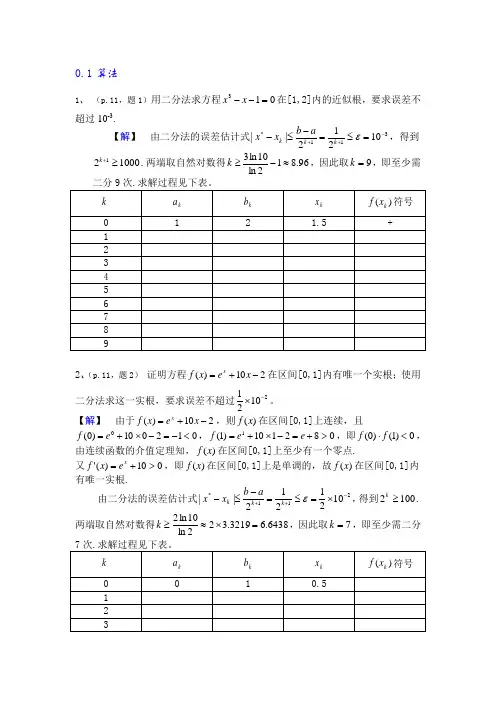
0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=- x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=- x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=- x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。

0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=- x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=- x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=- x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
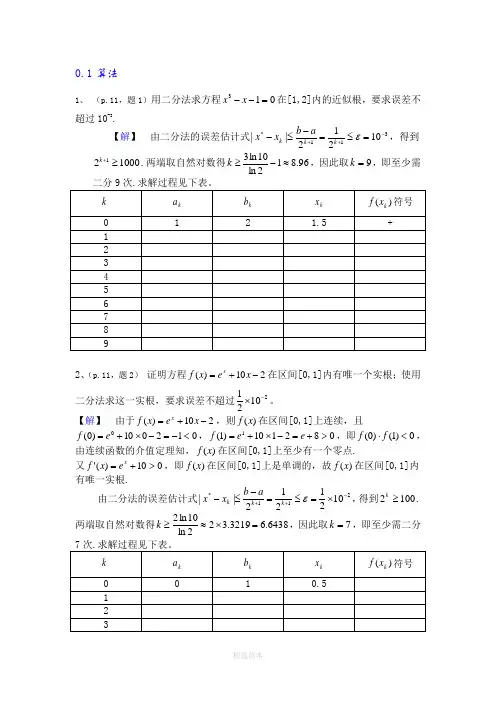
0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=- x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=- x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=- x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
数值分析简明教程教学设计
简介
数值分析是计算科学中的一个重要领域,涉及科学计算、数据处理和建模等方面。
本文档旨在为初学者提供一个简明易懂的数值分析教程,帮助他们快速入门并理解数值分析的基本概念和应用,在此基础上设计一份课程教学计划,让学生能够全面掌握该领域的知识和技能。
教学目标
通过本次课程的学习,学生将能够:
1.理解数值分析的概念和应用场景;
2.掌握数值计算中的各种基本方法和技术;
3.学会运用数值分析的方法解决实际问题;
4.培养数论思维,提高计算机编程能力。
教学内容
1.数学基础:函数、极限、导数、积分等数学基本概念;
2.常微分方程初值问题的数值解法:欧拉法、龙格-库塔法等;
3.常微分方程边值问题的数值解法:有限差分法、有限元法等;
4.偏微分方程数值解法:有限差分法、有限元法、谱方法等;
5.插值和拟合:拉格朗日插值、牛顿插值、最小二乘法等;
6.数值积分:复合求积公式、高斯公式等;
7.线性方程组的数值解法:高斯消元法、迭代法等;
8.非线性方程组数值解法:牛顿迭代法、弦截法等;
9.最优化问题的数值解法:牛顿法、拟牛顿法、梯度下降法等;
1。
比较详细的数值分析课后习题答案0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x 在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=-K x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=-K x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=-K x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=- x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=- x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=- x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
数值分析简明教程第二版(王超能)习题答案24页全解0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=-K x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=-K x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=-K x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.8110ln 3≈-≥k ,因此取9=k ,即至少需二分9次.求解过程见下表。
01<,[0,1]上至0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=- x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=- x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=- x e ,所以718.23=x 有四位有效数字;1=r ε2r ε3r ε评 (1(20718.0=【解】 评 3.(p.12【解】 由绝对误差限均为2105.0-⨯知有效数字应从小数点后两位算起,故42.11=x ,有三位;0184.02-=x 有一位;而0184.01018443=⨯=-x ,也是有一位。
1.1泰勒插值和拉格朗日插值1、(p.54,习题1)求作x x f sin )(=在节点00=x 的5次泰勒插值多项式)(5x p ,并计算)3367.0(5p 和估计插值误差,最后将)5.0(5p 有效数值与精确解进行比较。
【解】由x x f sin )(=,求得x x fcos )()1(=;x x f sin )()2(-=;x x fcos )()3(-=;x x f sin )()4(=;x x fcos )()5(=;x x f sin )()6(-=,所以插值误差:)(5x R 66060)6(!61)(!6|)sin(|)(!6|)(|x x x x x f ≤-=-=ξξ,若5.0=x ,则 )3367.0(5p 3303742887.0!53367.0!33367.03367.053≈+-=,而5665105.01002.2!63367.0)3367.0(--⨯<⨯≈≈R ,精度到小数点后5位,故取33037.0)3367.0(5=p ,与精确值 330374191.0)3367.0sin()3367.0(==f 相比较,在插值误差的精度内完全吻合!2(1(2【(1(23【(1因为3367.0=x 在节点0x 和1x 之间,先估计误差421021201.0⨯=≤;须保留到小数点后4为,计算过程多余两位。