平均指标和标志变异指标
- 格式:doc
- 大小:88.51 KB
- 文档页数:3


统计学基础平均指标和变异指标平均指标和变异指标是统计学中常用的两种指标,用于描述数据分布的中心趋势和离散程度。
在统计分析中,这两个指标的应用非常广泛。
1.平均指标:平均指标是用来表示数据分布的中心位置的指标,常见的平均指标有平均数、中位数和众数。
-平均数:平均数是指一组数据之和除以数据个数,表示了数据的平均水平。
平均数的计算方法是将所有数据相加,然后除以数据个数。
例如,对于一组数据:2,3,5,7,10,平均数的计算方式为(2+3+5+7+10)/5=5.4-中位数:中位数是将数据按照大小顺序排列后位于中间位置的数值,它划分了数据的中间位置。
如果数据个数为奇数,则中位数为排序后的中间值;如果数据个数为偶数,则中位数为排序后中间两个值的平均值。
中位数对于数据的极端值不敏感,适用于数据有异常值的情况,能够更好地表示数据的中心位置。
例如,对于一组奇数个数据:1,3,5,7,9,中位数为5;对于一组偶数个数据:2,4,6,8,中位数为(4+6)/2=5-众数:众数是一组数据中出现次数最多的数值,表示了数据中的高频值。
一个数据集可以有一个或多个众数。
如果一个数据集没有重复值,那么它没有众数。
例如,对于一组数据:1,2,3,4,4,4,5,众数为42.变异指标:变异指标是用来度量数据分布的离散程度,可以用来描述数据的稳定性和可变性。
常见的变异指标有极差、方差和标准差。
-极差:极差是一组数据的最大值和最小值之间的差异,表示了数据的全距。
极差越大,数据的离散程度越大;极差越小,数据的离散程度越小。
例如,对于一组数据:2,3,5,7,10,极差为(10-2)=8-方差:方差是一组数据与其平均数之间偏离程度的平均值的统计量,表示了数据分布的离散程度。
方差的计算公式是每个数值与平均数之差的平方之和除以数据个数。
例如,对于一组数据:2,3,5,7,10,平均数为5.4,方差的计算方式为[(2-5.4)^2+(3-5.4)^2+(5-5.4)^2+(7-5.4)^2+(10-5.4)^2]/5≈7.04-标准差:标准差是方差的平方根,是一个衡量数据分布离散程度的指标。

绝对指标是反映在⼀定时空条件下的社会经济现象总规模或绝对⽔平的统计指标。
按反映的时间状态不同,绝对指标可以分为时期指标和时点指标。
相对指标是社会经济现象的两个有联系的指标之⽐。
它能反映现象总体在时间、空间、结构、⽐例以及发展状况等⽅⾯的对⽐关系。
相对指标是绝对指标(总量指标)的派⽣指标,它把对⽐的总量指标的绝对⽔平及其差异进⾏抽象化。
根据对⽐指标的性质差异和相对指标说明问题的特点,可以将相对指标划分为如下⼏种具体形式:结构相对指标、强度相对指标、⽐较相对指标、⽐例相对指标、计划完成相对指标、动态相对指标。
平均指标是指⽤来测定静态分布数列中各单位的标志值集中趋势的指标。
平均指标主要有以下⼏种。
算术平均数(x)是指分布数列中各单位标志值通过⼀定⽅式汇总再与全部单位总数对⽐的指标。
调和平均数(XH)是分布数列中各单位标志值倒数的算术平均数的倒数。
⼏何平均数是指分布数列中n个标志值的连乘积的n次⽅根。
中位数是指分布数列中总体各单位标志值按⼤⼩顺序排列,处在中点位次的标志值。
众数是分布数列中出现频率的标志值。
变异指标主要是指标准差。
标准差,亦称均⽅差,是指分布数列中各单位标志值与其平均数的离差的平⽅的算术平均数的平⽅根。

练习题一、判断题1、按人口平均的粮食产量是一个平均数。
2、算术平均数的大小,只受总体各单位标志值大小的影响。
()3、在特定条件下,加权算术平均数等于简单算术平均数。
()4、众数是总体中出现最多的次数。
()5、权数对算术平均数的影响作用只表现为各组出现次数的多少,与各组次数占总次数的比重无关。
()6、标志变异指标数值越大,说明总体中各单位标志值的变异程度就越大,则平均指标的代表性就越小。
()7、中位数和众数都属于平均数,因此他们数值的大小受到总体内各单位标志值大小的影响。
()8、对任何两个性质相同的变量数列,比较其平均数的代表性,都可以采用标准差指标。
()9、比较两总体平均数的代表性,标准差系数越大,说明平均数的代表性越好。
()10、工人劳动生产率是一个平均数。
()二、单选题1、计算平均指标最常用的方法和最基本的形式是()A中位数 B众数 C调和平均数 D算术平均数2、计算平均指标的基本要求是所要计算的平均指标的总体单位应该是()A大量的 B同质的 C有差异的 D不同总体的3、在标志变异指标中,由总体中最大变量值和最小变量值之差决定的是()A标准差系数 B标准差 C平均差 D全距(极差)4、为了用标准差比较分析两个同类总体平均指标的代表性,其基本的前提条件是()A 两个总体的标准差应相等B 两个总体的平均数应相等C 两个总体的单位数应相等D 两个总体的离差之和应相等5、已知两个同类型企业职工平均工资的标准差分别为4.3和4.7,则两个企业职工平均工资的代表性是()A 甲大于乙B 乙大于甲C 一样的D 无法判断6、甲乙两数列的平均数分别为100和14.5,它们的标准差为12.8和3.7,则()A甲数列平均数的代表性高于乙数列B乙数列平均数的代表性高于甲数列C两数列平均数的代表性相同 D两数列平均数的代表性无法比较7、对于不同水平的总体不能直接用标准差来比较其变动度,这时需分别计算各自的()来比较。
A标准差系数 B平均数 C全距D均方差8、平均数指标反映了同质总体的()。

平均指标和变异指标的运用与分析(论文)平均指标和变异指标的运用与分析摘要:平均指标和变异指标是一对反映同一现象总体集中趋势和离散趋势的对应指标,在运用和分析中会遇到许多具体问题,要根据实际情况进行分析。
平均指标是一个反映现象总体在一定时空条件下内在的一般水平的综合性指标。
由于它将现象总体中的各总体单位在某一数量标志上表现的差异抽象掉了,所以,它用来说明现象总体内的集中趋势这一分布特征。
变异指标则是反映现象总体在一定时空条件下,各总体单位在某一个数量标志上表现出的差异性的综合性指标,它表明现象总体分布特征的离散趋势,即总体中各总体单位的个性差异,说明现象总体内或均衡或稳定或协调的程度,衡量平均指标对现象总体一般水平代表性的强弱。
平均指标和变异指标正是这样一对相互联系的对应指标,从不同侧面揭示同一现象总体各总体单位标志值的分布特征值,反映现象总体的基本数量特征和规律。
在具体运用平均指标和变异指标描述和分析现象总体时,会遇到两个方面的具体问题:第一方面,就是对不同的现象总体究竟应该用哪一个或哪几个平均指标和标志变异指标来进行描述和分析。
我们知道,平均指标有静态平均指标和动态平均指标——序时平均数。
本文主要是研究静态现象总体的问题,因此,主要使用静态平均指标及其变异指标。
在静态平均指标中,又有数值平均数和位置平均数之分。
在数值平均数中,又分为简单算术平均数和加权算术平均数,简单调和平均数和加权调和平均数,简单几何平均数和加权几何平均数。
我们知道,在某一个现象总体中,各总体单位在某一数量标志上的表现会有许多差异,我们不能用某个现象总体单位的标志值代表现象总体的一般水平。
但是,我们却需要一个反映现象总体综合性的一般水平的指标值来说明该总体的数量特征,代表该现象总体各总体单位在某个数量标志上抽象掉各自的个别差异后的一般水平。
如我们要了解某地区职工的平均工资、农村某地粮食单产、集市贸易中的平均成交价格等等。
同时,我们还可以看到,在一个同质总体中各总体单位由于受到共同起作用的一些基本因素的影响,使得总体中的各总体单位在某一数量标志上的表现差异总是有着一定的变化范围。



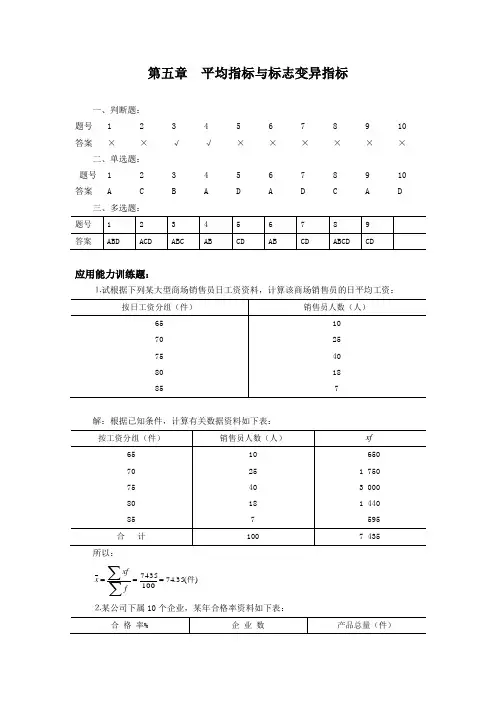
第五章 平均指标与标志变异指标一、判断题: 题号 1 2 3 4 5 6 7 8 9 10 答案××√√××××××二、单选题: 题号 1 2 3 4 5 6 7 8 9 10 答案ACBADADCAD三、多选题:应用能力训练题:⒈试根据下列某大型商场销售员日工资资料,计算该商场销售员的日平均工资:解:根据已知条件,计算有关数据资料如下表:所以:)(35.741007435件===∑∑f xf x⒉某公司下属10个企业,某年合格率资料如下表:要求:计算该产品的平均合格率解:根据题意,将有关数据计算入下表:%14.85140000119200===∑∑f xf x ⒊某市场上有三种鸡蛋,每公斤分别为16元、18元、20元,试计算: ⑴各买10公斤,平均每公斤多少钱? ⑵各买10元,平均每公斤多少钱? 解:⑴元)(1830102010181016............3213332211=⨯+⨯+⨯=++++++++=n n f f f f f x f x f x f x x⑵元)(85.17201018101610101010111=++++===∑∑∑∑m x m mm x x h ⒋某企业生产一种产品需顺次经过四个程序,这四个程序的废品率分别为1.2%、1.5%、1.3%和1.8%,该企业生产的平均废品率是多少?解:首先,计算该企业生产的平均合格率:%18.95%)8.11(%)3.11(%)5.11(%)2.11(......421=-⨯-⨯-⨯-=∏==n n n g x x x x x 该企业生产的平均废品率=1-95.18%=4.82%⒌某企业的销售额2011年比2010年增长7.5%,2012年比2011年增长9.8%,2013年比2012年增长6.3%,2014年比2013年增长11.4%。
计算2010年至2014年该企业销售额的平均增长速度。

第五章平均指标和标志变异指标
一、名词解释
1、算术平均数
2、调和平均数
3、几何平均数
4、权数
5、中位数
6、众数
7、标志变异指标
8、标准差
二、简答题
1、什么是平均指标?他有哪些特点和作用?
2、统计平均数有几种?为什么说算术平均数是计算平均指标的最常用方法?
3、如何理解权数的意义?在什么情况下,简单算术平均数和甲醛算术平均数的计算结果相等?
4、在实际统计中,如何应用调和平均数?
5、几何平均数最适合研究什么样的问题?
6、众数和中位数是如何计算的?它们为什么称为位置平均数?
7、什么是变异指标?其类型和作用如何?
8、为什么要计算变异系数?
9、简述算术平均数和调和平均数、几何平均数的数量关系?
10、算术平均数和众数、中位数有什么关系?如何进行相互计算?
三、计算题
3、某月份某企业按工人劳动生产率分组的生产班组数和工人数资料如下表:
7、某车间生产三批产品的废品率分别为1%、2%、1.5%,三批产品产量占全部产量的比重分别为25%、35%、40%试计算给车间三批产品的平均废品率。
8、因某种原因,某银行为吸收存款而提高利息率,五年的年利率分别为9%、10%、
12%、14%、20%,试计算五年的平均年利率?
株云杉,所得资料分组如下表:
11、某农作物的两种不同良种在五个村生产条件基本相同的地块上试种,所得结果如下表:是测定这两个品种收获率哪一个具有较大稳定性,指出哪一个品种有
值?。