当前位置：文档之家 › 自动控制原理之伯德图ppt课件

自动控制原理之伯德图ppt课件

  • 格式：ppt
  • 大小：262.00 KB
  • 文档页数：2

下载文档原格式

  / 2

合集下载

典型环节伯德图ppt课件

典型环节伯德图ppt课件
6
当有n个积分环节串联时，即: 其对数幅频特性为: 相频特性是一条与ω无关， 值为-n×900 且与ω轴平行 的直线。两个积分环节串联 的Bode图如图5-13所示。
是一条斜率为-n×20dB/dec， 且在ω=1（弧度/秒）处过零 分贝线（ω轴）的直线。
图5-13 两个积分环节串联的Bode图
7
2
一放大环节（比例环节）
放大环节的频率特性为:
其幅频特性是:
对数幅频特性为:
3
放大环节的对数幅频特性如图5-11所示，它是一条与角 频率ω无关且平行于横轴的直线，其纵坐标为20lgK。 当有n个放大环节串联时，即:
(5-62)
幅值的总分贝数为:
(5-63)
放大环节的相频特性是:
(5-64)
如图5-11所示，它是一条与角频率ω无 关且与ω轴重合的直线。
六二阶微分环节
二阶微分环节的频率特性是： 其对数幅频特性是：
相频特性是：
二阶微分环节与振荡节 的Bode图关于ω轴对称 ，如图5-21。渐近线的 转折频率为，相角变化 范围是00至+1800。 二阶微分环节的Bode图
19
七不稳定环节
不稳定环节的频率特性是:
其对数幅频特性和相频特性分别为:
不稳定惯性环节的Bode图
当 时， ，它是阻尼比 ξ的函数；当ξ=1时为-6（dB）; 当ξ=0.5时为0(dB); 当ξ=0.25时为+6(dB)；误差曲线如图5-18所示。
图5-17 振荡环节渐进线对数幅频特性
图5-18 振荡环节对数幅频特性误差修正曲线 15
由图知，振荡环节的误差可正可负，它们是阻尼比 ξ的函数，且以 的转折频率为对称，距离转折频率 愈远误差愈小。通常大于（或小于）十倍转折频率时， 误差可忽略不计。经过修正后的对数幅频特性曲线如图 5-19所示。

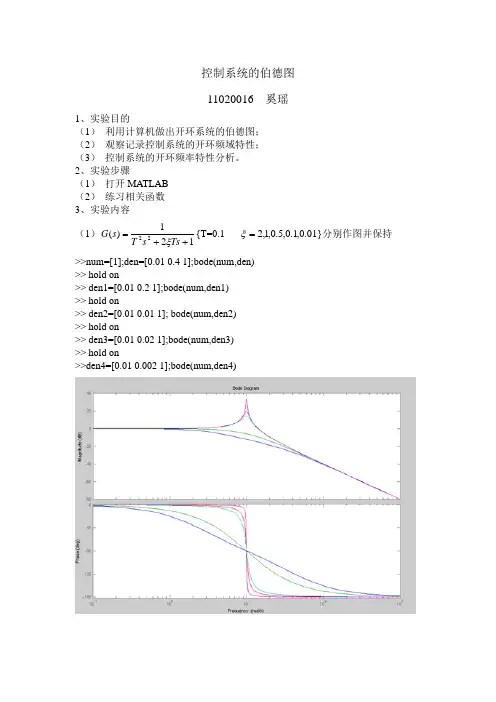
自控原理实验控制系统的伯德图

自控原理实验控制系统的伯德图

控制系统的伯德图11020016 奚瑶1、实验目的（1） 利用计算机做出开环系统的伯德图；（2） 观察记录控制系统的开环频域特性；（3） 控制系统的开环频率特性分析。

2、实验步骤（1） 打开MATLAB（2） 练习相关函数3、实验内容（1）121)(22++=Ts s T s G ξ{T=0.1 01.0,1.0,5.0,1,2=ξ}分别作图并保持 >>num=[1];den=[0.01 0.4 1];bode(num,den)>> hold on>> den1=[0.01 0.2 1];bode(num,den1)>> hold on>> den2=[0.01 0.01 1]; bode(num,den2)>> hold on>> den3=[0.01 0.02 1];bode(num,den3)>> hold on >>den4=[0.01 0.002 1];bode(num,den4)（2）)11.0)(101.0(6.31)(++=s s s s G 要求：1）做伯德图，在曲线上标出：幅频特性——初始段斜率、高频段斜率、开环截止频率、中频段穿越斜率 相频特性——低频段渐进相位角、高频段渐进相位角、-180°的穿越频率num=[31.6];den=[0.001 0.11 1 0];bode(num,den)grid初始段斜率=dec dB 202.211.001.1508.29-≈-=-- 高频段斜率= dec dB 3.57-≈dec dB 60-开环截止频率=16.3中频段穿越斜率= dec dB 4.40-≈dec dB 40-低频段相位角=-91.1°高频段相位角=-269°-180°线的穿越频率=322）由稳定裕度命令计算系统的稳定裕度c γ和g L ，并确定系统的稳定性 num=[31.6];den=[0.001 0.11 1 0] ;sys=tf(num,den);margin(num,den);[Gm(0),Pm(0),wg(0),wp(0)]=margin(sys);g L =11 c γ=180-158=22°稳定裕度g L > 6dB 相位裕度 c γ> 0°，但<30°所以系统稳定，但是相位裕度低于30°，接近于临界稳定点，系统趋于等幅震荡，稳定性相对较差。

15 第十五讲 伯德图

15 第十五讲 伯德图

1
(1−ω
2
/ω
2 2 n
)
+ 4ς ω / ω
2 2 2 2 2
2 n
Mdb = −20log10
−1
(1−T ω
)
+ 4ς 2T 2ω2
2ςTω ϕ (ω) = − tan 1−ω2Tω2
1) 低频渐近线:
当ωT << 1时，即 ω << 1/T， 1/T→转折频率 MdB = 0dB
Mdb -40db/dec ω
• 步骤 1: 计算转折频率。
1+ s → ωb =1rad / s
1 → ωb =1rad / s s 1 → ωb = 2 rad / s 1 1+ s 2
Kdb = 20lg 10 = 20 dB
步骤 2: 确定要画的频率范围。 所有转折频率都在1~10rad/s的这个十倍频程内， 所以此伯德图将在以下范围内绘制：
0.1 1.0 10
ω
φ
+90
1+s
+45
0 10
-45
1 s
-90
1 1 1+ s 2
图.SP.15.1.6
步骤8: 将所有环节的相角相叠加。
φ
+90
0.1 1.0 10
ω
+45
0
合成相位i
-45
-90
图.SP.15.1.6
MATLAB 仿真
10(1+ s) G(s) = 1 s1+ s 2
sys=tf([10 10],[0.5 1 0]); bode(sys) pause
H(s) =1

第十六讲 伯德图分析-稳定性-及幅值和相角裕度 ppt课件

第十六讲 伯德图分析-稳定性-及幅值和相角裕度 ppt课件


21
MATLAB 仿真
GH s

1 s s2 1 s /10
sys=tf([1 1],[0.2 1 0 0]); bode(sys) pause
PPT课件
22
PPT课件
23
用根轨迹来验证： Im
Re
-10
-1
图.16.9 系P统PT的课件根轨迹图
24
▽ 多个频率穿越点：
sys=tf([0.1 1.1 1],[0.00001 0.011 1 0 0 0]); bode(sys) pause
PPT课件
28
PPT课件
29
用根轨迹来验证：
在k<k1时， 系统是不稳定的； 在 k1<k<k2时， 系统是稳定的； 在 k>k2时， 系统再次不稳定。
GM1 K1db GM 2 K2db

1800
PM
图.16.3 增益裕度和相位裕度
PPT课件
log10 log10
13
系统的型和从伯德图得到 稳态误差
一般开环传递函数
GH s
Kb 1 s / z1 1 s / z2 1 sn 1 s / p1 1 s / p2 1
s s
/ /
zm pk
当ω 趋于 0 时
GH s Kb
sn
PPT课件
14
0型系统
M db
20 log10 KP
n0 GH (s) Kb
GH ( j) K p
图.16.4 0型系统的伯德图
PPT课件
log10
15
1型系统
幅值增益
GH (s) Kb Kb

自动控制原理：第六章频域分析法——伯特图及稳定性分析

自动控制原理：第六章频域分析法——伯特图及稳定性分析

0.1
0.05
0.05
0.1 0.3
(1 T 2 2
j2T)1
0.7
1
1
10
/ n
(ω) arctan[(2ζωT)/ (1 ωT2 )] 相角：0°~-180°
6.4 系统开环频率特性-典型环节的伯德图特性：
令
dA ( ) d
0,得
谐振
20
10
Bode Diagram 转折频率
0 K 0
90
K 0 180
101
100
101
102
/(rad/sec)
6.4 系统开环频率特性-典型环节的伯德图
2) 积分环节( j )1，微分环节( j )
Bode Diagram 20
1 j
L() /(dB)
积分
A( ω ) 1 ,( ω ) 90
ω
0 j
20
微分 A(ω) ω,(ω) 90
6.3 频率特性图示法-对数幅相频率特性曲线
6.3.3 对数幅相特性曲线（尼科尔斯（N.B.Nichols）曲线）
横坐标为相位()
纵坐标为对数幅值L()=20lgA()
绘制过程：
0
L() /(dB)
从伯德图中分别读取各频率 10 下L()和()的值，
20
在尼科尔斯坐标系中确定相
应的点并将频率作为参变 30 量标于各点旁，
r n 1 2 2
A(r ) Am 2
1
1 2
L() /(dB)
0
-10 -20
(1 T 22
j2T)1
0.05 0.1 0.3
-30
0.7
1 -40

《典型环节伯德图》课件

《典型环节伯德图》课件
Maya：一汇报人：
稳定性分析
稳定性定义：系统 在受到扰动后能够 恢复到其原始状态 的能力
稳定性分类：稳定、 不稳定、临界稳定
稳定性分析方法： 伯德图分析、奈奎 斯特图分析、根轨 迹分析等
伯德图分析：通过绘制 伯德图，观察系统在不 同频率下的增益和相位 变化，判断系统的稳定 性。
动态性能分析
伯德图：描述系统动态性能的图形工具 频率响应：系统对不同频率信号的响应 相位裕度：系统稳定性的指标 增益裕度：系统放大能力的指标 动态性能分析方法：如根轨迹法、频率响应法等
MATLAB还提供了丰富的函数库，可以方便地进行各种数学计算和仿真。
Simulink软件介绍
软件名称： Simulink
开发商： MathWorks
公司
软件功能：用 于建模、仿真 和分析动态系
统
应用领域：广 泛应用于控制 工程、信号处 理、通信等领
域
软件特点：图 形化界面，易 于操作，支持 多种编程语言
软件版本：最 新版本为 Simulink 2022a
其他绘制软件介绍
AutoCAD：一款专业的CAD软件，可以绘制 各种类型的伯德图
SolidWorks：一款三维设计软件，可以绘制 伯德图
Inventor：一款三维设计软件，可以绘制伯 德图
SketchUp：一款三维设计软件，可以绘制伯 德图
Blender：一款三维设计软件，可以绘制伯德 图
幅频特性的分析
幅频特性的定义：描述信号在频率域上的分布特性 幅频特性的表示方法：通常采用伯德图或奈奎斯特图 幅频特性的应用：用于分析信号的频率响应、滤波器设计等 幅频特性的测量方法：通过频谱分析仪或示波器等仪器进行测量
相频特性的分析
相频特性的定义：描述信号频率与相位之间的关系 相频特性的表示方法：通常用相频特性曲线表示 相频特性的应用：在信号处理、通信等领域有广泛应用 相频特性的测量方法：通过实验或仿真进行测量

如何绘制伯德图PPT课件

如何绘制伯德图PPT课件
G( j ) G1 ( j )G2 ( j )Gn ( j ) G( j ) G1 ( j ) G2 ( j ) Gn ( j ) L( ) 20 lg G( j) 20 lg G1 ( j) 20 lg G2 ( j ) 20 lg Gn ( j)
G( j ) 00
（5-63） （5-64）
100 00
900 1800
10 100 1000
图5-11 放大环节的Bode图
如图5-11所示，它是一条与角频率ω无关且与ω轴重合的直线。
5
（二）积分环节 积分环节的频率特性是
G( j) 1 j 1 1 e j90 j
7
当有n个积分环节串联时，即
dB L()
G(
j
)

(
1
j
)n
其对数幅频特性为
20 lg
G(
j )

20 lg
1
பைடு நூலகம்n
40
（ 5-70 ）
0
(5-71)
0.01 0.1
40 dB / dec
1
10
n 20 lg
G( j ) n 900
（5-72） 度 （）
6
设 ' 10 ，则有
20lg ' 20lg 10 20 20lg
dB L()
可见，其对数幅频特性是一条在
60
(5-68)
ω =1（弧度/秒）处穿过零分贝线 （ω 轴），且以每增加十倍频降 低20分贝的速度（-20dB/dec ） 变化的直线。
40
20dB / dec
1
L() dB

如何绘制伯德图PPT课件

如何绘制伯德图PPT课件
900
是一条斜率为-n×20dB/dec，且在 00
ω =1（弧度/秒）处过零分贝线（ω
0.01 0.1
1

轴）的直线。相频特性是一条与ω 900
无关，值为-n×900且与ω 轴平行的 1800 直线。两个积分环节串联的Bode图
如图5-13所示。
图5-13 两个积分环节串联的Bode图
8
（三） 惯性环节
1
L() dB
40
20
0
0.01 0.1
1
-20
-40
( )
90o
45o
0
0.01 0.1
1
-45o
-90o

10
100

10
100
2
用伯德图分析系统有如下优点： （1） 将幅频特性和相频特性分别作图，使系统（或环
节） 的幅值和相角与频率之间的关系更加清晰；
（2） 幅值用分贝数表示，可将串联环节的幅值相乘变为相 加运算，可简化计算；
一阶微分环节的对数幅频特性如图5-16所示，渐近线的转折频
率 为1，转折频率处渐近特性与精确特性的误差为
，
其误20差lg 均2为正3d分B 贝数，误差范围与惯性环节类似。
相频特性是
当 时， G( j )； arctg
（5-78）
0 G( j0) 00
12
当 1 时，G( j 1) 450 ；
成的折线称为对数幅频特性的渐近线。如图5-14所示。
9
惯性环节的相频特性为
G( j ) arctgT (5-75)
当 0时，G( j0) 00；
当 1 时，G( j 1 ) 450；

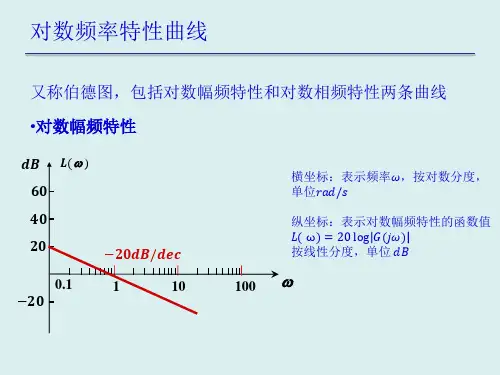
自动控制原理第五章第二部分

自动控制原理第五章第二部分

当L(w=0时：
L(w
)

20
lg
K
w
0K
wv
I型系统
斜率为-20db/dec的低频段渐近线或其延长线与横轴的 交点的频率值与开环放大系数K相等。
II型系统
斜率为-40db/dec的低频段渐近线或其延长线与横轴的 交点的频率值的平方与开环放大系数K相等。
例1:已知某最小相位系统由频率响应实验获得的对数幅 频曲线如图所示，试确定其传递函数。
3.开环对数幅频特性：
L(w)
60
40dB / dec
40
转折频率 w1 1
w2 2
w3 20
环节 惯性 一阶微分
振荡
20
60dB / dec
0
0.1
12
10 20
100 w
20
40dB / dec
40
80dB / dec
传递函数的频域实验确定
1.频率响应实验
Asinwt
L(w )
20dB / dec
0dB / dec
20
20dB / dec
0
0.1
1
20
w
40dB / dec
解： (1)确定系统积分环节的个数
低频段的渐近线为-20dB/dec 1
(2)确定系统传递函数
K ( 1 s 1)
G(s)
0.1 s(s 1)( 1
s 1)
20
L(w )
一阶微分环节 二阶微分环节
一点+一斜率确定初始段渐近线
(4)从低频渐近线开始，沿w 增大的方向，每遇到一个
转折频率改变一次渐近线斜率，直到绘出转折频率最高 的环节为止；

自动控制原理基础伯德图

自动控制原理基础伯德图

使用MATLAB 绘制频率特性曲线姓名 黄勇 班级 16电气本三 学号 4702160186一、频率特性在定义谐波输入下，输出响应中与输入同频率的谐波分量与谐波输入的幅值之比A(ω)为幅频特性，相位之差）（ωϕ为相频特性，并称其指数表达形式：()()()j G j A e ϕωωω=为系统的频率特性。

总结上述我们可知：频率特性由两个部分组合而成，分别是幅频特性和相频特性。

稳态系统的输出信号与输入信号的相位之差我们称其为相频特性。

稳态系统输出与输入的幅值之比称为幅频特性。

另外频率响应对稳定系统和不稳定系统都适应，其中稳定系统的频率特性可以通过实验的方法确定。

二、频率特性的几何表示法⏹ 幅相频率特性曲线简称幅相特性曲线，或幅相特性，或极坐标图。

⏹ 对数频率特性曲线又称为伯德曲线或伯德图。

⏹ 对数幅相曲线又称为尼科尔斯曲线或尼科尔斯图。

三、惯性环节频率特性的绘制惯性环节的表达式为： ()11G s Ts =+T 的取值分别为2、4、7，使用MATLAB 软件绘制MATLABA的函数指令如下：指令说明：num为分子指令；den为分母指令；此次画图调用了伯德图画法（bode指令）。

绘制图如下：T=2时。

MATLABA的函数指令如下：绘制图如下：同理当T=4时。

MATLABA的函数指令如下：绘制图如下：四、振荡环节频率特性的绘制振荡环节的传递函数为： ()221=21nnGs ssζωω++在201取值，本次取值分别为0.1 0.3 0.5 0.707 0.85 0.91 1。

方法一：使用伯德图画MATLAB函数程序指令如下：MATLAB图形显示如下：方法二：使用奈奎斯特图画取值分别为0.1 0.3 0.5 0.707 0.85 0.91 1。

MATLAB函数程序指令如下：MATLAB图形显示如下：。

自动控制原理第五章3PPT课件

自动控制原理第五章3PPT课件

2. υ = 1
系统的伯德图：
L(ω)/dB
ω=1
20lgK
-20dB/dec
L(ω)=20lgK
ω0
0 1 ω1 ωc
ω
低频段的曲线与横
-40dB/dec
轴相交点的频率为ω0
因为
20lgK lgω0-lg1
=20
故
20lgK=20lgω0 K=ω0
第三节 用实验法确定系统传递函数
3. υ = 2
12
第三节 用实验法确定系统传递函数
例 已知采用积分控制液位系统的结构
和对数频率特性曲线,试求系统的传
递函数。
L(ω)/dB
20
1
4
0
-20dB/dec -20
φ(ω)
0
-90
-180
hr(t)
1
-S
K h(t) Ts+1
ω
-40dB/dec
ω
解: 将测得的对数 = 0.曲 近25线线S2+近: 11似.25成S+渐1)
φ(s)=
1 (S+1) (S/4+1)
2）若两个系统的幅频特性相同，则>0时，最小相
角系统的相角总小于非最小相角系统的相角。
3）对于最小相角系统，若其传递函数的分子和分母
的最高次数分别为m和n，则时，相频特性()
-(n-m)90°。非最小相角系统不满足此条件。
例：设两个传递函数分别为
1Ts
1Ts
G1(s) 1T1s , G2(s) 1T1s ,
一个稳定系统，若其传递函数在右半s平面无零 点，称为最小相角系统（最小相位系统）；否则， 称为非最小相角系统（非最小相位系统）。

自动控制理频域伯德图

自动控制理频域伯德图


Lω 20lg1 ＝0 dB
——低频渐近线为一条0dB的水平直线。
Lω 20lg 1 Tn ω
2

2 2
2ζ T ω
n
2
高频段，即ωTn>>1时
L() 20lg( Tn ) 40lg(Tn )
2 2
当ω增加10倍
ωTn 40 40lgωTn L() 40lg10
相频与ω无关，值为-90°且平行于横轴的直线。
L ( )
20 0
20 0.1 10
1

( )
0 90
0.1
1
10

3 微分因子
G jω jω
微分环节是积分环节的倒数，它们的 曲线斜率和相位移也正好相差一个负号。
L ( )
20
0
20
0.1 20
1
10

( )
90
L() 40lg Tn 40lg1 0(dB)
即高频渐近线是一条斜率为-40dB/dec的直线。 当 ωω 1 时
n
Tn
说明
ω ωn
1 Tn
为二阶系统(振荡环节)的转折频率。

。10
0
0.1
0.2 0. 3
L ( )
dB
-40dB/dec
0 .7 1
10
系统 的相频特性为 90 arctan arctan 2 10
0
W=0
90
0
W=1
W=10 W=无穷大
110.860
123.70
0 90

自动控制原理__30页PPT

自动控制原理__30页PPT

谢谢！
36、自己的鞋子，自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢，但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何，且全力做你应该做的事吧。——美华纳
40、学而不思则罔，思而不学则殆。——孔子
自动控制原理__
1、合法而稳定的权力在使用得当时很 少遇到 抵抗。 ——塞 ·约翰 逊 2、权力会使人渐渐失去温厚善良的美 德。— —伯克
3、最大限度地行使权力总是令人反感 ；权力 不易确 定之处 始终存 在着危 险。— —塞·约翰逊 4、权力会奴化一切。——塔西佗
5、虽然权力是一头固执的熊，可是金 子可以 拉着它 的鼻子 走。— —莎士 比

控制系统的伯德图分析——自动控制原理

控制系统的伯德图分析——自动控制原理
() 0
伯德图
c
GMb>0
g
PM>0 Kg>1
PM -180
稳定闭环系统的GM和PM
奈氏图 jIm
L()
伯德图
c 1
0 GMb<0
c
ReΒιβλιοθήκη PM()0g
1
PM<0 Kg
-180
PM
Kg<1
不稳定闭环系统的GM和PM
GM，PM常作为控制系统的频域设计指标。
GM，PM大表明相对稳定性好,但响应速度低。 GM，PM小表明相对稳定性差,但响应速度高。 过大或过小都不好，较好的经验值为：
0时有低频渐近线方程
L( ) 20 lg K 20 lg K p
1
斜率=0， 与实轴无交点。
T
(2) N=1 (1型系统)
G( j)H ( j) K j (Tj 1)
L( ) 20 lg K 20 lg 20 lg T 2 2 1
0时有低频渐近线方程
L( ) 20 lg K 20 lg 20 lg K v 20 lg
斜率=-40 db/dec，交点: K a
L ()
1 T
Ka
-40db/dec
1
T Ka
L ()
1 T
Ka
-40db/dec
1
Ka
T
三、 伯德图与稳态误差的关系
表5-2 系统类型和低频渐近线特征
系统类型 斜率
0
0
1 -20
2 -40
L(=1) 与L=0的交点
20 lg K无p 交点
20 lg Kv
Kv
20 lg K a
Ka
斜率=-20 db/dec，交点: =Kv

自动控制原理(第2版)第5章频率响应法(2)简明教程PPT课件

自动控制原理(第2版)第5章频率响应法(2)简明教程PPT课件

( ) arctan 1
这表示L(ω)的低频渐近线为0dB的一条水平 线。
大连民族学院机电信息工程学院
自动控制原理
当 1 时，略去式中的1，则得 L( ) 20lg 1
可见，L(ω)高频部 分的渐近线是一条斜率 为–20dB/dec的直线， 当输入信号的频率每增 加十倍频程时对应输出 信号的幅值便下降20dB
1 20 lg K 20 lg K
大连民族学院机电信息工程学院
自动控制原理
2. 一阶因子
(1 jT )
1
一阶因子 (1 jT )1 分别为
的对数幅频和相频表达式
2
其中
L(ω)≈–20lg1dB=0dB
2 当 1 时，略去上式中的 ( ) 项，则得 1
L( ) 20lg 1 1 1 1 T
1 arg(1 jT ) arg( ) 1 jT
大连民族学院机电信息工程学院
自动控制原理
惯性环节L(ω)
L(ω)dB
1 ① G(s)= 0.5s+1
100 ② G(s)= s+5
40 26dB 20
[-20]
0dB 0o -20 - 30o - 45o o -40 - 60 - 90o 0.1 0.2
自动控制原理
第五章 频率响应法
Chapter 5 Frequency Response Methods
大连民族学院机电信息工程学院
College of Electromechanical ＆ Information Engineering
自动控制原理
5.2
对 数 坐 标 图
对数频率特性曲线由对数幅频曲线和对数相频 曲线两张图组成，是工程中广泛使用的一组曲线。 它又称为伯德曲线或伯德图。

自动控制原理之伯德图ppt课件

自动控制原理之伯德图ppt课件

求出。
2
系统开环对数幅频特性L(ω)通过0分贝线，即 L(c ) 0 或 A(c ) 1
时的频率c 称为穿越频率。穿越频率c 是开环对数相频
特性的一个很重要的参量。
3
5.4 系统开环频率特性的绘制
⑥ 画出各串联典型环节相频特性，将它们相加后得到 系统开环相频特性。
绘制开环系统对数相频特性时，可分环节绘 出各分量的对数相频特性，然后将各分量的纵坐 标相加，就可以得到系统的开环对数相频特性。
40dB/ dec
20dB/ dec
20dB/ dec
D
开环系统对数幅频特性图 60dB/ dec
5
5.4 系统开环频率特性的绘制
二、绘制系统开环频率特性伯德图的步骤
① 确定交接频率w1、w2、w3……，标在角频率w轴上。 ② 在w＝1处，量出幅值20lgK，其中K为系统开环放大系数。 (在图中标出相应的字母，如A点) ③ 通过A点作一条-20NdB/十倍频的直线，其中N为系统的 无差阶数，直到第一个交接频率w1。如果w1<1，则低频渐 近线的延长线经过A点。
斜率增加-40dB/十倍频。
2
5.4 系统开环频率特性的绘制
⑤ 绘出用渐近线表示的对数幅频特性以后，如果需要，可以进
行修正。通常只需修正交接频率处以及交接频率的二倍频和 1/2倍频处的幅值就可以了。
对于一阶项，在交接频率处的修正值为±3dB；
在交接频率的二倍频和1/2倍频处的修正值为±1dB。
对于二阶项，在交接频率处的修正值可由公式 20lg 1
4
例5-12 已知系统的开环传递函数为
G(s)H (s)
K (1 s) 1 1
LL( )
s T1s 1 T2 s 2

自动控制系统课件4-2

自动控制系统课件4-2

3
二、积分环节 传递函数： G(s) 1
s
频率特性：G(j ) 1
j
对数幅频特性： L( ) 20 lg M ( ) 20 lg 1 20 lg
4
二、积分环节
伯德图
5
三、微分环节 传递函数： G(s) s
频率特性： G(j ) j
对数幅频特性：L( ) 20 lg G j 20 lg 对数相频特性： 90
90
幅相曲线
12
六、振荡环节
根据幅频特性和相频特性公式计算出频率特性
j
1
O
13
六、振荡环节 渐近对数幅频特性：
当 << n时，略去/n，近似取
L( ) 20 lg G(j ) 20 lg 1 0 dB 在低频段的渐近特性是一条与横轴相重 合的直线。
14
六、振荡环节
这是一条在 n 处过横轴且斜率为
-40dB/十倍频程的直线。
15
六、振荡环节
对不同阻尼比，
振荡环节的精确 对数幅频特性
对数相频特性：
16
七、二阶微分环环节
二阶微分环节的伯德图
18
八、一阶不稳定环节 幅相特性:
19
八、一阶不稳定环节
一阶不稳定环节的伯德图
最小相位环节:
最小相位系统:
非最小相位环节: 非最小相位系统:
对数相频特性： ( ) arctan 特征点： 1 , L( ) 3dB, 45
10
五、一阶微分环节
一阶微分环节的伯德图 幅相曲线
11
六、振荡环节
对数幅频特性：
L( ) 20 lg G(j ) 20 lg
1
n
2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
5.4 系统开环频率特性的绘制
二、绘制系统开环频率特性伯德图的步骤
① 确定交接频率w1、w2、w3……，标在角频率w轴上。 ② 在w＝1处，量出幅值20lgK，其中K为系统开环放大系数。 (在图中标出相应的字母，如A点) ③ 通过A点作一条-20NdB/十倍频的直线，其中N为系统的 无差阶数，直到第一个交接频率w1。如果w1<1，则低频渐 近线的延长线经过A点。
斜率增加-40dB/十倍频。
2
5.4 系统开环频率特性的绘制
⑤ 绘出用渐近线表示的对数幅频特性以后，如果需要，可以进
行修正。通常只需修正交接频率处以及交接频率的二倍频和 1/2倍频处的幅值就可以了。
对于一阶项，在交接频率处的修正值为±3dB；
在交接频率的二倍频和1/2倍频处的修正值为±1dB。
对于二阶项，在交接频率处的修正值可由公式 20lg 1
4
例5-12 已知系统的开环传递函数为
G(s)H (s)
K (1 s) 1 1
LL( )
s T1s 1 T2 s 2
1
2T2 s 1 (T1
T2 )
dB ( ) AB
20dB/ dec
20log K
渐近特性
20dB/ dec
0
11
20dBT/1dec
40dB/ dec
1
T2
C
求出。
2
系统开环对数幅频特性L(ω)通过0分贝线，即 L(c ) 0 或 A(c ) 1
时的频率c 称为穿越频率。穿越频率c 是开环对数相频
特性的一个很重要的参量。
3
5.4 系统开环频率特性的绘制
⑥ 画出各串联典型环节相频特性，将它们相加后得到 系统开环相频特性。
绘制开环系统对数相频特性时，可分环节绘 出各分量的对数相频特性，然后将各分量的纵坐 标相加，就可以得到系统的开环对数相频特性。
1
5.4 系统开环频率特性的绘制
④ 以后每遇到一个交接频率，就改变一次渐近线斜率。 每当遇到 1 环节的交接频率时，渐近线斜率 jTj 1 增加-20dB/十倍频；
每当遇到 ( jTi 1) 环节的交接频率时，斜率增加
+20dB/十倍频；
每当遇到
( j)22 nLeabharlann 2nj2 n
环节的交接频率时，
40dB/ dec
20dB/ dec
20dB/ dec
D
开环系统对数幅频特性图 60dB/ dec
5