最优化方法与最优控制复习文件
- 格式:docx
- 大小:188.08 KB
- 文档页数:2

《最优化方法》复习提要 第一章最优化问题与数学预备知识§1.1模型无约束最优化问题 min /(x ), x =(旺,兀2,…心)'w R"・A约束最优化问题疋简(兀)》0,心1,2,・・・,加也(兀)=0,丿=1,2,・・・,") min /(x );s.t. gQ )nO,i = l,2,…,加,hj (x ) = 0,j = \,2,・・・,l ・其中.f (X )称为目标函数,西,兀2,…,暫称为决策变量,S 称为可行域,gQ ) no (心1,2,…,加),勺(兀) = 0。
= 1,2,…丿)称为约束条件. §1. 2多元函数的梯度、Hesse 矩阵及Tayloi •公式定义设f:R“TR,J^R“・如果%维向量〃,VAre R n,有+ Ax) -f(x) = p T\x + 0(||Ax||)・则称/(x )在点元处町微,并称df (x ) = p T\x 为/(x )在点元处的微分.如果/(X )在点元处对丁」=(兀“2,・・・,£)丁的各分量的偏导数。
/(元)d x i都存在,则称/(兀)在点元处一阶可导,并称向量为/(兀)在点元处一阶导数或梯度.定理1设f :R n^R,xeR n・如果/(兀)在点元处可微,则/(兀)在点元处梯度V/(x)存在,并且有#(x) = W)7'Ar .定义 设f:R"TR,J^R“・d 是给定的n 维非零向量,e = 2・如杲 dmin /(兀);即 vS.t. X G S.V/(x)=(df(x)T。
/(可。
/(元)Um /a + 2e )-V (x )久TO2存在,则称此极限为/(x )在点元沿方向d 的方向导数,记作冬学.da定理2设f :R n^R,xeR n.如果/(兀)在点元处可微,则/(兀)在点元处沿任何非零方向d 的方向导数存在,且= VA 元)。
,其中丘=厶~・daa定义 设/(兀)是/?"上的连续函数,xeR n. d 是〃维非零向量.如果3^>0,使得V2w (O0),有/(x + 2J )< (>) /(x ).则称d 为f (兀)在点元处的下降(上 升)方向.定理3设f:R n^R.xeR n,且/(兀)在点元处可微,如果日非零向量de R n9 使得Vf (x )Td < (>) 0,则d 是/(兀)在点元处的下降(上升)方向.定义 设f:R”TR,HeR”・如果/(兀)在点元处对丁自变量x = (x p x 2,---,x /J )7'的 各分量的二阶偏导数£単匕丿・=1,2,…,)都存在,则称函数/(兀)在点元处二阶 U Xj 可导,并称矩阵为/(x )在点元处的二阶导数矩阵或Hesse 矩阵.定义 设h:R" 记/1(兀)=(肉(兀),爲(兀),・・・,饥(兀))7',如果勺• (x ) (i = 1,2,…,加)在点元处对于自变量x =(兀],吃,…£)丁的各分量的偏导数d 2x } 扌/(元) dx }dx 2 巧(元) d 2f(x) 3 x 2d• d 2x 2• d x^d x n L n• •■d 2f(x) ■97(^) • •d 2f(x)d x n d X] d x n d x 2d 2f(x)V 2/(x)丿号⑴(i = 1,2,…,加;J = 1,2,…加 dx f都存在,则称向量函数加对在点元处是一阶可导的,并且称矩阵为/?(%)在点x 处的一阶导数矩阵或Jacobi 矩阵,例2 设aw R",xw R",bw R ,求f (x ) = a Tx-{-h 在任意点兀处的梯度和Hesse 矩阵.解 设0 =(绚卫2,・・・,%)/,兀=(旺,兀2,・・・,£)‘,则/(兀)=工绞母+b ,k=\因。




最优化及最优化方法讲稿ppt xx年xx月xx日CATALOGUE目录•最优化问题概述•线性规划问题及其求解方法•非线性规划问题及其求解方法•动态规划问题及其求解方法•最优化算法的收敛性分析•最优化算法的鲁棒性分析•最优化算法的应用举例 - 解决生产调度问题01最优化问题概述最优化问题是一个寻找某个或多个函数的特定输入,以使该函数的输出达到最小或最大的问题。
定义根据不同的分类标准,可以将最优化问题分为线性规划、非线性规划、多目标规划、约束规划等。
分类最优化问题的定义与分类描述所追求的最小或最大值的函数。
目标函数约束条件数学模型限制搜索范围的约束条件。
目标函数和约束条件的数学表达。
03最优化问题的数学模型0201最优化问题的求解方法牛顿法利用目标函数的Hessian矩阵(二阶导数矩阵)进行搜索。
梯度下降法迭代搜索,逐步逼近最优解。
混合整数规划将整数变量引入优化模型中,求解整数规划问题。
模拟退火算法以概率接受劣质解,避免陷入局部最优解。
进化算法模拟生物进化过程的启发式搜索算法。
02线性规划问题及其求解方法线性规划问题定义:在一组线性约束条件下,求解一组线性函数的最大值或最小值的问题。
数学模型:将实际问题转化为线性规划模型,包括决策变量、目标函数和约束条件。
线性规划问题的求解方法 - 单纯形法基本概念:介绍单纯形法的相关概念,如基、可行解、最优解等。
单纯形法步骤:阐述单纯形法的基本步骤和算法流程,包括初始基可行解的求解、最优解的迭代搜索和最终最优解的确定。
单纯形法改进:介绍一些改进的单纯形法,如简化单纯形法、对偶单纯形法等。
线性规划问题的定义与数学模型通过一个具体的生产计划问题,说明如何建立线性规划模型并进行求解。
生产计划问题通过一个配货问题,说明如何运用线性规划模型解决实际问题。
配货问题通过一个投资组合优化问题,说明如何运用线性规划进行风险和收益的平衡。
投资组合优化问题线性规划问题的应用举例03非线性规划问题及其求解方法非线性规划问题定义:非线性规划问题是一类求最优解的问题,其中目标函数和约束条件均为非线性函数。


控制系统中的最优控制与最优化技术随着科技的不断进步和应用范围的扩大,控制系统在各行各业中的重要性也日益凸显。
最优控制与最优化技术作为控制系统中的重要概念和方法,在提高系统性能和效率方面发挥着关键作用。
本文将就控制系统中的最优控制与最优化技术进行深入探讨。
一、最优控制的定义与概念最优控制是指在满足给定约束条件的前提下,通过使某种性能准则达到最大或最小值来确定控制器参数或控制策略的问题。
最优控制的实现可以使系统在最短时间内达到期望状态或在给定资源条件下获得最佳性能。
最优化技术是实现最优控制的关键方法之一,它利用数学和计算方法来寻找系统中使性能准则达到最大或最小值的最优解。
最优化技术广泛应用于各种领域,例如经济学、工程学、管理学等,其中最为常见的应用是在控制系统中。
二、最优控制的分类最优控制可以分为离散最优控制和连续最优控制两大类。
离散最优控制是指在离散时间点上确定控制器参数或控制策略的问题。
典型的离散最优控制方法包括动态规划、贝尔曼方程等。
连续最优控制是指在连续时间范围内确定控制器参数或控制策略的问题。
常见的连续最优控制方法有经典最优控制、最速控制、最小能耗控制等。
三、最优化技术在控制系统中的应用最优化技术在控制系统中有着广泛的应用。
以下是一些常见的应用领域。
1. 机器人控制机器人控制是利用最优化技术来实现机器人移动、定位和路径规划等问题。
通过对机器人运动过程中的能耗、时间等指标进行优化,可以实现机器人的高效控制和优化运动。
2. 制造业控制在制造业中,最优化技术可以用来优化物料和生产设备的调度、工艺参数的优化以及生产线的平衡等问题。
通过合理地设计和优化控制策略,可以提高制造业的生产效率和产品质量。
3. 能源系统控制能源系统控制是指在能源产生、传输和消费过程中,通过最优化技术实现能源的高效利用。
例如在电力系统中,可以通过最优化技术对电网的输电线路和发电机组进行优化调度,以最大限度地提高电网的稳定性和电能的利用率。

第二章 非线性规划在实践中,最优化问题的目标函数和(或)约束条件常常是非线性的,如例1-1和例2-1。
这类问题称为非线性规划问题。
求解无约束条件的非线性规划问题通常采用逐步逼近法(俗称试探法),若在求解过程中使用了目标函数的导数,称为解析法;不使用导数而直接利用目标函数进行比较、搜索,称为直接法。
对于有约束条件的非线性规划问题,可以将其转化为无约束条件的非线性规划问题后再进行求解。
本章介绍求解非线性规划的一些方法,对解的收敛性不作讨论。
例2-1求解例1-1,即有一块薄的塑料板,宽为a ,对称地把两边折起,做成槽(如图2-1)。
欲使槽的横截面积S 最大,1x 、2x 和θ的最优值是多少?解:最优化问题的目标函数和约束条件为θθsin )cos (m ax 221x x x S ⋅+=, a x x =+212;01≥x ;02≥x 。
分析:该问题的目标函数是非线性的,属非线性规划问题。
目标函数自变量中,只有2个是自由的,不妨以2x 和θcos =y 为自变量,将其转化为无约束条件的非线性规划问题。
212x a x -=;a x 5.002≤<。
目标函数改写为:22221)2(max y x y x x a J -+-=,原最优化问题简化成二元函数求极值问题,求解过程如下:1)2(101)2(1)2(2222222222222=-+---=∂∂=-+-+--=∂∂yy x y x x a y x y J y y x x a y x y x J; ⎩⎨⎧=+--=+-022*********y x y x x y a y x x a ;⎩⎨⎧==⇒2/13/2y a x ;⎩⎨⎧==ο603/2θa x ; 最优解: 3/1a x =;3/2a x =;o60=θ;12/3m ax 2a J =。
该例实质上是二元函数求极值问题,经解析方法计算使J 的一阶导数等于零的参数值,且J 的海森矩阵09/323/33/32/33<⎥⎦⎤⎢⎣⎡--=a a a H , 是负定矩阵,目标函数J 取极大值,即为最优解。

144 第七章 动态规划系统的数学模型、目标函数和求解方法是最优化问题的三个要素。
对于一个已知状态空间描述的控制系统来说,在确定了控制目标(性能指标)后,就需要寻求一个控制函数,使性能指标取最小(或最大)值。
在控制界普遍认为,庞特里亚金(Понтрягин)的最小值原理和贝尔曼(Bellman)的动态规划是求解最优控制问题的两种有效方法。
在第五章和第六章中,应用最小值原理给出了性能指标达到极值的必要条件,特别地,对于具有线性二次型性能指标的最优控制系统,能够得到最优控制的解析表达式,便于实现状态反馈控制。
本章介绍动态规划的主要内容—最优性原理,它在处理多级决策过程是非常有效的。
动态规划处理问题的思路是,把要处理的最优化问题转化为许多有序、相关的子问题,即多级决策过程,如果每一个子问题的解对全局都是最优的,那么,总的决策就是最优的。
本章先阐述多级决策过程的基本概念,其次介绍最优性原理,然后讨论用动态规划求解离散系统和连续系统的线性调节问题。
7-1 多级决策过程所谓多级决策过程如图7-1所示。
多级过程是由在时间或空间上(图7-2)顺序相关的若干级子过程组成的一个完整过程。
在每一级都需要有相应的决策,对整个过程性能指标而言,该决策应当是最优的。
显然某一级的决策确定后,必然会影响后一级过程的决策,从而影响到自当前一级过程到终端级过程的决策和整体性能指标。
由于在某一级时,子过程的初始状态是由前面多级过程及其决策的结果,初始状态往往不是唯一的,即可供选择的决策往往不止一个。
多级决策问题,就是要在允许选择的决策中选择一个最优的策略,使整体性能指标最优。
图7-1中的虚线框表示一级子过程,它可以代表任何类型的子过程。
图7-1将线性离散系统展示成一个时间上的多级决策过程,每一级子过程的状态方程是))u(B())x(A()1x(k k k k k +=+,1,,1,0-=N k 。
(7-1)系统从状态)0(x 经)1(x 、)2(x 、…转移到状态)(x N 的过程称为N 级过程。

第一章 最优化方法的一般概念人们在处理日常生活、生产过程、经营管理、社会发展等实际问题时,都希望获得最佳的处理结果。
在有多种方案及各种具体措施可供选择时,处理结果与所选取方案和具体措施密切相关。
获取最佳处理结果的问题称为最优化问题。
针对最优化问题,如何选取满足要求的方案和具体措施,使所得结果最佳的方法称为最优化方法。
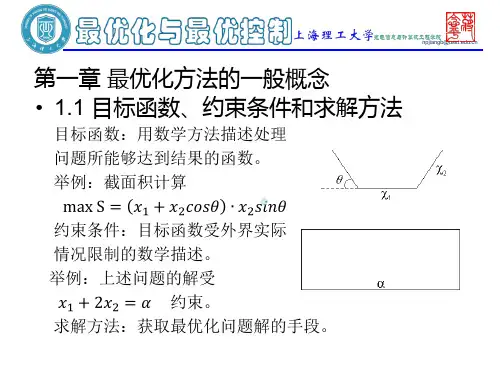
1-1 目标函数、约束条件和求解方法目标函数就是用数学方法描述处理问题所能够达到结果的函数,该函数的自变量是表示可供选择的方案及具体措施的一些参数或函数,最佳结果表现为目标函数取极值。
在处理实际问题时,通常会受到经济效率、物理条件、政策界限等许多方面的限制,这些限制的数学描述称为最优化问题的约束条件。
求解方法是获得最佳结果的必要手段,该方法使目标函数取极值,所得结果称为最优解。
针对各种类型的最优化问题,找出可靠、快捷的处理方法是最优化方法(理论)的研究范畴。
目标函数、约束条件和求解方法是最优化问题的三个基本要素。
无约束条件的最优化问题称为理想最优化问题,所得结果称为理想最优解。
下面用三个简单的例子,说明最优化问题的目标函数和约束条件。
例1-1 有一块薄的塑料板,宽为a ,对称地把两边折起,做成槽(如图1-1)。
欲使槽的横截面积S 最大,1x 、2x 和θ的最优值是多少?该问题要找出最优参数1x 、2x 和θ,使槽的横截面积S 最大,所以,目标函数为θθsin )cos (max 221x x x S ⋅+=; (1-1)由于底边与两个斜边的总长度应等于塑料板宽度a ,即约束条件为a x x =+212。
(1-2)有许多最优化问题可以方便地将等式约束条件代入目标函数中,使原问题转换为无约束条件的最优化问题,便于求解。
例1-1为无约束条件的最优化问题时,目标函数如下θθsin )cos 2(max 222x x x a S ⋅+-=。
(1-3)例1-2 仓库里存有20米长的钢管,现场施工需要100根6米长和80根8米长的钢管,问最少需要领取多少根20米长的钢管?用一根20米长的钢管,截出8米管或6米长管的方法只有三种,设:1x —1根长管截 成2根8米管的根数;2x —1根长管截成1根8米管和2根6米管的根数;3x —1根长管 截成3根6米管的根数。
最优化理论与方法知识点总结最优化理论与方法知识点总结 (1)一、最优化简介: (2)1.1最优化应用举例 (2)1.2基本概念 (2)1.3向量范数 (3)1.4矩阵范数 (3)1.5极限的定义 (3)1.6方向导数存在性和计算公式 (4)1.7梯度定义 (4)1.8海塞矩阵 (5)1.9泰勒展开式: (5)1.10凸集定义 (5)1.11凸集性质 (5)1.12凸函数定义 (6)1.13凸函数判断 (6)1.14矩阵正定与半正定判断 (6)1.15例题(判断矩阵是否正定) (7)1.16凸优化 (7)二、线性规划 (7)2.1线性规划数学模型的一般形式 (7)2.2解的基本定理 (7)2.3解的分类 (8)2.4图解法 (8)2.5例题(图解法) (8)2.6标准型的化法 (9)2.7例题(化为标准型) (9)2.8单纯形法 (10)2.9例题(单纯形法) (11)三、对偶线性规划 (13)3.1对偶问题 (13)3.2单纯形法解对偶问题 (13)3.3对偶单纯形法求解线性规划问题过程 (14)四、无约束优化 (14)4.1无约束优化概述 (14)4.2搜索区间的确定 (15)4.3区间消去法原理 (16)4.4黄金分割法 (17)4.5插值方法 (17)4.6常见的终止准则 (19)4.7最速下降法 (20)4.8牛顿类方法 (20)4.9例题(牛顿类方法) (21)一、最优化简介:1.1最优化应用举例具有广泛的实用性运输问题,车辆调度,员工安排,空运控制等工程设计,结构设计等资源分配,生产计划等通信:光网络、无线网络,ad hoc等.制造业:钢铁生产,车间调度等医药生产,化工处理等电子工程,集成电路VLSI etc.排版1.2基本概念目标函数和约束函数都是线性的,称之为线性规划问题,而有的模型中含有非线性函数,称之为非线性规划。
在线性与非线性规划中,满足约束条件的点称为可行点,全体可行点组成的集合称为可行集或可行域。
解2°:按二次函数计算。
取0x 0=;⎥⎦⎤⎢⎣⎡+++=Λ24222)x (2121x x x x ;⎥⎦⎤⎢⎣⎡=H =4222)x (A ; ⎥⎦⎤⎢⎣⎡=Λ20)x (0;⎥⎦⎤⎢⎣⎡-=Λ-=20)x (p 00; 25.0)p p /()x (p 0T 00T00=Λ-=A s ;⎥⎦⎤⎢⎣⎡-=5.00x 1;⎥⎦⎤⎢⎣⎡-=Λ01)x (1; ⎥⎦⎤⎢⎣⎡-=Λ+Λ-=5.01p )}p p /(p )x ({)x (p 00T001T 11A A ; 1)p p /()x (p 1T 11T 11=Λ-=A s ;T 2]11[x -=;收敛性检查:[]T 200)x (=Λ;得到[]T 11x -=*,4)x (=*f 。
2-2-6 变尺度法在梯度法中,是以)x (f 在k x 处的最速下降方向)x (p k k Λ-=作为搜索方向。
这种搜 索是局部性的,搜索会产生拉锯现象,使收敛放慢。
若要快速收敛,搜索方向应取k x 处的 牛顿方向,即)x ()x (p 1k k k ΛH -=-,式中 )x (k H 是 k x x =处的海森矩阵。
显然,要得到牛顿方向,需要计算二阶导数及海森 矩阵的逆矩阵,相当麻烦。
如果I =H )x (,则梯度方向和牛顿方向一致。
为了克服梯度法 和牛顿法的缺点,可按k k k k k H H g )x (p -=Λ-= (2-32)方向进行搜索。
为保证向下降方向搜索,且计算方便,要求矩阵k H 具有以下性质:1. k H 是正定的;2. 保证110p ,,p ,p -n 关于矩阵A 是共轭的;3. 1+k H 与k H 具有递推关系,即k k k H H H ∆+=+1, (2-33)式中 k H ∆称为校正矩阵。
为使110p ,,p ,p -n 关于矩阵A 共轭,并注意到式(2-32)则有0p p 1T =+k i A ,0g p 11T =++k k i AH ,k i ,,1,0 =。
最优化方法与最优控制复习文件1. 非线性优化的基本概念,最优解的一阶和二阶条件,最速下降方法,拟牛顿法情况,BFGS修正。
2. 变分问题的最优必要性条件推导,各种情况下的必要性条件,Hamilton 函数、拉格让日函数。
PPT 中讲到的最优控制实例,包括求解过程需要掌握。
3. 极大值原理搞清楚,以及PPT 中的计算实例。
4. 动态规划,原理和简单的求解技术。
5. LQR 问题也要看一下。
除此之外,还有几个作业题目大家做一下,如下所示:1. 非线性优化中,从直观考虑最速下降法是一种最快速的迭代优化方法,实际过程中为什么不理想?为什么采用二阶方法?二阶方法中的二阶导数矩阵怎么得到的?有什么要求? (15分)2. 对于函数形式为的优化问题,若采用最速下降法求解,请给出最优搜索方向p k 的表达式。
变量初值为X0=[1,1,1]T ,请写出第一步迭代过程,以及得到的X1的关于搜索步长α0表达式,在这种情况下,使得))0()0((F 0p x α+最小的搜索步长α0应该等于多少?(15分)3. 题目要求如下,采用动态规划方法寻求从A 点到B 点的最小时间路径(A 到B 仅能向前走),(20分)4. 对于以下简单的标量非线性系统,请通过求解相关HJB 方程得到其最优反馈控制策略。
提示,HJB 微分方程允许如此形式的解。
5.写出如下优化控制问题的Hamiltonian 函数、优化求解的必须性条件,并通过必要性条件的求解计算出该优化控制和状态轨线。
最小化目标函数6.根据你对优化控制求解方法的了解,目前对于优化控制问题(或者成为动态优化问题,DAOPs问题)有哪些求解方法,7.。
最优化方法与最优控制复习文件
1. 非线性优化的基本概念,最优解的一阶和二阶条件,最速下降方法,拟牛顿法情况,BFGS
修正。
2. 变分问题的最优必要性条件推导,各种情况下的必要性条件,Hamilton 函数、拉格让日
函数。
PPT 中讲到的最优控制实例,包括求解过程需要掌握。
3. 极大值原理搞清楚,以及PPT 中的计算实例。
4. 动态规划,原理和简单的求解技术。
5. LQR 问题也要看一下。
除此之外,还有几个作业题目大家做一下,如下所示:
1. 非线性优化中,从直观考虑最速下降法是一种最快速的迭代优化方法,实际过程中为什
么不理想?为什么采用二阶方法?二阶方法中的二阶导数矩阵怎么得到的?有什么要求? (15分)
2. 对于函数形式为
的优化问题,若采用最速下降法求解,请给出最优搜索方向p k 的表达式。
变量初值为X0=[1,1,1]T ,请写出第一步迭代过程,以及得到的X1的关于搜索步长α0表达式,在这种情况下,使得))0()0((F 0p x α+最小的搜索步长α0应该等于多少?(15分)
3. 题目要求如下,采用动态规划方法寻求从A 点到B 点的最小时间路径(A 到B 仅能向前
走),(20分)
4. 对于以下简单的标量非线性系统,请通过求解相关HJB 方程得到其最优反馈控制策略。
提示,HJB 微分方程允许如此形式的解。
5.写出如下优化控制问题的Hamiltonian 函数、优化求解的必须性条件,并通过必要性条
件的求解计算出该优化控制和状态轨线。
最小化目标函数
6.根据你对优化控制求解方法的了解,目前对于优化控制问题(或者成为动态优化问题,
DAOPs问题)有哪些求解方法,
7.。