当前位置：文档之家 › 线性代数实验题04-交通网络的流量分析

线性代数实验题04-交通网络的流量分析

  • 格式：doc
  • 大小：30.50 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

线性代数实验题04-交通网络的流量分析

线性代数实验题04-交通网络的流量分析

数学实验报告学号: , 姓名: , 得分: 实验内容:实验题：交通网络流量分析问题（线性方程组应用）城市道路网中每条道路、每个交叉路口的车流量调查，是分析、评价及改善城市交通状况的基础。

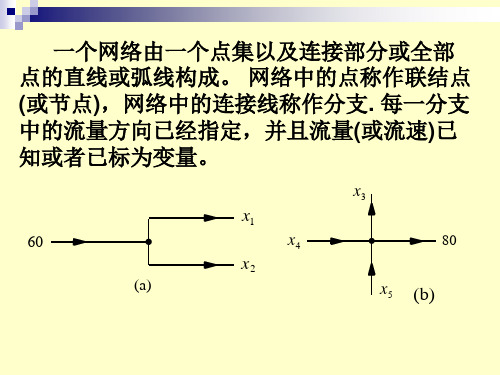
问题：某城市有下图所示的交通图，每条道路都是单行线，需要调查每条道路每小时的车流量。

图中的数字表示该条路段的车流数。

如果每个交叉路口进入和离开的车数相等，整个图中进入和离开的车数相等。

求（1）建立确定每条道路流量的线性方程组；（2）分析哪些流量数据是多余的；（3）为了唯一确定未知流量，需要增添哪几条道路的流量统计。

解：（1）由题意得：x1+ x7=400x1+ x9= x2+300x2+100=300+ x11x3+ x7=350+ x8x4+ x10= x9+ x3x11+500= x4+ x12x8+ x5=310x6+400= x10+ x5x12+150= x6+290整理得：x1+ x7=400x1- x2+ x9=300x2+ x11=200x3+ x7- x8=350-x3+x4+ x10- x9=0-x4+x11- x12=-500x5 +x8=310-x5+x6- x10=-400-x6+ x12= 140将方程组写成矩阵向量形式为AX = b1 0 0 0 0 0 1 0 0 0 0 0 400 x11 -1 0 0 0 0 0 0 1 0 0 0 300 x20 1 0 0 0 0 0 0 0 0 1 0 200 x3A= 0 0 1 0 0 0 1 -1 0 0 0 0 b= 350 X= x40 0 -1 1 0 0 0 0 -1 1 0 0 0 x50 0 0 -1 0 0 0 0 0 0 1 -1 -500 x60 0 0 0 1 0 0 1 0 0 0 0 310 x70 0 0 0 -1 1 0 0 0 -1 0 0 -400 x80 0 0 0 0 -1 0 0 0 0 0 1 140 x9x10x11x12在MATLAB环境中，首先输入方程组的系数矩阵A和方程组右端向量bA=[1,0,0,0,0,0,1,0,0,0,0,0;1,-1,0,0,0,0,0,0,1,0,0,0;0,1,0,0 ,0,0,0,0,0,0,1,0;0,0,1,0,0,0,1,-1,0,0,0,0;0,0,-1,1,0,0,0,0, -1,1,0,0;0,0,0,-1,0,0,0,0,0,0,1,-1;0,0,0,0,1,0,0,1,0,0,0,0; 0,0,0,0,-1,1,0,0,0,-1,0,0;0,0,0,0,-1,0,0,0,0,0,1]b = [400;300;200;350;0;500;310;-400;140]x9+500解得x1=-x2=200x3=- x9+ x10- x12。

应用线性代数解决实际问题

应用线性代数解决实际问题

应用线性代数解决实际问题线性代数作为数学的一个重要分支，广泛应用于各个领域，包括计算机科学、物理学、经济学等。

它不仅是数学家们研究的重要工具，更是解决实际问题的有效途径。

本文将通过具体案例，介绍线性代数在实际问题中的应用，从而展示其强大的解决能力。

案例一：网络流量优化现代社会离不开互联网，而网络流量的优化是提高互联网服务质量的重要问题之一。

假设我们有一组服务器，每个服务器的带宽和消耗成本有所不同，现在需要将用户的请求合理地分配到这些服务器上，以最大化带宽利用率并最小化消耗成本。

这就可以转化为一个线性代数中的线性规划问题。

首先，我们可以用一个向量表示服务器的带宽，用另一个向量表示服务器的消耗成本。

设请求到达的向量为x，那么我们的目标就是最大化带宽利用率和最小化消耗成本，可以构建如下优化模型：maximize cᵀx subject to Ax ≤ b其中，c是服务器的消耗成本向量，x是请求到达的向量，A是服务器带宽的矩阵，b是服务器的带宽上限。

通过求解这个线性规划问题，我们可以得到最佳的请求分配方案，从而实现网络流量的优化。

案例二：图像处理线性代数在图像处理中有着广泛的应用。

以黑白图片为例，可以将其表示为一个矩阵，其中的元素代表每个像素点的灰度值。

通过矩阵的加减、乘除运算，以及线性变换等操作，可以实现图像的平移、旋转、缩放等处理效果。

举个例子，假设我们想要将一张黑白图片的亮度增加一倍。

我们可以将这张图片表示为一个矩阵A，然后构造一个倍增矩阵B，即每个元素都是2。

通过这两个矩阵的乘法运算，即可实现亮度的增加。

这个过程可以用下面的表达式表示：A' = BA其中，A'表示亮度增加后的图像矩阵。

通过线性代数的运算，我们可以方便地实现图像处理中的各种效果。

总结线性代数作为数学的重要分支，具有广泛的应用领域。

本文通过网络流量优化和图像处理两个具体案例，展示了线性代数在实际问题中的应用。

线性代数的强大解决能力不仅能帮助我们解决现实生活中的问题，同时也为我们提供了一种思维方式和方法论。

交通流量调查与分析

交通流量调查与分析

道路交通量调查方法时间安排实习时间：2012年6月18-22日调查日期：交通调查的日期为2012年21日星期四正常工作日调查时间：上午7:30至8:30调差地点平安南大街和槐安路交叉口（珠光灯饰城站）实习目的交通调查是交通工程学科中的一个重要组成部分，交通工程学的发展在一定程度上依靠交通调查工作的开展和数据资料的积累与利用。

交通调查就是通过对多种交通现象进行调查，提供准确的数据信息，为交通规划、交通设施建设、交通控制与管理、交通安全、交通环境保护和交通流理论研究等各方面服务。

交通调查实习是在交通工程专业相关主干专业课学习结束之后进行的，该实习在于帮助学生增强感性认识，更好地理解和掌握交通调查的基本原理、内容与方法，培养学生实践和组织能力，帮助学生掌握交通调查技术和技能，为学生今后更好地参加工作打下牢固的业务基础。

调查内容1、交叉口交通量调查：采用人工计数法，实地调查记录十字型各进口道各流向的车数，调查早高峰交通量的情况。

2、交通延迟调查：采用点样本法实地调查某交叉口延误，并现场记录表。

调查流程周一：动员大会，宣布调查任务，周二：完成人员分配，设计调查方案（下午4点组长到交通办公室开会）周三: 确定调查方案（上午8点全体学生到教室开会）周四: 实地调查（7：30——8：30）周五：统计调查数据，撰写实习报告人员配备及分工调查班级：交通L092班（共26人）组长：郭志勇、杨盼盼调查南进口交通延误调查尚兵、陈铁仁、丁海明、张雪峰北进口交通延误调查张金铜、马立辉、宋阳、耿贺明注意安全1. 调查同学站在人行道上，不准站在机动车与非机动车的隔离带上。

2．禁止横穿马路，一定要走十字路口的人行横道。

交叉口基本情况调查交叉口几何条件调查平安南大街与槐安路交叉口平安南大街与槐安路交叉口卫星图平安南大街与槐安路交叉口概况：南北向的平安南大街是城市主干道，全段为沥青混凝土路面，北进口为4车道设有直右混合车道，直左混合车道。

交通流量问题

交通流量问题
数学实验报告
实验序号.2日期：2005年5月23日
班级
应用数学12级
姓名
罗望
学号
1217020220
实验名称
交通流量问题
问题背景描述：
已知某城市单行道的交通流量（每小时过车数）如下图：
）
假设：1.全部流入网络的流量等于全部流出网络的流量
2．全部流入一个节点的流量等于全部流出此节电的流量
试建立数学模型确定该交通网络未知部分的具体流量
所以：方程有无穷解。
3.求对应的齐次同解方程组通解：
4求特解
特解 =
5.那么，方程的解是X= +k +l （其中，k，l是常数学）
实验结果报告与实验总结：
通过本次实验进一步熟悉建立数学模型的方法，巩固了MATLAB的简单操作。
并能够用MATLAB求线性方程组的通解.不过在实验之中还遇到一些建模方面的问题，我会在以后的实验中不断总结和学习，争取不在同一个地方跌倒。
3.求通解。
4.将增广距阵最简化得t，求特解。
5.求非齐次的通解
实验过程记录（含：基本步骤、主要程序清单及异常情况记录等）：
2.在MATLAB2012a下实现：
>> A=[0 1 -1 1 0 0 0 0 0 0 ;0 0 0 1 1 0 0 0 0 0 ;0 0 0 0 0 -1 1 0 0 0 ;1 1 0 0 0 0 0 0 0 0 ;1 0 0 0 1 0 0 0 0 0 ;0 0 0 0 0 0 1 1 0 0 ;0 0 0 0 0 0 0 0 1 0 ;0 0 0 0 0 0 0 0 -1 1;0 0 0 0 0 0 0 0 0 1;0 0 1 0 0 1 0 1 0 0 ]
思考与深入：

线性方程组应用实例

线性方程组应用实例
线性代数
1.1 交通流量
图 4-1 是某城市的公路交通网络图，交叉路口由两条单向车道组成．图中给出了交通高 峰时段每小时进入和离开路口的车辆数，试计算两个交叉路口间车辆的数量．
1.1 交通流量
解：在每一路口，进入车辆与离开车辆肯定相等，所以得到非齐次线性方程组：
x1 450 x2 610 ， x1 x2
0 0
1 0
0 1
1 1
170
210
1 0 0 1 330 0 0 0 0 0
得同解方程组
x1 x2
x4 x4
330 170
， ，
x3 x4 210 ．
若知道某一路口的车辆数量，则其他路口的车辆数量即可求得．
1.2 化学方程式
在光合作用下，植物利用太阳提供的辐射能，将二氧化碳和水转化为葡萄糖和氧气，该 化学反应的方程式为
160 ，
x2 x3
520 390
x3 x4
480 600
， ，即
x2 x3 40 ， x3 x4 210 ，
x4 640 x1 310 ， x1
x4 330 ，
则有
1 1 0 0 160 1 0 0 1 330
A
0 0
1 1 0 0 1 1
40 210
0， 0，
2x2
12x4 ， 2x2
12x4 0 ，
得到 x1 x2 x3 6x4 ．若令 x4 1 ，则 x1 x2 x3 6 ，化学方程式的形式为 6CO2 6H2O 6O2 C6H12O6 ．
注：在实际问题中，要考虑各变量的实际意义．例如，化学方程式中的各变量应为非负
整数．
线性代数
x1CO2 x2H2O x3O2 x4C6H12O6 ． 为了平衡该方程式，需适当选择 x1 ，x2 ，x3 ，x4 ，使得方程式两边的碳、氢、氧原子数量 分别相等．

交通网络

交通网络


就是说x1, x2, x3, x4这四个未知量中, 任意 一个未知量的值统计出来之后都可以确定 出其他三个未知量的值。
Matlab练习题 某城市有下图所示的交通图, 每条道路都是 单行线, 需要调查每条道路每小时的车流量. 图 中的数字表示该条路段的车流数. 如果每个交叉 路口进入和离开的车数相等, 整个图中进入和离 开的车数相等。 现在需要解决如下问题： （1）建立确定每条道路流量的线性方程组。 （2）分析哪些流量数据是多余的。 （3）为了唯一确定未知流量, 需要增添哪 几条道路的流量统计 。
案例1 交通网络流量分析问题
城市道路网中每条道路、每个交叉 路口的车流量调查，是分析、评价及改 善城市交通状况的基础。根据实际车流 量信息可以设计流量控制方案，必要时 设置单行线，以免大量车辆长时间拥堵。
下图为某城市的局部单行示意图
【问题描述】： 某城市单行线如下图所示, 其中的数字表示该路段每小时按箭头方向行 驶的车流量(单位: 辆).

【模型求解】根据上述等式可得如下线性方 程组。 500 x1 x 2
x1 x4 100 x 2 x3 300 x3 x 4 3 0 0
其增广矩阵
1 1 0 0 1 0 500 0 0 1 100 初等行变换 1 1 0 300 0 1 1 300 0 1 0 0 0 0 0 1 100 1 0 1 600 0 1 1 300 0 0 0 0
(A, b) =
由此可得
x1 x 4 1 0 0 x2 x4 600 x x 300 4 3
x1 x 4 1 0 0 x2 x4 600 x x 300 4 3

线性代数的应用


四、信号流图模型
信号流图是用来表示和分析复杂系统内的信号 变换关系的工具。 x1 G1 x2 u 右图方程如下： x1 = u G2 x2， -G2
x2 = G1 x1
写成矩阵方程 x=Qx+Pu 移项整理，可以得到求信号向量x的公式。
x1 0 G 2 x1 x = G x + 2 1 0 2
4000 2200 6000
四、产品成本的计算
将M和P相乘，得到的矩阵设为Q，Q的第一行 第一列元素为 Q(1,1)=0.1×4000+0.3×2000+0.15×5800=1870
1870 Q = 3450 1670 2220 4020 1940 2070 3810 1830 1960 3580 1740
0 0.9200 -0.7071 -0.3162 lamda = , e = 0.7071 -0.9487 0 1.0000
三、人口迁徙模型
令
1 1 u1 = , u2 = 1 3
它是特征向量的整数化，得到
x k = A x0 = 0.25u2 0.05(0.92) u1
一、药方配制问题
u7=[100;55;0;35;6;50;25;10;20]; U=[u1,u2,u3,u4,u5,u6,u7] [U0,r]=rref(U) 计算结果为
一、药方配制问题
U0= 101000 012003 000101 000011 000000 四个零行 0 0 0 0 1 r= 1 2 4 5 7 从最简行阶梯型U0中可以看 出，R（U）=5，向量组线性 相关，一个最大无关组为 u1，u2，u4，u5，u7， u3=u1+2u2 u6=3u2+u4+u5 故可以配制新药

线性代数数学建模案例(1)


其增广矩阵
(A, b) =
1 1 0 0 500
1 0 0 1 100
1

0 0
0 1 0
0 1 1
1 0 1
100
300 300

初等行变换
0

0 0
1 0 0
0 1 0
1 1 0
600
300 0

由此可得
x1 x4 100
百甚至上千未知量和线性方程。
一个网络由一个点集以及连接部分或全部 点的直线或弧线构成。 网络中的点称作联结点
(或节点)，网络中的连接线称作分支. 每一分支 中的流量方向已经指定，并且流量(或流速)已 知或者已标为变量。
x3
x1
60
x4
80
x2
(a)
x5 (b)
网络流的基本假设是（1）网络中流入与流 出的总量相等；（2）每个节点上流入和流出 的总量也相等。例如，上面两图（a）、（b）。 流量在每个节点守恒。 在类似的网络模式中， 每个结点的流量都可以用一个线性方程来表示。
线性代数数学建模案例 （1）
一、网络流模型
网络流模型广泛应用于交通、运输、通讯、电力 分配、城市规划、任务分派以及计算机辅助设计等众 多领域。当科学家、工程师和经济学家研究某种网络 中的流量问题时,线性方程组就自然产生了,例如,城市 规划设计人员和交通工程师监控城市道路网格内的交 通流量,电气工程师计算电路中流经的电流,经济学家 分析产品通过批发商和零售商网络从生产者到消费者 的分配等. 大多数网络流模型中的方程组都包含了数
Matlab练习题
某城市有下图所示的交通图, 每条道路都是 单行线, 需要调查每条道路每小时的车流量. 图 中的数字表示该条路段的车流数. 如果每个交叉 路口进入和离开的车数相等, 整个图中进入和离 开的车数相等。

线性代数在交通流控制中的应用


文献标识 码： Ａ
文章编号 ： １ ６ ７ １ 一ｌ ４ ４ ０ （ ２ Ｏ ｌ ７ ） ０ ６ ｒ ＿ ＿ ０ Ｏ ７ ２ ＿ ＿ ０ ３
１ 单 行 道 交 通 网络 的 交通 流 量 平 衡 条 件
随着 计 算 机 的飞 速 发展 ， 我们 已然 生活 在 数
字化 时代 。 大数 据 、 云计算 的 出现极 大地 提升 了海
Ａ
ｘ４
１ ３
ｌ
Ｂ
Ｘ ３
图１
本 文针对几种 常见 的城市 交通局域 网络类 型 ， 探讨局 域 网各 结 点 交通 流 量 的 计算 方 法 并 给出
ｘ５
在 交通 流 量 平衡 条 件 下的 一组 流 量值 ， 交 通管制
条件下 流量控制 的可行 性 。
２ 不 同网络交叉点 的交通流量 的计算 。流量单
位： （ 辆Ｉ ｌ ｌ ＇ ， 时） ２ ． １ 含 丁 字 路 口的
体 系。 由于城市 车辆 的增 长和 路 网密 度 的增加 ， 交 叉 口之 问 的相 关性 逐渐 增 强 将 城 市 路 网 中 的多
个 交叉 口作 为 一 个 局域 网 ． 根 据交 通 流最平 衡条
反） 。 各 方 向的交通 流量 控制 ， 与单 行道 方法 相 同 。 各
路 口的交通 信号都 是分 别控 制各 行车 道 ，控 制 方法 与单行 道完 全一致 。 因此 ， 本 文不 再另 行探讨 。 交 通 流 量平 衡值 ， 流 量 的速 度 是交 通 信 号灯 的 控制时间 的重要 依据 。
中 国 ・包 头
职 大 学 报
２ ０ １ ７ 年 第 ６期
线性 代数 在 交通 流控 制 中的应 用

交通流量2


x 2 x3 x4 300 x 4 x5 500 x7 x6 200 800 x1 x 2 800 x1 x5 x7 x8 1000 400 x9 200 x10 x9 x10 600 x8 x3 x6 1000
数学实验报告
实验序号： 班级 信计 2 班 实验名称 交通流量问题 问 题 背 景 描 述 ： 已 知 某 城 市 单 行 道 的 交 通 流 量 （ 每 小 时 过 车 数 姓名 日期：2005 年 5 月 25 日星设：1.全部流入网络的流量等于全部流出网络的流量 2．全部流入一个节点的流量等于全部流出此节电的流量 试建立数学模型确定该交通网络未知部分的具体流量 实验目的：学会用线性代数中线性方程组的有关知识建立交通流量数学模型，并用数学 软件求其问题的全部解。 实验原理与数学模型： 1 由已知条件及假设建立 10 元线行方程组 2 用 MATLAB 软件求其通解 由网络流量假设,所给问题满足如下线行方程组
0 0 0 0 0 η 2= 1 1 1 0 0
赋值给自由未知量（x5,x6）为（0，0）得非齐次方程组的特解
x*
800 0 200 500 0 = 800 1000 0 400 600
0 1 -1 0 0
300 500 200 800 800 1000 400 200 600 1000
0 1 0 0 0 0 0
0 0 1 0 0 0 0
0 0 0 Columns 4 through 6 0 0 0 1 0 0 0 0 0 0 Columns 7 through 9 0 0 0 0 0 1 0 0 0 0 Columns 10 through 11 0 0 0 0 0 0 0 1 0 0 >>
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

数学实验报告
学号: , 姓名: , 得分:
实验内容:实验题：交通网络流量分析问题（线性方程组应用）
城市道路网中每条道路、每个交叉路口的车流量调查，是分析、评价及改善城市交通状况的基础。

问题：某城市有下图所示的交通图，每条道路都是单行线，需要调查每条道路每小时的车流量。

图中的数字表示该条路段的车流数。

如果每个交叉路口进入和离开的车数相等，整个图中进入和离开的车数相等。

求（1）建立确定每条道路流量的线性方程组；
（2）分析哪些流量数据是多余的；
（3）为了唯一确定未知流量，需要增添哪几条道路的流量统计。

解：
（1）由题意得：x1+ x7=400
x1+ x9= x2+300
x2+100=300+ x11
x3+ x7=350+ x8
x4+ x10= x9+ x3
x11+500= x4+ x12
x8+ x5=310
x6+400= x10+ x5
x12+150= x6+290
整理得： x 1+ x 7=400 x 1- x 2+ x 9=300
x 2+ x 11=200
x 3+ x 7- x 8=350
-x 3+x 4+ x 10- x 9=0 -x 4+x 11- x 12=-500 x 5 +x 8=310 - x 5+x 6- x 10=-400 -x 6+ x 12= 140
将方程组写成矩阵向量形式为AX = b
1 0 0 0 0 0 1 0 0 0 0 0 400 x 1
1 -1 0 0 0 0 0 0 1 0 0 0 300 x 2
0 1 0 0 0 0 0 0 0 0 1 0 200 x 3
A= 0 0 1 0 0 0 1 -1 0 0 0 0 b= 350 X= x 4
0 0 -1 1 0 0 0 0 -1 1 0 0 0 x 5
0 0 0 -1 0 0 0 0 0 0 1 -1 -500 x 6
0 0 0 0 1 0 0 1 0 0 0 0 310 x 7
0 0 0 0 -1 1 0 0 0 -1 0 0 -400 x 8
0 0 0 0 0 -1 0 0 0 0 0 1 140 x 9 x 10 x 11 x 12
在MATLAB 环境中，首先输入方程组的系数矩阵A 和方程组右端向量b
A=[1,0,0,0,0,0,1,0,0,0,0,0;1,-1,0,0,0,0,0,0,1,0,0,0;0,1,0,0,0,0,0,0,0,0,1,0;0,0,1,0,0,0,1,-1,0,0,0,0;0,0,-1,1,0,0,0,0,-1,1,0,0;0,0,0,-1,0,0,0,0,0,0,1,-1;0,0,0,0,1,0,0,1,0,0,0,0;0,0,0,0,-1,1,0,0,0,-1,0,0;0,0,0,0,-1,0,0,0,0,0,1] b = [400;300;200;350;0;500;310;-400;140]
解得 x 1=- x 9+500 x 2=200 x 3=- x 9+ x 10- x 12。