南京航空航天大学 结构力学 课后习题答案 第3章

B
M图(kN m)
（1） （2）
解： （1）求支座反力
∑M = 0 ∑F = 0
A y
取左边或者右边为隔离体，可得：
∑M ∑F
x
C
=0
⇒ FBx =
M h
（3） （4）
=0
最后容易做出结构的弯矩图。
3—18 试作图示刚架的 M 图。
C 0.8kN/m 0.5kN/m D E
14.625 4.225 12.8375
3—19 试作图示刚架的 M 图。
20kN
24 16
C
24
16
B FAx A FBy FAy
FBx
1m
2m
2m
2m
M图(kN m)
（1） （2） （3）
解：对整体：
∑M ∑F
y
A
=0
FBy × 4 + FBx ×1 = 20 × 2 FAy + FBy = 20 FAx − FBx = 0 FBx × 2 − FBy × 2 = 0
40kN m
10kN m M图(kN m)
32.5kN
20kN
20kN F(kN) S
解：求支座反力。取整体：
47.5kN
∑M ∑F
A
=0
FB × 8 − 20 ×10 − 10 ×10 × 3 − 40 = 0 FAy + FB − 10 ×10 − 20 = 0
然后即可做出弯矩图，利用弯矩图即可作出剪力图。
然后即可做出整个刚架的弯矩图。结点受力校核如下图。
D
qL 4 qL 2 qL 2
qL 4
qL 4
E
qL 2 qL 2

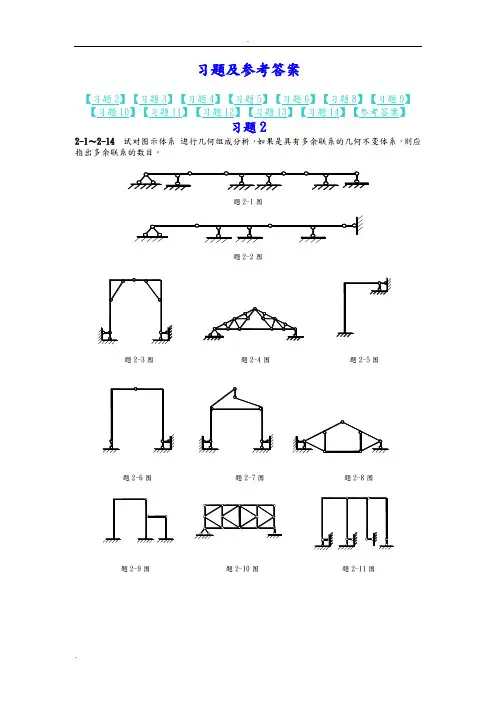
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1～2-14试对图示体系进行几何组成分析，如果是具有多余联系的几何不变体系，则应指出多余联系的数目。

题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。

(b)(a)20kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。

(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。

(c)(b)(a)20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。

P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。

(b)(a)题4-3图4-4 作图示刚架的M 图。

(a)题4-4图4-5 已知结构的M 图，试绘出荷载。

(b)(a)题4-5图4-6 检查下列刚架的M 图，并予以改正。

(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=，试求D 截面的内力。

题5-1图5-2 带拉杆拱，拱轴线方程x x l lfy )(42-=，求截面K 的弯矩。

C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。

习题66-1 判定图示桁架中的零杆。

(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。

(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。

(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。

(a)题6-4图6-5 用适宜方法求桁架中指定杆内力。

(c)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。

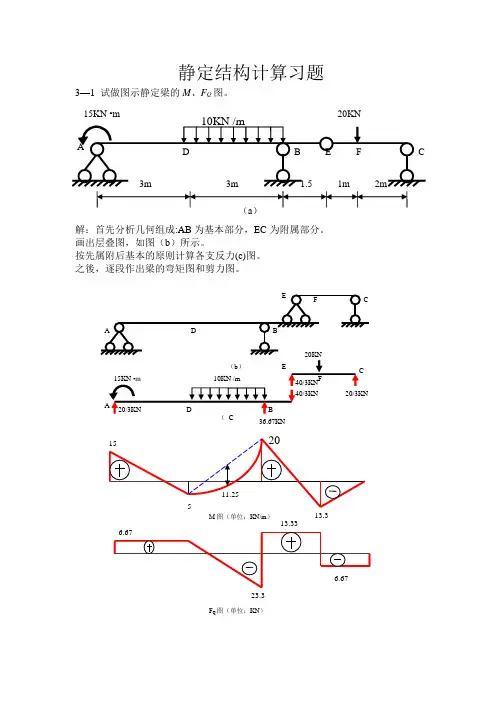
静定结构计算习题3—1 试做图示静定梁的M 、F Q 图。

解：首先分析几何组成:AB 为基本部分，EC 为附属部分。

画出层叠图，如图（b ）所示。

按先属附后基本的原则计算各支反力(c)图。

之後，逐段作出梁的弯矩图和剪力图。

36.67KN15KN •m 20KNM 图（单位：KN/m ）13.323.313.33F Q 图（单位：KN ）3—3 试做图示静定刚架的内力（M 、F Q 、F N ）图，并校核所得结果。

解：（1）计算支反力F AX =48kN （→） M A =60 KN •m (右侧受拉) （2）逐杆绘M 图 （3）绘F Q 图 （4）绘N 图（5）校核: 内力图作出后应进行校核。

(略)3—7 试做图示静定刚架的内力（M 、F Q 、F N ）图，并校核所得结果。

解：（1）计算支反力F AX =20kN （←） F AY =38kN(↑) F BY =62kN(↑) （2）逐杆绘M 图BCM 图（单位：KN/m ） F Q 图（单位：KN ）3030F AX F N图（单位：60）20）（3）绘F Q 图 （4）绘N 图（5）校核: 内力图作出后应进行校核。

(略)3—9 试做图示静定刚架的内力（M 、F Q 、F N ）图，并校核所得结果。

解：（1）计算支反力F AX =0.75qL （←） F AY =-0.25qL( ) F BY =0.25qL(↑) （2）逐杆绘M 图 （3）绘F Q 图 （4）绘N 图（5）校核: 内力图作出后应进行校核。

(略)3—11试做图示静定刚架的内力（M 、F Q 、F N ）图，并校核所得结果。

解：（1）计算支反力F BX =40KN （←） F AY =30KN (↑) F BY =50kN(↑) （2）逐杆绘M 图 （3）绘F Q 图 （4）绘N 图（5）校核: 内力图作出后应进行校核。

(略)C（a ）qBY 23—17 试求图示抛物线三铰拱的支座反力，并求截面D 和E 的内力。

FAy 6 FAx 2 0
1 ql 2A
1 ql 4
取整体：M A 0
Fy 0
取AC： MC 0
取整体： Fx 0
l
l
0.45ql
FBy
1 2l
ql 3l 2
3 ql 4
FAy
ql
3 4
ql
1 4
ql
FAx
2 ql 2 l4
1 ql 2
FBx
1 ql 2
l 2
1 ql B2 3 ql 4
取左段
FNK
ql cos
3l 4
1 q 3 l 2 2 4
9 ql 2 32
D
C
q
3 ql
4
A
1 ql
l
4
1 ql
4
1 ql 4
3 ql
4
FQ KN
1 ql 2
E
4
1 ql 2 4
9 ql2 32
1 ql
B
4
ql 2 8
M KNm
l
1 ql
4
1 ql
4
1 ql
4
FN KN
1 ql2 4
1 ql 4
3－12解：
q C
q
3 ql
4
A
l
1 ql
B
4
Fy 0
FAy
1 ql 4
1 ql 4
l
l
1 ql
4
取BC：
MC 0
FBx
1 4
ql
取整体：
Fx 0
FAx
ql
1 ql 4
3 ql 4
AD段的最大弯矩 M x 3 qlx 1 qx2 dM 3 ql qx 0

S(t) kx(t)
阻尼力D是一种使结构振动不断衰减的力，即结构在振动过程中，由于材料的内 摩擦、构件连接处的摩擦、地基土的内摩擦以及周围介质对振动的阻力等，使得 结构的振动能量受到损耗而导致其振幅逐渐衰减的一种力。阻尼力有集中不同的 理论，目前应用最广泛的是所谓的粘滞阻溺理论，它假定阻尼力的大小与质点的 速度成正比
定出结构质量集中 位置（质心）
将区域主要质量集中在质心； 将次要质量合并到相邻主要质量的质点上去
集中化描述举例
a、水塔建筑
h
h
h
b、厂房（大型钢筋混凝土屋面板）
主要(a质) 水量塔：水箱部分
水塔次要质量：塔柱部分
水箱全部质量 部分塔柱质量
集中到水箱质心
(b) 厂房
主要质量：屋面部分
厂房各跨质(b量) 厂集房中到各跨屋盖标高处
——临界阻尼状态
x(t)
=0 0 1
物体从开始的最大位移处缓慢地逼近平衡位置， 完全不可能再作往复振动——过阻尼状态
1
当 1
1
图 各种阻尼下单自由度体系的自由振动
t 临界阻尼系数： cr 2m
临界阻尼比（简称阻尼比） c
cr
任何一个振动系统，当阻尼增加到一定程度时，物体的运动是 非周期性的，物体振动连一次都不能完成，只是慢慢地回到平 衡位置就停止了。当阻力使振动物体刚能不作周期性振动而又 能最快地回到平衡位置的情况，称为“临界阻尼”，或中肯阻 尼状态。如果阻尼再增大，系统则需要很长时间才能达到平衡 位置，这样的运动叫过阻尼状态，系统如果所受的阻尼力较小 ，则要振动很多次，而振幅则在逐渐减小，最后才能达到平衡 位置，这叫做“欠阻尼”状态。
初始条件: 初始位移 x0 x(0) , 初始速度 x0 x(0)

习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1～2-14试对图示体系进行几何组成分析，如果是具有多余联系的几何不变体系，则应指出多余联系的数目。

题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。

(b)(a)20kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。

(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。

(c)(b)(a)20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。

P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。

(b)(a)题4-3图4-4 作图示刚架的M 图。

(a)题4-4图4-5 已知结构的M 图，试绘出荷载。

(b)(a)题4-5图4-6 检查下列刚架的M 图，并予以改正。

(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=，试求D 截面的内力。

题5-1图5-2 带拉杆拱，拱轴线方程x x l lfy )(42-=，求截面K 的弯矩。

C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。

习题66-1 判定图示桁架中的零杆。

(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。

(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。

(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。

(a)题6-4图6-5 用适宜方法求桁架中指定杆内力。

(c)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。

结构力学章节习题及参考答案第1章绪论（无习题）第2章平面体系的机动分析习题解答习题2.1 是非判断题(1) 若平面体系的实际自由度为零，则该体系一定为几何不变体系。

( )(2) 若平面体系的计算自由度W=0，则该体系一定为无多余约束的几何不变体系。

( )(3) 若平面体系的计算自由度W＜0，则该体系为有多余约束的几何不变体系。

( )(4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。

( )(5) 习题2.1(5) 图所示体系去掉二元体CEF后，剩余部分为简支刚架，所以原体系为无多余约束的几何不变体系。

( )习题2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC后，成为习题2.1(6)(b)图，故原体系是几何可变体系。

( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后，成为习题2.1(6)(c)图，故原体系是几何可变体系。

()(a)(b)(c)习题2.1(6)图习题2.2 填空(1) 习题2.2(1)图所示体系为_________体系。

习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。

习题2-2(2)图(3) 习题2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。

习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。

习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。

习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系，有_________个多余约束。

习题2.2(6)图(7) 习题2.2(7)图所示体系为_________体系，有_________个多余约束。

习题2.2(7)图习题2.3 对习题2.3图所示各体系进行几何组成分析。

(a)(b)(c)(d)(e)(f)习题2.3图(h)第3章(g)静定梁与静定刚架习题解答习题3.1 是非判断题(1) 在使用内力图特征绘制某受弯杆段的弯矩图时，必须先求出该杆段两端的端弯矩。

（1）在 作用下A点的转角为
由此解得
按上述思路，再求C截面两侧的转角，为此作出单位弯矩图，如图(c)所示，则
3-15已测得在图示荷载作用下各点竖向位移为H点1.2 cm，G、I点0.1 cm，F、C、J点0.06 cm，D、B点0.05 cm。试求当10 kN竖向力平均分布作用于15个结点上时，H点的竖向位移。
3-6 (a)
解将悬臂梁在K截面切开，取左边部分，并将K截面内力作为荷载作用在K截面上，如图(a-1)所示。(a-1)所示结构悬臂端的竖向位移就是原结构K截面的竖向位移。作出(a-1)所示结构的Mp和 图，并将Mp图按荷载分解。图乘结果为
3-6 (b)
解
3-6 (c)
解
3-6 (d)
解
3-6 (e)
解
3-9试求图示刚架在温度作用下产生的D点的水平位移。梁为高度h=0.8m的矩形截面梁，线膨胀系数为 =10-5 oC-1。
解
3-10图示桁架各杆温度上升t，已知线膨胀系数 。试求由此引起的K点竖向位移。（画出需要的图）
解
*3-11图示梁截面尺寸为b×h=0.2m×0.6m，EI为常数，线膨胀系数为 ，弹簧刚度系数k=48EI/l3(l=2m)。梁上侧温度上升10℃，下侧上升30℃，并有图示支座移动和荷载作用。试求C点的竖向位移。
解
3-6 (f)
解（1)相对水平位移
（2)相对竖向位移
对称结构在对称荷载作用下的反对称位移等于零
解
3-7试求图示结构在支座位移下的指定位移。
3-7 (a)
解
3-7 (b)
解
3-8图示结构各杆件均为截面高度相同的矩形截面，内侧温度上升t，外侧不变。试求C点的竖向位移。线膨胀系数为 。

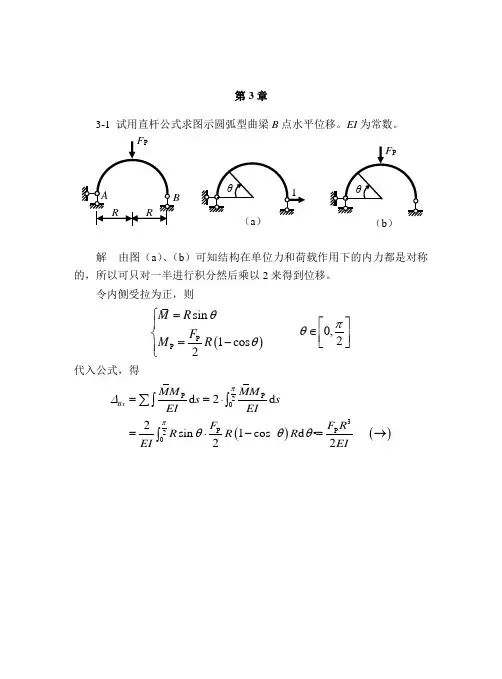
第三章 能量原理（习题解答）3-1 写出下列弹性元件的应变能和余应变能的表达式。

（a ）等轴力杆；（b ）弯曲梁；（c ）纯剪矩形板。

解：（a ）等轴力杆 应变能{}{}2220111()2222T VV VEf U AdV d dV dV E Lf E Lf L L εσεεσεε∆∆⎡⎤======⎢⎥⎣⎦⎰⎰⎰⎰余应变能22*21()2222V V fL fL N N L U BdV dV E E f Efσεσ=====⎰⎰其中L 为杆的长度，f 为杆的截面积，Δ为杆的变形量，E 为材料的弹性模量。

（b ）弯曲梁 应变能{}{}{}{}222222222220111()()22211()()22TTx V V V V l V d w d w U dV dV z dV Ez dVdx dxd w d w E z dydzdx EJ dx dx dxσεσεσ==-===⎰⎰⎰⎰⎰⎰⎰⎰线性余应变能222*220111111()2222l x x V V V My M y M U dV dV dzdydx dx J E E EJJ σε===⋅=⎰⎰⎰⎰⎰⎰（c ）纯剪矩形板 应变能{}{}t b a G dV G dV dV U V V VT⋅⋅⋅⋅=⋅=⋅==⎰⎰⎰22212121γγγτεσ 余应变能Gtfq t b a G dV G dV U V V 222*21212121=⋅⋅⋅==⋅=⎰⎰ττγτ3-2 求图3-2所示桁架的应变能及应变余能，应力—应变之间的关系式为 （a ） E σε= （b ）σ=解：取节点2进行受力分析，如图3-2a 所示。

根据平衡条件，有132131122113cos 45cos 45sin 45sin 4522N N P N N P N N ︒︒︒︒⎧+=⎨=+⎩⇒== （1）311313N Nf f σσ== （2）（a ） E σε=时311313N N Ef Ef εε==（3） 0VU AdV fl d εσε==⎰⎰ （4） 0VU BdV fl d σεσ*==⎰⎰ （5）联立（1）、（2）、（3）、（4），得到桁架的应变能为()()2222121231131322P P P P N N l l U f f f f ⎤+-⎫=+=+⎥⎪⎢⎥⎝⎭⎣⎦联立（1）、（2）、（3）、（5），得到桁架的余应变能为()()222212123113132224P P P P N N l l U E f f E f f *⎡⎤+-⎛⎫=+=+⎢⎥ ⎪⎢⎥⎝⎭⎣⎦（b ） σε=223113222213N N E f E f εε== （6）联立（1）、（2）、（4）、（6），得到桁架的应变能为()()331221222133P P P P l U E f f ⎡⎤+-=+⎢⎥⎢⎥⎣⎦联立（1）、（2）、（5）、（6），得到桁架的应变能为()()331221222136P P P P l U E f f *⎡⎤+-=+⎢⎥⎢⎥⎣⎦3-3 一种假想的材料遵循如下二维的应力—应变规律()()222x x y y y x xy xy EE εσμσεσμσγτ=-=-= 其中E 、G 和μ是材料常数。

第三章结构变形计算一、单位载荷法3-1、求图3-4所示结构的下列各种变形时，广义单位力应如何施加？1、求1点水平位移。

答：在1点沿水平方向施加2、求2点和4点在垂直方向上的相对位移。

答：在2点和4点垂直方向上施加单位力偶。

3、求结构端部1-1、杆的角位移答：在1点和1、点沿水平方向施加单位力偶4、求杆1-1、和3-3、的相对角位移3-2、图3-5示出一空间盒式结构，求下列变形时，广义单位力应如何施加？1、求翼肋Ⅰ、Ⅱ之间的相对转角。

答：在Ⅰ、Ⅱ翼肋上施加一对相反的平面单位力矩。

2、求1-1、-1、、杆的伸长。

答：在1点和1、、点施加沿杆方向的相反的单位力。

3、求节点1和2、之间沿1-2、方向的相对位移答：在1点和2、点施加沿1-2、方向的相反的单位力。

4、求上部开口1-2-2、-1、的剪切变形。

5、求肋Ⅰ、Ⅲ之间的相对翘曲角。

二、结构变形计算3-3、（例题）已知图3-7中所示平面桁架结构，各杆截面积均为f，材料相同，弹性模量均为E，在节点7上受一向下的力P作用。

求：用单位载荷法，计算节点2的垂直位移。

解：结构是逐次连接节点法形成的简单桁架，是静定结构，且不可移动。

（1）求解<P>状态由节点6平衡得：由节点2平衡得：由节点7平衡得：由节点3平衡得：由节点5平衡得：将各杆轴力标在图中。

（2）根据题意加单位载荷，求解<1>状态。

在节点2加向下的垂直力1，单位力由2-5,1-5,4-5杆承受并传到基础上，其余各杆的力均为零。

将各杆内力标在图上，或列在表中。

将<P>状态下的结构变形形态作为虚位移，施加在<1>状态上，因<1>状态，可利用虚位移原理，得：编号杆长度L1 1-2 A 0 2p 02 1-5 p pa3 2-3 A 0 2p 04 2-5 A -1 0 05 3-5 a 0 p 06 3-6 A 0 0 07 3-7 a 0 p 08 4-5 A -1 -3p 3pa9 5-6 A 0 -p 010 6-7 A 0 -p 0答：2点垂直位移大小为，方向向下。

结构力学：第1-11章课后答案(第五版李廉锟上下册) 第一章：结构力学基本原理1.1 选择题1.（D）材料的流变效应是指在恒定的应力下长时间内所发生的持续性变形。

2.（C）结构力学是研究结构在受力作用下的平衡条件、变形特点以及保证结构安全可靠的一门学科。

3.（B）静力学是结构力学的基础和起点，为后续结构力学的学习打下了坚实的理论基础。

4.（D）载荷是指作用在结构上的外力或内力引起的结构内力。

5.（D）结构承受荷载时产生的内力只有两种，即剪力和弯矩。

1.2 计算题1.（略）1.3 解答题1.（略）第二章：静定结构的受力分析2.1 选择题1.（C）静定杆系是指感力作用下平衡的杆件系统。

2.（B）双铰支座在支座点允许的转动是绕一个垂直轴线。

3.（C）简支梁在跨中承受的弯矩最大。

4.（C）连续梁是指有多个支座并且跨度超过3倍的梁。

5.（A）当两个力的作用线相交于一点时，这两个力称为共点力。

2.2 计算题1.（略）2.3 解答题1.（略）第三章：约束结构的受力分析3.1 选择题1.（C）约束支座限制了结构的自由度。

2.（B）在平面约束条件下，三个约束就可以确定结构的静定条件。

3.（A）约束力分解是将复杂的约束力分解为多个简单的约束力。

4.（D）简支梁在跨中承受的弯矩最大。

5.（D）当两个力构成一个力偶时，它们可以合成一个力偶。

若力偶平行于结构截面，力偶不会在结构内产生剪力和弯矩。

3.2 计算题1.（略）3.3 解答题1.（略）第四章：图解法与力法4.1 选择题1.（D）作用在梁上的集中力可以用力的大小和作用点位置的乘积表示。

2.（B）变形图中每个单元代表一个约束力。

3.（C）悬臂梁上的力和矩可以通过力的图解法求解。

4.（D）力法是通过构造力平衡方程解得结构的内力。

5.（A）设计中常用的受力分析方法有解析法、图解法和力法。

4.2 计算题1.（略）4.3 解答题1.（略）第五章：静定系数法与弹性能力法5.1 选择题1.（C）在确定支座反力时，要根据结构属于静定结构、不完全静定结构还是超静定结构来决定求解的方程数。

∑M = 0 ∑F = 0 ∑F = 0
A
FBy × l − q × l ×
l =0 2
（1） （2） （3）
y
FAy + FBy = 0 FAx + FBx − q × l = 0
FBx × l − FBy × l =0 2
x
取右边部分为隔离体：
∑M
C
=0
（4）
解以上方程可得：
ql ⎧ ⎪ FAx = 4 ⎪ 3ql ⎪ =＞ ⎨ FBx = 4 ⎪ ql ⎪ ⎪ FAy = FBy = 2 ⎩
3—10 试不计算反力绘出梁的 M 图。
16
12
4
A
B
8 2m 2m 4m 4m
12 4m
6m
2m
解：从悬臂端和 AB 开始作图。利用区段叠加法和铰结点的弯矩为零，即可做出全部的弯矩图。
3—12 试不计算反力绘出梁的 M 图。
5
华南农业大学 水利与土木工程学院（College of water conservancy and Civil Engineering, SCAU）
1m
D 80
30
40 E
20 40
40 C F
80 E
40
A
解： （1） 求支座反力
B
40
∑F = 0 ∑M = 0 ∑F = 0
y A x
FC − 10 × 4 − 20 = 0 FA − FB = 0
⇒ FC = 60 kN ⇒ FC = 10 kN
（1） （2） （3）
FB ×1 − 50 − 10 × 4 × 6 − 20 × 10 = 0 ⇒ FB = 10 kN
（1）

习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1～2-14试对图示体系进行几何组成分析，如果是具有多余联系的几何不变体系，则应指出多余联系的数目。

题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。

(b)(a)20kN10kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。

(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。

(c)(b)(a)20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。

P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。

(b)(a)题4-3图4-4 作图示刚架的M 图。

(a)题4-4图4-5 已知结构的M 图，试绘出荷载。

(b)(a)题4-5图4-6 检查下列刚架的M 图，并予以改正。

(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l l fy )(42-=，试求D 截面的内力。

题5-1图5-2 带拉杆拱，拱轴线方程x x l lfy )(42-=，求截面K 的弯矩。

C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。

习题66-1 判定图示桁架中的零杆。

(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。

(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。

(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。

(a)题6-4图6-5 用适宜方法求桁架中指定杆内力。

(c)(b)(a)P题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。

结构力学课后习题答案(总23页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1～2-14试对图示体系进行几何组成分析，如果是具有多余联系的几何不变体系，则应指出多余联系的数目。

题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。

(b)(a)20kN10kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。

(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。

(c)(b)(a)/20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。

P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。

(b)(a)题4-3图4-4 作图示刚架的M 图。

(a)题4-4图4-5 已知结构的M 图，试绘出荷载。

(b)(a)题4-5图4-6 检查下列刚架的M 图，并予以改正。

(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=，试求D 截面的内力。

题5-1图5-2 带拉杆拱，拱轴线方程x x l lf y )(42-=，求截面K 的弯矩。

C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。

习题66-1 判定图示桁架中的零杆。

(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。

(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。

(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。

E
2cm
A CB 2cm 2cm
42、求图示结构 A 点竖向位移（向上为正） AV 。
M EI
EI A
a
EI
EI = ∞ 1
3 EI
K = a3
a
a
43、求图示结构 C 点水平位移 CH ，EI = 常数。
M B
2l
C 6 EI k=
l3
A l
44、求图示结构 D 点水平位移 DH 。EI= 常数。
a/ 2 D
a
A
c1
A'
a
B B'
aห้องสมุดไป่ตู้
c2
35、图示结构 B 支座沉陷 = 0.01m ，求 C 点的水平位移。
C l
A
B
l/2 l/2
—— 25 ——
《结构力学》习题集
36、结构的支座 A 发生了转角 和竖向位移 如图所示，计算 D 点的竖向位移。
A
D
l
l l/ 2
37、图示刚架 A 支座下沉 0.01l ，又顺时针转动 0.015 rad ，求 D 截面的角位移。
P
P
l
l
l
l
18、用力法计算图示结构并作弯矩图。
—— 31 ——
100 kN C EI
《结构力学》习题集
100 kN D
2 EI A
2 EI
4m
B
1m
6m
1m
19、已知 EI = 常数，用力法计算并作图示对称结构的 M 图。
q
q
EA=
l
l
l
20、用力法计算并作图示结构的 M 图。EI =常数。
a
P q

3-2 试作图示多跨静定梁的弯矩图和剪力图。

(a) 4P F a2P F a 2P F aＭ4PF Ｑ34P F 2P F(b) ４2020M Q10/326/3４10A B C a a a a a F P a D E F F P 2m 6m 2m 4m 2m A B C D 10kN 2kN/m (c) 21018018040M1560704040Q(d) 7.5514482.524MQ3m 2m2m AB C E F15kN 3m 3m 4m 20kN/m D 3m 2m 2m 2m2m 2m 2m ABC D E FG H 6kN ·m 4kN ·m 4kN 2m 3-3 试作图示刚架的内力图。

试作图示刚架的内力图。

(a) 242018616MQ1820(b) 3030301101010QM 2104kN ·m 3m 3m 2kN A CBD 6m 10kN 40kN ·m ABC D(c) 664275MQ(d) 444444/32MQN2kN/m 6kN 6m 4kN AB CD2kN 6m 2kN 4kN ·m ACB D E(e) 44814``(f) 2222200.815MQN4m ABC4m D4kN A B C2m 3m 4m 2kN/m 3-4试找出下列各弯矩图形的错误之处，并加以改正。

(a) F P(b) (c) F P(d) M(e) (f) F PF P3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件，确定E 、F 两铰的位置。

B C EFDA28ql M2221()222116121618c B C BC C qql M l x x qx xM M M M ql ql x ql x l=-+===\=\=\= 中FD()2ql x -lBC EFxDAql lx3-6 试作图示刚架的弯矩和剪力图。