对球面划分三角形面网格示例.
- 格式:ppt
- 大小:2.19 MB
- 文档页数:19

实验四几何物体的表示——三角网格的表示与显示1.实验目的●熟悉三角网格的表示●熟悉三角网格的显示●熟悉纹理的显示2.实验内容●设计三角网格的数据结构●解析Obj文件格式的三角网格●显示三角网格及纹理贴图3.实验指导存储三角网格数据的文件格式多种多样,常见的文件格式有:●Wavefront OBJ (*.0bj)●3D Max (*.max, *.3ds)●VRML (*.vrl)●Inventor (*.iv)●PLY (*.ply, *,ply2)本实验主要以OBJ文件为例,了解其数据格式,建立三角网格在内存中的数据结构,从而将文件中的数据读取到内存,并最终显示出来。
3.1OBJ文件格式OBJ文件是Alias|Wavefront公司为他的一套基于工作站的3D建模和动画软件“Advanced Visualizer”开发的一种标准3D模型文件格式,很适合用于3D软件模型之间的数据交换。
目前几乎所有知名的3D软件如3dsMax,LightWave,Maya都支持OBJ文件的读写。
OBJ文件是一种纯文本文件,可以直接用写字板打开进行查看和编辑修改。
这种文件以纯文本的形式存储了模型的顶点、法线和纹理坐标和材质使用信息。
OBJ的每一行,都有极其相似的格式,每行的格式如下:其中,前缀标识了这一行所存储的信息类型,参数则是具体的数据。
OBJ文件的前缀可以有:面的格式说明:每个三角面片的数据由f开头,后面跟组成该三角面片的各顶点的顶点坐标索引,纹理坐标索引,顶点法向索引,其格式为:f 顶点坐标索引/纹理坐标索引/顶点法向索引……其中纹理坐标索引和顶点法向索引可以为空,如果为空的索引位于末尾时,’/’也可以省略,例如:f 1 2 3这样的行表示以第1、2、3号顶点组成一个三角形,等同于1// 2// 3//。
f 1/3 2/5 3/4这样的行表示以第1、2、3号顶点组成一个三角形,其中第一个顶点的纹理坐标的索引值为3,第二个顶点的纹理坐标的索引值为5,第三个顶点的纹理坐标的索引值为4。



结构有限元分析中的网格划分技术及其应用实例一、前言有限元网格划分是进行有限元数值模拟分析至关重要的一步,它直接影响着后续数值计算分析结果的精确性。
网格划分涉及单元的形状及其拓扑类型、单元类型、网格生成器的选择、网格的密度、单元的编号以及几何体素。
从几何表达上讲,梁和杆是相同的,从物理和数值求解上讲则是有区别的。
同理,平面应力和平面应变情况设计的单元求解方程也不相同。
在有限元数值求解中,单元的等效节点力、刚度矩阵、质量矩阵等均用数值积分生成,连续体单元以及壳、板、梁单元的面内均采用高斯(Gauss)积分,而壳、板、梁单元的厚度方向采用辛普生(Simpson)积分。
辛普生积分点的间隔是一定的,沿厚度分成奇数积分点。
由于不同单元的刚度矩阵不同,采用数值积分的求解方式不同,因此实际应用中,一定要采用合理的单元来模拟求解。
CAD软件中流行的实体建模包括基于特征的参数化建模和空间自由曲面混合造型两种方法。
Pro/E和SoildWorks是特征参数化造型的代表,而CATIA与Unigraphics等则将特征参数化和空间自由曲面混合造型有机的结合起来。
现有CAD软件对表面形态的表示法已经大大超过了CAE软件,因此,在将CAD实体模型导入CAE软件的过程中,必须将CAD模型中其他表示法的表面形态转换到CAE软件的表示法上,转换精度的高低取决于接口程序的好坏。
在转换过程中,程序需要解决好几何图形(曲线与曲面的空间位置)和拓扑关系(各图形数据的逻辑关系)两个关键问题。
其中几何图形的传递相对容易实现,而图形间的拓扑关系容易出现传递失败的情况。
数据传递面临的一个重大挑战是,将导入CAE程序的CAD模型改造成适合有限元分析的网格模型。
在很多情况下,导入CAE程序的模型可能包含许多设计细节,如细小的孔、狭窄的槽,甚至是建模过程中形成的小曲面等。
这些细节往往不是基于结构的考虑,保留这些细节,单元数量势必增加,甚至会掩盖问题的主要矛盾,对分析结果造成负面影响。


球面网壳结构类型和特点球面网壳主要有交叉桁架体系和角锥体系两大类。
1交叉桁架体系各种形式的单层球面网壳的网格形式均可适用于交叉桁架体系,只要将网壳中的每根杆件用平面网片来代替,即可形成双层球面网壳,注意网片竖杆方向是通过球心的。
单层球面网壳主要类型有:肋环型球面网壳(Ribbed Dome)、施威德勒型球面网壳(Schwedler Dome)、联方型球面网壳(Lamella Dome)、三向格子型球面网壳(three way grid Dome)、凯威特型球面网壳(Kiewitt Dome)和短程线球面网壳(Geodesic Dome)。
双层球面网壳在单层的基础上且网壳上下两层同心进行杆件的交叉复制,使得双层球面网壳的下层杆件连接规律与上层球面一致,上层和下层通过交叉连接,形成交叉桁架体系,即双层球面网壳。
1.1肋环型球面网壳它是由经向和纬向杆件组成,大部分网格呈梯形。
具有网格划分简单,节点构造简单的特点。
但是其杆件长短不一,内力分布不均匀,制作安装工作量相当大。
杆件计算模型应按空间刚接梁单元考虑,一般适用于中、小跨度结构。
图1:勒环型单层球面网壳1.2施威德勒型球面网壳由经向杆、纬向杆和斜杆构成,是肋环型球面网壳的改进形式。
加设斜杆的目的是为了提高结构刚度和其承受非对称荷载的能力。
斜杆布置方法主要有:左向单斜杆、双斜杆、左右向单斜杆和无纬向杆的双斜杆。
在具体工程设计时,应综合考虑荷载特点和支承方式以及材料等因素来确定选用结构布置形式。
这种网壳刚度较大,一般适用于大、中型网壳结构。
图2:施威德勒型单层球面网壳1.3联方型球面网壳联方型球面网壳系德国工程师Zollinger首创,由左斜杆和右斜杆组成菱形网格,两斜杆夹角为30~500之间,造型美观。
为了增强网壳的刚度和稳定性,可在环向加设杆件,使网格成为三角形。
适用于中、大跨度结构。
图3:联方型单层球面网壳1.4三向格子型球面网壳三向格子型是在球面上由三个方向相交成60度的大圆构成,或在球面的水平投影面上将跨度n等分,形成正三角形网格后再投影到球面上,即可得到三向网格型球面网壳。

基于球面三角网格逼近的等距曲面逼近算法*浙江大学CAD&CG 国家重点实验室 刘利刚 浙江大学数学系 王国瑾摘 要 本文给出了一种基于球面三角网格逼近的等距面逼近新算法。
利用三角网格逼近基球面,然后计算此三角网格按中心沿原曲面扫掠而成空间区域的边界作为等距曲面的逼近。
该算法计算简单,方便地解决了整体误差问题,而且所得到的逼近曲面是与原曲面同次数的NURBS 曲面。
关键词 等距曲面,球面,三角剖分,曲面逼近。
0 引 言等距曲线/曲面(offset)在数控机床运动轨迹计算、基于公差带分析的误差理论研究以及带厚度薄片实体(如汽车车身、箱包等)的计算机辅助几何设计中有着广泛的应用。
关于平面曲线的等距曲线已有大量的研究[1—5],但对等距曲面的研究工作则相对较少[6—7]。
设空间参数曲面R :),(v u r r =为正则的, 距离为d 的等距曲面d R 为),(),(),(v u d v u v u d n r r ⋅+=。
由于法向量),(v u n 的分母中出现根式,一张NURBS 曲面的等距曲面一般不再是NURBS 曲面,从而无法被通用的CAD/CAM 系统进行有效的处理。
Farouki [8]给出了三类简单实体(凸多面体、旋转体和拉伸体)表面的等距曲面的精确计算。
Martin [9]证明了Dupin 曲面(曲率线为圆弧的曲面)的等距曲面也是Dupin 曲面。
Pottmann [10]提出了PH 曲面(具有有理等距曲面的一类有理曲面)的概念,并且给出了具有有理等距曲面的可展曲面的显式表达。
吕伟[11]证明了抛物面、椭球面和双曲面的等距曲面是有理的。
Pottmann 等[12]证明了不可展有理直纹面的等距曲面在整个空间是可有理化的。
对于更为复杂的曲面,生成其等距曲面颇为困难。
Farouki [13]利用双三次Hermite 多项式曲面来插值逼近等距曲面。
1999年,Piegl 和Tiller [14]对NURBS 曲面的等距曲面逼近提出了一种新的算法,他们首先判断曲面上包含平面片或旋转面片(球面、环面、锥面和柱面等)的部分;然后根据曲率大小对其它曲面片部分的等距面片进行采样,利用NURBS 曲面进行插值;最后在允许误差范围内去除不需要的控制节点。

球面分割方案球面分割方案是指将球体表面按照一定规则进行划分,以便于进行球面上的计算和分析。
在计算机图形学、物理学、化学等领域都有着广泛的应用。
本文将介绍几种常见的球面分割方案以及它们的特点和应用。
一、经纬度划分经纬度划分是最常见的球面分割方案之一。
它将球体表面划分成一系列纬度和经度线构成的网格。
经度线是垂直于球心的线,从南极到北极穿过球面;纬度线是与经线相交的水平线,从一个极点到另一个极点。
经纬度划分可以用来表示地球上的经纬度坐标。
这种划分方案的特点是简单易用,能够提供全球范围内的坐标表示。
然而,经纬度划分在极地地区存在着畸变,导致区域缩小和形变,不适用于需要高精度分析的情况。
二、正多面体划分正多面体划分是将球面划分成多个等面积的小多面体,如正四面体、正六面体、正八面体等。
这种划分方案适用于需要分析局部区域的情况,例如计算物体表面的法向量、判断点是否在物体表面等。
正多面体划分的优点是可以得到均匀分布的采样点,适用于一些数值计算和模拟问题。
然而,在全球尺度的分析中,正多面体划分会导致分割的边界不连续,不方便进行全球范围内的计算。
三、等距离划分等距离划分是将球面划分成一系列等距离的小区域。
这种划分方案适用于需要精确度高、分辨率均匀的情况,例如全球气候模拟、地质勘探等。
等距离划分的特点是能够保持距离的一致性,对于一些需要考虑地球曲率的问题尤为重要。
然而,等距离划分也存在着数据存储和计算复杂度较高的问题,需要综合考虑实际应用中的需求。
结论不同的球面分割方案适用于不同的应用场景,选择合适的分割方案是保证计算和分析结果准确性的重要一步。
经纬度划分适用于全球范围内的坐标表示,正多面体划分适用于局部区域的分析,等距离划分适用于高精度和均匀分布的需求。
在实际应用中,还可以根据具体需求进行适当的改进和组合,以提高分割方案的效果和适用性。

三角网格数据结构流体力学
三角网格是多边形网格的一种,多边形网格又被称为“Mesh”,是计算机图形学中用于为各种不规则物体建立模型的一种数据结构。
现实世界中的物体表面直观上看都是由曲面构成的;而在计算机世界中,由于只能用离散的结构去模拟现实中连续的事物。
所以现实世界中的曲面实际上在计算机里是由无数个小的多边形面片去组成的。
比如下图的这些模型,在计算机渲染后由肉眼看是十分平滑的曲面,而实际上,计算机内部使用了大量的小三角形片去组成了这样的形状。
这样的小面片的集合就被称作Mesh。
Mesh既可以由三角形组成,也可以由其他平面形状如四边形,五边形等组成;由于平面多边形实际上也能再细分成三角形。
所以,使用全由三角形组成的三角网格(Triangle Mesh)来表示物体表面也是具有一般性的。
实际上,使用无数三角形面片来组成物体,现实世界存在的实物都能以这样的方式建模。
在计算机内存中一旦有了一个物体的Mesh,即意味着计算机有能力渲染显示这样的物体。
具体的渲染算法,以及渲染着色方式等问题,可以参考相关的资料(OPENGL的知识),内部都有详细的叙述。

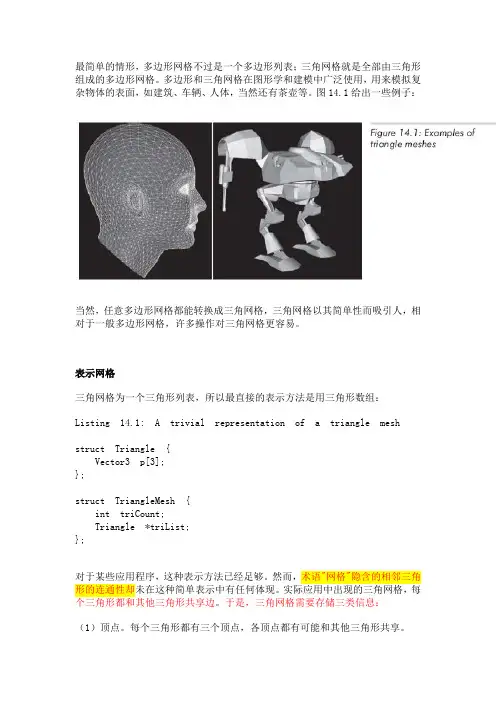
最简单的情形,多边形网格不过是一个多边形列表;三角网格就是全部由三角形组成的多边形网格。
多边形和三角网格在图形学和建模中广泛使用,用来模拟复杂物体的表面,如建筑、车辆、人体,当然还有茶壶等。
图14.1给出一些例子:当然,任意多边形网格都能转换成三角网格,三角网格以其简单性而吸引人,相对于一般多边形网格,许多操作对三角网格更容易。
表示网格三角网格为一个三角形列表,所以最直接的表示方法是用三角形数组:Listing 14.1: A trivial representation of a triangle meshstruct Triangle {Vector3 p[3];};struct TriangleMesh {int triCount;Triangle *triList;};对于某些应用程序,这种表示方法已经足够。
然而,术语"网格"隐含的相邻三角形的连通性却未在这种简单表示中有任何体现。
实际应用中出现的三角网格,每个三角形都和其他三角形共享边。
于是,三角网格需要存储三类信息:(1)顶点。
每个三角形都有三个顶点,各顶点都有可能和其他三角形共享。
(2)边。
连接两个顶点的边,每个三角形有三条边。
(3)面。
每个三角形对应一个面,我们可以用顶点或边列表表示面。
索引三角网格在索引三角网格中,我们维护了两个列表:顶点表与三角形表。
每个顶点包含一个3D位置,也可能有如纹理映射坐标、表面法向量、光照值等附加数据。
每个三角形由顶点列表的三个索引组成。
通常,顶点列出的顺序是非常重要的,因为我们必须考虑面的"正面"和"反面"。
从前面看时,我们将用顺时针方向列出顶点。
另外一些信息也存在这一级中,如预先计算的表面法向量,表面属性(纹理映射)等。
程序清单14.2给出了一段高度简化的代码:Listing 14.2: Indexed triangle mesh// struct Vertex is the information we store at the vertex level struct Vertex{// 3D position of the vertexVector3 p;// Other information could include texture mapping coordinates, // a surface normal, lighting values, etc.}// struct Triangle is the information we store at the triangle level struct Triangle{// Indices into the vertex listint vertex[3];// Other information could include a normal, material information , etc.}// struct TriangleMesh stores an indexed triangle meshstruct TriangleMesh{// The verticesint vertexCount;Vertex *vertexList;// The trianglesint triangleCount;Triangle *triangleList;};实践中,三角网格类会有一系列方法,用于存取和维护顶点、三角形列表。
任意曲面的三角形网格划分任意曲面的三角形网格划分是基于三角形网格生成算法实现的。
这些算法通常采用参数化方法表示曲面,并使用分割线段、迭代细分等方式将曲面划分为许多小的三角形网格。
具体实现过程中,可以采用不同的三角形网格生成算法,如Loop subdivision、Butterfly subdivision等。
这些算法在处理复杂曲面时具有不同的特点和适用范围。
任意曲面的三角形网格划分的优点主要表现在以下几个方面。
三角形网格结构清晰,易于理解和实现。
这种网格划分操作简单,可快速生成并处理大量网格数据。
三角形网格具有广泛的适用范围,可以适用于各种不同形状和性质的曲面。
任意曲面的三角形网格划分在计算机图形学、几何计算和可视化等领域有着广泛的应用。
在计算机图形学中,三角形网格是构建复杂三维模型的基础,也是进行渲染、动画等操作的基础。
在几何计算中,三角形网格可用于表面重建、形状匹配、有限元分析等任务。
在可视化领域,三角形网格可以用于生成高质量的渲染图像和动画,也可用于科学计算结果的可视化。
在使用任意曲面的三角形网格划分时,需要注意以下问题。
由于这种网格生成算法的计算量较大,因此需要优化算法以提高生成效率。
网格生成过程中需要存储大量的网格数据,因此需要合理组织数据结构以减少存储需求。
实现复杂度较高,需要仔细设计算法和数据结构以避免错误和漏洞。
任意曲面的三角形网格划分是一种非常重要的技术,在计算机图形学、几何计算和可视化等领域有着广泛的应用。
通过深入了解这种网格划分的原理和优点,掌握其应用场景及注意事项,我们可以更好地利用这种技术来处理和计算各种不同形状和性质的曲面。
曲面重构是一种从几何形状中提取特征并生成新的几何表示的技术,在计算机图形学、计算机视觉、生物医学工程等领域具有广泛的应用。
三角形网格是一种常见的曲面表示形式,具有灵活性和高效性,因此成为曲面重构领域的重要研究对象。
本文旨在探讨三角形网格上曲面重构技术的现状、研究方法、研究成果及未来发展方向。
球面三角基本公式一、球面三角的基础知识天文学,特别是球面天文学需要球面三角学的知识。
球面三角中,常要用到角度和圆弧的度量关系: 从平面三角学我们知道,一圆周的3601,叫做1度的弧。
1度弧的601叫做1角分的弧。
1角分弧的601叫做1角秒的弧。
根据弧和所对圆心角的关系,可以得出角的量度。
一圆周所对的圆心角为360°。
因此,1度的弧所对的圆心角,叫做1°的角;1角分的弧相对的圆心角,叫做1′;1角秒的弧所对的圆心角,叫做1″。
1° = 60′1′= 60″角和弧的量度单位,常用的有两种:弧度:长度和半径相等的圆弧所对的圆心角,叫做1弧度(rad)。
由于一圆周的长度等于2π个圆半径的弧长,根据以上弧度的定义,得到弧度和度的关系如下:2πrad=360° 1rad=π2360=57.3°= 3438′= 206265″; 或者 1°=3.571rad 1′=(601)°=34381rad 1″=(601)′=2062651rad 如果一个角的值以弧度表示时为θ,那么以度表示时其值为57°.3×θ;以角分表示时为3438′×θ;以角秒表示时为206265″×θ。
为了方便起见,我们用符号θ°,θ′,θ″表示一个角的度数、角分数、角秒数。
θ°=57.3°θ,θ′=3438′θ,θ″=206265″θ当角度很小时,角度的正弦或正切常可以近似地用它所对的弧来表示。
例如:sin1″≈tan1″≈1″=2062651rad 由此得:1rad=206265″=206265 sin1″根据相同的理由,得:sin θ″≈tan θ″≈θ″=206265θ=θsin1″ 上式常写为:θ=θ″sin1″球面上的圆:从立体几何学得知,通过球心的平面截球面所得的截口是一个圆,叫做大圆;不通过球心的平面截球面所得的截口也是一个圆,叫做小圆。