网格划分基本实用技巧——圆和椭圆

应变的计算方法本章介绍了几种网格应变的计算方法，通过分析网格变形的特点及规律,将网格的变形分解为分别沿两个主应变的方向一次变形而得，从而通过欧拉法推导了有限应变解析的方网格应变计算方法,并把三维空间网格的每个网格作为线性孔斯曲面介绍了三维空间网格的应变计算方法。

此外还介绍了工程应变、等效应变和厚度的计算。

4.2 基于欧拉法和有限应变理论解析的方网格计算方法根据有限应变的理论,不同的应力加载可以获得相同的应变结果。

对于近似于平面应力状态的板材成形来说，每个单元体的应变主方向(除去因为位移造成的转动)在成形过程中保持不变。

这样就可以将应变分成不同的加载阶段，利用真实应变的可叠加性，就可以推导出方网格变形的应变计算方法。

连续体的有限变形有两种表述方法。

一种方法的相对位移计算是以变形前后物体内一点作为参考点，即以变形前的坐标作为自变量，这种方法称为拉格朗日法。

另一种方法的相对位移计算是以变形后物体内一点作为参考点，以及已变形后的坐标作为自变量，这种方法称为欧拉法[48］。

这里给出基于欧拉法和有限应变理论解析的方网格计算原理。

4.2。

1 方网格内部的变形设任意方向正方形网格内接于圆网格，将其变形过程分解为两个阶段，如图4-5所示.第一个阶段沿着X方向变形,Y方向保持不变；第二个阶段沿着Y方向变形，X方向保持不变，即应变主方向与坐标轴相平行.变形的结果使圆网格变形为椭圆，正方形网格变形为平行四边形（假设单元网格内沿主应变方向的变形是均匀的）（a)初始网格（b）横向变形后的网格 (c）纵向变形后的网格图4-5 基于有限应变的网格分解变形过程4.2.2 应变主方向和真实应变的计算对于方网格中心的应变，假设网格内部变形是均匀的，所以变形前后四边形对角线的交点就是网格中心，对角线把方网格划分成四个三角形。

将变形后的网格中心和变形前的网格中心重合，建立直角坐标系，如图4—6所示。

图4-6 以欧拉法建立的变形前后网格中心重合的坐标系统根据欧拉方法，以变形之后的网格坐标来分析，将主应变方向定为坐标方向，设X方向为主应变的方向,Y方向为主应变的方向，两个方向分别有拉形比：(4—20）则两个方向的真实应变等于两次分别变形的叠加:(4-21）设变形前方网格边长为，为所取初始三角形的直角边长，则有:取其中初始三角形，其变形后为，根据变形后的网格点坐标、、，得到变形后三角形边长为：（4—22)沿两个主应变方向的拉形比为：（4-23)已知：(4—24)得:(4—25）由此得到根据三角形计算出来的主应变的方向，进而可以求出主应变：(4-26)根据四边形网格划分的三角形分别求出来的主应变的方向和大小，就得到了方网格中心O点的真实应变值。

1.基本几何结构的创建和网格化本章介绍了GAMBIT中一个简单几何体的创建和网格的生成。

在本章中将学习到：z启动GAMBITz使用Operation工具箱z创建一个方体和一个椭圆柱体z整合两个几何体z模型显示的操作z网格化几何体z检查网格的品质z保存任务和退出GAMBIT1.1 前提在学习本章之前，认为用户还没有GAMBIT的使用经验，不过，已经学习过前一章“本指南的使用”，并且熟悉GAMBIT界面以及本指南中所使用的规约。

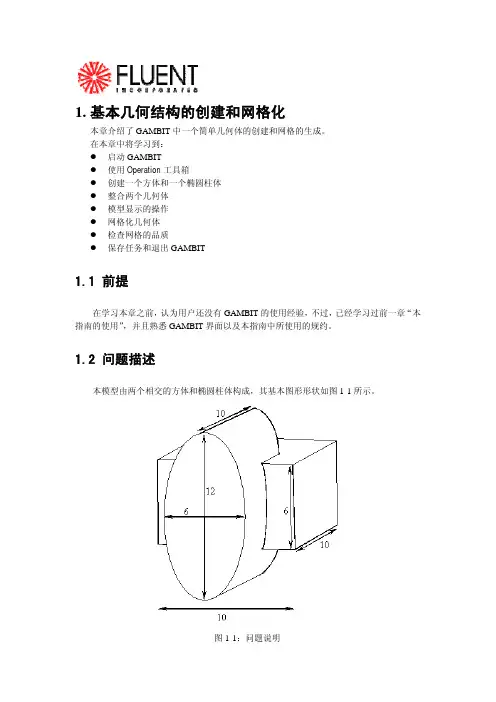
1.2 问题描述本模型由两个相交的方体和椭圆柱体构成，其基本图形形状如图1-1所示。

图1-1：问题说明1.3策略本章介绍使用GAMBIT生成网格的基本操作，特别地，将介绍：z如何使用“top-down”固体建模方法来方便地创建几何体z如何自动生成六面体网格“top-down”方法的意思是用户可以通过生成几何体（如方体、柱体等）来创建几何结构，然后，对它们进行布尔操作（如整合、剪除等），以这种方式，用户不用首先去创建作为基础的点、边和面，就可以快速创建出复杂的几何形体。

一旦创建出一个有效的几何模型，网格就可以直接并且自动地（很多情况下）生成。

在本例子中，将采用Cooper网格化算法来自动生成非结构化的六面体网格。

更复杂的几何结构在生成网格之前可能还需要进行手工分解，这将在后面进行介绍。

本章的学习步骤如下：z创建两个几何体（一个方体和一个椭圆柱体）z整合两个几何体z自动生成网格z检查网格的品质为了使本章的介绍尽量简短，一些必要的步骤被省略了：z调节几何体单边上节点的分布z设置连续介质类型（例如，标识哪些网格区是流体，哪些网格区是固体）和边界类型这些方面的详细内容，也包括其他方面，在随后的章节将涉及到。

1.4步骤输入gambit -id basgeom启动GAMBIT。

这就打开了GAMBIT的图形用户界面(GUI)（图1-2）。

GAMBIT把设定的名称（本例子中为basgeom）作为她将创建的所有文件的词头，如：basgeom.jou。

二阶椭圆问题带单位分解技巧的两重网格方法
王琤;黄自萍;李立康
【期刊名称】《应用数学和力学》
【年(卷),期】2008(29)4
【摘要】标准的两重网格方法是一种求解二阶椭圆问题的局部并行方法,其计算所得数值解在整个求解区域上并不连续.使用单位分解技术,将各个子区域上的局部解粘合在一起,从而得到全局连续解,并证明此解在H1范数意义下最优.更进一步,可以证明通过在粗网格上修正,能够改善其L2误差.数值例子验证了理论的正确性.【总页数】6页(P477-482)
【关键词】二阶椭圆问题;两重网格方法;单位分解
【作者】王琤;黄自萍;李立康
【作者单位】同济大学数学系,上海 200092;同济大学中德学院,上海 200092;复旦大学数学系,上海 200433
【正文语种】中文
【中图分类】O242.21;O246
【相关文献】
1.求解二阶椭圆奇性问题的组合网格法 [J], 钟志鹏;马昌凤;何婵
2.求解二阶变系数椭圆边值问题的代数两网格法 [J], 李明;崔向照;李郴良
3.瞬态N-S方程的二阶全离散稳定化两重网格有限元方法 [J], 刘华蓉;龙文光
4.Navier-Stokes方程带Backtracking技巧的两重网格算法 [J], 任春风;马逸尘;
应根军
5.各向异性网格下二阶椭圆齐边值问题的双线性元的超收敛性分析 [J], 彭玉成;俞迎达
因版权原因，仅展示原文概要，查看原文内容请购买。

rf 微波|射频|仿真|通信|电子|EMC|天线|雷达|数值 ---- 专业微波工程师社区: HFSS FULL BOOK v10中文翻译版568页(原801页)(分节 水印 免费 发布版)微波仿真论坛 --组织翻译 有史以来最全最强的 HFSS 中文教程感谢所有参与翻译,校对,整理的会员版权申明: 此翻译稿版权为微波仿真论坛()所有. 分节版可以转载. 严禁转载568页完整版.推荐: EDA问题集合(收藏版) 之HFSS问题收藏集合 /hfss.htmlQ: 分节版内容有删减吗? A:没有,只是把完整版分开按章节发布,免费下载.带水印但不影响基本阅读.Q: 完整版有什么优势? A:完整版会不断更新,修正,并加上心得注解.无水印.阅读更方便.Q: 本书结构? A: 前200页为使用介绍.接下来为实例(天线,器件,EMC,SI等).最后100页为基础综述Q: 完整版在哪里下载? A: 微波仿真论坛( /read.php?tid=5454 )Q: 有纸质版吗? A:有.与完整版一样,喜欢纸质版的请联系站长邮寄rfeda@ 无特别需求请用电子版Q: 还有其它翻译吗?A:有专门协助团队之翻译小组.除HFSS外,还组织了ADS,FEKO的翻译.还有正在筹划中的任务! Q: 翻译工程量有多大?A:论坛40位热心会员,120天初译,60天校对.30天整理成稿.感谢他们的付出!Q: 只讨论仿真吗?A:以仿真为主.微波综合社区. 论坛正在高速发展.涉及面会越来越广! 现涉及 微波|射频|仿真|通信|电子|EMC|天线|雷达|数值|高校|求职|招聘Q: 特色?A: 以技术交流为主,注重贴子质量,严禁灌水; 资料注重原创; 各个版块有专门协助团队快速解决会员问题; --- 等待你的加入RF rf---射频(Radio Frequency)微波|射频|仿真|通信|电子|EMC|天线|雷达|数值 ---- 专业微波工程师社区: http://bbs.eda .cn rf RF EDA .cnrf---射频(Radio Frequency )致谢名单 及 详细说明/read.php?tid=5454一个论坛繁荣离不开每一位会员的奉献多交流,力所能及帮助他人,少灌水,其实一点也不难打造国内最优秀的微波综合社区还等什么? 加入 RF EDA .CN 微波社区我们一直在努力微波仿真论坛第二节网格网格操作一）本章对Ansoft HFSS v.10.0软件的网格划分提供细节。

九宫格的分割方法
九宫格的分割方法主要涉及到将一个正方形或圆形进行等分，形成九个相等的部分。

具体步骤如下：
1.确定中心点：首先需要确定九宫格的中心点。

对于正方形，中心点是其对
角线交点；对于圆形，中心点则是其圆心。

2.划分线条：以中心点为基准，通过旋转和放射的方式将正方形或圆形划分
为九个相等的部分。

在正方形的四个角上绘制相互垂直的两条等分线，将正方形划分为九个相等的格子。

而对于圆形，可以使用三条通过圆心的射线，将圆划分为九个相等的扇形。

3.细化线条：在绘制好基本线条后，根据需要使用细线进一步细化分割，以
获得更精确的九宫格效果。

除了正方形和圆形外，九宫格还可以应用到其他形状上，如矩形、菱形等。

这些形状的九宫格分割方法与正方形类似，只不过在划分线条时需要根据形状的特点进行调整。

对于九宫格分割的应用，常见的包括版面设计、图案制作、游戏设计等领域。

通过九宫格分割，可以将一个整体划分为相对独立的九个部分，便于进行单独处理和设计。

同时，通过合理利用九宫格的规则，可以创造出更加规整、和谐的设计效果。

Hypermesh补面及划分网格实用手册作者：朱彦峰2008年8月第一章2Dmeshing 过程Hyperworks （为有限元分析做前处理和后处理） —— Hypermesh ： *为forge 提供的是#.nas 文件，2D 网格后的曲面。

使用步骤：1打开hypermesh 软件后，在user profiles 菜单中选择hypermesh 和nastran ；或通过preferences 下拉菜单//user profiles 进行如上操作；2选择files 设置输入文件的参数；将2处点开选择输入文件类型；设置scale factor 和才leanup tol ；在选择import 输入文件。

3输入模型后：Organize >> collectors (给名；改变颜色；选择components ；和pshell。

Shift+F11或Organize >> Entities （按surfs ，将选择的曲面copy 或移入该收集，作为参考）；首先通过左上角model 树将新收集隐藏（在选hide 前应先选configure browser 一次，否则隐藏不了。

210.500利用下面的工具进行放缩/移动和旋转等；（+、-可放缩）； 可用return 返回；利用3处按钮控制模型是否着色显示；并设置Auto 到by 2D top ；4 修补几何体：（1）Geom —— auto cleanup （2）利用，每次只勾选一个复选框，再利用相互切换，同时运用Geom状态下的各个工具修补曲面，消除红色和黄色边界线。

（edge edit —— （un ）supress 可以删除锐角边，便于应力分析及meshing ；）3部分修补工具：***Esc —— return 退出或返回；***F1 —— Hidden line 隐藏线；***F2 —— Delete Entities 删除；***F3 —— Replace 替换；***F4 —— Distance 距离；***F5 —— Mask 掩饰；（遮蔽不必要的部分；或非别mesh不同部分曲面）***F6 —— Edit Elements 编辑；***F8 —— Create Nodes***F9 —— Line edit***F10 —— check elements – Evaluates element quality of the generated mesh ***F12 —— Auto meshToggle 将相切连续以上的边转化为suppressed 边，作为一个平面计算。

网格划分的原则范文网格划分是一种地理信息系统中常用的数据处理方法，可以将地理空间按照一定的划分规则进行分割，从而方便对空间数据进行组织、管理和分析。

网格划分的原则是根据具体需求和数据特点，选择合适的划分尺度和规则。

一、尺度原则1.1数据精度与划分尺度匹配：划分网格时，应根据数据的精度要求选择合适的划分尺度。

如果数据精度较高，可以采用较小的划分尺度，以更精细的方式表示地理空间数据。

相反，如果数据精度较低，可以选择较大的划分尺度，以简化地理空间数据表示。

1.2数据密度与划分尺度匹配：划分网格时，还需考虑数据的密度。

如果数据密度较高，即其中一地区包含了大量的空间数据，可以采用较小的划分尺度，以便更好地表示数据。

而如果数据密度较低，可以适当扩大划分尺度，减少不必要的细节。

二、形状原则2.1正方形网格：正方形网格是最常见的划分形状，适用于大部分地理空间数据的表示和分析。

正方形网格具有统一的尺度和规则，方便计算和处理。

2.2矩形网格：矩形网格根据实际地理形状进行划分，可以更好地与地理实体对应，减少形状扭曲的问题。

但矩形网格的尺度和规则可能较为复杂，需要进行适当的调整和计算。

2.3其他形状网格：根据特殊的地理需求，还可以使用其他形状的网格进行划分，如三角形网格、六边形网格等。

这些形状的网格可以更好地适应特殊地理要素的特点，增加划分的灵活性。

三、分辨率原则3.1等分辨率网格：等分辨率网格是划分过程中最常用的一种方式，即将地理空间均匀划分为相同大小的网格。

等分辨率网格适用于数据分析和统计等需求，便于对空间数据进行比较和计算。

3.2不等分辨率网格：不等分辨率网格根据地理空间的特点进行划分，即在需要更精细表示的区域使用较小的网格尺度，在密度较低或不重要的区域使用较大的网格尺度。

不等分辨率网格适用于关注特定区域的分析和可视化需求。

四、连续性原则4.1连续网格：连续网格是指相邻网格之间无缺口或重叠，可以形成完整的划分区域。