影响系数法

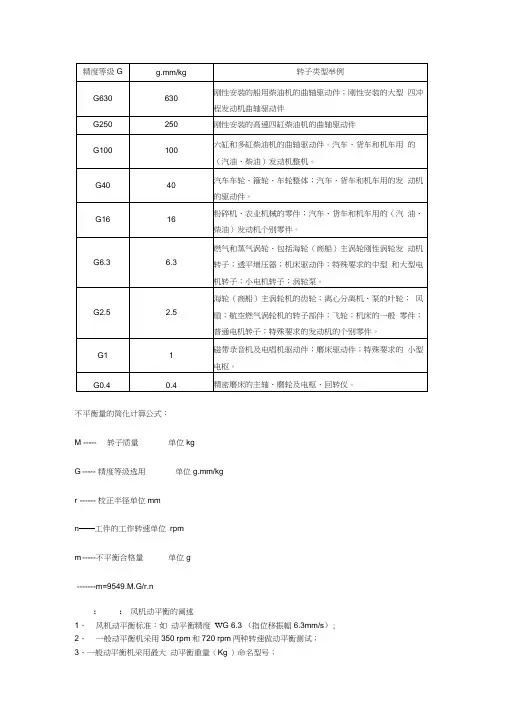
不平衡量的简化计算公式：M ----- 转子质量单位kgG ----- 精度等级选用单位g.mm/kgr ------ 校正半径单位mmn——工件的工作转速单位rpmm ----- 不平衡合格量单位g------- m=9549.M.G/r.n：：风机动平衡的阐述1、风机动平衡标准：如动平衡精度W G 6.3 （指位移振幅6.3mm/s）;2、一般动平衡机采用350 rpm和720 rpm两种转速做动平衡测试；3、一般动平衡机采用最大动平衡重量（Kg ）命名型号；4、动平衡方法：加重平衡和去重平衡；平衡对象：轴，风轮，皮带轮和其它转子6、平衡的原因：一个不平衡的转子将造成振动和转子本身及其支撑结构的应力（应力：材料内部互相拉推的力量，即作用与反作用力）；7、平衡的目的：A, 增加轴承寿命；B, 减少振动；C, 减少杂音；D, 减少操作应力；E, 减少操作者的困扰和负担；F, 减少动力损耗；G, 增加产品品质；H, 使顾客满意。

&不平衡的影响A, 只有一个传动组件的不平衡会导致整个组合产生振动，在转动所引起的振动会造成轴承、轴套、轴心、卷轴、齿轮等的过大磨损，而减少其使用寿命；B, 一旦很高的振动出现，则在结构支架和外框产生应力，经常导致其整个故障；C, 且被支架结构吸收的能量会使得等效率的减低；D, 振动也会经由地板传给邻近的机械，会严重影响其精确度或正常功能。

9、不平衡的原因：不平衡为转子（风轮、轴心或皮带轮等）的重量分布不均匀。

一、叶轮产生不平衡问题的主要原因叶轮在使用中产生不平衡的原因可简要分为两种：叶轮的磨损与叶轮的结垢。

造成这两种情况与引风机前接的除尘装置有关，干法除尘装置引起叶轮不平衡的原因以磨损为主，而湿法除尘装置影响叶轮不平衡的原因以结垢为主。

现分述如下。

1. 叶轮的磨损干式除尘装置虽然可以除掉烟气中绝大部分大颗粒的粉尘，但少量大颗粒和许多微小的粉尘颗粒随同高温、高速的烟气一起通过引风机，使叶片遭受连续不断地冲刷。

影响系数法在引风机现场动平衡中的分析与应用摘要：本文旨在深入探讨影响系数法在引风机现场动平衡中的分析与应用。

本文概述了对影响系数进行前期预测的原理和方法，并通过实例说明了影响系数法在引风机现场动平衡中的应用及优势。

研究表明，采用影响系数法分析引风机现场动平衡问题，可以从多个方面解决动平衡问题，大大提高工作效率、节省时间和成本。

关键词：影响系数法；引风机；现场动平衡正文：引风机的现场动平衡是一项极其重要的任务，它必须保证引风机的运转稳定性和振动是否超出预定的范围，例如Vibration Severity指标(VS)。

因此，需要对引风机现场动平衡进行及时有效的分析和处理，以确保引风机的稳定性和可靠性。

影响系数法是对引风机现场动平衡中常用的一种分析方法，它可以有效预测并分析引风机振动，从而更好地控制引风机现场动平衡。

首先，影响系数通过测量现场的动平衡条件来计算，然后根据实际动平衡情况，通过调整影响系数来优化实际的动平衡条件，并且可以估算出预期的振动水平。

本文从理论和实践的角度深入探讨了影响系数法在引风机现场动平衡中的分析与应用。

实例说明，影响系数法可以有效解决现场动平衡问题，同时可以大大提高工作效率、节省时间和成本。

综上所述，本文介绍了影响系数法在引风机现场动平衡中的应用，并指出了其优势和局限性，为引风机运行安全提供可靠的技术保障。

影响系数法也可以用于现场动平衡的优化，以改善当前系统的性能。

首先，通过计算动平衡条件下的影响系数，可以快速准确的判断系统的动平衡状态。

同时，可以通过改变影响系数来达到优化系统的目的，从而有效抑制振动噪声。

此外，影响系数法还可以用于风扇的在线检测和诊断，它可以实时监测风扇的运行状况，从而定位和解决存在的动平衡问题。

另外，通过影响系数法，可以准确掌握风扇轴承状态，从而实现及时更换轴承和轴承维护，保持风扇的正常运转状态。

总之，影响系数法是一种高效的引风机现场动平衡分析与应用方法，它可以从多种方面解决动平衡问题，有助于风扇的快速、准确的动平衡，大大提高工作效率、节省时间和成本，确保风扇的可靠运行。

实用文档
影响系数法
影响系数法步骤
所谓的现场动平衡使用的方法，比较常用的就是影响系数法。

1、首先测转频的振幅和相位。

2、测量该设备时要知道该设备为刚性还是柔性转子，是有区别的，工作转速是
在临界转速前运行还是在临界转速后运行，加试重的方法是不一样的，具体情况具体分析。

3、通过振幅的大小及相位的位置，在该位置加试重（也就是欠量），试重的一般
追寻以下公式：WP=0.15MS÷R（N/3000）2
WP为实验质量（g）
M为转子的质量（kg）
R为加试重的半径（mm）
S为原始振动幅值（um）
N为平衡转速（r/min）
通过计算得出大约需试配重的重量。

4、测取加试重后的振幅和相位。

5、计算出设备应加重量和位置。

当转子的长度大于半径时，可能要通过双面平衡才能达到满意的效果。

1、双面的动平衡需要选两个加重平面及两个测振点。

2、测量两个测点的初始振动，在两个面同时加试重，得出两面的振动和相位。

也可单面逐个试加配重，视情况灵活运用。

测出振动的幅值和相位。

3、计算出需要加双面的重量和相位。

现场动平衡大约需要1—2次的配重，一般就可比较满意。

也有特殊情况，3次基本解决。

影响系数法与振型分离法在转子动平衡中的应用韩继敏，杨金芳，贲喜鹏（哈尔滨电机厂有限责任公司，黑龙江哈尔滨150040）摘要：针对汽轮发电机转子平衡装备和装配条件相对稳定的特点，假定每台转子装配完成后，其测试条件、轴承刚度等都不变，则可以认为同一种型号的转子装配完后，其振动响应是相同的，即其影响系数相同。

使影响系数法与振型分离法相结合，计算出每阶振动的影响系数，再按此系数加重平衡，可减少启车次数、减少加重次数、减少计算次数。

关键词：汽轮发电机转子动平衡；振动；振型分离法；影响系数法0引言长期以来，汽轮发电机转子动平衡工序一直采用振型分离法进行转子动平衡。

其工期长、效率低直接影响人力、能源消耗以及产品进度，远远不能满足近现代化生产的需要。

为此，试验使用影响系数法与振型分离法相结合进行转子动平衡。

1传统的300MW、600MW汽轮发电机转子动平衡方法概述长期以来，中小型汽轮发电机转子动平衡沿用振型分离法。

转子从机械加工到下线结束，产生的不平衡量较多，这种平衡方法在当时条件下是比较适用的。

只是每台转子的平衡过程复杂、周期长，使转子动平衡环节近乎成为工厂生产的瓶颈。

转子以某一转速转动时，他的振动形状通常由多个振型组成。

如果转速发生变化，其振动形状也会随之改变。

与刚性转子不同，这种变化不是随转速的增加呈线性增大，而是组成它的各个振型做非线性变化，使得合成的振型表现为类似的非线性。

如果转速与某一阶固有频率相等，这时整个转子将只以与这阶频率对应的振型振动，其余各阶振型将不表现出来。

振型分离法动平衡流程如图1所示。

振型分离法动平衡特点有以下几点：图1振型分离法动平衡流程图1）启停机次数多采用这种方法动平衡，由于每阶振动均采用端部试加重、重量调整、计算、移重等多个环节平衡，因此造成开车、升速次数增多。

—56—2013．No．3影响系数法与振型分离法在转子动平衡中的应用试验与检测2）加重及重量调整次数多用这种方法平衡加重频次高，由外到内（即由端部到本体）需一步步多次加重才能达到平衡效果。

动平衡计算中影响系数的通解算法及其应用动平衡的质量，在动平衡计算方法上已作了大量的工作。

自1964年Goodman将最小二乘法引入柔性转子的动平衡计算中后，影响系数算法一直是动平衡试验中最常用的方法。

虽然这种方法有其固有的缺陷，但考虑的平衡面数、平衡转速数、“测点”数较多时具有一定的误差补偿能力。

按传统的影响系数算法，为求出各面的影响系数，需在每个加重面上分别单独加重，从而求得各面的单面影响系数。

但是在现场的动平衡试验中，常常是多平面同时加重，需要解决一些特殊条件下的影响系数的计算及提炼问题，即采用非常规的影响系数计算方法。

这些情形包括：（1）在熟知性能的机组上尝试一次加重或多面同时加重，当尝试的次数达到一定时，各加重平面的影响系数的分离计算。

（2）在多面同时加重时，若某些面的影响系数已知，加重次数足够时，未知面的影响系数的分离计算。

（3）包括试加重在内的加重次数超过了确定影响系数所必需的次数时，如何充分利用冗余的加重信息计算各面的影响系数。

对于以上的较为特殊的影响系数的计算问题，影响系数的分离计算在面数多于2个时，手工计算十分困难。

而加重次数冗余时影响系数的计算遵循何种准则，如何计算又是一个值得探讨的问题。

本文推导了涵盖以上3个方面特殊情形影响系数求解通式，它也适合于一般意义下的影响系数的求解。

1影响系数求解通式的推导设在某次动平衡试验中，有m个加重平面，n个“测点”，同一测点不同转速情况亦视为一新的“测点”。

对于多面同时试重的情形，须足够次的试（加）重后才能计算影响系数。

一般对于具有m个平面、n个“测点”的平衡计算问题，至少需m次的试重确定各面的影响系数值，并且每次试重并不要求只在一个面加重，允许每次在可加重的m个平面上任意加重。

为了使推导的公式适用于一般情形，假设在总共m个加重平面中，有k（k≤m）个加重面的影响系数未知。

另在试验中共有h次（试）加重，且加重次数满足h≥k。

在这种条件下，加重次数多于唯一确定未知影响系数所需的加重次数，即有冗余的加重信息，此时可利用冗余的信息对影响系数进行提炼，取代一般的矢量平均的办法，充分利用加重信息。

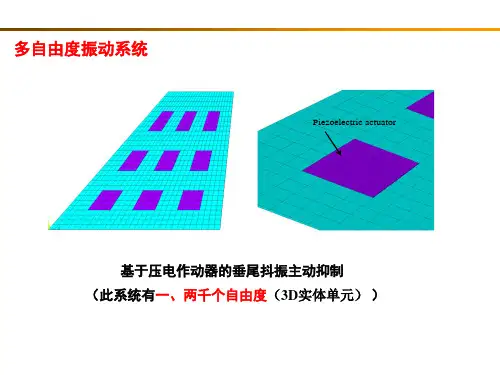
多自由度系统的运动微分方程牛顿第二定律矢量建模方法 影响系数法•刚度影响系数法•柔度影响系数法Lagrange方程方法•约束、自由度与广义坐标•Lagrange方程建模方法多自由度系统的运动微分方程牛顿第二定律建模多自由度系统的运动微分方程--牛顿第二定律建模以1m 为研究对象，有()())(1122111221111t F x x c x c x x k x k xm +−+−−+−=&&&&& （1） 以2m 为研究对象，有()())(2232321221212t F x c x k x x c x x k xm +−−−+−=&&&&& （2）将方程(1)、（2）整理可得多自由度系统的运动微分方程--牛顿第二定律建模()[]()[])(1221212212111t F x k x k k x c x c c xm =−++−++&&&& （3） ()[]()[])(2232122321212t F x k k x k x c c x c xm =++−+++−+&&&& （4） 将方程(3)、(4)写成矩阵形式⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡+−−++⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡+−−++⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡)()(002121322221213222212121t F t F x x k k k k k k x xc c c c c c x x m m &&&&&&即)(t F kx x C xM =++&&& 多自由度系统的运动微分方程--牛顿第二定律建模这种用矩阵写出的运动微分方程与单自由度系统的运动微分方程非常相似。

象例题中在各个离散质量上建立的坐标系为描述系统的物理坐标系，在此坐标下的系统质量矩阵、阻尼矩阵和刚度矩阵为系统的物理参数。

一、单自由度系统的振动2()()0()(nmx t kx t x t w x t +=⇔+120)cos sin cos n n A w t A w t x =+=2()()()0()2()()0n n mx t cx t kx t x t w x t w x t ξ++=++= 211)(nn w t w t e X e ξξ--=+自然频率 阻尼率 22n c c mw mkξ==w 2()2()(()cos(n n nw td x t w x t w x t t C ew t ξξψ-++=-：尼激0 ()cos(n x t C w t =-幅频曲线及其特性 ()H w 1：此时力与位移相位相反sin nwt c =/2/22T T T -=⎰周期函数将失去周期性，而离散频谱将转化为连续谱，此时傅里()()(mx t cx t kx t ++21)[1(/)n n c k w w ∞==-∑00sin n dx x ξωω+0sin n n x t ωω +自由振动是强迫振动的基础，任一时刻的强迫振动响应其实只是该时刻前被激起的一系列自由振动的叠加。

2()2()()n nx t w x t w x t ξ++=1()()()2iwtt H w F w e dw π+∞-∞=⎰()()()mx t cx t kx t ++=拉普拉斯变换：()(0)(()()()F s mx ms X s D s D s ++=+拉氏反变换：11()[()]2jw jwx t L X s j γγπ+--==⎰牛顿第二定律、定轴转动方程、能量原理、拉格朗日方程一般情况采用解析法求解，对于非线性方程，常采用数值方法求解振动系统反作用力近似为位移和速度的函数：)x 泰勒展开并取cx 结论：弹簧刚度与阻尼系数实际上是泰勒展开式中定义：单位位移所需要的力。

弹簧串联、并联，关键在于共力还是共位移用积分计算结构运动时的动能，得到某结构的等效质量/d m ；经变形法；能量法：max V不变，响应振幅与激振力振幅正比，为滞后激励多少，Ψ初相位微小的阻尼就可以限制振幅的无限扩大共振需要一个较长的建立过程，机器需有足够的加速功率顺利通过共振区。

影响力系数公式
影响力系数公式是计算一个人、品牌或事件在社交媒体上的影响力的一种方法。

它通常是通过计算特定指标的加权平均值得出的。

该公式的一般形式是：
影响力系数 = (关注者数量×0.4 + 点赞数×0.3 + 评论数
×0.2 + 转发数×0.1)÷总体数据
其中，关注者数量代表该个人或品牌在社交媒体上的粉丝数量，点赞数代表对其内容点赞的数量，评论数代表对其内容评论的数量，转发数代表对其内容转发的数量，总体数据代表对应指标的总量。

该公式的权重系数可以根据具体情况进行调整。

影响系数法
影响系数法是一种常用的风险评估方法,通过计算出风险事件发生的概率和对组织的影响程度,来评估组织面临的风险的大小和严重性,进而制定相应的风险应对措施。

该方法通常分为四个步骤：首先确定风险事件的可能性和影响程度,然后对两者进行排列组合,计算出每种风险事件的影响系数,最后将各种风险事件的影响系数相加,以求出整体风险对组织的威胁程度。

影响系数法被广泛用于企业风险管理、信息安全管理、项目管理等领域,帮助组织制定更全面、有效的风险应对措施,最大程度地减少、避免风险对组织造成的损失。