设置修正系数及阻尼方法

阻尼1 引言静止的结构，一旦从外界获得足够的能量（主要是动能），就要产生振动。

在振动过程中，若再无外界能量输入，结构的能量将不断消失，形成振动衰减现象。

振动时，使结构的能量散失的因素的因素称为结构的阻尼因素。

索罗金在其论著中将结构振动时的阻尼因素概括为几种类型，即界介质的阻尼力；材料介质变形而产生的内摩擦力；各构件连接处的摩擦及通过地基散失的能量。

百多年来，不同领域的专家，均根据自身研究的需要，着重研究某种阻尼因素，如外阻尼、摩擦阻尼、材料阻尼及辐射阻尼等。

对于材料阻尼的物理机制，文献[82]、[126]、[127]等分别做了简要描述。

材料阻尼是一个机制比较复杂的物理量，由多种基本的物理机制组合而成。

如金属材料中的热弹性、晶体的粘弹性、松弛效应、旋转流效应、电子效应等对阻尼均有贡献。

对一般的非金属材料（如玻璃、各种聚合物等），电子效应对能量的损失影响较小。

温度、绝热系数等也是影响阻尼的重要因素。

一般来说，非金属材料的能量损失比金属大。

此外地质岩石由不同种固体微粒组成，且有空隙体积，因此，其阻尼特性与一般材料不同。

岩石中能量损失主要由三个物理机制构成：岩石内部微粒间的粘性=岩石的内摩擦及较大的塑性变形，而岩石的内摩擦与岩石内部微粒间接触处的位错及塑性变形有关。

如献[82]所述，为了计算、分析结构在外界载荷作用下产生的反应，人们建立了描述固体材料应力应变关系的物理模型。

最简单的物理模型是单参数模型，即材料只产生弹性应力或只产生粘滞应力，但这两种模型不能代表材料中真实存在的粘弹性。

人们又建立了双参数线性模型，即Maxwell及Kelvin模型。

其中Maxwell模型由线性粘滞体和线弹性体串联而成，Kelvin模型是此二者并联而成的。

若设线粘滞体的应变为一般情况下，在结构振动分析设计中，与弹性力和惯性力相比，阻尼力在数值上较小。

然而，在一定条件下，阻尼因素将起很重要的作用。

如果没有阻尼力存在，振动体系在共振时将达到非常大的幅值。

PID调节参数及方法PID控制是一种常用的自动控制方法，它可以根据系统的实时反馈信息，即误差信号，来调整控制器的输出信号，从而实现系统的稳定性和性能优化。

PID调节参数是PID控制器中的比例系数、积分系数和微分系数。

调节这些参数可以达到所需的动态性能和稳态精度。

下面将介绍PID调节参数及常用的调节方法。

1.比例系数（Kp）：比例系数用来调节控制器输出信号与误差信号的线性关系。

增大比例系数可以加快系统的响应速度，但可能会引起系统的超调和不稳定。

减小比例系数可以提高稳定性，但可能会导致系统的响应速度变慢。

调节比例系数的方法一般有经验法和试探法。

经验法：根据经验将比例系数初值设为1，然后逐渐增大或减小，观察系统的响应情况。

当增大比例系数时，如果系统的超调量明显增加，则应适当减小比例系数；相反，如果系统的超调量过小，则应适当增大比例系数。

反复调节，直到得到满意的响应。

试探法：根据系统的特性进行试探调节。

根据系统的频率响应曲线或步跃响应曲线，选择适当的比例系数初值，然后逐渐增大或减小，观察系统的响应。

如果系统的过冲量大，则应适当减小比例系数；如果系统的响应速度慢，则应适当增大比例系数。

反复试探调节，直到得到满意的响应。

2.积分系数（Ki）：积分系数用来补偿系统的静差，增加系统的稳态精度。

增大积分系数可以减小系统的稳态误差，但可能会引起系统的震荡和不稳定。

减小积分系数可以提高稳定性，但可能会导致系统的静差增大。

调节积分系数的方法一般有试探法和校正法。

试探法：将积分系数初值设为0，然后逐渐增大，观察系统的响应。

如果系统的震荡明显增强，则应适当减小积分系数；相反，如果系统的响应速度慢，则应适当增大积分系数。

反复试探调节，直到得到满意的响应。

校正法：根据系统的静态特性进行校正调节。

首先将比例系数设为一个适当的值，然后减小积分系数，直到系统的静差满足要求。

这种方法通常用于对稳态精度要求较高的系统。

3.微分系数（Kd）：微分系数用来补偿系统的过冲和速度变化，增加系统的相对稳定性。

第32卷第3期桂林理工大学学报Vo L32 No．3 2012年8月Journal of Guilin Unive rs it y of Tech nology Aug．2012文章编号：1674—9057(2012)03—0316一04doi：10．3969／j．is sn．1674-9057．2012．03．005关于地基阻尼比测试分析方法的讨论和改进昊邦达(五洲工程设计研究院，北京100053)摘要：近年因编制国家液压振动台基础技术规范，由于地基阻尼比很重要，须对国内外某些主要测试和分析方法有所了解、研究，并作讨论和改进。

本文介绍了切线法、点峰法、双峰法、多峰法、比拟法等方法的优缺点：点峰法可用线位移响应曲线相对宽度左半宽得出，阻尼比偏低，不宜用于需用阻尼控制共振的大型强振台基础设计；多峰法计算出的阻尼比值较大，可用于大型振动台基础的设计；对弹性半空间理论实用化的莱斯默比拟法，通过实测和论证，作了修正，用于新编规范，提高了我国长期以来使用的小阻尼比值。

既能与国际接轨，又更为实用，且不失安全，经济效益显著。

关键词：地基阻尼比；切线法；点峰法；双峰法；多峰法；莱斯默比拟法中图分类号：TU435 文献标志码：A自20世纪80年代以来，我国已引进不少液压法等，主要内容见其中的第3部分。

经分析比较，振动台，国内亦力争自行制造，因而13益增多。

由最后确定只用点峰法，先后公开用于文献[2—于是新型激振器，基础设计不包括在现行国家动力5]。

至于切线法、双峰法，由于认为缺点是较粗机器基础设计规范之内。

设计中缺乏经验，已出现糙，至今一直未见公开应用。

文献[1]因未公开不少问题，因此需要编制一基础规范以利于工作。

出版而无馆藏，现在很难查到。

重点之一在于地基阻尼比的取用，这是由于振动台为了了解当时规范编制的背景，笔者查阅了频带宽、激振力大、振动强烈，须用地基阻尼比控译本文献[6]及其原文本，原文本出版于1970 制共振，充分发挥阻尼作用。

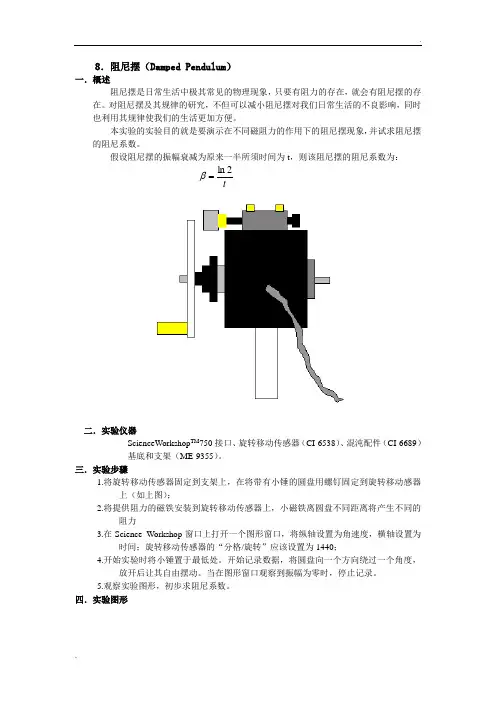
8．阻尼摆（Damped Pendulum）一．概述阻尼摆是日常生活中极其常见的物理现象，只要有阻力的存在，就会有阻尼摆的存在。

对阻尼摆及其规律的研究，不但可以减小阻尼摆对我们日常生活的不良影响，同时也利用其规律使我们的生活更加方便。

本实验的实验目的就是要演示在不同磁阻力的作用下的阻尼摆现象，并试求阻尼摆的阻尼系数。

假设阻尼摆的振幅衰减为原来一半所须时间为t，则该阻尼摆的阻尼系数为：t 2ln=β二．实验仪器ScienceWorkshop TM750接口、旋转移动传感器（CI-6538）、混沌配件（CI-6689）基底和支架（ME-9355）。

三．实验步骤1.将旋转移动传感器固定到支架上，在将带有小锤的圆盘用螺钉固定到旋转移动感器上（如上图）；2.将提供阻力的磁铁安装到旋转移动传感器上，小磁铁离圆盘不同距离将产生不同的阻力3.在Science Workshop窗口上打开一个图形窗口，将纵轴设置为角速度，横轴设置为时间；旋转移动传感器的“分格/旋转”应该设置为1440；4.开始实验时将小锤置于最低处。

开始记录数据，将圆盘向一个方向绕过一个角度，放开后让其自由摆动。

当在图形窗口观察到振幅为零时，停止记录。

5.观察实验图形，初步求阻尼系数。

四．实验图形图1图2图3 五．阻尼系数求法（第二组蓝色）在窗口上用鼠标点击标尺图标按钮，在图形窗口中读出最大振幅的值，如图4图4则振幅最大值的对应时间显示在横轴下（如上图），以同样的方法找出振幅大小减为一半时对应的时间，记录到下表中。

图5 图6求得的平均值与振幅修正可得比较精确结果。

六．实验数据处理实验数据处理应用图形：数据处理表振幅最大对应时间(s) 振幅减半对应时间(s)时间差t(s) t2ln=β1.170 10.643 9.473 0.0732由以上计算可得阻尼系数为0.0732。

墙式黏滞阻尼器在某学校消能减震设计中的应用分析刘荣林，杜晓菊(基准方中建筑设计股份有限公司，四川成都 610015)[摘要]：根据《四川省建设工程抗御地震灾害管理办法》及《建设工程抗震管理条例》要求，成都某中、小学校采用墙式黏滞阻尼器的消能减震设计。

选取该小学单体5为例，采用框架结构,综合考虑建筑使用功能和结构抗震要求,在1~3层共布置18套黏滞阻尼器。

建立未设置阻尼器和设置阻尼器两种结构模型,YJK5.2.1模型未建立阻尼器进行小震及等效中震包络设计,SAP2000(V24.0)建立阻尼器进行中震快速非线性时程分析法（FNA方法）减震分析，SAUSAGE(2022.2版)建立阻尼器进行大震弹塑性动力时程减震分析（修正的中心差分格式法）。

最终结果表明,设置墙式黏滞阻尼器能显著降低结构的地震响应,说明该结构设计合理，安全可靠；同时进行不同阻尼系数及阻尼指数情况下的附加阻尼对比。

[关键词]：墙式粘滞阻尼器；消能减震；学校建筑[中图分类号]：[文献标识码]：墙式黏滞阻尼器在某学校消能减震设计中的应用分析1.工程概况本项目位于成都双流区，为学校建筑，其建筑功能包括教室、办公室、实验室、会议室、食堂、报告厅、篮球场，采用现浇混凝土框架结构（属于多层结构），根据建筑功能及平、立面特点，中学通过设置防震缝划分为6个结构单体，小学通过设置防震缝及钢连廊划分为6个结构单体。

中学、小学结构平面布置如下图所示。

图 1‑1中学平面示意图图1‑2小学平面示意图 2.结构设计参数及体系选取小学单体5为例进行消能减震分析，主要设计参数详表 2‑1。

表2‑1主要设计参数小学单体5平面总长度约49.1m，宽度约26.0m；因首层层高4.8m大于其余楼层3.9m，在2层板面通过调整柱截面尺寸，将楼层的等效剪切刚度比值控制在规范要求的范围内。

本项目地基基础采用以中等风化泥岩作为基础持力层的旋挖灌注桩，旋挖灌注桩桩径800mm，单桩承载力为2100~2250KN，地下室范围桩长约为13~17m，无地下室范围桩长约为18~23m。

转子流量计示值误差测量及使用中注意事项摘要：将转子流量计连接在钟罩气体流量标准装置管路上，按规程调整流量检定点，记录一定时间内钟罩排出体积流量，记录标准器、流量计前的表压、温度进行修正。

转子流量计的刻度流量与钟罩气体流量标准装置容积时间法得到的标准流量进行比较，得到转子流量计的示值误差。

关键词：转子流量计示值误差测量结果；不确定度评定；转子流量计检定规程, 采用容积法, 利用介质通过流量计流入液体流量标准装置的工作量器内,测出流入工作量器内的液体体积、温度和时间, 计算出流量计的刻度状态下的实际流量和示值误差。

一、转子流量计的使用特点玻璃管转子流量计是直读式仪表, 锥管刻度有流量刻度和百分刻度2 种。

采用流量刻度标尺的流量计, 可根据转子高度直接读出流量值;对于采用百分刻度的玻璃管转子流量计, 要特别注意刻度数与流量的换算问题。

百分刻度标尺又分为等分和非等分刻度2 种。

对等分刻度的转子流量计, 应根据锥形管上的读数, 从制造厂提供的图表上查得相应的流量值;对于非等百分刻度的转子流量计,将读数乘以该转子流量计的上限刻度值, 即为实测流量。

远传式转子流量计, 无论是电远传还是气远传, 在正常运行时只允许调整转换器输出零位的高低, 其他一般不作调整。

流量计投放运行时, 其前后阀门应缓慢开启, 以免流体猛冲转子, 损坏仪表。

装有旁路的,应先开启旁路阀, 再投入仪表, 仪表投入后再关断旁路。

根据被测流体的脏污情况定期冲洗, 以保证精度。

对其远传仪表, 尚需定期清洗恒节流孔和过滤器。

当必须对变送器拆卸清洗时, 应注意不要碰弯导向杆, 以免转子产生“卡死” 现象, 使仪表失灵。

大口径玻璃转子流量计搬动时, 应先将转子顶住, 避免转子碰撞, 将锥管打坏。

夹套保温仪表夹套管中所通介质最高压力不应超过仪表说明书规定值(一般低于100 N/cm2并应用压力表监视。

在测量中, 若出现由于流体脉动而引起指示值不稳时, 可调大阻尼器阻尼量或在阻尼器中加适当的液体(如硅油), 以增加阻尼。

m/s,行走一次,即可将钢板上的船漆剥离掉,露出船板表面,除锈效果达到C级S a2.5喷射除锈标准,除锈效果良好㊂超高压旋转除锈清洗盘共安装4个喷嘴,以提高实际的除锈效率㊂在设计主动齿轮时,采用了合成材料,长时间的使用运转导致主动齿轮有一定疲劳损坏,而在一次操作中由于关机顺序错误,导致主动齿轮所受外负载突然增大,齿轮发生断裂,旋转喷头无法旋转工作㊂将喷头拆卸维修,如图7所示㊂图7 拆卸维修图由图7可知,主动齿轮由于疲劳损坏破坏掉6~7个齿,同时发现密封3处即端面密封处,端面部分有磨损,并且内环的磨损度大于外环的磨损度,这是由于端面部分的压力分布不均匀㊁内环压力高于外环压力所致㊂维修后,在使用过程中发现,在所有参数一定的情况下,工作时的系统压力要上调10M P a左右才能达到之前的除锈效果㊂分析原因如下:①由于端面密封处的端面有一定的磨损,导致密封效果不如以前,泄漏量增加,从而使得系统的效率下降,需通过提高系统压力来提高效率㊂②喷嘴长期使用,有一定的磨损,导致射流效率降低㊂4 结束语旋转密封的好坏直接影响到水射流除锈清洗的效率㊂该除锈清洗盘的成功研制及使用,解决了高压水射流密封困难的问题,在实际的使用中具有高效㊁结构简单及密封可靠等优点,并且整体设备以水作为传动介质,可以做到随时除锈随时回收锈漆效果,对环境无污染,符合船厂中除锈的需要,具有一定的推广价值㊂参考文献:[1] 付宜利,李志海.爬壁机器人的研究进展[J].机械设计,2008,25(4):1‐4.F uY i l i,L iZ h i h a i.R e s e a r c h i n g H e a d w a y o f W a l l‐c l i m b i n g R o b o t s[J].J o u r n a lo f M a c h i n e D e s i g n,2008,25(4):1‐4.[2] 薛胜雄.高压水射流技术工程[M].合肥:合肥工业 大学出版社,2006.[3] J E T E C H.R o t a t i n g S e a l s[E B/O L].[2014‐03‐04].h t t p://w w w.j e t e c h.c o m/w a t e r‐j e t t i n g‐t o o l s/r o t a-t i n g‐s e a l s.[4] H a mm e l m a n n(天津)有限公司.应用附件[E B/O L].[2012‐12‐04].h t t p://w w w.h a mm e l m a n n.c n/p r o d u c t s‐d e t a i l.a s p i d=&p a r e n t i d=1&c h i l d i d=30&p n a m e=%D3%A6%D3%C3%B8%B D%B C%F E.[5] K AMA T.R o t a t i n g n o z z l e s[E B/O L].[2012‐12‐04].h t t p://w w w.k a m a t.d e/P u m p‐a c c e s s o r i e s/H i g h‐p r e s s u r e‐n o z z l e s/1_340.h t m l.[6] 任启乐,薛胜雄,陈正文,等.高压旋转密封中填料密封技术的分析与改善[J].清洗世界,2009,25(12):34‐38.R e n Q i l e,X u eS h e n g x i o n g,C h e nZ h e n g w e n,e ta l.R e a s e a r c h o f P a c k i n g a n d S e a l i n g T e c h n o l o g y i nH i g hP r e s s u r e W a t e rR e v o l v i n g S e a l i n g[J].C l e a n-i n g W o r l d,2009,25(12):34‐38.[7] 薛胜雄,陈正文,盛业涛,等.美国高压水射流技术现状[C]//2006年中国机械工程学会年会暨中国工程院机械与运载工程学部首届年会论文集.北京:中国机械工程学会,2006:11‐17.[8] 王庆国,周丹.高压水间隙密封旋转喷头的研制及应用[J].机械开发,2000(4):66‐68.W a n g Q i n g g u o,Z h o uD a n.D e v e l o p m e n t a n dA p p l i-c a t i o no fR o t a t i n g N o z z l ew i t hH i g hP r e s s u r eW a t e rC r e v i c eS e a l[J].M a c h i n eD e v e l o p m e n t,2000(4):66‐68.[9] 王正钦,管华,刘庭成.高压水射流清洗技术中的旋转喷头[J].清洗世界,2007,23(1):31‐34.W a n g Z h e n g q i,G u a n H u a,L i uT i n g c h e n g.R o t a t i n gN o z z l e f o rH i g hP r e s s u r e W a t e r‐j e tC l e a n i n g T e c h-n o l o g y[J].C l e a n i n g W o r l d,2007,23(1):31‐34.[10] 马汝涛,徐义,祁万军,等.高压水射流清洗油管旋转喷头的设计及应用[J].石油机械,2007,35(10):29‐32.M aR u t a o,X u Y i,Q i W a n j u n.T h e D e s i g na n dA p p l i c a t i o no f H i g h P r e s s u r e W a t e rJ e t R o t a r yN o z z l e o nC l e a n i n g O i lP i p e[J].C h i n aP e t r o l e u mM a c h i n e r y,2007,35(10):29‐32.(编辑 袁兴玲)作者简介:孙 玲,女,1984年生㊂大连海事大学轮机学院博士研究生㊂主要研究方向为机电一体化㊁液压传动与控制㊁机器人控制㊂发表论文10余篇㊂弓永军,男,1974年生㊂大连海事大学交通运输装备与海洋工程学院教授㊁博士研究生导师㊂王祖温,男,1955年生㊂大连海事大学轮机学院教授㊁博士研究生导师㊂张增猛,男,1979年生㊂大连海事大学通运输装备与海洋工程学院副教授㊂㊃8171㊃磁流变阻尼器等效线性阻尼系数计算郭耀辉 陈恩伟 陆益民 刘正士 夏增强合肥工业大学,合肥,230009摘要:基于修正的B o u c _W e n 模型分析了磁流变阻尼器的性能,并计算了其等效线性阻尼系数;基于修正的B o u c _W e n 模型的仿真数据,通过曲线拟合回归分析方法建立了磁流变阻尼器等效线性阻尼系数与控制电压以及磁流变阻尼器运动振幅之间的关系模型,并验证了模型精度㊂研究结果显示,等效线性阻尼系数模型具有较高的精度,相对误差低于1%;对于应用强非线性磁流变阻尼器的振动系统,在给定频率下,利用等效线性阻尼系数模型可以有效提高系统振动及稳定性分析的计算效率㊂该研究为磁流变阻尼器的控制应用提供了理论依据㊂关键词:磁流变阻尼器;B o u c _W e n 模型;等效线性阻尼系数;曲线拟合;最小二乘法中图分类号:T H 113.1 D O I :10.3969/j.i s s n .1004-132X.2014.13.004C a l c u l a t i o no fE q u i v a l e n tL i n e a rD a m p i n g C o e f f i c i e n t o f aM a g n e t o r h e o l o g i c a lD a m pe r G u oY a o h u i C h e nE n w e i L uY i m i n L i uZ h e n g s h i X i aZ e n g q i a n gH e f e iU n i v e r s i t y o fT e c h n o l o g y,H e f e i ,230009A b s t r a c t :B a s e do nm o d i f i e dB o u c _W e nm o d e l t h i s p a p e r a n a l y z e d t h e p e r f o r m a n c e o fM Rd a m p -e r ,a n d t h e e q u i v a l e n t l i n e a r d a m p i n g c o ef f i c i e n t o fM Rd a m p e rw a s c a l c u l a t e d .B a s e d o n t h em o d i f i e d B o u c _W e nm o d e l s i m u l a t i o nd a t e ,t h e r e l a t i o n s h i p a m o ng th e M Rd a m p e r e q ui v a l e n t l i n e a rd a m p i n gc o e f f i c i e n t ,c o n t r o l v o l t a g ea nd MRd a m pe rm o v e m e n t a m p l i t u d ew a se s t a b l i s h e dt h r o u ght h ec u r v e f i t t i n g r e g r e s s i o na n a l y s i sm e t h o d ,a n d i t s a c c u r a c y w a sv e r i f i e d .R e s u l t sd i s p l a y t h a t t h ee qu i v a l e n t l i n e a r d a m p i n g c o e f f i c i e n tm o d e l h a s h i g h e r a c c u r a c y ,a n d t h e r e l a t i v e e r r o r i sw i t h i n 1%.F o r t h e v i -b r a t i o ns y s t e m sw h ic hc o n t a i n ed s t r o n g l y n o n l i ne a r a n d l a r g e d a m p i n g c o ef f i c i e n t o fMRd a m pe r ,t h e n e w m o d e lw i l l g r e a t l y r e d u c e t h ec a l c u l a t i o nof t h ev i b r a t i o na n a l y s i sa n dt h es t a b i l i t y s t u d y o f t h e s y s t e mi n a c o n s t a n t f r e q u e n c y v a l u e .B e s i d e s t h em o d e l a l s o p r o v i d e s a t h e o r e t i c a l b a s i s f o r t h e a p p l i -c a t i o n s o fMRd a m pe r c o n t r o l .K e y w o r d s :m a g n e t o r h e o l o g i c a l (MR )d a m p e r ;B o u c _W e n m o d e l ;e q u i v a l e n t l i n e a r d a m p i n g c o ef -f i c i e n t ;c u r v e f i t t i ng ;l e a s t s qu a r em e t h o d 收稿日期:2013 01 31基金项目:中央高校基本科研业务费专项资金资助项目(2011H G Q C 1035);国家自然科学基金资助项目(51279044);安徽省自然科学青年基金资助项目(11040606Q 36)0 引言磁流变阻尼器是一种新型的结构半主动振动控制装置[1],它具有结构简单以及阻尼力可控性好等优点,在车辆㊁桥梁以及建筑等结构系统的振动控制上具有广阔的应用前景[2‐4]㊂磁流变阻尼器复杂的非线性力学特性使得应用流变力学理论推导其阻尼特性极为困难㊂为了更准确地描述磁流变阻尼器的非线性力学特性,国内外学者进行了大量的研究,提出了多种数学模型㊂S pe n c e r 等[5]在B o u c _W e n 模型基础上提出的修正的B o u c _W e n 模型对激励有很好的适应性,能较好拟合实验数据并能较精确地描述磁流变阻尼器的非线性特性,但该模型待辨识参数较多,部分参数物理意义不明确,进行参数优化时容易发散㊂求取磁流变阻尼器等效线性阻尼系数能有效改善以上问题,并能更好把握阻尼器在给定激振频率以及不同控制电压和振幅下的耗能能力,有利于更好设计其控制策略㊂L i 等[6]给出了磁流变阻尼器等效线性阻尼系数与电流和振幅的关系;夏品奇等[7]应用能量等效和数值积分法求取磁流变阻尼器的等效线性阻尼系数,但没给出具体公式;陈大伟等[8]进一步给出其分段函数形式,但该函数难于对系统进行分析计算㊂本文首先在修正的B o u c _W e n 模型基础上沿用能量等效和数值积分方法计算磁流变阻尼器的等效线性阻尼系数,然后利用线性多项式及幂函数参数模型对其输入电压及运动振幅进行参数拟合,最后对阻尼器等效线性阻尼系数模型的精度以及该方法对其他力学模型的适应性进行了验证㊂1 修正的B o u c _W e n 模型本文采用的修正的B o u c _W e n 模型具体如下:㊃9171㊃f =c 1y ㊃+k1(x -x α)y ㊃=1c 0+c 1[αz +c 0x ㊃+k 0(x -y )]z ㊃=-γ|x ㊃-y ㊃|z |z |n -1- β(x ㊃-y ㊃)|z |n+A (x ㊃-y ㊃)α=αa +αbu c 1=c 1a +c 1b u c 0=c 0a +c 0bu u ㊃=-η(u -V üþýïïïïïïïïïïïï)(1)其中,x ㊁V ㊁f 分别为位移㊁电压和阻尼力,它们都是时间的函数;y ㊁z ㊁u 为中间变量;x α为阻尼器的初始位移㊂其余参数由实验数据辨识得到,具体见表1[5]㊂假设位移x =2.5s i n 5πt ,由式(1)得出的磁流变阻尼器的力学特性曲线如图1所示㊂表1 磁流变阻尼器模型参数参数数值参数数值c 0a (N ㊃s /c m )21.0αa (N ㊃s /c m )14.0c 0b (N ㊃s /(c m ㊃V ))3.5αb (N ㊃s /c m )695.0k 0(N ㊃s /c m )46.9γ(c m -2)363.0c 1a (N ㊃s /c m )283.0β(c m -2)363.0c 1b (N ㊃s /(c m ㊃V ))2.95A301.0k 1(N ㊃s /c m )5.0n2x α(c m )14.30η(s -1)190(a)阻尼力位移回线(b)阻尼力速度回线图1 不同电压下磁流变阻尼器力学特性曲线2 磁流变阻尼器的等效线性阻尼根据式(1),磁流变阻尼器的性能由一组非线性方程描述,由于式(1)求解困难,不方便实际应用㊂夏品奇等[7]应用能量法和梯形积分法求出了其等效线性阻尼系数㊂设阻尼器产生的阻尼力为f (t ),阻尼器杆件运动速度为x ㊃(t),两者关系为f (t )=C e qx ㊃(t )(2)式中,C e q 为等效线性阻尼系数㊂C e q 可由能量法求出:C e q =EπΩx 20(3)式中,E 为阻尼器运动一个周期2π/Ω所消耗的能量;Ω为圆频率;x 0为振幅㊂设Ω=5π,图2所示为不同电压和振幅下的能量,由式(3)可求得等效线性阻尼系数C e q ,如图3所示㊂由图3可知磁流变阻尼器的等效线性阻尼系数与输入电压和运动振幅有关㊂图2 磁流变阻尼器能量耗散曲线(Ω=5π)图3 磁流变阻尼器能量系数曲线(Ω=5π)3 等效线性阻尼的曲线拟合本文采用最小二乘法进行参数曲线拟合,并用误差平方和以及相关性判定系数来判定拟合结果[9]㊂3.1 等效线性阻尼系数与电压关系的拟合根据图3,振幅一定时,磁流变阻尼器的等效线性阻尼C e q 与电压V 成线性关系,因此采用最小二乘拟合多项式的拟合方式进行拟合㊂为减小误差,在原有取值基础上增加几个振幅取值:x 0=0.50,1.00,1.25,1.75,2.50,3.00,3.50,4.00,4.50,5.00c m ㊂电压仍为V =0,0.1,0.2,0.3,0.4,0.5,0.6V ,在MA T L A B 中对式(1)在不同振幅和电压下进行分析,然后由式(2)㊁式(3)得到㊃0271㊃修正的B o u c _W e n 模型在不同振幅和电压下的磁流变阻尼器的等效线性阻尼系数C e q ㊂电压V 为x 轴,等效线性阻尼系数C e q 为y轴,对数据进行平滑预处理㊂考虑到拟合的数据较少以及预测等效线性阻尼系数与电压成线性关系,采用线性最小二乘法和如下的一阶多项式进行拟合:C e q =p1V +p 2(4)其中,p 1㊁p 2为待辨识参数㊂以振幅x 0=0.5c m 为例,参数辨识的结果为C e q =85.41V +27.28(5)利用式(4)以及原始输入输出数据进行计算,拟合的误差平方和为0.1447,电压和等效线性阻尼系数的相关性判定系数为0.9999,表明拟合效果比较理想㊂按照此方法在不同振幅下进行曲线拟合,辨识获得的参数p 1㊁p2如表2所示㊂表2 C e q -V 拟合结果x 0(c m )p1p2误差平方和相关性判定系数0.5085.4127.280.14470.99991.0045.8326.640.013811.2537.6326.520.009511.7528.1426.390.005112.5020.9526.300.000713.0018.1726.250.000313.5016.1626.240.000414.0014.6126.230.000114.5013.4726.200.000115.0012.5226.19013.2 等效线性阻尼系数与振幅关系的拟合根据图2所示的能量耗散曲线,每周期耗散的能量E 在振幅一定时与电压V 也是线性关系,可表示为E =q 1V +q 2(6)代入式(3)可得C e q =q 1πΩx 20V +q 2πΩx 20(7)由此可知系数p 1和p 2是与振幅x 0有关的函数,由于q 1和q 2有可能也与x 0有关,所以系数p 1㊁p2与x 0的关系不能确定㊂因此,接下来对p 1和x 0以及p 2和x 0分别进行拟合,找出它们的关系㊂振幅x 0和系数p 1的拟合结果如图4所示,按照式(7)采用线性最小二乘法和二阶多项式对数据进行平滑处理㊂从图4看出,振幅x 0和参数p 1曲线近似于指数模型和幂函数模型,采用这两种模型分别进行拟合,拟合公式如下:p1=a e b x 0+ce d x 0(8)y =a +bx c0(9)其中,式(8)为指数模型,式(9)为幂函数模型,a ㊁b ㊁c ㊁d 为待辨识参数㊂经比较,幂函数模型拟合结果比指数模型理想㊂同理,对数据p 2和振幅x 0进行曲线拟合,结果仍是幂函数模型拟合得较好㊂图4 振幅x 0和系数p 1待拟合曲线综上可知,等效线性阻尼系数C e q 可表示为C e q =(42.45x -0.9524+3.292)V +(0.531x -1.141+26.11)(10)3.3 频率对等效线性阻尼系数的影响前面研究了给定频率下利用曲线拟合回归分析求解磁流变阻尼器等效线性阻尼系数的方法㊂但是激振频率变化会对等效线性阻尼系数产生一定影响㊂采用相同的方法,在振幅给定的情况下建立等效线性阻尼系数与激振频率ω以及电压V 的关系:C e q =(42.30ω-1+4.0)V +(ω-1+26.0)(11)由此可知,可以通过曲线拟合的方法建立振幅和电压或者频率和电压为变量的磁流变阻尼器的等效线性阻尼系数模型㊂但是,目前仅靠曲线拟合的方法还难以建立符合实际情况的磁流变阻尼器等效线性阻尼系数同时与三个参数,即频率㊁振幅和电压之间的拟合参数模型㊂4 讨论4.1 误差分析根据上文,修正的B o u c _W e n 模型可由式(1)表示,阻尼力f 用式(2)来等效,C e q 用式(10)计算㊂为了验证等效线性阻尼系数模型的准确性,分别对指数模型和幂函数模型的等效线性阻尼系数C e q 进行误差分析㊂分别求出在电压V =0.4,0.5,0.6,0.7,0.8,0.9,1.0V 和振幅x 0=1.00,2.00,3.50,5.00c m 下的等效线性阻尼系数,记为C e q ㊂把由式(3)求得的等效线性阻尼系数记为C e q0,则它们的相对误差由下式求得:δ=C e q -C e q 0C e q0(12)结果如表3㊁表4所示㊂㊃1271㊃表3 指数模型拟合的等效线性阻尼系数的相对误差%电压(V )x 0(c m )1.002.003.505.000.40.0052-0.00540.0052-0.00680.50.0051-0.00520.0059-0.00840.60.0082-0.00550.0071-0.00960.70.0067-0.00600.0083-0.10720.80.0079-0.00620.0094-0.01170.90.0094-0.00610.0101-0.12211.00.0098-0.00610.0109-0.1286表4 幂函数模型拟合的等效线性阻尼系数的相对误差%电压(V )x 0(c m )1.002.003.505.000.4-0.0010-0.00010.0001-0.00040.5-0.00190.0010-0.0001-0.00080.60.00060.00150.0004-0.00090.7-0.00150.00170.0009-0.00100.8-0.00080.00210.0013-0.00100.90.00030.00270.0014-0.00061.00.00030.00320.0015-0.0004 由表3㊁表4可知两种拟合方法计算等效线性阻尼系数的相对误差都很小,幂函数模型的精度比指数函数模型的精度要高,误差低于1%㊂由表4可知,等效线性阻尼系数的幂函数模型在电压一定时,振幅越大,精度越高㊂因此,用式(10)来表示等效线性阻尼系数C e q 能够满足精度要求㊂4.2其他力学模型比较磁流变阻尼器的参数化力学模型有多种,主要有B i n g h a m 模型㊁非线性双黏性模型㊁非线性滞回模型㊁B o u c _W e n 模型㊁修正的B o u c _W e n 模型和现象模型等[10]㊂为验证本文方法在其他力学模型上的适用性,下面将本文方法应用于研究最早㊁应用最多的B i n g h a m 模型㊂稳态剪切场下B i n gh a m 模型的阻尼力速度关系为f =C0x ㊃+F m s g n (x ㊃)(13)其中,f 为阻尼力;C 0为阻尼系数;F m 是与磁场相关的屈服力;x ㊃是活塞与缸体之间的相对速度㊂对常用的剪切阀式磁流变阻尼器进一步推得阻尼力速度关系:f =12ηL A 2p πD h3x ㊃+3L A p h τy s g n (x ㊃)(14)式中,L 为活塞杆有效长度;D 为缸体内径;A p 为活塞的有效面积;h 为孔道直径;τy 为磁流变液剪切屈服力㊂在位移x =2.5s i n 5πt 时磁流变阻尼器的阻尼力位移曲线和阻尼力速度曲线分别见图5a 和图5b [11]㊂能量耗散曲线和能量系数曲线分别如图6和图7所示㊂(a)阻尼力位移回线(b)阻尼力速度回线图5 磁流变阻尼器力学曲线(B i n gh a m 模型)图6 磁流变阻尼器能量耗散曲线(B i n gh a m 模型)图7 磁流变阻尼器能量系数曲线(B i n gh a m 模型)用以上分析修正B o u c _W e n 模型的方法对B i n gh a m 模型进行拟合㊂结果显示,幂函数模型的结果仍优于指数模型拟合的结果㊂等效线性阻尼系数可表示为C e q =(4482x -1+5.397)V +(5241x -0.9998+41.01)(15)㊃2271㊃。