矢量图原理

电路向量图的原理和应用1. 什么是电路向量图？电路向量图（Circuit Vector Diagram）是一种在电路分析中常用的工具，用于表示电路中各个元件之间的相对位置和方向关系。

它以向量的形式来描述电路中各个元件的位置、大小和方向，使得电路的分析更加直观和简洁。

2. 电路向量图的基本原理电路向量图的基本原理是使用向量表示电路元件的位置、大小和方向。

以下是电路向量图的基本原理和规则：•使用箭头来表示电流的方向，箭头指向电流的流向。

•使用带箭头的线段来表示电压的方向，箭头指向电压的正极。

•元件内部的箭头表示电流的流向，指向电流的流出端。

•并联元件之间的箭头指向同一个交流电源。

•串联元件之间的箭头相连。

•根据电路的实际情况，可以添加标记表示电流、电压、电阻等数值。

3. 电路向量图的应用3.1 电路分析电路向量图在电路分析中起到了关键的作用。

通过绘制电路向量图，可以直观地了解各个电路元件的相对位置和方向关系，从而方便进行电路分析。

通过观察电路向量图，可以确定电路的串并联关系，求解电流和电压的分布情况，以及计算电路中的功率和能量等。

3.2 电路设计在电路设计中，电路向量图可以帮助工程师更好地理解电路拓扑结构，从而进行更加精确和可靠的电路设计。

通过电路向量图，可以直观地看到各个元件之间的连接关系，帮助工程师合理选择电路元件和设计电路布局。

3.3 电路教学电路向量图作为一种直观和简洁的图示工具，也被应用于电路教学中。

学习者通过绘制和观察电路向量图，可以更加清晰地理解电路中各个元件之间的关系，加深对电路原理的理解。

4. 电路向量图的优势和局限性4.1 优势•直观简洁：电路向量图用直观的箭头和线段表示电流、电压等信息，使电路分析更加直观和简洁。

•灵活性强：电路向量图可以灵活地画出各种电路拓扑结构，满足不同电路分析和设计的需求。

•易于理解：对于初学者来说，电路向量图相较于其他表达方式更易于理解和掌握。

4.2 局限性•信息有限：电路向量图主要关注电流、电压等基本信息，对于一些复杂电路参数和特性的分析不够全面。

位图与矢量图形的原理与应用1. 引言在数字图像处理和计算机图形学中，位图和矢量图形是两种基本的图像表示方法。

它们各自具有独特的特点和应用场景。

本文将介绍位图与矢量图形的原理及其应用，帮助读者更好地理解和运用这两种图像格式。

2. 位图原理与应用2.1 位图原理位图（Bitmap）是一种栅格图像，由像素点阵组成。

每个像素点存储了一定的颜色信息，像素点的排列和色彩组合形成了整个位图图像。

由于像素点阵的局限性，位图在放大过程中容易失真，即像素点的分布无法满足放大后图像质量的需求。

2.2 位图应用位图广泛应用于摄影、图像处理、网页设计等领域。

由于位图能够很好地表现照片、插图等具有丰富细节的图像，因此在这些领域具有很高的实用价值。

常见的位图格式有JPEG、PNG、BMP等。

3. 矢量图形原理与应用3.1 矢量图形原理矢量图形（Vector Graphics）是由直线、曲线、形状等基本图形元素组成的图像。

这些元素被称为矢量，因为它们可以用数学公式来描述。

与位图不同，矢量图形在放大过程中不会失真，因为它们的形状和大小可以根据需要进行无限制的扩展。

3.2 矢量图形应用矢量图形广泛应用于图形设计、标志制作、动画制作等领域。

由于矢量图形具有无限放大的能力且不会失真，因此它们非常适合制作需要频繁缩放的图形，如公司标志、图表等。

常见的矢量图形格式有SVG、PDF、EPS等。

4. 位图与矢量图形的比较位图与矢量图形各有优缺点，下面是它们的比较：- 位图优点：能够表现丰富的图像细节，适合展示真实图片和艺术作品。

- 位图缺点：放大容易失真，文件大小较大，不适合大规模印刷和无限放大。

- 矢量图形优点：无限放大不失真，文件大小较小，适合制作标志、图表等。

- 矢量图形缺点：难以表现复杂细节，不适合展示照片和艺术作品。

5. 结论位图与矢量图形是数字图像处理和计算机图形学中两种基本的图像表示方法。

它们分别适用于不同的应用场景，了解它们的原理和特点，能够帮助我们更好地运用这两种图像格式。

矢量图解法简介在图像处理和图形设计领域，矢量图是一种基于数学公式描述的图像类型。

与位图图像不同，矢量图使用数学对象（如线段、多边形、曲线等）来表示图像的形状和颜色，而非以像素表示。

矢量图的主要优势是可以无损地进行缩放和变形，并且具有较小的文件大小。

由于矢量图使用数学对象而非位图存储图像数据，因此矢量图也可以更容易地进行编辑和修改。

本文将介绍矢量图解法的基本原理和常见应用场景，并探讨矢量图在图像处理和图形设计中的优势和局限性。

矢量图的工作原理矢量图使用数学公式来描述图像的形状和颜色。

图像中的每个元素（如线段、多边形、曲线等）都由数学方程式定义。

矢量图使用向量和曲线来表示形状。

通过定义始点坐标、终点坐标、绘图方向和曲线类型等参数，可以精确地绘制出各种形状。

矢量图中的颜色通常由渐变、填充和描边等技术实现。

渐变使用数学方程式定义色彩的渐变过程，填充使用颜色或纹理填充形状的内部，而描边则用于形状的边缘。

矢量图可以保存为各种文件格式，如SVG（可缩放矢量图形）、AI（Adobe Illustrator）、EPS（Encapsulated PostScript）等。

矢量图的优势和应用场景1. 缩放和变形无损矢量图可以无损地进行缩放和变形，因为图像的形状是基于数学公式计算得出的。

与位图图像不同，无论对矢量图进行多大或多小的缩放，都不会导致图像的质量损失。

这使得矢量图在需要频繁调整大小的设计和印刷制作中非常有用。

2. 文件大小小由于矢量图使用数学公式来描述图像，矢量图文件通常比位图图像文件更小。

这使得矢量图在需要在网络上进行传输或嵌入到其他文档中时非常方便。

3. 可编辑性强矢量图具有良好的可编辑性，可以方便地修改和调整图像的各个元素。

通过编辑软件，可以添加、删除、变换和调整矢量图的各个部分，使得图形设计和图像处理更加灵活和高效。

4. 特效和过渡效果矢量图可以通过使用渐变、透明度、阴影等技术实现各种特效和过渡效果。

位图与矢量图的区别
1、位图与矢量图的存储原理不同
先从概念说起：矢量图是根据几何特性来绘制图形，用线段和曲线描述图像，矢量图只能靠软件生成，矢量图文件占用内在空间较小；
位图图像也称为点阵图像，构成位图的基本单位是像素。

.
2、放大后是否失真
最大的区别，矢量图形与分辨率无关，可以将它缩放到任意大小和以任意分辨率在输出设备上打印出来，都不会影响清晰度，而位图是由一个一个像素点产生，当放大图像时，像素点也放大了，但每个像素点表示的颜色是单一的，所以在位图放大后就会出现咱们平时所见到的马赛克状。

.
3、表示的色彩效果不同
位图表现的色彩比较丰富，可以表现出色彩丰富的图象，可逼真表现自然界各类实物；而矢量图形色彩不丰富，无法表现逼真的实物，矢量图常常用来表示标识、图标、Logo等简单直接的图像。

.
4、文件的类型不同
位图的文件类型很多，如*.bmp、*.pcx、*.gif、*.jpg、*.tif、photoshop 的*.psd等；矢量图形格式也很多，如AdobeIllustrator的*.AI、*.EPS和SVG、AutoCAD的*.dwg和dxf、Corel DRAW的*.cdr等。

.
.
.
5、文件占用的存储空间不同
由于位图表现的色彩比较丰富，所以占用的空间会很大，颜色信息越多，占用空间越大，图像越清晰，占用空间越大；由于矢量图形表现的图像颜色比较单一，所以所占用的空间会很小。

.
.
.
6、经过软件矢量图可以很轻松的转化为位图，而位图要想转换为矢量图必须经过复杂而庞大的数据处理，而且生成的矢量图质量也会有很大的出入。

.。

矢量图的原理矢量图是一种基于数学公式描述图形的图像类型，与位图图像相对应。

它以几何图形的形式来描述图像，因此可以无限放大而不失真。

矢量图的原理是通过定义图形的数学属性来表示图像，因此具有很好的可伸缩性和编辑性。

首先，矢量图是由一系列的点、线、曲线和多边形组成的。

这些基本元素通过数学公式来描述其形状和位置，因此可以精确地表示图像。

相比之下，位图图像是由像素点构成的，放大时会出现锯齿状的边缘，而矢量图则可以保持平滑的边缘，不会出现失真。

其次，矢量图可以通过改变数学公式来实现图像的编辑和变换。

因为图形是由数学属性定义的，所以可以通过修改这些属性来实现图像的缩放、旋转、平移等操作。

这使得矢量图在设计领域中具有很好的灵活性和可编辑性，设计师可以随时修改图形而不必担心失真的问题。

另外，矢量图还可以实现图形的填充和描边效果。

通过定义图形的填充颜色、渐变、纹理等属性，可以实现丰富多彩的效果。

而描边可以定义线条的粗细、样式、颜色等属性，使得图形更加生动和立体。

此外，矢量图还可以实现图形的裁剪和组合。

通过定义图形的交集、并集、差集等操作，可以实现图形的裁剪和合并，从而创造出更加复杂的图形效果。

这种特性使得矢量图在图形设计和制作中具有很大的优势。

总的来说，矢量图的原理是通过数学公式来描述图形，具有很好的可伸缩性、编辑性和灵活性。

它在图形设计、平面设计、标志设计等领域有着广泛的应用，成为了设计师们不可或缺的工具之一。

希望本文能够帮助大家更好地理解矢量图的原理和特点。

详解矢量图与点阵图（位图）的差别在学习照片处理之前，首先我们需要学习的是不同图像之间的差别。

在本文里，将着重介绍两种不同图片格式的具体差别及原理。

在计算机中，图像是以数字方式记录、处理和保存的，可以将其分为两类，即矢量图与点阵图。

矢量(Vector)是矢量绘图的基础，“矢量”可以是一个点、一条线、或一个面，在点阵图之中，与之相对应的是像素(Pixel )首先，我们需要了解，什么是矢量图？什么是位图？一、矢量图在由矢量组成的各种图形中，每一个“矢量”都是一个相对独立的实体，它们都有自己的属性，如形状、颜色、大小、轮廓、在屏幕中的位置等。

因此可以对各个实体进行调整，改变它的大小、颜色、形状、弯曲程度、位置等属性。

“矢量图”的最大优势就在于它不会因进行放大或缩小等操作而使图形的清晰度发生变化。

举个例子来说，一条直线在CorelDRAW中只被记录其起点和结束点的坐标位置而已;在需要的情况下，您可以对其赋予其他属性，例如大小、颜色、形状、弯曲程度、页面位置等等。

这些属性是整条直线的属性，一旦被确认将应用于整条直线，并非个别点，这样就使得矢量文件相对来说很小，因为要记录的东西比“点阵图”少了许多。

二、点阵图（位图）点阵图图像也叫位图图像，是由个别的独立点—像素(照相元素)组合而成的，可以变化成不同的形状与色彩以形成一个图型。

从远距离看点阵图时，其色彩和形状看起来还是连续的。

因为每一个像素都是个别着色，所以可以创建出几乎可以乱真的照片效果，并能够通过修改选取区域的色彩加以强化。

缩小点阵图，将会移动构图的像素，以减少原图尺寸，但却因此扭曲了原始图像。

因为点阵图图像是由一连串排列好的像素创建出来的，其内容无法个别地处理控制(如移动)。

三、两者之间的差别处理位图其实是在编辑像素而不是图像本身。

因此，在表现图像色彩的细微变化时，位图是最佳选择，这是矢量图无法比拟的。

位图的清晰度与分辨率有关，而矢量图与分辨率无关。

依次将矢量图和点阵图进行放大，要吧发现矢量图的轮廓线依然保持平滑，而点阵图的边缘却由一个个色块小方格组成，呈现出锯齿状。

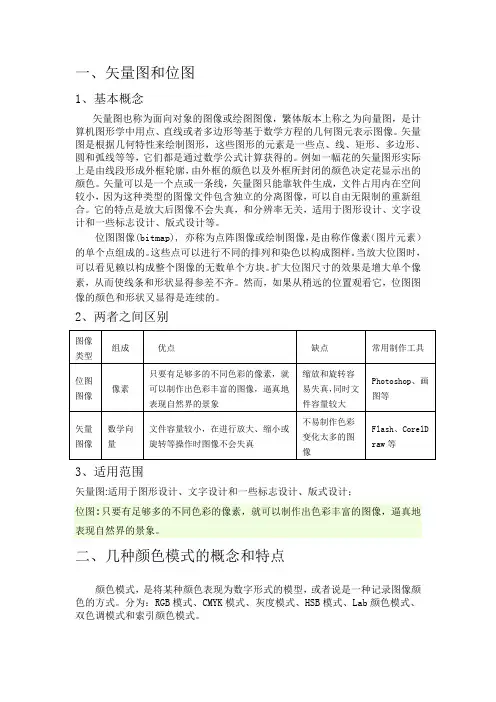
一、矢量图和位图1、基本概念3、适用范围矢量图:适用于图形设计、文字设计和一些标志设计、版式设计；位图:只要有足够多的不同色彩的像素，就可以制作出色彩丰富的图像，逼真地表现自然界的景象。

二、几种颜色模式的概念和特点颜色模式，是将某种颜色表现为数字形式的模型，或者说是一种记录图像颜色的方式。

分为：RGB模式、CMYK模式、灰度模式、HSB模式、Lab颜色模式、双色调模式和索引颜色模式。

1、RGB颜色模式虽然可见光的波长有一定的范围，但我们在处理颜色时并不需要将每一种波长的颜色都单独表示。

因为自然界中所有的颜色都可以用红、绿、蓝(RGB)这三种颜色波长的不同强度组合而得，这就是人们常说的三基色原理。

因此，这三种光常被人们称为三基色或三原色。

有时候我们亦称这三种基色为添加(Additive Colors)，这是因为当我们把不同光的波长加到一起的时候，得到的将会是更加明亮的颜色。

把三种基色交互重叠，就产生了次混合色：青(Cyan)、洋红(Magenta)、黄(Yellow)。

这同时也引出了互补色(Complement Colors)的概念。

基色和次混合色是彼此的互补色，即彼此之间最不一样的颜色。

例如青色由蓝色和绿色构成，而红色是缺少的一种颜色，因此青色和红色构成了彼此的互补色。

在数字视频中，对RGB三基色各进行8位编码就构成了大约1677万种颜色，这就是我们常说的真彩色。

顺便提一句，电视机和计算机的监视器都是基于RGB颜色模式来创建其颜色的。

2、CMYK颜色模式CMYK颜色模式是一种印刷模式。

其中四个字母分别指青（Cyan）、洋红（Magenta）、黄（Yellow）、黑（Black），在印刷中代表四种颜色的油墨。

CMYK 模式在本质上与RGB模式没有什么区别，只是产生色彩的原理不同，在RGB模式中由光源发出的色光混合生成颜色，而在CMYK模式中由光线照到有不同比例C、M、Y、K油墨的纸上，部分光谱被吸收后，反射到人眼的光产生颜色。

矢量图的原理矢量图是一种使用数学公式来描述图形的图像，与位图图像相比，矢量图具有许多优势。

在矢量图中，图形是由一系列的点、线、曲线和多边形等基本图形元素组成的，这些基本图形元素通过数学公式来描述其位置、形状和颜色等属性。

矢量图可以无限放大而不会失真，因为它们是基于数学公式描述的，而不是像位图图像那样是由像素点组成的。

这使得矢量图在印刷品、标识、图标、动画等领域有着广泛的应用。

矢量图的原理可以通过以下几个方面来解释和理解：1. 数学公式描述图形，矢量图使用数学公式来描述图形，这些数学公式包括了图形的位置、形状和颜色等属性。

通过这些数学公式，可以精确地描述和绘制出各种复杂的图形，而且不会出现失真和模糊的情况。

2. 基本图形元素的组合，矢量图是由一系列的点、线、曲线和多边形等基本图形元素组成的，这些基本图形元素可以通过组合和变换来构建出各种复杂的图形。

这种基于基本图形元素的组合方式，使得矢量图具有了很强的灵活性和可塑性。

3. 无限放大不失真，由于矢量图是基于数学公式描述的，因此可以无限放大而不会出现失真和模糊的情况。

这使得矢量图在印刷品、标识等需要高清晰度的场景中有着很大的优势。

4. 编辑和修改方便，由于矢量图是使用数学公式来描述图形的，因此可以很方便地进行编辑和修改。

可以通过修改数学公式的参数来改变图形的位置、形状和颜色等属性，而不需要重新绘制整个图形。

总的来说，矢量图的原理是基于数学公式描述图形，通过基本图形元素的组合和变换来构建出各种复杂的图形，具有无限放大不失真、编辑和修改方便等特点。

这些优势使得矢量图在印刷品、标识、图标、动画等领域有着广泛的应用，并且在数字化时代有着越来越重要的地位。

SVG的工作原理SVG 是一种基于XML 的图形标准，它可以被用来描述二维图形和动画。

SVG 可以被用来创建矢量图形，这意味着图形可以无限缩放，而不会失去其质量。

本文将阐述SVG 的工作原理和其优点。

SVG 的工作原理SVG 的工作原理包括以下几点：1. 使用XML 描述图形：SVG 语言是基于XML 的，它允许开发人员使用标记来描述图形。

这些标记可以定义图形的形状、颜色、大小和位置，以及任何可能需要的属性。

2. 实现矢量图形：SVG 并不是基于像素的，而是矢量图形。

矢量图形是基于数学公式的，这意味着它们可以在任何大小的屏幕上呈现，并且不会失去质量。

3. 支持多种图形元素：SVG 允许开发人员使用多种图形元素形成图形，其中包括路径、文本、形状、图像等。

4. 动画：SVG 可以被用来创建动画。

这些动画可以用来创建交互式图形，为Web应用程序增加互动性，也可以用于教育和娱乐领域。

5. 支持全部浏览器：SVG是一个开放标准，可跨平台运行。

目前，所有现代Web浏览器都支持SVG。

SVG 的优点SVG 具有以下几个优点：1. 扩展性好：由于基于矢量图形，SVG 可以无缝地放大或缩小，不会失真。

这使它们在屏幕尺寸变化时更具弹性，适合移动设备等各种应用场景。

2. 可用性好：SVG 具有良好的可用性，这意味着它可以使用各种工具编辑和创建。

不同于像素，矢量图形可以很容易地通过简单的编辑器来创建。

3. 交互性好: 由于SVG 可以通过JavaScript 实现交互式体验和平滑的动画。

这为Web应用程序增加了更好的用户体验。

4. 访问性好：SVG 矢量图像需要的文件大小比其他常见图像格式小，因此速度快，占用存储空间小。

更值得注意的是，由于SVG 图像是基于文本的，所以在各种设备上使用的时，搜索引擎能够更容易地识别它们，用于搜索引擎优化（SEO）。

结论SVG 是一个基于XML 的标准，它的矢量图形方法允许图像在放大或缩小时不会失真。

简述矢量图与位图的区别。

简述矢量图与位图的区别。

众所周知，数字图像是由很多点和线组成的，而且点可以离开一个小区域单独存在，这样就形成了矢量图，例如像素点；而像素点又称为像素（ Pixel），就是构成数码影像的基本元素。

你知道吗？你手机上下载到的任何一张图片都属于位图，它们是用来存储或处理我们日常生活当中所拍摄、收集起来的各种原始照片的。

那么什么是矢量图呢？顾名思义，就是用几何学原理构成的图。

比方说人物照片吧！你在街头随便找一位路人拍下他最真实的表情姿态然后经过电脑处理把每个点和面连接起来就变成了一幅完整的相片，从某种程度上讲，这就叫做“把位图转换成了矢量图”。

在现实生活中，位图图像通常是使用一些定义明确、色彩鲜艳、图案清晰的专门格式记录的，它包含了亮度信息，并保留了彩色灰阶信息及全部的图案、线条等信息，也正因为此，对于同一副图像，其文件大小只能被限制在指定范围内。

另外，为了达到更好的显示效果，位图图像中往往还要加入一些调节图层或调节层次的效果，在调节时往往需要复杂的算法来进行运算。

这无疑增加了处理位图的难度。

因此，在一般情况下，对图像进行分析处理应首选矢量图。

由于图像处理器硬件结构、指令系统和寻址方式不同，目前位图图像的输出设备主要是扫描仪、打印机、激光印刷机等，对位图图像的分析则需要软件的帮助。

有人说，矢量图与位图的根本差异就在于前者采用了面向对象技
术，对图像的位置和颜色信息采取了对应的编码方式，并且可以利用屏幕菜单功能实现复杂的操作。

但实际上矢量图与位图之间的差异远非只体现在前者的代码编写形式上，事实上二者的画面表现力，画质优劣也有着天壤之别。

矢量图原理矢量图是文件格式，一种用来描述空间关系模型的图形格式。

矢量图描述图纸图像，被视为一种用于创建具有精确空间关系的图形技术。

矢量图技术使用从空间坐标到颜色属性的属性列表，以及用于绘制和维护空间形状的算法，来描述和绘制图形。

矢量图由一系列由点或矢量形式表示的模型构成，包括点、线、面、圆形和椭圆形等几何建模元素。

点模型是空间点的表示，被定义为具有空间位置的简单单位；线模型是空间直线的表示，定义为由两个或多个点构成的连续部分；面模型是空间平面的表示，被定义为由相互联结的多边形构成的部分；圆形模型是空间圆的表示，定义为一个空间位置的初始点，以及一个空间位置的结束点；椭圆形模型是空间椭圆形的表示，定义为由起止点和中心位置构成的椭圆形。

矢量图技术的发展在很大程度上受到了计算机技术的推动，这为用户提供了更好更快更容易地处理和分析空间数据的机会和可能性。

矢量图技术有很多优势，能够提供精确的描述用户指定的空间关系，以及精确的处理数据的功能。

而且，由于它的算法可以用比较少的内存空间来储存和处理数据，因此可以很好地改善文件的效率，减少存储空间，并提供更快的绘制速度。

此外，矢量图技术还可以用于处理复杂的地理信息数据，以及帮助分析复杂的空间关系，并提供更准确的空间信息分析模型。

例如，矢量图技术可以被用于挖掘地理信息系统（GIS）中的隐藏信息，从而得出更准确的地理信息分析结果。

矢量图技术也可以被用于许多其他的应用，比如遥感图像处理、计算机图形学、航空航天科学、智能分析和测绘等。

总之，矢量图技术是一种在实现精确的空间关系建模和分析时非常有价值的技术。

矢量图可以量化地描述几何信息，并可以被用于多个不同的应用领域，以实现更准确的分析结果。

如今，矢量图技术已经发展到成熟、完善的阶段，可以满足不同领域的需求。

矢量图原理矢量图是一种使用数学公式来描述图形的图像类型，相对于位图而言，矢量图具有无限的放大缩小能力，因为它们是由数学公式描述的，而不是由像素点构成的。

在计算机图形学中，矢量图是一种非常重要的图像类型，它在各种设计软件和绘图工具中都有广泛的应用。

矢量图的原理主要包括几个方面，点、线、面以及变换。

首先，矢量图是由一系列的点和线段组成的。

这些点和线段是由数学公式描述的，通过坐标系来确定它们的位置和形状。

矢量图中的点和线段可以进行各种变换操作，比如平移、旋转、缩放等，而不会失真。

这是因为矢量图是基于数学公式描述的，所以在进行变换时，只需要对数学公式进行相应的计算，就可以得到变换后的图形。

其次，矢量图可以描述复杂的图形和曲线。

通过数学公式，我们可以描述出各种复杂的曲线和图形，比如圆、椭圆、贝塞尔曲线等。

而且，矢量图可以通过数学公式来进行插值，从而得到更加平滑的曲线和图形。

另外，矢量图可以进行各种填充和描边操作。

通过数学公式描述的图形，我们可以对其进行填充和描边操作，从而得到各种丰富多彩的效果。

比如，我们可以对图形进行纯色填充、渐变填充、图案填充等，也可以对图形进行不同粗细和样式的描边。

最后，矢量图可以无损地进行放大缩小。

由于矢量图是由数学公式描述的，所以在进行放大缩小操作时，不会失去图像的清晰度和质量。

这使得矢量图在印刷品和高清屏幕显示中有着重要的应用，因为它可以适应不同分辨率的输出设备而不会失真。

总的来说，矢量图的原理是基于数学公式来描述图形，通过点、线、面以及各种变换操作来构建图形，并且具有无损放大缩小的能力。

这使得矢量图在计算机图形学中有着广泛的应用，同时也为各种设计软件和绘图工具提供了强大的功能支持。

矢量图的原理矢量图是一种使用数学公式来描述图形的图像类型，与位图图像相比，它具有许多独特的优势。

在矢量图中，图形是由一系列的点、线和曲线来描述的，这些元素之间的关系是通过数学公式来确定的，因此无论放大还是缩小，矢量图都能保持图像的清晰度和平滑度。

那么，矢量图的原理是什么呢？首先，矢量图的基本单位是点、线和曲线。

这些基本单位可以通过数学公式来描述其位置、形状和大小，因此矢量图可以被无限放大而不会失真。

这是因为当我们放大一个矢量图时，实际上是重新计算了每个点、线和曲线的位置和形状，而不是简单地放大像素。

其次，矢量图的绘制是基于数学公式的。

这意味着我们可以使用数学函数来描述图形的轮廓、颜色和纹理，而不是依赖于像素点的阵列。

这种基于数学公式的绘制方式使得矢量图在编辑和修改时更加灵活和方便，因为我们可以直接修改数学公式来改变图形的形状和属性。

另外，矢量图的文件大小相对较小。

因为矢量图只需要存储数学公式和一些描述性的数据，而不需要存储大量的像素信息，所以它的文件大小通常比位图图像要小得多。

这使得矢量图在网络传输和存储时更加高效和节省空间。

此外，矢量图还具有编辑和修改的优势。

由于矢量图是基于数学公式描述的，所以我们可以轻松地对其进行编辑和修改，例如改变图形的大小、颜色、形状等。

这种灵活性使得矢量图在设计领域得到了广泛的应用，尤其是在标志设计、插图绘制和平面设计中。

总的来说，矢量图的原理是基于数学公式来描述图形的位置、形状和属性，它具有无限放大不失真、绘制灵活、文件大小小以及编辑修改方便等优势。

这些优势使得矢量图在许多领域得到了广泛的应用，并且在数字图形处理中扮演着重要的角色。

希望通过本文的介绍，读者能对矢量图的原理有更深入的了解，从而更好地应用于实际的工作和学习中。

矢量图的原理
矢量图是一种使用数学公式来描述图像的图形格式，它以线段、多边形、曲线
等几何图形来描述图像，而不是以像素点的阵列来描述。

矢量图在图像放大和缩小时能够保持图像的清晰度和质量，因此在印刷品、标识、图标等领域得到广泛应用。

本文将介绍矢量图的原理，以及其在图像处理中的重要性。

首先，矢量图是由一系列的数学公式来描述图像的，这些公式包括了图像的位置、形状、颜色等信息。

与之相对的是位图，位图是由像素点阵列来描述图像的，因此在放大时会出现锯齿和失真现象。

而矢量图则可以通过改变数学公式的参数来实现图像的放大和缩小，而不会损失图像的清晰度和质量。

其次，矢量图在图像处理中具有重要的意义。

在印刷品、标识、图标等领域，
矢量图能够保持图像的清晰度和质量，因此在这些领域得到了广泛的应用。

此外，矢量图还可以实现图像的编辑和修改，因为它是由数学公式描述的，可以通过改变公式的参数来实现图像的变换和调整。

另外，矢量图还具有良好的可压缩性。

由于矢量图是由数学公式描述的，因此
可以通过压缩算法来减小文件的大小，而不会损失图像的清晰度和质量。

这在网络传输和存储方面具有重要的意义，能够节省带宽和存储空间。

总之，矢量图是一种使用数学公式来描述图像的图形格式，它具有保持图像清
晰度和质量、良好的可编辑性和可压缩性等特点，在图像处理中具有重要的意义。

因此，在印刷品、标识、图标等领域得到了广泛的应用。

希望本文能够帮助大家更好地理解矢量图的原理和应用，为图像处理提供更多的思路和方法。