最新苏科版数学九年级上册《4.3 等可能条件下的概率(二)》精品课堂教学课件 (1)
- 格式:ppt
- 大小:2.03 MB
- 文档页数:16
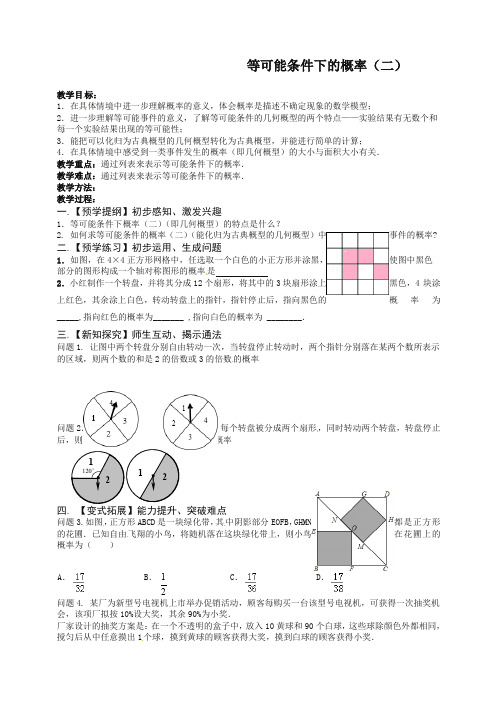
等可能条件下的概率(二) 教学目标:1.在具体情境中进一步理解概率的意义,体会概率是描述不确定现象的数学模型;2.进一步理解等可能事件的意义,了解等可能条件的几何概型的两个特点——实验结果有无数个和每一个实验结果出现的等可能性;3.能把可以化归为古典概型的几何概型转化为古典概型,并能进行简单的计算;4.在具体情境中感受到一类事件发生的概率(即几何概型)的大小与面积大小有关.教学重点:通过列表来表示等可能条件下的概率.教学难点:通过列表来表示等可能条件下的概率.教学方法:教学过程:一.【预学提纲】初步感知、激发兴趣1.等可能条件下概率(二)(即几何概型)的特点是什么?2. 如何求等可能条件的概率(二)(能化归为古典概型的几何概型)中事件的概率?二.【预学练习】初步运用、生成问题 1.如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是 2.小红制作一个转盘,并将其分成12个扇形,将其中的3块扇形涂上黑色,4块涂上红色,其余涂上白色,转动转盘上的指针,指针停止后,指向黑色的概率为 _____,指向红色的概率为_______ ,指向白色的概率为 ________.三.【新知探究】师生互动、揭示通法问题1. 让图中两个转盘分别自由转动一次,当转盘停止转动时,两个指针分别落在某两个数所表示的区域,则两个数的和是2的倍数或3的倍数的概率问题2.如图是两个可以自由转动的转盘,每个转盘被分成两个扇形,同时转动两个转盘,转盘停止4的概率问题3.如图,正方形ABCD 是一块绿化带,其中阴影部分EOFB ,GHMN 都是正方形的花圃.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( )A .B . 12C .D .问题4. 某厂为新型号电视机上市举办促销活动,顾客每购买一台该型号电视机,可获得一次抽奖机会,该项厂拟按10%设大奖,其余90%为小奖.厂家设计的抽奖方案是:在一个不透明的盒子中,放入10黄球和90个白球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到黄球的顾客获得大奖,摸到白球的顾客获得小奖.(1)厂家请教了一位数学老师,他设计的抽奖方案是:在一个不透明的盒子中,放入2黄球和3个白球,这些球除颜色外都相同,搅匀后从中任意摸出2个球,摸到的2个球都是黄球的顾客获得大奖,其余的顾客获得小奖.该抽奖方案符合厂家的设奖要求吗?请说明理由;(2)下图是一个可以自由转动的转盘,请你将转盘分为2个扇形区域,分别涂上黄、白两种颜色,并设计抽奖方案,使其符合厂家的设奖要求.(友情提醒:1.在用文字说明和扇形的圆心角的度数.2.结合转盘简述获奖方式,不需说明理由.)五.【回扣目标】学有所成、悟出方法1.可能条件的概率(二)的两个特点是什么?2.如何将等可能条件的概率(二)(能化归为古典概型的几何概型)转化为等可能条件下的概率(一)即古典概型?六.【当堂反馈】分层达标、收获成功1.已知地球表面陆地面积与海洋面积的比约为3:7.如果宇宙中飞来一块陨石落在地球上,则落在陆地上的概率是 .2.小明把如图所示的矩形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是.3.汶川大地震时,航空兵空投救灾物质到指定的区域(圆A)如图所示,若要使空投物质落在中心区域(圆B)的概率为12,则B⊙与A⊙的半径之比为424.甲、乙玩转盘游戏时,把质地相同的两个转盘A、B平均分成2份和3份,并在每一份内标有数字如图.游戏规则:甲、乙两人分别同时转动两个转盘各一次,当转盘停止后,指针所在区域的数字之和为偶数时甲获胜;数字之和为奇数时乙获胜.若指针落在分界线上,则需要重新转动转盘.(1)用画树状图或列表的方法,求甲获胜的概率;(2)这个游戏对甲、乙双方公平吗?请判断并说明理由.。


4.3 等可能条件下的概率(二)
.能把可以化归为古典概型的几何概型转化为古典概型,并能
.在具体情境中感受到一类事件发生的概率(即几何概型)的大小与面积大小有关.教学重点:会求等可能条件下的几何概型的概率.
个面积相等的扇形,若每个扇形面积为单位转动转盘,转盘指针指向的位置在不断改变(指针指向两个扇形
现将转盘涂色,颜色为红、蓝、白三种颜色.
个面积相等的扇形,这些扇形除颜色外完全相同,指
怎样计算指针指向红色区域的概率?
次,当转盘停止
1
课堂
3。


4.3 等可能条件下的概率(二)教学目的知识与技能目标1.在具体情境中进一步了解概率的意义,体会概率是描述不确定现象的数学模型;2.了解一类事件发生概率的计算方法,并能进行简单的计算; 过程与方法能设计符合要求的简单概率模型.培养学生分析、解决问题的能力. 情感态度与价值观在具体情境中体验生活与数学的关系,教导学生遇事不慌,积极主动地想办法,从容解决.教学重点、难点重点:通过面积、体积计算事件发生的概率. 难点:设计符合要求的简单事件发生的概率模型.教学过程Ⅰ.创设问题情景,引入新课手中有两个不透明的袋子,一个袋子中装有8个黑球,2个白球;另一个袋子里装有2个黑球,8个白球.这些球除颜色外完全相同.在哪一个袋子里随意摸出一球,摸到黑球的概率较大?为什么?在第一个袋子里摸到黑球的概率较大.这是因为,在第一个袋子里,P (摸到黑球)=108=54;而在第二个袋子里,P (摸到黑球)=51102 .图1图1中的每一块方砖除颜色外完全相同,小球分别在卧室和书房中滚来滚去,并随意停留在某块方砖上.在哪个房间里,小球停留在黑砖上的概率大呢? Ⅱ.讲授新课——讨论停留在黑砖上的概率 1.议一议首先观察卧室和书房的地板图,你会发现什么?那么,小球在卧室里滚来滚去,停留在黑砖上的概率为多少呢?如何计算呢?图2议一议:假如小球在如图2所示的地板上自由地走来走去,并随意停留在某块方砖上,它最终停留在黑色方砖上的概率是多少?(图中每一块除颜色外完全相同)P (最终停留在黑色方砖上)=41164=. 怎样想到计算最终停留在黑色方砖上概率用164的. P (最终停留在黑砖上)=41164=个方砖面积个方砖面积.2.想一想 出示讨论题目:如图是一个转盘.转盘分成8个相同的图形,颜色分为红、绿、黄三种.指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个图形的交线时,当作指向右边的图形).求下列事件的概率: (1)指针指向红色; (2)指针指向黄色或绿色.【解析】(1)将所用可能结果和指针指向红色的结果列举出来,后者除以前者即可; (2)将所用可能结果和指针指向红色或黄色的结果列举出来,后者除以前者即可. 解:按颜色把8个扇形分为红1.红2.绿1.绿2.绿3.黄1.黄2.黄3,所有可能结果的总数为8,(1)指针指向红色的结果有2个,∴P (指针指向红色)=;(2)指针指向黄色或绿色的结果有3+3=6个, ∴P (指针指向黄色或绿色)==. Ⅲ.应用深化 1.例题日常生活中有许多形式的抽奖游戏,我们可以利用概率的知识计算某些游戏获奖的概率.下面我们就来看这样的例子图4例某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得100元、50元、20元的购物券(转盘被分成20个相等的扇形). 甲顾客购物120元,他获得购物券的概率是多少?他得到100元、50元、20元购物券的概率分别是多少?解:根据题意,甲顾客的消费额在100元到200元之间,因此可以获得一次转动转盘的机会. 转盘被等分成20个扇形,其中1个红色、2个黄色、4个绿色,因此,对于甲顾客来说,P (获得购物券)=20720421=++; P (获得100元购物券)=201;P (获得50元购物券)=101202=;P (获得20元购物券)=51204=.你还能举出一个不确定事件,它发生的概率也是83吗? 2.补充练习一张写有密码的纸片被随意地埋在下面矩形区域内(每个方格大小一样) (1)埋在哪个区域的可能性大?(2)分别计算出埋在三个区域内的概率; (3)埋在哪两个区域的概率相同.图5解:(1)埋在“2”号区域的可能性大. (2)P (埋在“1”号区域)=41; P (埋在“2”号区域)=2142 ; P (埋在“3”号区域)=41.(3)埋在“1”和“3”区域的概率相同. Ⅳ.课时小结 谈一下这节课的收获. V.课后作业 课本习题。

苏科版数学九年级上册4.3《等可能条件下的概率(二)》教学设计一. 教材分析《等可能条件下的概率(二)》是苏科版数学九年级上册第四章第三节的内容。
这部分内容是在学生已经掌握了等可能条件下的概率计算方法的基础上进行进一步的探究。
本节课的主要内容是让学生理解并掌握相互独立事件的概率计算方法,以及如何利用树状图来求解概率。
这部分内容在现实生活中有着广泛的应用,对于培养学生的逻辑思维能力和解决问题的能力具有重要意义。
二. 学情分析九年级的学生已经具备了一定的数学基础,对于事件的概率有一定的认识。
但是,对于相互独立事件的概率计算方法和利用树状图求解概率还比较陌生。
因此,在教学过程中,需要引导学生通过实际问题来理解相互独立事件的概率计算方法,并通过大量的练习来掌握利用树状图求解概率的方法。
三. 教学目标1.理解相互独立事件的定义,掌握相互独立事件的概率计算方法。
2.学会利用树状图来求解概率问题。
3.能够运用所学的知识解决实际生活中的概率问题。
四. 教学重难点1.重点:相互独立事件的概率计算方法,利用树状图求解概率。
2.难点:理解相互独立事件的含义,以及如何利用树状图来求解概率。
五. 教学方法采用问题驱动的教学方法,通过实际问题引导学生理解相互独立事件的概率计算方法,并通过大量的练习来掌握利用树状图求解概率的方法。
同时,运用讨论法、案例分析法等教学方法,提高学生的参与度和积极性。
六. 教学准备1.准备相关的实际问题,用于引导学生思考和讨论。
2.准备PPT,用于展示相互独立事件的概率计算方法和树状图求解概率的方法。
3.准备练习题,用于巩固所学知识。
七. 教学过程1.导入(5分钟)通过一个实际问题来引导学生思考:抛掷两枚均匀的骰子,求两个骰子的点数之和为7的概率。
让学生尝试用自己的方法来解决这个问题,从而引出相互独立事件的概率计算方法。
2.呈现(10分钟)通过PPT展示相互独立事件的概率计算方法,并用具体的例子来解释和说明。
等可能条件下的概率(二)教学目标:1.在具体情境中进一步理解概率的意义,体会概率是描述不确定现象的数学模型;2.进一步理解等可能事件的意义,了解等可能条件的几何概型的两个特点——实验结果有无数个和每一个实验结果出现的等可能性;3.能把可以化归为古典概型的几何概型转化为古典概型,并能进行简单的计算;4.在具体情境中感受到一类事件发生的概率(即几何概型)的大小与面积大小有关.教学重点:通过列表表示等可能条件下的概率.教学难点:通过列表表示等可能条件下的概率.教学方法:教学过程:一.【预学提纲】初步感知、激发兴趣1.等可能条件下概率(二)(即几何概型)的特点是什么?2. 如何求等可能条件的概率(二)(能化归为古典概型的几何概型)中事件的概率?二.【预学练习】初步运用、生成问题1.如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是2.小红制作一个转盘,并将其分成12个扇形,将其中的3块扇形涂上黑色,4块涂上红色,其余涂上白色,转动转盘上的指针,指针停止后,指向黑色的概率为 _____,指向红色的概率为_______ ,指向白色的概率为 ________.三.【新知探究】师生互动、揭示通法问题1. 让图中两个转盘分别自由转动一次,当转盘停止转动时,两个指针分别落在某两个数所表示的区域,则两个数的和是2的倍数或3的倍数的概率问题2.如图是两个可以自由转动的转盘,每个转盘被分成两个扇形,同时转动两个转盘,转盘停止后,则指针所指区域内的数字之和为4的概率四. 【变式拓展】能力提升、突破难点问题3.如图,正方形ABCD是一块绿化带,其中阴影部分EOFB,GHMN 都是正方形的花圃.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为()A .B.12C.D.问题4. 某厂为新型号电视机上市举办促销活动,顾客每购买一台该型号电视机,可获得一次抽奖机会,该项厂拟按10%设大奖,其余90%为小奖.厂家设计的抽奖方案是:在一个不透明的盒子中,放入10黄球和90个白球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到黄球的顾客获得大奖,摸到白球的顾客获得小奖.(1)厂家请教了一位数学老师,他设计的抽奖方案是:在一个不透明的盒子中,放入2黄球和3个白球,这些球除颜色外都相同,搅匀后从中任意摸出2个球,摸到的2个球都是黄球的顾客获得大奖,其余的顾客获得小奖.该抽奖方案符合厂家的设奖要求吗?请说明理由;(2)下图是一个可以自由转动的转盘,请你将转盘分为2个扇形区域,分别涂上黄、白两种颜色,并设计抽奖方案,使其符合厂家的设奖要求.(友情提醒:1.在用文字说明和扇形的圆心角的度数.2.结合转盘简述获奖方式,不需说明理由.)五.【回扣目标】学有所成、悟出方法1.可能条件的概率(二)的两个特点是什么?2.如何将等可能条件的概率(二)(能化归为古典概型的几何概型)转化为等可能条件下的概率(一)即古典概型?六.【当堂反馈】分层达标、收获成功1.已知地球表面陆地面积与海洋面积的比约为37.如果宇宙中飞一块陨石落在地球上,则落在陆地上的概率是 .2.小明把如图所示的矩形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是.3.汶川大地震时,航空兵空投救灾物质到指定的区域(圆A)如图所示,若要使空投物质落在中心区域(圆B)的概率为12,则B⊙与A⊙的半径之比为424.甲、乙玩转盘游戏时,把质地相同的两个转盘A、B平均分成2份和3份,并在每一份内标有数字如图.游戏规则:甲、乙两人分别同时转动两个转盘各一次,当转盘停止后,指针所在区域的数字之和为偶数时甲获胜;数字之和为奇数时乙获胜.若指针落在分界线上,则需要重新转动转盘.(1)用画树状图或列表的方法,求甲获胜的概率;(2)这个游戏对甲、乙双方公平吗?请判断并说明理由.。
苏科版数学九年级上册4.3 等可能条件下的概率(二)教学设计一. 教材分析苏科版数学九年级上册4.3等可能条件下的概率(二)是本册教材中的重要内容,主要让学生掌握等可能条件下概率的求法,进一步理解概率的内涵。
本节课通过具体的实例,引导学生利用等可能条件下概率的求法解决实际问题,培养学生的数学应用能力。
二. 学情分析学生在学习本节课之前,已经掌握了概率的基本概念,了解了等可能条件下的概率求法。
但部分学生对概率的理解仍停留在表面,难以将概率知识应用于实际问题。
因此,在教学过程中,教师需要关注学生的学习需求,通过丰富的实例,引导学生深入理解概率的内涵,提高学生的数学应用能力。
三. 教学目标1.知识与技能:让学生掌握等可能条件下概率的求法,能运用概率知识解决实际问题。
2.过程与方法:通过实例分析,培养学生运用概率知识分析问题、解决问题的能力。
3.情感态度与价值观:激发学生学习概率的兴趣,培养学生的数学思维。
四. 教学重难点1.重点:等可能条件下概率的求法。
2.难点:如何将概率知识应用于实际问题。
五. 教学方法1.情境教学法:通过具体的实例,引导学生深入理解概率的内涵。
2.问题驱动法:设置问题情境,激发学生的思考,培养学生解决问题的能力。
3.合作学习法:学生进行小组讨论,促进学生之间的交流与合作。
六. 教学准备1.准备相关的实例,用于讲解等可能条件下的概率求法。
2.设计问题情境,激发学生的思考。
3.准备课堂练习题,巩固所学知识。
七. 教学过程1.导入(5分钟)利用一个简单的实例,如抛硬币实验,引导学生回顾概率的基本概念,为新课的学习做好铺垫。
2.呈现(15分钟)呈现本节课的主要内容:等可能条件下概率的求法。
通过具体的实例,讲解如何求解等可能条件下的概率。
3.操练(10分钟)学生进行小组讨论,让学生运用所学的概率知识解决实际问题。
教师巡回指导,解答学生的问题。
4.巩固(10分钟)出示课堂练习题,让学生独立完成。