力矩分配法

C M AB = CM BA = −28.6
q = 12kN / m
A
EI
B
EI
C
10m
q = 12kN / m
10m
u MB
A 2 ql / 12
B
u MB
C
M
C CB
=0
A
B
C
最终杆端弯矩: 最终杆端弯矩 M AB = −100 − 28.6 = −128.6 M BA = 100 − 57.1 = 42.9 M BC = 0 − 42.9 = −42.9 M CB = 0
B
d M BC
d u M BA = µ BA ( − M B )
d u M BC = µ BC ( − M B ) d d M BA M BC ---分配弯矩 分配弯矩
令
µ BA µ BC
S BA = S BA + S BC S BC = S BA + S BC
µ BA µ BC ---分配系数 分配系数
---传递系数 ---传递系数 1 1
A
i i i
B
2i C=1/2
传递弯矩
B
C=0 C=C=-1 与远端支承 情况有关
3i A 1
远端定向时: 远端定向时: i A
B
固定状态: 固定状态 F M AB = − ql 2 / 12 = −100kN .m F M BA = 100kN .m F F M BC = M CB = 0 放松状态: 放松状态 d u M BA = µ BA ( − M B ) = −57.1 d u M BC = µ BC ( − M B ) = −42.9
EI
B
EI
C

力矩分配法简介力矩分配法是一种常用的工程分析方法，用于计算和分析物体受到的力的分布情况以及力矩的平衡。

根据力矩分配法，物体处于平衡状态时，所有作用于物体上的力矩和为零。

利用这个原理，可以计算物体上各点的力的大小和分布。

基本原理力矩是一个力在距离某一点的作用线上产生的旋转效果。

当物体受到多个力作用时，在平衡状态下，力的合力和力矩的合力都为零。

根据力矩的定义，可以得到如下的力矩分配方程：其中，表示物体上所有力矩的代数和。

力矩分配法的步骤力矩分配法一般包括以下几个步骤：1.给定各个力的大小和作用点位置。

2.计算每个力的力矩。

力的力矩可以通过力乘以力臂得到，力臂是力的作用点到某一参考点的直线距离。

3.将各个力矩代入力矩分配方程，求解未知力的大小和作用点位置。

可以利用代数方程或者力矩图等方法进行计算。

4.验证计算结果，检查力矩的合力是否为零，以验证平衡状态。

5.如果力矩不为零，则需要重新调整力的大小和作用点位置，再次计算和验证。

力矩分配法的应用力矩分配法在工程中有广泛的应用。

以下是一些常见的应用例子：1.结构平衡：力矩分配法可以用于计算结构上各个部分受力的平衡情况，如梁、桁架等结构的受力分析。

2.机械设计：力矩分配法可以用于计算机械装置中各个零件受力的分布情况，如齿轮传动、支撑结构等。

3.车辆平衡：力矩分配法可以应用于汽车、飞机等交通工具的平衡分析，确保车辆的稳定性和安全性。

4.物体悬挂：力矩分配法可以计算物体悬挂时各个支点的受力情况，如吊车、吊车臂等。

总结力矩分配法是一种常用的力学分析方法，通过计算力矩的平衡来推导出物体上各点的力的分布情况。

它在工程中的应用非常广泛，可以用于结构平衡、机械设计、车辆平衡等领域。

使用力矩分配法可以帮助工程师更好地理解和分析各种力的作用情况，从而设计出更加稳定和安全的结构和设备。

S S BA 1 BC BC 1 SB 2 SB 2 传递系数：CAB 1 CC B 0
BA 分配系数：
m 118
A -32 29.5 0.5 32 59 91
91
固端弯矩：
C
ql 2 24 42 M AB 32 12 12 M BC - 3Pl 3 200 4 -150 16 16
B
2
C
l
ql / 8 ql 2 /14 3ql 2 / 56 ql 2 /14 ql 2 /14 ql 2 / 28 A
SCA 4 EI l SCB 3EI l
A
l
解：仅C点有转角位移，结点转动刚度： 力矩分配系数： CA SCA 4 , CB SCB 3 传递系数：
1 3 11 384 117 384 1 12
1 12 1 24 16 384 1 48 40 384
3 16 11 128 35 128
ql
2
解：仅A点有转角位移，结点转动刚度：
1, 3, 4 分配系数： AB 8 AC AD 8 8 1 C 1, C , C AC 0 AD 传递系数： AB 2 11 2 1 1 3 2 F ql ql 固端力及约束力矩： 1P 48 3 12 16 2 分配力矩： 11ql / 48
SC S AB S AC S AD i 3i 4i 8i
• 最后根据各杆端力矩 分配结果画弯矩图。
• 注意跨中荷载的弯矩 叠加。
117 35 16 48 75 48 40 96
1 8
4 8
3 8
1 6 11 384 75 384
1 3 11 384 117 384 1 12

u B
---不平衡力矩,顺时针为正
固端弯矩---荷载引起的单跨梁两 端的杆端弯矩,绕杆端顺时针为正.
M
F AB

ql 2
/ 12

100kN .m
M
F BA

100kN .m
M
F BC

M
F CB
0
M
u B

M
F BA

M
F BC
100kN.m
放松状态:需借助分配系数,
传递系数等概念求解
q 12kN / m B
ql 2
/ 12

100kN .m
A EI
B EI
C
M
F BA

100kN .m
10m
10m
M
F BC

M
F CB
0
放松状态:
q 12kN / m
M
u B
M
d BA


BA
(
M
u B
)

57.1
M
d BC


BC
(
M
u B
)

42.9
M
C AB

CM BA

28.6
M
C CB

0

28.6
传 递
M
C CB

0
M 128.6 42.9 42.9 0
最终杆端弯矩:
M AB 100 28.6 128.6
q 12kN / m 42.9
M BA 100 57.1 42.9
M

力矩分配法
力矩分配法是计算超静定结构的一种渐近方法。

力矩分配法是根据位移法基本原理，从开始建立近似状态，逐步通过增量调整来修正，最后收敛于真实状态。

力矩分配法的未知量为杆端弯矩，正负号规定同位移法。

力矩分配法只适用于求解无结点线位移的结构。

在力矩分配法求解超静定问题中，有四大步骤：
第一步：分析结构体系（是否为几何不变体系，是否有结点角位移），结构体系中的结点角位移就是结构的基本未知量。

第二步：求解四大参数（线刚度i 、转动刚度nm S 、分配系数nm 、
固端弯矩g nm M ）
第三步：求解杆端弯矩
第四步：求跨中弯矩，作M 图，Q 图。

基于位移法的力矩分配法，直接求得杆端弯矩，精度满足工程 要求，应用广泛。适合于手算，与电算并存。常见还有无剪力 分配法、迭代法等。
§7-2 力矩分配法的基本概念
1.正负号的规定
力矩分配法中对杆端弯矩、固端弯矩的正负号规
﹑ 定，与位移法相同，即假设对杆端顺时针转为
正，反之为负；对结点则以逆时针转为正，反之 为负。
MB B MFBC=0
MB
M
F BA
M
F BC
M BFA
（顺时针为正）
A M’AB
MB 放松约束
C
B
(c)
M’BA M’BC
②放松B点的约束，使之由MB到零（原结构没有这
个约束）。
方法：在B点施加力矩-MB
-MB单独作用： 分配力矩： M'BA , M'BC
传递力矩：
M
' AB
③叠加: (b)、 (c)相加后与原结构受力相同。
i AC
1 3
iCE
1 3
AG
4/3 4/3 41/3
0.5
AC
41/ 3 4/3 41/3
0.5
20kN/m A 2I G
I
CI H
I
E
基本结构
CA
41/
3
41/ 3 2/ 3
41/
3
4/3 10 / 3
0.4
CH
2/3 10 / 3
0.2 ,
CE
4/3 10 / 3
0.4
(2)固端弯矩
则: M Aj Aj M 即: M AB AB M
M
D
A
B
A
M AC AC M
M AD AD M

CB 1
CD 0
③传递系数
1 CCB 2
CBC 0
第9章 力矩分配法
§9-3 对称结构的计算
取一半结构进行计算，注意杆件截半后，线刚度增倍。 例9-3-1 求矩形衬砌在上部土压力作用下的弯矩图。
q
A EI1 F
B
EI2
K
l2
C
解：设梁的线刚度为i1=EI1/l1 柱的线刚度为i2=EI2/l2
⑸最后一轮循环最后一个结点分配后只向其他结点传递。
第9章 力矩分配法
⑹不能同时放松相邻结点（因定不出其转动刚度和传递系数）， 但可以同时放松所有不相邻的结点，以加快收敛速度。
A
B
C
D
E
B、D同时分配后向C传递，C分配后再同时向B、D传递，如此循 环。
A
B
C
D
E
F
B、D同时分配后同时向C、E传递，C、E同时分配后再同时向B、 D传递，如此循环。
A
B
15.86 3m 3m
C M (kNm) 6m
结点
A
B
C
解：① 不平衡力矩
m
g AB
Pl 8
20 6 8
15
m
g BA
Pl 8
15
mBgC
ql2 8
9
mBg
m
g BA
mBgC
6
杆端
AB
BA BC CB ②分配系数
分配系数
4/7 3/7
固端弯矩 -15
15
-9 0
平衡
分配传递 -1.72 -3.43 -2.57 0
第9章 力矩分配法
§9-1 力矩分配法的基本概念

M BA 1 C BA M AB 2
传递系数
远端固定
C AC
M CA 1 M AC M DA 0 M AD
远端滑动
C AD
远端铰支
远端弯矩等于近端弯矩乘以传递系数。
§7-1 力矩分配法的基本概念
2பைடு நூலகம்
基本运算（单结点的力矩分配）
计算FP作用下的杆端弯矩。
（1）在结点B加一个阻止转动的约束，阻止B点的转动。
C M CB
28.6 d CM BC 0 ( 42.9) 0
传递弯矩
与远端支承 情况有关
固定状态: F M AB ql 2 / 12 100kN .m
F M BA 100kN .m F F M BC M CB 0
举例分析2：
q 12kN / m
A
A
M AB S AB M S
A
S AB
M S AC S AD
M AD S AD M S
A
M AC
S AC M S
A
§7-1 力矩分配法的基本概念
M AB S AB M S
A
M AC
S AC M S
A
M AD
S AD M S
A
A端弯矩与各杆A端的转动刚度成正比。 统一用下列公式
M Aj Aj M
Aj
S
A
S Aj
——分配系数
力偶M，按各杆的分配系数分配于各杆的A端。 很明显

Aj
1
§7-1 力矩分配法的基本概念
（3）传递系数 由位移法中的刚度方程得
M AB 4i AB A M BA 2i AB A M AC i AC A M CA iCA A M AD 3i AD A M DA 0

-ql
2／8
=
-10×8
2／8
=
-
80kN·m
F
MCB =0
将它们填入表中第二行相应杆端下面。
由表可求得B点的不平衡力矩。但因B点有 外力偶，故不平衡力矩等于：
MB = -80 +150 = 70 kN·m
3、计算分配弯矩与传递弯矩
将结点B的不平衡力矩反号乘以各杆分配系 数得各杆近端分配弯矩。将所得分配弯矩 乘以相应杆的传递系数即得远端传递弯矩。
Mjc C = Mij
远端固定端时，C = 1/2 远端铰支座时， C = 0 远端定向支座时， C = -1
三、最终弯矩
将第一步固定结点各杆端的固端弯矩与 第二步放松节点时相应杆端的分配弯矩 或传递弯矩相加即得出杆端的最终弯矩。
例20-1用力矩分配法计算图(a)所示的两 跨连续梁，画出弯矩图。
3、将杆端的固端弯矩与分配弯矩或 传递弯矩相加，得到杆端最终弯矩。
一、固定结点
在结点1上附加刚臂，限制结点1的转动，原刚 架被解体成三个单跨梁，此时单跨梁A1两端 产生的弯矩即是位移法中所提到的固端弯矩。
q
M1
A 1
C
M1
M1A 1
M1C
B
M1B
查表得：MAF1 = 0
M1FA = 1 ql 2 由于附加刚臂阻8止了结点1转动，附加
F
MBA=
Pa
2b/l
= 50×42×6/10
= 48 kN·m
F
MBC=-ql
2/12=-25×122
/12=-300
kN·m
F
MCB=
ql
2/12=
25×12
2/12=

80kNm A EI 4m B 2m EI
100kN C 2m
20kN/m 2EI 4m D
40kNm
80kNm A EI 4m B 2m EI
100kN C 2m
20kN/m 2EI 4m
40kNm D
分配系数 固端弯矩 分配弯矩 和 3.12 传递弯矩 0 32.5
0.5 0 65
0.5 -50 65 -12.5
µ M µ CB M CD
M C CD
放松
-MCBC
A B
FP
C
MCCB
D 约束B 约束
M C AB
M µ BA
M µ BC
M C CB
二轮
MCBC
A B
FP
-MCCB
放松 C D 约束C 约束
M C BC
M µ CB M µ CD
M C CD
例2．如图连续梁，用力矩分配法计算并绘弯矩图。 ．如图连续梁，用力矩分配法计算并绘弯矩图。
第6章 力矩分配法 章
学习目标
1．牢记力矩分配法的使用条件是没有结点 线位移。 2．掌握力矩分配法计算连续梁和无结点线 位移刚架。
学习重点
力矩分配法计算连续梁 1）计算转动刚度、分配系数和传递系 数； 2）计算各杆固端弯矩和不平衡力矩。 3）不平衡力矩的分配和传递 4）最后杆端弯矩的计算。
第一节 力矩分配法的基本概念
µCB =
S CB 1 = = 0.5 SCB + SCD 1 + 1
µCD
S CD 1 = = = 0.5 SCB + S CD 1 + 1
例2．如图连续梁，用力矩分配法计算并绘弯矩图。 ．如图连续梁，用力矩分配法计算并绘弯矩图。

第八章力矩分配法
1
§8-1 概述 计算超静定结构，不论采用力法或位移法，均要组成和解算典型方程，当未知量较多时，其工作量非常大。
为了寻求较简捷的计算方法，自上世纪三十年代以来，又陆续出现了各种渐进法，力矩分配法就是其一。 渐进法的共同特点是，避免了组成和解算典型方程，而以逐次渐进的方法来计算杆端弯矩，其结果的精度
A
i=2
B
i=3 C
6m
3m
3m
40kN/m D
i=4
6m
杆端
m
MF
B1次 C1次
AB C 1 2 BA BC C 1 2 CB CD C 0 DC
0.4 0.6
0.5 0.5
100
0
0 -300
300 -180
0
40
80 120
60
-45
-90 -90
集中力偶m
逆时针为正
讨论
A A
2、静定段处理
D
Δ1 =1 B
4m
i= 3
i= 6
基本系
C
D
r111FR1F 0
3)作M1、MF图
基本系为无侧移刚架
30kN /m
A
r 11
i= 4
M1、MF图运用 力矩分配法绘制
F R 1 F 4)求系数和自由项
i= 3
i= 6
△1作用
C
D
i= 3
i= 6
荷载作用
C
D
5)求未知量 6)叠加法作M图
MM11+MF
l
EI＝ C
位移法求解
（1）建立基本体系
如何分配？
B
l
l
FRK

第十七章力矩分配法一、力矩分配法的基本概念力矩分配法是在位移法基础上发展起来的一种数值解法，它不必计算节点位移，也无须求解联立方程，可以直接通过代数运算得到杆端弯矩。

力矩分配法的适用对象:是连续梁和无节点线位移刚架。

内力正负号的规定:同位移法的规定一致。

杆端弯矩使杆端顺时针转向为正，固端剪力使杆端顺时针转向为正。

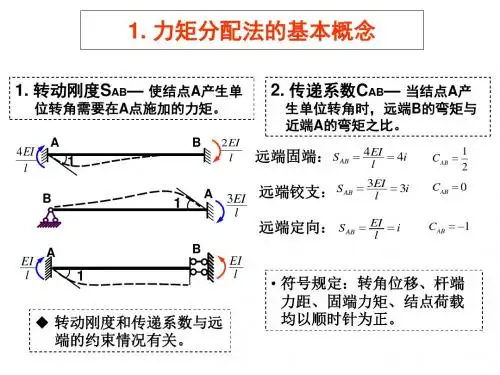
1、转动刚度(S)定义:杆件固定端转动单位角位移所引起的力矩称为该杆的转动刚度，(转动刚度也可定义为使杆件固定端转动单位角位移所需施加的力矩)。

转动刚度与远端约束及线刚度有关远端固定: S = 4 i远端铰支: S = 3i远端双滑动支座: S = i远端自由: S = 0 (i为线刚度)力矩分配法的基本思路,刚节点B将产生一个转角位移FM固端弯矩():是被约束隔离各杆件在荷载单独作用下引起的杆端弯矩。

FFFF MMMM,，，BBABCBDFM一般地不等于零，称为节点不平衡力矩现放松转动约束，即去掉刚臂，这个状态称为放松状态，节点B将产生角位移，并在各杆端(包括近端和远端)引起杆端弯矩，记作M’，则固端弯矩与位移弯矩的代数和就是最终杆端弯矩2、近端位移弯矩的计算及分配系数AB杆:远端为固定支座，转动刚度SBA = 4iBC杆:远端为铰支座，转动刚度SBC = 3iBD杆:远端为双滑动支座，转动刚度SBD = i 各杆近端(B端)的杆端弯矩表达式:FFF,MMMiMSM4,,,，,，,，BABABABABABAFFF,MMMiMSM3,,,，,，,，CCBBCBCBBCBCFFF,MMMiMSM,,,，,，,，BBDBDBBDBDDD式中:23FlqlFFFM,,M,0M,CBDBAB1612显然，杆的近端位移弯矩为:,,,MS,MS,,MS,,,BABABDBDBCBC由B节点的力矩平衡条件ΣM = 0得:FFFS,，M，S,，M，S,，M,0BABABCBCBDBDM，M，M,0 BABCBD解得未知量θ为:FFFF(,M,M,M)(,,M)BCBCBCB,,, S，S，S,SBABCBDB解得的未知量代回杆近端位移弯矩的表达式，得到将未知量代回杆近端分配弯矩的表达式，得到:SFBA,M,S,,(,,M)BABAB,SBSFBC,M,S,,(,,M)BCBCB,SBSFBD,M,S,,(,,M)BDBDB,SB上式中括号前的系数称为分配系数，记作μ，即:SSSBCBABD,,,,,,BABCBD,S,,SSBBB一个杆件的杆端分配系数等于自身杆端转动刚度除以杆端节点所连各杆的杆端转动刚度之和。

土木工程力学（2）辅导（四）——力矩分配法1. 力矩分配法的基本运算●三个基本概念转动刚度：111zSM kk=kS1：1k杆的1用的弯矩。

分配系数：MSSMkkk)1(111=∑k1μ：当结点1杆的1端的力矩。

传递系数：kkkMCM111=kC1矩的比值。

当单位力偶作用在结点1弯矩乘以传递系数。

●一个基本运算如图1所示，各杆的转动刚度为：141413131212,4,2iSiSiS===各杆的力矩分配系数为：∑∑∑===)1(11414)1(11313)1(11212,,kKkSSSSSSμμμ分配给各杆的分配力矩即近端弯矩为：MSSMMSSMMMSSMkkk∑∑∑====)1(11414)1(1131312)1(11212,,μμμμ各杆的传递系数为：1,21,0141312-===CCC各杆的传递弯矩即远端弯矩为：144113131331121221,21,0MMMMCMMCM CCC-=====2．具有一个结点角位移结构的计算步骤：● 加约束：在刚结点i 处加一附加刚臂，求出固端弯矩，再求出附加刚臂给结点的约束力矩f i M 。

● 放松约束：为消掉约束力矩f i M ，加-f i M ，求出各杆端弯矩。

● 合并：将上两种情况相加。

固端弯矩+分配弯矩=近端弯矩 固端弯矩+传递弯矩=远端弯矩 例1. 用力矩分配法计算图2所示连续梁的弯矩图。

分配系数固端弯矩分配及传递弯矩最后弯矩M图（单位：KN.m）mKNplMmKNqlMmKNqlMBCfCBfBAf.60163.6012.1351222-=-====-=附加刚臂对结点的约束力矩为：mKNM B f.7560135=-=●放松结点：在结点B上加外力偶B fM-，求出分配弯矩和传递弯矩。

定义lEIi=转动刚度为：iiSiiSBCBCABBA44,33====分配系数为：57.043.0=+==+=BCABBCBCBCBABABASSSSSSμμ分配弯矩为：()()mkNMmkNMBCBA.25.327543.0.75.427557.0-=-⨯=-=-⨯=μμ传递弯矩为：()mkNMMCBcABc.38.2175.4221-=-⨯==●合并，固端弯矩+分配弯矩=近端弯矩，固端弯矩+传递弯矩=远端弯矩。

用位移法求解时的基本结构如图17-2(b)所示。 相应的位移法典型方程为
r11Z1+R1p=0 作基本结构的M1图，如图17-2(c)所示。
由转动刚度的定义可知：
r11=SAB+SAC+SAD=∑SAj 方程中的自由项：R1p=-M 代入位移法典型方程得：∑SAjZ1-M=0
Z1=(1/∑SAj)M
3.传递系数C
图17-2(a)中，结点力矩M不仅使各杆近端产生弯矩，同 时也使各杆远端产生弯矩。我们把杆件的远端弯矩与近端弯 矩的比值称为该杆从近端传至远端的弯矩传递系数，简称传 递系数，用C表示。由位移法可进一步求出
MBA=2iABZ1=(2iAB /∑SAj)M， MCA=0， MDA=2iADZ1=(2iAD/∑SAj)M 而 MAB=SABZ1=(4iAB/∑SAj)M， MAC=SACZ1=(3iAC/∑SAj)M， MAD=SADZ1=(4iAD/∑SAj)M
=-48kN•m，
MFDA=pa2b/l2=100×32×2/52=72kN•m MFAC= MFCA=0
பைடு நூலகம்
根据平衡条件，可求得附加刚臂上产生的 反力矩RFA
RFA= MFAB + MFAC + MFAD = 60-48=12kN•m
RFA在数值上等于汇交于结点A的各杆端的 固端弯矩的代数和，可以看作是各固端弯矩本 身所不能相互平衡的差额，故称为结点的不平 衡力矩。可见，RFA= R1p。因此
Z1=-R1p/r11=-RFA/∑SAj
各杆件杆端的最后弯矩可根据叠加原理
M= M1Z1+Mp求得： MAB =(SAB/∑SAj)(-RFA)+ MFAB
=μAB(-RFA)+ MFAB = MμAB+ MFAB MAC =(SAC/∑SAj)(-RFA)+ MFAC