2018年中考数学专题复习《相似三角形》同步练习含答案
- 格式:pdf
- 大小:284.24 KB
- 文档页数:6

备考2023年中考数学一轮复习-图形的变换_图形的相似_相似三角形的判定与性质-综合题专训及答案相似三角形的判定与性质综合题专训1、(2017哈尔滨.中考模拟) 如图,抛物线y=ax2+bx+c经过A(﹣3,0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO(1)求抛物线的解析式;(2)点P在线段AB上,过点P作y轴的平方线,交抛物线于点Q,当PQ取最大值时,求点P的坐标;(3)在(2)的条件下,把线段PA绕点P顺时针旋转90°,得线段PD,连接BD交直线PQ于点M,作MN⊥AB于N,求MN的长.2、(2018灌云.中考模拟) 如图(1)如图,正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD:GC:EB的结果;(2)将图中的正方形AEGH绕点A旋转一定角度,如图,求HD:GC:EB;(3)把图中的正方形都换成矩形,如图,且已知DA::,求此时HD:GC:EB的值简要写出过程.3、(2018无锡.中考模拟) 如图,A、B两点的坐标分别为(0,6),(0,3),点P为x轴正半轴上一动点,过点A作AP的垂线,过点B作BP的垂线,两垂线交于点Q,连接PQ,M为线段PQ的中点.(1)求证:A、B、P、Q四点在以M为圆心的同一个圆上;(2)当⊙M与x轴相切时,求点Q的坐标;(3)当点P从点(2,0)运动到点(3,0)时,请直接写出线段QM扫过图形的面积.4、(2019慈溪.中考模拟) 双曲线y= (k>0)的图象如图所示,点A的坐标是(0,6),点B(a,0)(a>0)是x轴上的一个动点,G为线段AB的中点,把线段BG绕点B按顺时针方向旋转90°后得到线段BC,然后以AB,BC为边作矩形ABCD。
(1)求C点坐标(用a的式子表示) ;(2)若矩形ABCD水平向右平移二个单位,使双曲线y= 经过A,C两点,求a的值。
5、(2011嘉兴.中考真卷) 已知直线y=kx+3(k<0)分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P 作x轴的垂线交直线AB于点C,设运动时间为t秒.(1)当k=﹣1时,线段OA上另有一动点Q由点A向点O运动,它与点P以相同速度同时出发,当点P到达点A时两点同时停止运动(如图1).①直接写出t=1秒时C、Q两点的坐标;②若以Q、C、A为顶点的三角形与△AOB相似,求t的值.(2)当时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D (如图2),①求CD的长;②设△COD的OC边上的高为h,当t为何值时,h的值最大?6、(2019泉州.中考模拟) 如图,在ABCD中,AC与BD相交于点O,AC⊥BC,垂足为C.将△ABC沿AC翻折得到△AEC,连接DE.(1)求证:四边形ACED是矩形;(2)若AC=4,BC=3,求sin∠ABD的值.7、(2018洛阳.中考模拟) 在等腰直角三角形ABC中,∠ACB=90°,AC=BC,D是AB 边上的中点,Rt△EFG的直角顶点E在AB边上移动.(1)如图1,若点D与点E重合且EG⊥AC、DF⊥BC,分别交AC、BC于点M、N,易证EM=EN;如图2,若点D与点E重合,将△EFG绕点D旋转,则线段EM与EN的长度还相等吗?若相等请给出证明,不相等请说明理由;(2)将图1中的Rt△EGF绕点D顺时针旋转角度α(0∘<α<45∘). 如图2,在旋转过程中,当∠MDC=15∘时,连接MN,若AC=BC=2,请求出线段MN的长;(3)图3, 旋转后,若Rt△EGF的顶点E在线段AB上移动(不与点D、B重合),当AB=3AE时,线段EM与EN的数量关系是;当AB=m·AE时,线段EM与EN的数量关系是.8、(2019福田.中考模拟) 如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC.BD 交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E.连接OE.(1)求证:四边形ABCD是菱形;(2)若AB=.OE=2,求线段CE的长.9、(2018毕节.中考模拟) 如图,在▱ABCD中过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.(1)求证:△ABF∽△BEC;(2)若AD=5,AB=8,sinD= ,求AF的长.10、(2018遵义.中考模拟) 如图,在△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,且CD=3cm.动点P、Q分别从A、C两点同时出发,其中点P以1cm/s的速度沿AC向终点C移动;点Q以cm/s的速度沿CB向终点B移动.过点P 作PE∥CB交AD于点E,设动点的运动时间为x秒.(1)用含x的代数式表示EP;(2)当Q在线段CD上运动几秒时,四边形PEDQ是平行四边形;(3)当Q在线段BD(不包括点B、点D)上运动时,求当x为何值时,四边形EPDQ面积等于.11、(2017陕西.中考真卷) 综合题(1)问题提出如图①,△ABC是等边三角形,AB=12,若点O是△ABC的内心,则OA的长为;(2)问题探究如图②,在矩形ABCD中,AB=12,AD=18,如果点P是AD边上一点,且AP=3,那么BC边上是否存在一点Q,使得线段PQ将矩形ABCD的面积平分?若存在,求出PQ的长;若不存在,请说明理由.(3)问题解决某城市街角有一草坪,草坪是由△ABM草地和弦AB与其所对的劣弧围成的草地组成,如图③所示.管理员王师傅在M处的水管上安装了一喷灌龙头,以后,他想只用喷灌龙头来给这块草坪浇水,并且在用喷灌龙头浇水时,既要能确保草坪的每个角落都能浇上水,又能节约用水,于是,他让喷灌龙头的转角正好等于∠AMB(即每次喷灌时喷灌龙头由MA转到MB,然后再转回,这样往复喷灌.)同时,再合理设计好喷灌龙头喷水的射程就可以了.如图③,已测出AB=24m,MB=10m,△AMB的面积为96m2;过弦AB的中点D作DE⊥AB 交于点E,又测得DE=8m.请你根据以上信息,帮助王师傅计算喷灌龙头的射程至少多少米时,才能实现他的想法?为什么?(结果保留根号或精确到0.01米)12、(2018青海.中考真卷) 如图,抛物线与坐标轴交点分别为,,,作直线BC.(1)求抛物线的解析式;(2)点P为抛物线上第一象限内一动点,过点P作轴于点D,设点P 的横坐标为,求的面积S与t的函数关系式;(3)条件同,若与相似,求点P的坐标.13、(2020营口.中考模拟) 如图(提出问题)(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.14、(2020扬州.中考真卷) 如图1,已知点O在四边形ABCD的边AB上,且,OC平分,与BD交于点G,AC分别与BD、OD 交于点E、F.(1)求证:;(2)如图2,若,求的值;(3)当四边形ABCD的周长取最大值时,求的值.15、(2020昆明.中考真卷) 如图1,在矩形ABCD中,AB=5,BC=8,点E,F分别为AB,CD的中点.(1)求证:四边形AEFD是矩形;(2)如图2,点P是边AD上一点,BP交EF于点O,点A关于BP的对称点为点M,当点M落在线段EF上时,则有OB=OM.请说明理由;(3)如图3,若点P是射线AD上一个动点,点A关于BP的对称点为点M,连接AM,DM,当△AMD是等腰三角形时,求AP的长.相似三角形的判定与性质综合题答案1.答案:2.答案:3.答案:4.答案:5.答案:6.答案:7.答案:8.答案:9.答案:10.答案:11.答案:12.答案:13.答案:14.答案:15.答案:。

中考数学一轮复习专题相似三角形综合复习一选择题:1.下列说法正确的是()(A)两个矩形一定相似.(B) 两个菱形一定相似.(C)两个等腰三角形一定相似.(D) 两个等边三角形一定相似.2.如图,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E,B,D,F,若AC=4,CE=6,BD=3,则DF的值是()A.4 B.4.5 C.5 D.5.53.若两个扇形满足弧长的比等于它们半径的比,则这称这两个扇形相似。
如图,如果扇形AOB与扇形是相似扇形,且半径(为不等于0的常数)。
那么下面四个结论:①∠AOB=∠;②△AOB∽△;③;④扇形AOB与扇形的面积之比为.成立的个数为()A.1个B.2个C.3个D.4个4.如图,在长为8cm、宽为4cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是()A.2cm2 B.4cm2 C.8cm2 D.16cm25.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是()A. B. C. D.6.如图,矩形ABCD∽矩形ADFE,AE=1,AB=4,则AD=()A. 2B. 2.4C. 2.5D. 37.如图是测量小玻璃管口径的量具ABC,AB的长为12 cm,AC被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(DE∥AB),那么小玻璃管口径DE是( )A.8 c m B.10 cm C.20 cm D.60 cm8.如图,在平行四边形ABCD 中,点E在CD上,若DE:CE =1:2,则△CEF与△ABF的周长比为()A.1:2 B.1:3 C.2:3 D.4︰99.如图,AB是⊙O的直径,D,E是半圆上任意两点,连接AD,DE,AE与BD相交于点C,要使△ADC与△BDA相似,可以添加一个条件.下列添加的条件中错误的是( )A.∠ACD=∠DAB B.AD=DE C.AD·AB=CD·BD D.AD2=BD·CD10.如图,D是△ABC一边BC上一点,连接AD,使△ABC∽△DBA的条件是( )A.AC:BC=AD:BDB.AC:BC=AB:ADC.AB2=CD·BCD.AB2=BD·BC11.如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:①∠APB=∠EPC;②∠APE=∠APB;③P是BC的中点;④BP:BC=2:3.其中能推出△ABP∽△ECP的有( )A.4个 B.3个 C.2个 D.1个12.如图,在▱ABCD中,AB=4,AD=3,过点A作AE⊥BC于E,且AE=3,连结DE,若F为线段DE上一点,满足∠AFE=∠B,则AF=()A.2 B. C.6 D.213.已知( )A. B. C. D.14.如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达点E处(即CE=3米),测得自己影子EF的长为2米,已知小明的身高是1.5米,那么路灯A的高度AB是()A.4.5米 B.6米 C.7.2米 D.8米15.如图,在矩形COED中,点D的坐标是(1,3),则CE的长是()A.3 B. C. D.416.如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )A. B. C. D.17.如图,AB=AC=4,P是BC上异于B,C的一点,则AP2+BP·PC的值是( )A.16 B.20 C.25 D.3018.如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B=α,DE交AC于点E.下列结论:①AD2=AE•AB;②3.6≤AE<10;③当AD=2时,△ABD≌△DCE;④△DCE为直角三角形时,BD 为8或12.5.其中正确的结论个数是().A.1个B. 2个C. 3个D. 4个19.如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于()A.3:2:1 B.5:3:1 C.25:12:5 D.51:24:1020.如图,小明作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积.然后分别取△A1B1C1三边的中点A2、B2、C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积.用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…,由此可得,第10个正△A10B10C10的面积是()A. B. C. D.二填空题:21.若,则= .22.若a:b:c=1:3:2,且a+b+c=24,则a+b﹣c= .23.如图,边长12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上.若BF=3,则小正方形的边长为.24.如图,上体育课,甲、乙两名同学分别站在C、D的位置时,乙的影子恰好在甲的影子里边,已知甲,乙同学相距1米,甲身高1.8米,乙身高1.5米,则甲的影长是_ 米.25.如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB,CD上滑动,当CM=_________时,△AED与以M,N,C为顶点的三角形相似.26.阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m,窗口高AB=1.8m,则窗口底边离地面的高BC=______m.27.如图,小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度为米.28.如图,在四边形中,,如果边AB上的点P,使得以为顶点的三角形与为顶点的三角形相似,这样的点P有个.29.如图,△ABC是边长为a的等边三角形,将三角板的30°角的顶点与A重合,三角板30°角的两边与BC交于D、E两点,则DE长度的取值范围是_________.30.如图,△ABC是一张直角三角形彩色纸,AC=15cm,BC=20cm.若将斜边上的高CD 分成n等分,然后裁出(n ﹣1)张宽度相等的长方形纸条.则这(n﹣1)张纸条的面积和是cm2.三简答题:31.如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,使AE=CF,连接AF,BE相交于点P.(1)求证:AF=BE,并求∠APB的度数;(2)若AE=2,试求AP·AF的值.32.已知:如图,△ABC中,AB=2,BC=4,D为BC边上一点,BD=1.(1)求证:△ABD∽△CBA;(2)若DE∥AB交AC于点E,请再写出另一个与△ABD相似的三角形,并直接写出DE的长.33.如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC 于点N.(1)求证:△ABM∽△EFA;(2)若AB=12,BM=5,求DE的长.34.如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与底面保持平行并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.35.一天晚上,李明和张龙利用灯光下的影子长来测量一路灯D的高度.如图23-12,当李明走到点A处时,张龙测得李明直立时身高AM与影子长AE正好相等;接着李明沿AC方向继续向前走,走到点B处时,李明直立时身高BN的影子恰好是线段AB,并测得AB=1.25m,已知李明直立时的身高为1.75m,求路灯的高CD的长.(结果精确到0.1m).36.如图,Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,一动点P从点A出发沿边AC向点C以1cm/s的速度运动,另一动点Q同时从点C出发沿CB边向点B以2cm/s的速度运动.问:(1)运动几秒时,△CPQ的面积是8cm2?(2)运动几秒时,△CPQ与△ABC相似?37.如图,AD是△ABC的高,点E,F在边BC上,点H在边AB上,点G在边AC上,AD=80cm,BC=120cm.(1)若四边形EFGH是正方形,求正方形的面积.(2)若四边形EFGH是长方形,长方形的面积为y,设EF=x,则y=______.(含x的代数式),当x=______时,y最大,最大面积是______.38.如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个动点到达终点时,另一个动点也随之停止运动.(1)AC= cm,BC= cm;(2)当t=5 (s)时,试在直线PQ上确定一点M,使△BCM的周长最小,并求出该最小值.(3)设点P的运动时间为t (s),△PBQ的面积为y (cm2),当△PBQ存在时,求y与t的函数关系式,并写出自变量t的取值范围;(4)探求(3)中得到的函数y有没有最大值?若有,求出最大值;若没有,说明理由.39.在等腰△ABC中,AB=AC=10,BC=12,D为底边BC的中点,以D为顶点的角∠PDQ=∠B.(1)如图1,若射线DQ经过点A,DP交AC边于点E,直接写出与△CDE相似的三角形;(2)如图2,若射线DQ交AB于点F,DP交AC边于点E,设AF=x,AE为y,试写出y与x的函数关系式;(不要求写出自变量的取值范围)40.在平面直角坐标系中,二次函数的图象与轴交于A(-3,0),B(1,0)两点,与y轴交于点C.(1)求这个二次函数的解析式;(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;(3)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;参考答案1、D2、B.3、D4、C5、B6、A7、A8、C9、C 10、D 11、C 12、D.13、B 14、B 15、C 16、B 17、A 18、D;19、D 20、A.21、.22、8.23、.24、6 25、或 26、4 m. 27、14+2 28、329、(2﹣3)a≤DE≤a..30、cm2.31、解:(1)∵△ABC为等边三角形,∴AB=AC,∠C=∠CAB=60°,又∵AE=CF,∴△ABE≌△CAF(SAS),∴AF=BE,∠ABE=∠CAF.又∵∠APE=∠BPF=∠ABP+∠BAP,∴∠APE=∠BAP+∠CAF=60°,∴∠APB=180°-∠APE=120°(2)∵∠C=∠APE=60°,∠PAE=∠CAF,∴△APE∽△ACF,∴=,即=,∴AP·AF=12 32、【解答】(1)证明:∵AB=2,BC=4,BD=1,∴,∵∠ABD=∠CBA,∴△ABD∽△CBA;(2)解:∵DE∥AB,∴△CDE∽△CBA,∴△ABD∽△CDE,∴DE=1.5.33、【解答】(1)证明:∵四边形ABCD是正方形,∴AB=AD,∠B=90°,AD∥BC,∴∠AMB=∠EAF,又∵EF⊥AM,∴∠AFE=90°,∴∠B=∠AFE,∴△ABM∽△EFA;(2)解:∵∠B=90°,AB=12,BM=5,∴AM==13,AD=12,∵F是AM的中点,∴AF=AM=6.5,∵△ABM∽△EFA,∴,即,∴AE=16.9,∴DE=AE﹣AD=4.9.34、根据题意,得∠DEF=∠DCA=90°,∠EDF=∠ADC,∴△DEF∽△DCA.∴=.已知DE=0.5米,EF=0.25米,DC=20米.∴=.解得AC=10米.∵四边形BCDG是矩形,∴BC=DG,而DG=1.5米,则BC=1.5米.35、答案:设CD长为x米,∵AM⊥EC,CD⊥EC,BN⊥EC,EA=MA∴MA∥CD∥BN ∴EC=CD=x∴△ABN∽△ACD,解得:x=6.125≈6.1.经检验,x=6.125是原方程的解,∴路灯高CD约为6.1米36、【解答】解:(1)设x秒后,可使△CPQ的面积为8cm2.由题意得,AP=xcm,PC=(6﹣x)cm,CQ=2xcm,则(6﹣x)•2x=8,整理,得x2﹣6x+8=0,解得x1=2,x2=4.则P、Q同时出发,2秒或4秒后可使△CPQ的面积为8cm2(2)设运动y秒时,△CPQ与△ABC相似.若△CPQ∽△CAB,则=,即=,解得y=2.4秒;若△CPQ∽△CBA,则=,即=,解得y=秒.综上所述,运动2.4秒或秒时,△CPQ与△ABC相似.37、【解答】解:(1)∵四边形EFGH是正方形,∴HG∥EF,GH=HE=ID,∴△AHG∽△ABC,∴AI:AD=HG:BC,∵BC=120cm,AD=80cm,∴,解得:HG=48cm,∴正方形EFGH的面积=HG2=482=2304(cm2);(2)∵四边形EFGH是长方形,∴HG∥EF,∴△AEF∽△ABC,∴AI:AD=HG:BC,即,解得:HE=﹣x+80,∴长方形EFGH的面积y=x(﹣x+80)=﹣2+80x=﹣(x﹣60)2+240,∵﹣<0,∴当x=60,即EF=60cm时,长方形EFGH有最大面积,最大面积是240cm2;故答案为:﹣x2+80x,60cm,240cm2.38、解:(1)设AC=4x,BC=3x,在Rt△ABC中,AC 2 +BC 2 =AB 2,即:(4x)2 +(3x)2 =10 2,解得:x=2,∴AC=8cm,BC=6cm;(2)存在,理由:∵AQ=14-2x=14-10=4,AP=x=5,∵AC=8,AB=10,∴PQ是△ABC的中位线,∴PQ∥AB,∴PQ⊥AC,∴PQ是AC的垂直平分线,∴PC=AP=5,∴当点M与P重合时,△BCM的周长最小,∴△BCM的周长为:MB+BC+MC=PB+BC+PC=5+6+5=16,∴△BCM的周长最小值为16.(3)①当点Q在边BC上运动时,过点Q作QH⊥AB于H,∵AP=x,∴BP=10-x,BQ=2x,∵△QHB∽△ACB,②当点Q在边CA上运动时,过点Q作QH′⊥AB于H′,∵AP=x,∴BP=10-x,AQ=14-2x,∵△AQH′∽△ABC,39、【解答】解:(1)与△CDE相似的三角形为△ABD,△ACD,△ADE;理由如下:∵AB=AC,D为底边BC的中点,∴∠B=∠C,AD⊥BC,∴∠ADB=∠ADC=90°,∴△ABD∽△ACD,∵∠PDQ=∠B,∴∠PDQ=∠C,又∵∠DAE=∠CAD,∴△ADE∽△ACD;∵∠CDE+∠PDQ=90°,∴∠C+∠PDQ=90°,∴∠CED=90°=∠ADC,又∵∠C=∠C,∴△CDE∽△CAD,∴△△ABD∽△ACD∽△ADE∽△CDE;(2)∵∠FDC=∠B+∠BDF,∠FDC=∠FDE+∠EDC,∴∠EDC=∠BDF,∴△BDF∽△CDE,∴,∵D为BC的中点,∴BD=CD=6,∴∴y=;(3)△DEF与△CDE相似.理由如下:如图所示:由(2)可知:△BDF∽△CDE,则,∵BD=CD,∴,又∵∠EDF=∠C,∴△DEF∽△CED.40.解:(1)由抛物线过点A(-3,0),B(1,0),则解得∴二次函数的关系解析式.(2)连接PO,作PM⊥x轴于M,PN⊥y轴于N.设点P坐标为(m,n),则.PM =,,AO=3.当时,=2.∴OC=2.===.8分∵=-1<0,∴当时,函数有最大值.此时=.∴存在点,使△ACP的面积最大.(3)存在点Q,坐标为:,.分△BQE∽△AOC,△EBQ∽△AOC,△QEB∽△AOC三种情况讨论可得出.。

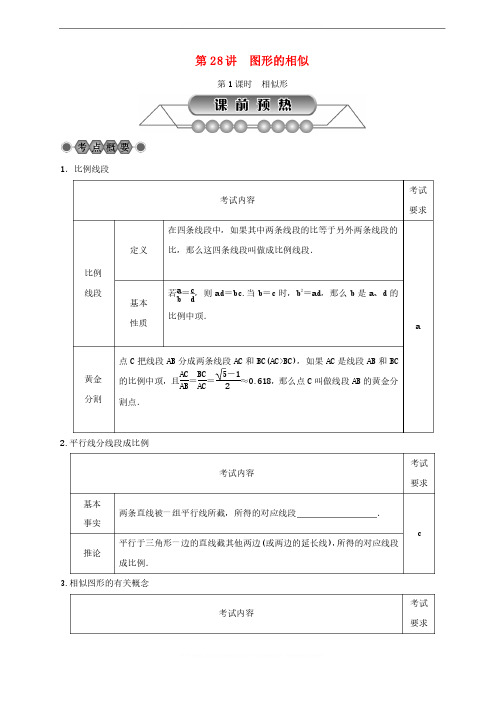
第28讲 图形的相似第1课时课时 相似形相似形1.比例线段.比例线段考试内容考试内容考试考试要求要求比例比例 线段线段定义定义在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段.比,那么这四条线段叫做成比例线段.a基本基本 性质性质若a b =c d,则ad ad==bc.bc.当当b =c 时,时,b b 2=ad ad,那么,那么b 是a 、d 的比例中项.比例中项.黄金黄金 分割分割 点C 把线段AB 分成两条线段AC 和BC(AC>BC)BC(AC>BC),如果,如果AC 是线段AB 和BC 的比例中项,且AC AB =BC AC =5-12≈0.6180.618,,那么点C 叫做线段AB 的黄金分割点.割点.2.2.平行线分线段成比例平行线分线段成比例平行线分线段成比例考试内容考试内容考试考试要求要求基本基本 事实事实两条直线被一组平行线所截,所得的对应线段两条直线被一组平行线所截,所得的对应线段. c推论推论平行于三角形一边的直线截其他两边平行于三角形一边的直线截其他两边((或两边的延长线或两边的延长线)),所得的对应线段成比例.成比例.3.3.相似图形的有关概念相似图形的有关概念相似图形的有关概念考试内容考试内容考试考试要求要求相似图形________________________________________相同的图形称为相似图形.相同的图形称为相似图形.相同的图形称为相似图形.a相似多相似多边形边形两个边数相同的多边形,如果它们的角分别如果它们的角分别 ,边 ,那么这两个多边形叫做相似多边形.多边形叫做相似多边形.相似多边形对应相似多边形对应 的比叫做相似比.的比叫做相似比.(1)(1)相似多边形周长的比等于相似比;相似多边形周长的比等于相似比;相似多边形周长的比等于相似比; (2)(2)相似多边形面积的比等于相似比的平方相似多边形面积的比等于相似比的平方相似多边形面积的比等于相似比的平方相似三相似三 角形角形 两个三角形的三个角分别两个三角形的三个角分别_ _ ,三条边,三条边 ,则这两个三角形相似.当相似比等于1时,这两个三角形时,这两个三角形 . 4.4.相似三角形的判定相似三角形的判定相似三角形的判定考试内容考试内容考试考试要求要求判定1________________________________________于三角形一边的直线和其他两边相交,于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.三角形与原三角形相似.a 判定2 三边三边 的两个三角形相似.的两个三角形相似.判定3 两边两边 且夹角且夹角 的两个三角形相似.的两个三角形相似. 判定4 两角分别两角分别 的两个三角形相似.的两个三角形相似.判定5满足斜边和一条直角边满足斜边和一条直角边 的两个直角三角形相似.的两个直角三角形相似.拓展拓展直角三角形中被斜边上的高分成的两个三角形都与原三角形相似.两个三角形都与原三角形相似.5.5.相似三角形的性质相似三角形的性质相似三角形的性质考试内容考试内容考试考试要求要求性质性质1.1.相似三角形的对应角相似三角形的对应角相似三角形的对应角 ,对应边对应边. a2.2.相似三角形对应高的比、相似三角形对应高的比、相似三角形对应高的比、对应中线的比、对应中线的比、对应中线的比、对应角平分线的比和周长的对应角平分线的比和周长的比都等于比都等于.3.3.相似三角形面积的比等于相似比的相似三角形面积的比等于相似比的相似三角形面积的比等于相似比的____________________. ____________________.三角形三角形 的重心的重心 三角形三条中线的交点叫做重心.三角形三条中线的交点叫做重心.三角形的重心分每一条中线成1∶2的两条线段.拓展拓展如图,△ABC 中,∠中,∠ACB ACB ACB==9090°,°,CD 是斜边AB 上的高,则有下列结论.则有下列结论.①AC 2=AD·AB;=AD·AB;②BC 2=BD·AB;=BD·AB;③CD 2=AD·BD;=AD·BD;④AB AB··CD CD=AC·BC.=AC·BC.=AC·BC.考试内容考试内容考试考试要求要求基本基本 思想思想转化思想:证角相等,证比例线段往往转化为证相似三角形;测量问题,往往构建相似三角形,即实际问题转化为相似三角形问题来解决.往往构建相似三角形,即实际问题转化为相似三角形问题来解决.b1.(2017·杭州.(2017·杭州))如图,在△ABC 中,点D ,E 分别在边AB AB,,AC 上,DE DE∥∥BC BC,,若BD BD==2AD 2AD,,则( ( )A .AD AB =12 B .AE EC =12 C .AD EC =12 D .DE BC =12 2.(2015·嘉兴.(2015·嘉兴))如图,直线l 1∥l 2∥l 3,直线AC 分别交l 1,l 2,l 3于点A ,B ,C ;直线DF 分别交l 1,l 2,l 3于点D ,E ,F.AC 与DF 相交于点H ,且AH AH==2,HB HB==1,BC BC==5,则DEEF的值为的值为( ( ( )A .12B .2C .25D .35 3.(2015·嘉兴.(2015·嘉兴))如图是百度地图的一部分如图是百度地图的一部分((比例尺1∶4000000).按图可估测杭州在嘉兴的南偏西偏西_______________________________________度方向上,杭州到嘉兴的图上距离约2cm ,则杭州到嘉兴的实际距离约为________________________________________..【问题】如图,点D 在△ABC 的边AC 上.上.(1)(1)要判断△ADB 要判断△ADB 与△ABC 相似,添加一个条件是相似,添加一个条件是____________________________________________________________;; (2)若△ADB∽△ABC,若△ADB∽△ABC,AB AB AB==4,AD AD==2,则AC AC==________________;; (3)(3)通过通过通过(1)(1)(1)、、(2)(2)解答,你能说出相似三角形哪些知识?解答,你能说出相似三角形哪些知识?解答,你能说出相似三角形哪些知识?【归纳】通过开放式问题,归纳、疏理比例、相似多边形有关概念,相似三角形性质、判定.类型一 比例性质、黄金分割等相关概念例1 (1)(2016·山西(1)(2016·山西))宽与长的比是5-12(约0.618)0.618)的矩形叫做黄金矩形,的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:作正方形ABCD ABCD,,分别取AD AD、、BC 的中点E 、F ,连结EF EF;以点;以点F 为圆心,以FD 为半径画弧,交BC 的延长线于点G ;作GH⊥AD,交AD 的延长线于点H ,则图中下列矩形是黄金矩形的是,则图中下列矩形是黄金矩形的是( ( ( )A .矩形ABFEB .矩形EFCDC .矩形EFGHD .矩形DCGH【解后感悟】先根据正方形的性质以及勾股定理,求得DF 的长,再根据DF DF==GF 求得CG 的长,最后根据CG 与CD 的比值为黄金比,判断矩形DCGH 为黄金矩形.为黄金矩形.(2)(2) 已知x 3=y 4=z 6≠0,求x +y -z x -y +z 的值.的值.【解后感悟】这类题我们一般是设辅助未知数k ,即比值为k ,把所有字母都用含有k 的式子表示出来,从而达到计算或化简的目的.示出来,从而达到计算或化简的目的.1.在中华经典美文阅读中,在中华经典美文阅读中,小明同学发现自己的一本书的小明同学发现自己的一本书的宽与长之比为黄金比.宽与长之比为黄金比.已知这本书的已知这本书的长为20cm ,则它的宽约为,则它的宽约为( ( ( )A .12.36cmB .13.6cmC .32.36cmD .7.64cm 2.(2015·扬州.(2015·扬州))如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A 、B 、C 都在横格线上,若线段AB AB==4cm ,则线段BC BC==cm .类型二 相似多边形例2 已知矩形ABCD 中,中,AB AB AB==1,在BC 上取一点E ,沿AE 将△ABE 向上折叠,使B 点落在AD 上的F 点,若四边形EFDC 与矩形ADCB 相似,则AD AD==( ( )A .5-12B .5+12C .3D .2 【解后感悟】解题关键是根据相似多边形的性质:对应边的比等于相似比.【解后感悟】解题关键是根据相似多边形的性质:对应边的比等于相似比.3.(2015·葫芦岛.(2015·葫芦岛))如图,在矩形ABCD 中,中,AD AD AD==2,CD CD==1,连结AC AC,以对角线,以对角线AC 为边,按逆时针方向作矩形ABCD 的相似矩形AB 1C 1C ,再连结AC 1,以对角线AC 1为边作矩形AB 1C 1C 的相似矩形AB 2C 2C 1,…,按此规律继续下去,则矩形AB n C n C n -1的面积为的面积为____________________________________________________________..类型三 相似三角形的判定与性质例3 (2016·南充(2016·南充))已知正方形ABCD 的边长为1,点P 为正方形内一动点,若点M 在AB 上,且满足△PBC∽△PAM,延长BP 交AD 于点N ,连结CM.(1)(1)如图如图1,若点M 在线段AB 上,求证:AP⊥BN;上,求证:AP⊥BN;AM AM AM==AN AN;;(2)①如图2,在点P 运动过程中,满足△PBC∽△PAM 的点M 在AB 的延长线上时,的延长线上时,AP AP AP⊥⊥BN 和AM =AN 是否成立?是否成立?((不需说明理由不需说明理由) )②是否存在满足条件的点P ,使得PC PC==12?请说明理由.?请说明理由.【解后感悟】本题考查相似三角形的性质、正方形的性质、圆的有关知识,解题的关键是熟练应用相似三角形性质解决问题,最后一个问题利用圆的位置关系解决问题.应用相似三角形性质解决问题,最后一个问题利用圆的位置关系解决问题.4.(1)(1)如图,在△ABC 如图,在△ABC 中,点D ,E 分别在边AB AB,,AC 上,且AE AB =AD AC =12,则S △ADE ∶S 四边形BCED 的值为( ( )A .1∶3B .1∶2C .1∶3D .1∶4(2)(2) (2016·河北(2016·河北))如图,△如图,△ABC ABC 中,∠中,∠A A =7878°,°,°,AB AB AB==4,AC AC==6.6.将△ABC 将△ABC 沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似...的是的是( ( ( )5.(1)(2015·自贡)将一副三角板按图叠放,则△AOB 与△DOC 的面积之比等于 .(2)(2015·无锡市南长区模拟(2)(2015·无锡市南长区模拟))如图,△如图,△ABC ABC 中,中,AB AB AB==5,BC BC==3,CA CA==4,D 为AB的中点,过点D 的直线与BC 所在直线交于点E ,若直线DE 截△ABC 所得的三角形与△ABC 相似,则DE DE== .类型四 与相似三角形相关的问题例4 如图,点A ,B ,C ,D 为⊙O 上的四个点,上的四个点,AC AC 平分∠BAD,平分∠BAD,AC AC 交BD 于点E ,CE CE==4,CD CD==6,则AE 的长为的长为( ( ( )A .4B .5C .6D .7【解后感悟】本题运用圆周角定理、相似三角形的判定与性质,解答本题的关键是得出∠CAD =∠CDB,证明△ACD∽△DCE.=∠CDB,证明△ACD∽△DCE.6.(1)(1)已知:在△ABC 已知:在△ABC 中,中,BC BC BC==1010,,BC 边上的高h =5,点E 在边AB 上,过点E 作EF∥BC,交AC 边于点F.F.点点D 为BC 上一点,连结DE DE、、DF.DF.设点设点E 到BC 的距离为x ,则△DEF 的面积S 关于x 的函数图象大致为函数图象大致为( ( ( )(2)(2015·杭州模拟(2)(2015·杭州模拟))在研究相似问题时,甲、乙同学的观点如下:在研究相似问题时,甲、乙同学的观点如下:甲:将边长为3,4,5的三角形按图①的方式向外扩张,得到新的三角形,它们的对应边间距为1,则新三角形与原三角形相似.,则新三角形与原三角形相似.乙:将邻边为3和5的矩形按图②的方式向外扩张,得到新矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.则新矩形与原矩形不相似.对于两人的观点,下列说法正确的是对于两人的观点,下列说法正确的是( ( ( ) )A .两人都对.两人都对B .两人都不对.两人都不对C .甲对,乙不对.甲对,乙不对D .甲不对,乙对.甲不对,乙对(3)(3) (2015·滨州(2015·滨州))如图,在x 轴的上方,直角∠BOA 绕原点O 按顺时针方向旋转,若∠BOA 的两边分别与函数y =-1x 、y =2x的图象交于B 、A 两点,则∠OAB 的大小的变化趋势为的大小的变化趋势为( ( ( ) )A .逐渐变小.逐渐变小B .逐渐变大.逐渐变大C .时大时小.时大时小D .保持不变.保持不变7.(2016·龙东.(2016·龙东))已知,在平行四边形ABCD 中,点E 在直线AD 上,上,AE AE AE==13AD AD,连结,连结CE 交BD 于点F ,则EF∶FC 的值是的值是 .【课本改变题】教材母题--浙教版教材九上第149页第5题课本中有一道作业题:课本中有一道作业题:有一块三角形余料ABC ABC,它的边,它的边BC BC==120mm ,高AD AD==80mm .要把它加工成正方形零件,使正方形的一边在BC 上,其余两个顶点分别在AB AB,,AC 上.问加工成的正方形零件的边长是多少mm?小颖解得此题的答案为48mm ,小颖善于反思,她又提出了如下的问题.,小颖善于反思,她又提出了如下的问题.(1)(1)如果原题中要加工的零件是一个矩形,如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm ?请你计算.?请你计算.(2)(2)如果原题中所要加工的零件只是一个矩形,如图如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.【方法与对策】本题是课本改变题,试题设置上主要是三角形和矩形的组合,通过基本图形是相似三角形,揭示对应边成比例的关系式来解决问题,再深入探究,规律性较强,这种题型是中考常用的命题方式.常用的命题方式.【找不准相似三角形中的对应边】【找不准相似三角形中的对应边】如图,△如图,△ABC ABC 中,点D 在线段BC 上,且△ABC∽△D 上,且△ABC∽△DBA BA BA,则下列结论一定正确的是,则下列结论一定正确的是,则下列结论一定正确的是( ( ( )A .AB 2=BC·BD =BC·BD B .AB 2=AC·BD =AC·BDC .AB AB··AD AD=BD·BC =BD·BC =BD·BC D .AB AB··AD AD=AD·CD =AD·CD =AD·CD参考答案 第28讲 图形的相似 第1课时 相似形【考点概要】【考点概要】2.成比例成比例 3.形状形状 相等相等 成比例成比例 边 相等相等 成比例成比例 全等全等 4.平行平行 成比例成比例 成比例成比例 相等 相等相等 成比例成比例 5.相等相等 成比例成比例 相似比相似比 平方平方【考题体验】【考题体验】1.B 2.D 3.45 80km 【知识引擎】【知识引擎】【解析】(1)添加条件是∠ABD =∠C 或∠ADB =∠ABC 或者AD AB =AB AC ; (2)由△ADB ∽△ABC ,得AD AB =ABAC,得AC =8; (3)相似三角形知识:性质、判定等.相似三角形知识:性质、判定等. 【例题精析】【例题精析】例1 (1)(1)设正方形的边长为设正方形的边长为2,则CD CD==2,CF CF==1.1.在直角三角形在直角三角形DCF 中,中,DF DF DF==12+22=5,∴FG FG==5,∴CG CG==5-1,∴CG CD =5-12,∴矩形DCGH 为黄金矩形.故选D . . (2)(2)(2)设设x 3=y 4=z 6=k(k≠0),根据题意,得x =3k 3k,,y =4k 4k,,z =6k 6k,所以,所以x +y -z x -y +z =3k 3k++4k 4k--6k 3k 3k--4k 4k++6k =k 5k =15. .例2 B 例3(1)(1)如图如图1中,∵四边形ABCD 是正方形,∴AB AB==BC BC==CD CD==AD AD,,∠DAB DAB=∠ABC=∠BCD=∠D==∠ABC=∠BCD=∠D==∠ABC=∠BCD=∠D=909090°,°,∵△∵△PBC PBC PBC∽△∽△∽△PAM PAM PAM,∴∠,∴∠,∴∠PAM PAM PAM=∠PBC,=∠PBC,PM PC =AM BC =PA PB,∵∠,∵∠PBC PBC PBC+∠PBA=+∠PBA=+∠PBA=909090°,∴∠°,∴∠°,∴∠PAM PAM PAM+∠PBA=+∠PBA=+∠PBA=909090°,°,∴∠∴∠APB APB APB==9090°,∴°,∴°,∴AP AP AP⊥⊥BN BN,∵∠,∵∠,∵∠ABP ABP ABP=∠ABN,∠=∠ABN,∠=∠ABN,∠APB APB APB=∠=∠=∠BAN BAN BAN==9090°,∴△°,∴△°,∴△BAP BAP BAP∽△∽△∽△BNA BNA BNA,∴,∴PA PB PB==ANAB AB,,∴AN AB =AM BC,∵AB AB==BC BC,,∴AN AN==AM. AM. (2)①仍然成立,(2)①仍然成立,AP AP⊥⊥BN 和AM AM==AN.AN.理由如图理由如图2中,∵四边形ABCD 是正方形,∴是正方形,∴AB AB AB==BC BC==CD CD==AD AD,∠,∠,∠DAB DAB DAB=∠ABC=∠BCD=∠D==∠ABC=∠BCD=∠D==∠ABC=∠BCD=∠D=909090°,∵△°,∵△°,∵△PBC PBC PBC∽△∽△∽△PAM PAM PAM,∴∠,∴∠,∴∠PAM PAM PAM==∠PBC,PM PC =AM BC =PA PB,∵∠,∵∠PBC PBC PBC+∠PBA=+∠PBA=+∠PBA=909090°,∴∠°,∴∠°,∴∠PAM PAM PAM+∠PBA=+∠PBA=+∠PBA=909090°,∴∠°,∴∠°,∴∠APB APB APB==9090°,∴°,∴°,∴AP AP AP⊥⊥BN BN,,∵∠∵∠ABP ABP ABP=∠ABN,∠=∠ABN,∠=∠ABN,∠APB APB APB=∠BAN==∠BAN==∠BAN=909090°,∴△°,∴△°,∴△BAP BAP BAP∽△∽△∽△BNA BNA BNA,∴,∴PA PB =AN AB ,∴AN AB =AM BC,∵,∵AB AB AB==BC BC,∴,∴,∴AN AN =AM. AM. ②这样的点P 不存在.理由:假设PC PC==12,如图3中,以点C 为圆心12为半径画圆,以AB为直径画圆,为直径画圆,CO CO CO==BC 2+BO 2=52>12+12,∴两个圆外离,∴∠,∴两个圆外离,∴∠APB APB APB<<9090°,这与°,这与AP⊥PB 矛盾,∴假设不可能成立,∴满足PC PC==12的点P 不存在.不存在. 例4 设AE AE==x ,则AC AC==x +4,∵,∵AC AC 平分∠BAD,∴∠平分∠BAD,∴∠BAC BAC BAC=∠CAD,∵∠=∠CAD,∵∠=∠CAD,∵∠CDB CDB CDB=∠BAC(圆周角定=∠BAC(圆周角定理),∴∠,∴∠CAD CAD CAD=∠CDB,∵∠=∠CDB,∵∠=∠CDB,∵∠ACD ACD ACD=∠DCE,∴△ACD∽△DCE,∴=∠DCE,∴△ACD∽△DCE,∴CD CE =AC DC ,即64=x +46,解得:,解得:x x =5.故选B .【变式拓展】【变式拓展】1.A 2.12 2.12 3.3.5n 22n 2n--1 4.(1)C (2)C 5.(1)1∶35.(1)1∶3 (2)2或103 6.(1)D (2)A (3)D 7.23或43 【热点题型】【热点题型】【分析与解】【分析与解】(1)(1)(1)设矩形的边长设矩形的边长PN PN==2y mm ,则PQ PQ==y mm ,由条件可得△APN∽△ABC,∴PN BC BC==AEAD AD,,即2y 120=8080--y 80,解得y =2407,∴PN PN==2407×2=4807(mm ),答:这个矩形零件的两条边长分别为2407mm ,4807mm ; (2)(2)设设PN PN==x mm ,由条件可得△APN∽△ABC,由条件可得△APN∽△ABC,∴∴PN BC =AE AD ,即x 120=8080--PQ 80,解得PQ PQ==8080--23x.∴S =PN·PQ==PN·PQ=x(80x(80x(80--23x)x)=-=-23x 2+80x 80x=-=-23(x (x--60)2+24002400,∴,∴,∴S S 的最大值为2400mm 2,此时PN PN==60mm ,PQ PQ==8080--23×6060==40(mm ). 【错误警示】A .∵△.∵△ABC ABC ABC∽△∽△∽△DBA DBA DBA,∴,∴AB BD =BC AB ,∴,∴AB AB 2=BD·BC.=BD·BC.。

相似三角形一. 知识梳理1.平行线分线段成比例定理定理:两条直线被三条平行线所截,所得的对应线段成比例。
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
2.相似三角形定义:三角对应相等、三边对应成比例的两个三角形叫做相似三角形。
相似比:相似三角形对应边的比叫做相似比。
3.相似三角形的判定平行法:平行于三角形一边的直线和其他两边相交,所得的三角形与原三角形相似。
两角法:两角分别相等的两个三角形相似。
边角法:两边成比例且夹角相等的两个三角形相似。
三边法:三边对应成比例的两个三角形相似。
4.相似三角形的性质①相似三角形的对应角相等,对应边成比例;②相似三角形对应边上高的比,对应边上中线的比与对应角平分线的比都等于相似比;③相似三角形周长的比等于相似比;④相似三角形面积的比等于相似比的平方。
5.位似图形定义:如果两个图形不仅相似,而且对应顶点的连线相交于一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心。
这时的相似比又叫位似比6. 黄金分割:点C 把线段AB 分成两条线段AC 和BC,如果ACBC AB AC =,那么称线段AB 被点C 黄金分割,点C 叫做线段AB 的黄金分割点,AC 与AB 的比叫做黄金比. 1:618.0215:≈-=AB AC 二.课后作业1.下列图形中不一定属于相似形的是( )A.两个圆B.两个等边三角形C.两个正方形D.两个矩形2.如果两个相似三角形的面积比是1∶4,那么它们的周长比是( )A. 1∶16B. 1∶4C. 1∶6D. 1∶23.已知△ABC ∽△DEF ,且AB:DE=1:2,则△ABC 的周长与△DEF 的周长之比( )A.1:2B.1:4C.2:1D.4:14.如图,给出下列条件:其中,不能单独判定△ABC∽△ACD 的条件为( )A.∠B=∠ACDB.∠ADC=∠ACBC.AC CD =AB BCD.AC AD =AB AC5.如图,DE ∥BC ,且AD=2,BD=5,则△ADE 与△ABC 的相似比为( )A.2:5B.5:2C.2:7D.7:26.如图,在△ABC 中,DE ∥BC ,AD=2,AE=3,BD=4,则AC=( ) A.7 B.8 C.9 D.10 E A D CB A BC DE7.已知△ABC ∽△DEF ,且它们的周长之比为1:2,那么它们的相似比为 。

中考数学高频考点《动点产生的相似、全等三角形问题》专项测试卷-带答案一阶方法突破练相似三角形问题1. 如图,在平面直角坐标系中,A(-3,0),B(3,0),C(0,4),点D为x轴上一点,当△ABC∼△ACD时,求点D的坐标.2.如图,在平面直角坐标系中,直线y=−43x+8与x轴交于点A,与y轴交于点 B,已知点 C的坐标为( (−4,0),点 P 是直线 AB上的一个动点.若以A,P,C为顶点的三角形与△AOB相似,求点P的坐标.3.如图,抛物线y=−12x2+32x+2交x轴于点A,B,交y轴于点C,点M是第一象限内抛物线上一点,过点M作MN⊥x轴于点N.若△MON与△BOC相似,求点M的横坐标.● 全等三角形问题x+2与x轴,y轴分别交于A,B两点,直线AC⊥AB于点A,若点 D 是x轴上方直线AC4.如图,直线y=12上的一个动点,点E 是x轴上的一个动点,当△BOA≅△AED时,求点E的坐标.5.如图,在平面直角坐标系中,抛物线y=−x²+2x+3与 x轴交于点A,B(点A在点B的左侧),点C是第一象限内抛物线上一点,过点C作( CD⊥x轴于点 D,直线y=x与CD所在直线交于y=x点 E,若直线: y=x;上存在一点 F,使得△ODE≅△FCE,求点 C的坐标.6.如图,在平面直角坐标系中,抛物线y=−x²−2x+3与x 轴交于点A,B(点A在点B的左侧),与y轴交于点C,连接AC,BC,若在第二象限内存在一点D,使得以A,C,D为顶点的三角形与△ABC全等,求点 D 的坐标.二阶设问进阶练例如图,在平面直角坐标系中,直线y=kx+1l与x轴交于点A,与y轴交于点 C,过点 C的抛物线y=3 4x2−52x+1与直线AC交于点B(4,3).(1)已知点P是x轴上一点(点 P不与点O重合),连接CP,若△AOC∼△ACP,,求点P的坐标;(2)已知点Q(m,0)是x轴上一点,连接BQ,若以点A,B,Q为顶点的三角形与△AOC相似,求点Q的坐标;(3)已知点E(0,n)为y轴正半轴上一点,点. D(0,−1),,若以点B,C,E为顶点的三角形与△ACD相似,求点 E 的坐标;(4)若点 F 是抛物线上一点,过点 F 作FG⊥y轴于点 G,点 J是y轴上一点,要使以F,G,J为顶点的三角形与△OAC全等,求点 F的纵坐标;(5)若点S为第一象限内抛物线上一点,过点S作ST⊥x轴于点T,点Z 是x轴上一点,要使以S,T,Z 为顶点的三角形与△AOC全等,求点 Z 的坐标;(6)如图⑥,已知L为AO的中点,连接OB,点R为平面直角坐标系内一点,是否存在点R,使得以L,O,R为顶点的三角形与△COB全等?若存在,请求出点R的坐标;若不存在,请说明理由.综合强化练1. 创新题·阅读理解题定义:将抛物线y=ax²向右平移h个单位,再向上平移k个单位得到抛物线y=a(x −ℎ)²+k(h,k均大于0),则将抛物线y=ax²称为“原函数”,把由它平移得到的抛物线y=a(x−ℎ)²+k称为抛物线y=ax²的“衍生函数”,将平移路径称为“衍生路径”,平移前后对应点之间的距离√ℎ2+k2称“衍生距离”.如图,已知抛物线L y=−1x2+2x与x轴交于点A,顶点为B,连接AB,OB.2x2为抛物线L的“原函数”,则抛物线L 的“衍生路径”为,平移前后对应点的“衍生(1)若抛物线y=−12距离”为;(2)若点Q是线段AB上一点,点C为OB的中点,连接CQ,点B 关于线段CQ的对称点为B′,当△B′CO为等边三角形时,求CQ的长;(3)若将抛物线L作为“原函数”,将其向左平移n(n⟩0))个单位得到它的“衍生函数”L',L'与x轴的负半轴交于点E,与y轴交于点 D,点 P 为抛物线L'上一点,若△POE≅△POD,求两抛物线的“衍生距离”.作图区答题区2.如图,在平面直角坐标系中,已知抛物线y=ax²+bx−2与x轴交于A(1,0) B(−3,0))两点,与y轴交于点C,连接AC.(1)求该抛物线的解析式;(2)若点 P是第二象限内抛物线上的动点,PQ⊥x轴于点Q,M是x轴上的点,当以P,Q,M为顶点的三角形与△AOC全等时,求 P点与M点的坐标;(3)如图②,连接BC,过点A作. AD‖BC交抛物线于点 D,E为BC下方抛物线上的一个动点,连接DE,交线段B C于点 F,连接CE,AF,求四边形ACEF 面积的最大值.作图区答题区3.如图,在平面直角坐标系中,一次函数y=−√3x+√3的图象分别与x轴,y轴交于A,B两点,过点 B 的另一直线交x轴于点( C(−3,0).(1)求直线 BC的解析式;(2)创新题·动点求面积关系若点P从C点出发,以每秒1个单位的速度沿射线CA运动,过点 P作y轴的平行线交直线BC于点Q,连接BP.设△BPQ的面积为S,点 P的运动时间为t秒,求S与t的函数关系式,并写出自变量t的取值范围;(3)在直线BC上是否存在点 M,使得以A,B,M 为顶点的三角形与△AOB相似?若存在,请求出点M的坐标;若不存在,请说明理由.作图区答题区4. 创新题·阅读理解题定义:若抛物线y=ax²+bx+c(ac≠0)与x轴交于A,B两点,与y轴交于点 C.线段OA,OB,OC的长满足OC²=OA⋅OB,则这样的抛物线称为“黄金抛物线”.如图,“黄金抛物线y=ax²+bx+2(a ≠0)与x轴的负半轴交于点A,与x轴的正半轴交于点 B,与y轴交于点 C,且OA=4OB.(1)求抛物线的解析式;(2)点P为AC 上方抛物线上的动点,过点 P作PD⊥AC于点 D.①求 PD的最大值;②连接PC,当以点 P,C,D为顶点的三角形与△ACO相似时,求点 P 的坐标.作图区答题区5.如图①,在平面直角坐标系xOy中,直线y=−x+4与x轴,y轴分别交于点A,B,抛物线y=ax²+bx+c(a≠0)经过点A,B,( C(−2,0).(1)求抛物线的解析式;(2)连接BC,点 P 为直线AB上方抛物线上一动点,过点 P作PE‖BC交AB于点E,过点P作PF‖x轴交直线AB于点F,求△PEF周长的最大值及此时点 P的坐标;(3)如图②,将抛物线向右平移2个单位得到一个新的抛物线y′,,新抛物线与原抛物线交于点G,连接BG并延长交新抛物线y'于点 D,连接OG,作射线OD.动点M位于射线 OD下方的新抛物线上,动点 N位于射线OD上,是否存在动点M,N,使∠OMN=90°,,且以点O,M,N为顶点的三角形与△OBG相似?若存在,求出点M的坐标;若不存在,请说明理由.作图区答题区参考答案一阶方法突破练1. 解:∵A(-3,0),B(3,0),C(0,4)∴AB=6,AC=5.∵△ABC∽△ACD∴ABAC =ACAD,即65=5AD,解得AD=256.由题意得,点 D 在点A 的右侧∵OA=3,∴OD=AD−OA=76,∴点D 的坐标为(76,0).2. 解:在y=−43x+8中,令x=0,解得y=8,令y=0,解得x=6,∴A(6,0),B(0,8),∴AB=√62+82=10.分两种情况考虑,如解图所示①当△AOB ∽△ACP ₁时 ∠ACP ₁=∠AOB =90°,当x=-4时 y =−43x +8=403,∴点 P ₁的坐标为 (−4,403); ②当△AOB ∽△AP ₂C 时,设点P ₂的坐标为 (m ,−43m +8).∵点A 的坐标为(6,0),点 C 的坐标为(-4,0)∴AC=10.∵ △AOB ∽△AP ₂C∴CP 2BO =AC AB ,即 CP 28=1010,∴CP 2=8,∴√[m −(−4)]2+(−43m +8−0)2=8,整理,得 (53m −4)2=0,解得 m 1=m 2=125,∴点P ₂的坐标为 (125,245).综上所述,点P 的坐标为 (−4,403)或 (125,245). 3. 解:在 y =−12x 2+32x +2中,令x=0,得y=2,∴C(0,2),∴OC=2 令 −12x 2+32x +2=0,解得x=4或x=-1∵点B 在x 轴正半轴,∴B(4,0),∴OB=4.设 M (t ,−12t 2+32t +2),1N(t,0)∴MN =−12t 2+32t +2,ON =t. 分两种情况讨论:①当△BOC ∽△MNO 时 OC NO =BO MN ,即解得 t =−1+√172或 t =−1−√172(舍去); ②当△BOC ∽△ONM 时 OC NM =OB NO ,艮 2−12t 2+32t+2=4t , 解得 t =1+√5或 t =1−√5(舍去).综上所述,点M 的横坐标为 −1+√172或 1+√5.4. 解:如解图,∵ AC ⊥AB,∴∠BAC=∠AOB=90°∴ ∠ABO + ∠BAO = ∠CAE +∠BAO=90° 2t =4−12t 2+32t+2,∴∠ABO=∠CAE在y=1x+2中2令x=0,则y=2,令y=0,则x=-4∴OA=4,OB=2∵△BOA≌△AED,∴AE=OB=2,∴OE=AE+OA=6∴E(-6,0).5. 解:∵ CD⊥x 轴,直线 y=x 与 CD 交于点 E,∴∠OED=∠EOD=45°,OD=DE设D(m,0)如解图当点 C 在直线 y = x 上方时△ODE≌△FCE∴∠ODE=∠FCE=90°,ED=CE,∴C(m,2m),将 C 点坐标代入抛物线的解析式,得2m=−m²+2m+3,解得m=√3或m=−√3(舍去)∴C( √3,2 √3)当点 C 在直线y=x下方时,不存在满足条件的点 C.综上所述,点C的坐标为(√3,2√3).6. 解:∵抛物线y=−x²−2x+3与x轴交于点 A,B,与y轴交于点 C∴令x=0,解得y=3,令y=0,解得x=1或x=-3∴C(0,3),A(-3,0),B(1,0),∴OA=OC=3,OB=1.如解图,分两种情况讨论:①当△CD₁A≌△ABC时∵OA=OC=3,∴∠CAO=45°∵△CD₁A≌△ABC∴∠ACD₁=∠CAO=45°,∴CD₁‖AB,CD₁=AB=4,∴D₁(-4,3);②当△AD₂C≌△ABC时∠BAC=∠CAD₁=45°,AB=AD₁=4,∴∠D₂AB=90°,∴D₂(-3,4)综上所述,点D的坐标为(-4,3)或(-3,4).二阶设问进阶练例解:(1)∵直线AC经过点B(4,3),∴将点 B 的坐标代入直线 AC的解析式,得3=4k+1,解得k=1,2∴直线AC 的解析式为 y =12x +1,在 y =12x +1中,令y=0,解得x=-2 ∴ 点A 的坐标为(-2,0) ∴AO=2,CO=1∴AC =√AO 2+CO 2=√22+12=√5. 如解图①,设点 P(p,0),连接CP,∴PA=p+2.∵ △AOC ∽△ACP ∴ACAO =APAC ,即 √52=√5, p =12, ∴ 点P 的坐标为(( 12,0);(2)如解图②,分两种情况讨论:①△AOC ∽△AQ ₁B 时,∠AQ ₁B=∠AOC=90° ∴BQ ₁⊥x 轴. ∵B(4,3)∴点 Q ₁的坐标为(4,0);②△AOC ∽△ABQ ₂时,过点B 作BQ ₂⊥AB,交x 轴于点Q ₂,则点Q ₂(m,0) ∵AO AB =AC AQ 2,即 3√5=√5m+2. 解得 m =112,此时点Q ₂的坐标为 (112,0). 综上所述,点Q 的坐标为(4,0)或 (112,0);(3)∵A(-2,0),C(0,1),B(4,3),D(0,-1),E(0 n),∴AC =AD =√5,BC =2√5,CD =2,CE =|n −1| ∴分两种情况讨论:①当△ACD ∽△BCE 时 ACCD =BCCE , 即 √52=2√5|n−1|,解得n=5或n=-3(舍去);②当△ACD ∽△ECB 时AC EC=DC BC,即√5|n−1|=2√5,n=6或n=-4(舍去)综上所述,点E 的坐标为(0,5)或(0,6);(4)∵A(-2,0),C(0,1),∴OA=2,OC=1,分两种情况讨论: ①△OAC ≌△GJF 时∴OC=FG=1,∴点F 的横坐标为1或-1 将点 F 的横坐标代入 y =34x 2−52x +1,解得 y =−34或 y =174;②△OAC ≌△GFJ 时∴OA=FG=2,∴点F 的横坐标为2或-2,将点 F 的横坐标代入 y =34x 2−52x +1,解得y=-1或y=9 ∴ 点 F 的纵坐标为 −34或 174或-1或9; (5)∵OA=2,OC=1 分两种情况讨论:①如解图③,当△AOC ≌△STZ 时,ST=AO=2,OC=TZ=1,∴ys=2 在 y =34x 2−52x +1中,令y=2,得 34x 2−52x +1=2,解得 x =5+√373或 x =5−√373舍去),(1∴S (5+√373,2),T (5+√373,0), ∴Z (2+√373,0)或 (8+√373,0);②如解图④,当△AOC ≌△ZTS 时,ST=CO=1,AO=TZ=2,∴ys=1 在 y =34x 2−52x +1中,令y=1,得 34x 2−52x +1=1,解得 x =103或x=0(舍去)∴S (103,1),T (103,0),∴Z (43,0)或 (163,0),∴点Z 的坐标为 (2+√373,0)或 (8+√373,0)或 (43)0)或(( 163,0);(6)存在.∵ B(4,3)∴OB=√(4−0)2+(3−0)2=5,∴在△COB中,( CO=1,BC=2√5,OB=5∵L为AO 的中点,OA=2,CO=1∴LO=CO=1,L(-1,0)设R点坐标为(x,y)则LR²=(x+1)²+y²,OR²=x²+y²,∵ LO=CO,如解图⑤,分两种情况讨论: ①当△LOR≌△COB时,RL=BC,OR=OB.∴{(x+1)2+y2=20x2+y2=25,解得{x1=−3y1=4,{x2=−3y2=−4,即R点坐标为(-3,4)或(-3,-4);②当△OLR≌△COB时,RL=OB,OR=CB.∴{(x+1)2+y2=25x2+y2=20,解得{x3=2y3=4,{x4=2y4=−4,即R点坐标为(2,4)或(2,-4).∴综上所述,R点坐标为(-3,4)或(-3,-4)或(2,4)或(2,-4).三阶综合强化练1.解:(1)将原函数向右平移2个单位,再向上平移2个单位,2 √2; 【解法提示】∵y=−12x2+2x=−12(x−2)2+2,.将原函数y=−12x2向右平移2个单位,再向上平移2个单位即可得到y=−12x2+2x,根据公式得“衍生距离”为√22+22=√8=2√2.(2)【思路点拨】审题后,根据题意画出草图,由△AOB的三边关系可判定△AOB 为等腰直角三角形,由对称性和等边三角形的性质结合锐角三角函数求解即可.根据题意画出图象,如解图①在y=−12x2+2x中令y=0,解得x=0或x=4,∴A(4,0).∵ B 为抛物线 L 的顶点∴B(2,2),∴OB=BA=2√2.∵ C 是OB的中点∴OC=BC=√2.∵△OB'C为等边三角形,∴∠OCB'=60°.又∵点 B 与点 B'关于线段CQ 对称∴∠B'CQ=∠BCQ=60°.∵OA=4,OB=2√2,AB=2√2,∴OB²+AB²=OA²,∴∠OBA=90°在 Rt△CBQ中,∠CBQ=90°,∠BCQ=60°,BC= √2∴cos∠BCQ=BCCQ =√2CQ=12,∴CQ=2√2;(3)【思路点拨】由全等三角形对应边角关系可得OD=OE,∠POD=∠POE,由线段相等关系结合抛物线与坐标轴交点,列方程求解即可.∵将抛物线L作为“原函数”,将其向左平移n个单位得到它的“衍生函数”L'(n>0),L:y=- 12(x- 2)²+2,∴L′:y=−12(x−2+n)2+2,∵抛物线L的“衍生函数”L'与x轴的负半轴交于点E,与y轴交于点 D∴令x=0,得y=−12n2+2n,令y=0,得x=-n或x=4-n∴OD=|−12n2+2n|,OE:=n或OE=4-n∵△POE≌△POD,∴OD=OE如解图②,当−12n2+2n>0,即0<n<4时,有−12n2+2n=n,解得n=0(舍去)或n=2,或有−12n2+2n=4-n,解得n=4(舍去)或n=2∴抛物线L 的“衍生函数”L'为y=−12x2+2,∴两抛物线的“衍生距离”为√22+02=2;如解图③,当−12n2+2n<0时,即n<0(不符合题意)或n>4时,4-n<0,∴有12n2−2n=n,解得n=0(舍去)或n=6∴两抛物线的“衍生距离”为√62+02=6,综上所述,两抛物线的“衍生距离”为2或6.2. 解:(1)把A(1,0),B(-3,0)代入y=ax²+bx−2中,得{a+b−2=09a−3b−2=0,解得{a=23b=43∴抛物线的解析式为y=23x2+43x−2;(2)【思路点拨】∵以P,Q,M 为顶点的三角形与△AOC全等,由于∠AOC=∠PQM=90°,故分两种情况,①△PQ M≌△AOC,②△MQP≌△AOC,分别求解即可.在y=23x2+43x−2中,令x=0,则y=-2∴C(0,-2),∴OC=2 ∵A(1,0),∴OA=1设P(x,23x2+43x−2),分两种情况讨论:①如解图①,当△PQM≌△AOC 时,PQ=OA =1,QM=OC=2∴23x2+43x−2=1,解得x=−√222−1或x=√222−1(舍去)∴P(−√222−1,1),∴Q(−√222−1,0),∴M(−√222−3,0)或M(−√222+1,0);②如解图②,当△MQP≌△AOC时,PQ=OC=2,QM=OA=1∴23x2+43x−2=2,解得x=−√7−1或x=√7−1(舍去) ∴P(−√7−1,2),∴Q(−√7−1,0),∴M(−√7−2,0)或M(−√7,0),综上所述,点 P,M的坐标为:P(−√222−1,1),M(√222−3,0)或M(−√222+1,0);P(−√7−1,2),M(−√7−2,0)或M(−√7,0);(3)【思路点拨】分别求出BC,AD 的解析式确定点D坐标,连接DC,将四边形ACEF的面积转化为△DEC 的面积,表示出面积关系式,利用二次函数的性质即可求出最大值.∵B(-3,0),C(0,-2)∴直线 BC 的解析式为y=−23x−2,∵AD∥BC,∴设直线AD 的解析式为y=−23x+b2,将A(1,0)代入得b2=23,∴直线AD 的解析式为y=−23x+23,令−23x+23=23x2+43x−2,解得x=-4或x=1(舍去)∴D(−4,103),如解图③,连接DC∵AD∥BC∴S AFC=S DFC,∴S四边形ACEF=S DEC,∵D(-4 103),C(0,-2)∴直线 DC 的解析式为y=−43x−2.过点 E 作 EQ⊥x轴交 CD于点 Q设E(m,23m2+43m−2),则Q(m,−43m−2),∴S圆锥侧ACEF=S DEC=12×4×(−43m−2−23m2−43m+2)=−43(m2+4m)=−43(m +2)2+163,∴−43<0,∴当m=-2时,四边形 ACEF 面积的最大值为 163.3. 解:(1)∵一次函数 y =−√3x +√3的图象经过A ,B 两点,∴当x=0时,y= √3,∴B(0 √3) 设直线BC 的解析式为y=kx+b(k ≠0),将 B(0 √3),C(-3,0)两点坐标代入 得 {b =√3−3k +b =0, 解得 {k =√33.b =√3 ∴ 直线 BC 的解析式为 y =√33x +√3;(2)由题意可得CP=t,则OP=|t-3|,∴P(t-3,0),∵ PQ ∥y 轴 ∴Q 点的横坐标为t-3,将x=t-3,代入直线BC 的解析式得 y =√33t,∴Q (t −3,√33t), 当0≤t<3 时,△BPQ 在 y 轴左侧,此时 PQ =√33t,OP=3-t ∴S BPQ =12PQ ⋅OP =12×√33t ×(3−t )=−√36t 2+√32t. 当t=3时,点B,Q 重合 ∴S=0;当t>3时,△BPQ 在y 轴右侧,此时 PQ =√33t,OP =t-3∴S BPQ =12PQ ⋅OP =12×√33t ×(t −3)=√36t 2−√32t. 当t=3时同样满足上式.综上所述,S 与t 的函数关系式为 S ={√36t 2+√32t(0≤t <3)√36t 2−√32t (t ≥3);(3)存在. ∵tan ∠OBC =OC OB=√3=√3,∴∠OBC =60∘,∴∠BCO=30°,∴BC=2OB=2 √3. 令 y =−√3x +√3=0,则x=1,∴A(1,0) ∵tan ∠OBA =OAOB =√3=√33,∴∠OBA =30∘,∴∠ABC=90°,AB=2OA=2.①当点 M 在 y 轴左侧,△MBA ∽△AOB 时,则 MB AO = BA OB ,卧 MB 1=√3∴MB =2√33, 如解图,过点M ₁作M ₁H ⊥y 轴于点H ∴M 1H =M 1B ⋅sin60∘=2√33×√32=1,BH =M 1B ⋅cos60∘=2√33×12=√33, ∴HO =BO −BH =√3−√33=2√33.∵点 M 在第二象限 ,∴M 1(−1,2√33);当△ABM ∽△AOB 时,则 BM OB =ABAO , 即√3=21,∴BM =2√3,此时点 M 与点 C 重合∴M ₁(−3,0);②当点 M 在 y 轴右侧,△MBA ∽△AOB 时,则 MB AO=BAOB,即MB 1=√3∴MB =2√33, 如解图,过点M ₃作M ₃N ⊥y 轴于点 N ∴M 3N =M 3B ⋅sin60∘=2√33×√32=1,BN =M 3B ⋅cos60∘=2√33×12=√33, ∴ON =√3+√33=4√33,∴M 3(1,4√33); 当△ABM ∽△AOB 时,则 MBBO =ABAO , 即√3=21,∴MB =2√3,如解图,过点M ₄作M ₄P ⊥y 轴于点P∴PM 4=M 4B ⋅sin60∘=2√3×√32=3,PB =M 4B ⋅cos60∘=2√3×12=√3,∴OP =OB +PB =√3+√3=2√3,∴M 4(3,2√3).综上所述,符合条件的点M 的坐标为 (−1,2√33)或(-3,0)或 (1,4√33)或(3,2 √3).4.解:(1)由题意得 OC ²=OA ⋅OB, ∵抛物线 y =ax ²+bx +2与y 轴交于点 C ∴C(0,2),∴OC=2 ∵OA=4OB,∴4=4OB ·OB ∴OB=1,OA=4 ∴A(-4,0),B(1,0)将点A(-4,0),B(1,0)代入抛物线y=ax²+bx+2中,得{16a−4b+2=0a+b+2=0,解得{a=−12b=−32∴抛物线的解析式为y=12x2−32x+2;(2)①【思路点拨】过点 P作y轴的平行线与直线AC交于点E,∠PED=∠ACO,由锐角三角函数将求PD的最大值转化为求PE的最大值,利用二次函数的性质求解即可.如解图①,过点 P 作 y 轴的平行线交直线 AC 于点E易知直线AC的解析式为y=12x+2,设P(m,−12m2−32m+2),则E(m,12m+2),∴PE=−12m2−32m+2−12m−2=−12m2−2m,∵−12<0,..当m=−b2a=−2时,PE有最大值∵∠PED=∠ACO,A(-4,0),C(0,2) ∴ sin∠PED=sin∠ACO∴AC=2√5,∴PD:PE=AO:AC=4:2 √5∴PD=2√55PE=2√55(−12m²−2m),∴当m=-2时,PD 有最大值,最大值为4√55;②【思路点拨】分两种情况,(i)△CPD∽△ACO,由对应角相等关系可得,PC∥AO,将OC=2=γ代入即可,(ii)△PCD∽△ACO,构造“A”字型与△PCD 相似的三角形,再构造“一线三垂直”模型,联立直线与抛物线的解析式求解即可.∵PD⊥AC,∴∠PDC=90°=∠AOC∴当以点 P,C,D为顶点的三角形与△ACO相似时,则△CPD∽△ACO或△PCD∽△ACO(i)如解图②,若△CPD∽△ACO,则∠PCD=∠CAO,∴CP∥AO∵C(0,2),∴点P 的纵坐标为2∵点P为AC上方抛物线上的动点∴2=−12x2−32x+2,解得x₁=0(不合题意,舍去),x₁=−3,∴此时点 P的坐标为(-3,2);(ii)如解图③,过点A 作AC 的垂线,交 CP 的延长线于点 G,过点 G 作 GH ⊥x 轴于点 H,若△PCD ∽△ACO,则 ∠PCD =∠ACO,PD AO =CD CO ,∴PD CD =AO CO =42=2, ∵ PD ⊥AC,GA ⊥AC,∴GA ∥PD∴△GAC ∽△PDC∴GA PD =AC DC ,∴GA AC =PD CD =2,∵GA ⊥AC,GH ⊥x 轴∴∠GAC=∠GHA=90°∴∠AGH+∠GAH=90°,∠GAH+∠CAO=90°∴∠AGH=∠CAO又∵∠GHA=∠AOC=90°,∴△GHA ∽△AOC∴GH AO =AH CO =GA AC ,即 GH 4=AH 2=2,∴GH=8,AH=4,∴HO=AH+OA=8,∴G(-8,8)易知直线CG 的解析式为 y =−34x +2, 令 −34x +2=−12x 2−32x +2,解得 x ₁=0(不合题意,舍去), x 2=−32, 把 x =−32代入 y =−34x +2 得 y =−34×(−32)+2=258,∴此时点 P 的坐标为 (−32,258). 综上所述,符合条件的点P 的坐标为(-3,2)或 (−32,258).5. 解:(1)∵直线y=-x+4与x 轴,y 轴分别交于点A,B,∴A(4,0),B(0,4)∴抛物线的解析式为 y =ax ²+bx +4将A(4,0),C(-2,0)分别代入 y =ax ²+bx +4中,得 {16a +4b +4=04a −2b +4=0,解得 {a =−12,b =1,∴抛物线的解析式为y=−12x2+x+4;(2)由题意知,△OBC三边之比为1:2: √5,如解图①,过点 P 作PH∥y轴交AB 于点H,作EK⊥PH于点 K ∴△PEK∽△BCO∴EKPK =COBO=12,由题意可知△EHK 与△FPH为等腰直角三角形. ∴EK=KH,PF=PH,设PH=l ∴PK+HK=l,EK=13l,∴EH=√23l,EF=2√23l,PE=√53l,则C PEF=(1+2√23+√53)l,设P(m,−12m2+m+4),则H(m,-m+4)∴PH=−12m2+2m,∴C PEF=(1+2√23+√53)⋅(−12m2+2m)=(1+2√23+√53)⋅[−12(m−2)2+2].∴−12<0,0<m<4,∴当m=2时,C△PEF 取得最大值,最大值为2+ 4√23+2√53,此时,点P的坐标为(2,4);(3)【思路点拨】分两种情况,①△MON∽△BOG,旋转OG构造∠MON=∠BOG,联立直线OM与抛物线的解析式求解即可,②△MNO∽△BOG,旋转OD 构造∠MON=∠BGO,联立直线OM与抛物线的解析式求解即可.存在.将抛物线向右平移两个单位得y′=−12(x−2)2+(x−2)+4=−12x2+3x,新抛物线与原抛物线交于点G,B(0,4)∴G(2,4),D(4,4)分两种情况讨论:①当△MON∽△BOG时如解图②,将 OG绕点 O 顺时针旋转45°得到点 G',延长 OG'交抛物线于点 M,过点 M 作OM⊥MN交射线OD 于点 N,过点 G作GH⊥OD 于点 H∵G(2,4),D(4,4),B(0,4)∴OD=4 √2,GD=2,OB=4,OG=2 √5∴GH=√22GD=√2,∵∠GHO=90°,∴OH=3 √2过点 G'作 G'Q⊥x轴于点 Q,则∠GOH=∠G'OQ,∠GHO=∠G'QO=90°,OG=OG' ∴△GOH≌△G'OQ∴G′Q=GH=√2,OQ=OH=3√2,∴G′(3√2,√2),∴直线OM 的解析式为y=13x,联立{y=13xy=−12x2+3x,解得{x1=0y1=0舍去) {x2=163y2=169∴M(163,169);②当△MNO∽△BOG时,∠NOM=∠OGB,如解图③,将OD 绕点 O顺时针旋转∠BGO 的度数交抛物线于点 M,过点 M作OM⊥MN交射线OD于点N同①理可得,直线OM 的解析式为y=−13x.联立{y=−13xy=−12x2+3x,解得{x1=0y1=0舍去) {x2=203y2=−209∴M(203,−209).综上所述,点M的坐标为(163,169)或(203,−209).。
相似形一.选择题(本大题有10个小题,每小题3分,共30分。
请选出每小题中一个符合题意的正确选项,不选、多选、错选均不给分)1. 下列说法中,错误的是( )A.所有的等边三角形都相似B.和同一图形相似的两图形也相似C.所有的等腰直角三角形都相似D.所有的矩形都相似2. 下列图形中,是位似图形的是( )A B C D3. 如图1,小强设计两个直角三角形来测量河宽BC ,他量得AB=2米,BD=3米,CE=9米,则河宽BC 为( )A5米 B.4米 C.6米 D.8米图1 图2 图34.如图2,已知AB∥EF∥CD,则图中相似的三角形有( )A.1对 B.2对 C.3对 D.4对5.如图3,铁道口的栏杆短臂长1米,长臂长16米,当短臂端点下降0.5米时,长臂端点升高( )A.11.25米 B.6.6米 C.8米 D.10.5米6.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与ABC 相似的是( )A B C D7.已知,如图4,在ABC 中,P为AB上的一点,在下列四个条件下:①ACP ∠=B ∠;②APC ACB ∠=∠;③2AC AP AB =⋅;④AB CP AP CB ⋅=⋅。
能满足APC 与ACB 相似的条件是( )A.①②④ B.①③④ C.②③④ D.①②③图4 图5 8.如图5所示,AB是斜靠在墙壁上的长梯,梯脚B距墙1.6米,梯子上点D距离墙1.4米,BD长0.55米,则梯子的长为( )A.3.85米 B.4.00米 C.4.40米 D4.50米9.如图6,在矩形ABCD中,AE BD ⊥于E,矩形ABCD的面积为40平方厘米,:1:5ABE DBA S S =,则AE的长为( )A4厘米 B.5厘米 C.6厘米 D.7厘米图6 图7 10.如图7,点E是正方形ABCD中边CD的中点,P是BC边上的一点,下列条件中,不能推出ABP 与ECP 相似的是( )A.APB EPC ∠=∠B.90APE ∠=C. P 是BC 的中点D. :2:3BP BC =二.填空题(本大题有10个小题,每小题3分,共30分,将正确答案填在题中的横线上)11.已知线段1,a b c d ====,则这四条线段______比例线段(填“成”或“不成”).12.学校平面图的比例尺是1:500,平面图上校园面积为21300cm ,则学校的实际面积为_______2m .13.如果ABC A B C ''',相似比为3 :2。
中考数学专题复习练习三等角型相似三角形题型压轴题HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】三等角型相似三角形三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景,一个与等腰三角形的底角相等的顶点在底边所在的直线上,角的两边分别与等腰三角形的两边相交如图所示:等角的顶点在底边上的位置不同得到的相似三角形的结论也不同,当顶点移动到底边的延长线时,形成变式图形,图形虽然变化但是求证的方法不变。
此规律需通过认真做题,细细体会。
典型例题【例1】如图,等边△ABC 中,边长为6,D 是BC 上动点,∠EDF =60° (1)求证:△BDE ∽△CFD(2)当BD =1,FC =3时,求BE【思路分析】本题属于典型的三等角型相似,由题意可得∠B =∠C =∠EDF =60° 再用外角可证∠BED =∠CDF ,可证△BDE 与△CFD 相似排出相似比便可 求得线段BE 的长度解:(1)∵△ABC 是等边三角形,∠EDF =60°∴∠B =∠C =∠EDF =60°∵∠EDC =∠EDF +∠FDC =∠B +∠BED ∴∠BED =∠FDC ∴△BDE ∽△CFD (2)∵△BDE ∽△CFD∴BECD BD FC = ∵BD =1,FC =3,CD =5∴BE =35点评:三等角型的相似三角形中的对应边中已知三边可以求第四边。
【例2】如图,等腰△ABC 中,AB =AC ,D 是BC 中点,∠EDF =∠B ,求证:△BDE ∽△DFE【思路分析】比较例1来说区别仅是点D 成为了BC 的中点,所以△BDE △CFD 相似的结论依然成立,用相似后的对应边成比例,以及BD =CD 可证得△BDE 和△DFE 相似 解: ∵AB =AC ,∠EDF =∠B∴∠B =∠C =∠EDF∵∠EDC =∠EDF +∠FDC =∠B +∠BED ∴∠BED =∠FDC ∴△BDE ∽△CFD ∴DF DECD BE =又∵BD =CD ∴DF DE BD BE =即DFBD DE BE = ∵∠EDF =∠BCA DB E F∴△BDE ∽△DFE点评:三等角型相似中若点D 是等腰三角形底边上任意一点则仅有一对相似三角形,若点D 是底边中点则有三对相似三角形,△BDE 与△CFD 相似后若得DFDECF BD =加上BD =CD 可证得△CFD 与△DFE 相似【例3】如图,在△ABC 中,AB =AC =5cm ,BC =8,点P 为BC 边上一动点(不与点B 、C 重合),过点P 作射线PM 交AC 于点M ,使∠APM =∠B ; (1)求证:△ABP ∽△PCM ; (2)设BP =x ,CM =y .求 y 与x(3)当△APM 为等腰三角形时, 求PB 的长.【思路分析】第(1)(2)小题都是用常规的三等角型相似的方法。
2017挑战压轴题中考数学精讲解读篇因动点产生的相似三角形问题1. 如图,在平面直角坐标系xOy中,将抛物线y=x2的对称轴绕着点P( 0,2)顺时针旋转45°后与该抛物线交于A、B两点,点Q是该抛物线上一点.(1)求直线AB的函数表达式;(2)如图①,若点Q在直线AB的下方,求点Q到直线AB的距离的最大值;(3)如图②,若点Q在y轴左侧,且点T (0,t) (t V2)是射线PO上一点, 当以P、B、Q为顶点的三角形与△ PAT相似时,求所有满足条件的t的值.图①图②备用图2. 如图,已知BC是半圆O的直径,BC=8过线段BO上一动点D,作AD丄BC 交半圆O于点A,联结AO,过点B作BH丄AO,垂足为点H,BH的延长线交半圆O于点F.(1)求证:AH=BD(2)设BD=x, BE?BF=y求y关于x的函数关系式;(3)如图2,若联结FA并延长交CB的延长线于点G,当厶卩人丘与厶FBG相似时,求BD的长度.3•如图,在平面直角坐标系xOy中,直线AB过点A (3, 0)、B (0, m) (m>0), tan / BAO=2(1)求直线AB的表达式;(2)反比例函数y= 的图象与直线AB交于第一象限内的C、D两点(BD v BC),x当AD=2DB时,求&的值;(3)设线段AB的中点为E,过点E作x轴的垂线,垂足为点M,交反比例函数y的图象于点F,分别联结OE OF,当厶OE2A OBE时,请直接写出满足条x4. 如图,在Rt A ABC中,/ ACB=90, AC=1, BC=7,点D是边CA延长线的一点,AE丄BD,垂足为点E, AE的延长线交CA的平行线BF于点F,连结CE交AB于点G.(1)当点E是BD的中点时,求tan / AFB的值;(2)CE?AF的值是否随线段AD长度的改变而变化?如果不变,求出CE?AF的值; 如果变化,请说明理由;(3)当△BGE和△ BAF相似时,求线段AF的长.5. 如图,平面直角坐标系xOy中,已知B (- 1, 0), —次函数y=-x+5的图象与x 轴、y轴分别交于点A、C两点,二次函数y=-x2+bx+c的图象经过点A、点B.(1)求这个二次函数的解析式;(2)点P是该二次函数图象的顶点,求△ APC的面积;(3)如果点Q在线段AC上,且△ ABC与厶AOQ相似,求点Q的坐标.6 .已知:半圆O的直径AB=6,点C在半圆O上,且tan / ABC=2匚,点D为弧AC 上一点,联结DC (如图)(1)求BC的长;(2)若射线DC交射线AB于点M,且△ MBC与厶MOC相似,求CD的长;(3)联结OD,当OD// BC时,作/ DOB的平分线交线段DC于点N,求ON的长.7•如图,已知二次函数y=«+bx+c(b, c为常数)的图象经过点A (3,- 1), 点C (0,- 4),顶点为点M,过点A作AB// x轴,交y轴与点D,交该二次函数图象于点B,连结BC.(1)求该二次函数的解析式及点M的坐标;(2)若将该二次函数图象向上平移m (m > 0)个单位,使平移后得到的二次函数图象的顶点落在△ ABC的内部(不包含厶ABC的边界),求m的取值范围;(3)点P时直线AC上的动点,若点P,点C,点M所构成的三角形与△ BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程)•备用医I因动点产生的等腰三角形问题8 .如图1,在厶ABC中,/ ACB=90, / BAC=60,点E是/BAC角平分线上一点,过点E作AE的垂线,过点A作AB的垂线,两垂线交于点D,连接DB,点F是BD的中点,DH丄AC,垂足为H,连接EF, HF.(1)如图1,若点H是AC的中点,AC=2「,求AB, BD的长;(2)如图1,求证:HF=EF(3)如图2,连接CF, CE猜想:△ CEF是否是等边三角形?若是,请证明;若不是,说明理由.9 •已知,一条抛物线的顶点为E (- 1,4),且过点A (-3, 0),与y轴交于点C,点D是这条抛物线上一点,它的横坐标为m,且-3v m v- 1,过点D作DK 丄x轴,垂足为K, DK分别交线段AE、AC于点G、H.(1) 求这条抛物线的解析式;(2) 求证:GH=HK10.如图,已知在Rt A ABC中,/ ACB=90, AB=5, si nA丄,点P是边BC上的5一点,PEI AB,垂足为E,以点P为圆心,PC为半径的圆与射线PE相交于点Q, 线段CQ与边AB交于点D.(1) 求AD的长;(2) 设CP=x △ PCQ的面积为y,求y关于x的函数解析式,并写出定义域;(3) 过点C作CF丄AB,垂足为F,联结PF、QF,如果△ PQF是以PF为腰的等腰三角形,求CP的长.C C11 •如图(1),直线y=- x+n交x轴于点A,交y轴于点(0,4),抛物线y=「x2+bx+c3 3经过点A,交y轴于点B (0,-2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD丄PD于点D,连接PB,设点P的横坐标为m.(1)求抛物线的解析式;(2)当厶BDP为等腰直角三角形时,求线段PD的长;(3)如图(2),将厶BDP绕点B逆时针旋转,得到△ BD P'当旋转角/ PBP = / OAC且点P的对应点P落在坐标轴上时,请直接写出点P的坐标.12 •综合与探究如图,在平面直角坐标系中,已知抛物线y=ax2+bx - 8与x轴交于A,B两点,与y轴交于点C,直线I经过坐标原点0,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE已知点A,D的坐标分别为(-2, 0),(6,- 8).(1)求抛物线的函数表达式,并分别求出点B和点E的坐标;(2)试探究抛物线上是否存在点F,使厶FOE^A FCE若存在,请直接写出点F 的坐标;若不存在,请说明理由;(3)若点P是y轴负半轴上的一个动点,设其坐标为(0, m),直线PB与直线是等腰三角形.因动点产生的直角三角形问题13. 已知,如图1,在梯形ABCD中,AD// BC,/ BCD=90, BC=11, CD=6, tan / ABC=2点E在AD边上,且AE=3ED EF// AB交BC于点F,点M、N分别在射线FE和线段CD上.(1)求线段CF的长;(2)如图2,当点M在线段FE上,且AM丄MN,设FM?cos/ EFC=x CN=y求y关于x的函数解析式,并写出它的定义域;(3)如果△ AMN为等腰直角三角形,求线段FM的长.C C14. 如图,在矩形ABCD中,点0为坐标原点,点B的坐标为(4, 3),点A、C 在坐标轴上,点P在BC边上,直线h:y=2x+3,直线12:y=2x-3.(1)分别求直线l1与x轴,直线12与AB的交点坐标;(2)已知点M在第一象限,且是直线12上的点,若△ APM是等腰直角三角形,求点M的坐标;(3)我们把直线h和直线12上的点所组成的图形为图形F.已知矩形ANPQ的顶点N在图形F上,Q是坐标平面内的点,且N点的横坐标为x,请直接写出x的取值范围(不用说明理由).因动点产生的平行四边形问题15. 如图,在平面直角坐标系xOy 中,抛物线y=ax - 2ax -3a (a v 0)与x 轴交 于A , B 两点(点A 在点B 的左侧),经过点A 的直线I : y=kx+b 与y 轴交于点C , 与抛物线的另一个交点为D ,且CD=4AC(1) 直接写出点A 的坐标,并求直线I 的函数表达式(其中k , b 用含a 的式子 表示);(2) 点E 是直线I 上方的抛物线上的一点,若△ ACE 的面积的最大值为「,求a4的值;(3) 设P 是抛物线对称轴上的一点,点 Q 在抛物线上,以点A ,D ,P ,Q 为顶OA=5, AB=4,点D 为边AB 上一点,将△ BCD 沿直 线CD 折叠,使点B 恰好落在OA 边上的点E 处,分别以OC, OA 所在的直线为x 轴,y 轴建立平面直角坐标系.(1) 求点E 坐标及经过O , D , C 三点的抛物线的解析式;(2) 一动点P 从点C 出发,沿CB 以每秒2个单位长的速度向点B 运动,同时 动点Q 从E 点出发,沿EC 以每秒1个单位长的速度向点C 运动,当点P 到达点 B 时,两点同时停止运动.设运动时间为 t 秒,当t 为何值时,DP=DQ(3) 若点N 在(2)中的抛物线的对称轴上,点 M 在抛物线上,是否存在这样 的点M 与点N ,使得以M , N , C, E 为顶点的四边形是平行四边形?若存在, 请求出M 点的坐标;若不存在,请说明理由.16.如图,在矩形OABC 中, 请说明理由.17•如图,抛物线y=-X123+2X+3与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D和点C关于抛物线的对称轴对称,直线AD与y轴交于点E.1 求直线AD的解析式;2 如图1,直线AD上方的抛物线上有一点F,过点F作FG丄AD于点G,作FH平行于X轴交直线AD于点巴求厶FGH周长的最大值;3 点M是抛物线的顶点,点P是y轴上一点,点Q是坐标平面内一点,以A, M , P, Q为顶点的四边形是以AM为边的矩形•若点T和点Q关于AM所在直线对称,求点T 的坐标.18•如图,点A和动点P在直线I上,点P关于点A的对称点为Q,以AQ为边作Rt A ABQ,使/ BAQ=90 , AQ: AB=3: 4,作厶ABQ的外接圆0.点C在点P 右侧,PC=4过点C作直线m丄I,过点O作OD丄m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF冷CD,以DE, DF为邻边作矩形DEGF设AQ=3x.(1)用关于X的代数式表示BQ, DF.(2)当点P在点A右侧时,若矩形DEGF勺面积等于90,求AP的长.(3)在点P的整个运动过程中,①当AP为何值时,矩形DEGF是正方形?②作直线BG交。
中考数学专题复习:二次函数综合题(相似三角形问题)1.如图①,二次函数y =﹣x 2+bx +c 的图象与x 轴交于点A (﹣1,0)、B (3,0),与y 轴交于点C ,连接BC ,点P 是抛物线上一动点.(1)求二次函数的表达式.(2)当点P 不与点A 、B 重合时,作直线AP ,交直线BC 于点Q ,若①ABQ 的面积是①BPQ 面积的4倍,求点P 的横坐标.(3)如图①,当点P 在第一象限时,连接AP ,交线段BC 于点M ,以AM 为斜边向①ABM 外作等腰直角三角形AMN ,连接BN ,①ABN 的面积是否变化?如果不变,请求出①ABN 的面积;如果变化,请说明理由.2.如图,二次函数2314y x bx =++的图像经过点()8,3A ,交x 轴于点B ,C (点B 在点C 的左侧),与y 轴交于点D .(1)填空:b = ______;(2)点P 是第一象限内抛物线上一点,直线PO 交直线CD 于点Q ,过点P 作x 轴的垂线交直线CD 于点T ,若PQ QT =,求点P 的坐标;(3)在x 轴的正半轴上找一点E ,过点E 作AE 的垂线EF 交y 轴于F ,若AEF 与EFO △相似,求OE 的长.3.如图,已知抛物线2y ax bx c =++与x 轴相交于点()1,0A -,()3,0B ,与y 轴的交点()0,6C .(1)求抛物线的解析式;(2)点(),P m n 在平面直角坐标系第一象限内的抛物线上运动,设PBC 的面积为S ,求S 关于m 的函数表达式(指出自变量m 的取值范围)和S 的最大值;(3)点M 在抛物线上运动,点N 在y 轴上运动,是否存在点M 、点N 使得①CMN =90°,且∆CMN 与OBC ∆相似,如果存在,请求出点M 和点N 的坐标.4.如图,抛物线L 1:y =ax 2﹣2x +c (a ≠0)与x 轴交于A 、B (3,0)两点,与y 轴交于点C (0,﹣3),抛物线的顶点为D .抛物线L 2与L 1关于x 轴对称.(1)求抛物线L 1与L 2的函数表达式;(2)已知点E 是抛物线L 2的顶点,点M 是抛物线L 2上的动点,且位于其对称轴的右侧,过M 向其对称轴作垂线交对称轴于P ,是否存在这样的点M ,使得以P 、M 、E 为顶点的三角形与△BCD 相似,若存在请求出点M 的坐标,若不存在,请说明理由.5.如图,在平面直角坐标系中,已知直线4y x =+与x 轴、y 轴分别相交于点A 和点C ,抛物线21y x kx k =++-的图象经过点A 和点C ,与x 轴的另一个交点是点B .(1)求出此抛物线的解析式; (2)求出点B 的坐标;(3)若在y 轴的负半轴上存在点D .能使得以A ,C ,D 为顶点的三角形与①ABC 相似,请求出点D 的坐标.6.如图1,已知抛物线23y ax bx =++经过点()1,5D ,且交x 轴于A ,B 两点,交y 轴于点C ,已知点()1,0A -,(),P m n 是抛物线在第一象限内的一个动点,PQ BC ⊥于点Q .(1)求抛物线的解析式;(2)当PQ =m 的值;(3)是否存在点P ,使BPQ 与BOC 相似?若存在,请求出P 点的坐标;若不存在,请说明理由.7.如图,在平面直角坐标系中,直线y =12x +2与x 轴交于点A ,与y 轴交于点C .抛物线y =ax 2+bx +c的对称轴是x=-32且经过A、C两点,与x轴的另一交点为点B.(1)求二次函数y=ax2+bx+c的表达式;(2)点P为线段AB上的动点,求AP+2PC的最小值;(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A,M,N为顶点的三角形与①ABC 相似?若存在,求出点M的坐标;若不存在,请说明理由.8.如图,抛物线y=−x2+bx+c与x轴相交于A(−1,0),B(3,0)两点,与y轴交于点C,顶点为点D,抛物线的对称轴与BC相交于点E,与x轴相交于点F.(1)求抛物线的函数关系式;(2)连结DA,求sin A的值;(3)若点H线段BC上,BOC与BFH△相似,请直接写出点H的坐标.9.如图,抛物线y=1-2x2+bx+c与x轴交于点A(﹣2,0)和点B(8,0),与y轴交于点C,顶点为D,连接AC,BC,BC与抛物线的对称轴l交于点E.(1)求抛物线的表达式;(2)点P 是第一象限内抛物线上的动点,连接PB ,PC ,当S △PBC =720S △ABC 时,求点P 的坐标; (3)点N 是对称轴l 右侧抛物线上的动点,在射线ED 上是否存在点M ,使得以点M ,N ,E 为顶点的三角形与①OBC 相似?若存在,求点M 的坐标;若不存在,请说明理由.10.如图,抛物线23y ax bx =++与x 轴交于1,0A 、()3,0B -两点,与y 轴交于点C ,设抛物线的顶点为D .(1)求该抛物线的表达式与顶点D 的坐标; (2)试判断BCD △的形状,并说明理由;(3)探究坐标轴上是否存在点P ,使得以P 、A 、C 为顶点的三角形与BCD △相似?若存在,请求出点P 的坐标;若不存在,请说明理由.11.如图,抛物线y =ax 2﹣2ax ﹣3a (a ≠0)与x 轴交于点A ,B .与y 轴交于点C .连接AC ,BC .已知ABC 的面积为2.(1)求抛物线的解析式;(2)平行于x 轴的直线与抛物线从左到右依次交于P ,Q 两点.过P ,Q 向x 轴作垂线,垂足分别为G ,H .若四边形PGHQ 为正方形,求正方形的边长;(3)抛物线上是否存在一点N ,使得①BCN =①CAB ﹣①CBA ,若存在,请求出满足条件N 点的横坐标,若不存在请说明理由.12.如图,二次函数2y x bx c =-++的图像与x 轴交于点A (-1,0),B (2,0),与y 轴相交于点C .(1)求这个二次函数的解析式;(2)若点M 在此抛物线上,且在y 轴的右侧.①M 与y 轴相切,过点M 作MD ①y 轴,垂足为点D .以C ,D ,M 为顶点的三角形与①AOC 相似,求点M 的坐标及①M 的半径长.13.如图,在平面直角坐标系中,抛物线2()0y ax bx c ac =++≠与x 轴交于点A 和点B (点A 在点B 的左侧),与y 轴交于点C .若线段OA OB OC 、、的长满足2OC OA OB =⋅,则这样的抛物线称为“黄金”抛物线.如图,抛物线22(0)y ax bx a =++≠为“黄金”抛物线,其与x 轴交点为A ,B (其中B 在A 的右侧),与y 轴交于点C .且4OA OB =(1)求抛物线的解析式;(2)若P 为AC 上方抛物线上的动点,过点P 作PD AC ⊥,垂足为D . ①求PD 的最大值;①连接PC ,当PCD 与ACO △相似时,求点P 的坐标.14.如图,在平面直角坐标系xOy 中,已知抛物线2y x bx c =++与x 轴交于点A 、B 两点,其中1,0A ,与y 轴交于点()0,3C .(1)求抛物线解析式;(2)如图1,过点B 作x 轴垂线,在该垂线上取点P ,使得①PBC 与①ABC 相似,请求出点P 坐标;(3)如图2,在线段OB 上取一点M ,连接CM ,请求出12CM BM +最小值.15.如图,抛物线y =ax 2+k (a >0,k <0)与x 轴交于A ,B 两点(点B 在点A 的右侧),其顶点为C ,点P 为线段OC 上一点,且PC =14OC .过点P 作DE ①AB ,分别交抛物线于D ,E 两点(点E 在点D 的右侧),连接OD ,DC .(1)直接写出A ,B ,C 三点的坐标;(用含a ,k 的式子表示) (2)猜想线段DE 与AB 之间的数量关系,并证明你的猜想;(3)若①ODC =90°,k =﹣4,求a 的值.16.如图,抛物线223y x bx c =++与x 轴交于A ,B 两点,与y 轴交于C 点,连接AC ,已知B (﹣1,0),且抛物线经过点D (2,﹣2).(1)求抛物线的表达式;(2)若点E 是抛物线上第四象限内的一点,且2ABES=,求点E 的坐标;(3)若点P 是y 轴上一点,以P ,A ,C 三点为顶点的三角形是等腰三角形,求P 点的坐标.17.如图,在直角坐标系xOy 中,抛物线y =ax 2+bx +2(a ≠0)与x 轴交于点A (﹣1,0)和B (4,0),与y 轴交于点C ,点P 是抛物线上的动点(不与点A ,B ,C 重合).(1)求抛物线的解析式;(2)当点P 在第一象限时,设①ACP 的面积为S 1,①ABP 的面积为S 2,当S 1=S 2时,求点P 的坐标; (3)过点O 作直线l ①BC ,点Q 是直线l 上的动点,当BQ ①PQ ,且①BPQ =①CAB 时,请直接写出点P 的坐标.18.如图,在平面直角坐标系xOy中,直线y=﹣x+3与两坐标轴交于A、B两点,抛物线y=x2+bx+c 过点A和点B,并与x轴交于另一点C,顶点为D.点E在对称轴右侧的抛物线上.(1)求抛物线的函数表达式和顶点D的坐标;(2)若点F在抛物线的对称轴上,且EF①x轴,若以点D,E,F为顶点的三角形与①ABD相似,求出此时点E的坐标;(3)若点P为坐标平面内一动点,满足tan①APB=3,请直接写出①P AB面积最大时点P的坐标及该三角形面积的最大值.19.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A、B,与y轴交于点C,且OC=2OB=6OA=6,点P是第一象限内抛物线上的动点.(1)求抛物线的解析式;(2)连接BC与OP,交于点D,当S△PCD:S△ODC的值最大时,求点P的坐标;(3)点M在抛物线上运动,点N在y轴上运动,是否存在点M、点N.使①CMN=90°,且①CMN与①BOC 相似,若存在,请求出点M、点N的坐标.20.如图,抛物线y=x2+bx+12(b<0)与x轴交于A,B两点(A点在B点左侧),且OB=3OA.(1)请直接写出b=,A点的坐标是,B点的坐标是;(2)如图(1),D点从原点出发,向y轴正方向运动,速度为2个单位长度/秒,直线BD交抛物线于点E,若BE=5DE,求D点运动时间;(3)如图(2),F点是抛物线顶点,过点F作x轴平行线MN,点C是对称轴右侧的抛物线上的一定点,P 点在直线MN上运动.若恰好存在3个P点使得①P AC为直角三角形,请求出C点坐标,并直接写出P点的坐标.答案1.(1)y =﹣x 2+2x +3.(2)P 352或 (3)①ABN 的面积不变,为4.2.(1)2-(2)5⎛ ⎝⎭或5⎛ ⎝⎭(3)4或493.(1)2246y x x =-++(2)S 关于m 的函数表达式为239(03)S m m m =-+<<,S 的最大值是274 (3)存在,M (1,8),N (0,172)或M (74,558),N (0,838)或M (94,398),N (0,38)或M (3,0),N (0,﹣32)4.(1)抛物线L 1:223y x x =--,抛物线L 2:2y x 2x 3=-++;(2)435(,)39M 或(4,5)M -.5.(1)254y x x =++(2)点B 的坐标为(-1,0)(3)点D 的坐标是(0,-203) 6.(1)215322y x x =-++ (2)1或5(3)存在;P (53,529)7.(1)抛物线表达式为:213222y x x =--+;(2)AP +2PC 的最小值是4;(3)存在M(0,2)或(-3,2)或(2,-3)或(5,-18),使得以点A 、M 、N 为顶点的三角形与ABC 相似.8.(1)y =-x 2+2x +3(3)点H 的坐标为(1,2)或(2,1)9.(1)21382y x x =++ (2)P 1(1,10.5),P 2(7,4.5)(3)存在,(3,8)或(3,5或(3,11)30.(1)y =﹣x 2﹣2x +3,(﹣1,4);(2)直角三角形,理由见解析;(3)存在,(0,0)或(0,﹣13)或(-9,0)11.(1)y =﹣13x 2+23x +1(2)﹣6﹣(3)存在,5或11712.(1)22y x x =-++; (2)M 的坐标为(12,94),(32, 54 ),(3,-4),①M 的半径长为12或32或313.(1)213222y x x =--+(2)①PD ①P 坐标为(3,2)-或325()28,-14.(1)243y x x =-+(2)P 点坐标为()3,9或()3,215.(1)点A 、B 、C 的坐标分别为(、、(0,k ) (2)DE =12AB(3)a =1316.(1)224233y x x =--(2)E ,-1)(3)P 点的坐标(0,2)或(02)或(0,﹣2或(0,54)17.(1)213222y x x =-++ (2)点P 的坐标为(103,139)(3)点P 的坐标为(32,﹣2)或(32,﹣2)或(173,﹣509)18.(1)y =x 2﹣4x +3,(2,﹣1)(2)(5,8)或(73,89-)(3)①P AB ,此时P )19.(1)y =﹣2x 2+4x +6 (2)点P 的坐标为(32,152) (3)存在,M 、N 的坐标分别为(3,0)、(0,﹣32)或(94,398)、(0,38)或(1,8)、(0,172)或(74,558)、(0,838)20.(1)﹣8,(2,0),(6,0)(2)3秒或212秒 (3)C 点坐标为(143,﹣329),P 点的坐标为(103,﹣4)或(﹣103,﹣4)或(11027,﹣4)。