钢结构课后答案
- 格式:docx
- 大小:20.00 KB
- 文档页数:10

钢结构课后习题答案(仅供参考)第三章 钢结构的连接3.1 试设计双角钢与节点板的角焊缝连接(图3.80)。
钢材为Q235B ,焊条为E43型,手工焊,轴心力N=1000KN (设计值),分别采用三面围焊和两面侧焊进行设计。
解:(1)三面围焊 2160/w f f N mm = 123α=213α= 确定焊脚尺寸:,max min 1.2 1.21012f h t mm ≤=⨯=, ,min min 1.5 1.512 5.2f h t mm ≥==, 8f h mm = 内力分配:30.7 1.2220.78125160273280273.28w f f f N h b f N KN β=⋅⋅⋅=⨯⨯⨯⨯⨯==∑3221273.281000196.69232N N N KN α=-=⨯-= 3112273.281000530.03232N N N KN α=-=⨯-=焊缝长度计算:11530.032960.720.78160w wf f N l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为 1296830460608480wf l mm h mm '=+=≤=⨯=,取310mm 。
22196.691100.720.78160w wf f N l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为 2110811860608480wf l mm h mm '=+=≤=⨯=,取120mm 。
(2)两面侧焊确定焊脚尺寸:同上,取18f h mm =, 26f h mm = 内力分配:22110003333N N KN α==⨯=, 11210006673N N KN α==⨯= 焊缝长度计算:116673720.720.78160w wf fN l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为:mm h mm l f w48086060388283721=⨯=<=⨯+=',取390mm 。
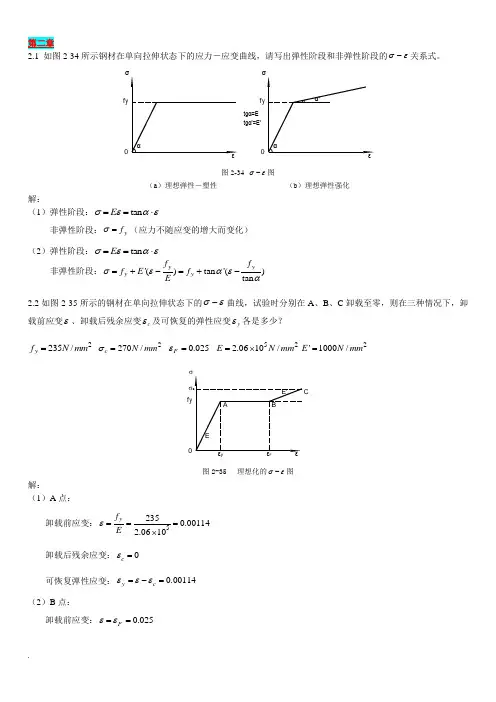
2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσ图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε==卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
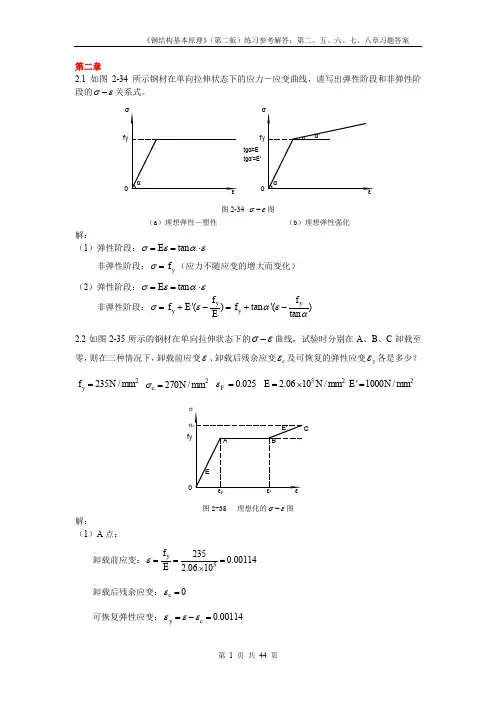
第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσF图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。

钢结构课后习题答案(仅供参考)第三章 钢结构的连接3.1 试设计双角钢与节点板的角焊缝连接(图3.80)。
钢材为Q235B ,焊条为E43型,手工焊,轴心力N=1000KN (设计值),分别采用三面围焊和两面侧焊进行设计。
解:(1)三面围焊 2160/wf f N mm = 123α=213α= 确定焊脚尺寸:,max min 1.2 1.21012f h t mm ≤=⨯=, ,min min 1.5 1.512 5.2f h t mm ≥==, 8f h mm = 内力分配:30.7 1.2220.78125160273280273.28w f f f N h b f N KN β=⋅⋅⋅=⨯⨯⨯⨯⨯==∑3221273.281000196.69232N N N KN α=-=⨯-= 3112273.281000530.03232N N N KN α=-=⨯-=焊缝长度计算:11530.032960.720.78160w wf fN l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为 1296830460608480wf l mm h mm '=+=≤=⨯=,取310mm 。
22196.691100.720.78160w wf fN l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为 2110811860608480wf l mm h mm '=+=≤=⨯=,取120mm 。
(2)两面侧焊确定焊脚尺寸:同上,取18f h mm =, 26f h mm = 内力分配:22110003333N N KN α==⨯=, 11210006673N N KN α==⨯= 焊缝长度计算:116673720.720.78160w wf f N l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为:mm h mm l f w48086060388283721=⨯=<=⨯+=',取390mm 。

钢结构课后习题答案(仅供参考)第三章 钢结构的连接3.1 试设计双角钢与节点板的角焊缝连接(图3.80)。
钢材为Q235B ,焊条为E43型,手工焊,轴心力N=1000KN (设计值),分别采用三面围焊和两面侧焊进行设计。
解:(1)三面围焊 2160/wf f N mm = 123α=213α= 确定焊脚尺寸:,max min 1.2 1.21012f h t mm ≤=⨯=,,min 5.2f h mm ≥==, 8f h mm = 内力分配:30.7 1.2220.78125160273280273.28w f f f N h b f N KN β=⋅⋅⋅=⨯⨯⨯⨯⨯==∑3221273.281000196.69232N N N KN α=-=⨯-= 3112273.281000530.03232N N N KN α=-=⨯-=焊缝长度计算:11530.032960.720.78160w wf fN l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为 1296830460608480wf l mm h mm '=+=≤=⨯=,取310mm 。
22196.691100.720.78160w wf fN l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为 2110811860608480wf l mm h mm '=+=≤=⨯=,取120mm 。
(2)两面侧焊确定焊脚尺寸:同上,取18f h mm =, 26f h m m = 内力分配:22110003333N N KN α==⨯=, 11210006673N N KN α==⨯= 焊缝长度计算:116673720.720.78160w wf f N l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为:mm h mm l f w48086060388283721=⨯=<=⨯+=',取390mm 。
223332480.720.76160w wf fN l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为:mm h mm l f w48086060260262481=⨯=<=⨯+=',取260mm 。

钢结构课后习题答案(仅供参考)第三章 钢结构的连接3.1 试设计双角钢与节点板的角焊缝连接(图3.80)。
钢材为Q235B ,焊条为E43型,手工焊,轴心力N=1000KN (设计值),分别采用三面围焊和两面侧焊进行设计。
解:(1)三面围焊 2160/w f f N mm = 123α=213α= 确定焊脚尺寸:,max min 1.2 1.21012f h t mm ≤=⨯=, ,min min 1.5 1.512 5.2f h t mm ≥==, 8f h mm = 内力分配:30.7 1.2220.78125160273280273.28w f f f N h b f N KN β=⋅⋅⋅=⨯⨯⨯⨯⨯==∑3221273.281000196.69232N N N KN α=-=⨯-= 3112273.281000530.03232N N N KN α=-=⨯-=焊缝长度计算:11530.032960.720.78160w wf f N l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为 1296830460608480wf l mm h mm '=+=≤=⨯=,取310mm 。
22196.691100.720.78160w wf f N l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为 2110811860608480wf l mm h mm '=+=≤=⨯=,取120mm 。
(2)两面侧焊确定焊脚尺寸:同上,取18f h mm =, 26f h mm = 内力分配:22110003333N N KN α==⨯=, 11210006673N N KN α==⨯= 焊缝长度计算:116673720.720.78160w wf fN l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为:mm h mm l f w48086060388283721=⨯=<=⨯+=',取390mm 。
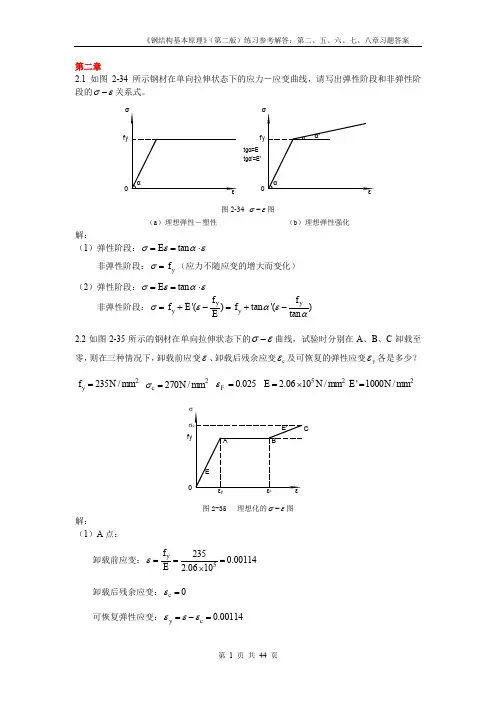
第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσF图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。

第三章 钢结构的连接3.1 试设计双角钢与节点板的角焊缝连接(图3.80)。
钢材为Q235B ,焊条为E43型,手工焊,轴心力N=1000KN (设计值),分别采用三面围焊和两面侧焊进行设计。
解:(1)三面围焊 2160/wf f N m m = 123α= 213α= 确定焊脚尺寸:,max min 1.2 1.21012f h t mm ≤=⨯=,,min 5.2f h mm ≥==, 8f h mm =内力分配:30.7 1.2220.78125160273280273.28w f f f N h b f N KN β=⋅⋅⋅=⨯⨯⨯⨯⨯==∑3221273.281000196.69232N N N KN α=-=⨯-= 3112273.281000530.03232N N N KN α=-=⨯-=焊缝长度计算:11530.032960.720.78160w wf f N l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为 1296830460608480wf l mm h mm '=+=≤=⨯=,取310mm 。
22196.691100.720.78160w wf fN l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为 2110811860608480wf l mm h mm '=+=≤=⨯=,取120mm 。
(2)两面侧焊确定焊脚尺寸:同上,取18f h mm =, 26f h m m = 内力分配:22110003333N N KN α==⨯=, 11210006673N N KN α==⨯= 焊缝长度计算:116673720.720.78160w wf fN l mm h f ≥==⋅⨯⨯⨯∑,则实际焊缝长度为:mm h mm l f w48086060388283721=⨯=<=⨯+=',取390mm 。
223332480.720.76160w wf fN l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为:mm h mm l f w48086060260262481=⨯=<=⨯+=',取260mm 。

第三章 钢结构的连接3。
1 试设计双角钢与节点板的角焊缝连接(图3。
80)。
钢材为Q235B,焊条为E43型,手工焊,轴心力N=1000KN (设计值),分别采用三面围焊和两面侧焊进行设计。
解:(1)三面围焊 2160/w f f N mm = 123α=213α= 确定焊脚尺寸:,max min 1.2 1.21012f h t mm ≤=⨯=, ,min min 1.5 1.512 5.2f h t mm ≥==, 8f h mm =内力分配:30.7 1.2220.78125160273280273.28w f f f N h b f N KN β=⋅⋅⋅=⨯⨯⨯⨯⨯==∑ 3221273.281000196.69232N N N KN α=-=⨯-= 3112273.281000530.03232N N N KN α=-=⨯-=焊缝长度计算:11530.032960.720.78160w wf fN l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为 1296830460608480wf l mm h mm '=+=≤=⨯=,取310mm 。
22196.691100.720.78160w wf f N l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为 2110811860608480wf l mm h mm '=+=≤=⨯=,取120mm 。
(2)两面侧焊确定焊脚尺寸:同上,取18f h mm =, 26f h mm = 内力分配:22110003333N N KN α==⨯=, 11210006673N N KN α==⨯= 焊缝长度计算:116673720.720.78160w wf f N l mm h f ≥==⋅⨯⨯⨯∑,则实际焊缝长度为:mm h mm l f w48086060388283721=⨯=<=⨯+=',取390mm 。

钢结构(第三版)戴国欣主编__课后习题答案第三章钢结构的连接3.1试设计双角钢与节点板的角焊缝连接(图3.80)。
钢材为Q235B,焊条为E43型,手工焊,轴心力N=1000KN(设计值),分别采用三面围焊和两面侧焊进行设计。
解:(1)三面围焊确定焊脚尺寸:,,内力分配:焊缝长度计算:,则实际焊缝长度为,取310mm。
,则实际焊缝长度为,取120mm。
(2)两面侧焊确定焊脚尺寸:同上,取,内力分配:,焊缝长度计算:,则实际焊缝长度为:,取390mm。
,则实际焊缝长度为:,取260mm。
3.2 试求图3.81所示连接的最大设计荷载。
钢材为Q235B,焊条为E43型,手工焊,角焊缝焊脚尺寸,。
焊脚尺寸:焊缝截面的形心:则(1)内力分析:V=F,(2)焊缝截面参数计算:(3)应力计算T引起的应力:V引起的应力:(4)3.3 试设计如图3.82所示牛腿与柱的连接角焊缝①、②、③。
钢材为Q235B,焊条为E43型,手工焊。
(1)内力分析:V=F=98KN,(2)焊缝截面参数计算:取焊缝截面的形心:(3)应力计算M引起的应力:V引起的应力:(4)3.4 习题3.3的连接中,如将焊缝②及焊缝③改为对接焊缝(按三级质量标准检验),试求该连接的最大荷载。
(1)内力分析:V=F,(2)焊缝截面参数计算:(3)应力计算M引起的应力:V引起的应力:(4)3.5焊接工字形梁在腹板上设一道拼接的对接焊缝(图3.83),拼接处作用有弯矩,剪力V=374KN,钢材为Q235B钢,焊条用E43型,半自动焊,三级检验标准,试验算该焊缝的强度。
(1)内力分析:V=374KN,(2)焊缝截面参数计算:(3)应力计算腹板和翼缘交接处:折算应力:不满足3.6 试设计图3.81的粗制螺栓连接,F=100KN(设计值),。
(1)内力分析:V=100KN,,(2)参数计算:单个螺栓抗剪承载力(M22),(3)内力计算T引起的应力:V引起的应力:(4)3.7 试设计如图3.84所示:构件钢材为Q235B,螺栓为粗制螺栓。
1.1、屋盖结构主要组成部分是哪些?它们的作用是什么?A、屋架:支撑于柱或托架,承受屋面板或檩条传来的荷载;b、天窗:屋架跨度较大时,为了采光和通风的需要;C、支撑系统:用于增强屋架的侧向刚度,传递水平荷载和保证屋盖体系的整体稳定。
1.2、屋盖结构中有哪些支撑系统?支撑的作用是什么?(1)a、上弦横向水平支撑b、下弦横向水平支撑c、上弦纵向水平支撑d、下弦纵向水平支撑e、垂直支撑f、系杆(2)a、保证结构的空间整体性b、为弦杆提供适当的侧向支撑点c、承担并传递水平荷载d、保证结构安装时的稳定与方1.3、如何区分刚性系杆和柔性系杆?哪些位置需要设置刚性系杆?答:(1)刚性系杆:能承受压力,柔性系杆:只能承受拉力(2)上弦平面内檩条和大型屋面板可起到刚性系杆作用,因而可在屋架的屋脊和支座节点处设置系杆,当屋架横向支撑设置在第二柱间时所有系杆均为刚性系杆。
1.4实腹式和格构式檩条各适用于哪种情况?其优缺点是什么?答:(1)实腹式檩条常用于跨度为3~6m的情况,构造简单,制造及安装方便(2)桁架式檩条用于跨度较大(>6m)的情况,分为三种形式:A、平面桁架式檩条,受力明确,用料省,但侧向刚度较差,必须设置拉条;B、T形桁架式檩条,整体性差,应沿跨度全长设置钢箍;C、空间桁架式檩条,刚度好,承载力大,不必设置拉条,安装方便,但是构造复杂,适用跨度和荷载较大的情况1.5为什么檩条要布置拉条?答:为了给檩条提供侧向支撑,减小檩条沿屋面坡度方向的跨度,除了侧向刚度较大的空间桁架式和T形桁架式檩条外,在实腹式檩条和平面桁架式檩条之间设置拉条。
1.6三角形、梯形、平行弦桁架各适用于哪些屋盖体系?答:(1)三角形屋架:屋面坡度较大的有檩屋盖结构或中小跨度的轻型屋面结构(2)梯形屋架:用于屋面坡度较小的屋盖结构、工业厂房屋盖结构最常用形式(3)矩形屋架:用于托架或支撑体系中(4)曲拱屋架:用于有特殊要求的房屋中1.7屋架的腹杆有哪些体系?各有什么特征?答:(1)三角形腹杆:单斜杆式,长杆受拉,短杆受压,经济;人字式,腹杆数少,节点少,构造简单;芬克式,腹杆受力合理,可分开运输。
第七章7.9解:钢材为Q235钢,焊条为E43型,则角焊缝的强度设计值w 2f 160N/mm f =。
图示连接为不等肢角钢长肢相连,故K 1=0.65,K 2=0.35。
焊缝受力:110.65600390kN N K N ==⨯=220.35600210kN N K N ==⨯=所需焊缝计算长度,肢背:31w1wf1f 39010217.6mm 20.720.78160N l h f ⨯===⨯⨯⨯⨯ 肢尖:32w2wf2f 21010156.3mm 20.720.76160N l h f ⨯===⨯⨯⨯⨯ 侧面焊缝实际施焊长度,肢背:1w1f12217.628233.6mm l l h =+=+⨯=,取240mm ;肢尖:2w2f22156.326165.6mm l l h =+=+⨯=,取170mm 。
7.11解:①()()fmin fmax 6mm1~2121~210~11mmh h t ====-=-=取f 8mm h =焊缝有效截面的形心位置:()120.781921920.78256.1mm 20.7819230020.780.78x ⎛⎫⨯⨯⨯⨯⨯+⨯ ⎪⎝⎭==⨯⨯⨯++⨯⨯⨯⨯()()324x 10.7830020.7820.781921500.7866128649mm 12I =⨯⨯⨯+⨯⨯+⨯⨯⨯⨯+⨯=()2y 2340.7830020.7856.111920.7820.781920.7819256.116011537mm1222I =⨯⨯+⨯⨯⨯⎡⎤⨯⎛⎫+⨯⨯⨯⨯+⨯⨯⨯+-=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦4x y 661286491601153782140186mm J I I =+=+=()6yT2A6T2x A 60101500.782111.6N/mm 821401860.78601019256.12101.3N/mm 82140186Tr J Tr J τσ⨯⨯+⨯===⨯⎛⎫⨯⨯+- ⎪⎝⎭===139.1MPa 160MPa ==≤ 所选焊脚尺寸满足强度要求(可选焊脚尺寸为7mm 验算强度,可能不满足) ②采用四面围焊,取f 6mm h =()()334x 1120020.7630020.7620030059400746mm 1212I =⨯+⨯⨯⨯+⨯⨯-⨯⨯= ()()334y 1120020.7630020.7630020032608868mm 1212I =⨯+⨯⨯⨯+⨯⨯-⨯⨯=4x y 594007463260886892009614mm J I I =+=+= ()6yT2A6T 2xA 60101500.76299.2N/mm 920096141940.7660102264.6N/mm 92009614Tr J Tr J τσ⨯⨯+⨯===⨯⎛⎫⨯⨯+ ⎪⎝⎭===112.4MPa 160MPa ==≤虽强度富裕较多,但已是最小焊脚尺寸,因此采用方案二的焊角尺寸可减少2mm③方案一耗用的焊条:()223f w 118300200222400mm 22h l ⋅=⨯⨯+⨯= 方案二耗用的焊条:()223f w 116230020018000mm 22h l ⋅=⨯⨯⨯+=所以方案二耗用的焊条少于方案一。
2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan y yy y f f f E f E σεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm =2270/c N mm σ=0.025F ε=522.0610/E N mm =⨯2'1000/E N mm =f yσ图2-35 理想化的σε-图解:(1)A 点: 卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε==卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构(第三版)戴国欣主编__课后习题答案第三章钢结构的连接3.1试设计双角钢与节点板的角焊缝连接(图3.80)。
钢材为Q235B,焊条为E43型,手工焊,轴心力N=1000KN(设计值),分别采用三面围焊和两面侧焊进行设计。
解:(1)三面围焊确定焊脚尺寸:,,内力分配:焊缝长度计算:,则实际焊缝长度为,取310mm。
,则实际焊缝长度为,取120mm。
(2)两面侧焊确定焊脚尺寸:同上,取,内力分配:,焊缝长度计算:,则实际焊缝长度为:,取390mm。
,则实际焊缝长度为:,取260mm。
3.2 试求图3.81所示连接的最大设计荷载。
钢材为Q235B,焊条为E43型,手工焊,角焊缝焊脚尺寸,。
焊脚尺寸:焊缝截面的形心:则(1)内力分析:V=F,(2)焊缝截面参数计算:(3)应力计算T引起的应力:V引起的应力:(4)3.3 试设计如图3.82所示牛腿与柱的连接角焊缝①、②、③。
钢材为Q235B,焊条为E43型,手工焊。
(1)内力分析:V=F=98KN,(2)焊缝截面参数计算:取焊缝截面的形心:(3)应力计算M引起的应力:V引起的应力:(4)3.4 习题3.3的连接中,如将焊缝②及焊缝③改为对接焊缝(按三级质量标准检验),试求该连接的最大荷载。
(1)内力分析:V=F,(2)焊缝截面参数计算:(3)应力计算M引起的应力:V引起的应力:(4)3.5焊接工字形梁在腹板上设一道拼接的对接焊缝(图3.83),拼接处作用有弯矩,剪力V=374KN,钢材为Q235B钢,焊条用E43型,半自动焊,三级检验标准,试验算该焊缝的强度。
(1)内力分析:V=374KN,(2)焊缝截面参数计算:(3)应力计算腹板和翼缘交接处:折算应力:不满足3.6 试设计图3.81的粗制螺栓连接,F=100KN(设计值),。
(1)内力分析:V=100KN,,(2)参数计算:单个螺栓抗剪承载力(M22),(3)内力计算T引起的应力:V引起的应力:(4)3.7 试设计如图3.84所示:构件钢材为Q235B,螺栓为粗制螺栓。
①角钢与连接板的螺栓连接;②竖向连接板与柱的翼缘板的螺栓连接。
③竖向连接板与柱的翼缘板的螺栓连接。
,。
①角钢与连接板的螺栓连接;单个螺栓抗剪承载力(M20)螺栓个数个,取5个螺栓,按规范规定间距排列(图省略)。
②竖向连接板与柱的翼缘板的螺栓连接。
内力分析,由支托承担。
单个螺栓抗拉承载力(M20,)螺栓个数个,取6个螺栓,排2排,按规范规定间距排列(图省略)。
③竖向连接板与柱的翼缘板的螺栓连接。
,。
,,由支托承担。
3.8 按摩擦型连接高强度螺栓设计习题3.7中所要求的连接(取消承托板),且分别考虑:①;②,。
螺栓强度级别及接触面处理方式自选。
Q235钢,喷砂处理,M20,8.8级,P=125KN,µ=0.45,,一个螺栓承担的拉力②,,,一个螺栓的最大拉力第四章轴心受力构件4.1验算由2∟组成的水平放置的轴心拉杆的强度和长细比。
轴心拉力的设计值为270KN,只承受静力作用,计算长度为3m。
杆端有一排直径为20mm的孔眼(图4.37),钢材为Q235钢。
如截面尺寸不够,应改用什么角钢?注:计算时忽略连接偏心和杆件自重的影响。
解:(1)强度查表得∟的面积A=6.14cm2 ,,,N=270KN,强度不满足,所需净截面面积为,所需截面积为,选,面积A=7.29cm2(2)长细比4.2 一块-的钢板用两块拼接板-进行拼接。
螺栓孔径为22mm,排列如图4.38所示。
钢板轴心受拉,N=1350KN(设计值)。
钢材为Q235钢,解答下列问题;(1)钢板1-1截面的强度够否?(2)是否需要验算2-2截面的强度?假定N力在13个螺栓中平均分配,2-2截面应如何验算?(3)拼接板的强度够否?解:(1)钢板1-1截面强度验算:,N=1350KN,强度满足。
(2)钢板2-2截面强度验算:(a),种情况,(a)是最危险的。
,N=1350KN,但不超过5%,强度满足。
对应图(d)的验算:,,强度满足。
(3)拼接板的强度够否?因为拼接板厚度,所以不必验算拼接板。
4.3 验算图4.39所示用摩擦型高强度螺栓连接的钢板净截面强度。
螺栓直径20mm,孔径22mm,钢材为Q235AF,承受轴心拉力N=600KN(设计值)。
解:(1)净截面验算:,,强度满足。
(2)全截面验算,强度满足。
4.4 一水平放置两端铰接的Q345钢做成的轴心受拉构件,长9m,截面由2∟组成的肢尖向下的T形截面,问是否能承受设计值为870KN的轴心力?解:(1)强度验算查表得∟的面积A=13.94cm2 ,,,但不超过5%,强度满足。
(2)刚度验算4.5 某车间工作平台柱高2.6m,按两端铰接的轴心受压柱考虑。
如果柱采用I16(16号热轧工字钢),试经过计算解答:(1)钢材采用Q235钢时,设计承载力为多少?(2)改用Q345钢时,设计承载力是否显著提高?(3)如果轴心压力为330KN(设计值),I16能否满足要求?如不满足,从构造上采取什么措施就能满足要求?解:(1)钢材采用Q235钢时,设计承载力为多少?查表得I16的面积A=26.1cm2 ,,,a类截面,查表得,b类截面,查表得。
(2)改用Q345钢时,设计承载力是否显著提高?,a类截面,按查表得,b类截面,按查表得,承载力无太明显的提高。
(3)如果轴心压力为330KN(设计值),I16能否满足要求?如不满足,从构造上采取什么措施就能满足要求?8距uuuuuuuuuuuujuu因为,所以整体稳定不满足。
在侧向加一支撑,重新计算。
,b类截面,查表得,整体稳定满足。
4.6 设某工业平台柱承受轴心压力5000KN(设计值),柱高8m,两端铰接。
要求设计一H 型钢或焊接工字形截面柱。
解:H型钢柱(1)初选截面设(b类)则,,选,其面积,,(2)验算,b类截面,查表得,b类截面,查表得,整体稳定满足。
焊接工字形(1)初选截面根据H型钢截面,初选焊接工字形截面,如图所示。
(2)计算参数,,(2)整体稳定验算,b类截面,查表得,b类截面,查表得,整体稳定满足。
(3)局部稳定验算,局部稳定满足。
4.7图4.40(a)、(b)所示两种截面(焰切边缘)的截面积相等,钢材均为Q235钢。
当用作长度为10m的两端铰接轴心受压柱时,是否能安全承受设计荷载3200KN。
解:计算(a)图截面(1)计算参数:,(2)整体稳定验算,b类截面,查表得,b类截面,查表得,整体稳定满足。
(3)局部稳定验算,局部稳定满足。
计算(b)图截面(1)计算参数:,(2)整体稳定验算,b类截面,查表得,b类截面,查表得,整体稳定不满足。
(3)局部稳定验算,局部稳定满足。
4.8 设计由两槽钢组成的缀板柱,柱长7.5m,两端铰接,设计轴心压力为1500KN,钢材为Q235B,截面无削弱。
解:(1)初选截面:设(b类)则,选2[32a,,其面积,(2)验算实轴的整体稳定,b类截面,查表得,绕实轴的整体稳定满足。
(3)确定柱宽设,取b=330mm,如下图所示。
(4)验算虚轴的整体稳定,,截面对虚轴的参数:130,,,绕虚轴的整体稳定满足。
(5)缀板的设计选用缀板尺寸为-,则,取,分支线刚度缀板线刚度则横向剪力取焊脚尺寸,采用绕角焊,则焊缝计算长度为验算焊缝:,第五章5.1 一平台的梁格布置如图5.53所示,铺板为预制钢筋混凝土板,焊于次梁上。
设平台恒荷载的标准值(不包括梁自重)为2.0。
试选择次梁截面,钢材为Q345钢。
解:1、普通工字形钢3、验算:1)强度2)挠度重选I50a3)整稳:不必计算。
4)局稳:因为是型钢,不必验算。
5.3解:图5.54(a)所示的简支梁,其截面为不对称工字形[图5.54(b)],材料为Q235B 钢;梁的中点和梁端均有侧向支承;在集中荷载(未包括梁自重)F=160(设计值)的作用下,梁能否保证其整体稳定性?5.4解:设计习题5.1的中间主梁(焊接组合梁),包括选择截面、计算翼缘焊缝、确定腹板加劲肋的间距。
钢材为Q345钢,E50型焊条(手工焊)。
解:(1)试选截面:(2)强度验算:(3)整稳验算:(4)刚度验算:(5)翼缘和腹板的连接焊缝计算:(6)主梁加劲肋设计Ⅲ区格:Ⅰ区格:Ⅱ区格:Ⅲ区格:横向加劲助尺寸:中部支承加劲助:第六章6.1 有一两端铰接长度为4m的偏心受压柱子,用Q235钢的HN400×200×8×13做成,压力的设计值为490kN,两端偏心距均为20cm。
试验算其承载力。
M1=98kN.mM1=98kN.mN=490kN4000解:查型钢表得:A=83.37cm2,Ix=22775cm4 ,ix=16.53cm,iy=4.56cm,Wx=1139cm3。
M= 490×0.2=98kN.m强度验算:平面内整体稳定验算:βmx= 1NEx/=π2E Ix/(1.1×l0x2)=3.142×2.06×105 ×22775×104/(1.1×40002)=26283KNλx= l0x/ix=4000/165.3=24.2,属于a类截面,查表,得φx=0.974N/(φxA)+βmxMx/[γ1x W1x(1-0.8N/NEx/)]=490×103/(0.974×8337)+1.0×98×106/[1.05×1139×103×(1-0.8×490 / 26283 )]=60.3+83.2=143.5 N/mm2<f=215 N/mm2平面外整体稳定验算:λy= l0y/iy=4000/45.6=87.7,属于b类截面查表,得φy=0.637φb=1.07-λy2/44000=1.07-87.72/44000=0.895<1.0βtx=1.0N/(φyA)+βtxMx/ (φbW1x)=490×103/(0.637×8337)+1.0×98×106/(0.895×1139×103)=92.3+96.1=188.4 N/mm2< f=215 N/mm2该构件强度、平面内整体稳定、平面外的整体稳定均满足要求。
6.2如图所示悬臂柱,承受偏心距为25cm的设计压力1600kN,弯距作用平面外有支撑体系对柱上端形成支点,要求选定热轧H型钢或焊接工字形截面,材料为Q235钢(注:当选用焊接工字形截面时,可试用翼缘2-400×20,焰切边,腹板-460×12)。
解:选用选用焊接工字形截面时,可试用翼缘2-400×20,焰切边,腹板-460×12平面内计算长度l0x=14000mm,平面外计算长度l0y=7000mm承受均匀弯距M=1600×0.25=400kN.m计算截面特性:A=400×20×2+460×12=21520mm2Wx=Ix/(h/2)=1.019×109/(500/2)=4.076×106mm3ix=( Ix/A)1/2=(1.019×109/21520) 1/2=217.6mmiy=( Iy/A)1/2=(2.134×108/21520) 1/2=99.6mmλx=lox/ ix=14000/217.6=64.3<[λ]=150λy=loy/ iy=7000/99.6=70.3<[λ]=150 刚度满足要求强度验算:平面内整体稳定验算:βmx= 1NEx/=π2E Ix/(1.1×l0x2)=3.142×2.06×105 ×1.019×109/(1.1×140002)=9599KNλx= l0x/ix=14000/217.6=64.3<[λ]=150属于b类截面,查表,得φx=0.784N/(φxA)+βmxMx/[γ1x W1x(1-0.8N/NEx/)]=1600×103/(0.784×21520)+1.0×400×106/[1.05×4.076×106×(1-0.8×1600 / 9599)] =94.8+107.8=202.6 N/mm2<f=215 N/mm2平面外整体稳定验算:λy= l0y/iy=7000/99.6=70.3<[λ]=150属于b类截面查表,得φy=0.749φb=1.07-λy2/44000=1.07-70.32/44000=0.958<1.0βtx=1.0N/(φyA)+βtxMx/ (φbW1x)=1600×103/(0.749×21520)+1.0×400×106/(0.958×4.076×106)=99.3+102.4=201.7 N/mm2< f=215 N/mm2局部稳定验算:腹板:翼缘:--。