下载文档原格式
超声导波检测技术超声导波（Ultrasonic Guided Wave）检测技术利用低频扭曲波（Torsinal Wave）或纵波（Longitudinal Wave）可对管路、管道进行长距离检测，包括对于地下埋管不开挖状态下的长距离检测。
超声导波（也称为制导波）的产生机理与薄板中的兰姆波激励机理相类似，也是由于在空间有限的介质内多次往复反射并进一步产生复杂的叠加干涉以及几何弥散形成的。
但是对于管道检测，在一般管壁厚度下要产生适当的波型，则需要使用比通常超声波探伤低得多的频率，导波通常使用的频率f＜100KHz，因此导波对单个缺陷的检出灵敏度与通常使用频率在MHz级别的超声检测相比是比较低的，但是导波检测的优点是能传播20~30米长距离而衰减很小，因此可在一个位置固定脉冲回波阵列就可做大范围的检测，特别适合于检测在役管道的内外壁腐蚀以及焊缝的危险性缺陷。
低频导波长距离超声检测法用于管道在役状态的快速检测，内外壁腐蚀可一次探测到，也能检出管子断面的平面状缺陷。
超声导波应用的主要波型包括-扭曲波（Torsinal Wave，也简称为扭波）和纵波（Longitudinal Wave）。
扭曲波的特点是能够一边沿管子周向振动，一边沿管子轴向传播，声能受管道内部液体影响较小（在导波检测时，液体在管道中流动是允许的），回波信号能包含管轴方向的缺陷信息，通常能得到清晰的回波信号，信号识别较容易，在应用中需要换能器数量少，重量轻、费用省、因管内液体介质而产生的扩散效应较小，波型转换较少，检测距离较长，对轴向缺陷灵敏度高。
纵波特点是一边沿管子轴向振动，一边沿管子轴向传播，回波幅度与缺陷性状关系不大，回波信号不如扭波清晰，因为受管内流体流动的影响，也受探头接触面的表面状态影响较大（油漆、凹凸等）受被测管内液体介质流动的影响很大。
超声导波检测装置主要由固定在管子上的探伤套环（探头矩阵）、检测装置本体（低频超声探伤仪）和用于控制和数据采样的计算机三部分组成。
厚壁小径管超声波检测工艺研究本文对厚壁的小径管通常采用的超声波检测工艺进行改进，在检测焊缝上部区域的时候采用超声爬波检测法进行检测，检测中下部区域的时候采用横波一次波，并在进行波形分析的时候对横波检测的根部未焊透进行经验分析，最大限度地检出了焊缝中的未焊透缺陷。
标签：厚壁;小径管;爬波，超声波;一次波电站锅炉受热面的管子管径通常直径都小于100mm。
随着锅炉的不断发展，目前采用的小径管外径与壁厚的比值几乎都不大于20。
比如某个电厂所采用的高温过热器管规格为45mm×13mm。
锅炉的受热面管排密集，数量多而且对接焊口的数量也大，一台几百瓦功率的锅炉受热面通常有几万道焊缝，而且在检修的过程中也涉及到更换焊接的焊缝大约几万道。
小径管的焊缝质量直接关系着锅炉的安全，因此对厚壁小径管的无损检测质量进行控制是必然的。
1 常规射线无损检测存在的问题在锅炉的制造或者检修的过程中，规范要求对外径不大于159mm的管子对接接头焊缝进行100%的超声或者射线探伤，常规手段采用的都是射线探伤，但是通常对于厚壁小径管，使用射线进行探伤透射的效果并不好，这是因为几点原因：（1）小径管的壁厚，透照的厚度差较大，因此在底片上成像的黑度差也较大。
射线照相的灵敏度与底片的黑度关系较大，黑度的高低都会影响灵敏度使得厚度的宽容度减小，有些工厂在生产的过程中能够保证小径管的焊缝不断旋转拍照，避免透照的厚度差大的问题出现，保证质量。
但是在检修的时候，由于焊缝只能从一个方向透照，因此厚度差的问题很难避免。
（2）管径厚度的变化较大会引起散射比的增加，从而产生边蚀效应。
（3）由于厚壁小径管集中在受热面，彼此之间的间距较小，因此实现多次透照的工作面有限，绝大多数检测只能够保证透照一次，因此有效检测范围很小，散射线也很杂乱，对于底片的成像质量影响较大。
由于透照角度与边蚀效应的存在，焊缝缺陷的有效检出范围也很低，尤其是危害性较大的面积性缺陷，检出的概率不高，所以给锅炉埋下了安全隐患。
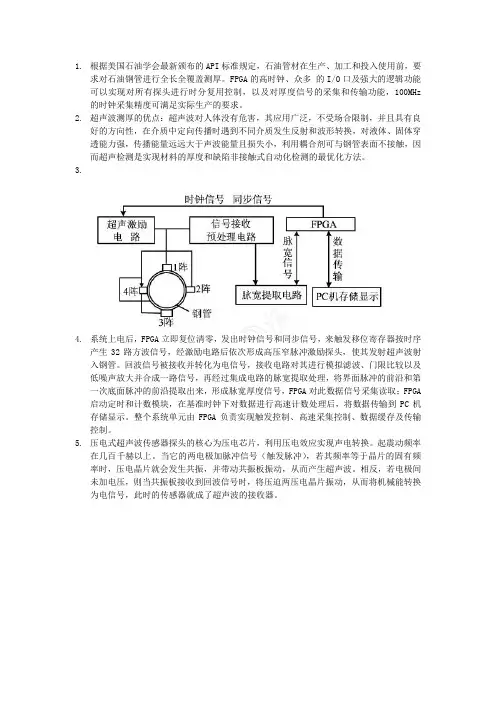
1.根据美国石油学会最新颁布的API标准规定，石油管材在生产、加工和投入使用前，要求对石油钢管进行全长全覆盖测厚。
FPGA的高时钟、众多的I/O口及强大的逻辑功能可以实现对所有探头进行时分复用控制，以及对厚度信号的采集和传输功能，100MHz 的时钟采集精度可满足实际生产的要求。
2.超声波测厚的优点：超声波对人体没有危害，其应用广泛，不受场合限制，并且具有良好的方向性，在介质中定向传播时遇到不同介质发生反射和波形转换，对液体、固体穿透能力强，传播能量远远大于声波能量且损失小，利用耦合剂可与钢管表面不接触，因而超声检测是实现材料的厚度和缺陷非接触式自动化检测的最优化方法。
3.4.系统上电后，FPGA立即复位清零，发出时钟信号和同步信号，来触发移位寄存器按时序产生32路方波信号，经激励电路后依次形成高压窄脉冲激励探头，使其发射超声波射入钢管。
回波信号被接收并转化为电信号，接收电路对其进行模拟滤波、门限比较以及低噪声放大并合成一路信号，再经过集成电路的脉宽提取处理，将界面脉冲的前沿和第一次底面脉冲的前沿提取出来，形成脉宽厚度信号，FPGA对此数据信号采集读取；FPGA 启动定时和计数模块，在基准时钟下对数据进行高速计数处理后，将数据传输到PC机存储显示。
整个系统单元由FPGA负责实现触发控制、高速采集控制、数据缓存及传输控制。
5.压电式超声波传感器探头的核心为压电芯片，利用压电效应实现声电转换。
起震动频率在几百千赫以上。
当它的两电极加脉冲信号（触发脉冲），若其频率等于晶片的固有频率时，压电晶片就会发生共振，并带动共振板振动，从而产生超声波。
相反，若电极间未加电压，则当共振板接收到回波信号时，将压迫两压电晶片振动，从而将机械能转换为电信号，此时的传感器就成了超声波的接收器。
6.影响测量准确性的因素（1）：声速的影响。
对测量结果要求不高的场合，可以采用从各种资料中查到的声速进行测量，但是，从各种资料中查到的声速往往与材料的实际声速有明显的差异。
超声测厚的原理超声测厚是一种常用的无损检测技术，广泛应用于各种工业领域中，例如航空、航天、石化、冶金、制造业等等。
其原理是利用超声波在材料内部传播的特性，通过测量超声波在材料中的传播时间和反射信号的强度，来确定材料的厚度。
本文将详细介绍超声测厚的原理。
一、超声波的传播特性超声波是一种高频声波，其频率通常在1MHz到10MHz之间。
在材料内部传播时，超声波会遇到不同的界面，例如材料内部的各种缺陷、材料与涂层之间的界面、材料与空气之间的界面等等。
当超声波遇到这些界面时，一部分能量会被反射回来，一部分能量会继续向前传播，这种现象称为超声波的反射和传播。
超声波在材料内部传播的速度取决于材料的密度和弹性模量，一般来说，材料越密度越大、弹性模量越高，超声波在其中的传播速度越快。
因此，超声波可以用来测量材料的密度和弹性模量。
二、超声测厚的原理超声测厚是利用超声波在材料内部传播的特性，通过测量超声波在材料中的传播时间和反射信号的强度，来确定材料的厚度。
具体的测量过程如下：1. 发送超声波：超声波由一个发射器产生，经过一个透射器后，进入被测材料中。
2. 接收反射信号：当超声波遇到材料内部的界面时，一部分能量会被反射回来，这些反射信号会被一个接收器接收到。
3. 测量传播时间：根据超声波在材料中的传播速度，可以计算出超声波从发射器到接收器的传播时间。
4. 计算厚度：根据传播时间和超声波在材料中的传播速度，可以计算出被测材料的厚度。
5. 分析反射信号：反射信号的强度和形状可以提供关于材料内部的信息，例如缺陷的位置、大小、形状等等。
三、超声测厚的应用超声测厚广泛应用于各种工业领域中，例如航空、航天、石化、冶金、制造业等等。
以下是一些具体的应用案例：1. 航空航天领域：超声测厚可以用来检测飞机和火箭的各种结构件的厚度和缺陷，例如机翼、发动机叶片、液压管路等等。
2. 石化领域：超声测厚可以用来检测各种管道和容器的厚度和缺陷，例如石油管道、化工容器、储罐等等。
无损检测超声检测公式汇总情况超声检测公式1.周期和频率的关系，二者互为倒数： T=1/f2.波速、波长和频率的关系：C=f λ 或λ=f c3.C L ∶Cs ∶C R ≈1.8∶1∶0.94.声压： P ＝P 1－P 0 帕斯卡（Pa ）微帕斯卡（μPa ）1Pa ＝1N/m 2 1Pa ＝106μP 6.声阻抗:Z ＝p/u ＝ρcu/u ＝ρc 单位为克/厘米2·秒（g/cm 2·s ）或千克/米2·秒（kg/m 2·s ）7.声强；I ＝21Zu2＝Z P 22单位; 瓦/厘米2（W/cm 2）或焦耳/厘米2·秒（J/cm 2·s ）8.声强级贝尔（BeL ）。
△＝lgI 2/I 1 （BeL ）9.声强级即分贝（dB ）△＝10lgI 2/I 1 ＝20lgP 2/P 1 （dB ）10.仪器示波屏上的波高与回波声压成正比：△20lgP 2/P 1＝20lgH 2/H 1 （dB ） 11.声压反射率、透射率： r=Pr / P0 t =Pt / P0=-=+21//)1(1Z t Z r t r r =12120Z Z Z Z P P r +-= t =12202Z Z Z P P t +=Z 1—第一种介质的声阻抗；Z 2—第二种介质的声阻抗12.声强反射率： R=2121220???? ??+-==Z Z Z Z r I I r声强透射率：T()212214Z Z Z Z +=T+R=1 t －r =1 13.声压往复透射率；T 往=21221)(4Z Z Z Z +14.纵波斜入射: 1sin L L c α=1sin L Lc α'=1n si S S c '=2sin L L c β=2sin S S c β CL1、CS1—第一介质中的纵波、横波波速； C L2、C S2—第二介质中的纵波、横波波速；αL 、α′L —纵波入射角、反射角；βL 、βS —纵波、横波折射角；α′S —横波反射角。
第42卷 第1期2003年2月复旦学报(自然科学版)Journal of Fudan University(Natural Science)Vol.42No.1Feb.2003 文章编号:042727104(2003)0120007207超声导波频散特性与管材内径-壁厚比的关系他得安1,刘镇清2(1.复旦大学电子工程系,上海 200433;2.同济大学声学研究所,上海 200092)摘 要:在自由管材的情况下,对于内径2壁厚比变化对管材中较低阶纵向导波模式频散特性的影响进行了分析.分析结果表明:管材中导波的频散特性与内径2壁厚比有关;当内径2壁厚比和频厚积较小时,内径2壁厚比的变化对低阶导波模式的频散特性有较大的影响,但随内径2壁厚比和频厚积的增加,这种影响将减小.另一方面,内径2壁厚比对导波频散特性的影响随导波模式阶次的增加而减小.关键词:超声导波;频散特性;管材;内径2壁厚比中图分类号:TB551 文献标识码:A近年来,管道的无损检测成为一个重要的问题.传统的超声方法是用基本的纵波来测量壁厚度,这种方法须逐点测量管道,非常费时且设备昂贵.超声导波提供了一个更具吸引力的方法,因为它可以在管道的任一位置上激发,沿管轴传播[1].置于空气中的钢管中导波可以传播几十米[2,3];当管道被埋于矿石棉中时,也可以获得类似的结果[4].由于频散波的波包形状随波的传播而发生变化,传播较快的信号从较慢的信号中分离出来,使波包扩展开来.这将对信号的检测造成两个不利的影响;减小分辨率和减小幅度.这个影响在文献[5]中进行了有意义的讨论.在时间上和空间上波包的扩展降低了分辨率,当试图去检测与结构特性相近的缺陷如焊点时,常常遇到这种问题.在那些情况下,只有当缺陷的反射能从结构特性中分辨出时,才能可靠的检测出缺陷.另一方面,当用导波进行检测时,在管材中存在多种模式的导波.为了在长距离上保持波包形态不变,长距离导波无损检测技术的发展渴望利用频散最小的模式.因此,合理选择检测的模式是提高检测可靠性的关键所在[6],而内径2壁厚比在较低频厚积下,对导波模式的频散行为具有较大的影响[7].虽然在众多的研究中考虑了管材内径或壁厚对低频厚积下导波模式频散特性的影响,但迄今为止,作者尚未见到内径2壁厚比变化对导波模式频散特性影响的公开研究报道.因为管材的超声检测基本上都是在较低频厚积下进行的[2],所以,在较低频厚积下,研究内径2壁厚比变化对导波模式频散特性的影响,在工业界超声无损检测中是非常重要的.1 超声纵向导波在管材中的频散特性分析假设管材是轴对称、无限长的.管材的周围为真空时,在内外表面上没有位移限制;1个垂直应力和2个切应力在界面上变为零,即在内半径为a,外半径为b的2个边界上,边界条件为: σrr=σrθ=σrz=0 r=a,b.(1) 1.1 基本方程对于均匀、各向同性的线弹性介质,其一般的弹性动力学运动方程为[8]: (λ+2μ) ( ・U)+μ ×( ×U)=ρ92U/9t2,(2) 收稿日期:2002208201基金项目:上海市博士后基金资助项目作者简介:他得安(1972—),男,博士后.其中U为位移矢量,ρ为材料密度,λ和μ为Lamé常数,上式左边第一项表示膨胀(压缩)部分,第二项表示旋转(等体积)部分.用Helmholtz分解,时间谐振位移矢量U可用压缩标量势Φ和等体积矢量势Ψ表示为: U= Φ+ ×Ψ,(3)其中Φ=<e i(ζz-ωt),Ψ=ψe i(ζz-ωt),i为虚数单位,ω为角频率,轴向波数ζ=ω/c p,c p为相速度.1.2 频散方程根据(1)～(3)式,产生一组特征方程,形成以幅度A、B、A1、B1、A3、B3表示的矩阵形式[5]: [C ij]・[E]=0 i,j=1,2,…,6,(4)其中E=[A B A1 B1 A3 B3]T,C ij为系数矩阵,其表达式参见文献[7].为使上式有非零解,其系数行列式必须为零,即: C ij=0 i,j=1,2,…,6,(5)上式即为管材中导波的频散方程.1.3 B essel函数的选择在C ij的表达式中含有一系列Bessel函数,所以,选取合适的Bessel函数对方程(5)中解的稳定性非常重要.因为Bessel函数J n和Y n沿虚轴以指数形式增加,向内和向外传播的波的影响不能清楚地分开,因此当Bessel函数的变元增大时,它的解变得不稳定,这一问题类似于板中大频厚积的情况[9],对大半径管材尤其重要;然而随着变元逐渐增大,Bessel函数I n(z)增大,而K n(z)减小[10],使修正Bessel函数分离,它的解变得更加稳定.各量的选取如附录所示.1.4 轴对称模式在实际应用中,由于激发和接收等方面的便利,使纵向模式比扭转模式优越.因此,在超声无损检测的实际应用中,一般都用纵向轴对称导波模式,本文也仅讨论纵向轴对称模式.当周向阶次n=0时,(5)式可写成: D1・D2=0,(6)其中: D1=C11C12C14C15C31C32C34C35C41C42C44C45C61C62C64C65, D2=C23C26C53C56.当上式中,频散方程 D1=0(7)时所对应的模式就是纵向轴对称模式.它的位移在(r,z)平面内,因此周向位移分量为零,即uθ=0.2 内径2壁厚比对管中导波频散特性的影响分析2.1 相同内径2壁厚比下不同内径和壁厚时的相速度频散曲线在分析不同内径2壁厚比对导波频散特性的影响前,先分析相同内径2壁厚比时不同内径和壁厚对频散特性的影响.根据(7)式,可得纵向轴对称模式L(0,m)的相速度频散曲线.图1(a)、1(b)分别是内径2壁厚比(r/d)为2和8时不同内径和壁厚下的相速度频散曲线,其中横坐标为频厚积(f・d).其材料为铜管,密度为8.4g/cm3,纵波速度为4.4m/ms,横波速度为2.2m/ms.从图中看出,内径和壁厚不同,而内径2壁厚比相同时,管中各导波模式的相速度频散曲线完全重合.因此,对于一定的材料,在一定的频厚积下,管材中各导波模式的频散特性只与内径2壁厚比有关.只要内径2壁厚比一定,不管内径和壁厚分别如何变化,对管材中导波的频散特性没有影响.根据这一现象,在以下研究不同内径2壁厚比对管材中导波频散的影响时,只考虑其内径2壁厚比,而没有分别考虑其内径和壁厚.8复旦学报(自然科学版) 第42卷图1 相同内径2壁厚比,不同r 和d 时的相速度频散曲线Fig.1 Phase velocity of guided waves at same inner 2radius 2thickness ratio (r/d ),various inner 2radius and thickness2.2 不同内径2壁厚比下的速度频散曲线图2～图4分别为不同内径2壁厚比时,L (0,1)和L (0,2)以及较高阶模式在自由铜管中的相速度c p 和群速度c g 的频散曲线,其中各图中的(a )图为c p 频散曲线;图(b )为c g 频散曲线.图2 不同内径2壁厚比(r/d =2,4,6,10,20)下L (0,1)模式的频散曲线Fig.2 The dispersive characteristics curve of the L (0,1)mode at different inner 2radius 2thicknessratio图3 不同内径2壁厚比(r/d =2,4,6,10,20)下L (0,2)模式的频散曲线Fig.3 The dispersive characteristics curve of the L (0,2)mode at different inner 2radius 2thickness ratio9第1期 他得安等:超声导波频散特性与管材内径-壁厚比的关系从图中看出,在低频情况下(相对于长波长),不同内径2壁厚比(r/d )下的频散曲线有较大的差别,且管中的纯模式最显著.随着频率的增加,纵向导波模式开始显得象板中的波,尤其当半径2壁厚比增大时,这种情况更为明显.图4 不同内径2壁厚比(r/d =2,4,6,10,20)下L (0,3)和L (0,4)模式的频散曲线Fig.4 The dispersive characteristics curve of the L (0,3)and L (0,4)mode at different inner 2radius 2thickness ratio从图2中看出,随内径2壁厚比的增加,低频下L (0,1)模式的相速度和群速度频散曲线向更低频方向移动.在低频下,随内径2壁厚比的增大,管材中L (0,1)模式的相速度减小,大部分频率点上,L (0,1)模式的群速度减小;当频率较大时,群速度增大.但当频率较高时,各内径2壁厚比下的频散曲线重合,这说明当频率较大(如在1.0MHz 以上)时,内径2壁厚比对L (0,1)模式的频散特性基本上没有影响.内径2壁厚比越大时,各内径2壁厚比上的频散曲线重合的频率越低.和L (0,1)模式的情况相似,在低频下,随内径2壁厚比的增加,L (0,2)模式的相速度和群速度频散曲线也都向更低频方向移动,相速度随内径2壁厚比的增加而减小,而群速度随内径2壁厚比的增加而增加.另一方面,当频率较高时,内径2壁厚比的变化对L (0,2)模式频散特性的影响减小.内径2壁厚比越大时,各内径2壁厚比上的频散曲线重合的频率点也越低.从图2和图3中也可以看出,内径2壁厚比变化对L (0,1)模式的影响比对L (0,2)模式的影响大.从图4中可以看出,当内径2壁厚比大于2时,L (0,3)以上模式的频散曲线不随内径2壁厚比的变化而变化,因此,当内径2壁厚比较大时,内径2壁厚比的变化对它们的频散特性基本上没有影响.图5是在频厚积为0.2MHz ・mm 、波传播距离为400mm 时,不同内径2壁厚比(r/d )下自由铜管中纵向轴对称模式L (0,2)和L (0,1)的模拟脉冲回波信号.从图上看出,在这一频率下,内径2壁厚比为7.5以下时L (0,2)和L (0,1)都有频散现象;但内径2壁厚比在7.5以上时,L (0,2)是非频散的,而L (0,1)还有频散现象;当内径2壁厚比为20时,L (0,2)是非频散的,而L (0,1)也几乎是非频散的,但随着内径2壁厚比的增加,L (0,1)模式也越来越变得非频散.可以看出,内径2壁厚比对管中导波的频散特性具有很大的影响.2.3 截止频率与内径2壁厚比的关系图6为各较低阶纵向轴对称模式的内径2壁厚比与截止频率f c 的关系.随着内径2壁厚比的增大,L (0,2)模式的截止频率开始时快速减小,当内径2壁厚比达到5以上时,减小的速率放慢.另一方面,L (0,2)模式在较低频厚积下,几乎是非频散的,且非频散区随内径2壁厚比的增大而增大.因此,L (0,2)模式在管材的检测中非常具有潜力,这是因为:首先,在低频厚区,L (0,2)模式在一很宽频带范围内是非频散的,也就是说在这一频带内,它的速度不随频率的变化而变化,因此,波包在传播过程中保持不变;其次,在低频下很宽的区域内,管中L (0,2)模式是速度最快的模式[2],所以在检测过程中首先检测到的是L (0,2)模式,这样,就可以把一些不需要的模式或模式转换后的新模式分开;再次,它的模式行为对表面和内部缺陷都很灵敏.当内径2壁厚比大于2时,内径2壁厚比的变化对管材中较高阶模式的截止频率基本上没有影01复旦学报(自然科学版) 第42卷响,只有在内径2壁厚比小于2时,截止频率随内径2壁厚比的增大而减小.图5 频厚积为0.2MHz ・mm 时,不同内径2壁厚比(r/d )下模拟的脉冲回波信号Fig.5 Simulative pulse echo signal in various inner 2radius 2thickness ratio (r/d )at 0.2MHz ・mm图6 各较低阶纵向轴对称模式的截止频率与内径2壁厚比的关系Fig.6 Relationship between inner 2radius 2thickness ra 2tio and cut 2off frequency of various lower longi 2tudinal guided waves modes 3 结 论本文对自由管材的情况下,内径2壁厚比变化对自由管材中较低阶纵向导波模式频散特性的影响进行了分析讨论,结果表明:1)对于一定的材料,在一定的频厚积下,管材中导波的频散特性只与内径2壁厚比有关.只要内径2壁厚比一定,不管内径和壁厚分别如何变化,对管中导波的频散特性没有影响;2)L (0,2)模式的截止频率随内径2壁厚比的增大而减小,而当内径2壁厚比大于2时,内径2壁厚比对L (0,3)和L (0,4)模式的截止频率没有影响;3)在低频下,L (0,1)和L (0,2)模式的频散曲线随内径2壁厚比的增大而向更低频方向移动.除少数频率点外,内径2壁厚比增大时,L (0,1)和L (0,2)模式的相速度减小,而群速度增大.内径2壁厚比越大时,各内径2壁厚比上的频散曲线重合的频率点越低;4)当内径2壁厚比较小时,对其他高阶导波模式的频散特性有影响,这种影响随阶数的增加而减弱;当内径2壁厚比较大时,对其他高阶模式没有影响.另一方面,由于L (0,2)模式在较低频厚积下,几乎是非频散的,且非频散区随内径2壁厚比的增大而增大,因此,L (0,2)模式的波形包络在较低频厚积下几乎保持不变,这对超声无损检测是非常有利的.本文得到同济大学工程力学系贺鹏飞教授、复旦大学电子工程系王威琪院士、余建国教授和汪源源教11第1期 他得安等:超声导波频散特性与管材内径-壁厚比的关系21复旦学报(自然科学版) 第42卷授的指导,在此表示感谢!参考文献:[1] 刘镇清.圆管中超声导波[J].无损检测,1999,21(12):5602562.[2] Alleyne D N.Lowe M J S,Cawley P.The reflection of guided waves from circumferential notches in pipes[J].T rans A S M E J of A ppl Mech,1998,65:6352641.[3] Bai H,Shah A H,Popplewell N.Scattering of guided waves by circumferential cracks in steel pipes[J].T ransA S M E J of A ppl Mech,2001,68(4):6192631.[4] Alleyne D N,Cawley P,Lank A M,et al.The Lamb wave inspection of chemical plant pipework[J].Reviewof Progress in Quantitation ND E,1997,16(A):126921276.[5] Wilcox P D,Lowe M J S,Cawley P.Long range lamb wave inspection:The effect of dispersion and modal selec2tivity[J].Review of Progress in Quantitative ND E,1999,18(A):1512158.[6] Ditri J,Rose J L,Chen G.Mode selection cirteria for defect detection optimization using Lamb waves[J].Re2view of Progress in Quantitative ND E,1992,11(B):210922115.[7] 他得安,刘镇清,田光春.超声导波在管材中的传播特性[J].声学技术,2001,20(3):1312134.[8] G azis D C.Three2dimensional investigation of the propagation of waves in hollow circular cylinders[J].J A2coust Soc A m,1959,31(5):5682573.[9] Lowe M J S.Matrix techniques for modeling ultrasonic waves in mutilayered media[J].I EEE T rans on U F2FC,1995,42:5252542.[10] 奚定平.贝塞尔函数[M].北京:高等教育出版社;德国:Springer2Verlag Berlin Heidelberg,1998.附录:B essel函数及各参数的选择C p>C l C l>C p>C t C l>C t>C pk l=k2l k l=-k2l k l=-k2lk t=k2t k t=k2t k t=-k2tγ=1γ1=-1γ1=-11γ=1γ2=1γ2=-12Z n(k l r)=J n(k l r)Z n(k l r)=I n(k l r)Z n(k l r)=I n(k l r)W n(k l r)=Y n(k l r)W n(k l r)=K n(k l r)W n(k l r)=K n(k l r)Z n(k t r)=J n(k t r)Z n(k t r)=J n(k t r)Z n(k t r)=I n(k t r)W n(k t r)=Y n(k t r)W n(k t r)=Y n(k t r)W n(k t r)=K n(k t r) 其中Z n表示向内的Bessel函数,代替J n,I n;W n表示向外的Bessel函数,代替Y n,K n.R elationship Bet w een DispersiveCharacteristics of Ultrasonic G uided Waves and Inner2radius2thickness R atio of PipesT A De2an1,LI U Zhen2qing2(1.Depart ment of Elect ronic Engineering,Fudan U niversity,S hanghai200433,China;2.Institute of Acoustics,Tongji U niversity,S hanghai200092,China)Abstract:The influence of inner2radius2thickness ratio on the dispersive characteristics of guided waves for lower in free pipes has been analyzed.The results show that the dispersive characteristics of ultrasonic guided waves in pipes are re2 lated to Inner2Radius2Thickness Ratio(IRTR)of pipes.When IRTR and frequency2thickness product are small,the change of IRTR has a great influence on the dispersive characteristics of lower guided waves,while with the increase of IRTR and frequency2thickness product,the influence of IRTR on guided waves will be reduced.On the other hand,the influence of IRTR on guided waves will be reduced with the increase of the order of guided waves.K eyw ords:ultrasonic guided waves;dispersive characteristics;pipes;inner2radius2thickness ratio～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～(上接第6页)Performance Degradation and Damage Mechanisms of in Service12Cr1MoV Steel PipeCH AO Chen,Y ANG Zhen2guo(Depart ment of M aterial Science,Fudan U niversity,S hanghai200433,China)Abstract:Short2term mechanical tests were conducted for12Cr1MoV steel s pecimens(parent material)taken from an in2service main steam pipe of a power plant.Metallographic examinations and fractographic analyses were carried out for the cut specimens.Creep damage and failure mechanisms of the pipe material at elevated temperature were evaluat2 ed and studied.The results show that(1)the sharp reduction of impact toughness of the in2service material at normal temperature can be attributed to the fast growth of inner microcracks under impact;(2)the mechanisms such as creep cavity accumulating and effective cross2section shrinking of the pipe dominate the process of low strain rate failure;and(3)the degree of enrichment of constituent elements such as Cr and Mn in the grain boundary carbides can be used asa parameter to characterize the damage nucleation,then,to estimate the damage incubation time.K eyw ords:main steam pipe;12Cr1MoV;performance degradation;damage mechanism 31第1期 他得安等:超声导波频散特性与管材内径-壁厚比的关系。
