下载文档原格式
ar模型例题解析AR模型，即自回归模型，常用于时间序列数据的分析和预测。
以下是一个简单的AR模型例题解析：题目：假设我们有一个时间序列数据集，我们想使用AR模型对其进行拟合和预测。
1. 数据准备：首先，我们需要收集或生成一个时间序列数据集。
这个数据集可以来自任何领域，如金融、气象、交通等。
在本例中，我们使用随机数生成一个简单的时间序列数据集。
2. 数据预处理：对数据进行清洗和整理，去除异常值和缺失值。
然后，对数据进行归一化或标准化，使其符合AR模型的假设条件。
3. 模型选择：选择合适的AR模型阶数。
常用的方法有自相关图法、AIC准则、BIC准则等。
在本例中，我们使用自相关图法来确定AR模型的阶数。
4. 模型拟合：使用选定的AR模型阶数，使用最小二乘法或其它优化算法对模型进行拟合。
在本例中，我们使用R语言的“ar”包来进行模型拟合。
5. 模型评估：使用各种评价指标对模型的拟合效果进行评估。
常用的评价指标包括均方误差（MSE）、均方根误差（RMSE）、平均绝对误差（MAE）等。
在本例中，我们使用RMSE来评估模型的拟合效果。
6. 模型预测：使用拟合好的AR模型对未来的数据进行预测。
在本例中，我们使用R语言的“forecast”包来对未来10个时间点的数据进行预测。
7. 结果分析：将预测结果与实际数据进行对比，分析模型的预测精度和适用性。
根据需要，可以对模型进行优化或调整，以提高预测精度。
通过以上步骤，我们可以对时间序列数据集进行AR模型的拟合和预测。
需要注意的是，AR模型适用于平稳时间序列数据的分析和预测。
对于非平稳时间序列数据，可以考虑使用其它模型，如ARIMA模型等。
第3章 单元测验一、单项选择题1. 的阶差分是（ C ）t X k A Bkt t t k X X X -∇=-11kk k t t t k X X X ---∇=∇-∇C D111kk k t t t X X X ---∇=∇-∇1112k k k t t t X X X ----∇=∇-∇2. MA(2)模型，则移动平均部分的特征根是（ A ）121.10.24t t t t X εεε--=-+A ， B ，10.8λ=20.3λ=10.8λ=-20.3λ=C ， D ，10.8λ=-20.3λ=-10.8λ=-20.2λ=3. AR(2)模型，其中，则（ B ） 121.10.24t t t t X X X ε--=-+0.04t D ε=t t EX ε=A B 00.04C D0.140.24. 若零均值平稳序列，其样本ACF 和样本PACF 都呈现拖尾性，则对可能建立（ B{}t X {}t X ）模型。
A. MA(2)B.ARMA(1,1)C.AR(2)D.MA(1) 5. 对于一阶滑动平均模型MA(1): ，则其一阶自相关函数为( C )。
15.0--=t t te e Y A. B. C. D. 5.0-25.04.0-8.06. 关于平稳时间序列模型，说法正确的是（ B ）A. 可以对未来很长一段时间的序列值进行精确预测。
B. 当前观测序列时间为t,MA(q)模型对大于t+q 时间点序列值的预测值恒为常数。
C ．自相关系数具有非唯一性，偏自相关系数不具有非唯一性 D ．均值非平稳的序列，可以通过对数变换将其变成平稳的。
二、多项选择题1. 关于延迟算子的性质，下列表示中正确的有 ( AD )A B10=B n-=（1-）tt n tx x B x -C∑=-=-ni n in nnB C B 0)1()1(D 对任意两个序列和，有{}t x {}t y 11()t t t t B x y x y --+=+2. ARMA 模型可逆性条件是（ CD ）A 的特征根都在单位圆内B 的根都在单位圆内 （）0t B εΦ=（）0B Θ=C 的特征根都在单位圆内D 的根都在单位圆外 0=Θt B ε）（（）0B Θ=3. 关于平稳可逆的ARMA 模型的序列预测问题，下列公式正确的有（ ABCD ）A12(|,,,)(0)t l t t t t lE x x x x x l +--+=≤ B12ˆ(|,,,)()(0)t l t t t t E x x x x xl l +--=>C 12(|,,,)(0)t l t t t t lE x x x l εε+--+=≤ D12(|,,,)0(0)t l t t t E x x x l ε+--=> 4. 对平稳时间序列模型矩估计方法评价正确的是 （ BCD ）A 估计精度高B 估计思想简单直观C 不需要假设总体分布D 计算量小5. 下列属于模型优化方法的有（ ABC ）A 残差方差图定阶法B F 检验定阶法C 最佳准则函数定阶法D 最小二乘估计法 6. 下列关于说法正确的是（ ABCDE ） A AR 模型总是可逆的B 平稳MA 模型的均值就等于模型的截距项参数C 偏自相关系数用来描述时间序列值间的直接影响D 只要ARMA 模型的AR 部分的系数的绝对值和小于1，该模型一定平稳。
课程名称：__ 时间序列分析 __ 实验项目：__ AR模型 ____ ___ 实验类型：__ 验证型________ ___ 学生学号：__ 徐洁洁 ____ 学生姓名：__ 2012962006 学生班级：_ 统计学______ _____ 课程教师：__ 范英兵______ _____ 实验日期：_______ 2014年9月28日_ ____
图2 我国1959年-2012年年末总人口相关图
中可以看出，我国年末总人口y一直保持明显的增长趋势；从图
相关系数递减到零的速度相当缓慢，在这段很长的延迟期里自相关系数一直为正，而后又一直为负，显示出明显的三角对称性，这是具有单调趋势的非平稳序列的一种典型的自相关形式此，基于以上情况分析可以初步判断该序列是非平稳的.
图4 y的一阶差分相关图
的一阶差分序列后期大致在1000的附近波动；从图
的一阶差分序列具有很强的短期相关性. 因此，基于以上情况分析可以初步判断一阶差分后的）根据平稳序列的自相关函数和偏自相关函数确定模型类型
注：验证性实验仅上交电子文档，设计性试验需要同时上交电子与纸质文档进行备份存档。
ARMAARIMA模型介绍及案例分析AR、MA和ARIMA是时间序列分析中常见的模型，用于分析和预测时间序列数据的特征和趋势。
下面将对这三种模型进行介绍，并提供一个案例分析来展示它们的应用。
自回归模型（AR）是一种基于过去的观测值来预测未来观测值的模型。
它基于一个假设：未来的观测值可以由过去的观测值的线性组合来表示。
AR模型的一般形式可以表示为：y_t=c+ϕ_1*y_(t-1)+ϕ_2*y_(t-2)+...+ϕ_p*y_(t-p)+ε_t其中，y_t表示时间t的观测值，c是常数项，ϕ_1至ϕ_p是自回归系数，p是自回归阶数，ε_t是误差项。
AR模型的关键是确定自回归阶数p和自回归系数ϕ。
移动平均模型（MA）是一种基于过去的误差项来预测未来观测值的模型。
它基于一个假设：未来的观测值的误差项可以由过去的误差项的线性组合来表示。
MA模型的一般形式可以表示为：y_t=c+ε_t+θ_1*ε_(t-1)+θ_2*ε_(t-2)+...+θ_q*ε_(t-q)其中，y_t表示时间t的观测值，c是常数项，ε_t是误差项，θ_1至θ_q是移动平均系数，q是移动平均阶数。
MA模型的关键是确定移动平均阶数q和移动平均系数θ。
自回归移动平均模型（ARIMA）结合了AR和MA模型的特点，同时考虑了时间序列数据的趋势性。
ARIMA模型一般形式可以表示为：y_t=c+ϕ_1*y_(t-1)+ϕ_2*y_(t-2)+...+ϕ_p*y_(t-p)+ε_t+θ_1*ε_(t-1)+θ_2*ε_(t-2)+...+θ_q*ε_(t-q)其中，y_t表示时间t的观测值，c是常数项，ϕ_1至ϕ_p是自回归系数，p是自回归阶数，ε_t是误差项，θ_1至θ_q是移动平均系数，q是移动平均阶数。
ARIMA模型的关键是确定自回归阶数p、移动平均阶数q和相关系数ϕ和θ。
下面举一个电力消耗预测的案例来展示AR、MA和ARIMA模型的应用：假设有一段时间内的电力消耗数据，我们想要用AR、MA和ARIMA模型来预测未来一段时间内的电力消耗。
第三次试验报告一、实验目的：根据AR模型、MA模型所学知识,利用R语言对数据进行AR、MA模型分析，得出实验结果并对数据进行一些判断，选择最优模型。
二、实验要求：三、实验步骤及结果：⑴建立新的文件夹以及R-project，将所需数据移入该文件夹中。
⑵根据要求编写代码，如下所示：为例）代码及说明：（以r t2⑶实验结果及相关说明：时间序列1；1.确定模型①时序图（TS图）：由图可知：该时间序列可能具有平稳性，均值在0附近。
②自相关函数图（ACF图）：由图可知：很快减小为0（q=0）2.定阶③偏相关函数（PACF图）由图可知，PACF图0步结尾。
3.参数估计：4. 模型诊断：（法一）利用tsdiag(fit1) 函数进行整体检验：对模型诊断得出下面一组图，每组包含三个小图：i第一个小图为标准化残差图，是ât/σ所得。
模型图看不出明显规律。
ii第二个小图为残差ât的自相关函数图，是单个ρk是否等于0的假设检验。
（蓝线置信区间内都可认为是0）可知：模型中单个ρk都等于0假设成立。
iii第三个小图为前m个ρk同时为0的L-B假设检验。
则由模型图知：在95%置信区间下认为ât为白噪声，模型充分性得到验证。
（法二）利用Box-Ljung test 进行检验：5. 拟合优度检验：①调整后R2：Adj-R2=1 - σ̂a2/σ̂r2②信噪比: SNR=σ̂r2/σ̂a2=[1/(1- Adj-R2)]-1由结果可知：Adj-R2= 0.001428571;信噪比SNR= 0.001430615;即由Adj-R2=14.28571% 较低，说明说明信号占整体数据信息比例较小，模型拟合效果不够好。
由SNR可知，噪音约为信号700倍，模型效果非常不好。
6. 预测：时间序列2：1.确定模型①时序图（TS图）：由图可知：该时间序列具有平稳性。
②自相关函数图（ACF图）：由图可知：很快减小为0，并呈周期性、指数衰减,并且3步结尾。
正态ar模型和偏态ar模型正态AR模型和偏态AR模型是时间序列分析中常见的模型，它们能够对数据进行建模和预测，并在实际应用中发挥重要作用。
下面是对这两种模型的生动、全面和有指导意义的介绍。
正态AR模型是指在时间序列分析中，如果数据的分布近似服从正态分布，则可以使用正态AR模型来建模。
也就是说，数据中的每个观测值都是由该观测值的前一期值以及一些随机误差项所决定的。
正态AR模型通常用AR(p)表示，其中的(p)代表模型的阶数，表示当前观测值与前p个观测值之间的关系。
正态AR模型的预测基于过去的观测值，使得我们能够根据现有信息来预测未来的值。
正态AR模型假设数据的误差项满足独立同分布的正态分布，这意味着模型的残差在均值为0的情况下呈现出高斯分布。
正态AR模型虽然能够对许多现实世界的数据进行较好的拟合和预测，但是它的一个主要限制是对数据的分布有较强的假设要求。
如果数据的分布偏离了正态分布，那么正态AR模型可能无法很好地拟合数据并进行准确的预测。
偏态AR模型是指在时间序列分析中，数据的分布存在明显的偏态时，可以使用偏态AR模型来建模。
偏态AR模型考虑了数据的非正态性，可以更好地拟合和预测非正态分布的数据。
偏态AR模型通常用ARMA(p,q)表示，其中的(p)和(q)代表模型的阶数，表示当前观测值与前p个观测值和前q个误差值之间的关系。
偏态AR模型的预测仍然是基于过去的观测值，但是它还考虑了误差项的偏态性质，使得预测更加准确。
另外，如果数据的偏态性较为显著，可以使用非线性模型进行建模，如偏态ARIMA模型。
偏态ARIMA模型是在偏态AR模型的基础上引入了移动平均项，以进一步提高模型的准确性。
偏态ARIMA模型的预测除了考虑过去的观测值和误差项，还考虑了移动平均项的影响，从而能够更好地适应偏态分布的数据。
综上所述，正态AR模型和偏态AR模型是时间序列分析中常用的模型，它们分别适用于数据近似服从正态分布和存在明显偏态的情况。
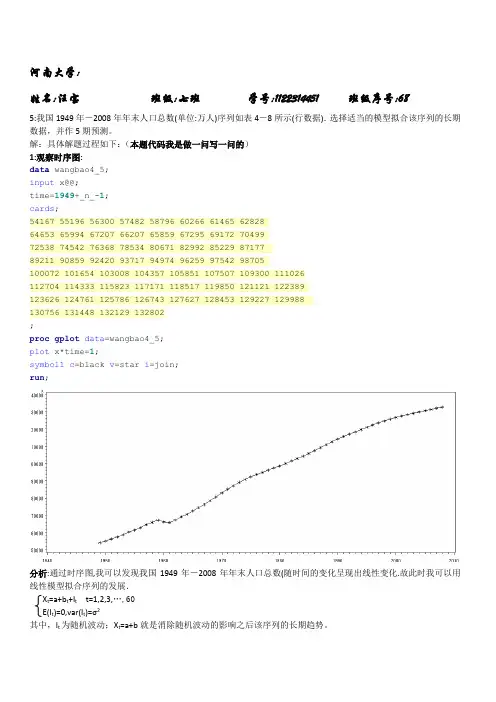
河南大学:姓名:汪宝班级:七班学号:1122314451 班级序号:685:我国1949年－2008年年末人口总数(单位:万人)序列如表4－8所示(行数据)．选择适当的模型拟合该序列的长期数据，并作5期预测。
解：具体解题过程如下：（本题代码我是做一问写一问的）1:观察时序图:data wangbao4_5;input x@@;time=1949+_n_-1;cards;54167 55196 56300 57482 58796 60266 61465 6282864653 65994 67207 66207 65859 67295 69172 7049972538 74542 76368 78534 80671 82992 85229 8717789211 90859 92420 93717 94974 96259 97542 98705100072 101654 103008 104357 105851 107507 109300 111026112704 114333 115823 117171 118517 119850 121121 122389123626 124761 125786 126743 127627 128453 129227 129988130756 131448 132129 132802;proc gplot data=wangbao4_5;plot x*time=1;symbol1c=black v=star i=join;run;分析:通过时序图,我可以发现我国1949年－2008年年末人口总数(随时间的变化呈现出线性变化.故此时我可以用线性模型拟合序列的发展．X t=a+b t+I t t=1,2,3,…,60E(I t)=0,var(I t)=σ2其中，I t为随机波动；X t=a+b就是消除随机波动的影响之后该序列的长期趋势。
2:进行线性模型拟合：proc autoreg data=wangbao4_5;model x=time;output out=out p=wangbao4_5_cup;run;proc gplot data=out;plot x*time=1 wangbao4_5_cup*time=2/overlay ;symbol2c=red v=none i=join w=2l=3;run;分析：由上面输出结果可知：两个参数的p值明显小于0.05，即这两个参数都是具有显著非零，4：模型检验又因为Regress R-square=total R-square=0.9931,即拟合度达到99.31%所以用这个模型拟合的非常好。
实验报告报告题目：ＡＲ模型拟合课程名称：应用时间序列分析专业：统计学年级：统计１２１学号：65学生姓名：***指导教师：**学院：理学院实验时间：2015年5月２６日学生实验室守则一、按教学安排准时到实验室上实验课，不得迟到、早退和旷课。
二、进入实验室必须遵守实验室的各项规章制度，保持室内安静、整洁，不准在室内打闹、喧哗、吸烟、吃食物、随地吐痰、乱扔杂物，不准做与实验内容无关的事，非实验用品一律不准带进实验室。
三、实验前必须做好预习（或按要求写好预习报告），未做预习者不准参加实验。
四、实验必须服从教师的安排和指导，认真按规程操作，未经教师允许不得擅自动用仪器设备，特别是与本实验无关的仪器设备和设施，如擅自动用或违反操作规程造成损坏，应按规定赔偿，严重者给予纪律处分。
五、实验中要节约水、电、气及其它消耗材料。
六、细心观察、如实记录实验现象和结果，不得抄袭或随意更改原始记录和数据，不得擅离操作岗位和干扰他人实验。
七、使用易燃、易爆、腐蚀性、有毒有害物品或接触带电设备进行实验，应特别注意规范操作，注意防护；若发生意外，要保持冷静，并及时向指导教师和管理人员报告，不得自行处理。
仪器设备发生故障和损坏，应立即停止实验，并主动向指导教师报告，不得自行拆卸查看和拼装。
八、实验完毕，应清理好实验仪器设备并放回原位，清扫好实验现场，经指导教师检查认可并将实验记录交指导教师检查签字后方可离去。
九、无故不参加实验者，应写出检查，提出申请并缴纳相应的实验费及材料消耗费，经批准后，方可补做。
十、自选实验，应事先预约，拟订出实验方案，经实验室主任同意后，在指导教师或实验技术人员的指导下进行。
十一、实验室内一切物品未经允许严禁带出室外，确需带出，必须经过批准并办理手续。
目录第一部分：实验（或算法）原理 ..................... 错误!未定义书签。
第二部分：实验步骤....................................... 错误!未定义书签。
(p)模型的参数估计 ........................... 错误!未定义书签。
2. AR(p)模型参数的最小二乘估计 ... 错误!未定义书签。
3. AR(p)模型的定阶........................... 错误!未定义书签。
4.拟合模型的检验............................. 错误!未定义书签。
第三部分：算法实例与讲解 ....................... 错误!未定义书签。
讲解 ....................................................... 错误!未定义书签。
模型评价 ............................................... 错误!未定义书签。
第四部分：优点与限制................................... 错误!未定义书签。
第五部分：参考文献....................................... 错误!未定义书签。
第一部分：实验（或算法）原理自回归模型（英语：Autoregressive model ，简称AR 模型），是统计上一种处理时间序列的方法，用同一变量例如x 的之前各期，亦即x_{1}至x_{t-1}来预测本期x_{t}的表现，并假设它们为一线性关系。
因为这是从回归分析中的线性回归发展而来，只是不用x 预测y ，而是用x 预测x （自己）；所以叫做自回归。
其中：是常数项；被假设为平均数等于0，标准差等于的随机误差值；被假设为对于任何的都不变。
文字叙述为：的当期值等于一个或数个落后期的线性组合，加常数项，加随机误差。
第二部分：实验步骤如果时间序列 }{t X 是平稳AR 序列，根据此序列的一段有限样本值 n x x x ,,,21 对}{t X 的模型进行统计，称为自回归模型拟合自回归模型拟合主要包括： (1) 判断自回归模型AR 的阶数； (2) 估计模型的参数； (3) 对拟合模型进行检验。
(p)模型的参数估计目的：为观测数据建立AR(p)模型t p t p t t t X X X X εααα++++=--- 2211假定自回归阶数p 已知，考虑回归系数Tp ),,(1αα =α和零均值白噪声}{t ε的方差2σ的估计。
数据n x x x ,,,21 的预处理：如果样本均值不为零，需将它们中心化，即将它们都同时减去其样本均值∑==nt t n x n x 1/1，再对序列按式的拟合方法进行拟合。
对于AR(p)模型，自回归系数α由AR(p)序列的自协方差函数 p r r r ,,,10 通过Yule-Walker 方程⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----p p p p p p a a a r r r r r r r r r r r r 2102120111021 唯一决定，白噪声方差 2σ 由j pjj r r ∑=-=102ασ决定。
实际应用中，对于较大的p,为了加快计算速度可采用如下的Levison递推方法⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧≤≤≤-=--=-===-++++==--++++-∑∑p k k j a a a aa r r a r r a r a r k j k k k k j k j k j k j k j j k j j k k k k k k k k ,1ˆˆˆˆ)ˆˆˆ)(ˆˆˆ(ˆ)ˆ1(ˆˆˆ/ˆˆˆˆ,11,1,1,111,0,111,12,21220111020ασσσσ 递推最后得到矩估计22,2,1,1ˆˆ,)ˆ,,ˆ,ˆ()ˆ,,ˆ(pT p p p p T p a a a σσαα== 上式是由求偏相关函数的公式：⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----kk k k k k k k k a a a2121211121111ρρρρρρρρρ 导出。
2. AR(p)模型参数的最小二乘估计如果 p αααˆ,ˆ,ˆ21 是自回归系数 p ααα,,,21 的估计，白噪声j ε 的估计计定义为n j p x x x x p j p j j j j ≤≤++++-=---1),ˆˆˆ(ˆ2211αααε 通常n j p j ≤≤+1,ˆε为残差。
我们把能使∑+=-------=npj p t p t t t x x x x s 122211}{)(ααα α达到极小值的 αˆ称为α的最小二乘估计。
相应地，白噪声方差 2σ 的最小二乘估计∑+=-------=--=-=npt p t p t t T T T T x x x pn p n s p n 121112)ˆˆ(1))((1)ˆ(1ˆαασ y x x x x y y y α式中p αααˆ,ˆ,ˆ21 为αˆ的p 个分量。
3. AR(p)模型的定阶 偏相关函数的分析方法：一个平稳序列是AR(p)序列当且仅当它的偏相关函数是p 步截尾的。
如果}ˆ{,k k ap 步截尾：当 p k ˆ> 时， 0ˆ,≈k k a ； 而 0ˆˆ,ˆ≠p p a ，就以p ˆ作为p 的估计。
4.拟合模型的检验现有数据 n x x x ,,,21 ，欲判断它们是否符合以下模型 2,1,2211++=++++=---p p t X X X X t p t p t t t εααα 式中 }{t ε 被假定为独立序列,且∞<==422,,0t t t E E E εσεε t ε 与},{t s X s < 独立。
原假设 0H ：数据n x x x ,,,21 符合AR(p)。
故在 0H 成立时，下列序列n p t X X X X p t p t t t t ,,1,2211 +=----=---αααε为独立序列 }{t ε 的一段样本值序列。
步骤：1. 首先，根据公式2,1,0),(ˆ/)(ˆ)(ˆ2,1,0,1)(ˆ01===-=∑--=+++k r r k pn r k k kp n tkp t p t kεεερεεε计算出残差的样本自相关函数，2. 利用上一章关于独立序列的判别方法，判断 n p εε,,1 +是否为独立序列的样本值3. 根据判断结果，如果接受它们为独立序列的样本值，则接受原假设，即接受n x x x ,,,21 符合AR(p),否则，应当考虑采用新的模型拟合原始数据序列。
第三部分： 算法实例与讲解下表为某地历年税收数据（单位亿元）。
使用AR（p）预测税收收入，讲解因为税收具有一定的稳定性和增长性，且与前几年的税收具有一定的关联性，因此可以采用时间序列方法对税收的增长建立预测模型。
下面为使用MATLAB 建立模型并求解过程clc, cleara=[58 ];a=a'; a=a(:); a=a'; %把原始数据按照时间顺序展开成一个行向量Rt=tiedrank(a) %求原始时间序列的秩n=length(a); t=1:n;Qs=1-6/(n*(n^2-1))*sum((t-Rt).^2) %计算Qs的值t=Qs*sqrt(n-2)/sqrt(1-Qs^2) %计算T统计量的值t_0=tinv,n-2) %计算上alpha/2分位数e=[1:13];b=diff(a) %求原始时间序列的一阶差分% plot(e,b,'*');m=ar(b,2,'ls') %利用最小二乘法估计模型的参数bhat=predict(m,[b'; 0],1) %1步预测，样本数据必须为列向量,要预测1个值，b后要加1个任意数，1步预测数据使用到t-1步的数据ahat=[a(1),a+bhat{1}'] %求原始数据的预测值，并计算t=15的预测值delta=abs((ahat(1:end-1)-a)./a) %计算原始数据预测的相对误差plot(a,'b');hold onplot(ahat,'r');grid ontitle('历史数据-蓝色线；预测数据-红色线')模型评价由于本案例哄第t年税收的值与前若干年的值之间具有较高的相关性，所以采用了AR模型，在其他情况下，也可以采用MA模型或者ARMA模型等其他时间序列方法。
另外，还可以考虑投资、生产、分配结构、税收政策等诸多因素对于税收收入的影响，采用多元时间序列分析方法建模关系模型，从而改善税收预测模型，提高预测质量。
第四部分：优点与限制自回归方法的优点是所需资料不多，可用自身变量数列来进行预测。
