当前位置：文档之家 › 物理化学讲稿02(热力学第二定律)

物理化学讲稿02(热力学第二定律)

  • 格式：pdf
  • 大小：437.79 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

物理化学02章_热力学第二定律01

物理化学02章_热力学第二定律01
V2 V3 相除得 V1 V4
热机效率(efficiency of the engine )
任何热机从高温 (Th ) 热源吸热 Qh ,一部分转化 为功W,另一部分Qc 传给低温 (Tc ) 热源.将热机所作 的功与所吸的热之比值称为热机效率,或称为热机 转换系数，用 表示。 恒小于1。
任意可逆循环的热温商
任意可逆循环热温商的加和等于零,即：
Qi )R 0 ( i Ti
或
Q ( T )R 0
证明如下：(1)在如图所示的任意可逆 循环的曲线上取很靠近的PQ过程； (2)通过P，Q点分别作RS和TU两条可逆绝热膨胀线， (3)在P，Q之间通过O点作等温可逆膨胀线VW，使两个 三角形PVO和OWQ的面积相等， 这样使PQ过程与PVOWQ过程所作的功相同。 同理，对MN过程作相同处理，使MXO’YN折线所经过程 作的功与MN过程相同。VWYX就构成了一个卡诺循环。
2.3 卡诺循环与卡诺定理
•卡诺循环 •热机效率 •冷冻系数 •卡诺定理
卡诺循环（Carnot cycle）
1824 年，法国工程师 N.L.S.Carnot (1796~1832)设 计了一个循环，以理想气体
为工作物质，从高温h ) 热源 (T
Qh 吸收 Qc 一部分
的热量，一部分通过 的热量放给低温c ) (T
熵的引出
用一闭合曲线代表任意可逆循环。 在曲线上任意取A，B两点，把循环分成AB和 BA两个可逆过程。
根据任意可逆循环热温商的公式：
Q ( T )R 0
可分成两项的加和
A Q Q A ( T )R1 B ( T )R2 0 B
熵的引出
移项得：
B Q Q A ( T )R1 A ( T )R2 B

物理化学第2章 热力学第二定律

物理化学第2章 热力学第二定律
BSm$ (B)
§3.7 熵变的计算
一、单纯状态变化过程
1. 等温过程 2.变温过程
S QR T
①等容变温过程
S T2 Qr T2 nCp,mdT
T T1
T1
T
nC
p,m
ln
T2 T1
②等压变温过程
S T2 Qr T T1
T2 nCV ,mdT
T1
T
nCV
,m
ln
T2 T1
U3 0
p
W3
nRTc
ln V4 V3
A(p1,V1,Th )
B(p2,V2,Th )
Th
Qc W3
D(p4,V4,TC )
C(p3,V3,TC )
Tc
环境对系统所作功如 DC曲线下的面积所示
a db
c
V
过程4：绝热可逆压缩 D( p4,V4,TC ) A( p1,V1,Th )
Q4 0
p
用一闭合曲线代表任意可逆循环。 在曲线上任意取A，B两点，把循环分成AB和 BA两个可逆过程。 根据任意可逆循环热温商的公式：
δ Q
T R
0
将上式分成两项的加和
B Q
( AT
)R1
A Q
( BT
)R2
0
移项得：
B A
(
Q T
)R1
B A
(
Q T
)R
2
说明任意可逆过程的热温商的值决定于始终 状态，而与可逆途径无关，这个热温商具有状态 函数的性质。
所以Clausius 不等式为
dS 0
等号表示绝热可逆过程，不等号表示绝热不
可逆过程。
熵增加原理可表述为：

物理化学(第五版) 演示文稿2.2 热力学第二定律概述

物理化学(第五版) 演示文稿2.2 热力学第二定律概述

瓦特改进、发明的蒸汽机
“它武装了全人类，使虚弱无力的双手变得力大无穷，健全了 人类的大脑以处理一切难题。它为机械动力在未来创造奇迹打 下了坚实的基础，将有助并报偿后代的劳动。”
2
已经意识到蒸气机工作需要两个不同温度的热源
高温热源T1 Q1
热机
-W=Q1+Q2
Q2
低温热源T2
图 1 热机示意图
热机效率： def W Q1 Q2
（2）理想气体等温可逆膨胀：系统从单一 热源吸的热全部为对环境做的功，但是系统 的状态世纪初，热机效率极低， 热利用率η<5%，人们希望从 理论上找出提高η的办法。
1824年，卡诺设计了一个 理想循环过程。从循环过程 的热功转换情况，得出可逆 热机效率（极限），为人们
提供了提高的方向和限度。
3
二、热力学第二定律的经典表述
①克劳修斯说法(1850)（热传导的不可逆性） 不可能把热由低温物体转移到高温物体， 而不留下其他变化。
②开尔文说法(1851)（热功转换的不可逆性） 不可能从单一热源吸热使之完全变为功， 而不留下其他变化。
Clausius
(1822-1888)
③第二类永动机是不可能造成的。
Lord Kelvin (1824-1907)
现代热力学之父
应明确:
（1）致冷机：热从低温物体高温物体， 但是环境消耗了能量(电能)；
§2-2 热力学第二定律概述
一、热机效率
瓦特改进、发明的蒸汽机对近代科学和生产贡献 巨大，具有划时代的意义，它导致了第一次工业技术 革命的兴起，极大的推进了社会生产力的发展。
James Watt
（1736-1819）
1801年，英国人理查 ·特 里 维 西 克 制 成 了 “伦敦蒸汽马车”， 它是最早的载人蒸汽 车辆之一，也是第一 辆真正投入市场的蒸 汽机车辆，能乘坐6 人，最高速度27公里 /时。

物理化学02章_热力学第二定律02

物理化学02章_热力学第二定律02

S体系
Qr Qsurr Qsys Q Δ S环 = = = Tsurr Tsurr Tsurr T
Δ S 总 =Δ S 体 + Δ S 环 ≥ 0
上一讲回顾
(1) 熵变的计算： 可逆过程，直接计算过程的热温商 不可逆过程，设计可逆过程计算。 (2) 等温过程,变温过程及相变过程熵变的计算 (3) 利用熵变判断过程的方向
a）恒 T 可逆 b）恒 T 不可逆 V2 V2 V2 Δ S 总 = nRTLn +(-nRLn ） Δ S 总 = nRTLn + 0 V1 V1 V1
= 0
V2 = nRTLn > 0 V1
等温过程的熵变
例： 1mol理想气体在等温下通过：(1)可逆膨胀，(2)真 空膨胀，体积增加到10倍，分别求其熵变。 解：（1）可逆膨胀
简化：
V2 P2 等 T：Δ S= nRLn =- nRLn V1 P1 T2 等 P：Δ S= CP Ln T1
T2 等 V：Δ S= CV Ln T1
变温过程的熵变
1. 先等温后等容 2. 先等温后等压 3. 先等压后等容
T2 nCV ,m dT V2 S nR ln( ) T1 V1 T T2 nC p ,m dT p1 S nR ln( ) T1 p2 T V2 p2 S nC p ,m ln( ) nCV ,m ln( ) V1 p1
S T
T2
1
nCV ,m dT T
(2) 物质的量一定的等压变温过程
S T
T2
1
nC p ,m dT T
等 P 过程：
W`=0， QP = dH = CPdT = QR
QR QP C P dT dS = = = T T T CP S )P 或 ( T T

第二章 热力学第二定律 物理化学课件

第二章 热力学第二定律 物理化学课件

设始、终态A，B的熵分别为SA 和 SB，则：
SB SA S
B Qr AT
对微小变化
dS Qr
T
上式习惯上称为熵的定义式，即熵的变化值可 用可逆过程的热温商值来衡量。
2 不可逆过程的热温商
• 如果热机进行不可逆循环，则其效率必 然比卡诺循环效率低，即
Q1 Q2 Q1
T1
T 2
T1
或
1+
T K
2
dT T
J K-1
24.3J K-1
• 此过程热温商为
Q
T
2
373 K 273 K
32.22
22.18 103
T K
373
3.49
106
• 故开动此致冷机所需之功率为
1780
1 60
W
50%=59.3
W
§2.4 熵的概念
• 1 可逆过程的热温商及熵函数的引出
• 在卡诺循环中，两个热源的热温商之和 等于零，即
Q1 Q2 QB 0
T1 T2
TB
• 那么，任意可逆循环过程的多个热源的 热温商之和是否仍然等于零?
§2.4 熵的概念
S Qr Qr TT
• 对理想气体定温可逆过程来说 Qr=-Wr
nRT ln V2
S
V1 nR ln V2 nR ln p1
T
V1
p2
例题3
• (1) 在300K时，5mol的某理想气体由 10dm3定温可逆膨胀到100dm3。计算此过 程中系统的熵变；
• (2)上述气体在300K时由10dm3向真空膨 胀变为100dm3。试计算此时系统的S。 并与热温商作比较。
Q1

物理化学2_热力学第二定律

物理化学2_热力学第二定律

∆S = ∫
T2
T1
nCV.m dT T
2．等压变温 δQR = nC p ,m dT
∆S = ∫
T2
nC p.m T
T1
dT
3．理想气体状态变化（仅有体积功 WR = −∫ p外dV = − pdV ）
δQR＝dU－δWR = dU + pdV = nCV,m dT + nRT
于是
dV V
∆S = ∫
Zn+CuSO 4 (aq)
ZnSO 4(aq)+Cu ∆H m *= -216.8 kJ mol -1
热力学第二定律所要解决的问题是寻找一个在一定条件下的过程进行的共 同判据----普遍适用的判据。 这个判据一定是体系的状态函数。它的改变值反映在一定条件下过程的方向 性。 一热力学第二定律的表述 (Expression of Second Law of Thermodynamics) 1824 年 Carnot 认为热机必须在两个热源间工作，从高温热源吸热只有部分 作功，而其余部分传给低温热源。 ＊ 1850 年克劳修斯（R.Clausius）: 不可能把热从低温物体传到高温物体而不产生其他影响。 ＊ 1851 年开尔文（Kelvin） ： 不可能从单一热源吸取热量使之完全转化为功而不引起其他变化。 热力学第二定律的确立，证明第二类永动机是不可造出的。第二类永动机： 一种能够从单一热源吸热，并将所吸收的热全部变为功而无其他影响的机器 （Second Kind of permanent motion machine） 上述两种表达方法是完全有效的。 设有一部违反 Kelvin 热机 A 和制冷机 B 联合工作，如下图：
高温热源T2
高温热源 T2
W =Q2 Q2 B Q1

《物理化学》02章_热力学第二定律

W(总) = －Q(总) = Q2 + Q1
V2 V4 nRT2 ln nRT1 ln V1 V3
V2 V4 nRT2 ln nRT1 ln V1 V3 W 热机效率： V2 Q2 nRT2 ln V1
BC：绝热可逆膨胀，T2 V2-1 = T1 V3-1 DA：绝热可逆压缩， T2 V1-1 = T1 V4-1 两式相除: V2 /V1 =V3 /V4
不违背第一定律的事情是否一定能成功？
例1： 1/2O2(g)+ H2(g) H2O(l)
r H m (298.15 K) =-286KJ.mol-1
加热不能使其反向进行 例2： OH-+ H+H2O(l) 极易进行
但最终[OH-][H+]=10-14mol2.dm-6 该反应不能进行到底
§2.1 自发过程的共同特征
一.自发过程的方向和限度
自发过程:在一定环境条件下,环境不做非体积功,系
统中自动发生的过程.反之,只有环境做非体积功才 能发生的过程为非自发过程.通常所说的”过程方 向” 既是指自发过程的方向. 举例: ①.气流:高压 低压
②.传热:高温
③.扩散:高浓度
低温
低浓度
④.反应:Zn+CuSO4
对微小变化
Q dS ( )R T
B
Q SB SA S ( )R A T
二.热力学第二定律的数学表达式
对两个热源间的不可逆 循环:热温商之和小于零. Q1 T1 Q2 T2
+
＜0
对任意的不可逆 循环:ຫໍສະໝຸດ ∑δQ T1 ir
＜0
对不可逆循环，A
ir
B
r
A

物理化学热力学第二定律


对微小变化
Qr dS T
上式为熵的定义式。 熵的变化必须由可逆过程的热温商求得。
(2) 不可逆过程的热温商
• 如果热机进行不可逆循环，则其效率必然比卡 诺循环效率小，即 Q1 Q2 T2 T Q2 T2
1
• 其中Q表示不可逆过程的热效应。由上式得
Q1* Q2* 0 T1 T2
• 因此，对一任意不可逆循环来说，必有

Q*
T
0
假定一不可逆循环A→B→A，其中A→B为不可 逆过程（标记ir）、B→A为可逆过程（标记r）。
警告：对不可逆过程 A→B (1→2) 不可颠倒积分限。
2 T T 2 Q 2 Q r ir > 1 T 1 T 2 Q > 不可逆 S 1 T = 可逆 Q > 不可逆 dS T = 可逆 1
①A→B 定温可逆膨胀 ②B→C 绝热可逆膨胀 ③C→D 定温可逆压缩 ④D→A 绝热可逆压缩
• 过程①：定温（T2）可逆膨胀 理想气体Δ U= 0, 故 Q2 = -W1 W1 = -RT2*ln(V2/V1) • 过程② ：绝热可逆膨胀 由于绝热 Q= 0, 故ΔU = W2 Δ U= Cv*Δ T = Cv*(T1-T2) • 过程③ ：定温（T1）可逆压缩 理想气体ΔU=0，故 Q1 = -W3 W3 = -RT1*ln(V4/V3) • 过程④ ：绝热可逆压缩 由于绝热 Q= 0, ΔU = W4 ΔU= Cv* ΔT = Cv*(T2-T1)
卡诺定理： 1. 在两个不同温度的热源之间工作的任意 热机，以卡诺热机的效率为最高。 2. 卡诺热机的效率只与两个热源的温度有 关，而与工作物质(水蒸气或其它气体) 无关。

物理化学02热力学第二定律

（或用1.41式推导）
所以：
W
W1
W3

RT2
ln V2 V1

RT1
ln V4 V3

R(T2

T1
)
ln
V2 V1
2019/5/7
21
于是，卡诺热机的热机效率应为：
W

R(T2

T1 )
ln
V2 V1
T2 T1
Q2
RT2
ln
V2 V1
T2
另外： W Q1 Q2 T2 T1
W Q1 Q2
从高温热源取出的热Q2转化为功的比例，称为“热机效率” 号η表尔，即
W
Q2
2019/5/7
20
W W1 W 2W3 W4
•根据绝热可逆过程方程式
过程2： 过程4：
T2V2 1 T1V3 1
T2V1 1 T1V4 1
相除得 V2 V3 V1 V4
孤立系统一旦发生一个不可逆过程，则一定是自发过程。 dS>0
2019/5/7
35
§2.6 熵的物理意义及规定熵的计算(p66)
（1）几率、宏观状态、微观状态 几率，就是指某种事物出现的可能性。
2N
集中到一侧：有序性高；分开：无序性高、混乱度高
2019/5/7
36
由上可知，一种指定的宏观状态可由多种微观状态来实现。 与某一宏观状态相对应的微观状态的数目，称为该宏观状态 的“微观状态数“，也称为这一宏观状态的“热力学几率”， 以符号Ω表示。
但系统体积变大、压力变小了。
2019/5/7
4
自发过程的共同特征 ：
(1) 自发过程单向地朝着平衡。 (2) 自发过程都有作功本领。 (3) 自发过程都是不可逆的。 自发过程方向最后归结为热功转换的方向性

第二章：热力学第二定律(物理化学)

如果是一个隔离系统，环境与系统间既无热 的交换，又无功的交换，则熵增加原理可表述为： 一个隔离系统的熵永不减少。
精选可编辑ppt
31
克劳修斯不等式的意义
克劳修斯不等式引进的不等号，在热力学上可以
作为变化方向与限度的判据。
dS Q T
dSiso 0
“>” 号为不可逆过程 “=” 号为可逆过程
“>” 号为自发过程 “=” 号为处于平衡状态
I < 20% 1度电/1000g煤
高煤耗、高污染（S、N氧化物、粉尘和热污染）
精选可编辑ppt
16
火力发电厂的能量利用
400℃
550℃
ThTC67330055%
Th
673
I < 40% 1度电/500g煤
ThTC82330063%
Th
823
精选可编辑ppt
17
火力发电厂的改造利用
精选可编辑ppt
十九世纪，汤姆荪（Thomsom）和贝塞罗特（Berthlot） 就曾经企图用△H的符号作为化学反应方向的判据。他们认 为自发化学反应的方向总是与放热的方向一致，而吸热反应 是不能自动进行的。虽然这能符合一部分反应，但后来人们 发现有不少吸热反应也能自动进行，如众所周知的水煤气反 应就是一例。这就宣告了此结论的失败。可见，要判断化学 反应的方向，必须另外寻找新的判据。
精选可编辑ppt
4
2.2 自发变化不可逆症结
T1高温热源 Q1
M
W
Q2
T2低温热源
精选可编辑ppt
5
2.3 热力学第二定律（The Second Law of Thermodynamics)
开尔文(Kelvin) ：“不可能从单一热源取出热使之完全 变为功，而不发生其它的变化。”
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

• 三.
相变过程:
• 1. 平衡相变:
S=∫0T(熔) (Cp(s)/T)dT+H熔/T熔+ ∫T(熔)T(沸)(Cp(l)/T)dT+H沸/T沸+ ∫T(沸)T (Cp(g)/T)dT
• G=0 • S=H/T • 2. 非平衡相变: 需设计一可逆过程 • • 求G时尽可能设计等温变压可逆过程.
• 熵判据从原理上虽然可以解决一切自然过程 的方向和限度问题, 但使用起来殊不方便, 为 了热力学判据使用的方便, 人们由熵函数发展 出吉布斯自由能(Gibbs free energy，用于等 压过程方向的判断).
• W:宏观状态拥有的微观运动状态的数量
• k：Boltzmann常数
• W的值愈大，体系混乱程度愈高。 • 熵是体系混乱度的量度。 • 孤立体系的熵只增不减意味着体系 的混乱度只增不减。
3
2014/7/8
• 对于恒温恒压过程: • dS－Q/T≧0 (熵判据) • dU= Q+W Q= dU+pdV-Wf • dS－dU/T－pdV/T+Wf/T≧0 两边同乘以T • TdS－dU－pdV≧-Wf • d(TS)－dU－d(pV) ≧ -Wf ∵dT=0 dp=0 • •
理想气体,等容过程 理想气体,等压过程
• 对于只涉及处于内部平衡态之纯物质的等温 过程, 其熵变随温度同趋于零.
• 物质在绝对零度附近时, 许多性质将发生根本性的变化:
• 热胀系数趋于零 • 等压热容与等容热容将相同 • 物质的热容在绝对零度时将趋于零
等压变温
• 由热力学第三定律所求得的物质的熵称为规定熵. • 以前曾将规定熵称为绝对熵, 对考虑到人们对自然的认识是有 限的, 随着科学的发展, 人类可能对熵有更深刻地认识, 故改称 为规定熵. • 规定熵可用热化学方法测定得到, 也可由统计热力学理论直接 计算得到. 规定熵的求算方法为: • S=∫0T Q/T • =∫0T (Cp/T)dT (2) • 上式表明 , 只要获得物质从 0K开始的等压热容的数据即可得 到物质的熵. 若物质在0～T温度区间有相的变化, 则需要将相 变的熵变加和进去. 如气体的熵可由下式求得: •
吉布斯自由能变化与化学反应
化学反应均在恒温恒压下进行 , 因而只要 求算某化学反应的吉布斯自由能的变化。 吉布斯自由能在化学领域中具有极其广泛 的应用，即可由其数值的符号来判断反应的方 向和限度。 对于恒温恒压的可逆过程: (dT=0, dp=0) G=Wf 对于电化学反应过程, 可由G求出电池电动势: G=－nFEr
多组分体系热力学
H2O(g), 298K 760mmHg
G
H2O(l), 298K 760mmHg
一. 偏摩尔量(partial molar quantity): 物质的纯组分的性质与当其与其它物质形 成溶液等多组分体系时, 有许多性质会发生变 化. 如体积等. 例如:50ml的水和50ml的乙醇混 合, 溶液的体积不是简单的加和, 而只有约96ml.
• 实际体系不可能为真正的绝热体系或孤 立体系, 但若将环境的熵变也一起考虑, 体系加环境可视为孤立体系, 所以有: •
理想溶液的混合过程
返回
(dS)体系+(dS)环境≧0 (S)环境=－Q实/T环
返回
• 环境熵变的计算公式: •
• 熵的微观意义（Boltzmann 熵定理 ）： •
S=klnW
吉布斯自由能
• 在相同高温热源(T2)和低温热源(T1)间工作的热 机,其效率不可能超过卡诺热机,且所有可逆热机 的效率()均相等,为:
大脑的功率
• The total energy consumption of the brain is about 25 watts *.
* Principles of Neural Science, by Eric R. Kandel and James H. Schwartz, 2nd edition, Elsevier, 1985.
18-25岁基础代谢率最高 25岁以后，基础代谢率每十年约下降5-10% 五十岁时，基础代谢率降低了15-30%(身材逐渐走样的原因)
心脏的功率估算
假设心脏1分钟使6 L血液在体内循环一次，血压平均值 1.5×104帕(112mmHg)，心跳每分70次，人心脏工作的 平均功率为多少？ 压力：F=pA A为血管截面积，p为血压。 此压力由心脏提供，所以心脏一分钟内收缩做功为： W=Fh=pAh=pV 则心脏的功率 P=W/t=pV/t=pV/t = 1.5×104 ×6×10-3 m3/60 = 1.5W
克劳修斯不等式: dS≧Q/T “=”时为可逆过程； “>”为不可逆(自发)过程； “<”为不可能过程。
2
2014/7/8
• 对于绝热体系: Q=0 • • • 或： ∴ dS≧Q/T=0
dS≧0 (绝热体系)
(dS)孤立≧0
• 上式为熵判别式, 是热力学上第一个判 别式, 也是最重要的判别式. • 上式也称为熵增原理
G1 G2
G3
H2O(l), 298K 23.76mmHg
H2O(g), 298K 23.76mmHg
• • • •
G= G1+ G2+ G3 =RTln(p2/p1) + 0 + Vm(H2O)(p2－p1) =－8585.6+1.766=－8583.8 J<0 ∵ G<0, 此过程是一自发过程.
• • • •
功可以无条件地全变为热； 热不能无条件地全变为功。 热量自发地从高温物体传给低温物体； 不可能自发由低温物体流向高温物体。
• 能满足以上要求的热力学函数就是：
熵 （entropy） • • 熵函数可以定量的确定化学反应及其 它任何过程进行的方向与限度。
1
2014/7/8
• 熵: 体系熵变等于可逆过程的热温商之和. • S= Qr/T • 卡诺定理:
• 一 自然界的自发过程:
• 我们周围的自然界所发生的过程都是自发进行的, 如:
• 化学过程： • • • • H2+0.5O2=H2O C+O2=CO2 2Fe+1.5O2=Fe2O3 N2+3H2=2NH3
• • • •
水 电 热 风
流 流 流 流
高处 → 低处 高压 → 低压 热处 → 冷处 高压 → 低压
=1-T1/T2
各年龄基础代谢值（BMR）
• 人若是以热机方式工作，体温37oC，环 境温度以20oC计，最大效率为： • =1-T1/T2 • =1–293.15/310.15 • =5.48% • 以每天食物摄入量为2000千卡计，人的 功率为 • 2000 1034.184 5.48%/(24 60 60)=5.3 瓦
年龄 7-9 10-12 13-15 16-19 20-24 25-34 35-54 55-69 70~
男性(Kcal/kg/min) 0.0295 0.0244 0.0205 0.0183 0.0167 0.0159 0.0154 0.0151 0.0145
女性(Kcal/kg/min) 0.0279 0.0231 0.0194 0.0168 0.0162 0.0153 0.0147 0.0144 0.0144
dG= -SdT+Vdp G=∫Vdp =V(p2－p1)
(假设密度与压力无关)
•
热力学第三定律
limT→0KS=0
二. 变温过程: U=CV T H=CpT dG= -SdT+Vdp G=∫－SdT =(H-TS)= H- (TS)
理想气体熵变
• 普朗克于1912年提出物质在绝对零度时的熵等于零. • • 热力学第三定律的表述为:
• Gibbs关系式(了解) :
• • • •
dU=TdS－pdV dH=TdS+Vdp dF=－SdT－pdV dG=－SdT+Vdp
H=U+pV F=U-TS G=H-TS
4
2014/7/8
• 热力学主要关系式(了解) :
•
热力学函数值的计算
一. 等温过程: 理想气体： U=0 , H=0 凝聚体系: G=(H-TS) =(U+pV-TS)
2014/7/8
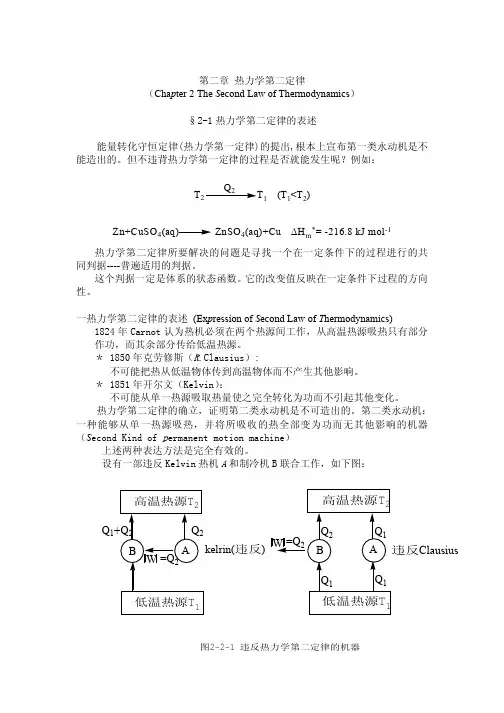
• 热力学第二定律是决定自然界一切过 程方向与限度的基本规律.
• Clauxius表述:
物理化学 热力学第二定律
(变化)
• 不可能使热量从低温物体流向高温 物体而无其它变化.
• Kelvin表述:
• 不可能从单一热源取出热使之完全 变为功而无其它变化. • 第二类永动机不可能.
热力学第二定律
(3)
5
2014/7/8
• 例: 已知298K下水的p*=23.76mmHg, 试计算298K, 1atm下的水蒸汽变为同温同压下的液态水的G? • 解: 此为一非平衡相变, 特设计下列可逆过程:
H2O(g), 298K 760mmHg
C6H6(l) 268.15K S1 C6H6(l) 278.65K
V总n1V*m,1 + n2V*m,2
V*m,1为纯i的摩尔体积。
例: 求-5℃下, 液态苯凝结的S?
已知: T平衡相变=5.5℃; Hm(熔)=9916J.mol-1; -5℃下的相变热为9847 J.mol-1; Cp,m(l)=126.8 J.K-1.mol-1; Cp,m(s)=122.6 J.K-1.mol-1.
• 热力学三大判别式:
• • • • • • • • • • • (S)孤≧0 >0: 为自发过程 =0: 可逆过程 <0: 不可能过程
(dT=0, dp=0, Wf=0) 自发过程 (G)T,p<0 =0 (dT=0, dp=0, Wf=0) 平衡,可逆 >0 (dT=0, dp=0) 不自发不可逆过程 >Wf,R (dT=0, dp=0) 不可能过程 (dT=0, dV=0, Wf=0) 自发过程 (F)T,V <0 =0 (dT=0, dV=0, Wf=0) 平衡,可逆 >0 (dT=0, dV=0) 不自发不可逆过程 >Wf,R (dT=0, dV=0) 不可能过程