当前位置：文档之家 › 7.2 迭代法及其收敛性

7.2 迭代法及其收敛性

  • 格式：ppt
  • 大小：4.65 MB
  • 文档页数：40

下载文档原格式

  / 40

合集下载

迭代法的收敛性与稳定性 - 松弛迭代法、迭代法的收敛性与稳定性

迭代法的收敛性与稳定性 - 松弛迭代法、迭代法的收敛性与稳定性
Bk 0(零矩阵)(k )
定义 6.5 设有矩阵序列 Ak (aij(k ) ) Rnn 及 Ak (aij ) Rnn ，如果 n2 个数列极限存在
且有
lim
k
a (k) ij
aij
(i,
j
1,2,..., n)
则
Ak
称收敛于
A
记为 lim(k
)
。
定理 6.5
lim
k
Ak
A
lim
三 松弛法例题与程序
例 6.9 取 1.4, x(0) (1,1,1)T 用超松弛法解方程组
2x1 x2
1
x1 2x2 x3 0
x2 2x3 1.8
� � 解：由 xi(k1)
(1 )xik
aii
(bi
i 1 j 1
a x(k 1) ij j
n
aij
x
(k j
x j(k ) ) / aii xi(k )
j i
j i 1
i 1
n
(bi aij x j(k 1) aij x j(k ) ) / aii
ji
ji
(i 1,, n; k 0,1,).
� � i1
n
xi
b x(k 1) ij j
bij
x(k) j
gi
x(k) i
j 1
j i 1
a x(k1) ij j
aij x(jk ) ) / aii .
j 1
j i 1
(2) 再由 x(k) 与 ~xi(k 1) 加权平均定义 xi(k 1) ，即
x(k 1) i
(1 )xi(k)
x%i(k 1)

第5节_迭代法的收敛性

第5节_迭代法的收敛性
x ≠0
Bx x
≥
Bx1 ቤተ መጻሕፍቲ ባይዱ1
= 1,与已知矛盾！
线性方程组迭代法收敛性
推论1：对任意初始向量x (0)和右端项g，若 M < 1, 由迭代式 x ( k +1) = Mx ( k ) + g产生的向量序列{ x ( k ) }收敛.
证明：矩阵范数性质3：ρ ( A) ≤ || A ||
迭代法收敛与否只决定于迭代矩阵的谱半径，与初始向 量及右端项无关。 对同一方程组，由于不同的迭代法迭代矩阵不同，可能 出现有的方法收敛，有的方法发散的情形。
且至少有一个i值，使上式中不等号严格成立，则称A为弱 对角占优阵。若对所有i，上式不等号均严格成立，则称A 为严格角占优阵。
定义：如果矩阵A不能通过行的互换和相应的列互换成 A11 为形式 A = 0 A12 ,其中A11，A22为方阵，则称A为不可约。 A22
1 1 0 2 1 0 P = I13 例： A = 1 1 0 PT AP = 0 1 1 → 0 1 2 0 1 1
k →∞
证：设u为A特征值λ对应的特征向量， 则：Ak u = λ Ak -1u =...=λ k u 即：λ k为矩阵Ak的特征值。
ρ 所以：（Ak） [ ρ ( A)]k =
线性方程组迭代法收敛性
1- ρ ( A) > 0， 2 定理：设A为任意n阶方阵， 存在矩阵范数 ，使得 则对任意正数ε , 存在矩阵 1 + ρ ( A) A ≤ ρ ( A) + ε = <1 范数 ，使得： 2 证： 充分性：若ρ ( A) < 1 ，取ε = 则有： A = 0 lim
Gauss-Seidel迭代收敛性：

7.2 迭代法及其收敛性

7.2 迭代法及其收敛性

1 2 3 4 5 6 7 8 9 10 30 40 45
1.358484290 1.355301399 1.355302727 1.355301425 1.355301394
由上表数据可看出，若取迭代函数为(c )， (d )和 (e )三种情形，算法表现良好，均能较快得到方程 的近似根.
下面讨论用迭代的方法求 ( x )的不动点x * .取 方程(7.2.1)解的初始近似值x0 , 通过如下迭代
xk xk 1 , k 1,2,, 产生迭代序列 xk . (7.2.2)
如果序列 xk 收敛到x * ,即 lim xk x * ,因 ( x )
x k x * x k 1 x * L x k 1 x * L x k 2 x L x0 x .
* k *
2

7.2.3
由0 L 1可得 lim Lk 0,因此对上式取极限可得
k
lim xk x * lim Lk x0 x * 0
4 x 在[1,2] 的值域为[ 1.6, 2].此外
(7.2.1)
其中 ( x )为连续函数,其取法不唯一,例如可取
方程(7.2.1)的解称为函数 ( x )的不动点, 求方程 (7.2.1)的解的问题称为不动点问题.
因此, 对于方程f ( x ) 0,为求出它的一个实根, 常 常将其化为求解等价的不动点问题,因为不动点 问题的形式往往更易于分析求解.
但对于情形(a )，迭代序列发散;在情形(b)中， 出现负数开根号，从而迭代不能继续下去.
因此, 迭代函数 ( x )的选取将会对迭代过程的收 敛性产生很大的影响.事实上, 要使迭代法产生的序 列 xk 收敛,则迭代函数 ( x )应满足一定的条件.

数值分析第7章-方程近似根

数值分析第7章-方程近似根
机动 上页 下页 首页 结束
例7-2 求x x 1 0在1.5附近的根x *。
3
解：（ 1）将方程改写成下列形 式 x 3 x1 据此建立迭代公式 x k 1 3 x k 1 (k 0,1,2, )
k xk
k
xk
k
xk
0 1.5 1 1.35721 2 1.33086
它表明定理中的条件(2)可用(2.5)代替。
机动 上页 下页 首页 结束
1 在例7-2中，当 (x) x 1时， (x) (x 1) 2/3 , 3 1 1 1 在区间[1, 2]中， (x) ( ) 3 1, 又因 3 4
3
1 3 2 (x) 3 3 2 故定理1中条件1成立。所以迭代法收敛。 而当 (x) x 3 1时， (x) 3x 2在区间[1，中 2] (x) 1 不满足定理条件。
对定理1的条件(2)，在使用时如果
（2.4）
(x) C1[a, b]且对任意x [a, b]有 (x) L 1
则由中值定理可知对x, y [a, b]有 (2.5)
(x) (y ) ( )( x y ) L x - y , (a, b)
机动 上页 下页 首页 结束
例7 - 4 牛顿法求方程x x 5 0的近似根.
3
1）判断根的大致范围
f (0) 5, f (2) 5 x* （ 0,2 ）
2）求导判断收敛性
f 3x 2 1 0 单调 f ( x) 6 x 0, 连续
定理2 在定理1的条件下, 对任意初值 x 0 [ a, b], 迭代序列 (2.2)均收敛于 ( x)的不动点x*, Lk | x k x* | | x1 x0 | . 1 L

37第七节 迭代法及其收敛性

37第七节 迭代法及其收敛性
从而 ||x(k+1) -x(k)|| =||(x(k+1) -x*)-(x(k) -x*)|| ||x(k) -x*||-||x(k+1) -x*|| ||x(k) -x*||-q||x(k) -x*||
=(1-q) ||x(k) -x*||
数学学院 信息与计算科学系
故得
1 q ( k 1) (k ) x x x x x ( k ) x ( k 1) 1 q 1 q k q q x ( k ) x x ( k ) x ( k 1) x (1) x(0) 1 q 1 q


数学学院 信息与计算科学系
二、迭代法的收敛性
定义2 如果
lim A
k
k
(k )
A O
则称矩阵序列｛A(k)｝依范数收敛于A，记
lim A( k ) A
由范数的等价性可以推出，矩阵序列｛A(k)｝ 依某种范数收敛，则依任何一种范数它都收敛，故 下面不强调是在那种范数意义下收敛。
x
k 1
Bx( k ) f
k 0,1,2
其中B称为迭代矩阵。
数学学院 信息与计算科学系
若序列｛x(k)｝收敛，即
lim x ( k ) x
k
显然有
x Bx f
此极限 x＊就是方程组 Ax=b 的解。 定义1 如果序列｛x(k)｝的极限存在(记 x＊)， 则称迭代法收敛，x＊就是方程组 Ax=b 的解，否则 称此迭代法发散。
数学学院 信息与计算科学系
x(k+1) -x*= B( x(k) -x* ) , x(k+1) –x(k)= B( x(k) –x(k-1) )
即有

数值计算方法 迭代法及其收敛性 - 迭代法及其收敛性

数值计算方法 迭代法及其收敛性 - 迭代法及其收敛性

x*
lim
k
x
k
1
lim
k
(
xk
)
(lim k
xk
)
( x* )
故k充分大时，xk可作为方程根的近似值
按上述方法构造迭代格式来求解方程的方法称为简单迭代法或逐
次迭代法。
不动点迭代法： 将方程 f ( x) 0 改写为: x ( x).
1 若要求x*满足f ( x* ) 0,则x* ( x* );反之亦然，
重点
实多项式方程
f ( x) a0 x n a1 x n1 an1 x an (a0 0),
的求根问题.
（其中系数ai (i 0,1,, n)为实数）
若 方程f ( x*) 0, 则x*称为函数f ( x)的零点
1
若方程 f (x) (x x* )m g(x),
其 中m为 正 整 数 ， 且g( x* ) 0.
真真解解：：xx==1.13.234274272
典型例题
例3
用不同方法求方程x2 3 0的根x* 3.
(1) xk1 xk2 xk 3,(x) x2 x 3
(2)
xk 1
3 xk
,(x)
3, x
(3)
xk 1
xk
1 4
( xk2
3), ( x)
x
1 4
(x2
3)
(4)
xk 1
1 2
典型例题
(2)
xk1
3 xk
,(x)
3, x
( x* ) 1
(3)
xk 1
xk
1 4
(
x
2 k
3),( x)
x
1 (x2 4

迭代法和收敛性

迭代法和收敛性

x1(k x2(k
1) 1)
0.2x2(k) 0.1x3(k) 0.3
0.2x1(k )
0.1x3(k) 1.5 , k
0,1, 2,
x3(k
1)
0.2x1(k )
0.4x2(k )
2
迭代计算
x(0) 0 [0, 0, 0]T
x(1) 1
0.3
x(1) 2
1.5
x1(k x2(k
其中系数矩阵非奇异，且主对角元aii≠0，(i
=1,2,…,n)，由第i 个方程解出xi，有
x1
1 a11
(b1
a12 x2
a13 x3
x2
1 a22
(b2
a21x1
a23x3
xn
1 ann
(bn
an1x1
an2 x2
a1n xn ) a2n xn )
ann1xn1)
建立迭代格式
aij
x
( j
k
)
)
j i 1
加速
x ( k 1) i
( k 1)
xi
(1 ) xi(k )
i 1, 2, , n
或合起来写成迭代加速的形式
x (k 1) i
aii
(bi
i 1
a x (k 1) ij j j 1
n
aij
x
(k j
)
)
(1
)
xi( k
)
j i1
参数 称为松弛因子， 1 时迭代格式就是高斯-
x (k1) i
1 aii
(bi
n
aij x j(k ) ),
j1
(i 1,2,, n)

迭代法的收敛条件

迭代法的收敛条件
4
解线性方程组的迭代法
定理3.5 设 A 为n阶方阵， 则
lim A k 0
k
的充要条件为
( A) 1.
k k
［证明］必要性. 若 lim A 0
由定义3.2得
而
k
lim A
k
k
0
k k
0 ( A ) [ ( A)] A
lim[ ( A)] 0
k
松弛法收敛的必要条件是 0 2。 设松弛法的迭代矩阵 M 有特征值
［证明］
1 , 2 ,
n . 因为 det( M ) 12 n (M )n
det(M ) 1
10
由定理3.6，松弛法收敛必有
p19
解线性方程组的迭代法
又因为
M (D L ) 1[(1 ) D U]
k k
于是由极限存在准则，有 所以 ( A) 1.
5
解线性方程组的迭代法
充分性.
若
( A) 1,
1 ( A) 0, 取 2
由定理3.4存在一种存在一种
, 使得
A ( A)
而
A
k
A ,
k
k
1 ( A) 1 2 于是
k
lim A
非严格对角占优,但 A为对称正定矩阵, 1.4 故松弛法收敛。 上述结论的证明可参看[1],[7].
23
例 对线性方程组
x1( k 1)
( k 1) 20x1 2x2 3x3 24 x2 x 8x x 12 2 ( k ) 3 ( k ) 30 2 3 1 ( k 1) x3 x1 x2 2 x1 3x2 15x3 30 15 15 15 讨论Jacobi迭代法及Gauss-Seidel迭代法的收敛性. 解: Jacobi迭代的迭代矩阵为

迭代法的收敛性

迭代法的收敛性
k
x* Mx* g 由迭代公式有 M (x
k k
x ( k ) x* Mx ( k 1) g Mx* g
( k 1)
x ) M (x
* 2 * k
( k 2) (k )
x ) M (x
* k
(0)
x )
*
于是有 lim M ( x
1 1 例：Ax b, A 2 1 2
1 2 1 1 讨论用三种迭代法求解的收敛性。 2 1 1 2 解：因A为对称且其各阶主子式皆大于零，故A为对称正定矩 1 2 阵。由判别条件3，Gauss-Seidel迭代法与松弛法(0 2) 均收敛。A不是弱对角占优阵，故不能用条件1判断。 0 1 -1 Jacobi迭代法的迭代矩阵为B I - D A 2 1 2 1 2 0 1 2 1 2 1 2 0

1,
1,由推论1无法判别收敛性。
对一些特殊的系数矩阵可给出几个常用的判 别收敛条件
设有线性方程组Ax b, 下列结论成立（收敛充分条件） 1.若A为严格对角占优阵或不可约弱对角占优阵，则 Jacobi迭代法和Gauss-Seidel迭代法均收敛。 2.若A为严格对角占优阵， 0 1, 则松弛法收敛。 3.若A为对称正定阵，则松弛法收敛的充要条件为 0 2。 10 1 2 2 1 0 B 1 2 1 上两例中： A 1 10 2 1 1 5 0 1 2 A为严格对角占优阵，故Jacobi与Gauss-Seidel迭 代均收敛。B为非严格对角占优阵，但为对称正定 阵， =1.4故松弛法收敛。
推论1 对任意初始向量x 和右端项g，若 M 1,由迭代

《迭代法及其收敛性》课件

《迭代法及其收敛性》课件
猜测一个初始解，作 为迭代的起点。
2 建立迭代公式
根据问题的特性和已 知条件，建立迭代公 式。
3 判断迭代是否收敛
判断迭代得到的解是 否足够接近真实解， 停止迭代。
迭代法的例子
牛顿迭代法
用于求解方程的数值方 法，通过不断迭代逼近 方程的根。
埃特金迭代法
用于求解线性方程组的 数值方法迭代法
用于求解线性方程组的 数值方法，通过不断迭 代逼近方程组的解。
迭代法的收敛性
收敛性是指迭代得到的解越来越接近真实解，而收敛速度是指迭代得到的解 的收敛速度有快有慢。
收敛速度的度量方法
1 零点误差
迭代得到的解与真实 解之间的差距。
2 牛顿数列
迭代得到的解之间的 差值的变化规律。
3 收敛阶
《迭代法及其收敛性》 PPT课件
迭代法及其收敛性
迭代法是一种求解数值问题的方法，通过反复迭代得到更精确的解。这个PPT 课件将讲解迭代法的定义、步骤、例子以及收敛性的度量方法。
什么是迭代法？
迭代法是一种求解某些数值问题的方法，从一个猜测的解开始，通过反复迭 代得到更精确的解。
迭代法的步骤
1 猜测初始解
迭代得到的解的收敛 速度的量化指标。
如何判断迭代是否收敛？
1 绝对误差减小
迭代得到的解的绝对 误差逐渐减小。
2 相对误差减小
迭代得到的解的相对 误差逐渐减小。
3 后验估计准则
通过计算后验估计准 则判断迭代的结果是 否满足要求。
总结
1 迭代法是一种常用的数值求解方法 2 收敛性和收敛速度是迭代法的重要评价指标 3 判断迭代收敛的方法有多种，需要根据问题具体情况选择

第七章 函数方程求根

第七章 函数方程求根
如果取定初始近似x0，满足下列条件：
（1） F(x0 ) 1 存在，并且有实数B, η，使得
F (x0 ) 1 B, F (x0 ) 1 F(x0 )
（2）在圆S(x0,ω)中满足李普希茨条件：
F(x) F(y) K x y , x, y S(x0 , )
（3） h KB 1 , 1 1 2h
t * 1 1 2h ,t ** 1 1 2h
h
h
如果取t0=0，则对f(t)按牛顿法产生的序列{tk}有下列性质：
（1）{tk}是单调上升序列，满足：t0<t1<t2<…<tk<t*
（2）
lim
k
t
k
t*
（3） t * tk1
m 2k 1 0 k
m0 (1 m02 j )
3．切线法的几何意义。为了求曲线y=F(x)与x轴的交点， 用过 (xk , F (xk )) 处的切线与x轴的交点来近似。
因为过 (xk , F (xk )) 的切线方程为 y F (xk ) F (xk )( x xk ) ，令y=0即得它与x轴的交点的横坐标即为
xk1 xk F (xk ) F (xk )
第七章 函数方程 求根
学习目标：掌握函数方程求根的 二分法、迭代法、牛顿法、 以及弦割法。重点是一般迭 代法、牛顿法等及其收敛性 。
§7.1 二分法与反插值法
二分法是求连续函数f(x)实根的可先靠方法。这个方法 要求先找到两个自变量的值a1与b1，使得f(a1)与f(b1)异号， 即f(a1)f(b1)<0；假定a1<b1。
m0ห้องสมุดไป่ตู้
1 1
1 2h 1 2h
因此牛顿法产生的序列{xk}如图3所示。

数值分析中的迭代法收敛性分析

数值分析中的迭代法收敛性分析

数值分析中的迭代法收敛性分析迭代法是数值分析领域中常用的一种数值计算方法，通过迭代逼近的方式求解数值问题。

在使用迭代法时，我们需要关注其收敛性，即迭代过程是否能够逼近问题的解。

本文将探讨数值分析中的迭代法收敛性分析方法。

一、迭代法的基本概念迭代法是一种通过逐次逼近的方式求解数值问题的方法。

在求解问题时，我们通过不断使用公式迭代计算，直到满足某个特定的条件为止。

迭代法在实际应用中广泛使用，例如求解方程组、求解最优化问题等。

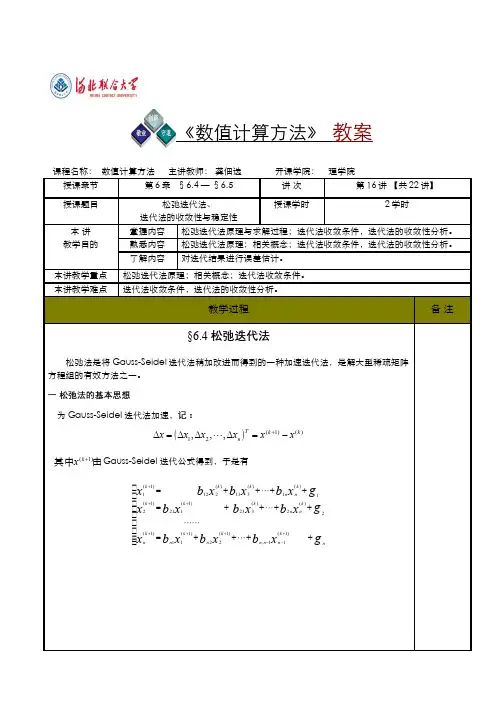
二、迭代法的数学模型我们可以用以下数学模型描述迭代法的过程：设迭代公式为：x_(n+1) = g(x_n)，其中x_n表示第n次迭代的结果，g(x)为迭代函数。

三、迭代法的收敛性在使用迭代法时，我们希望迭代过程能够收敛到问题的解。

迭代法的收敛性分析是判断迭代过程是否能够收敛的关键。

1.线性收敛如果迭代法满足以下条件：1）对于任意的x_0，如果|x_n - x*| / |x_(n-1) - x*| ≤ C (0 < C < 1)，其中x*为问题的解，那么称迭代法是线性收敛的。

2）线性收敛的迭代法需要满足条件|x_1 - x*| / |x_0 - x*| ≤ C (0 < C <1)。

2.超线性收敛如果迭代法满足以下条件：对于任意的x_0，如果|x_n - x*| / |x_(n-1) - x*|^p ≤ C (0 < C < 1, p > 1)，那么称迭代法是超线性收敛的。

3.二次收敛如果迭代法满足以下条件：对于任意的x_0，如果|x_n - x*| / |x_(n-1) - x*|^2 ≤ C (0 < C < 1)，那么称迭代法是二次收敛的。

四、判断迭代法的收敛性在实际应用中，判断迭代法的收敛性是非常重要的。

下面介绍几种常用的判断方法。

1.收敛准则根据数列极限的定义，如果一个数列{x_n}满足：对于任意ε > 0，存在正整数N，当n > N时，有|x_n - x*| < ε，则称{x_n}收敛于x*。

数值分析教案_非线性方程的数值解法

数值分析教案_非线性方程的数值解法

定理 2（不动点迭代法的全局收敛性定理） 设 ( x) C[a, b] 满足定理 1 中的两个条 件，则对任意的 x0 [a, b] ，由（2.1）式生成的迭代序列 {xk } 收敛到 ( x) 在 [a, b] 上的不 动点，且有
| x* xk | | xk 1 xk | , 1 L
ak bk ） 。记第 n 次过程得到的隔根区间为 2
[an , bn ] ，则 [a0 , b0 ] [a1, b1 ] [a2 , b2 ] [an , bn ]
an x* bn ， n 0,1, 2,
bn an bn 1 an 1 2 b0 a0 2n
k
则称迭代方程（2.1）收敛。 2.2 不动点的存在性与迭代法的收敛性 定义 若存在常数 L ，使对任何 x1 , x2 [a, b] 有
| ( x1 ) ( x2 ) | L | x1 x2 |
则称 ( x) 在 [a, b] 上满足 Lipschitz（利普希茨）条件， L 称为 Lipschitz 常数。 显然， 若 ( x) 在 [a, b] 上满足 Lipschitz 条件， 则 ( x) 在 [a, b] 上连续。 若 ( x ) 在 [ a, b] 上一阶导数存在且有界，则 ( x) 在 [a, b] 上满足 Lipschitz 条件。 定理 1（不动点存在性定理） 设 ( x) C[a, b] 满足以下两个条件： （1）对任意 x [a, b] ，有 ( x) [a, b] ； （2） ( x) 在 [a, b] 上满足 Lipschitz 条件，且 Lipschitz 常数 L 1 ； 则 ( x) 在 [a, b] 上存在唯一的不动点。 证明：先证明不动点的存在性，记 g ( x) x ( x) ，由定理条件有 g (a) a (a) 0 及 g (b) b (b) 0 ，若有一等号成立，则 g (a) 0 或 g (b) 0 ，即 有不动点，否则必 有 g (a) g (b) 0 ，因 g ( x) C[a, b] ，则必有 x* [a, b] 使 g ( x* ) x* ( x* ) 0 ，x* 即为 的 不动点。

第七讲二分法与迭代过程的收敛性

第七讲二分法与迭代过程的收敛性
1 ( x) ( 2 x 5) 2 1 2 1 1 2 3 3 4 6 3 ( 2 1.5 5)
所以迭代公式
2 3
1
2 3
取x0=2 计算, 结果列表：
k xk xk-xk-1 0.08008 0.01227 0.00187 0.00027 0.00005
1.二分法的基本思想 条件: 函数f(x)在[a,b]上连续, 严格单调, 且
f(a)f(b)<0, 这时方程在区间内有且仅有一个实根x*.
二分法的基本思想 将含方程根的区间平分为两个小区间, 然后判断 根在哪个小区间, 舍去无根的区间, 而把有根的区间 再一分为二, 再判断根属于哪个更小的区间, 如此周 而复始, 直到求出满足精度要求的近似根.
k 1
ak
xk
bk
(b a )
由此得二分过程的结束原则：
先给定精度要求ε(>0)
(1)当|bk+1 – ak+1|<ε时结束二分计算, 取 x*≈xk;
(2)事先由ε估计出二分的最小次数 k+1, 取 x*≈xk. ba ba * k 1 由 x xk k 1 得2 ， 2 ln(b a ) ln
一、二分法
2.计算过程 具体计算过程
y a1 0 a b1 x* x 0
f (x )
y
0 a
f ( x) a1 x0 b * b1 x x
b x
1 第1次二分, 取中点 x0 (a b ) 2 若f(a)f(x0 )<0, 则 x*∈( a, x0 ), 令a1=a, b1=x0; 否则 x*∈(x0, b), 令a1=x0, b1=b.
答案: 计算结果见列表：

迭代过程的收敛性

迭代过程的收敛性
2 2 ( x x ) ( x ) ~ k 1 k xk xk xk 2 k , k 0,1,. xk 2 2 xk 1 xk xk
xk 1 x (4.1) lim c , 0 c 1 k x x* k 1) xk x* ,, k 0,1,, (若等号成立,则 xk x* , 是精确解)
m (1) g ( x) [a, b], x [a, b]； (2)0 L 1, 使 x, x [a, b] 有 g( x) g( x) L x x x* xk 1 max g ( x) L 1 ， 则有 lim * g ( x* ) 或 x k x x [ a ,b ] k
1 简单迭代法的基本思想方法：
2. 收敛性（定理1）
对迭代 x g ( x)若有
4、高阶收敛性（定理 3） * ( m1) * ( m)
若 g( x ) g ( x ) 0, g
x [ x , x ], 有 g ( x) g ( x ) L x x * , 0 L 1, * x xk 1 * 或 g ( x ) 1, 则有 lim * g ( x* ) k x x k
§1 迭代过程的收敛性
(1) 将 f ( x ) 0 化为等价方程x g ( x)； (2) 从某 x0 出发,作序列 {xk } : xk 1 g ( xk ), k 0,1, — 迭代公式 * 若 { xk } 收敛于 x * 且 g ( x ) 连续,则 x 是f(x)=0的根。
ek ek
* x x lim k 1 * c, 0 c 1 定理4: 若序列{ xk } 线性收敛于 x ： k x x k ~

数值分析中的迭代方法与收敛性分析

数值分析中的迭代方法与收敛性分析

数值分析中的迭代方法与收敛性分析迭代方法是数值分析中一种重要的算法，用于求解数值问题。

迭代方法基于一个初始猜测解，并通过不断迭代逼近真实解。

本文将介绍迭代方法的基本原理以及如何进行收敛性分析。

一、迭代方法的原理迭代方法的基本原理是通过不断更新猜测解来逼近真实解。

假设我们要求解一个方程f(x)=0，其中f(x)表示一个函数。

我们可以通过选择一个初始猜测解x0，然后使用迭代公式x_{k+1}=g(x_k)来生成下一个近似解x_{k+1}，其中g(x_k)是一个迭代函数。

通过不断迭代，我们希望逐渐接近真实解。

二、常见的迭代方法在数值分析中，有许多常见的迭代方法被广泛应用于求解不同类型的数值问题。

以下是几种常见的迭代方法：1. 不动点迭代法不动点迭代法通过将方程f(x)=0转化为等价的x=g(x)的形式来求解。

其中g(x)是一个迭代函数，可以通过不断迭代x_{k+1}=g(x_k)逼近真实解。

不动点迭代法的收敛性通常需要满足收敛性条件，如Lipschitz条件或收缩映射条件。

2. 牛顿迭代法牛顿迭代法通过利用函数的导数信息来加速收敛速度。

迭代公式为x_{k+1}=x_k-\frac{f(x_k)}{f'(x_k)}，其中f'(x_k)表示函数f(x_k)的导数。

牛顿迭代法的收敛性通常需要满足局部收敛性条件，如满足Lipschitz条件和拟凸性条件。

3. 雅可比迭代法雅可比迭代法用于求解线性方程组Ax=b，其中A是系数矩阵，b是常数向量。

迭代公式为x_{k+1}=D^{-1}(b-(L+U)x_k)，其中D、L和U分别是矩阵A的对角线、下三角和上三角部分。

雅可比迭代法的收敛性要求系数矩阵A满足严格对角占优条件。

三、迭代方法的收敛性分析在使用迭代方法求解数值问题时，我们需要进行收敛性分析，以确定迭代方法是否能够逼近真实解。

常用的迭代收敛性分析方法包括：1. 收敛域分析收敛域分析用于确定迭代方法的收敛域，即迭代过程中能够保证收敛的初始猜测解的范围。

迭代法的收敛定理

迭代法的收敛定理

一、基本收敛定理
The Fundamental convergence theorem
Theorem :for any initial value x (0) R n, the fundamental iterative method defined
by x(k+1)=Bx(k)+f (k=0,1,2,…) converges to the unique solution of x=Bx+f if only if
1.25 x1 3.69 x2 12.37 x3 0.58 10.01x1 9.05 x2 0.12 x3 1.43 1.22 x 4.33x 2.67 x 3.22 1 2 3
无法直接判断Jacobi 迭代法和G-S迭代法的收敛性，但如果 将方程组的次序修改为
对角占优矩阵
diagonally dominant matrix
如果线性方程组AX=b的系数矩阵A具有某种特殊性质 （如对称正定、对角占优等），则可从A本身直接得出某些 迭代法收敛性结论。 定义3.1 如果矩阵A满足条件
aii aij
j i
(i 1,2,
, n)
(2)
则称A是严格对角占优阵(strictly diagonally dominant matrix)； 如果矩阵A满足条件 aii aij (i 1,2, , n) (3)
在偏微分方程数值解中，有限差分往往导出对角占优的 线性代数方程组，有限元法中的刚性矩阵往往是对称正定阵， 因此这两个判断定理是很实用的。 对于给定的线性方程组，借助于定理3.3和定理3.4可 以直接判断Jacobi 迭代法和G-S迭代法的收敛性。 但同时应当注意，迭代法收敛与否与方程组中方程排列 顺序有关，如线性方程组

数值计算中的迭代法与收敛性分析

数值计算中的迭代法与收敛性分析

数值计算中的迭代法与收敛性分析数值计算是现代科学技术中不可或缺的一部分，主要解决数学问题的计算和应用问题的模拟。

其中，在数学问题的计算中，经常需要使用迭代法。

本文将从迭代法的基本概念、应用、收敛的定义和分类、收敛性分析以及优化中的迭代法等几个方面论述迭代法与收敛性分析。

一、迭代法的基本概念和应用迭代法是指通过对一个初值的反复迭代求解来逼近某个方程的解或某个函数的极值的方法。

通常来说，迭代法都需要给出迭代序列的计算公式，将初值代入迭代公式计算，得到下一项的迭代结果，不断迭代，直到达到预定的迭代次数或满足收敛精度要求为止。

在数值计算中，迭代法的应用十分广泛，例如求解非线性代数方程、求解常微分方程初值问题、解方程组、求解最优化问题等。

二、收敛的定义和分类在迭代方法求解问题时，我们需要考虑其迭代序列的收敛性问题。

收敛是指迭代序列随着迭代次数的增加，逐渐逼近欲求解的精确解。

在数值计算中，可以用迭代序列中后面几项的误差与该序列最后一项的关系来描述收敛情况。

如果迭代序列中的误差随着迭代次数的增加而逐渐趋于零，那么该迭代序列就是收敛的；反之，如果误差在某个阶段始终无法收敛，那么该迭代序列就是发散的。

按照算法的不同，迭代可以分为简单迭代和牛顿迭代等多种迭代方法。

而根据问题的不同性质，迭代的收敛性可以分为线性收敛和非线性收敛两种情况。

在常见的迭代算法中，如牛顿迭代等，通常都需要对迭代的收敛性进行分析，并根据问题特点选择适当的算法。

三、收敛性分析收敛性分析是数值计算中非常重要的一部分，其主要目的就是分析迭代序列的收敛性，找到迭代公式使其遵循收敛性的要求。

对于某些特定的迭代算法，分析收敛的方法也不相同。

下面我们以简单迭代法和牛顿迭代法两种常见的迭代算法为例，简单分析一下如何对其进行收敛性分析。

（1）简单迭代法的收敛性分析对于简单迭代法，其基本的思路就是对于方程f(x)=0，在x_0处展开泰勒公式，得到x_(k+1)和x_k間的关系式，根据其收敛的条件来选择迭代公式。

第二节迭代法及其收敛性1

第二节迭代法及其收敛性1
x g ( x).
（2.1）
若要求 x *满足 f ( x*) 0 ，则 x* g ( x*) ；反之亦然， 称 x* 为函数 g ( x )的一个不动点. 求 f ( x)的零点就等价于求 ( x )的不动点，选择一个 初始近似值 x0 ，将它代入(2.1)右端，即可求得
x1 g ( x0 ).
仍取迭代初值 x0 1.5，则有
x1 2.375, x2 12.39.
结果会越来越大，不可能趋于某个极限. 这种不收敛的迭 代过程称作是发散的. 一个发散的迭代过程，纵使进行了 千百次迭代，其结果也是毫无价值的.
y p1 p0
y=x y= (x)
y p0
y=x

x1 x2 x* y= (x) y=x x x0 y y=(x) p0 x*
图1-2 过 P0 引平行 x轴的直线，设此直线交直线 y x于点 Q1， 然后过 Q1再作平行于 y 轴的直线，它与曲线 y ( x)的 ( x1 ) x 交点记作 P 1，则点 P 1的横坐标为 1，纵坐标则等于
x2 .
按图1-2中箭头所示的路径继续做下去，在曲线 y g ( x) 上得到点列 P ，其横坐标分别为依公式 xk 1 g ( xk ) 1, P 2 求得的迭代值 x1 , x2 . 如果点列 {Pk }趋向于点 P *，则相应的迭代值 xk 收敛 得到所求的根 x * .
注意
，从计算结果看到迭代法（1） 3 1.7320508
及（2）均不收敛，且它们均不满足定理3中的局部收敛条 件，迭代法（3）和（4）均满足局部收敛条件，且迭代法
（4）比（3）收敛快，因在迭代法（4）中 g ( x*) 0.
定义7.2.2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

k4.1045
1/ 2
表 7.2.1 用不动点迭代法计算例7.2.1的结果
0 (a) 1.5 -0.625 6.447 -378.2 5.3697e7 -1.547e23 (b) 1.5 0.912871 2.454577 (c) (d) (e) 1.5 1.5 1.5 1.241638702 1.333333333 1.365079365 1.424290116 1.305205188 1.387624336 1.332682451 1.370291856 1.344991115 1.362217505 1.350582520 1.358732441 1.355350555 1.354767869 1.355301399 1.355384418 1.355301398 1.355288480 1.355303407 1.355301085 1.355301446 1.355301390
*
k
xk x L x0 x L max x0 a , b x0 ,
* k * k
从而 7.2.4 成立.
再由 7.2.3 , 对m k 1, 我们有
x m x k x m x m 1 x m 1 x m 2 x k 1 x k x m x m 1 x m 1 x m 2 x k 1 x k Lm 1 x1 x0 Lm 2 x1 x0 Lk x1 x0 Lk x1 x0 1 L L2 Lm k 1 .
(7.2.1)
其中 ( x )为连续函数,其取法不唯一,例如可取
方程(7.2.1)的解称为函数 ( x )的不动点, 求方程 (7.2.1)的解的问题称为不动点问题.
因此, 对于方程f ( x ) 0,为求出它的一个实根, 常 常将其化为求解等价的不动点问题,因为不动点 问题的形式往往更易于分析求解.
7.2
迭代法及其收敛性
本节主要内容
不动点迭代
不动点迭代的收敛性
不动点迭代的加速
非线性方程
f ( x) 0
可等价改写为
7.2.1 不动点迭代
非线性方程f ( x ) 0可等价改写为 x ( x ),
x x f ( x ), 或者 x x 5 f ( x ).


1/2
e.
x3 3 x2 8 x 5 x x . 2 3x 6x
取初始值x0 1.5,利用MATLAB编写如下m文件 Example7 _ 2 _1.m并运行，详细结果见表7.2.1.
%Example7 _ 2 _1 eps 1e 8; N 300;x0 1.5; phi1 = @(x)(x- x^ 3 - 3* x^ 2 + 8); phi 2 = @(x)((8 / x- 3* x) ^ 0.5); phi3 = @(x)(((1 / 3) * (8 - x^ 3)) ^ 0.5); phi 4 = @(x)((8 / (3 + x)) ^ 0.5); phi 5 = @(x)(x- (x^ 3 + 3* x^ 2 - 8) / (3* x^ 2 + 6 * x)); Hfun = @fixed p oint; [k, x] = feval(Hfun, phi 4, x 0,eps, N)
但对于情形(a )，迭代序列发散;在情形(b)中， 出现负数开根号，从而迭代不能继续下去.
因此, 迭代函数 ( x )的选取将会对迭代过程的收 敛性产生很大的影响.事实上, 要使迭代法产生的序 列 xk 收敛,则迭代函数 ( x )应满足一定的条件.
7.2.2 不动点迭代的收敛性
快.当L接近于1时, 收敛速度可能会较慢, 而且即使 xk 1 xk 很小, 误差 x * xk 也可能很大.
例7.2.2
1
对于例7.2.1中的选取1 x x x 3 3 x 2 8,
我们有1 1 5, 1 2 10, 因此1 x 不是从 1,2 到其自身内的映射.此外,1 ' x 1 3 x 2 6 x ,因此对 所有x [1,2], 均有 1 ' x 1.尽管定理7.2.2不能保证 算法一定失败, 但我们没有期望它收敛的理由 . 1/2 8 的选取, 易知 2 对于例7.2.1中 4 x 3 x
4 x 在[1,2] 的值域为[ 1.6, 2].此外
定理7.2.1
1如果函数 ( x )在区间 a , b 上连续,且对任意 x a , b 的有 ( x ) a , b , 则 x 在 a , b 上有
不动点.
2 进一步地, 如果 ( x )在(a, b)上存在, 且存在一个
if abs(x-x0)<eps return else x0=x; if k==N warning('算法超出最大迭代次数!') end end end
例 7.2.1
方程
f ( x) x3 3 x2 8 0
在[1, 2]内由唯一实根.有许多方法可以将方程转 化为不动点形式，例如 :
1 2 3 4 5 6 7 8 9 10 30 40 45
1.358484290 1.355301399 1.355302727 1.355301425 1.355301394
由上表数据可看出，若取迭代函数为(c )， (d )和 (e )三种情形，算法表现良好，均能较快得到方程 的近似根.
证明
g(a ) (a ) a 0, g(b) (b) b 0.
由零点定理可知, 存在p a , b 使得g ( p ) ( p) p 0, 进而有 ( p) p, 此说明p为的不动点.
2
进一步地, 假设 ( x ) L 1, x a , b .反证
k
连续, 于是
k k
x* lim xk lim xk 1 lim xk 1 x * ，
k



从而得到x *为函数 ( x )的不动点.上述迭代称为不 动点迭代, 迭代公式 7.2.2 称为不动点迭代公式,
( x )又称为迭代函数.
x k x * x k 1 x * L x k 1 x * L x k 2 x L x0 x .
* k *
2

7.2.3
由0 L 1可得 lim Lk 0,因此对上式取极限可得
k
lim xk x * lim Lk x0 x * 0
法假设p, q均为 a , b 上的不动点, 且p q, 则由中值 定理可知, 存在一个介于p, q之间的数 , 使得
( p) (q )
因此
pq
( )
p q ( p ) (q ) '( ) p q L p q p q ,
由定理7.2.2可知, lim xm x * ,因此
m


x * xk lim xm xk lim Lk x1 x0
m m
m k 1

i 0
Li
Lk x1 x0 . 1 L 此式说明 7.2.5 成立.
由上述推论可知, L越小, 序列 xk 收敛得越
2.3 令k : k 1.
2.4 令x0 : x .
步骤3 输出信息“算法超出最大迭代次数！”， 算法终止.
算法7.2的Matlab程序如下：
算法7.2的MATLAB程序
%fixed _ point.m function k, x fixed _ point(phi, x0,eps, N) %功能：用不动点解方程x = (x) fprintf ('kx \ n '); fork 1: N x phi(x0); fprintf ('%3d,%10.9f \ n ',k, x)
* x 收敛 到 a , b 中唯一的不动点 x . k
证明 由定理7.2.1可知, x 在 a , b 中有唯一不动 点x .由于 x 将 a , b 映射到其本身,因此序列 xk
*
是有定义的, 且xk [a , b], k 0.由条件⑵, 结合中值 定理可知
这是一个矛盾, 从而有p q, 此说明 a , b 上的不动 点是唯一的.
定理7.2.1的 ( x ) a, b
x
在 a , b 上连续
定理7.2.2 若函数 x 在区间 a , b 上连续，且满足
正的常数L 1使得 ( x ) L, x a , b ,
则 ( x )在 a , b 上的不动点是唯一的.
1 如果 (a ) a或者 (b) b, 则 在端点处有 不动点.否则,由 ( x ) a , b , x a , b 可知, (a ) a 且 (b) b.因此,函数g( x ) ( x ) x在 a , b 上连续, 且
下面讨论用迭代的方法求 ( x )的不动点x * .取 方程(7.2.1)解的初始近似值x0 , 通过如下迭代
xk xk 1 , k 1,2,, 产生迭代序列 xk . (7.2.2)
如果序列 xk 收敛到x * ,即 lim xk x * ,因 ( x )
a. x 1 x x x 3 3 x 2 8; 1/2 8 x 2 x 3 x ; x
b.
1 3 c. x 3 x 8 x ; 3 1/2 8 d . x 4 x ; 3 x