平面几何习题集
- 格式:doc
- 大小:145.78 KB
- 文档页数:5

大学工程制图习题集答案一、平面图形的绘制1. 根据给定的尺寸,绘制一个矩形,其长为60mm,宽为40mm。
- 解答:使用直线命令绘制两条垂直的线段,分别代表矩形的长和宽,确保它们相交于一个点。
2. 绘制一个圆,其直径为30mm,并在圆周上标出四个等分点。
- 解答:使用圆命令绘制直径为30mm的圆,然后使用点命令在圆周上绘制四个等分点。
二、立体图形的绘制1. 绘制一个正方体的三视图(正视图、侧视图、俯视图)。
- 解答:首先绘制正视图,然后根据正方体的几何特性绘制侧视图和俯视图,确保三视图的尺寸一致。
2. 绘制一个圆柱的三视图,并标注其直径和高度。
- 解答:使用圆和矩形命令绘制圆柱的正视图和侧视图,俯视图为一个圆,标注直径和高度。
三、剖面图和断面图1. 给定一个长方体,其内部有一个圆柱形空洞,绘制其剖面图。
- 解答:选择适当的剖面线,绘制长方体的剖面图,显示内部的圆柱形空洞。
2. 绘制一个带有圆孔的板的断面图。
- 解答:确定断面的位置,绘制断面图,显示板的厚度和圆孔的尺寸。
四、尺寸标注1. 对绘制的平面图形进行尺寸标注,包括长度、宽度和半径等。
- 解答:使用尺寸标注命令,对图形的各个部分进行准确的尺寸标注。
2. 对立体图形的三视图进行尺寸标注,包括长度、宽度、高度和直径。
- 解答:确保三视图中的尺寸标注清晰、准确,反映立体图形的实际尺寸。
五、公差标注1. 对平面图形的尺寸进行公差标注。
- 解答:根据公差标准,对平面图形的尺寸进行适当的公差标注。
2. 对立体图形的尺寸进行公差标注。
- 解答:同样根据公差标准,对立体图形的尺寸进行公差标注,确保制造精度。
结束语工程制图是一项重要的技能,它要求精确和细致。
通过不断的练习和学习,可以提高制图能力,为未来的工程实践打下坚实的基础。
希望这份习题集答案能够帮助同学们更好地理解和掌握工程制图的相关知识。
请注意,以上内容仅为示例,具体的习题集答案应根据实际的习题内容来编写。

2021IMO中国国家集训队平面几何练习题几何讲义1.一圆o切于两条平行线l1,l2,第二个圆?o1切l1于a,外切?o于c,第三个圆?o2切外切?o于d,外切?o1于e,ad交bc于q,求证q是?cde的外心。
(35届imol2于b,预选题)证明由ao1∥bo2,言?ao1e??bo2e??,从而存有?aeo1??beo2,即a,e,b三点共线。
同理由of∥bo2,可得b,d,f三点共线。
又因为11?edb?180eo2b?180ao1e??eaf,所以a,e,d,f四点共圆,22be?ba?bd?bf,即点b在?o1与?o的根轴上。
又因为c在?o1与?o的根轴上,所以bc是?o1与?o的根轴。
同理ad是?o2与?o的根轴,因此q为根心,且有qc?qd?qe,即q 是?cde的外心。
2.非全等?abc的内切圆圆心为i,其与bc,ca,ab分别切线于点a1,b1,c1,aa1,bb1分别交圆于a2,b2,?a证明1b1c1中?c1a1b1,?c1b1a1的角平分线分别交b3,b3,1c1,ac11于点a(1)a2a3就是?b1a2c1的角平分线;(2)如果p,q就是?a1a2a3和?b1b2b3的两个外接圆的交点,则点i在直线pq上。
(01年保加利亚)c1a2aa2aa2b1a2cacaca,从而有12?11?13,即a2a3是?b1a2c1的角平分线。
c1a1ac1ab1b1a1b1a2b1a1b1a3o,连oi,ia2,oa2,oa1,则oi?a1a2。
由于?a1a3a2?(2)设立?a1a2a3的外心为ac11a2c1a2a3c1a1a3ac11a2a2oi1c1a2b1c1a1b190ac11a2,所以21?a2oa1?180a1a3a2?90ac于是有?ia2o?90?,11a2?90a2io,2即ia2与?o相切于a2。
同理ib2与?b1b2b3的外接圆相切于b2,从而i在?o与?b1b2b3的外接圆的根轴上,即i,p,q三点共线。
db cab ’ a ’c’ d ’ Xb 1'd 1'c 1'a 1'c 1d 1m 1n 1'b 1(a 1)m 1'm’n ’nmX1X2n 12-4 直线与平面、平面与平面的相对位置1.求直线AB与平面的交点,并判别直线的可见性。
4.求两平面的交线。
6.作一直线使与两交叉直线AB,CD相交,同时平行于直线KL。
作直线AE平行于直线KL;求CD与平面(AE和AB确定)的交点M;作MN平行于KL。
7.过点C作CD平行于AB,且点D于A,B等距。
距离说明:为使图形清晰,将AB 的正面投影改变了一些方向。
过AB 的中点E 作AB 的中垂面;求CD 与中垂面的交点D 。
其中MN 为PH 中垂面的交线。
8.求点K 到直线AB 的距离。
距离9.求点A 到三角形BCD 的距离。
说明:为使图形清晰,将A 点的水平投影 往上移动了一些。
11.已知线段AB,CD正交,作线段AB的正面投影。
13.过点K作直线与交叉两直线AB和CD相交。
交叉二直线DE,FG相交,并垂直于三角形ABC。
作直线BC垂直于平面;求三角形ABC的实形(略);90°减角ABC即为所求(略)。
15.求直线与平面之间的夹角。
作直线EM垂直于三角形ABC;求FG与平面(DE和EM确定)的交点K;过K作EM的平行线KN。
16.已知菱形ABCD的一边AD在直线AE上,另一边AB平行于三角形LMN,点B在直线FG上,求作菱形的两面投影。
Y坐标差16.过点A作平行于三角形LMN的平面;求FG与平面的交点B;求AB的实长,AE的实长,在AE上截取AD=AB,得D;再作AB,AD的平行线即可。
2-5 投影变换1.用换面法求直线AB的实长及其与H面的倾角α。
2.已知AB垂直于BC,补全BC的水平投影。
4.已知点A与三角形DEF的距离为10,求A的正面投影。
7.已知两平行直线AB及CD相距15mm,求CD的水平投影。
![高等几何习题集[1]2](https://uimg.taocdn.com/946569ff846a561252d380eb6294dd88d0d23d08.webp)
高等几何习题集习题1.11.证明:任一三角形都有一个内切椭圆,其切点为三边的中点,中心为三角形的重心;同时有一个外接椭圆以三角形的重心为中心。
2.平行于平行四边形ABCD 对角线AC 作一直线与AB 、BC 交于点E 、F ,证明:三角形AED 和CDF 的面积相等。
3.在椭圆的内接三角形的顶点作切线构成外切三角形,证明:如果这两上三角形有两对边平行,则第三对边也平行。
4.过三角形ABC 内任一点P 作DE//BC ,交AB 、AC 于E 、E ,作FG//CA 交BC 、BA 于F 、G ,作HK//AB 交BC 、CA 于H 、K ,证明:=++ABHK CA FG BC DE 常数。
5.设X 、Y 是三角形ABC 的边AB 、CA 上的动点,满足BX :XA=CY :Y A 。
证明:BY 与CX 的交点在一条定直线上。
6.设D 、E 、F 各是三角形ABC 的边BC 、CA 、AB 上的点,且DE//AB ,DF//CA ,证明:CD E BFD AEF S S S ∆∆∆⋅=2。
7.将三角形的每边三等分,将每个分点与三角形的对顶点相连,这六条直线构成一个六边形,证明:此六边形的三双对顶点的连线共点。
8.在三角形ABC 的边BC 、CA 、AB 上取点D 、E 、F 使BD :DC = CE :EA = AF :FB = 1 :n 。
设AD 交BE 于L ,BE 交CF 于K ,CF 交AD 于M ,证明:1122++-=n n n S S ABC LKM )(∆∆ 。
9.设点D 、E 、F 分别位于三角形ABC 的边BC 、CA 、AB 上,且BD :DC=CE :EA=AF :FB ,三线AD 、BE 、CF 构成三角形PQR ,证明:三角形ABC 、DEF 和PQR 具有共同的重心。
10.过椭圆的弦AB 的中点C 任作二弦PQ 和ST ,PS 、QT 分别交AB 于M 、N ,证明:MC=CN 。

平面几何练习题及解答一、直线与角度1. 给定一条直线L1和两条直线L2和L3,若L1与L2垂直,L2与L3平行,则L1与L3之间的夹角为多少度?解答:由于L1与L2垂直,可得出L2的斜率为无穷大,即L2为竖直线。
而L2与L3平行,说明它们具有相同的斜率。
因此,L3的斜率也为无穷大,即L3也是竖直线。
由此可知,L1与L3之间的夹角为90度。
2. 给定一条直线L和两点A、B,若L与AB的垂线相交于点M,且角AMB为40度,则角LMA的度数是多少?解答:由垂线的性质可得出,角LMA与角AMB互补,它们的度数和为90度。
已知角AMB为40度,因此角LMA的度数为90度减去40度,即50度。
二、三角形3. 已知三角形ABC,其中∠B = 90度,AB = 3 cm,BC = 4 cm,求AC的长度。
解答:根据勾股定理可得:AC² = AB² + BC²AC² = 3² + 4²AC² = 9 + 16AC² = 25AC = √25AC = 5 cm4. 已知三角形ABC,其中AB = 6 cm,BC = 8 cm,AC = 10 cm,求∠B的度数。
解答:根据余弦定理可得:BC² = AB² + AC² - 2 * AB * AC * cosB8² = 6² + 10² - 2 * 6 * 10 * cosB64 = 36 + 100 - 120 * cosB64 = 136 - 120 * cosB120 * cosB = 136 - 64120 * cosB = 72cosB = 72 / 120cosB = 0.6根据反余弦函数可得:∠B = arccos(0.6)∠B ≈ 53.13度三、圆的性质5. 在平面直角坐标系中,给定圆心为O(2, 3),半径为5的圆C,点P(6, 7)是否在圆C上?解答:利用距离公式可计算OP的距离:OP = √((6-2)² + (7-3)²)OP = √((4)² + (4)²)OP = √(16 + 16)OP = √32OP ≈ 5.66由于OP的长度不等于圆C的半径,即5.66不等于5,因此点P不在圆C上。

高三数学解析几何习题集
一、直线与平面
1. 已知直线L1的方程为x + 2y - 3 = 0,点A(2, -1)在该直线上,求直线L1与直线L2:2x - y + 4 = 0的交点坐标。
2. 平面α过点A(1, -2, 3),且与直线L:x = 2 + 3t,y = -1 - t,z = 3t相交于点P(5, 1, -2),求平面α的方程。
3. 已知平面α与平面β垂直,平面α通过点A(1, 2, -1),平面β通过直线L:x = 2 - 4t,y = t,z = 3t,求平面β的方程。
二、曲线的方程
1. 曲线C为椭圆,已知其焦点F1(-3, 0),F2(3, 0),且顶点为(0, 2),求曲线C的方程。
2. 曲线C为双曲线,已知其离心率为2,焦点为F1(3, 0),F2(-3, 0),求曲线C的方程。
3. 曲线C为抛物线,已知其焦点为F(2, -1),过顶点V(0, 0),求曲线C的方程。
三、空间向量与坐标系
1. 已知向量AB = 2i + j - k,向量AC = i - 2j + 3k,求向量BC的坐标表示。
2. 平行四边形ABCD中,已知向量AB = 2i - 3j + 4k,向量AC = 3i + 4j - k,求向量BD的坐标表示。
3. 在XYZ坐标系中,已知A(2, -1, 3),B(-1, 2, -3),C(4, 3, -2),求三角形ABC的面积。
以上是高三数学解析几何习题集的部分题目,希望能对高三学生的数学学习有所帮助。
请自行努力解答,并核对答案,巩固知识理解和运用能力。
祝你学业进步,取得优异成绩!。
初中几何经典习题集(不做后悔)1.如图3,在Rt △ABC 中,∠B=90°,它的内切圆分别与边BC 、CA 、AB 相切于点D 、E 、F ,连接AD 与内切圆相交于另一点P ,连接PC 、PE 、PF 、FD ,且PC ⊥PF . 求证:(1)△PFD ∽△PDC ; (2)EP PDDE DC=2.如图,AB 是⊙O 的直径,AC 是弦,点D 是⋂AC 上一点,弦DE ⊥AB 交AC 于F ,交AB 于H ,交⊙O 于E ,P 是ED(1)若PC =PF ,判断PC 与⊙O 的位置关系,并说明理由;(2)若⋂⋂=CD DA ,31sin =∠BAC,求ADE ∠sin 的值.3.如图,BC 是半圆O 的直径,EC 是切线,C 是切点,割线EDB 交半圆O 于D ,A 是半圆O 上一点,AD=DC ,EC=3,BD=2.5(1)求tan ∠DCE 的值;(2)求AB 的长.4.如图,P 是⊙O 外一点,割线PA 、PB 分别与⊙O 相交于A 、C 、B 、D 四点,PT•切⊙O 于点T ,点E 、F 分别在PB 、PA 上,且PE=PT ,∠PFE=∠ABP . (1)求证:PD ·PF=PC ·PE ; (2)若PD=4,PC=5,AF=2120,求PT 的长.5.已知AB 是⊙O 的直径,弦CD ⊥AB 于E ,F 是DC 延长线上的一点,FA 、FB 与⊙O 分别交于M 、G ,GE 与⊙O 交于点N 。
(1)求证:AB 平分∠MAN ;(2) 若⊙O 的半径为5,FE=2CE=6,求线段AN 的长。
ABO PBAEA6.已知:如图,∠ACB =60°,CE 为∠ACB 的角平分线,O 为射线CE 上的一点,⊙O 切AC 于点D .(1)求证:BC 与⊙O 相切; (2)若⊙O 的半径为6,P 为⊙O 上一点,且使得∠DPC =90°,求DP 的长7.如图,点P 为△ABC 的内心,延长AP 交△ABC 的外接圆于D ,在AC 延长线上有一点E ,满足AD 2=AB ·AE ,求证:DE 是⊙O 的切线.1.已知:如图,点O 为等腰直角三角形ABC 的重心, 90=∠CAB ,直线m 过点O ,过C B A 、、三点分别作直线m 的垂线,垂足分别为点F ED 、、.(1)当直线m 与BC 平行时(如图1),请你猜想线段CF BE 、和AD 三者之间的数量关系并证明;(2) 当直线m 绕点O 旋转到与BC 不平行时,分别探究在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段CF BE AD 、、三者之间又有怎样的数量关系?请写出你的结论,不需证明.2.如图1,在Rt △ABC 中,∠ABC=90°, ∠B=30°,AD 为BC 边上的中线,E 为AD 上一动点,设DE=nEA ,连结CE 并延长交AB 于点F ,过点F 作FG ∥AC 交AD (或延长线)于点G 。
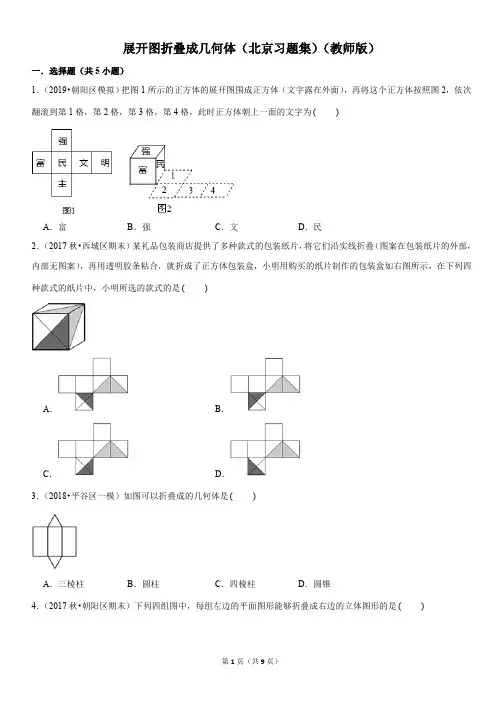
一、选择题1. 一个由小正方体组成的几何体,从不同方向看到的是,这是由()个小正方体组成的几何体。
A.3 B.4 C.5 D.62. 用小正方体摆成的组合体,从正面看是,从左面看是,从上看是。
这个组合体是()。
A.B.C.D.3. 下图是从上面看一些小正方体所搭几何体的平面图。
方格中的数字表示该位置小正方体的个数,则这个几何体从左面看是()。
A.B.C.D.4. 一个由五个小正方体组成的几何体,从前面看是,从左面看是,这个几何体的形状可能是()。
A.B.C.5. 如图,它是由6个同样大的小正方体摆成的几何体。
将①号小正方体移走后,从正面、上面和左面观察新几何体与原几何体相比,下列说法正确的是()。
A.从正面看到的图形没有发生改变B.从上面看到的图形没有发生改变C.从左面看到的图形没有发生改变D.从任何一面看到的图形都发生了改变二、填空题6. 一个立体图形,从上面和左面看到的形状如下图:它可能是下面的哪一个?在合适的图形下面画“√”。
7. 一些小方块拼组成的图形,从正面看是,从左面看也是这些小方块至少有( )个。
8. 把正确答案的序号填在()里。
(1)如果用4个小正方体,可以怎样摆?( )(2)如果用5个小正方体,可以怎样操?( )(3)如果用6个小正方体,可以怎样摆?( )(4)如果用7个小正方体,可以怎样摆?( )9. 小王用棱长1厘米的小正方体摆成一个物体,从前面、右面和上面分别观察这个物体,看到的形状如下图,这个物体的表面积是( )平方厘米。
10. 一个立体图形,从上面看到的形状是,从左边看到的形状是。
搭这样的立体图形,最少需要 ( )个小立方体。
三、解答题11. 在下图中添上一个同样大的正方体,使得从左面看到的图形不变。
想一想,一共有多少种不同的添法?(添上的正方体和原来的图形至少有一个面连在一起)12. 梦梦说:“我用相同的正方体搭了下面立体图形中的一个,这个立体图形从正面看是4个正方形,从右面看是2个正方形,从上面看是3个正方形,且从正面看上面的正方形在中间。
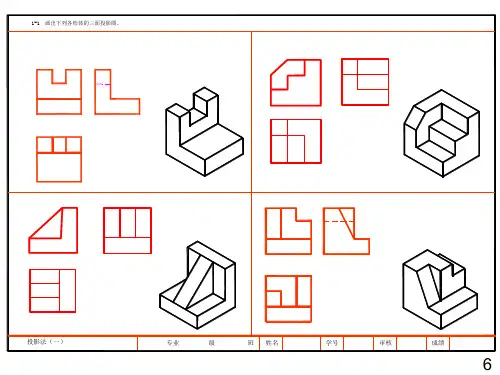
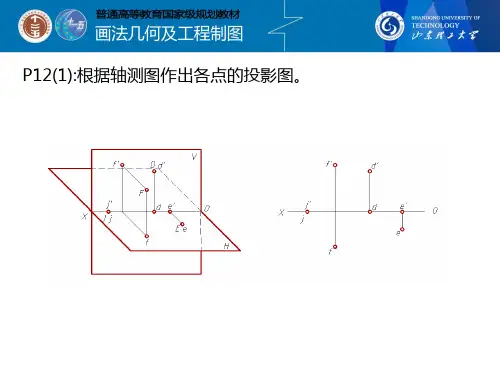
画法几何习题集答案问题一:如何确定一个平面图形在空间中的投影?答案:确定一个平面图形在空间中的投影,首先需要确定投影面和视图。
通常,我们使用正投影法,将图形投影到三个相互垂直的平面上,即前视图(正视图)、侧视图和俯视图。
通过这三个视图,可以完整地表达出空间图形的形状和尺寸。
问题二:如何绘制一个长方体的三视图?答案:绘制长方体的三视图需要从三个不同的方向观察长方体。
首先,绘制前视图,显示长方体的正面和侧面;然后,绘制侧视图,显示长方体的侧面和背面;最后,绘制俯视图,显示长方体的顶面和底面。
每个视图都应该展示长方体的相应边长和高度。
问题三:如何通过已知的两个视图来恢复第三个视图?答案:通过已知的两个视图来恢复第三个视图,需要利用空间几何关系和已知的尺寸。
首先,分析已知视图中的尺寸和形状,确定缺失视图的轮廓。
然后,根据已知视图中的尺寸和比例,计算缺失视图中的线段长度和角度。
最后,将计算出的数据绘制成缺失的视图。
问题四:如何判断两个平面图形是否平行或垂直?答案:判断两个平面图形是否平行或垂直,可以通过观察它们的投影。
如果两个图形在所有视图中的投影都保持相同的相对位置,并且没有相交线,那么这两个图形是平行的。
如果两个图形在某个视图中的投影相交于一条直线,并且在其他视图中没有相交,那么这两个图形是垂直的。
问题五:如何计算空间中两点之间的距离?答案:计算空间中两点之间的距离,可以使用空间两点距离公式。
设两点的坐标分别为 \( P_1(x_1, y_1, z_1) \) 和 \( P_2(x_2, y_2, z_2) \),则两点之间的距离 \( d \) 可以通过以下公式计算:\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \]结束语:画法几何习题的解答需要对空间图形有深刻的理解,以及对几何原理和绘图技巧的熟练掌握。
通过不断的练习和思考,可以提高解决画法几何问题的能力。
画法几何习题集第八版答案画法几何是一门重要的学科,它与数学和艺术有着密切的联系。
对于学习画法几何的人来说,习题集是必不可少的学习资料。
而《画法几何习题集第八版》则是一本被广泛使用的教材。
在这篇文章中,我将为大家提供《画法几何习题集第八版》的答案,帮助学习者更好地理解和掌握画法几何的知识。
第一章:基本几何概念1. 直线和线段的区别在于直线没有端点,而线段有两个端点。
2. 平行线是指在同一个平面内永远不会相交的线。
3. 垂直线是指两条直线相交时,相交角度为90度的线。
第二章:角的性质和分类1. 锐角是指小于90度的角。
2. 钝角是指大于90度但小于180度的角。
3. 平角是指等于90度的角。
第三章:三角形的性质和分类1. 等边三角形是指三条边长度相等的三角形。
2. 等腰三角形是指两条边长度相等的三角形。
3. 直角三角形是指其中一个角度为90度的三角形。
第四章:四边形的性质和分类1. 矩形是指四条边都相等且所有角都为直角的四边形。
2. 平行四边形是指对边平行的四边形。
3. 菱形是指四条边都相等的四边形。
第五章:圆的性质和相关定理1. 圆是指平面上所有到圆心距离相等的点的集合。
2. 弧是指圆上两个点之间的一段曲线。
3. 弦是指圆上连接两个点的线段。
第六章:相似三角形和比例1. 相似三角形是指对应角度相等的三角形。
2. 比例是指两个数之间的大小关系。
第七章:三角函数1. 正弦函数是指一个角的对边与斜边之比。
2. 余弦函数是指一个角的邻边与斜边之比。
3. 正切函数是指一个角的对边与邻边之比。
第八章:向量和坐标1. 向量是指有大小和方向的量。
2. 坐标是指在平面上用数对表示点的位置。
通过以上习题集的答案,我们可以更好地理解和掌握画法几何的知识。
画法几何不仅仅是一门学科,更是一门能够培养我们逻辑思维和创造力的艺术。
通过学习画法几何,我们可以培养自己的观察力和分析能力,提高我们的空间想象力和美感。
因此,我希望大家能够认真学习画法几何,掌握其中的技巧和方法,从而在艺术创作和数学应用中有所突破。
解答题 1、(2008广东)如图5,在△ABC 中,BC>AC , 点D 在BC 上,且DC =AC,∠ACB 的平分线
CF 交AD 于F ,点E 是AB 的中点,连结EF.求证:△ABD ∽△AEF .
2、(2008湖北武汉)(本题6分)如图,点D ,E 在BC 上,且FD ∥AB ,FE ∥AC 。
求证:△ABC ∽△FDE .
3(2008 湖南 怀化)如图10,四边形ABCD 、DEFG 都是正方形,连接AE 、CG,AE 与CG 相交
于点M ,CG 与AD 相交于点N . 求证:(1)CG AE =;
(2).MN CN DN AN ∙=∙
4(2008年江苏省南通市)如图,四边形ABCD 中,AD =CD ,∠DAB =∠ACB =90°,过点D 作DE ⊥AC ,垂足为F ,DE 与AB 相交于点E. (1)求证:AB ·AF =CB ·CD
(2)已知AB =15cm ,BC =9cm ,P 是射线DE 上的动点.设DP =xcm (x >0),
四边形BCDP 的面积为ycm 2
.
①求y 关于x 的函数关系式;
②当x 为何值时,△PBC 的周长最小,并求出此时y 的值.
F E D C B A D P A E F C B
第5题图
A B
C
D E P
O
R 图
5、(2008安徽)如图,四边形ABCD 和四边形ACED 都是平行四边形,点R 为DE 的中点,
BR 分别交AC CD ,于点P Q ,.
(1)请写出图中各对相似三角形(相似比为1除外); (2)求::BP PQ QR .
6(2008年广东梅州市)本题满分8分.
如图10所示,E 是正方形ABCD 的边AB 上的动点, EF ⊥DE 交BC 于点F . (1)求证: ∆ADE ∽∆BEF ;
(2)设正方形的边长为4, AE =x ,BF =y .当x 取什么值时, y 有最大值?并求出这个最大值.
7.(2008年广东梅州市)本题满分8分.
如图8,四边形ABCD 是平行四边形.O 是对角线AC 的中点,过点O 的直线EF 分别交AB 、DC 于点E 、F ,与CB 、AD 的延长线分别交于点G 、H .
(1)写出图中不全等的两个相似三角形(不要求证明);
(2)除AB =CD ,AD =BC ,OA =OC 这三对相等的线段外,图中还有多对相等的线段,请选出其中一对加以证明.
y x
A
O
C B
8(08山东省日照市)在△ABC 中,∠A=90°,AB =4,AC =3,M 是AB 上的动点(不与A ,B 重合),过M 点作MN∥BC 交AC 于点N .以MN 为直径作⊙O ,并在⊙O 内作内接矩形AMPN .令AM =x .
(1)用含x 的代数式表示△MNP 的面积S ; (2)当x 为何值时,⊙O 与直线BC 相切?
(3)在动点M 的运动过程中,记△MNP 与梯形BCNM 重合的面积为y ,试求y 关于x 的函数表达式,并求x 为何值时,y 的值最大,最大值是多少?
9\(2008年福建省福州市)(本题满分13分)
如图,已知△ABC 是边长为6cm 的等边三角形,动点P 、Q 同时从A 、B 两点出发,分别沿AB 、BC 匀速运动,其中点P 运动的速度是1cm/s ,点Q 运动的速度是2cm/s ,当点Q 到达点C 时,P 、Q 两点都停止运动,设运动时间为t (s ),解答下列问题: (1)当t =2时,判断△BPQ 的形状,并说明理由; (2)设△BPQ 的面积为S (cm 2),求S 与t 的函数关系式;
(3)作QR //BA 交AC 于点R ,连结PR ,当t 为何值时,△APR ∽△PRQ ?
10、(2008 黑龙江)如图,在平面直角坐标系中,点(30)C -,
,点A B ,分别在x 轴,y 轴的正半轴上,且满足2
310OB OA -+-=.
(1)求点A ,点B 的坐标.
(2)若点P 从C 点出发,以每秒1个单位的速度沿射线CB 运动,连结AP .设ABP △的面积为S ,点P 的运动时间为t 秒,求S 与t 的函数
关系式,并写出自变量的取值范围. (3)在(2)的条件下,是否存在点P ,使以点A B P
,,为顶点的三角形与AOB △相似?若存在,请直接写出
A B
C M N P 图 8 O (第9题)
点P 的坐标;若不存在,请说明理由.
11.(2008扬州)如图,在△ABD 和△ACE 中,AB=AD ,AC=AE ,∠BAD=∠CAE ,连结BC 、DE 相交于点F ,BC 与AD 相交于点G.
(1)试判断线段BC 、DE 的数量关系,并说明理由
(2)如果∠ABC=∠CBD ,那么线段FD 是线段FG 和FB 的比例中项吗?为什么?
G
F
A
C
E
B
D
12((08浙江温州)如图,在Rt ABC △中,90A ∠=,6AB =,8AC =,D E ,分别是边AB AC ,的中点,点P 从点D 出发沿DE 方向运动,过点P 作PQ BC ⊥于Q ,过点Q 作QR BA ∥交AC 于R ,当点Q 与点C 重合时,点P 停止运动.设BQ x =,
QR y =.
(1)求点D 到BC 的距离DH 的长;
(2)求y 关于x 的函数关系式(不要求写出自变量的取值范围);
(3)是否存在点P ,使PQR △为等腰三角形?若存在,请求出所有满足要求的x 的值;若不存在,请说明理由.
A B
C
D E
R P H Q
(第1题图)
G F E D C B A 13、(08中山)将两块大小一样含30°角的直角三角板,叠放在一起,使得它们的斜边AB 重合,直角边不重合,已知AB=8,BC=AD=4,AC 与BD 相交于点E ,连结CD .
(1)填空:如图9,AC= ,BD= ;四边形ABCD 是 梯形. (2)请写出图9中所有的相似三角形(不含全等三角形).
(3)如图10,若以AB 所在直线为x 轴,过点A 垂直于AB 的直线为y 轴建立如图10
的平面直角坐标系,保持ΔABD 不动,将ΔABC 向x 轴的正方向平移到ΔFGH 的位置,FH 与BD 相交于点P ,设AF=t ,ΔFBP 面积为S ,求S 与t 之间的函数关系式,并写出t 的取值值范围.
.
14、(2008 湖北 恩施) 如图11,在同一平面内,将两个全等的等腰直角三角形ABC 和AFG 摆放在一起,A 为公共顶点,∠BAC =∠AGF =90°,它们的斜边长为2,若∆ABC 固定不动,∆AFG 绕点A 旋转,AF 、AG 与边BC 的交点分别为D 、E (点D 不与点B 重合,点E 不与点C 重合),设BE =m ,CD =n.
(1)请在图中找出两对相似而不全等的三角形,并选取其中一对进行证明. (2)求m 与n 的函数关系式,直接写出自变量n 的取值范围.
(3)以∆ABC 的斜边BC 所在的直线为x 轴,BC 边上的高所在的直线为y 轴,建立平面直
角坐标系(如图12).在边BC 上找一点D ,使BD =CE ,求出D 点的坐标,并通过计算验证
BD 2+CE 2=DE 2.
(4)在旋转过程中,(3)中的等量关系BD
2
+CE 2
=DE 2
是否始终成立,若成立,请证明,若不成立,请说明理由.
G
y x
O F
E D C B A
D
C
B
A
E
图9
E D
C H
F
G B
A
P
y
x 图10。