画法几何习题集答案

几何画法习题集答案几何画法是数学中一个重要的分支，它涉及到图形的构造、测量和证明。

以下是一份几何画法习题集的答案，供同学们参考。

习题一：构造等边三角形答案：首先，选择一点A作为顶点。

然后，以点A为圆心，以AB为半径画圆，与圆相交的点B即为等边三角形的底边端点。

接着，以点B为圆心，以BC为半径画圆，与第一个圆相交的点C即为等边三角形的另一个顶点。

连接AB、BC、CA，得到等边三角形ABC。

习题二：构造平行四边形答案：首先，画一条直线AB。

然后，在直线AB上任取一点C，以点C为圆心，以AC为半径画圆，与直线AB相交于点D。

连接CD和DA，得到平行四边形ABCD。

习题三：构造直角三角形答案：首先，画一条直线AB。

然后，以点A为圆心，以AB为半径画圆。

接着，以点B为圆心，以BC为半径画圆，其中BC等于AB。

两个圆的交点即为直角三角形的顶点C。

连接AC和BC，得到直角三角形ABC。

习题四：构造正六边形答案：首先，画一条直线AB。

然后，以点A为圆心，以AB为半径画圆。

接着，以点B为圆心，以AB为半径画圆。

两个圆的交点C和D为正六边形的顶点。

重复上述步骤，构造出正六边形的另外两个顶点E和F。

连接AB、BC、CD、DE、EF和FA，得到正六边形ABCDEF。

习题五：构造等腰梯形答案：首先，画一条直线AB作为底边。

然后，以点A和点B为圆心，以AC和BD为半径画圆，其中AC等于BD。

两个圆的交点C和D为等腰梯形的顶点。

连接AC、BD、CD，得到等腰梯形ABCD。

以上是几何画法习题集的部分答案，希望能够帮助同学们更好地理解和掌握几何画法的技巧。

在实际操作中，同学们应该亲自动手尝试，以加深对几何图形构造的理解。

db c ab’a’c’d’Xb1'd1'c1'a1'c1d1m1n1'b1（a1）m1'm’n’nmX1 X2n12-4 直线与平面、平面与平面的相对位置1.求直线AB与平面的交点，并判别直线的可见性。

4.求两平面的交线。

6.作一直线使与两交叉直线AB,CD相交，同时平行于直线KL。

作直线AE平行于直线KL；求CD与平面（AE和AB确定）的交点M；作MN平行于KL。

7.过点C作CD平行于AB，且点D于A,B等距。

说明：为使图形清晰，将AB的正面投影改变了一些方向。

过AB的中点E作AB的中垂面；求CD与中垂面的交点D。

其中MN为P H中垂面的交线。

8.求点K到直线AB的距离。

距离距离9.求点A到三角形BCD的距离。

说明：为使图形清晰，将A点的水平投影往上移动了一些。

11.已知线段AB,CD正交，作线段AB的正面投影。

13.过点K作直线与交叉两直线AB和CD相交。

14.作一直线使与交叉二直线DE,FG相交，并垂直于三角形ABC。

作直线BC垂直于平面；求三角形ABC的实形（略);90°减角ABC即为所求（略)。

15.求直线与平面之间的夹角。

作直线EM垂直于三角形ABC;求FG与平面（DE和EM确定）的交点K；过K作EM的平行线KN。

16.已知菱形ABCD的一边AD在直线AE上，另一边AB平行于三角形LMN，点B在直线FG上，求作菱形的两面投影。

16.过点A 作平行于三角形LMN 的平面；求FG 与平面的交点B;求AB 的实长，AE 的实长，在AE 上截取AD=AB,得D;再作AB,AD 的平行线即可。

2-5 投影变换1.用换面法求直线AB 的实长及其与H 面的倾角α。

2.已知AB 垂直于BC ，补全BC 的水平投影。

Y坐标差4.已知点A与三角形DEF的距离为10，求A的正面投影。

7.已知两平行直线AB及CD相距15mm,求CD的水平投影。

11.在直线AB上找一点K使它与三角形MNC及三角形MND等距。

画法几何考试题及答案一、选择题（每题2分，共10分）1. 在正投影法中，平面图形的三个视图是：A. 正视图、侧视图、俯视图B. 左视图、右视图、俯视图C. 正视图、后视图、仰视图D. 俯视图、仰视图、侧视图答案：A2. 点的投影规律中，水平投影和垂直投影之间的关系是：A. 相等B. 垂直C. 倾斜D. 平行答案：D3. 线段在正投影中的实长与在水平投影中的影长之间的关系是：A. 相等B. 垂直C. 倾斜D. 不确定答案：A4. 在画法几何中，平面图形的对称性质不包括：A. 对称中心B. 对称轴C. 对称线D. 对称面答案：D5. 以下哪个不是平面图形的基本视图？A. 正视图B. 侧视图C. 斜视图D. 俯视图答案：C二、填空题（每题2分，共10分）1. 在画法几何中，______投影法是一种常用的投影方法，它能够直观地表达出物体的三个面。

答案：正2. 当一个平面图形与投影面平行时，其投影与原图形______。

答案：相似3. 在画法几何中，一个点在三个投影面上的投影构成一个______。

答案：三点4. 线段的实长是指线段在______投影中的真正长度。

答案：正5. 当一个平面图形与投影面垂直时，其投影为______。

答案：一条线三、简答题（每题10分，共20分）1. 请简述正投影法的基本原理及其在工程制图中的应用。

答案：正投影法是一种将三维空间中的物体投影到二维平面上的技术。

它基于的原理是物体的三个视图（正视图、侧视图、俯视图）能够全面表达物体的形状和尺寸。

在工程制图中，正投影法被广泛应用于绘制零件图、装配图等，因为它能够提供清晰、准确的尺寸信息，便于工程设计和制造。

2. 描述如何确定一个平面图形在正投影中的投影方向。

答案：确定一个平面图形在正投影中的投影方向，首先需要确定观察者的位置和视角。

通常，观察者位于投影面的一侧，面向投影面。

然后，根据物体相对于观察者的方向，确定其在投影面上的投影。

例如，如果物体正面朝向观察者，那么正视图将直接投影在投影面上；如果物体侧面朝向观察者，那么侧视图将投影在投影面上。

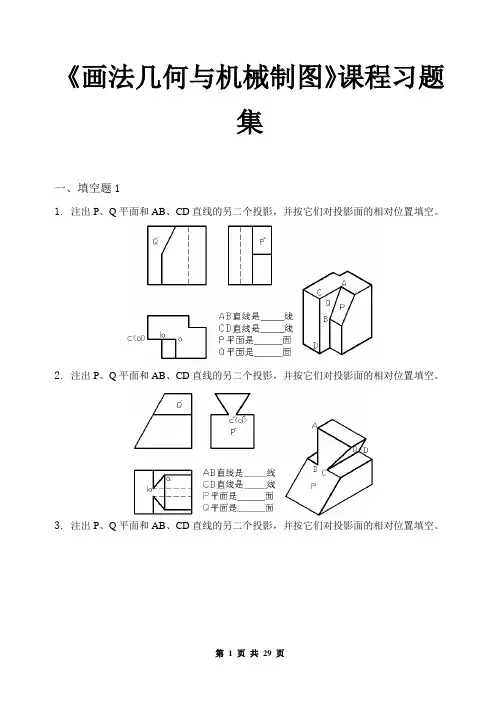
《画法几何与机械制图》课程习题集一、填空题11.注出P、Q平面和AB、CD直线的另二个投影，并按它们对投影面的相对位置填空。

2.注出P、Q平面和AB、CD直线的另二个投影，并按它们对投影面的相对位置填空。

3.注出P、Q平面和AB、CD直线的另二个投影，并按它们对投影面的相对位置填空。

4.注出P、Q平面和AB、CD直线的另二个投影，并按它们对投影面的相对位置填空。

5.判断并填写两直线的相对位置关系。

二、综合设计题6.分析下列螺纹及其连接的错误，在其右方做出正确的视图。

7.分析下列螺纹及其连接的错误，在其右方做出正确的视图。

8.读懂拨叉图，并填空：1、图中B—B是断面图；K是视图；2、在图上标出零件长、宽、高三个方向的尺寸基准；3、零件属于类零件，这种零件一般需要的视图表示，其材料是（写出牌号）；4、图中右上角符号“”表示。

9.读懂轴的零件图，填空并补画出断面图B-B。

1、表达轴类零件结构一般采用个基本视图，此视图必定是视图。

2、该零件要求表面粗糙度的最小值是。

3、在图中用箭头和指引线指出高度和宽度尺寸基准。

4、6φ表示。

26k5、该零件的AA-是断面图，该零件有个退刀槽，6、图右上角表示。

7、补画出轴上（B-B）断面图。

10.读懂下面阀杆的零件图，并填空：1、该零件长度方向的尺寸基准是、高度方向的尺寸基准是。

2、图中右上角注出的“其余”的含义是。

3、图中尺寸12是；50是；SR20是。

（总体尺寸、定位尺寸或者定形尺寸）4、11表示基本尺寸是，基本偏差代号是，公差等级代号是。

18d5、阀杆零件的材料是（填牌号）。

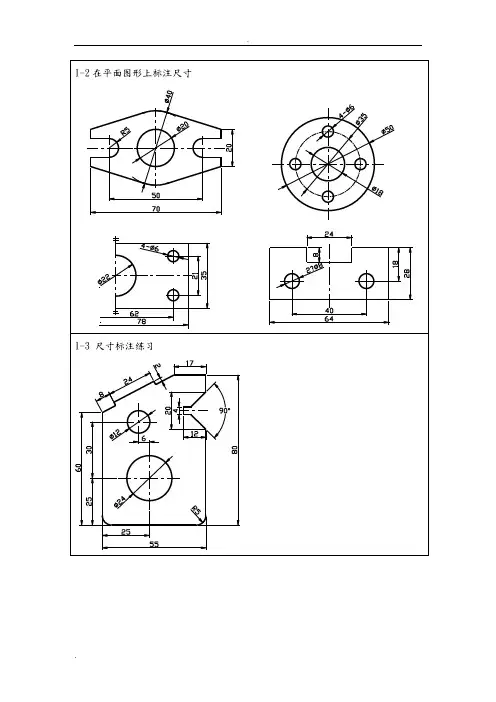
三、作图题111.分析下列形体，标注其尺寸（从图中直接量取，取整数）。

12.对下面的形体进行尺寸标注（取整，四舍五入）。

13.分析下列形体，标注其尺寸（从图中直接量取，保留一位小数）。

14.标注组合体的尺寸（取整数，四舍五入）。

15.对下面形体进行尺寸标注（取整，四舍五入）。

16.读懂两视图，补画第三视图。

画法几何考试题及答案一、选择题1. 在平面上，两条相交直线最多可以交于几个点？A. 1个B. 2个C. 3个D. 无限个答案：D. 无限个2. 下列哪个是等腰三角形？A. 直角三角形B. 锐角三角形C. 钝角三角形D. 等边三角形答案：A. 直角三角形3. 以下哪个图形不是多边形？A. 三角形B. 圆形C. 正方形D. 梯形答案：B. 圆形4. 若两个角的和等于180度，则称这两个角为什么关系？A. 互补角B. 相邻角C. 对顶角D. 补角答案：A. 互补角5. 下列哪个是多面体？A. 圆锥B. 圆柱C. 正方体D. 圆球答案：C. 正方体二、填空题1. 用尺规画一个与已知直线段平行的直线段的步骤是先__________，再__________。

答案：画一个切线，然后沿着这个切线平行移动直线段。

2. 下列哪个是不等于180度的角？A. 钝角B. 直角C. 平角D. 锐角答案：C. 平角3. 已知ΔABC中，∠B = 90度，若AC = 5cm，BC = 12cm，则AB = __________。

答案：AB = √(AC² + BC²) = √(5² + 12²) = √(25 + 144) = √169 = 13cm4. 平行四边形的对边长度相等，且对角线__________。

答案：互相等长且平分对方。

5. 正方体有多少个面？答案：六个。

三、解答题1. 画出一个等边三角形并标明边长。

解答：（示意图）A/ \/___\B CAB = AC = BC2. 画出一个矩形并标明长和宽。

解答：（示意图）A_______B| || ||_______|AB为长，BC为宽。

3. 给出一个圆，画出一个切线。

解答：（示意图）_______| /| /| /| /O这里O为圆心，OA为半径，切线为BC。

4. 已知ΔABC中，∠A = 60度，AC = 5cm，BC = 8cm，画出三角形ABC。

画法几何及工程制图习题集答案(共10篇)画法几何及工程制图习题集答案（一）: 画法几何及工程制图习题集第四版答案是高等教育出版社西安交通大学工程画教研室许睦旬许凤仙温伯平编的给我你邮箱画法几何及工程制图习题集答案（二）: 画法几何与工程制图该怎么学理论上,必须掌握点线面的投影特征（平线、垂线、一般位置线,平面、垂面一般位置面）对分析复杂形体特别有用.实践中,多想多问多画多演示,利用铅笔当线,利用三角板、纸张当面演示画法几何的相对位置关系.利用橡皮泥叠加、切割体会截交线、相贯线的形状.利用静物写生学习勾画立体草图技能.若能在补图补线时先勾画出立体图,能较大程度提高准确率.顺利度过三视图难关.其余部分基本都是国标规定,基本画法等就比较容易学习了.画法几何及工程制图习题集答案（三）: 画法几何及工程制图21.下列说法错误的是()A.尺寸线必须用细实线画出,不得用其他图线代替,也不得与其他图线重合成画在其延长线上B.尺寸数字允许被任何图线穿过C.尺寸界线用细实线绘制,并应由图形的轮廓线、轴线或对称中心线处引出,其末端超出尺寸线约2mm.22.下列不属于装配尺寸的是（）A.配合尺寸B.连接尺寸C.特性尺寸23.视图主要是表达物体的外部结构形状,而物体内部的结构形状,在前面视图中是用虚线表示的.当物体内部结构复杂时,视图中就会出现较多的虚线,有时内、外结构的虚、实线重叠在一起,既影响图形的清晰,又不利于看图和标注尺寸.为了完整清晰地表达物体的内部结构形状,《技术制图》国家标准规定了（）的画法.A.剖视图B.局部视图C.放大图24.断面图一般用于表达物体某处的切断面形状或轴、杆上的孔、槽等结构.为了得到物体结构的实形,剖切平面一般应（）物体的主要轴线或剖切处的轮廓线.A.平行于B.垂直于25.零件图一般不包括以下（）的内容A.一组图形B.装配序顺序C.技术要求26.由曲面围成或由曲面和平面围成的立体称为（）A.曲面体B.多面体C.平面立体27.图板板面要平整、图板工作边要光滑平直.用胶纸或胶布将图纸固定在图板（）的适当位置A.左下方B.右上方C.图板中间28.根据点的运动有无规律,曲线可以分为（）A.规则曲线和不规则曲线B.平面曲线和空间曲线29.两曲面体的相贯线一般为封闭的空间曲线,当两旋转面共轴时,它们的相贯线为（）A.直线和一段圆弧B.全部直线C.圆30.根据有关标准规定,用正投影法绘制出物体的图形,称为（）A.视图B.剖视图C.断面图31.正面投影图是三面投影图的主要投影图.选择正面投影图时必须考虑组合体的（）和正面投射方向.A.形状B.安放位置C.大小32.移出断面图的轮廓线用粗实线绘制A.粗实线B.细实线C.点画线33.组合体的读图主要是用形体分析法,对于那些不易看懂的局部形状则应用（）A.线面分析法B.换面法C.素线法34.用简化伸缩系数所画的图在长度上成为实际投影长度的（）倍A.1B.1.22C.0.8235.绘图铅笔铅芯的软硬用字母“B”和“H”表示.B前的数值越大,表示铅芯（）A.越硬B.越软C.与软硬无关36.图纸有正反两面,用橡皮擦拭容易起毛的一面是（）A.正面B.反面37.根据母线是直线还是曲线．曲面可分为（）A.直纹面和曲线面B.规则曲面和不规则曲面C.旋转面和非旋转面38.对于柱面,当截平面平行于柱面的素线时,交线为（）A.直线B.曲线C.圆39.下列方式不属于曲面形成方式的是（）A.不断改变方向的点的连续运动的轨迹B.曲面与曲面或者曲面与平面相交的交线C.由多个平面为成的表面40.下列不属于旋转直纹面的是()A.圆柱面B.圆锥面C.切线面21～25 BCABC26～30 AAAAA31～35 BAABB35～40 BABCC画法几何及工程制图习题集答案（四）: 几何画法与工程制图求解二、多选题（共 8 道试题,共 32 分.）V1. 根据不同剖切方式,单一剖切面的剖视图有：（）A. 全剖视图B. 半剖视图C. 局部剖视图D. 平行剖切面的剖视图E. 相交剖切面的剖视图满分：4 分2. 两条空间直线的相对位置有三种情况,分别为：（）A. 重合B. 平行C. 相交D. 交叉满分：4 分3. 按投影方法分,工程图中最常用的有下列三种,分别为：A. 透视图B. 轴侧图C. 正投影图D. 机械图满分：4 分4. 截交点和截交线的求法有：（）A. 积聚投影法B. 曲面上取线法C. 辅助投影法D. 辅助平面法满分：4 分5. 下列哪些是AutoCAD中命令调用的方法（）A. 屏幕菜单B. 在命令行输入命令C. 工具菜单D. 下拉菜单满分：4 分6. 轴侧投影按照三个轴的变形系数是否相等,分为：（）A. 三等轴侧投影B. 二等轴侧投影C. 不等轴侧投影D. 正轴侧投影满分：4 分7. 可编辑对象的命令有（）A. 夹点B. 比例C. 图块D. 镜像满分：4 分8. Auto CAD提供了哪几种坐标系（）A. 世界坐标系B. 目标坐标系C. 用户坐标系D. 全球坐标系满分：4 分假如是补全四边形的话好像还少了条件.画法几何及工程制图习题集答案（五）: 工程制图习题集第二版答案冯秋官,仝基斌主编是冯秋官,仝基斌这种教材和配套训练都是每订数十本给老师配一本（有些是配的电子版）答案,没有直接拿到答案的,只有老师那里有.还是一步一步来吧,如果只是为了能参考一下答案可以试试去跟老师商量一下吧～也可以趁这个机会多和老师沟通一下,毕竟制图这个东西,光靠最终的答案而缺乏过程和思路提高很慢.多和老师沟通一下,向老师表明好好学习的信念,就算拿不到答案,老师以后也会多关注你的!加油!画法几何及工程制图习题集答案（六）: 几何画法和工程制图是不是一门课【画法几何及工程制图习题集答案】两门课:画法几何注重物体的线条表现,工程制图以画法几何为基础,注重物体的视图表现；画法几何是一门理论课,而工程制图则是一门实践课.画法几何及工程制图习题集答案（七）: 工程制图与画法几何中斜椭圆柱的投影怎么画万变不离其宗,严格按照投影规律画.先分析在各个投影面中的形状,然后按照长对正,高平齐,宽相等来作图.画法几何及工程制图习题集答案（八）: 几何画法：求与两直线AB、AC等距的点的轨迹画法几何及机械制图习题集第45页5-29求与两直线AB、AC等距的点的轨迹 .请问怎么作图.24小时之内给出解会有加分这个题目就是做∠BAC的平分线以A为圆心,任意长度a为半径做圆弧,交AB,AC于D,E点再分别以D,E为圆心,以任意长度b为半径做圆弧（b要足够大）,使两弧相交于O连接AO形成的直线即所求轨迹.画法几何及工程制图习题集答案（九）: 在画法几何与土木工程制图作业中,求两一般位置直线间的距离这一题型用换面法该怎么画那么求一般位置直线与一般位置平面间的距离呢求两一般位置直线间的距离：1.将其中一条直线经两次换面,换成投影面的垂直线,这时一条直线积聚成一点,另一条依然是一般位置直线；2.过积聚点做另一条直线投影的垂线,即得到两直线间的距离画法几何及工程制图习题集答案（十）: 画法几何及土木建筑制图题2一、单选题1.画剖面图时,图上应标注出:A.剖切位置B.剖切符号C.剖面图名称D.ABC2.绘制结构平面布置图的常用比例为（）.A.1：5、1：10B.1：10、1：20C.1：50、1：100D.1：200、1：5003.尺寸数字“Φ50”与“R20”中符号“Φ”、“R”的含义是：A.Φ表示直径,R表示半径B.Φ表示半径,R表示直径C.Φ,R 都可以表示半径D.Φ,R都可以表示直径4.房屋工程图按专业不同,一般包括（）.A.建筑施工图、结构施工图、总平面图B.建筑施工图、结构施工图、设备施工C.建筑施工图、水电施工图、设备施工图D.建筑施工图、装修施工图、水电施工图5.标注尺寸时,尺寸线画（）.A.粗实线B.细实线C.中实线D.点划线6.建筑平面图、立面图、剖面图的常用比例取（）.A.1：5、1：10B.1：20、1：50C.1：50、1：100D.1：200、1：5007.楼梯平面图上应该用（）表示表示剖切位置.A.45°折断线B.30°折断线C.90°折断线D.60°折断线8.楼梯详图上楼梯段的水平长度为（）,梯段的高度为（）.A.踏面宽X踏面数,踏面宽X踢面数B.踏面宽X踏面数,踏面宽X踢面高C.踏面宽X步级数,踏面宽X踢面数D.踏面宽X踏面数,步级数×踢面高9.当平面在某两个投影面的投影具有积聚性时,该平面一定是（）.A.那个投影面的垂直面B.那个投影面的平行面C.一般位置平面D.某个投影面的垂直面,或某个投影面的平行面.10.当两个基本体叠加组合时,相邻表面的连接关系：（）.A.只能是平齐共面的B.一定是错开的C.只能是相切的D.可以是共面、错开、相切或是相交四种情况之一11.代号为HRB335的钢筋是：A.光圆钢筋B.带肋钢筋C.余热处理钢筋D.无指定含义12.在钢筋混凝土结构图中,符号“ Ф ”表示为（）级钢筋.A.HPB235B.HRB335C.HRB400D.RRB40013.剖面图上,画钢筋布置的规定是：平行于投影面的钢筋画（）,垂直于投影面的钢筋断面画（）A.粗实线,圆圈B.细实线,小黑圆点C.粗实线,小黑圆点D.细实线,圆圈14.画阶梯剖面图时,两剖切面的转折处（）.A.画粗实线B.画细实线C.不应画线D.任意15.在结构施工图中尺寸线或标注引出线一般用（）表示.A.细实线B.中实线C.虚线D.细单点长画线二、判断题1.平面立体与回转体相贯其实质是平面与回转体的截交问题.A.错误B.正确2.求解相贯线投影时,不用考虑确定特殊点的问题.A.错误B.正确3.房屋的建筑结构图应反映房屋承重构件的形状、尺寸及内部构造等A.错误B.正确4.特征投影对组合体读图并不重要.A.错误B.正确5.绘制楼梯详图时只需画出楼梯平面图、楼梯剖面图即可.A.错误B.正确1-5、DBADC6-10、CADAD11-15、AACBA1-5、BABAA我是建筑专业的一名学生,这是我自己做的,个别题目做错了,不要怪我。

《画法几何及土木工程制图习题集》习题解答(第三版)几何画法【1-1】按照立体图作诸点的三面投影。

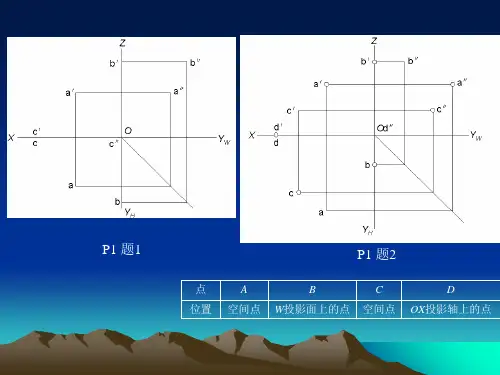
几何画法【1-2】已知点A、B、C、D的两面投影，作出各点的第三投影，并写出这些点的空间位置。

A几何画法【1-3】作出诸点的三面投影：点A(25,15,20);点B距离投影面W、V、H分别为20mm、10mm、15mm;点C位于点A之左10mm、之前15mm、之上10mm;点D在点A之下8mm、与投影面V、H等距，与投影面W的距离是与H面距离的2.5倍。

几何画法【1-4】已知点A与W面距离为20mm;点B距点A12mm;点C与点A是对V面的重影点，在点A的正前方15mm;点D在点A的正下方20mm。

补全诸点的三面投影，并表明可见性。

几何画法【1-5】已知点A与H、V面等距，点B在V面上，与点A是对V面的重影点；点C在点A之右55mm、之后15mm、之下10mm;点D(40,20,30);点E在点D的正下方20mm。

作出点A的水平投影，以及点B、C、D、E的两面投影，并表明可见性。

几何画法【1-6】已知点A(40,20,60);点B(0,0,50);点C在点A的正前方10mm;点D在点A之下50mm、之右15mm,且在V面上；点E在点D的正左方20mm。

作诸点的两面投影，并表明可见性。

几何画法【2-1】判别下列直线对投影面的相对位置。

几何画法【2-2】过点A作下列直线的三面投影。

⑴一般位置直线AB,B在A之上5mm、A之左20mm、A之后10mm;⑵正平线AC,C在A的右上方，α=30°,长25mm;⑶正垂线AD,D在A之正前方15mm;⑷侧平线AE,E在A的后下方，β=45°,长20mm。

几何画法【2-3】已知直线AD和点C、B的两面投影，判别C、B是否在AD上，已知点E在AD上，AE:ED为3:5,作出AD的侧面投影和点E的三面投影。

几何画法【2-4】作直线AB的真长及其对投影面H、V的倾角α、β,在AB上作与点A相距25mm的点C的两面投影。