初中数学三角形全等证明综合题(含答案)

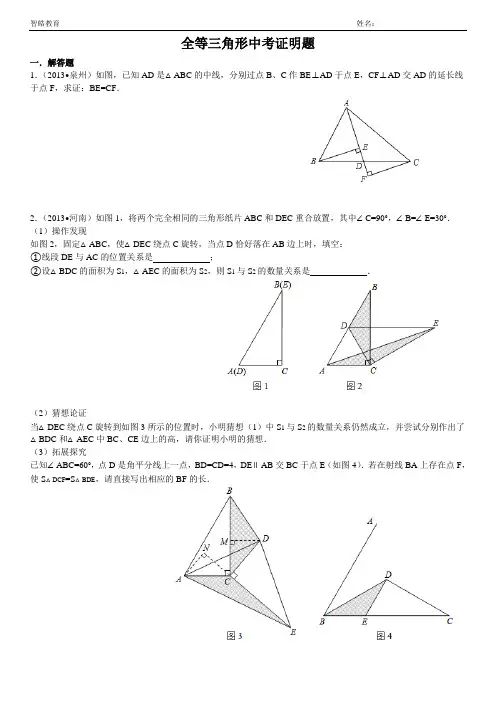
智皓教育姓名：全等三角形中考证明题一．解答题1．（2013•泉州）如图，已知AD是△ABC的中线，分别过点B、C作BE⊥AD于点E，CF⊥AD交AD的延长线于点F，求证：BE=CF．2．（2013•河南）如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°，∠B=∠E=30°．（1）操作发现如图2，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB边上时，填空：①线段DE与AC的位置关系是_________；②设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是_________．（2）猜想论证当△DEC绕点C旋转到如图3所示的位置时，小明猜想（1）中S1与S2的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC、CE边上的高，请你证明小明的猜想．（3）拓展探究已知∠ABC=60°，点D是角平分线上一点，BD=CD=4，DE∥AB交BC于点E（如图4）．若在射线BA上存在点F，使S△DCF=S△BDE，请直接写出相应的BF的长．3．（2013•大庆）如图，把一个直角三角形ACB（∠ACB=90°）绕着顶点B顺时针旋转60°，使得点C旋转到AB 边上的一点D，点A旋转到点E的位置．F，G分别是BD，BE上的点，BF=BG，延长CF与DG交于点H．（1）求证：CF=DG；（2）求出∠FHG的度数．4．（2012•阜新）（1）如图，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE=90°．①当点D在AC上时，如图1，线段BD、CE有怎样的数量关系和位置关系？直接写出你猜想的结论；②将图1中的△ADE绕点A顺时针旋转α角（0°＜α＜90°），如图2，线段BD、CE有怎样的数量关系和位置关系？请说明理由．（2）当△ABC和△ADE满足下面甲、乙、丙中的哪个条件时，使线段BD、CE在（1）中的位置关系仍然成立？不必说明理由．甲：AB：AC=AD：AE=1，∠BAC=∠DAE≠90°；乙：AB：AC=AD：AE≠1，∠BAC=∠DAE=90°；丙：AB：AC=AD：AE≠1，∠BAC=∠DAE≠90°．5．（2009•仙桃）如图所示，在△ABC中，D、E分别是AB、AC上的点，DE∥BC，如图①，然后将△ADE绕A 点顺时针旋转一定角度，得到图②，然后将BD、CE分别延长至M、N，使DM=BD，EN=CE，得到图③，请解答下列问题：（1）若AB=AC，请探究下列数量关系：①在图②中，BD与CE的数量关系是_________；②在图③中，猜想AM与AN的数量关系、∠MAN与∠BAC的数量关系，并证明你的猜想；（2）若AB=k•AC（k＞1），按上述操作方法，得到图④，请继续探究：AM与AN的数量关系、∠MAN与∠BAC 的数量关系，直接写出你的猜想，不必证明．6．（2008•台州）CD经过∠BCA顶点C的一条直线，CA=CB．E，F分别是直线CD上两点，且∠BEC=∠CFA=∠α．（1）若直线CD经过∠BCA的内部，且E，F在射线CD上，请解决下面两个问题：①如图1，若∠BCA=90°，∠α=90°，则BE_________CF；EF_________|BE﹣AF|（填“＞”，“＜”或“=”）；②如图2，若0°＜∠BCA＜180°，请添加一个关于∠α与∠BCA关系的条件_________，使①中的两个结论仍然成立，并证明两个结论成立．（2）如图3，若直线CD经过∠BCA的外部，∠α=∠BCA，请提出EF，BE，AF三条线段数量关系的合理猜想（不要求证明）．7．（2007•绍兴）课外兴趣小组活动时，许老师出示了如下问题：如图1，己知四边形ABCD中，AC平分∠DAB，∠DAB=60°，∠B与∠D互补，求证：AB+AD=AC．小敏反复探索，不得其解．她想，若将四边形ABCD特殊化，看如何解决该问题．（1）特殊情况入手添加条件：“∠B=∠D”，如图2，可证AB+AD=AC；（请你完成此证明）（2）解决原来问题受到（1）的启发，在原问题中，添加辅助线：如图3，过C点分别作AB、AD的垂线，垂足分别为E、F．（请你补全证明）8．（2007•常德）如图，已知AB=AC，（1）若CE=BD，求证：GE=GD；（2）若CE=m•BD（m为正数），试猜想GE与GD有何关系．（只写结论，不证明）9．（2006•泰安）（1）已知：如图①，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=60°，求证：①AC=BD；②∠APB=60度；（2）如图②，在△AOB和△COD中，若OA=OB，OC=OD，∠AOB=∠COD=α，则AC与BD间的等量关系式为_________；∠APB的大小为_________；（3）如图③，在△AOB和△COD中，若OA=k•OB，OC=k•OD（k＞1），∠AOB=∠COD=α，则AC与BD间的等量关系式为_________；∠APB的大小为10．（2005•南宁）（A类）如图，DE⊥AB、DF⊥AC．垂足分别为E、F．请你从下面三个条件中，再选出两个作为已知条件，另一个为结论，推出一个正确的命题（只需写出一种情况）．①AB=AC；②BD=CD；③BE=CF已知：DE⊥AB、DF⊥AC，垂足分别为E、F，AB=AC，BD=CD求证：BE=CF已知：DE⊥AB、DF⊥AC，垂足分别为E、F，AB=AC，BE=CF求证：BD=CD已知：DE⊥AB、DF⊥AC，垂足分别为E、F，BD=CD，BE=CF求证：AB=AC（B类）如图，EG∥AF，请你从下面三个条件中，再选两个作为已知条件，另一个为结论，推出一个正确的命题（只需写出一种情况）．①AB=AC；②DE=DF；③BE=CF已知：EG∥AF，AB=AC，DE=DF求证：BE=CF参考答案与试题解析一．解答题（共10小题）1．（2013•泉州）如图，已知AD是△ABC的中线，分别过点B、C作BE⊥AD于点E，CF⊥AD交AD的延长线于点F，求证：BE=CF．考点：全等三角形的判定与性质．专题：证明题．分析：根据中线的定义可得BD=CD，然后利用“角角边”证明△BDE和△CDF全等，根据全等三角形对应边相等即可得证．解答：证明：∵AD是△ABC的中线，∴BD=CD，∵BE⊥AD，CF⊥AD，∴∠BED=∠CFD=90°，在△BDE和△CDF中，，∴△BDE≌△CDF（AAS），∴BE=CF．点评：本题考查了全等三角形的判定与性质，利用三角形全等证明边相等是常用的方法之一，要熟练掌握并灵活运用．2．（2013•河南）如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°，∠B=∠E=30°．（1）操作发现如图2，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB边上时，填空：①线段DE与AC的位置关系是DE∥AC；②设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是S1=S2．（2）猜想论证当△DEC绕点C旋转到如图3所示的位置时，小明猜想（1）中S1与S2的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC、CE边上的高，请你证明小明的猜想．（3）拓展探究已知∠ABC=60°，点D是角平分线上一点，BD=CD=4，DE∥AB交BC于点E（如图4）．若在射线BA上存在点F，使S△DCF=S△BDE，请直接写出相应的BF的长．考点：全等三角形的判定与性质．专题：几何综合题；压轴题．分析：（1）①根据旋转的性质可得AC=CD，然后求出△ACD是等边三角形，根据等边三角形的性质可得∠ACD=60°，然后根据内错角相等，两直线平行解答；②根据等边三角形的性质可得AC=AD，再根据直角三角形30°角所对的直角边等于斜边的一半求出AC=AB，然后求出AC=BE，再根据等边三角形的性质求出点C到AB的距离等于点D到AC的距离，然后根据等底等高的三角形的面积相等解答；（2）根据旋转的性质可得BC=CE，AC=CD，再求出∠ACN=∠DCM，然后利用“角角边”证明△ACN和△DCM全等，根据全等三角形对应边相等可得AN=DM，然后利用等底等高的三角形的面积相等证明；（3）过点D作DF1∥BE，求出四边形BEDF1是菱形，根据菱形的对边相等可得BE=DF1，然后根据等底等高的三角形的面积相等可知点F1为所求的点，过点D作DF2⊥BD，求出∠F1DF2=60°，从而得到△DF1F2是等边三角形，然后求出DF1=DF2，再求出∠CDF1=∠CDF2，利用“边角边”证明△CDF1和△CDF2全等，根据全等三角形的面积相等可得点F2也是所求的点，然后在等腰△BDE中求出BE的长，即可得解．解答：解：（1）①∵△DEC绕点C旋转点D恰好落在AB边上，∴AC=CD，∵∠BAC=90°﹣∠B=90°﹣30°=60°，∴△ACD是等边三角形，∴∠ACD=60°，又∵∠CDE=∠BAC=60°，∴∠ACD=∠CDE，∴DE∥AC；②∵∠B=30°，∠C=90°，∴CD=AC=AB，∴BD=AD=AC，根据等边三角形的性质，△ACD的边AC、AD上的高相等，∴△BDC的面积和△AEC的面积相等（等底等高的三角形的面积相等），即S1=S2；故答案为：DE∥AC；S1=S2；（2）如图，∵△DEC是由△ABC绕点C旋转得到，∴BC=CE，AC=CD，∵∠ACN+∠BCN=90°，∠DCM+∠BCN=180°﹣90°=90°，∴∠ACN=∠DCM，∵在△ACN和△DCM中，，∴△ACN≌△DCM（AAS），∴AN=DM，∴△BDC的面积和△AEC的面积相等（等底等高的三角形的面积相等），即S1=S2；（3）如图，过点D作DF1∥BE，易求四边形BEDF1是菱形，所以BE=DF1，且BE、DF1上的高相等，此时S△DCF=S△BDE，过点D作DF2⊥BD，∵∠ABC=60°，∴∠F1DF2=∠ABC=60°，∴△DF1F2是等边三角形，∴DF1=DF2，∵BD=CD，∠ABC=60°，点D是角平分线上一点，∴∠DBC=∠DCB=×60°=30°，∴∠CDF1=180°﹣30°=150°，∠CDF2=360°﹣150°﹣60°=150°，∴∠CDF1=∠CDF2，∵在△CDF1和△CDF2中，，∴△CDF1≌△CDF2（SAS），∴点F2也是所求的点，∵∠ABC=60°，点D是角平分线上一点，DE∥AB，∴∠DBC=∠BDE=∠ABD=×60°=30°，又∵BD=4，∴BE=×4÷cos30°=2÷=，∴BF1=，BF2=BF1+F1F2=+=，故BF的长为或．点评：本题考查了全等三角形的判定与性质，三角形的面积，等边三角形的判定与性质，直角三角形30°角所对的直角边等于斜边的一半的性质，熟练掌握等底等高的三角形的面积相等，以及全等三角形的面积相等是解题的关键，（3）要注意符合条件的点F有两个．3．（2013•大庆）如图，把一个直角三角形ACB（∠ACB=90°）绕着顶点B顺时针旋转60°，使得点C旋转到AB 边上的一点D，点A旋转到点E的位置．F，G分别是BD，BE上的点，BF=BG，延长CF与DG交于点H．（1）求证：CF=DG；（2）求出∠FHG的度数．考点：全等三角形的判定与性质．分析：（1）在△CBF和△DBG中，利用SAS即可证得两个三角形全等，利用全等三角形的对应边相等即可证得；（2）根据全等三角形的对应角相等，即可证得∠DHF=∠CBF=60°，从而求解．解答：（1）证明：∵在△CBF和△DBG中，，∴△CBF≌△DBG（SAS），∴CF=DG；（2）解：∵△CBF≌△DBG，∴∠BCF=∠BDG，又∵∠CFB=∠DFH，∴∠DHF=∠CBF=60°，∴∠FHG=180°﹣∠DHF=180°﹣60°=120°．点评：本题考查了全等三角形的判定与性质，正确证明三角形全等是关键．4．（2012•阜新）（1）如图，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE=90°．①当点D在AC上时，如图1，线段BD、CE有怎样的数量关系和位置关系？直接写出你猜想的结论；②将图1中的△ADE绕点A顺时针旋转α角（0°＜α＜90°），如图2，线段BD、CE有怎样的数量关系和位置关系？请说明理由．（2）当△ABC和△ADE满足下面甲、乙、丙中的哪个条件时，使线段BD、CE在（1）中的位置关系仍然成立？不必说明理由．甲：AB：AC=AD：AE=1，∠BAC=∠DAE≠90°；乙：AB：AC=AD：AE≠1，∠BAC=∠DAE=90°；丙：AB：AC=AD：AE≠1，∠BAC=∠DAE≠90°．考点：全等三角形的判定与性质．专题：几何综合题；压轴题．分析：（1）①BD=CE，BD⊥CE．根据全等三角形的判定定理SAS推知△ABD≌△ACE，然后由全等三角形的对应边相等证得BD=CE、对应角相等∠ABF=∠ECA；然后在△ABD和△CDF中，由三角形内角和定理可以求得∠CFD=90°，即BD⊥CF；②BD=CE，BD⊥CE．根据全等三角形的判定定理SAS推知△ABD≌△ACE，然后由全等三角形的对应边相等证得BD=CE、对应角相等∠ABF=∠ECA；作辅助线（延长BD交AC于F，交CE于H）BH构建对顶角∠ABF=∠HCF，再根据三角形内角和定理证得∠BHC=90°；（2）根据结论①、②的证明过程知，∠BAC=∠DFC（或∠FHC=90°）时，该结论成立了，所以本条件中的∠BAC=∠DAE≠90°不合适．解答：解：（1）①结论：BD=CE，BD⊥CE；②结论：BD=CE，BD⊥CE…1分理由如下：∵∠BAC=∠DAE=90°∴∠BAC﹣∠DAC=∠DAE﹣∠DAC，即∠BAD=∠CAE…1分在△ABD与△ACE中，∵∴△ABD≌△ACE（SAS）∴BD=CE…1分延长BD交AC于F，交CE于H．在△ABF与△HCF中，∵∠ABF=∠HCF，∠AFB=∠HFC∴∠CHF=∠BAF=90°∴BD⊥CE…3分（2）结论：乙．AB：AC=AD：AE，∠BAC=∠DAE=90°…2分点评：本题考查了全等三角形的判定与性质．SSS，SAS，ASA，AAS，HL均可作为判定三角形全等的定理．注意：在全等的判定中，没有AAA（角角角）和SSA（边边角）（特例：直角三角形为HL，因为勾股定理，只要确定了斜边和一条直角边，另一直角边也确定，属于SSS），因为这两种情况都不能唯一确定三角形的形状；另外三条中线（或高、角平分线）分别对应相等的两个三角形也全等．5．（2009•仙桃）如图所示，在△ABC中，D、E分别是AB、AC上的点，DE∥BC，如图①，然后将△ADE绕A 点顺时针旋转一定角度，得到图②，然后将BD、CE分别延长至M、N，使DM=BD，EN=CE，得到图③，请解答下列问题：（1）若AB=AC，请探究下列数量关系：①在图②中，BD与CE的数量关系是；②在图③中，猜想AM与AN的数量关系、∠MAN与∠BAC的数量关系，并证明你的猜想；（2）若AB=k•AC（k＞1），按上述操作方法，得到图④，请继续探究：AM与AN的数量关系、∠MAN与∠BAC 的数量关系，直接写出你的猜想，不必证明．考点：全等三角形的判定．专题：压轴题；探究型．分析：（1）①根据题意和旋转的性质可知△AEC≌△ADB，所以BD=CE；②根据题意可知∠CAE=BAD，AB=AC，AD=AE，所以得到△BAD≌△CAE，在△ABM和△ACN中，DM=BD，EN=CE，可证△ABM≌△ACN，所以AM=AN，即∠MAN=∠BAC．（2）直接类比（1）中结果可知AM=k•AN，∠MAN=∠BAC．解答：解：（1）①BD=CE；②AM=AN，∠MAN=∠BAC，∵∠DAE=∠BAC，∴∠CAE=∠BAD，在△BAD和△CAE中∵∴△CAE≌△BAD（SAS），∴∠ACE=∠ABD，∵DM=BD，EN=CE，∴BM=CN，在△ABM和△ACN中，∵∴△ABM≌△ACN（SAS），∴AM=AN，∴∠BAM=∠CAN，即∠MAN=∠BAC；（2）AM=k•AN，∠MAN=∠BAC．点评：本题考查三角形全等的判定方法和性质．判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．本题还要会根据所求的结论运用类比的方法求得同类题目．6．（2008•台州）CD经过∠BCA顶点C的一条直线，CA=CB．E，F分别是直线CD上两点，且∠BEC=∠CFA=∠α．（1）若直线CD经过∠BCA的内部，且E，F在射线CD上，请解决下面两个问题：①如图1，若∠BCA=90°，∠α=90°，则BE=CF；EF=|BE﹣AF|（填“＞”，“＜”或“=”）；②如图2，若0°＜∠BCA＜180°，请添加一个关于∠α与∠BCA关系的条件∠α+∠BCA=180°，使①中的两个结论仍然成立，并证明两个结论成立．（2）如图3，若直线CD经过∠BCA的外部，∠α=∠BCA，请提出EF，BE，AF三条线段数量关系的合理猜想（不要求证明）．考点：直角三角形全等的判定；三角形内角和定理．专题：几何综合题；压轴题．分析：由题意推出∠CBE=∠ACF，再由AAS定理证△BCE≌△CAF，继而得答案．解答：解：（1）①∵∠BCA=90°，∠α=90°，∴∠BCE+∠CBE=90°，∠BCE+∠ACF=90°，∴∠CBE=∠ACF，∵CA=CB，∠BEC=∠CFA；∴△BCE≌△CAF，∴BE=CF；EF=|BE﹣AF|．②所填的条件是：∠α+∠BCA=180°．证明：在△BCE中，∠CBE+∠BCE=180°﹣∠BEC=180°﹣∠α．∵∠BCA=180°﹣∠α，∴∠CBE+∠BCE=∠BCA．又∵∠ACF+∠BCE=∠BCA，∴∠CBE=∠ACF，又∵BC=CA，∠BEC=∠CFA，∴△BCE≌△CAF（AAS）∴BE=CF，CE=AF，又∵EF=CF﹣CE，∴EF=|BE﹣AF|．（2）EF=BE+AF．点评：本题综合考查全等三角形、等边三角形和四边形的有关知识．注意对三角形全等，相似的综合应用．7．（2007•绍兴）课外兴趣小组活动时，许老师出示了如下问题：如图1，己知四边形ABCD中，AC平分∠DAB，∠DAB=60°，∠B与∠D互补，求证：AB+AD=AC．小敏反复探索，不得其解．她想，若将四边形ABCD特殊化，看如何解决该问题．（1）特殊情况入手添加条件：“∠B=∠D”，如图2，可证AB+AD=AC；（请你完成此证明）（2）解决原来问题受到（1）的启发，在原问题中，添加辅助线：如图3，过C点分别作AB、AD的垂线，垂足分别为E、F．（请你补全证明）考点：直角三角形全等的判定．专题：证明题；压轴题；开放型．分析：（1）如果：“∠B=∠D”，根据∠B与∠D互补，那么∠B=∠D=90°，又因为∠DAC=∠BAC=30°，因此我们可在直角三角形ADC和ABC中得出AD=AB=AC，那么AD+AB=AC．（2）按（1）的思路，作好辅助线后，我们只要证明三角形CFD和BCD全等即可得到（1）的条件．根据AAS可证两三角形全等，DF=BE．然后按照（1）的解法进行计算即可．解答：证明：（1）∵∠B与∠D互补，∠B=∠D，∴∠B=∠D=90°，∠CAD=∠CAB=∠DAB=30°，∵在△ADC中，cos30°=，在△ABC中，cos30°=，∴AB=AC，AD=．∴AB+AD=．（2）由（1）知，AE+AF=AC，∵AC为角平分线，CF⊥CD，CE⊥AB，∴CE=CF．而∠ABC与∠D互补，∠ABC与∠CBE也互补，∴∠D=∠CBE．∵在Rt△CDF与Rt△CBE中，∴Rt△CDF≌Rt△CBE．∴DF=BE．∴AB+AD=AB+（AF+FD）=（AB+BE）+AF=AE+AF=AC．点评：本题考查了直角三角形全等的判定及性质；通过辅助线来构建全等三角形是解题的常用方法，也是解决本题的关键．8．（2007•常德）如图，已知AB=AC，（1）若CE=BD，求证：GE=GD；（2）若CE=m•BD（m为正数），试猜想GE与GD有何关系．（只写结论，不证明）考点：全等三角形的判定与性质．专题：证明题；压轴题；探究型．分析：（1）要证GE=GD，需证△GDF≌△GEC，由已知条件可根据AAS判定．（2）若CE=m•BD（m为正数），那么GE=m•GD．解答：证明：（1）过D作DF∥CE，交BC于F，则∠E=∠GDF．∵AB=AC，∴∠ACB=∠ABC∵DF∥CE，∴∠DFB=∠ACB，∴∠DFB=∠ACB=∠ABC．∴DF=DB．∵CE=BD，∴DF=CE，在△GDF和△GEC中，，∴△GDF≌△GEC（AAS）．∴GE=GD．（2）GE=m•GD．点评：本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．本题的辅助线是解决题目的关键．9．（2006•泰安）（1）已知：如图①，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=60°，求证：①AC=BD；②∠APB=60度；（2）如图②，在△AOB和△COD中，若OA=OB，OC=OD，∠AOB=∠COD=α，则AC与BD间的等量关系式为AC=BD；∠APB的大小为α；（3）如图③，在△AOB和△COD中，若OA=k•OB，OC=k•OD（k＞1），∠AOB=∠COD=α，则AC与BD间的等量关系式为AC=k•BD；∠APB的大小为180°﹣α．考点：全等三角形的判定；三角形内角和定理．专题：探究型．分析：（1）分析结论AC=BD可知，需要证明△AOC≌△BOD，围绕这个目标找全等的条件；（2）与图①比较，图形条件发生了变化，仍然可以证明△AOC≌△BOD，方法类似；（3）转化为证明△AOC∽△BOD．解答：解：（1）①∵∠AOB=∠COD=60°，∴∠AOB+∠BOC=∠COD+∠BOC．即：∠AOC=∠BOD．又∵OA=OB，OC=OD，∴△AOC≌△BOD．∴AC=BD．②由①得：∠OAC=∠OBD，∵∠AEO=∠PEB，∠APB=180°﹣（∠BEP+∠OBD），∠AOB=180°﹣（∠OAC+∠AEO），∴∠APB=∠AOB=60°．（2）AC=BD，α（3）AC=k•BD，180°﹣α．点评：三角形全等的判定是中考的热点，一般以考查三角形全等的方法为主，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．10．（2005•南宁）（A类）如图，DE⊥AB、DF⊥AC．垂足分别为E、F．请你从下面三个条件中，再选出两个作为已知条件，另一个为结论，推出一个正确的命题（只需写出一种情况）．①AB=AC；②BD=CD；③BE=CF已知：DE⊥AB、DF⊥AC，垂足分别为E、F，AB=AC，BD=CD求证：BE=CF已知：DE⊥AB、DF⊥AC，垂足分别为E、F，AB=AC，BE=CF求证：BD=CD已知：DE⊥AB、DF⊥AC，垂足分别为E、F，BD=CD，BE=CF求证：AB=AC（B类）如图，EG∥AF，请你从下面三个条件中，再选两个作为已知条件，另一个为结论，推出一个正确的命题（只需写出一种情况）．①AB=AC；②DE=DF；③BE=CF已知：EG∥AF，AB=AC，DE=DF求证：BE=CF友情提醒：若两题都做的同学，请你确认以哪类题记分，你的选择是A类类题．考点：全等三角形的判定与性质．专题：证明题；开放型．分析：本题是开放题，应先确定选择哪对三角形，对应三角形全等条件求解；再根据全等三角形的性质得出结论．解答：解：（A类）已知：…，AB=AC，BD=CD求证：BE=CF．证明：∵AB=AC，∴∠B=∠C．∵DE⊥AB，DF⊥AC，∴∠BED=∠CFD=90°．在△BDE和△CDF中∴△BDE≌△CDF．∴BE=CF．已知：…，AB=AC，DE=DF，求证：BE=CF．证明：∵EG∥AF，∴∠GED=∠F，∠BGE=∠BCA．∵AB=AC，∴∠B=∠BCA，∴∠B=∠BGE，∴BE=EG．在△DEG和△DFC中∴△DEG≌△DFC，∴EG=CF，∴BE=CF．点评：这是一道考查三角形全等的识别方法的开放性题目，答案可有多种．同时还考查了全等三角形的性质．。

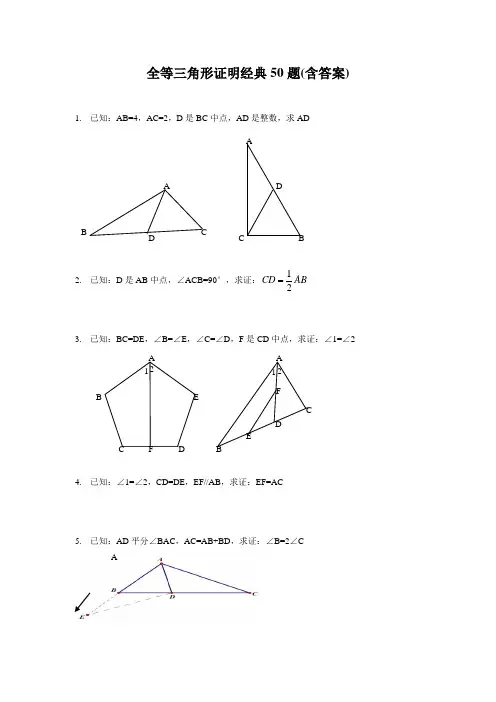
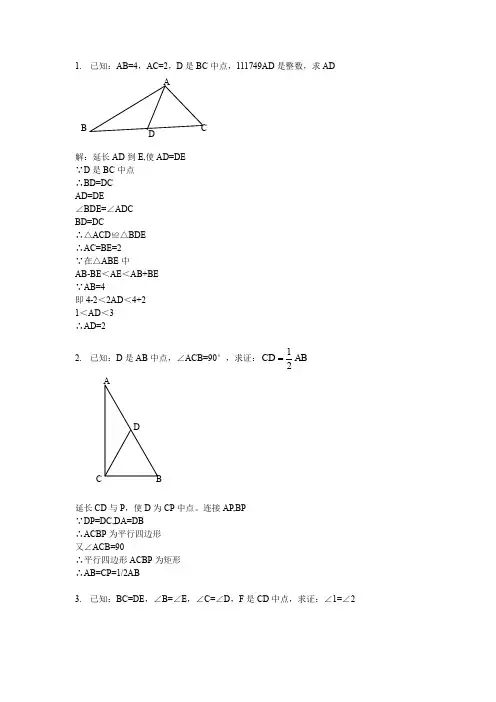
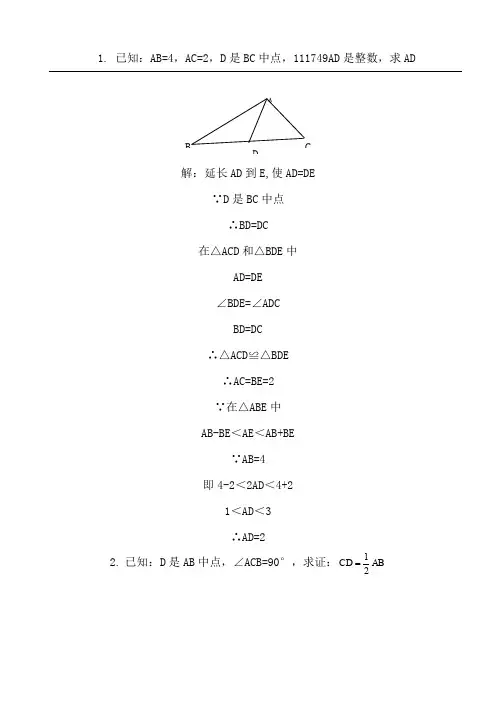
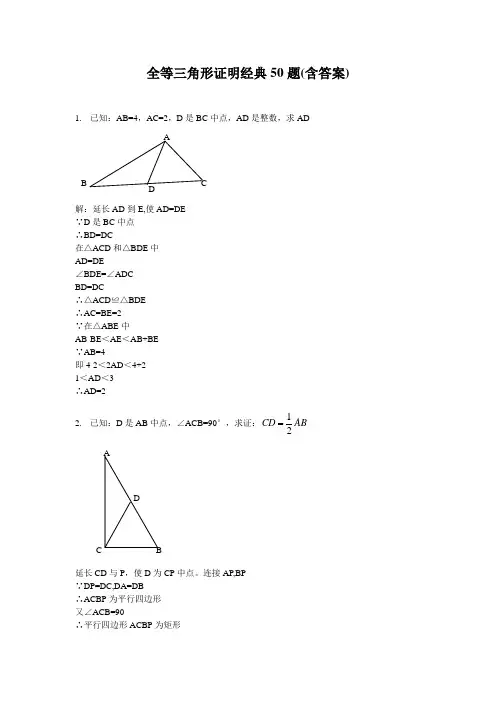
1. 已知：AB=4,AC=2,D 是BC 中点,111749AD是整数,求AD解：延伸AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=22. 已知：D 是AB 中点,∠ACB=90°,求证：AD B C延伸CD与P,使D为CP中点.衔接AP,BP∵DP=DC,DA=DB∴ACBP为平行四边形又∠ACB=90∴平行四边形ACBP为矩形∴AB=CP=1/2AB3.已知：BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证：∠1=∠2证实：衔接BF和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF衔接BE在三角形BEF中,BF=EF∴∠EBF=∠BEF.∵∠ABC=∠AED.∴∠ABE=∠AEB.∴ AB=AE.在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等.∴∠BAF=∠EAF (∠1=∠2). 4. 已知：∠1=∠2,CD=DE,EF//AB,求证：EF=AC过C 作CG∥EF 交AD 的延伸线于点GCG∥EF,可得,∠EFD ＝CGDDE ＝DC∠FDE ＝∠GDC （对顶角）∴△EFD≌△CGDEF ＝CG∠CGD ＝∠EFD 又,EF∥AB∴,∠EFD ＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC 为等腰三角形,AC ＝CG 又 EF ＝CG∴EF＝AC5. 已知：AD 等分∠BAC,AC=AB+BD,求证：∠B=2∠CB ACDF21 E A证实：延伸AB取点E,使AE＝AC,衔接DE∵AD等分∠BAC∴∠EAD＝∠CAD∵AE＝AC,AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C6.已知：AC等分∠BAD,CE⊥AB,∠B+∠D=180°,求证：AE=AD+BE证实：在AE上取F,使EF＝EB,衔接CF∵CE⊥AB∴∠CEB＝∠CEF＝90°∵EB＝EF,CE ＝CE,∴△CEB≌△CEF∴∠B＝∠CFE∵∠B＋∠D＝180°,∠CFE＋∠CFA＝180°∴∠D＝∠CFA∵AC 等分∠BAD∴∠DAC＝∠FAC∵AC＝AC∴△ADC≌△AFC（SAS ）∴AD＝AF∴AE＝AF ＋FE ＝AD ＋BE7. 已知：AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解：延伸AD 到E,使AD=DE∵D 是BC 中点∴BD=DC 在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE 中 AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=28. 已知：D 是AB 中点,∠ACB=90°,求证：AD B C∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE＜AE＜AB+BE∵AB=4即4-2＜2AD＜4+21＜AD＜3∴AD=29.已知：BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证：∠1=∠2证实：衔接BF和EF.∵ BC=ED,CF=DF,∠BCF=∠EDF.∴ 三角形BCF全等于三角形EDF(边角边).∴ BF=EF,∠CBF=∠DEF.衔接BE.在三角形BEF中,BF=EF.∴∠EBF=∠BEF.又∵∠ABC=∠AED.∴ AB=AE.在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF.∴ 三角形ABF 和三角形AEF 全等.∴∠BAF=∠EAF (∠1=∠2).10. 已知：∠1=∠2,CD=DE,EF//AB,求证：EF=AC过C 作CG∥EF 交AD 的延伸线于点GCG∥EF,可得,∠EFD ＝CGDDE ＝DC∠FDE ＝∠GDC （对顶角）∴△EFD≌△CGDEF ＝CG∠CGD ＝∠EFD 又EF∥AB∴∠EFD ＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC 为等腰三角形,AC ＝CG 又 EF ＝CG∴EF＝AC11. 已知：AD等分∠BAC,AC=AB+BD,求证：∠B=2∠C证实：延伸AB 取点E,使AE ＝AC,衔接DE∵AD 等分∠BACB ACDF21 ECD B A∵AE＝AC,AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C12.已知：AC等分∠BAD,CE⊥AB,∠B+∠D=180°,求证：AE=AD+BE在AE上取F,使EF＝EB,衔接CF∵CE⊥AB∴∠CEB＝∠CEF＝90°∵EB＝EF,CE＝CE,∴△CEB≌△CEF∴∠B＝∠CFE∵∠B＋∠D＝180°,∠CF E＋∠CFA＝180°∴∠D＝∠CFA∵AC等分∠BAD∴∠DAC＝∠FAC又∵AC＝AC∴△ADC≌△AFC（SAS）∴AD＝AF∴AE＝AF＋FE＝AD＋BE12. 如图,四边形ABCD中,AB∥DC,BE.CE分离等分∠ABC.∠BCD,且点E在AD上.求证：BC=AB+DC.在BC上截取BF=AB,衔接EF∵BE等分∠ABC∴∠ABE=∠FBE又∵BE=BE∴⊿ABE≌⊿FBE（SAS）∴∠A=∠BFE∵AB//CD∴∠A+∠D=180º∵∠BFE+∠CFE=180º∴∠D=∠CFE又∵∠DCE=∠FCECE 等分∠BCDCE=CE∴⊿DCE≌⊿FCE（AAS ）∴CD=CF∴BC=BF+CF=AB+CD13.已知：AB//ED,∠EAB=∠BDE,AF=CD,EF=BC,求证：∠F=∠CAB‖ED,得：∠EAB+∠AED=∠BDE+∠ABD=180度,∵∠EAB=∠BDE,∴∠AED=∠ABD,∴四边形ABDE 是平行四边形.∴得：AE=BD,∵AF=CD,EF=BC,∴三角形AEF 全等于三角形DBC,∴∠F=∠C.14. 已知：AB=CD,∠A=∠D,求证：∠B=∠C DCB A FE证实：设线段AB,CD 地点的直线交于E,（当AD<BC 时,E 点是射线BA,CD 的交点,当AD>BC 时,E 点是射线AB,DC 的交点）.则： △AED 是等腰三角形.∴AE=DE而AB=CD∴BE=CE (等量加等量,或等量减等量）∴△BEC 是等腰三角形∴∠B=∠C.15. P 是∠BAC 等分线AD 上一点,AC>AB,求证：PC-PB<AC-AB在AC 上取点E,使AE ＝AB.∵AE ＝ABAP ＝AP∠EAP ＝∠BAE,∴△EAP≌△BAP∴PE＝PB.PC ＜EC ＋PE∴PC＜（AC －AE ）＋PB∴PC－PB ＜AC －AB.16. 已知∠ABC=3∠C,∠1=∠2,BE⊥AE,求证：AC-AB=2BE证实：在AC 上取一点D,使得角DBC=角C∵∠ABC=3∠C∴∠ABD=∠ABC -∠DBC=3∠C -∠C=2∠C;∵∠ADB=∠C+∠DBC=2∠C;∴AB=AD∴AC – AB =AC-AD=CD=BD 在等腰三角形ABD 中,AE 是角BAD 的角等分线,∴AE 垂直BD∵BE⊥AE∴点E 必定在直线BD 上,在等腰三角形ABD PD A CB中,AB=AD,AE 垂直BD∴点E 也是BD 的中点∴BD=2BE∵BD=CD=AC -AB∴AC -AB=2BE17. 已知,E 是AB 中点,AF=BD,BD=5,AC=7,求DC∵作AG∥BD 交DE 延伸线于G∴AGE 全等BDE ∴AG=BD=5∴AGF∽CDF AF=AG=5∴DC=CF=218．如图,在△ABC 中,BD=DC,∠1=∠2,求证：AD⊥BC．解：延伸AD 至BC 于点E,∵BD=DC ∴△BDC 是等腰三角形∴∠DBC=∠DCB 又∵∠1=∠2 ∴∠DBC+∠1=∠DCB+∠2 即∠ABC=∠ACB∴△ABC 是等腰三角形∴AB=AC 在△ABD 和△ACD 中 ｛AB=AC∠1=∠2 BD=DC∴△ABD 和△ACD 是全等三角形（边角边）∴∠BAD=∠CAD∴AE 是△ABC 的中垂线∴AE⊥BC∴AD⊥BC19．如图,OM 等分∠POQ,MA⊥OP,MB⊥OQ,A.B 为垂足,AB 交OM 于点N ．求证：∠OAB=∠OBA证实：∵OM 等分∠POQ∴∠POM＝∠QOM∵MA⊥OP,MB⊥OQ∴∠MAO＝∠MBO＝90F A E DCB∵OM＝OM∴△AOM≌△BOM （AAS）∴OA＝OB∵ON＝ON∴△AON≌△BON （SAS）∴∠OAB=∠OBA,∠ONA=∠ONB∵∠ONA+∠ONB＝180∴∠ONA＝∠ONB＝90∴OM⊥AB20．（5分）如图,已知AD∥BC,∠PAB的等分线与∠CBA的等分线订交于E,CE的连线交AP于D．求证：AD+BC=AB．做BE的延伸线,与AP订交于F点,∵PA//BC∴∠PAB+∠CBA=180°,又∵,AE,BE均为∠PAB和∠CBA的角等分线∴∠EAB+∠EBA=90°∴∠AEB=90°,EAB为直角三角形在三角形ABF中,AE⊥BF,且AE为∠FAB的角等分线∴三角形FAB为等腰三角形,AB=AF,BE=EF在三角形DEF与三角形BEC中,∠EBC=∠DFE,且BE=EF,∠DEF=∠CEB,∴三角形DEF与三角形BEC为全等三角形,∴DF=BC∴AB=AF=AD+DF=AD+BC21．如图,△ABC中,AD是∠CAB的等分线,且AB=AC+CD,求证：∠C=2∠B延伸AC到E 使AE=AC 衔接 ED∵ AB=AC+CD∴ CD=CE可得∠B=∠E△CDE为等腰∠ACB=2∠B22．（6分）如图①,E.F分离为线段AC上的两个动点,且DE⊥AC 于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M．（1）求证：MB=MD,ME=MF（2）当E.F两点移动到如图②的地位时,其余前提不变,上述结论可否成立？若成立请赐与证实;若不成立请解释来由．（1）衔接BE,DF．∵DE⊥AC于E,BF⊥AC于F,∴∠DEC=∠BFA=90°,DE∥BF,在Rt△DEC和Rt△BFA 中,∵AF=CE,AB=CD,∴Rt△DEC≌Rt△BFA（HL）,∴DE=BF．∴四边形BEDF是平行四边形．∴MB=MD,ME=MF;（2）衔接BE,DF．∵DE⊥AC于E,BF⊥AC于F,∴∠DEC=∠BFA=90°,DE∥BF,在Rt△DEC和Rt△BFA 中,∵AF=CE,AB=CD,∴Rt△DEC≌Rt△BFA（HL）,∴DE=BF．∴四边形BEDF是平行四边形．∴MB=MD,ME=MF．23．已知：如图,DC∥AB,且DC=AE,E为AB的中点,（1）求证：△AED≌△EBC．（2）不雅看图前,在不添帮助线的情形下,除△EBC外,请再写出两个与△AED的面积相等的三角形．（直接写出成果,不请求证实）：证实：∵DC∥AB∴∠CDE＝∠AED∵DE＝DE,DC＝AE∴△AED≌△EDC∵E为AB中点∴AE＝BE∴BE＝DC∵DC∥AB∴∠DCE＝∠BEC∵CE＝CE∴△EBC≌△EDC∴△AED≌△EBC24．（7分）如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的等分线,BD的延伸线垂直于过C点的直线于E,直线CE交BA的延伸线于F．求证：BD=2CE．证实：∵∠CEB=∠CAB=90°∴ABCE四点共元∵∠AB E=∠CB E∴AE=CE∴∠ECA=∠EAC取线段BD的中点G,衔接AG,则：AG=BG=DG∴∠GAB=∠ABG而：∠ECA=∠GBA (同弧上的圆周角相等）∴∠ECA=∠EAC=∠GBA=∠GAB而：AC=AB∴△AEC≌△AGB∴EC=BG=DG∴BE=2CE25.如图：DF=CE,AD=BC,∠D=∠C.求证：△AED≌△BFC.证实：∵DF=CE,∴DF-EF=CE-EF,即DE=CF,在△AED和△BFC中,∵ AD=BC, ∠D=∠C ,DE=CF ∴△AED≌△BFC（SAS）26.（10分）如图：AE.BC交于点M,F点在AM上,BE∥CF,BE=CF.求证：AM是△ABC的中线.证实：∵BE‖CF∴∠E=∠CFM,∠EBM=∠FCM∵BE=CF∴△BEM≌△CFM∴BM=CM∴AM是△ABC的中线.27.（10分）如图：在△ABC中,BA=BC,D是AC的中点.求证：BD⊥AC.∵△ABD和△BCD的三条边都相等∴△ABD=△BCD∴∠ADB=∠CD∴∠ADB=∠CDB=90°∴BD⊥AC28.（10分）AB=AC,DB=DC,F是AD的延伸线上的一点.求证：BF=CF在△ABD与△ACD中AB=ACBD=DCAD=AD∴△ABD≌△ACD∴∠ADB=∠ADC∴∠BDF=∠FDC在△BDF与△FDC中BD=DC∠BDF=∠FDCDF=DF∴△FBD≌△FCD∴BF=FC29.（12分）如图：AB=CD,AE=DF,CE=FB.求证：AF=DE.∵AB=DCAE=DF,CE=FBCE+EF=EF+FB∴△ABE=△CDF∵∠DCB=∠ABFAB=DC BF=CE△ABF=△CDE∴AF=DE30.公园里有一条“Z”字形道路ABCD,如图所示,个中AB∥CD,在AB,CD,BC三段路旁各有一只小石凳E,F,M,且BE＝CF,M在BC的中点,试解释三只石凳E,F,M正好在一条直线上.证实：衔接EF∵AB∥CD∴∠B=∠C∵M是BC中点∴BM=CM在△BEM 和△CFM中BE=CF∠B=∠CBM=CM∴△BEM≌△CFM（SAS）∴CF=BE31．已知：点 A.F.E.C在统一条直线上, AF＝CE,BE∥DF,BE＝DF．求证：△ABE≌△CDF．∵AF=CE,FE=EF.∴AE=CF.∵DF//BE,∴∠AEB=∠CFD（两直线平行,内错角相等）∵BE=DF∴：△ABE≌△CDF（SAS）32.已知：如图所示,AB＝AD,BC＝DC,E.F分离是DC.BC的中点,求证： AE＝AF.DEAF衔接BD;∵AB=ADBC=D∴∠ADB=∠ABD∠CDB=∠ABD;两角相加,∠ADC=∠ABC;∵BC=DCE\F是中点∴DE=BF;∵AB=ADDE=BF∠ADC=∠ABC∴AE=AF.33．如图,在四边形ABCD中,E是AC上的一点,∠1=∠2,∠3=∠4,求证: ∠5=∠6．证实：在△ADC,△ABC中∵AC=AC,∠BAC=∠DAC,∠BCA=∠DCA∴△ADC≌△ABC（两角加一边）∵AB=AD,BC=CD在△DEC与△BEC中∠BCA=∠DCA,CE=CE,BC=CD∴△DEC≌△BEC（双方夹一角）∴∠DEC=∠BEC34．已知AB∥DE,BC∥EF,D,C在AF上,且AD＝CF,求证：△ABC≌△DEF．∵AD=DF∴AC=DF∵AB//DE∴∠A=∠EDF又∵BC//EF∴∠F=∠BCA∴△ABC≌△DEF（ASA）35．已知：如图,AB=AC,BD AC,CE AB,垂足分离为D.E,BD.CE订交于点F,求证：BE=CD．证实：∵BD⊥AC∴∠BDC=90°∵CE⊥AB∴∠BEC=90°∴∠BDC=∠BEC=90°∵AB=AC∴∠DCB=∠EBC∴BC=BC∴Rt△BDC≌Rt△BEC（AAS)∴BE =CD36、如图,在△ABC 中,AD 为∠BAC 的等分线,DE⊥AB于E,DF⊥AC 于F.求证：DE=DF ．证实：∵AD 是∠BAC 的等分线 ∴∠EAD=∠FAD∵DE⊥AB,DF⊥AC∴∠BFD=∠CFD=90°∴∠AED 与∠AFD=90°在△AED 与△AFD 中∠EAD=∠FADAC DE FAD=AD∠AED=∠AFD∴△AED≌△AFD（AAS ）∴AE=AF在△AEO 与△AFO 中∠EAO=∠FAOAO=AOAE=AF∴△AEO≌△AF O （SAS ）∴∠AOE=∠AOF=90°∴AD⊥EF37.已知：如图, AC BC 于 C , DE AC 于 E , AD AB 于 A , BC=AE ．若AB=5 ,求AD 的长？ ∵AD⊥AB∴∠BAC=∠ADE 又∵AC⊥BC 于C,DE⊥AC 于E 依据三角形角度之和等于180度∴∠ABC=∠DAE∵BC=AE,△ABC≌△DAE（ASA ）∴AD=AB=538．如图：AB=AC,ME⊥AB,MF⊥AC,垂足分离为 E.F,ME=MF.求证：MB=MC证实：∵AB=AC∴∠B=∠C DCB AE∵ME⊥AB,MF⊥AC∴∠BEM=∠CFM=90°在△BME和△CMF中∵∠B=∠C ∠BEM=∠CFM=90° ME=MF∴△BME≌△CMF（AAS）∴MB=MC．39.如图,给出五个等量关系：①②③④⑤．请你以个中两个为前提,另三个中的一个为结论,推出一个准确的结论（只需写出一种情形）,并加以证实．已知：①AD=BC,⑤∠DAB=∠CBA求证：△DAB≌△CBA证实：∵AD=BC,∠DAB=∠CBA又∵AB=AB∴△DAB≌△CBA40．在△ABC中,,,直线经由点,且于,于.(1)当直线绕点扭转到图1的地位时,求证：①≌;②;(2)当直线绕点扭转到图2的地位时,（1）中的结论还成立吗？若成立,请给出证实;若不成立,解释来由.（1）①∵∠ADC=∠ACB=∠BEC=90°,∴∠CAD+∠ACD=90°,∠BCE+∠CBE=90°,∠ACD+∠BCE=90°．∴∠CAD=∠BCE．∵AC=BC,∴△ADC≌△CEB．②∵△ADC≌△CEB,∴CE=AD,CD=BE．∴DE=CE+CD=AD+BE．（2）∵∠ADC=∠CEB=∠ACB=90°,∴∠ACD=∠CBE．又∵AC=BC,∴△ACD≌△CBE．∴CE=AD,CD=BE．∴DE=CE﹣CD=AD ﹣BE41．如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.求证：（1）EC=BF;（2）EC⊥BF（1）∵AE⊥AB,AF⊥AC,∴∠BAE=∠CAF=90°,∴∠BAE+∠BAC=∠CAF+∠BAC,即∠EAC=∠BAF, AE B MCF在△ABF和△AEC中,∵AE=AB,∠EAC=∠BAF,AF=AC,∴△ABF≌△AEC（SAS）,∴EC=BF;（2）如图,依据（1）,△ABF≌△AEC,∴∠AEC=∠ABF,∵AE⊥AB,∴∠BAE=90°,∴∠AEC+∠ADE=90°,∵∠ADE=∠BDM（对顶角相等）,∴∠ABF+∠BDM=90°,在△BDM中,∠BMD=180°-∠ABF-∠BDM=180°-90°=90°,∴EC⊥BF．42．如图：BE⊥AC,CF⊥AB,BM=AC,CN=AB.求证：（1）AM=AN;（2）AM⊥AN.证实：（1）∵BE⊥AC,CF⊥AB∴∠ABM+∠BAC=90°,∠ACN+∠BAC=90°∴∠ABM=∠ACN∵BM=AC,CN=AB∴△ABM≌△NAC∴AM=AN（2）∵△ABM≌△NAC∴∠BAM=∠N∵∠N+∠BAN=90°∴∠BAM+∠BAN=90°即∠MAN=90°∴AM⊥AN43．如图,已知∠A=∠D,AB=DE,AF=CD,BC=EF.求证:BC∥EF在△ABF和△CDE中,AB=DE∠A=∠DAF=CD∴△ABF≡△CDE（边角边）∴FB=CE在四边形BCEF中FB=CEBC=EF∴四边形BCEF是平行四边形∴BC‖EF44．如图,已知AC∥BD,EA.EB分离等分∠CAB和∠DBA,CD过点E,则AB与AC+BD相等吗？请解释来由在AB上取点N ,使得AN=AC∵∠CAE=∠EAN ∴AE为公共,∴△CAE≌△EAN∴∠ANE=∠ACE又∵AC平行BD∴∠ACE+∠BDE=180而∠ANE+∠ENB=180∴∠ENB=∠BDE∠NBE=∠EBN∵BE为公共边∴△EBN≌△EBD∴BD=BN∴AB=AN+BN=AC+BD45.（10分）如图,已知: AD是BC上的中线 ,且DF=DE．求证:BE∥CF．证实：∵AD是△ABC的中线BD=CD ∵DF=DE（已知）∠BDE=∠FDC ∴△BDE≌△FDC 则∠EBD=∠FCD ∴BE∥CF（内错角相等,两直线平行）.46.(10分)已知：如图,AB＝CD,DE⊥AC,BF⊥AC,E,F是垂足,．求证：．证实：∵DE⊥AC,BF⊥AC∴∠CED=∠AFB=90º又∵AB=CD,BF=DE∴Rt⊿ABF≌Rt⊿CDE（HL ）∴AF=CE∠BAF=∠DCE∴AB//CD47.(10分)如图,已知∠1=∠2,∠3=∠4,求证：AB=CD∵,∠3=∠4∴OB=OC在△AOB 和△DOC 中∠1=∠2OB=OC∠AOB=∠DOC△AOB≌△DOC∴AO=DO AO+OC=DO+OB AC=DB在△ACB 和△DBC 中AC=DB A D ECBF,∠3=∠4BC=CB△ACB≌△DBC∴AB=CD48.(10分)如图,已知AC⊥AB,DB⊥AB,AC＝BE,AE ＝BD,试猜测线段CE 与DE 的大小与地位关系,并证实你的结论.CE>DE.当∠AEB 越小,则DE 越小.证实：过D 作AE 平行线与AC 交于F,衔接FB由已知前提知AFDE 为平行四边形,ABEC 为矩形 ,且△DFB 为等腰三角形.RT△BAE 中,∠AEB 为锐角,即∠AEB<90°∵DF//AE ∴∠FDB=∠AEB<90°△DFB 中 ∠DFB=∠DBF=(180°-∠FDB)/2>45°RT△AFB 中,∠FBA=90°-∠DBF <45°∠AFB=90°-∠FBA>45°∴AB>AF∵AB=CE AF=DE∴CE>DE49.(10分)如图,已知AB ＝DC,AC ＝DB,BE ＝CE,求证：AE ＝DE. ∵AB=DC,AC=DB,BC=BCA CE D B A B E CD∴△ABC≌△DCB,∴∠ABC=∠DCB又∵BE=CE,AB=DC∴△ABE≌△DCE∴AE=DE50．如图9所示,△ABC 是等腰直角三角形,∠ACB＝90°,AD 是BC 边上的中线,过C 作AD 的垂线,交AB 于点E,交AD 于点F,求证：∠ADC＝∠BDE．作CG⊥AB,交AD 于H,则∠ACH=45º,∠BCH=45º∵∠CAH=90º-∠CDA, ∠BCE=90º-∠CDA ∴∠CAH=∠BCE 又∵AC=CB, ∠ACH=∠B=45º∴△ACH≌△CBE, ∴CH=BE 又∵∠DCH=∠B=45º, CD=DB∴△CFD≌△BED∴∠ADC=∠BDE AB CD E F图9。

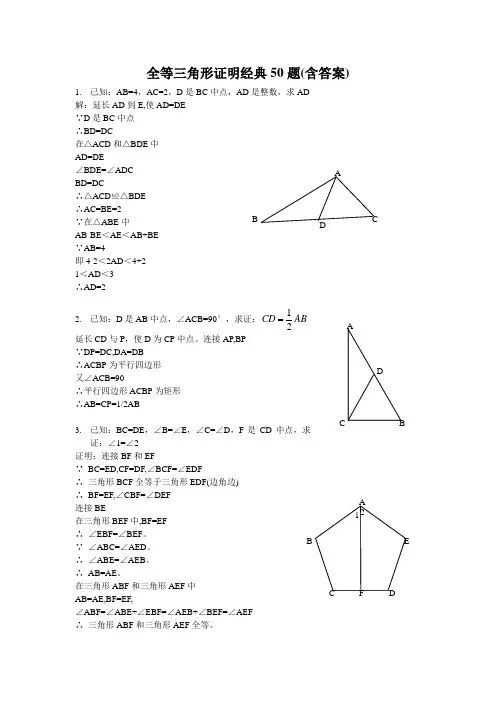
全等三角形证明经典50题(含答案)1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=22. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB延长CD 与P ，使D 为CP 中点。

连接AP ,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形AD BC∴AB=CP=1/2AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF∵ BC=ED,CF=DF ,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF ,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。

∵ ∠ABC=∠AED 。

∴ ∠ABE=∠AEB 。

∴ AB=AE 。

在三角形ABF 和三角形AEF 中AB=AE,BF=EF ,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。

∴ ∠BAF=∠EAF (∠1=∠2)。

4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ，可得，∠EFD ＝CGDDE ＝DC∠FDE ＝∠GDC （对顶角）B ACDF21 E∴△EFD≌△CGDEF＝CG∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC为等腰三角形，AC＝CG又EF＝CG∴EF＝AC5.已知：AD平分∠BAC，AC=AB+BD，求证：∠B=2∠CA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE证明：在AE 上取F ，使EF ＝EB ，连接CF∵CE ⊥AB∴∠CEB ＝∠CEF ＝90°∵EB ＝EF ，CE ＝CE ，∴△CEB ≌△CEF∴∠B ＝∠CFE∵∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180°∴∠D ＝∠CFA∵AC 平分∠BAD∴∠DAC ＝∠FAC∵AC ＝AC∴△ADC ≌△AFC （SAS ）∴AD ＝AF∴AE ＝AF ＋FE ＝AD ＋BE7. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD B CAD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE ∴AC=BE=2∵在△ABE中AB-BE＜AE＜AB+BE ∵AB=4即4-2＜2AD＜4+2 1＜AD＜3∴AD=28.已知：D是AB中点，∠ACB=90°，求证：12 CD AB9. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。

全等三角形证明经典50题(含答案)1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD2. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠24. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠CDAB B A CDF2 1 EAC D E F 21 A D BC A6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

求证：BC=AB+DC 。

13.已知：AB//ED ，∠EAB=∠BDE ，AF=CD ，EF=BC ，求证：∠F=∠C14. P 是∠BAC 平分线AD 上一点，AC>AB ，求证：PC-PB<AC-AB15. 已知∠ABC=3∠C ，∠1=∠2，BE ⊥AE ，求证：AC-AB=2BED C B A FE PD A CB16. 已知，E 是AB 中点，AF=BD ，BD=5，AC=7，求DC18．如图，在△ABC 中，BD =DC ，∠1=∠2，求证：AD ⊥BC ．19．如图，OM 平分∠POQ ，MA ⊥OP ,MB ⊥OQ ，A 、B 为垂足，AB 交OM 于点N ．求证：∠OAB =∠OBA20．（5分）如图，已知AD ∥BC ，∠P AB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD +BC =AB ．21．如图，△ABC 中，AD 是∠CAB 的平分线，且AB =AC +CD ，求证：∠C =2∠B22．（6分）如图①，E 、F 分别为线段AC 上的两个动点，且DE ⊥AC 于E ，BF ⊥AC 于F ，若AB =CD ，AF =CE ，BD 交AC 于点M ．（1）求证：MB =MD ，ME =MF（2）当E 、F 两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．F AEDCB P E D CB A DC B A23．已知：如图，DC ∥AB ，且DC =AE ，E 为AB 的中点， （1）求证：△AED ≌△EBC ． （2）观看图前，在不添辅助线的情况下，除△EBC 外，请再写出两个与△AED 的面积相等的三角形．（直接写出结果，不要求证明）：24．（7分）如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ．求证：BD =2CE ．证明：25、如图：DF=CE ，AD=BC ，∠D=∠C 。

1. 已知：AB=4，AC=2，D 是BC 中点，111749AD 是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DCAD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=22. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB延长CD 与P ，使D 为CP 中点。

连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2AD BC证明：连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。

∵ ∠ABC=∠AED 。

∴ ∠ABE=∠AEB 。

∴ AB=AE 。

在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。

∴ ∠BAF=∠EAF (∠1=∠2)。

4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ，可得，∠EFD ＝CGDDE ＝DC∠FDE ＝∠GDC （对顶角）∴△EFD ≌△CGDEF ＝CGBACDF21 E∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC为等腰三角形，AC＝CG又EF＝CG∴EF＝AC5.已知：AD平分∠BAC，AC=AB+BD，求证：∠B=2∠CA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C6.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE 上取F ，使EF ＝EB ，连接CF∵CE ⊥AB∴∠CEB ＝∠CEF ＝90°∵EB ＝EF ，CE ＝CE ，∴△CEB ≌△CEF∴∠B ＝∠CFE∵∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180°∴∠D ＝∠CFA∵AC 平分∠BAD∴∠DAC ＝∠FAC∵AC ＝AC∴△ADC ≌△AFC （SAS ）∴AD ＝AF∴AE ＝AF ＋FE ＝AD ＋BE7. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=28. 已知：D 是AB 中点，∠ACB=90°，求证：1CD AB9. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。

1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=22. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB延长CD 与P ，使D 为CP 中点。

连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2AD BC证明：连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。

∵ ∠ABC=∠AED 。

∴ ∠ABE=∠AEB 。

∴ AB=AE 。

在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。

∴ ∠BAF=∠EAF (∠1=∠2)。

4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ，可得，∠EFD ＝CGDDE ＝DC∠FDE ＝∠GDC （对顶角）∴△EFD ≌△CGDEF ＝CGB ACDF21E∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC为等腰三角形，AC＝CG又EF＝CG∴EF＝AC5.已知：AD平分∠BAC，AC=AB+BD，求证：∠B=2∠CA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C6.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE 上取F ，使EF ＝EB ，连接CF∵CE ⊥AB∴∠CEB ＝∠CEF ＝90°∵EB ＝EF ，CE ＝CE ，∴△CEB ≌△CEF∴∠B ＝∠CFE∵∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180°∴∠D ＝∠CFA∵AC 平分∠BAD∴∠DAC ＝∠FAC∵AC ＝AC∴△ADC ≌△AFC （SAS ）∴AD ＝AF∴AE ＝AF ＋FE ＝AD ＋BE7. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE＜AE＜AB+BE ∵AB=4即4-2＜2AD＜4+2 1＜AD＜3∴AD=28.已知：D是AB中点，∠ACB=90°，求证：12 CD AB9.已知：BC=DE，∠B=∠E，∠C=∠D，F是CD中点，求证：∠1=∠2证明：连接BF 和EF 。

1. 已知：AB=4，AC=2，D 是BC 中点，111749AD 是整数，求AD解：延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC 在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4 即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=2 2. 已知：D 是AB 中点，∠ACB=90°，求证：12CD ABA DB C延长CD 与P ，使D 为CP 中点。

连接AP,BP ∵DP=DC,DA=DB ∴ACBP 为平行四边形 又∠ACB=90 ∴平行四边形ACBP 为矩形 ∴AB=CP=1/2AB 3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠24.5. 证明：连接BF 和EF∵BC=ED,CF=DF,∠BCF=∠EDF∴三角形BCF 全等于三角形EDF(边角边)∴BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴∠EBF=∠BEF 。

C D FB C∵∠ABC=∠AED 。

∴∠ABE=∠AEB 。

∴AB=AE 。

在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴三角形ABF 和三角形AEF 全等。

∴∠BAF=∠EAF(∠1=∠2)。

6. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ，可得，∠EFD ＝CGDDE ＝DC∠FDE ＝∠GDC （对顶角）∴△EFD ≌△CGDEF ＝CG∠CGD ＝∠EFD又，EF ∥AB∴，∠EFD ＝∠1∠1=∠2∴∠CGD ＝∠2∴△AGC 为等腰三角形，AC ＝CG又EF ＝CG∴EF ＝AC7. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠CB ACDF2 1EA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD（SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C8.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE上取F，使EF＝EB，连接CF∵CE⊥AB∴∠CEB＝∠CEF＝90°∵EB＝EF，CE＝CE，∴△CEB≌△CEF∴∠B＝∠CFE∵∠B＋∠D＝180°，∠CFE＋∠CFA＝180°∴∠D＝∠CFA∵AC平分∠BAD∴∠DAC＝∠FAC∵AC＝AC∴△ADC≌△AFC（SAS）∴AD＝AF∴AE＝AF＋FE＝AD＋BE9.已知：AB=4，AC=2，D是BC中点，AD是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC 在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4 即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=2 10. 已知：D 是AB 中点，∠ACB=90°，求证：1CD ABADB C在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE ∵AB=4 即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=2 11.已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。

全等三角形证明经典50题(含答案)1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=22. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB延长CD 与P ，使D 为CP 中点。

连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形AD BC∴AB=CP=1/2AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。

∵ ∠ABC=∠AED 。

∴ ∠ABE=∠AEB 。

∴ AB=AE 。

在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。

∴ ∠BAF=∠EAF (∠1=∠2)。

4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ，可得，∠EFD ＝CGDDE ＝DC∠FDE ＝∠GDC （对顶角）B ACDF21 E∴△EFD≌△CGDEF＝CG∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC为等腰三角形，AC＝CG又EF＝CG∴EF＝AC5.已知：AD平分∠BAC，AC=AB+BD，求证：∠B=2∠CA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE证明：在AE 上取F ，使EF ＝EB ，连接CF∵CE ⊥AB∴∠CEB ＝∠CEF ＝90°∵EB ＝EF ，CE ＝CE ，∴△CEB ≌△CEF∴∠B ＝∠CFE∵∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180°∴∠D ＝∠CFA∵AC 平分∠BAD∴∠DAC ＝∠FAC∵AC ＝AC∴△ADC ≌△AFC （SAS ）∴AD ＝AF∴AE ＝AF ＋FE ＝AD ＋BE7. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD BCAD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE＜AE＜AB+BE ∵AB=4即4-2＜2AD＜4+21＜AD＜3∴AD=28.已知：D是AB中点，∠ACB=90°，求证：12 CD AB9. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。

全等三角形证明经典50题(含答案)1.已知：AB=4，AC=2，D是BC中点，AD是整数，求AD解：延长AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE＜AE＜AB+BE∵AB=4即4-2＜2AD＜4+21＜AD＜3∴AD=22.已知：D是AB中点，∠ACB=90°，求证：12 CD AB延长CD与P，使D为CP中点。

连接AP,BP∵DP=DC,DA=DB∴ACBP为平行四边形又∠ACB=90∴平行四边形ACBP为矩形∴AB=CP=1/2AB3.已知：BC=DE，∠B=∠E，∠C=∠D，F是CD中点，求证：∠1=∠2证明：连接BF和EF∵BC=ED,CF=DF,∠BCF=∠EDF∴三角形BCF全等于三角形EDF(边角边)∴BF=EF,∠CBF=∠DEF连接BE在三角形BEF中,BF=EF∴∠EBF=∠BEF。

∵∠ABC=∠AED。

∴∠ABE=∠AEB。

∴AB=AE。

在三角形ABF和三角形AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴三角形ABF和三角形AEF全等。

A DBC∴ ∠BAF=∠EAF (∠1=∠2)。

4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC 过C 作CG ∥EF 交AD 的延长线于点G CG ∥EF ，可得，∠EFD ＝CGD DE ＝DC∠FDE ＝∠GDC （对顶角） ∴△EFD ≌△CGD EF ＝CG∠CGD ＝∠EFD 又，EF ∥AB∴，∠EFD ＝∠1 ∠1=∠2∴∠CGD ＝∠2∴△AGC 为等腰三角形， AC ＝CG 又 EF ＝CG ∴EF ＝AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠ C证明：延长AB 取点E ，使AE ＝AC ，连接DE ∵AD 平分∠BAC ∴∠EAD ＝∠CAD ∵AE ＝AC ，AD ＝AD∴△AED ≌△ACD （SAS ） ∴∠E ＝∠C ∵AC ＝AB+BD ∴AE ＝AB+BD ∵AE ＝AB+BE ∴BD ＝BE ∴∠BDE ＝∠E∵∠ABC ＝∠E+∠BDE ∴∠ABC ＝2∠EABA CDF2 1 E∴∠ABC＝2∠C6.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE上取F，使EF＝EB，连接CF∵CE⊥AB∴∠CEB＝∠CEF＝90°∵EB＝EF，CE＝CE，∴△CEB≌△CEF∴∠B＝∠CFE∵∠B＋∠D＝180°，∠CFE＋∠CFA＝180°∴∠D＝∠CFA∵AC平分∠BAD∴∠DAC＝∠FAC∵AC＝AC∴△ADC≌△AFC（SAS）∴AD＝AF∴AE＝AF＋FE＝AD＋BE12. 如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD上。

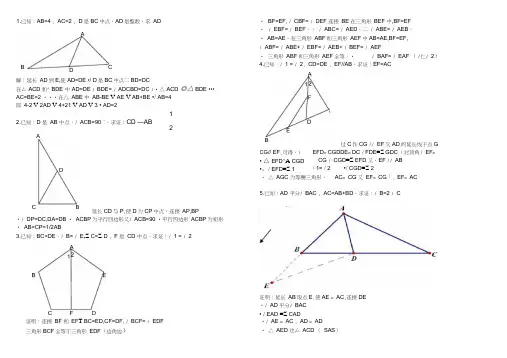
证明：连接 BF 和 EF T BC=ED,CF=DF, / BCF= / EDF 三角形BCF 全等于三角形 EDF （边角边）1.已知：AB=4 , AC=2 , D 是BC 中点，AD 是整数，求 ADD • BF=EF, / CBF= / DEF 连接 BE 在三角形 BEF 中,BF=EF • / EBF= / BEF 。

： / ABC= / AED 。

二 / ABE= / AEB 。

• AB=AE 。

在三角形 ABF 和三角形 AEF 中AB=AE,BF=EF, / ABF= / ABE+ / EBF= / AEB+ / BEF= / AEF • 三角形 ABF 和三角形 AEF 全等。

•/ BAF= / EAF （ /仁/ 2）4.已知：/ 1 = / 2, CD=DE , EF//AB ，求证：EF=AC解：延长 AD 到E,使AD=DE •/ D 是BC 中点二BD=DC 在厶 ACD 和^ BDE 中 AD=DE / BDE= / ADCBD=DC /•△ ACD ◎△ BDE ••• AC=BE=2 •••在△ ABE 中 AB-BE V AE V AB+BE •/ AB=4 即 4-2 V 2AD V 4+21 V AD V 3 • AD=21 2.已知：D 是 AB 中点，/ ACB=90 °，求证：CD —AB 2A CG// EF ,可得，/• △ EFD ^A CGD•，/ EFD =Z 1过C 作CG // EF 交AD 的延长线于点GEFD = CGDDE = DC / FDE =Z GDC （对顶角） EF = CG / CGD =Z EFD 又，EF // AB / 1= / 2 •/ CGD =Z 2 • △ AGC 为等腰三角形， AC = CG 又 EF = CG 「. EF = AC 延长CD 与P ,使D 为CP 中点。

连接 AP,BP •/ DP=DC,DA=DB • ACBP 为平行四边形又/ ACB=90 •平行四边形 ACBP 为矩形 • AB=CP=1/2AB 3.已知：BC=DE ，/ B= / E ,Z C=Z D , F 是 CD 中点，求证：/ 1 = / 2 5.已知：AD 平分/ BAC , AC=AB+BD ，求证：/ B=2 / C证明：延长 AB 取点E ,使AE = AC ,连接DE •/ AD 平分/ BAC• / EAD =Z CAD•/ AE = AC , AD = AD • △ AED 也厶 ACD （ SAS ）•••/ E = Z C•/ AC = AB+BD •AE = AB+BD•/ AE = AB+BE •BD = BE •••/ BDE =Z E •••/ ABC =Z E+ / BDE •••/ ABC = 2 / E •••/ ABC = 2 / C ••• AE = AF + FE = AD + BE12.如图，四边形ABCD中，AB 在AD上。

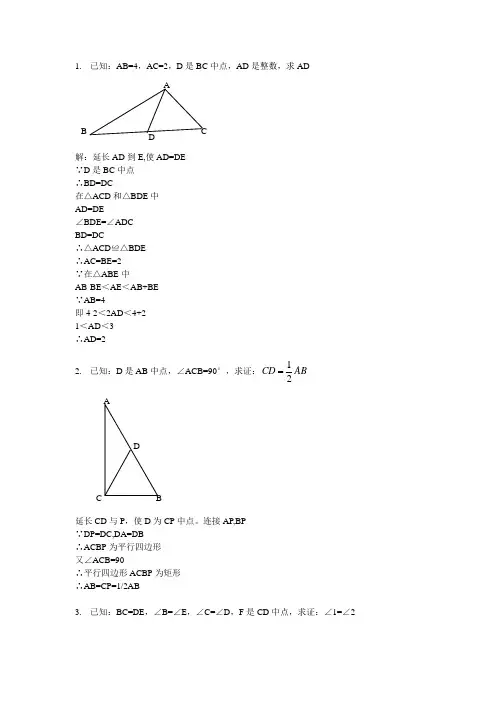
1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=22. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB延长CD 与P ，使D 为CP 中点。

连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2AD BC证明：连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。

∵ ∠ABC=∠AED 。

∴ ∠ABE=∠AEB 。

∴ AB=AE 。

在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。

∴ ∠BAF=∠EAF (∠1=∠2)。

4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ，可得，∠EFD ＝CGDDE ＝DC∠FDE ＝∠GDC （对顶角）∴△EFD ≌△CGDEF ＝CGB ACDF21 E∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC为等腰三角形，AC＝CG又EF＝CG∴EF＝AC5.已知：AD平分∠BAC，AC=AB+BD，求证：∠B=2∠CA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C6.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE 上取F ，使EF ＝EB ，连接CF∵CE ⊥AB∴∠CEB ＝∠CEF ＝90°∵EB ＝EF ，CE ＝CE ，∴△CEB ≌△CEF∴∠B ＝∠CFE∵∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180°∴∠D ＝∠CFA∵AC 平分∠BAD∴∠DAC ＝∠FAC∵AC ＝AC∴△ADC ≌△AFC （SAS ）∴AD ＝AF∴AE ＝AF ＋FE ＝AD ＋BE7. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADC AD BCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=28. 已知：D 是AB 中点，∠ACB=90°，求证：1CD AB9. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。

全等三角形证明经典50题(含答案)1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC 在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=2ADBC2. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB延长CD 与P ，使D 为CP 中点。

连接AP ,BP ∵DP=DC,DA=DB ∴ACBP 为平行四边形 又∠ACB=90∴平行四边形ACBP 为矩形 ∴AB=CP=1/2AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边) ∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF ∴ ∠EBF=∠BEF 。

∵ ∠ABC=∠AED 。

∴ ∠ABE=∠AEB 。

∴ AB=AE 。

在三角形ABF 和三角形AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴ 三角形ABF 和三角形AEF 全等。

∴ ∠BAF=∠EAF (∠1=∠2)。

4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG ∥EF 交AD 的延长线于点G CG ∥EF ，可得，∠EFD ＝CGD DE ＝DC∠FDE ＝∠GDC （对顶角）BA CDF2 1 EEF＝CG∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC为等腰三角形，AC＝CG又EF＝CG∴EF＝AC5.已知：AD平分∠BAC，AC=AB+BD，求证：∠B=2∠CA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C6.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE 上取F ，使EF ＝EB ，连接CF ∵CE ⊥AB∴∠CEB ＝∠CEF ＝90° ∵EB ＝EF ，CE ＝CE ， ∴△CEB ≌△CEF ∴∠B ＝∠CFE∵∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180° ∴∠D ＝∠CFA ∵AC 平分∠BAD ∴∠DAC ＝∠FAC ∵AC ＝AC∴△ADC ≌△AFC （SAS ） ∴AD ＝AF∴AE ＝AF ＋FE ＝AD ＋BE7. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DEADB C∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=28. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB解：延长AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE＜AE＜AB+BE∵AB=4即4-2＜2AD＜4+21＜AD＜3∴AD=29.已知：BC=DE，∠B=∠E，∠C=∠D，F是CD中点，求证：∠1=∠2证明：连接BF和EF。

1.已知：AB=4 , AC=2 , D 是BC 中点，AD 是整数，求ADA 解：延长AD 至IJE,使AD=DE・・・D 是BC 中点BD=DC在厶ACD 和厶BDE 中AD=DEZBDE= ZADC BD=DCAA ACD A BDE•*. AC=BE=2・・•在△ ABE 中AB-BE < AE<AB+BE・・・AB=4即 4・2 <2AD < 4+21 < AD < 3・・・AD=2延长CD 与P,使D 为CP 中点。

连接VDP=DC,DA=DBA AC BP 为平行四边形又 Z ACB=90・・・平行四边形ACBP 为矩形AAB=CP=1/2AB 2.已知：D 是AB 中点，Z ACB=90 0,求证：CD [AB 2AAP,BP3.已知：BC=DE , Z B= ZE, Z C= ZD , F 是CD 中点，求证：Z 1= Z2证明：连接BF和EF・・・ BC=ED,CF=DF, Z BCF= Z EDF・・・三角形BCF全等于三角形EDF（边角边）・・・ BF=EF, ZCBF=Z DEF连接BE在三角形BEF中,BF=EF/. Z EBF=Z BEFo・・・ Z ABC= Z AED o・・・ Z ABE= Z AEBo/. AB=AE o在三角形ABF和三角形AEF屮AB=AE,BF=EF,ZABF= Z ABE+ Z EBF= ZAEB+ Z BEF= Z AEF・・・三角形ABF和三角形AEF全等。

・・・ Z BAF= Z EAF（Z 1= Z 2）o4. 己知：Z 1= Z 2 , CD=DE , EF//AB ,求证：EF=AC过C作CG〃EF交AD的延长线于点GCG// EF,可得，Z EFD= CGDDE= DCZFDE= Z GDC （对顶角）AA EFD^A CGDEF= CGZCGD = Z EFD又，EF// AB・・・，Z EFD= Z 1Z1= Z 2・・・Z CGD= Z 2・・・△ AGC为等腰三角形,AC= CG又EF=CG・・・EF= AC5.已知：AD 平分Z BAC, AC=AB+BD ,求证：Z B=2 Z C证明：延长AB取点E,使AE=AC,连接DEVAD 平分Z BACAZ EAD=Z CAD・・・AE=AC, AD = ADA A AED^A ACD ( SAS)AZ E=Z CVAC = AB+BD・・・AE= AB+BD・・・AE= AB+BEABD = BE・・・Z BDE=Z EVZ ABC=Z E+ Z BDEAZ ABC = 2 ZEAZ ABC = 2 ZC6.己知：AC 平分Z BAD , CE丄AB , Z B+ Z D=180 ° ,求证：AE=AD+BE・・・CE丄AB ・・・Z CEB=Z CEF= 90° ・・・EB=EF, CE = CE, AACEB^ACEF ・・・Z B=Z CFEVZ B+Z D= 180 ° , ZCFE+Z CFA= 180 0AZ D = Z CFAVAC 平分Z BAD・・・Z DAC = Z FACVAC = AC・・・△ ADC 竺△ AFC ( SAS)/.AD = AF ・・・AE= AF+ FE= AD + BE解：延长AD至IJE,使AD=DE・・・D是BC中点・・・BD=DC在厶ACD和厶BDE中AD=DEZBDE= Z ADCBD=DC7.已知：AB=4 , AC=2 , D是BC屮点, AD是整数，求ADA 证明:在AE上取F,使EF= EB,连接CFAAACD^ABDE•*. AC=BE=2・・•在△ ABE中AB-BE < AE<AB+BE・・・AB=4即4・2 < 2AD < 4+21 < AD < 3・・・AD=218.已知：D 是AB 中点，Z ACB=90 0,求证：CD -AB2解：延长AD到E,使AD=DE・・・D是BC屮点・・・BD=DC在厶ACD和厶BDE中AD=DEZBDE= Z ADCBD=DCAA ACD A BDE•*. AC=BE=2•・•在A ABE中9.已知：BC=DE , Z B= ZE, Z C= ZD , F 是CD 中点，求证：Z 1= Z2A证明：连接BF和EF。

1.已知：AB=4 , AC=2 , D是BC中点，AD是整数,求AD解：延长AD至【J E,使AD=DE• D是BC中点••• BD=DC在左ACD和左BDE中AD=DEZ BDE= Z ADCBD=DC••• A ACD^A BDE. .AC=BE=2•在△ ABE 中AB-BE < AE< AB+BE••AB=4即4-2<2AD <4+21<AD <3•••AD=21 2.已知：D是AB中点，Z ACB=90 ,求证：CD —AB延长CD与P,使D为CP中点。

连接AP.BP ••DP=DC,DA=DB• •ACBP为平行四边形又/ ACB=90平行四边形ACBP为矩形•••AB=CP=1/2AB证明：连接BF和EF. • BC=ED,CF=DF, / BCF= / EDF三角形BCF全等于三角形EDF（边角边）••• BF=EF, Z CBF= / DEF连接BE在三角形BEF中,BF=EF/ EBF= / BEF。

. • Z ABC= Z AED。

••• Z ABE= Z AEB。

AB=AE 。

在三角形ABF和三角形AEF中AB=AE,BF=EF,Z ABF= Z ABE+ Z EBF= Z AEB+ Z BEF= Z AEF三角形ABF和三角形AEF全等。

Z BAF= Z EAF （ Z 1 = Z 2）。

EF=AC 4,已知：/ 1 = Z 2, CD=DE , EF//AB ,求证:过C作CG // EF交AD的延长线于点GCG// EF,可得，/ EFD= CGDDE= DC/ FDE=Z GDC （对顶角）. EFD^A CGDZCGD=Z EFD又，EF// AB. Z EFD=Z 1/ 1= / 2•••Z CGD=Z 2AGC为等腰三角形,AC= CG又EF= CGEF= AC证明：延长AB取点E,使AE = AC,连接DE . • AD 平分Z BAC••• Z EAD = Z CAD. . AE = AC , AD = AD. AED^A ACD (SAS)Z E= Z C. . AC = AB+BDAE = AB+BD. . AE = AB+BE. .BD = BE•••Z BDE = / E. Z ABC = Z E+ Z BDE•••Z ABC = 2 / E•.•Z ABC = 2 Z C6. 已知：AC 平分Z BAD , CE± AB , Z B+ / D=180 °,求证：AE=AD+BE证明：在AE上取F,使EF = EB,连接CF. • CE ± ABCEB = Z CEF = 90°. • EB = EF, CE = CE,. CEB^A CEF•••Z B=Z CFE. Z B+Z D= 180° , Z CFE + Z CFA = 180°•••Z D = Z CFA. • AC 平分Z BAD/ DAC = / FAC. . AC = AC. ADC^A AFC (SAS)AD = AFAE = AF + FE= AD + BE7, 已知：AB=4 , AC=2 , D是BC中点，AD是整数，求AD解：延长AD至ij E,使AD=DED是BC中点. . BD=DC在^ ACD和^ BDE中AD=DEZ BDE= Z ADCBD=DC. ACD^A BDE••• AC=BE=2•.•在△ ABE 中AB-BE V AE V AB+BE. . AB=4即4-2 V 2AD V 4+21 v AD v 3AD=21—8. 已知：D是AB中点，/ACB=9,求证：CD-AB2 解：延长AD至ij E,使AD=DED是BC中点. . BD=DC在^ ACD和^ BDE中AD=DE/ BDE= / ADCBD=DC. ACD^A BDE ••• AC=BE=2•.•在△ ABE 中AB-BE V AE V AB+BE . . AB=4即4-2 V 2AD V 4+2 1 v AD v 3AD=2证明：连接BF和EF。