IMI-SPP+色散曲线
- 格式:docx
- 大小:841.91 KB
- 文档页数:20


一维双原子链的色散关系The dispersion relation of the one-dimensionaldiatomic chain学生姓名:吴刚所在专业:应用物理学班级:物理091指导教师:陈冰泉,刘彦平申请学位:理学学士论文提交日期:2021-6-5论文辩论日期:2021-6-18学位授予单位:青岛理工大学摘要物理学中对晶格振动的研究一直是一个重要且有意义的课题。
关于晶格振动的研究通常建立在原子链的研究上。
本文在介绍关于原子链研究根底理论的根底上,讨论了一维单原子链晶格的色散关系,从一维双原子链的角度介绍了晶格的色散关系,然后在前面讨论的根底上对三维晶格的色散关系进行了推导。
关于原子链色散关系的研究,让我们对于晶格振动有个更加清楚地认识。
论文重点介绍了一维双原子链的色散关系,在公式推导的根底上,作者完成计算机编程和模拟计算,得到色散关系的曲线。
关键词:晶格振动,一维单原子链,一维双原子链,三维晶格,色散关系AbstractThe study of lattice vibration has been an important and meaningful topic in physics. The investigation of lattice vibration is usually based on the study of atomic chain. With the introduction of the theoretical basis of atomic chain, this thesis discusses the dispersion relation of one-dimensional monatomic chain lattice, as well as the dispersion relation of one dimensional diatomic chain lattice. Based on the knowledge above, the equations for describing the dispersion relation of three dimensional lattice are then derived. The study of dispersion relations allows us to have a more clear understanding of lattice vibration. This thesis mainly presents the study and discussion of the dispersion relation of one dimensional diatomic chain. In addition to the equation derivation, we carry out programming and simulations for obtaining some important dispersion-relation curves.目录前言 0第一章理论根底 (2)第二章一维单原子链的色散关系 (5)2.1 建立振动模型 (5)2.2 建立振动方程并求解 (5)2.3 玻恩-卡曼条件 (7)2.4.qw 的函数关系 (8)第三章一维双原子链的色散关系 (12) (12)3.2 原子运动方程的求解 (12)3.3 周期性边界条件 (14)3.4 对于声学波和光学波的讨论 (15)第四章三维晶格振动的推导 (19)4.1 一维多原子链问题的处理 (19)4.2 建立三维模型和求解运动方程 (19)4.3 波矢q的取值和范围 (21)4.4 理论上的计算 (23)第五章结论和讨论 (26)致谢 (27)参考文献 (29)前言讨论晶体结构时,我们把晶体内的原子看作是处于自己的平衡位置上固定不动的。




《光纤通信》大作业阶跃光纤模式色散曲线计算光纤材料色散计算光纤光栅特性分析指导老师:专业:姓名:学号:一、阶跃光纤模式色散曲线计算1.原理分析模式色散是指多模式传输时同一波长分量的各种传导模式的相位常数不同,群速度不同,引起到达终端的脉冲展宽的现象。
对光纤中光的传播理论的研究,可以有多种方法,比如射线法,标量近似分析法等,但为了更广泛地描述光纤波导中光的传播,更详细地研究光纤的传输特性,就必须运用波动光学理论对光纤进行分析。
要对光在光纤中的传播特性有详细的理解,必须依靠麦克斯韦方程,结合问题中的边界条件,求解电磁矢量场.求解的方法一般是:1、先求出亥姆霍兹方程组以及电磁场纵向分量Ez 和Hz 的具体形式。
2、2、把Ez 和Hz 有具体形式代入麦克斯韦方程以求取其他电磁场横向分量θE 、Er 、θH 、Hr 。
3、3、利用界面上电磁场θE 和θH 切向连续条件,求取模式本征方程。
对于时谐场光波,在均匀、无源介质中,同样满足矢量的亥姆霍兹方程(式1-1,1-2)022=+∇E k E (1-1)022=+∇H k H (1-2)对于在圆柱形光纤中传播的电磁波.电场和磁场具有如下形式的函数关系(式1-3,1-4):)(),(),(t z j e r E y x E ωβθ-= (1-3))(),(),(t z j e r H y x H ωβθ-=(1-4)代入,得到亥姆霍兹方程(式1-5,1-6)。
02202=+∇z z E n k E (1-5)02202=+∇z z H n k H (1-6) 经过推导,可以得到关于r 的贝塞尔方程或修正的贝塞尔方程(式1-7)。
(1-7) 最后可解得电场和磁场的纵向分量Ez 和Hz 。
⎪⎪⎩⎪⎪⎨⎧>≤=);()()();()()(a r e r a W K W K A a r e r a U J U J A E im m m im m m z θθ0)(])[()()(2222120222=--+∂∂+∂∂r R m r n k r r R r r r R r β光纤中传播模式及传输特性都是由它自身的本征方程确定的。


色散曲线及其物理意义
色散曲线(dispersion curve)即物质材料的折射率n与波长λ之间的依赖关系曲线。
色散的实验事实在折射现象中明显的反映出来,例如,太阳光(或白光)通过棱镜或水晶时发生的色散现象(如图所示),即一束阳光可被棱镜分为红、橙、黄、绿、蓝、靛、紫七色光。
该实验现象表明,同一物质对不同的单色光的折射率是不同的,红色光的折射率最小,紫色光的折射率最大。
当它们通过棱镜时,传播方向有不同程度的偏折,因而在离开棱镜便各自分散开来。
1672年牛顿首先通过棱镜折射观察到上述的色散现象,同时他还利用正交棱镜法将色散曲线,即物质材料的折射率n与波长λ之间的依赖关系曲线非常直观地显示了出来。

色散曲线表征材料光学特性及波长选择光学特性是材料在光学波段内对光的吸收、反射和透射等行为的表现。
波长选择是在特定光学应用中,根据材料的光学特性选择合适的波长。
为了能够更好地研究和应用材料的光学特性,科学家们采用了色散曲线来表征材料的光学特性,并根据色散曲线来选择合适的波长。
色散曲线是描述材料对不同波长光的折射率变化关系的一种图形。
折射率是光线在物质中传播时速度的比值,而波长则与光的频率成反比。
材料的折射率与波长之间的关系可以通过色散曲线来展示。
一般来说,色散曲线是由波长沿横轴,折射率沿纵轴组成的。
从色散曲线中,我们可以得到材料的色散性质。
色散性质通常分为正常色散和反常色散两种情况。
正常色散是指折射率随着波长的增加而减小,而反常色散是指折射率随着波长的增加而增大。
正常色散通常发生在可见光波段,而反常色散通常发生在紫外光和红外光波段。
根据材料的色散性质,可以对材料进行光学设计和波长选择。
在光学应用中,人们常常需要选择合适的波长来实现特定的功能。
比如,在光通信领域中,波长选择非常重要。
传输信号所使用的波长需要在光纤中具有很小的损耗,同时还要满足光纤材料的色散特性。
由于光纤的传输损耗与波长的选择有关,因此选择合适的波长可以减小信号的衰减,提高传输效率。
另外,波长选择还与材料的吸收特性密切相关。
材料对特定波长的吸收强度取决于其能级结构和电子-光子相互作用。
根据材料吸收谱的特点,可以选择合适的波长来实现光学传感器、光催化等应用。
此外,波长选择在光谱分析中也是非常重要的。
光谱仪常常用于分析物质的组成和性质。
根据物质的吸收特性,可以选择合适的波长来进行分析。
不同波长的光在物质中的吸收程度不同,通过比较不同波长下光的吸收情况,可以得到物质的特征光谱。
在现代光学研究中,选择合适的波长对于实现特定功能和优化设备性能至关重要。
通过光学特性的研究,科学家们可以理解和控制材料的光学行为,并根据需求选择合适的波长。
这不仅有助于材料的应用开发,还有助于推动光学技术的发展。

色散曲线表征材料光学特性及波长选择引言:光学是研究光的传播、反射、吸收和干涉等现象的学科。
材料的光学特性对于光的传播以及与材料的相互作用至关重要。
色散曲线是一种常用的方法来描述材料的光学特性,它可以帮助我们了解材料对不同波长光的吸收和散射情况。
本文将介绍色散曲线的概念、其在材料光学特性表征中的重要性,并探讨如何选择适当的波长对材料进行研究。
一、色散曲线概述色散是指材料对光波波长的依赖关系。
当光线经过一个介质时,不同波长的光波会因材料的光学性质而产生不同的折射率。
色散曲线则是描述光波传播过程中折射率变化与波长变化的关系。
一般来说,折射率随着波长的增加而减小,这种现象称为正常色散;相反,折射率随波长增加而增大则称为反常色散。
二、色散曲线的重要性色散曲线是表征材料光学特性的重要工具,其具有以下几个重要作用:1. 材料鉴定和分类:不同材料的色散曲线各异,通过测量材料的色散曲线,我们可以确定材料的光学特性,从而将其分类和鉴定。
2. 特定波长的选择:通过分析材料的色散曲线,我们可以选择合适的波长来研究材料。
例如,对于某些材料,特定波长的光会被材料吸收,因此选择其他波长进行观察可以避免吸收干扰,得到更准确的结果。
3. 光学器件设计:色散曲线对于光学器件的设计非常关键,特别是在光纤通信领域。
通过选择适当的材料和波长,可以优化光学器件的性能和效率。
三、如何选择波长进行研究在材料研究过程中,选择合适的波长进行研究是非常重要的,下面给出一些选择波长的准则:1. 避免吸收峰和散射:当研究材料吸收性质时,需要避开材料吸收峰的波长进行实验,以免吸收干扰研究结果。
同时,如果材料对特定波长的光有强烈的散射现象,也应选择其他波长。
2. 最大灵敏度波长:材料在某些波长下可能具有最大的灵敏度。
在研究材料光学特性时,选择具有最大灵敏度的波长可以获得更准确的测量结果。
3. 窗口波长:对于某些材料,只有在特定的波长范围内才能观察到其光学特性。
《光纤通信》大作业阶跃光纤模式色散曲线计算光纤材料色散计算光纤光栅特性分析指导老师:专业:姓名:学号:一、阶跃光纤模式色散曲线计算1.原理分析模式色散是指多模式传输时同一波长分量的各种传导模式的相位常数不同,群速度不同,引起到达终端的脉冲展宽的现象。
对光纤中光的传播理论的研究,可以有多种方法,比如射线法,标量近似分析法等,但为了更广泛地描述光纤波导中光的传播,更详细地研究光纤的传输特性,就必须运用波动光学理论对光纤进行分析。
要对光在光纤中的传播特性有详细的理解,必须依靠麦克斯韦方程,结合问题中的边界条件,求解电磁矢量场.求解的方法一般是:1、先求出亥姆霍兹方程组以及电磁场纵向分量Ez 和Hz 的具体形式。
2、2、把Ez 和Hz 有具体形式代入麦克斯韦方程以求取其他电磁场横向分量θE 、Er 、θH 、Hr 。
3、3、利用界面上电磁场θE 和θH 切向连续条件,求取模式本征方程。
对于时谐场光波,在均匀、无源介质中,同样满足矢量的亥姆霍兹方程(式1-1,1-2)022=+∇E k E (1-1)022=+∇H k H (1-2)对于在圆柱形光纤中传播的电磁波.电场和磁场具有如下形式的函数关系(式1-3,1-4):)(),(),(t z j e r E y x E ωβθ-= (1-3))(),(),(t z j e r H y x H ωβθ-=(1-4)代入,得到亥姆霍兹方程(式1-5,1-6)。
02202=+∇z z E n k E (1-5)02202=+∇z z H n k H (1-6) 经过推导,可以得到关于r 的贝塞尔方程或修正的贝塞尔方程(式1-7)。
(1-7) 最后可解得电场和磁场的纵向分量Ez 和Hz 。
⎪⎪⎩⎪⎪⎨⎧>≤=);()()();()()(a r e r a W K W K A a r e r a U J U J A E im m m im m m z θθ0)(])[()()(2222120222=--+∂∂+∂∂r R m r n k r r R r r r R r β光纤中传播模式及传输特性都是由它自身的本征方程确定的。
色散曲线简介色散曲线是描述光在不同波长下折射率变化的曲线。
在光学领域中,光的折射是由于光通过了不同介质引起的,而不同波长的光在介质中的传播速度以及折射程度也会有所不同,这就形成了色散现象。
色散曲线可以用来分析不同波长下光的折射情况,对于光学设计和实验研究有着重要的意义。
色散的定义色散是光在折射过程中,由于介质折射率对光波长的依赖性而产生的现象。
当入射的光波呈现出不同波长的成分时,不同波长的光在介质中的折射情况不同,导致出射光的波长分离,进而产生折射角的变化。
形成色散曲线的原因色散曲线的形成是由于光在介质中传播速度与波长相关的性质。
由于折射率是光在介质中传播速度的倒数,所以不同波长的光在介质中的折射率也会不同。
光的速度是光在真空中的速度除以介质的折射率。
而根据光的频率与波长的关系,我们知道光波长越短,频率越高。
所以,在光通过介质时,波长较短的光速度会比波长较长的光速度更快,而波长较短的光折射率会比波长较长的光折射率更大,因此由此产生了色散现象。
色散曲线的分类色散曲线根据折射率与波长的关系可以分为以下几种类型:正常色散正常色散是指随着波长减小,折射率也随之减小的情况。
在正常色散情况下,折射角随着入射光波长的减小而变小,即波长越短,折射角越小。
负色散负色散是指随着波长减小,折射率也随之增加的情况。
在负色散情况下,折射角随着入射光波长的减小而增加,即波长越短,折射角越大。
零色散零色散是指在特定的波长下,折射率不随波长而变化。
在零色散情况下,折射角与入射光波长无关。
色散曲线的应用色散曲线的研究对光学设计和实验研究有着重要的意义。
色散的存在和性质决定了许多光学器件的功能和性能。
棱镜棱镜是一种常用的光学器件,它能将不同波长的光分离出来,实现光的分光。
根据色散曲线的性质,波长越短的光在棱镜中的折射角会更大,从而使得不同波长的光发生分离。
光纤光纤是一种能够将光信号进行传输的光学器件。
由于不同波长的光在光纤中的传播速度不同,所以光在光纤中的传播速度也会发生变化,这就导致了信号的色散现象。
第三章 晶格振动与晶体的热学性质1.什么是简谐近似?解:当原子在平衡位置附近作微小振动时,原子间的相互作用可以视为与位移成正比的虎克力,由此得出原子在其平衡位置附近做简谐振动。
这个近似即称为简谐近似。
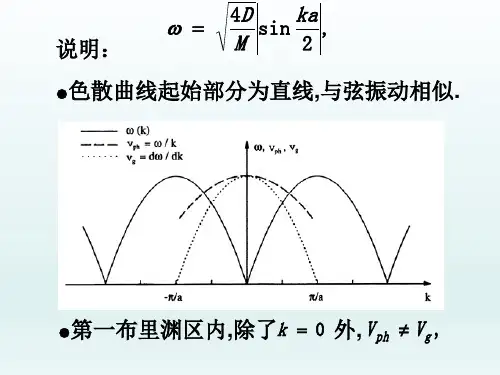
2.试定性给出一维单原子链中振动格波的相速度和群速度对波矢的关系曲线,并简要说明其意义。
解:由一维单原子链的色散关系2sin2qamβω= ,可求得一维单原子链中振动格波的相速度为22sinqa qamaqv p βω== (1)2c os qam a dq d v g βω==。
由(1)式及结合上图3.1中可以看出,由于原子的不连续性,相速度不再是常数。
但当0→q 时,mav p β=为一常数。
这是因为当波长很长时,一个波长范围含有若干个原子,相邻原子的位相差很小,原子的不连续效应很小,格波接近与连续媒质中的弹性波。
由(2)式及结合上图3.1中可以看出,格波的群速度也不等于相速度。
但当0→q ,mav v p g β==,体现出弹性波的特征,当q 处于第一布区边界上,即aq π=时,0=g v ,而mav p βπ2=,这表明波矢位于第一布里渊区边界上的格波不能在晶体中传播,实际上它是一种驻波。
3.周期性边界条件的物理含义是什么?引入这个条件后导致什么结果?如果晶体是无限大,q 的取值将会怎样?解:由于实际晶体的大小总是有限的,总存在边界,而显然边界上原子所处的环境与体内原子的不同,从而造成边界处原子的振动状态应该和内部原子有所差别。
考虑到边界对内部原子振动状态的影响,波恩和卡门引入了周期性边界条件。
其具体含义是设想在一长为Na 的有限晶体边界之外,仍然有无穷多个相同的晶体,并且各块晶体内相对应的原子的运动情况一样,即第j 个原子和第j tN +个原子的运动情况一样,其中t =1,2,3…。
引入这个条件后,导致描写晶格振动状态的波矢q 只能取一些分立的不同值。
如果晶体是无限大,波矢q 的取值将趋于连续。
PWSCF计算晶体的声子色散曲线和态密度(2007-02-21 22:43)标签:pwscf分类:PWSCFpwscf是采用线性响应的方法来进行晶格动力学性质的计算。
在计算晶体的声子色散和态密度时的步骤:i)用pw.x 进行自洽计算; ii)用ph.x对小的q点网格进行计算,得到这些q点的动力学矩阵元;iii)用q2r.x计算出实空间中的力常数矩阵; iv)用matdyn.x计算声子色散曲线;v)用matdyn.x计算声子态密度。
下面以Sc为例子并针对pwscf的最新版本3.2.1来说明(早期版本在计算声子色散曲线较麻烦,因为它不能自动处理q点网格,然后对每个q点一次性计算,而是需要手动产生这些点,一个个计算)。
1) 用pw.x进行电子密度的自洽计算&controltitle='Sc, hexagonal cell'calculation = 'scf'restart_mode='from_scratch',prefix='sc',pseudo_dir = './',outdir='./tmp'tprnfor=.true./&systemibrav=4,celldm(1)=6.05606,celldm(3)=1.71298,nat=2,ntyp=1, nbnd= 30,ecutwfc=30.0,occupations ='smearing', degauss =0.01smearing ='mp'/&electronsdiagonalization='cg'diago_cg_maxiter= 60mixing_mode = 'plain'mixing_beta = 0.5conv_thr = 1.0d-6/ATOMIC_SPECIESSc 44.955910 Sc.pw91-nsp-van.UPFATOMIC_POSITIONS (crystal)Sc 0.3333333333333286 0.6666666666666714 0.2500000000000000Sc 0.6666666666666714 0.3333333333333286 0.7500000000000000K_POINTS (automatic)8 8 6 0 0 0注意Sc是金属,在此例子中,我们选用MP方法来确定电子的占有数(见occupations ='smearing', smearing='mp'),这里未经测试而选用了展宽系数为0.01 Ry (见degauss=0.01)。