利用包含随机波动的时变参数模型预测通货膨胀
- 格式:pdf
- 大小:348.07 KB
- 文档页数:4
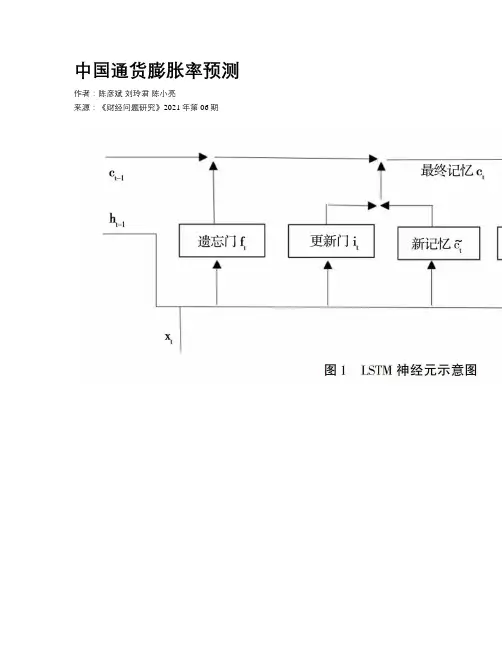
中国通货膨胀率预测作者:陈彦斌刘玲君陈小亮来源:《财经问题研究》2021年第06期摘要:前瞻性預测通货膨胀率有助于央行等政府部门更好地使用货币政策稳定物价,以防范通货膨胀对于市场主体尤其是中低收入群体的冲击,有助于金融机构和投资者更好地进行投资决策,因而具有重要意义。
已有文献主要使用AR和VAR等线性模型对通货膨胀率进行预测,对于变量间非线性关系以及历史数据信息的挖掘相对欠缺,因而已有文献的预测策略及其准确性有待改进。
LSTM模型能够充分挖掘变量之间的非线性关系并且处理复杂的长期时序动态信息,从而弥补已有研究的不足。
为此,本文使用LSTM模型对中国通货膨胀率进行预测,考虑到新常态以来中国的CPI和PPI走势多次背离,只使用CPI很难对一般物价水平进行全面把握,因此,本文使用LSTM模型对CPI和PPI两个指标进行了预测分析。
研究结果表明,LSTM模型在预测中国通货膨胀率时表现出了较好的性能,且其预测效果明显优于BVAR 模型。
有鉴于此,本文建议将LSTM模型更广泛地用于通货膨胀率预测领域。
除了CPI和PPI,未来还应该更加关注对核心CPI指标的预测,从而为货币政策的制度提供更有价值的决策参考。
关键词:通货膨胀率;CPI;PPI;LSTM模型;BVAR模型中图分类号:F037.2 文献标识码:A文章编号:1000-176X(2021)06-0018-12一、引言通货膨胀率(下文简称“通胀率”)是监测宏观经济运行的重要指标之一,对通胀率进行前瞻性预测具有重要意义。
其一,货币政策的重要目标之一是稳定物价,但货币政策在调控物价过程中存在一定的时滞,因而央行需要较为精确的通货膨胀(下文简称“通胀”)预测作为前提,才能更好地使用货币政策稳定物价水平。
其二,通胀率不仅会影响投资者在投资周期方面的决策,且会影响到投资者在投资产品方面的决策,因而对于金融机构和投资者而言,预测通胀率具有重要的指导意义。
其三,家庭财产差距较大和结构性通胀频发等问题的存在,使通胀对中低收入群体的危害较大,从而进一步凸显了预测通胀率的必要性和重要性。

时间序列计量经济学模型概述时间序列计量经济学模型是在经济学研究中广泛使用的一种方法,用于分析经济变量随时间的变化。
该模型基于时间序列数据,即经济变量在一段时间内的观测值。
时间序列计量经济学模型的核心是建立经济变量之间的关系,以解释和预测经济现象的变化。
其中最常用的模型是自回归移动平均模型(ARMA)、自回归条件异方差模型(ARCH)和季节性时间序列模型。
自回归移动平均模型(ARMA)是一个包含自回归项和移动平均项的线性模型。
该模型以过去的观测值和随机项为输入,预测当前观测值。
ARMA模型基于假设,即经济变量的行为受到历史观测值的影响。
自回归条件异方差模型(ARCH)是一种考虑了随时间变化方差的模型。
该模型通过引入一个条件异方差项,模拟经济变量中的波动性。
ARCH模型的应用范围广泛,特别是在金融市场波动性分析中。
季节性时间序列模型用于分析具有明显季节性特征的经济变量,如销售额、就业人数等。
这些模型通常基于季节、趋势和随机成分的组合,以预测未来观测值。
在建立时间序列计量经济学模型时,常常需要进行模型识别、参数估计和模型诊断等步骤。
识别模型的目标是确定适当的模型结构,参数估计则是利用历史数据估计模型的参数值。
模型诊断用于检验模型的拟合程度和误差分布是否符合模型假设。
时间序列计量经济学模型在经济研究中有广泛的应用,例如预测未来经济指标、分析经济周期和波动性、评估政策效果等。
它提供了一种量化的方法,使经济学家可以更好地理解和解释经济变量的演变。
时间序列计量经济学模型是经济学研究中一种重要的统计工具,广泛应用于宏观经济、金融市场和企业经营等领域。
它可以帮助我们理解和解释经济变量随时间的变化规律,进行预测和政策分析。
本文将进一步探讨时间序列计量经济学模型的相关概念和应用。
在构建时间序列计量经济学模型之前,首先需要了解时间序列数据的特点。
时间序列数据是按照时间顺序排列的一系列观测值,通常具有趋势性、季节性、周期性和随机性等特征。

金融市场的计量经济学金融市场是一个充满变动和不确定性的领域,深受经济学家、学者和决策者的关注。
计量经济学作为一种强大的工具和方法,被广泛应用于金融市场的分析和预测。
本文将探讨金融市场的计量经济学应用,并介绍其在金融领域的重要性。
一、引言计量经济学是应用数学和统计学原理,分析经济数据、理解经济现象和预测经济变量的一门学科。
在金融市场中,计量经济学的应用可以帮助我们深入了解市场的运作机制、预测市场走势,以及评估金融政策的效果。
二、金融市场的计量经济学模型1. 资本资产定价模型(Capital Asset Pricing Model,CAPM)CAPM是计量经济学中广泛使用的一种模型,用于计算资产的预期回报。
通过考虑资产的系统风险和市场风险溢价,CAPM模型可以估算投资组合的预期回报率,并为投资者提供了理论依据。
2. 随机波动模型(Stochastic Volatility Model)金融市场的波动性是一个重要的问题,随机波动模型提供了一种描述金融市场波动性的方法。
该模型允许波动性在不同的时间段和市场状态下变化,从而更真实地反映市场的风险。
3. 共整合模型(Cointegration Model)共整合模型是计量经济学中用于分析时间序列数据的一种方法。
在金融市场中,共整合模型可以用来研究两个或多个金融变量之间的长期关系,揭示它们之间的均衡关系。
三、计量经济学在金融市场的应用1. 金融市场预测计量经济学提供了大量的工具和方法,可以用于金融市场的预测和分析。
通过对历史数据的回归分析和时间序列模型的应用,可以帮助我们预测金融市场的走势和变动。
2. 金融政策评估计量经济学在金融政策评估中发挥着重要作用。
通过建立经济模型和计量模型,可以评估不同政策对金融市场和经济增长的影响,并提供政策制定者参考。
3. 风险管理金融市场的风险管理是一个复杂而关键的问题。
计量经济学提供了一些方法,如价值-at-风险(Value-at-Risk)模型和条件异方差(Conditional Heteroskedasticity)模型,可以帮助金融机构评估和管理风险。

二、我国通货膨胀率模拟及预测实证分析(一)理论模型本文考虑封闭经济模型,模型包括三个模块:总供给(AS)曲线、总需求(AD)曲线以及通货膨胀预期形成机制。
AS曲线形式如下:。
其中,yt表示产出偏离其长期趋势的部分,或者称之为产出缺口,πt为实际通货膨胀率,π*t 为预期通货膨胀率,εt为供给冲击。
AD曲线的形式如下:。
其中,mt表示实际货币供给偏离其长期趋势的偏离值,ξt 为需求冲击。
通货膨胀预期π*t影响总需求的渠道是通过影响实际利率,进而影响到投资量。
根据理论模型,通货膨胀的结构式如下:(1)图12007-2010年我国CPI和PPI走势图(1)式表明,当期通货膨胀率主要受以下因素的影响:产出缺口的前期值(反应了滞后效应)、当期实际货币余额缺口以及通货膨胀率的前期值。
ηt表示一系列供给冲击和需求冲击的组合。
(二)线性模型的估计结果所有数据来自中经网统计数据库,为了扩大样本量,收集季度频率的数据,数据样本为1992年第一季度(1992Q1)至2010年第一季度(2010Q1)。
所有数据都经过X12季节调整,以剔除季节因素的影响。
产出缺口和实际货币余额缺口的计算则采用了HP滤波方法。
为更好地评价两种建模方法的结果,将样本分为两个区间,1992Q1-2008Q4的数据样本用于估计参数,2009Q1-2010Q1的数据样本用于事后预测。
为避免出现伪回归问题,对所有变量进行单位根检验,ADF检验结果表明,所有变量均为平稳序列,可以直接回归。
经过经济意义和统计显著性的考虑,得到线性模型的最佳估计结果如下:(2)t=(2.47)(2.61)(2.45)(20.91)(-5.34)其中,R2=0.97,括号中的数值为各估计参数的t统计量,所有系数在5%的显著性水平下均通过检验,拉格朗日乘子(LM)检验和Breusch-Pagan-Godfrey检验都表明,模型不存在序列相关和异方差问题。
为了更好地与神经网络模型进行比较,计算线性模型均方误差(MSE),MSE=1.5964。

我国经济增长和通货膨胀的关联性分析内容摘要:随着改革开放的深入进行,我国经济获得了惊人的发展,取得了令世人瞩目的成绩。
但是,在高速经济增长的同时也出现了严重的通货膨胀,那么,通货膨胀与经济增长的关系是怎样的?本文以我国1978-2012年的经济数据为依据,结合相关宏观经济理论,借助计量分析的方法建立了一个非线性三次回归模型,对我国的经济增长和通货膨胀之间的关系进行了研究。
最终,说明在我国历年的发展过程中,经济增长与通货膨胀之间存在较显著的相关性,并据此提出一些较为可行的建议或方法。
关键词:经济增长通货膨胀相关性计量经济分析前言在宏观经济理论中,宏观经济政策主要目标有充分就业,物价稳定和经济持续均衡的增长。
物价稳定是指价格总水平的稳定,一般用价格指数来衡量。
物价稳定成为宏观经济政策的目标,是由于通货膨胀对经济有不良影响,它会使货币贬值,价格信号失真,造成国民经济的非正常发展。
而经济增长目标是指在一个特定时期内经济社会所生产的产量和收入的持续增长,通常用一定时期内实际国内生产总值年均增长率来衡量。
一国理想的经济状态是在经济增长的同时保持较低的通货膨胀率,但是,经济持续增长与通货膨胀两者之间的关系是宏观经济学中的悖论,即宏观理论中也认为物价稳定和经济增长这两个目标在短期内同时实现是有矛盾的。
在探讨通货膨胀成因时,往往认为经济增长是以总需求扩张为前提的,总需求的扩张会引起总体物价水平的上涨,进而引起通货膨胀,即所谓需求拉动的通货膨胀。
由此可见,经济增长目标和物价稳定目标往往是冲突的,经济增长在某种意义上可以看作是通货膨胀的原因之一。
近年来,美国经济增长速度一旦达到或超过一定水平(如2.5%),政府就提高利率,这主要就是出于对经济过热而引起通货膨胀的担心。
这种反应其实隐含着经济增长是导致通货膨胀的原因的观念。
然而,西方经济学也承认,经济增长并非一定会伴随着通货膨胀。
通货膨胀的原因除了总需求的拉动,也可以由成本推动等因素所引起。


萨缪尔森《宏观经济学》(第19版)第16章 通货膨胀复习笔记跨考网独家整理最全经济学考研真题,经济学考研课后习题解析资料库,您可以在这里查阅历年经济学考研真题,经济学考研课后习题,经济学考研参考书等内容,更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验,从前辈中获得的经验对初学者来说是宝贵的财富,这或许能帮你少走弯路,躲开一些陷阱。
以下内容为跨考网独家整理,如您还需更多考研资料,可选择经济学一对一在线咨询进行咨询。
一、通货膨胀的定义及影响1.通货膨胀的定义通货膨胀意味着一般价格水平的上涨。
通货膨胀的严重程度可以用通货膨胀率来衡量。
人们一般采用价格指数来计算通货膨胀率,常用价格指数有:消费价格指数和GDP 紧缩指数。
通货膨胀率即价格水平变动的百分比,用公式可以表示为:()()()1=100%1t t t t --⨯-年的价格水平年的价格水平通货膨胀年年的价格水平2.通货膨胀的类型(1)按照严重程度不同,通货膨胀可以分为三类:低通货膨胀、急剧通货膨胀和恶性的通货膨胀。
①低通货膨胀是指年通货膨胀率为一位数的通货膨胀。
其特点是价格上涨缓慢且可以预测,人们对货币比较信任,愿意签订以货币形式表示的长期合同。
②急剧通货膨胀是指总价格水平以每年20%、100%,甚至200%的二位数或三位数的速率上涨时的通货膨胀。
这种急剧的通货膨胀局面一旦形成并稳固下来,便会产生严重的经济扭曲。
其特点为:一般地说,大多数经济合同都会实行指数化;货币贬值非常迅速,人们仅在手中保留最低限度的货币以应付日常交易所需;金融市场逐渐消亡,资本逃向国外;人们囤积商品,购置房产,而且绝对不会按照很低的名义利率出借货币。
③恶性通货膨胀是指各种价格以每年百分之一百万,甚至百分之万亿的惊人速率持续上涨的通货膨胀。
(2)按是否可预期,通货膨胀又可以分为两类:可预期的通货膨胀和不可预期的通货膨胀。
①可预期的通货膨胀是指通货膨胀过程被经济主体预期到了,以及由于这种预期而采取各种补偿性行动引发的物价上升运动。

第35 卷第4 期Vol.35 No.42020 年4 月Apr. ,2020统计与信息论坛Statistics & Information Forum文新雷1,赵春艳1,张跃胜2(1.西安交通大学经济与金融学院,陕西西安710061#.天津城建大学经济与管理学院,天津300384)【统计理论与方法】中国通货膨胀波动的测算——基于TVP-AR-SV 模型摘要:准确测度通胀波动规律是研究通货膨胀及货币政策的重要基础。
为克服现有随机波动(SV )模型 隐含假设中存在的天然缺陷,平衡模型估计的准确性与操作的简便性,通过对比SV 、UCSV 、ARSV 、TVP-AR-SV 四种主要模型,认为其中时变系数自回归随机波动(TVP-ARSV )模型最适用于中国通胀波动的测度。
对中国的季度通胀数据建立该模型,利用马尔科夫链蒙特卡洛模拟(MCMC )方法对模型参数进行贝叶 斯估计,得到通胀的波动序列,同时对通货膨胀进行预测,并与其他形式的SV 模型的估计结果进行对比。
结 果表明,TVP-ARSV 模型估计的随机波动能够全面地解释中国通胀率的整体波动规律,参数估计精度及模型对未来通胀的预测能力均优于其他备选模型。
关键词:通货膨胀波动;TVP-ARSV 模型;马尔科夫链蒙特卡洛方法中图分类号:F222文献标志码:A 文章编号:1007-3116(2020)04-0023-11一、引言近年来,中国经济发展开始从速度向质量进行转变,党的十九大及中央经济工作会议均强调经济工作要坚持稳中求进的总基调,以适应经济发展新常态。
而稳定的物价水平是保障经济平稳健康发展的重要前提。
通货膨胀历来是货币政策制定者关注的一个 重要指标,是调控物价的重要依据。
但是通货膨胀中的波动部分往往是一种噪声,会干扰主要的信号。
如 果货币政策对这些干扰信号做出反应,不仅无法实现 其调控效果, 反而会影响经济平稳运行)为能够提前 规避掉干扰因素,并准确地针对通胀中的主要信号来 进行调控,需要准确测度出通货膨胀的波动,将其从通胀中分离出来。


时变参数向量自回归模型1. 引言时变参数向量自回归模型(Time-Varying Parameter Vector Autoregressive Model,TVAR)是一种用于分析时间序列数据的经济计量模型。
它可以捕捉到时间序列数据中的动态性和非线性关系,因此在经济学、金融学等领域被广泛应用。
本文将介绍时变参数向量自回归模型的基本原理、建模方法以及应用案例,帮助读者全面了解该模型。
2. 基本原理2.1 自回归模型自回归模型(Vector Autoregressive Model,VAR)是一种多元时间序列分析方法。
它假设时间序列数据之间存在线性关系,并可以通过过去若干期的数据来预测未来的值。
VAR模型可以表示为:Y t=c+Φ1Y t−1+Φ2Y t−2+⋯+Φp Y t−p+εt其中,Y t是一个n维向量,表示第t期的观测值;c是一个常数向量;Φ1,Φ2,…,Φp是n×n的系数矩阵,表示自回归系数;εt是一个n维向量,表示误差项。
2.2 时变参数向量自回归模型时变参数向量自回归模型是在VAR模型的基础上引入了时变参数的扩展模型。
它认为自回归系数在时间上是可变的,可以通过某种方式来描述其动态性。
时变参数向量自回归模型可以表示为:Y t=c+Φ1(t)Y t−1+Φ2(t)Y t−2+⋯+Φp(t)Y t−p+εt其中,Φi(t)表示第i个滞后期的自回归系数在时间t上的取值。
3. 建模方法3.1 参数估计对于时变参数向量自回归模型,参数估计是一个关键步骤。
常用的方法有贝叶斯方法、频域方法和局部似然方法等。
贝叶斯方法通过引入先验分布来估计参数,可以获得参数的后验分布。
频域方法利用频域上的特征来估计参数,可以捕捉到数据的周期性。
局部似然方法则在每个时间点上估计参数,可以灵活地适应时变性。
3.2 模型选择在建立时变参数向量自回归模型时,需要选择合适的滞后阶数和模型形式。
滞后阶数决定了过去多少期的数据被考虑进模型中,一般通过信息准则(如AIC、BIC等)来选择最优阶数。
计量经济模型与经济预测引言计量经济学是应用数学和统计学原理来分析经济理论和实证的分支学科。
它通过建立经济模型,使用统计方法对模型进行实证分析,并用模型进行经济预测。
本文将介绍计量经济模型的基本概念及其在经济预测中的应用。
计量经济模型的基本概念计量经济模型是描述经济变量之间关系的数学模型。
它通常基于经济理论假设和观察到的经济数据,用数学形式来表示经济变量之间的关系。
计量经济模型有多种形式,常见的包括线性回归模型、时间序列模型和面板数据模型等。
线性回归模型是最常用的计量经济模型之一。
它假设经济变量之间存在线性关系,通过最小化观测数据与模型预测值之间的差距来估计模型参数。
线性回归模型可以用以下数学形式表示:Y = β0 + β1X1 + β2X2 + ... + βnXn + ε其中,Y表示被解释变量,X1、X2、…、Xn表示解释变量,β0、β1、β2、…、βn分别表示模型的截距和系数,ε表示随机干扰项。
时间序列模型是用于分析时间序列数据的计量经济模型。
它假设数据中存在随机变化和趋势性,并通过建立数学模型来描述时间序列数据之间的关系。
常见的时间序列模型包括ARMA模型、ARIMA模型和VAR模型等。
面板数据模型是用于分析面板数据(即同时包含多个个体和多个时间点的数据)的计量经济模型。
它可以用来分析个体之间的差异和时间变动对经济变量的影响。
面板数据模型的常见形式包括固定效应模型和随机效应模型等。
经济预测的方法经济预测是利用统计方法和计量经济模型对未来经济变量进行预测的过程。
经济预测可以根据数据的特点分为宏观经济预测和行业经济预测。
常用的经济预测方法包括时间序列分析、结构方程模型和机器学习等。
时间序列分析是一种用于预测具有时间依赖性的经济变量的方法。
它基于时间序列模型,通过分析过去的时间序列数据,利用模型对未来的趋势和周期性变化进行预测。
时间序列分析常用的方法包括移动平均法、指数平滑法和ARIMA模型等。
金融市场中价格波动的预测模型研究金融市场中价格的波动性一直以来都是投资者关注的重点之一。
对价格波动进行准确预测可以为投资者提供决策依据,帮助其优化投资组合,最大化投资回报。
因此,研究金融市场中价格波动的预测模型具有重要的理论和实际意义。
价格波动性是指价格在一定时间内的变动幅度。
金融市场中的价格波动受到众多因素的影响,包括经济基本面、政治事件、市场情绪和技术指标等。
传统的时间序列分析模型如ARIMA、GARCH等,以及机器学习和人工智能模型如支持向量机(SVM)、随机森林(Random Forest)等,都被广泛应用于金融市场价格波动的预测研究中。
首先,ARIMA模型是一种常用的时间序列分析模型,它可以预测未来一段时间内的价格波动情况。
ARIMA模型结合了自回归(AR)和滑动平均(MA)的特点,适用于价格波动性具有一定规律性的情况。
该模型首先对数据进行平稳性检验,再利用自相关函数(ACF)和偏自相关函数(PACF)确定ARIMA模型的阶数。
最后,利用参数估计和模型诊断方法得到最终的预测结果。
其次,GARCH模型是一种用于金融时间序列预测的非线性模型,其基本思想是在ARIMA模型的基础上引入条件异方差,以更准确地捕捉价格波动的特征。
GARCH模型通过研究价格波动的历史数据,估计条件异方差的参数,并利用这些参数进行未来价格波动性的预测。
常见的GARCH模型包括常规GARCH、EGARCH、TGARCH等。
研究表明,GARCH模型相较于传统的时间序列分析模型,能够更好地解释金融市场中价格波动的非线性特征。
此外,机器学习和人工智能模型在金融市场价格波动预测中也发挥着重要作用。
支持向量机(SVM)是一种基于统计学习理论的非线性分类方法。
SVM模型通过构建具有较高鲁棒性的决策边界,对价格波动进行分类预测。
随机森林(Random Forest)是另一种常用的机器学习模型,其通过采用多个决策树的集成学习方法,提高了预测的准确性。
计量经济学4种常用模型计量经济学是经济学的一个重要分支,主要研究经济现象的数量关系及其解释。
在计量经济学中,常用的模型有四种,分别是线性回归模型、时间序列模型、面板数据模型和离散选择模型。
下面将对这四种模型进行详细介绍。
第一种模型是线性回归模型,也是计量经济学中最常用的模型之一。
线性回归模型是通过建立自变量与因变量之间的线性关系来解释经济现象的模型。
在线性回归模型中,自变量通常包括经济学理论认为与因变量相关的变量,通过最小二乘法估计模型参数,得到经济现象的解释。
线性回归模型的优点是简单易懂,计算方便,但其前提是自变量与因变量之间存在线性关系。
第二种模型是时间序列模型,它主要用于分析时间序列数据的模型。
时间序列模型假设经济现象的变化是随时间演变的,通过分析时间序列的趋势、周期性和随机性,可以对经济现象进行预测和解释。
时间序列模型的常用方法包括自回归移动平均模型(ARMA)、自回归条件异方差模型(ARCH)等。
时间序列模型的优点是能够捕捉到时间的动态变化,但其局限性是对数据的要求较高,需要足够的时间序列观测样本。
第三种模型是面板数据模型,也称为横截面时间序列数据模型。
面板数据模型是将横截面数据和时间序列数据结合起来进行分析的模型。
面板数据模型可以同时考虑个体间的差异和时间的变化,因此能够更全面地解释经济现象。
面板数据模型的常用方法包括固定效应模型、随机效应模型等。
面板数据模型的优点是能够控制个体间的异质性,但其需要对个体间的相关性进行假设。
第四种模型是离散选择模型,它主要用于分析离散选择行为的模型。
离散选择模型假设个体在面临多种选择时,会根据一定的规则进行选择,通过建立选择概率与个体特征之间的关系,可以预测和解释个体的选择行为。
离散选择模型的常用方法包括二项Logit模型、多项Logit模型等。
离散选择模型的优点是能够分析个体的选择行为,但其局限性是对选择行为的假设较强。
综上所述,计量经济学中常用的模型有线性回归模型、时间序列模型、面板数据模型和离散选择模型。
基于结构式VAR模型的我国核心通货膨胀的估计一、核心通货膨胀的概念及意义核心通货膨胀是指在通货膨胀中排除食品和能源价格因素后的通货膨胀水平。
食品和能源价格通常具有较高的波动性,而且受季节、自然灾害等因素影响较大,排除这两个特殊领域价格变动,更有利于得到通货膨胀的基本趋势。
核心通货膨胀具有更好的预测能力,对货币政策制定和经济稳定具有更强的参考价值。
二、结构式VAR模型的基本原理结构式VAR模型是以多元时间序列数据为基础,采用向量的形式来表示多个变量之间的关系,通过向量自回归方程描述变量之间的动态调整关系。
具体而言,VAR模型可以用如下形式表示:\[ Y_t = A_1Y_{t-1} + A_2Y_{t-2} + \cdots + A_pY_{t-p} + u_t \]\( Y_t \)为 \( n \times 1 \) 的向量,表示 \( n \) 个变量在时间 \( t \) 的取值;\( A_i \) 为 \( n \times n \) 的矩阵,表示 \( i \) 期滞后的自回归系数;\( p \) 为滞后阶数;\( u_t \) 为 \( n \times 1 \) 的向量,表示影响变量的扰动项。
在结构VAR模型中,通过设立外生变量的约束,可以得到变量之间的因果关系,从而揭示不同变量之间的联动关系。
通过对模型的参数估计,可以得到变量之间的短期和长期关系,为宏观经济分析提供了一种有效的工具。
三、我国核心通货膨胀的估计我们确定了一个包括核心通货膨胀率、物价指数、货币供应量、利率和产出等变量的结构VAR模型。
考虑到核心通货膨胀率的表达,我们可以设定该变量为一种完全内生变量。
然后,我们通过收集相关的历史数据,利用最小二乘估计法对VAR模型的参数进行估计。
在进行参数估计时,我们需要考虑到变量之间的内生性和外生性关系,以及滞后阶数的选择等问题。
在估计模型参数后,我们通过实证分析得到了一些重要结论。
人民币汇率变动的价格传递效应——基于SV-TVP-FAVAR模型的实证分析刘金全;石睿柯;徐阳【摘要】本文基于一个带有随机波动率的时变参数因子扩张向量自回归模型(SV-TVP-FAVAR模型)实证考察了人民币汇率变动对我国进口价格、生产者价格以及消费者价格传递效应的时变特征.检验结果表明,人民币汇率变动对价格的传递过程在不同时点存在着明显差异,人民币汇率变动对进口价格、生产者价格以及消费者价格的传递不仅不完全,而且存在一定的时滞;自2005年7月汇率制度改革之后,人民币汇率变动对进口价格和消费者价格的传递作用显著增强,与此同时,人民币汇率对进口价格、生产者价格以及消费者价格的传递作用沿着商品价值链的方向呈依次递减趋势.%This paper examines the time-varying effects of RMB exchange rate pass-through based on a time-varying param-eters factor-augmented vector auto-regression with stochastic volatility model(SV-TVP-FAVAR model).The results show that there is a significant difference for exchange rate pass-through at different time points.The RMB exchange rate pass-through into prices is incomplete and has a certain time lag.Since the reform of the RMB exchange rate in July 2005, the RMB exchange rate pass-through into import prices and consumer prices has significantly enhanced.At the same time, the RMB exchange rate pass-through decreases along the commodity flow chain.【期刊名称】《工业技术经济》【年(卷),期】2018(037)005【总页数】9页(P63-71)【关键词】汇率传递;进口价格;国内价格;SV-TVP-FAVAR模型;时变特征;汇率市场化【作者】刘金全;石睿柯;徐阳【作者单位】吉林大学商学院,长春 130012;吉林大学数量经济研究中心,长春130012;纽约大学理工学院,NY 112014;吉林大学经济学院,长春 130012【正文语种】中文【中图分类】F832.6;F224引言汇率传递(Exchange Rate Pass-Through,简称ERPT)一直是各国政府和学者关注的热点问题,其研究的问题是当汇率发生一单位变化时,进口价格(或出口价格)以及国内整体价格(消费者价格或生产者价格)所受到的影响程度。
时间序列分析在经济预测中的应用在当今复杂多变的经济环境中,准确预测经济走势对于企业决策、政府规划以及个人投资都具有至关重要的意义。
时间序列分析作为一种强大的数据分析工具,在经济预测领域发挥着不可或缺的作用。
时间序列,简单来说,就是按照时间顺序排列的数据点序列。
这些数据点可以是股票价格、销售额、国内生产总值(GDP)等经济指标。
时间序列分析的核心目标是通过研究这些数据的历史模式和趋势,来预测未来的可能值。
时间序列分析之所以能够在经济预测中发挥作用,主要基于以下几个关键特点。
首先,它能够捕捉数据中的趋势性。
经济数据往往呈现出一定的长期趋势,例如经济的增长或衰退。
通过时间序列分析,可以识别并量化这种趋势,从而为预测未来的发展方向提供依据。
其次,它可以揭示周期性。
许多经济现象都具有周期性特征,如季节性波动或商业周期。
时间序列分析能够帮助我们发现这些周期规律,并据此对未来的周期阶段进行预估。
再者,它能够考虑到随机性因素。
经济活动受到众多不确定因素的影响,导致数据中存在随机波动。
时间序列模型可以对这种随机性进行建模和处理,从而提高预测的准确性。
在实际应用中,常用的时间序列分析方法包括移动平均法、指数平滑法和自回归移动平均(ARMA)模型等。
移动平均法是一种简单而直观的方法。
它通过计算一定时间段内数据的平均值来平滑数据,从而减少随机波动的影响。
例如,我们可以计算过去几个月的平均销售额来预测下一个月的销售额。
然而,移动平均法的缺点是它对历史数据的权重相同,可能无法充分反映近期数据的重要性。
指数平滑法则对移动平均法进行了改进。
它给予近期数据更高的权重,使得预测更能及时反映数据的最新变化。
这种方法在处理具有一定稳定性的数据时表现较好。
ARMA 模型则更加复杂和精确。
它将时间序列看作是过去值和随机误差项的线性组合。
通过对模型参数的估计,可以预测未来的值。
但ARMA 模型的应用需要一定的前提假设和数据特征满足,否则可能导致不准确的预测。
金融研究利用包含随机波动的时变参数模型预测通货膨胀!高 展(华东师范大学商学院,上海 200241)内容提要:本文在广义的菲利普斯曲线的理论框架下,应用灵活的包含随机波动的时变参数模型(TVP-SV)分析了中国的通货膨胀预测。
实证结果与传统的线性回归模型对比发现,TVP-S V模型能够更好地对数据进行拟合并显著的改善通货膨胀的预测精度。
关键词:通货膨胀;TV P-S V模型;菲利普斯曲线中图分类号: F822.5 文献标识码:A 文章编号:1003-4161(2010)01-0111-04一、引言准确的预测通货膨胀是宏观经济领域长期关注的重要问题,其对各种宏观经济决策的制定意义重大。
因此国内外的学者纷纷提出针对通货膨胀预测的各种方法。
在这些众多的方法中,绝大部分的理论框架都基于扩展的菲利普斯曲线。
比如A ng,Bekaert和W e i(2007),A t keson和O han i an(2001),G roen, Paap和R avazzo lo(2008),Stock和W atson(1999)以及Stock和W a tson(2008)。
尽管上述各文献的方法在细节上千差万别,但是他们设定的解释变量却均为通货膨胀率(或是通货膨胀率的变化)而解释变量为通货膨胀率的滞后值,失业率以及其他一些预测变量。
将通货膨胀率(与通货膨胀率的滞后值,失业率以及其他一些预测变量进行线性回归,利用回归的结果进行迭代运算就可以实现对通货膨胀的预测。
这是国内外学者所普遍采用的方法。
然而这种方法却有其内在的缺陷。
首先,预测变量的系数有可能是时变的。
实际上菲利普斯曲线的斜率随时间变化已得到了普遍的认同。
其次,在线性回归模型中随机扰动项的方差也有可能是时变的。
因此,为了弥补以上文献在研究方法上的缺陷,本文在国内首次利用一个包含随机波动的TVP(时变参数模型)模型来对其二者间的关系进行考察。
近年来,国际上在实证宏观领域许多考虑到参数时变特征的非线性模型已经被广为应用了。
比如,Bo iv i n和G iannoni(2006),Cog ley和Sargen t (2001),以及Lubik和Schorfhe i de,(2004)均应用了TV P(时变参数)模型来考察货币政策的传导机制。
S i m s和Zha(2006)则在实证中考虑了方差的时变特征,即使用随机波动模型来进行分析。
而P ri m iceri(2005)在其实证分析中不仅考虑了系数的时变性而且考虑了方差的波动,即利用包含随机波动的TV P模型进行分析。
本文所使用的包含随机波动的TV P模型具有高度的灵活性,它不仅能容纳传统的线性模型,而且能对变量之间的时变关系进行精确的刻画。
此外,由于考虑了随机波动因素,在模型中没有明确包含的其他变量的影响也可以通过随机波动参数的值而反映出来。
以下部分的结构安排如下:第二部分对本文所使用的模型进行了具体的描述;第三部介绍了所用数据并给出了实证结果进行说明;第四部分是结论。
二、实证模型及所用数据菲利普斯曲线是通货膨胀的主要预测模型。
菲利普斯曲线认为当期的通货膨胀率取决于失业率以及通货膨胀率和失业率的滞后值。
其他一些学者比如S tock和W atson(1999)将其他一些变量增加到菲利普斯曲线的解释变量中从而得到广义的菲利普斯曲线。
本文以广义的菲利普斯曲线为基础设定预测通货膨胀率的实证模型,其用公式表示如下:y t=C+ 1d GDP-1+ 2d M1-1+ 3y t-1+ t(1)此处的y t描述通货膨胀水平,我们可以将其定义为l n(P t/ P t-1),其中P t指的是价格指数。
dGPD-1表示GD P增值率的滞后值,d M1-1指M1增值率的滞后值,y e指预期的通货膨胀率。
在本文中我们用滞后一期的通货膨胀率代替预期的通货膨胀率,那么等式(1)则变为:y t=c+ 1dGDP-1+ 2d M1-1+ 3y t-1+ t(2)等式(2)描述了在获得了直到t-1期信息时,可以对第t期的通货膨胀水平进行预测。
本文所采用的TV P-S V模型考虑到通货膨胀率与预测变量间的关系可能是时变的以及扰动项方差的波动,由此可以得到, y t=Z t t+ t(3)t=t-1+!t(4)t=∀t e2(5)h t+1=h t+#t(6)式(3)中的Z t=[1,d GDP-1,d M1-1,y t-1]是由所有的预测变量所构成的1∀4的行向量(包括了截距项和通货膨胀率的滞后值)。
式(4)描述了回归系数t的演进机制,其中t=[C t, 1t, 2t, 3t]是4∀1的列向量,它描述了通货膨胀率与预测变量间的关系。
!t是一个随机扰动项,假设,!t#N(0,Q),Q是!t的方差。
式(5)中∀t服从N(0,1),h t实际上度量着 t的波动的大小。
式(6)描述了h t的演进机制,其中#t是随机扰动项,服从N(0,∃2)。
在本文中我们使用季度数据。
其中的价格指数我们采用CP I来度量。
此外根据中国数据的可获得性,所选样本数据的时间区间为从1992年第1季度到2009年第1季度。
数据来源于CCER宏观经济研究数据库。
三、TVP-SV模型的参数估计在本文使用的TV P-S V模型中共要估计,Q,h,∃24组参数。
我们利用M C M C方法分别对上述参数进行估计。
由于参数估计存在一定的难度,因此在以下做一简要的说明。
第一考虑Q和∃2的估计。
Q和∃2的估计思路是一样的,因此仅以Q的估计为例做出说明。
要估计Q就需要得到后验分布P(Q|data,,h∃2)。
实际上,P(Q|data,,h∃2)∃P(Q|)∃P(|Q)P(Q)(7)在这里我们假设P(Q-1)服从W分布。
由此可以得到P (Q-1|data,,h∃2)也是可以识别的W分布。
从该W分布中直接抽取Q-1的随机样本再求其倒数就可以得到Q的后验抽样。
第二考虑对的估计。
在其他参数取定的情况下,对的抽样并不是依赖条件后验分布P(|data,,h∃2)而实现的。
利用Durbi n and K oop m an(2002)的平滑仿真算法可以实现的估计。
第三考虑对h的估计。
具体的按以下的方法得到:首先对方程(4)两边平方并取对数可以得到:l n 2t=h t+ln∀2t。
然后,令u t=l n( 2t),%t=l n∀2t,那么可以得到u t=h t+%t,同时由于h t+1 =h t+%t,因此在其他参数值知道的条件下这是个标准的状态空间模型,同样可以根据D urb i n and K oop m an(2002)的平滑仿真算法来对h进行抽样估计。
在进行估计的时候唯一的困难在于%t =ln∀2t并不是服从正态分布的。
为解决这个问题,我们利用K i m,Shephard and Ch i b(1998)的混合抽样法将%t的密度函数可以由7种不同的正态分布的密度函数混合来近似替代,从而最终得到h的抽样值。
把上述各组参数估计的模块组合在一起从而形成M C M C循环,反复的进行参数抽样,从而最终得到各个参数的估计值。
四、实证结果在本部分中我们分别利用线性回归方法和本文的方法进行实证分析,然后进行比较就可发现本文所使用的方法的优越性。
首先利用线性回归模型得到的回归结论为y t=-0.002+0.013dGDP t-1+0.023d M t-1-0.555y t-1(-3.22) (4.99) (1.88) (-7.93)其中括号中的数字为t值。
由此回归结果我们可以得到预测出的通货膨胀率值。
我们将预测出的值与实际值在同一图中反映可以得到,其中的指的是实际值,而指的预测值。
图1 应用线性回归法得到的通货膨胀率的预测值与实际值其次,利用本文的方法进行运算得到各时变参数的值如下图所示。
图2 常数项的系数从图2可以发现应用本文的方法所得到的常数项的系数显然不是一个常数其随时间的变化呈现出明显的波动特征。
在本文的模型中,我们可以将常数项的系数理解为预期的趋势性的通货膨胀率。
在各个不同的时期,经济环境的差异显著,各经济主体在不同的环境下对通货膨胀预期改变显然更加的符合经济现实。
图3 dGDPt-1的系数从图3可以发现经济增长率的系数也表现出明显的时变特征。
这意味着在不同的时期,经济增长率对通货膨胀率的影响力度有着明显的差异。
从理论上看经济增长率与通货膨胀率的关系应该是正相关的。
经济增长值率越高,通货膨胀率也应该越大。
通过图3也可以发现在大部分时期,经济增长率的系数也是为正的。
然而经济增长率对通货膨胀的影响力度同样与经济环境有着密切的关系。
当实体经济处于萧条时期,整体经济的资源利用率不足存在比较大的负产出缺口的时候,即使经济增长率较快,对通货膨胀的影响依然不大。
然而当经济处于繁荣时期,整体经济的资源接近充分利用的状态时,即使经济增长率较低也会对通货膨胀形成较大的影响。
比如在第25个样本点即1997年的第4季度,该季度的经济增长率为0.2996,然而其对通货膨胀的影响力度仅为0.008。
这恰好是由于1997年发生了亚洲金融危机,我国的经济周期恰好处于萧条阶段。
整个社会的资源利用率有限,因此虽然在第4季度有着较高的经济增值率然而却对通货膨胀的影响力度甚微。
与之恰好相反的可以发现在第46个样本点即2004年第3季度,该季度的经济增值率仅为0.0841,然而其对通货膨胀的影响力度却达到了0.025。
这种结果的出现却是由于2004年我国正处于经济繁荣的周期。
在这种经济环境下,较小的经济增长率也对通货膨胀形成了较大的影响。
图4 d M 1t-1的系数从图4可以发现货币供给增长率的系数同样有着明显的时变特征。
这也意味着在不同的时期,货币供给增长率对通货膨胀率的影响力度差异显著。
通货膨胀从本质上看就是一种货币现象。
当过多的货币追逐过少的商品的时候,商品自然就会出现通货膨胀的现象。
因此,货币供给的增长速度对通货膨胀的影响显然是正的。
货币供给的增长率越高,通货膨胀率也会越高。
从图4也可以发现货币供给增长率的系数都是正的。
然而与经济增长率对通货膨胀的影响类似,货币供给增长率对通货膨胀的影响力度同样与经济周期高度相关。
其二者间内在的逻辑是完全一样的。
当实体经济处于萧条时期,整体经济的资源利用率不足存在比较大的负产出缺口的时候,即使货币供给增长率较快,对通货膨胀的影响依然不大。
然而当经济处于繁荣时期,整体经济的资源接近充分利用的状态时,即使货币供给增长率较低也会对通货膨胀形成较大的影响。
类似的,我们可以用同样的样本点来进行验证。
比如在第25个样本点即1997年的第4季度,该季度的货币供给增长率为0.08,然而其对通货膨胀的影响力度仅为0.016。
这也是由于1997年发生了亚洲金融危机,我国的经济周期恰好处于萧条阶段。