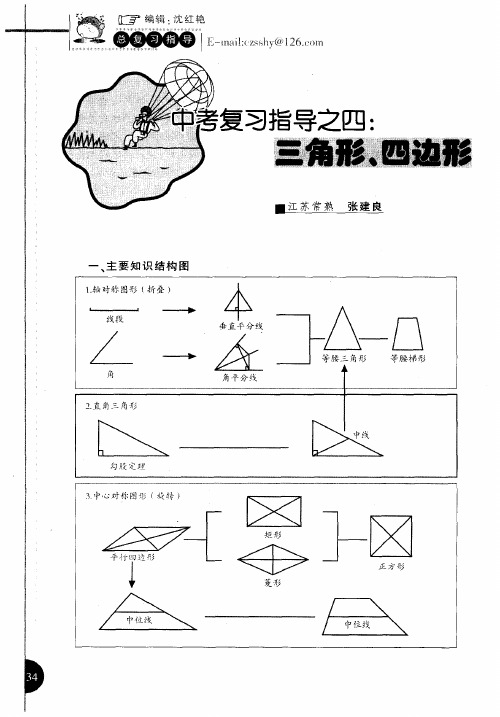
三角形和四边形中考复习

第二部分空间与图形第四章三角形与四边形第1讲线、角、相交线和平行线一级训练1．(2011年安徽芜湖)一个角的补角是36°35′，这个角是________．2．如图4－1－12，已知线段AB＝10 cm，AD＝2 cm，D为线段AC的中点，那么线段CB＝________cm.图4－1－123．(2012年湖南株洲)如图4－1－13，已知直线a∥b，直线c与a，b分别交于点A，B，且∠1＝120°，则∠2＝()图4－1－13A．60°B．120°C．30°D．150°4．(2011年四川南充)如图4－1－14，直线DE经过点A，DE∥BC，∠B＝60°，下列结论成立的是()图4－1－14A．∠C＝60°B．∠DAB＝60°C．∠EAC＝60°D．∠BAC＝60°5．下列命题中，正确的是()A．若a·b＞0，则a＞0，b＞0 B．若a·b＜0，则a＜0，b＜0C．若a·b＝0，则a＝0且b＝0 D．若a·b＝0，则a＝0或b＝06．(2012年湖北孝感)已知∠α是锐角，∠α与∠β互补，∠α与∠r互余，则∠β－∠r的值等于()A．45°B．60°C．90°D．180°7．(2011年浙江丽水)如图4－1－15，有一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1＝20°，那么∠2的度数是()A．30°B．25°C．20°D．15°图4－1－158．如图4－1－16，下列条件中，不能判断l1∥l2的是()图4－1－16A．∠1＝∠3 B．∠2＝∠3 C．∠4＝∠5 D．∠2＋∠4＝180°9．(2011年湖北孝感)如图4－1－17，直线AB，CD相交于点O，OT⊥AB于点O，CE∥AB交CD于点C.若∠ECO＝30°，则∠DOT＝()图4－1－17A．30°B．45° C. 60° D. 120°10．(2012年湖南怀化)如图4－1－18，已知AB∥CD，AE平分∠CAB，且交CD于点D，若∠C＝110°，则∠EAB＝()A．30°B．35°C．40°D．45°图4－1－1811．下列四个生活、生产现象：①用两个钉子就可以把木条固定在墙上；②植树时，只要定出两棵树的位置，就能确定同一行所在的直线；③从A地到B地架设电线，总是尽可能沿着线段AB架设；④把弯曲的公路变直，就能缩短路程．其中可用公理“两点之间，线段最短”来解决的现象有()A．①②B．①③C．②④D．③④12．如图4－1－19，一束光线垂直照射在水平地面，在地面上放一个平面镜，欲使这束光线经过平面镜反射后成水平光线，则平面镜与地面所成锐角的度数为()图4－1－19A．45°B．60°C．75°D．80°二级训练13．(2012年四川广元)一辆汽车在公路上行驶，两次拐弯后，仍在原来的方向上平行行驶，那么两个拐弯的角度()A．先向左转130°，再向左转50°B．先向左转50°，再向右转50°C．先向左转50°，再向右转40°D．先向左转50°，再向左转40°14．如图4－1－20，在△ABC中，∠C＝90°.若BD∥AE，∠DBC＝20°，则∠CAE的度数是()A．40°B．60°C．70°D．80°图4－1－2015．如图4－1－21，把一张长方形纸片沿EF折叠后，点D，C分别落在点D′，C′的位置．若∠EFB＝65°，则∠AED′＝()图4－1－21A．70°B．65°C．50°D．25°w16．观察下图4－1－22，寻找对顶角(不含平角)：(1)(2)(3)图4－1－22(1)如图4－1－22(1)，图中共有______对对顶角；(2)如图4－1－22(2)，图中共有______对对顶角；(3)如图4－1－22(3)，图中共有______对对顶角；(4)研究(1)～(3)小题中直线条数与对顶角的对数之间的关系，若有n条直线相交于一点，则可形成______对对顶角；(5)若有2 008条直线相交于一点，则可形成______对对顶角．三级训练17．如图4－1－23，∠AOB＝90°，∠BOC＝30°，射线OM平分∠AOC，ON平分∠BOC.图4－1－23(1)求∠MON的度数；(2)如果(1)中，∠AOB＝α，其他条件不变，求∠MON的度数；(3)如果(1)中，∠BOC＝β(β为锐角)，其他条件不变，求∠MON的度数；(4)从(1)、(2)、(3)的结果中，你能看出什么规律？第2讲三角形第1课时三角形一级训练1．已知在△ABC中，若∠A＝70°－∠B，则∠C＝()A．35°B．70°C．110°D．140°2．如图4－2－14，在△ABC中，∠A＝70°，∠B＝60°，点D在BC的延长线上，则∠ACD＝()A．100°B．120°C．130°D．150°图4－2－143．已知如图4－2－15的两个三角形全等，则α的度数是()图4－2－15A．72°B．60°C．58°D．50°4．(2011年湖南怀化)如图4－2－16，∠A，∠1，∠2的大小关系是()图4－2－16A. ∠A>∠1>∠2B. ∠2>∠1>∠AC. ∠A>∠2>∠1D. ∠2>∠A>∠15．(2011年江西)如图4－2－17，下列条件中，不能证明△ABD≌△ACD的是()图4－2－17A．BD＝DC，AB＝AC B．∠ADB＝∠ADC，∠BAD＝∠CADC．∠B＝∠C，∠BAD＝∠CAD D．∠B＝∠C，BD＝DC6．(2011年上海)下列命题中，是真命题的是()A．周长相等的锐角三角形都全等B．周长相等的直角三角形都全等C．周长相等的钝角三角形都全等D．周长相等的等腰直角三角形都全等7．(2012年山东德州)不一定在三角形内部的线段是()A．三角形的角平分线B．三角形的中线C．三角形的高D．三角形的中位线8．(2012年山东济宁)用直尺和圆规作一个角的平分线的示意图如图4－2－18，则能说明∠AOC＝∠BOC的依据是()A．SSS B．ASAC．AAS D．角平分线上的点到角两边距离相等图4－2－189．(2011年安徽芜湖)如图4－2－19，已知在△ABC中，∠ABC＝45°，F是高AD和BE 的交点，CD＝4，则线段DF的长度为()图4－2－19A．2 2B．4C．3 2D．4 210．以三条线段3,4，x－5为边组成三角形，则x的取值范围为________．11．若△ABC的周长为a，点D，E，F分别是△ABC三边的中点，则△DEF的周长为__________．12．(2011年江西)如图4－2－20，两块完全相同的含30°的直角三角形叠放在一起，且∠DAB＝30°.有以下四个结论：①AF⊥BC；②△ADG≌△ACF; ③O为BC的中点；④AG∶DE ＝3∶4.其中正确结论的序号是__________．图4－2－20二级训练13．(2011年山东威海)在△ABC中，AB＞AC，点D，E分别是边AB，AC的中点，点F 在边BC上，连接DE，DF，EF，则添加下列哪一个条件后，仍无法判定△BFD与△EDF全等？()A．EF∥AB B．BF＝CF C．∠A＝∠DFE D．∠B＝∠DEF14．(2011年浙江)如图4－2－21，点D，E分别在AC，AB上．(1)已知BD＝CE，CD＝BE，求证：AB＝AC；(2)分别将“BD＝CE”记为①，“CD＝BE”记为②，“AB＝AC”记为③.添加条件①、③，以②为结论构成命题1，添加条件②、③，以①为结论构成命题2.命题1是________命题，命题2是_________命题(选择“真”或“假”填入空格)．图4－2－2115．(2012年湖北随州)如图4－2－22，在△ABC中，AB＝AC，点D是BC的中点，点E 在AD上．求证：(1)△ABD≌△ACD；(2)BE＝CE.图4－2－22三级训练16．(2011年湖南衡阳)如图4－2－23，在△ABC 中，∠B ＝90°，AB ＝3，AC ＝5，将△ABC 折叠，使点C 与点A 重合，折痕为DE ，则△ABE 的周长为________．图4－2－2317．如图4－2－24，两根旗杆间相距12 m ，某人从点B 沿BA 走向点A ，一定时间后他到达点M ，此时他仰望旗杆的顶点C 和D ，两次视线的夹角为90°，且CM ＝DM ，已知旗杆AC 的高为3 m ，该人的运动速度为1 m/s ，求这个人运动了多长时间？图4－2－24第二部分 空间与图形 第四章 三角形与四边形第1讲 线、角、相交线和平行线 【分层训练】 1．143°25′ 2.B 3.B 4.B 5.D 6.C 7.B 8.B 9．C 10.B 11.D 12．A 解析：如图D9，过点O 作OD ⊥OC ，根据平面镜反射定律，可得∠AOD ＝∠BOD .又∵AO 垂直于水平面，OB 平行于水平面，∴∠AOB ＝90°.∴∠AOD ＝∠BOD ＝45°.又∵OD ⊥OC ，∴∠BOC ＝90°－∠BOD ＝45°.由于OB 平行于水平面，可得∠1＝∠BOC ＝45°.图D911．D 13.B14．C 解析：由题意，可得∠EAB ＋∠DBA ＝180°，又由∠C ＝90°，可得∠CAB ＋∠CBA ＝90°，于是∠CAE ＋∠DBC ＝90°.故∠CAE ＝90°－∠DBC ＝70°.15．C 解析：∠D ′EF ＝∠DEF ＝∠EFB ＝65°，于是∠AED ′＝180°－∠D ′ED ＝50°. 16．(1)2 (2)6 (3)12 (4)n (n －1) (5)4 030 056解析：(1)如图4－1－22(1)，图中共有1×2＝2对对顶角； (2)如图4－1－22(2)，图中共有2×3＝6对对顶角； (3)如图4－1－22(3)，图中共有3×4＝12对对顶角；(4)研究(1)～(3)小题中直线条数与对顶角的对数之间的关系，若有n 条直线相交于一点，则可形成(n －1)n 对对顶角；(5)若有2 008条直线相交于一点，则可形成(2 008－1)×2 008＝4 030 056对对顶角．17．解：(1)∠MON ＝∠COM －∠CON ＝12∠AOC －12∠BOC ＝12×120°－12×30°＝45°.(2)∠MON ＝∠COM －∠CON ＝12∠AOC －12∠BOC ＝12(α＋30°)－12×30°＝12α.(3)∠MON ＝∠COM －∠CON ＝12∠AOC －12∠BOC ＝12(90°＋β)－12β＝45°.(4)∠MON 的大小等于∠AOB 的一半，与∠BOC 的大小无关． 第2讲 三角形 第1课时 三角形 【分层训练】1．C 2.C 3.D 4.B 5.D 6.D 7.C 8.A 9.B10．6<x <12 解析：由题意，可得1<x －5<7，解得6<x <12. 11.a 2 解析：由题意，可得△DEF 的三边为△ABC 的中位线，故其周长为a 2. 12．①②③④ 13.C 14．(1)证明：连接BC ，∵ BD ＝CE ，CD ＝BE ，BC ＝CB ， ∴ △DBC ≌△ECB (SSS)． ∴ ∠DBC ＝∠ECB . ∴ AB ＝AC . (2)真 假15．证明：(1)∵D 是BC 的中点， ∴BD ＝CD .在△ABD 和△ACD 中， ⎩⎪⎨⎪⎧BD ＝CD ，AB ＝AC ，AD ＝AD (公共边)，∴△ABD ≌△ACD (SSS)．(2)由(1)，可知：△ABD ≌△ACD ， ∴∠BAD ＝∠CAD ，即∠BAE ＝∠CAE . 在△ABE 和△ACE 中， ⎩⎪⎨⎪⎧AB ＝AC ，∠BAE ＝∠CAE ， AE ＝AE ，∴△ABE ≌△ACE (SAS)．∴BE ＝CE (全等三角形的对应边相等).16．7 解析：因为将△ABC 折叠，使点C 与点A 重合，折痕为DE ，所以EC ＝AE ，故△ABE 的周长为AB ＋BE ＋AE ＝AB ＋BE ＋EC ＝AB ＋BC ＝3＋4＝7.17．解：∵∠CMD ＝90°， ∴∠CMA ＋∠DMB ＝90°. 又∵∠CAM ＝90°，∴∠CMA ＋∠ACM ＝90°. ∴∠ACM ＝∠DMB . 又∵CM ＝MD ，∴Rt △ACM ≌Rt △BMD . ∴AC ＝BM ＝3.∴他到达点M 时，运动时间为3÷1＝3(s)． 答：这人运动了3 s.。

精品基础教育教学资料，仅供参考，需要可下载使用！中考数学冲刺专题训练（附答案）：三角形与四边形一、选择题（本大题共8个小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的）1．一个等腰三角形的底边长是6，腰长是一元二次方程28150x x -+=的一根，则此三角形的周长是（ ） A ．16 B ．12C ．14D ．12或16【答案】A 【解析】解方程28150x x -+=，得：3x =或5x =，若腰长为3，则三角形的三边为3、3、6，显然不能构成三角形； 若腰长为5，则三角形三边长为5、5、6，此时三角形的周长为16， 故选：A ．2．如图，在△ABC 中，BE 是∠ABC 的平分线，CE 是外角∠ACM 的平分线，BE 与CE 相交于点E ，若∠A =60°，则∠BEC 是（ ）A ．15°B ．30°C ．45°D ．60°【答案】B 【解析】∵BE 是∠ABC 的平分线， ∴∠EBM=12∠ABC ， ∵CE 是外角∠ACM 的平分线， ∴∠ECM=12∠ACM ， 则∠BEC=∠ECM-∠EBM=12×（∠ACM-∠ABC ）=12∠A=30°， 故选：B ．3．如图，在△ABC 中，∠C ＝90°，AC ＝12，AB 的垂直平分线EF 交AC 于点D ，连接BD ，若cos ∠BDC ＝57，则BC 的长是（ ）A ．10B ．8C ．3D ．6【答案】D 【解析】∵∠C ＝90°，cos ∠BDC ＝57， 设CD ＝5x ，BD ＝7x ， ∴BC ＝6x ，∵AB 的垂直平分线EF 交AC 于点D ， ∴AD ＝BD ＝7x ， ∴AC ＝12x ， ∵AC ＝12， ∴x ＝1， ∴BC ＝6； 故选D.4．一个菱形的边长为6，面积为28，则该菱形的两条对角线的长度之和为( ) A ．8 B ．12C ．16D ．32【答案】C 【解析】 如图所示：四边形ABCD 是菱形，12AO CO AC ∴==， 12DC BO BD ==，AC BD ⊥， 面积为28，∴12282AC BD OD AO ⋅=⋅=① 菱形的边长为6，2236OD OA ∴+=②，由①②两式可得：222()2362864OD AO OD OA OD AO +=++⋅=+=，8OD AO ∴+=，2()16OD AO ∴+=，即该菱形的两条对角线的长度之和为16， 故选C ．5．如图，点B 、F 、C 、E 在一条直线上，AB ∥ED ，AC ∥FD ，那么添加下列一个条件后，仍无法判定△ABC ≌△DEF 的是（ ）A ．AB =DE B ．AC =DF C ．∠A =∠D D ．BF =EC【答案】C 【解析】解：选项A 、添加AB=DE 可用AAS 进行判定，故本选项错误； 选项B 、添加AC=DF 可用AAS 进行判定，故本选项错误； 选项C 、添加∠A=∠D 不能判定△ABC ≌△DEF ，故本选项正确；选项D 、添加BF=EC 可得出BC=EF ，然后可用ASA 进行判定，故本选项错误． 故选C ．6．如图，ABCD 中，对角线AC 、BD 相交于点O ，OE BD ⊥交AD 于点E ，连接BE ，若ABCD 的周长为28，则ABE ∆的周长为（ ）A ．28B ．24C ．21D ．14【答案】D 【解析】∵四边形ABCD 是平行四边形， ∴OB OD =，AB CD =，AD BC =， ∵平行四边形的周长为28， ∴14AB AD += ∵OE BD ⊥，∴OE 是线段BD 的中垂线， ∴BE ED =，∴ABE ∆的周长14AB BE AE AB AD =++=+=， 故选：D ．7．如图，在ABCD 中，将ADC ∆沿AC 折叠后，点D 恰好落在DC 的延长线上的点E 处．若=60B ︒∠，=3AB ，则ADE ∆的周长为（ ）A ．12B ．15C ．18D ．21【答案】C 【解析】由折叠可得，90ACD ACE ︒∠=∠=，90BAC ︒∴∠=，又60B ︒∠=，30ACB ︒∴∠=，26BC AB ∴==，6AD ∴=，由折叠可得，60E D B ︒∠=∠=∠=，60DAE ︒∴∠=，ADE ∴∆是等边三角形， ADE ∴∆的周长为6318⨯=，故选：C ．8．如图，在正方形ABCD 中，E 、F 分别是BC 、CD 上的点，且∠EAF ＝45°，AE 、AF 分别交BD 于M 、N ，连按EN 、EF 、有以下结论：①AN ＝EN ，②当AE ＝AF 时，BEEC＝2﹣2，③BE+DF ＝EF ，④存在点E 、F ，使得NF ＞DF ，其中正确的个数是（ ）A ．1B ．2C ．3D ．4【答案】B 【解析】 ①如图1，∵四边形ABCD 是正方形，∴∠EBM ＝∠ADM ＝∠FDN ＝∠ABD ＝45°，∵∠MAN＝∠EBM＝45°，∠AMN＝∠BME，∴△AMN∽△BME，∴AM MN BM EM=，∵∠AMB＝∠EMN，∴△AMB∽△NME，∴∠AEN＝∠ABD＝45°∴∠NAE＝∠AEN＝45°，∴△AEN是等腰直角三角形，∴AN＝EN，故①正确；②在△ABE和△ADF中，∵AB ADABE ADF90 AE AF︒=⎧⎪∠=∠=⎨⎪=⎩，∴Rt△ABE≌Rt△ADF（HL），∴BE＝DF，∵BC＝CD，∴CE＝CF，假设正方形边长为1，设CE＝x，则BE＝1﹣x，如图2，连接AC，交EF于H，∵AE＝AF，CE＝CF，∴AC是EF的垂直平分线，∴AC⊥EF，OE＝OF，Rt △CEF 中，OC ＝12EF ＝22x ， △EAF 中，∠EAO ＝∠FAO ＝22.5°＝∠BAE ＝22.5°， ∴OE ＝BE ， ∵AE ＝AE ，∴Rt △ABE ≌Rt △AOE （HL ）， ∴AO ＝AB ＝1， ∴AC ＝2＝AO+OC ，∴1+22x ＝2， x ＝2﹣2，∴BE EC ＝1(22)22---＝(21)(22)2-+＝22； 故②不正确； ③如图3，∴将△ADF 绕点A 顺时针旋转90°得到△ABH ，则AF ＝AH ，∠DAF ＝∠BAH ， ∵∠EAF ＝45°＝∠DAF+∠BAE ＝∠HAE ， ∵∠ABE ＝∠ABH ＝90°， ∴H 、B 、E 三点共线， 在△AEF 和△AEH 中，AE AE FAE HAE AF AH =⎧⎪∠=∠⎨⎪=⎩，∴△AEF ≌△AEH （SAS ）， ∴EF ＝EH ＝BE+BH ＝BE+DF ， 故③正确；④△ADN 中，∠FND ＝∠ADN+∠NAD ＞45°， ∠FDN ＝45°， ∴DF ＞FN ，故存在点E 、F ，使得NF ＞DF ， 故④不正确； 故选B ．二、填空题（本大题共4个小题，每小题6分，共24分）9．如图，在△ABC 中，以点B 为圆心，以BA 长为半径画弧交边BC 与点D ，连结AD ，若∠B =40°，∠C =36°，则∠DAC 的度数是____________．【答案】34° 【解析】由作图过程可知BD=BA ， ∵∠B=40°， ∴∠BDA=∠BAD=12(180°-∠B)=70°， ∴∠DAC=∠BDA-∠C=70°-36°=34°. 故答案为34°. 10．如图，在矩形ABCD 中，1AB =，BC a =，点E 在边BC 上，且35BE α=．连接AE ，将ABE ∆沿AE 折叠，若点B 的对应点B '落在矩形ABCD 的边上，则 a 的值为________．【答案】53或53【解析】 分两种情况：①当点B '落在AD 边上时，如图1． 四边形ABCD 是矩形，90BAD B ︒∴∠=∠=，将ABE ∆沿AE 折叠，点B 的对应点B '落在AD 边上，1452BAE B AE BAD '︒∴∠=∠=∠=，AB BE ∴=，315a ∴=， 53a ∴=；②当点B '落在CD 边上时，如图2． ∵四边形ABCD 是矩形，90BAD B C D ︒∴∠=∠=∠=∠=，AD BC a ==．将ABE ∆沿AE 折叠，点B 的对应点B '落在CD 边上，90B AB E '︒∴∠=∠=，1AB AB '==，35EB EB a '==，2221DB B A AD a ''∴=-=-，3255EC BC BE a a =-=-=． 在ADB '∆与B CE '∆中，90A 90B AD EBC B DD C ︒︒⎧∠=∠=-∠'''⎨∠=∠=⎩， ADB B CE ''∴∆⋃∆，DB AB CE B E'''∴=，即2112355a a a -=，解得153a =，20a =（舍去）． 综上，所求a 的值为53或53． 故答案为53或53． 11．如图，正方形ABCD 的边长为4，点E 是CD 的中点，AF 平分BAE ∠交BC 于点F ，将ADE ∆绕点A 顺时针旋转90°得ABG ∆，则CF 的长为_____．【答案】6-25 【解析】作FM AD M FN AG N ⊥⊥于，于 ，如图，易得四边形CFMD 为矩形，则4FM ＝∵正方形ABCD的边长为4，点是的中点，2DE ∴＝，∴224225AE =+=∵△ADE 绕点A 顺时针旋转90°得△ABG ，∴252349090AG AE BG DE GAE ABG D ∠∠∠︒∠∠︒＝＝，＝＝，＝，＝，＝＝ 而90ABC ∠︒＝ ， ∴点G 在CB 的延长线上，∵AF 平分∠BAE 交BC 于点F ，∴∠1＝∠2，∴∠2+∠4＝∠1+∠3，即F A 平分∠GAD ， ∴FN ＝FM ＝4， ∵11••22AB GF FN AG ＝, ∴425254GF ⨯==, ∴4225625CF CG GF +=-＝﹣＝﹣ ． 故答案为6-25．12．如图，在平面直角坐标系中，OA ＝1，以OA 为一边，在第一象限作菱形OAA 1B ，并使∠AOB ＝60°，再以对角线OA 1为一边，在如图所示的一侧作相同形状的菱形OA 1A 2B 1，再依次作菱形OA 2A 3B 2，OA 3A 4B 3，……，则过点B 2018，B 2019，A 2019的圆的圆心坐标为_____．【答案】（-32018，3）2019） 【解析】过A 1作A 1C ⊥x 轴于C ，∵四边形OAA1B是菱形，∴OA＝AA1＝1，∠A1AC＝∠AOB＝60°，∴A1C＝32，AC＝12，∴OC＝OA+AC＝32，在Rt△OA1C中，OA1＝2213OC AC+=，∵∠OA2C＝∠B1A2O＝30°，∠A3A2O＝120°，∴∠A3A2B1＝90°，∴∠A2B1A3＝60°，∴B1A3＝23，A2A3＝3，∴OA3＝OB1+B1A3＝33＝（3）3∴菱形OA2A3B2的边长＝3＝（3）2，设B1A3的中点为O1，连接O1A2，O1B2，于是求得，O1A2＝O1B2＝O1B133）1，∴过点B1，B2，A2的圆的圆心坐标为O1（0，23，∵菱形OA3A4B3的边长为333，∴OA4＝934，设B2A4的中点为O2，连接O2A3，O2B3，同理可得，O2A3＝O2B3＝O2B2＝3＝（3）2，∴过点B2，B3，A3的圆的圆心坐标为O2（﹣3，33），…以此类推，菱形OA2019A2020B2019的边长为（3）2019，OA2020＝（3）2020，设B2018A2020的中点为O2018，连接O2018A2019，O2018B2019，求得，O2018A2019＝O2018B2019＝O2018B2018＝（3）2018，∴点O2018是过点B2018，B2019，A2019的圆的圆心，∵2018÷12＝168…2，∴点O2018在射线OB2上，则点O2018的坐标为（﹣（3）2018，（3）2019），即过点B2018，B2019，A2019的圆的圆心坐标为：（﹣（3）2018，（3）2019），故答案为：（﹣（3）2018，（3）2019）．三、解答题（本大题共3个小题，每小题12分，共36分．解答应写出文字说明、证明过程或演算步骤）13．如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F、H在菱形ABCD的对角线BD上.=；（1）求证：BG DEFH=，求菱形ABCD的周长。

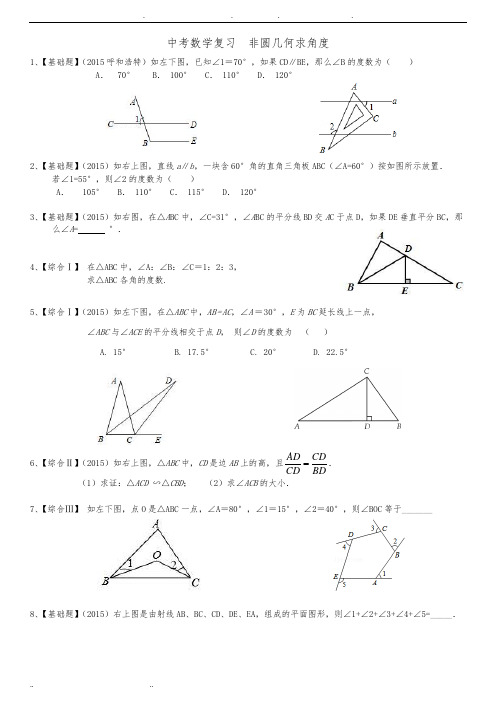
中考数学复习非圆几何求角度1、【基础题】（2015呼和浩特）如左下图，已知∠1＝70°，如果CD∥BE，那么∠B的度数为（）A．70°B． 100°C． 110°D． 120°2、【基础题】（2015）如右上图，直线a∥b，一块含60°角的直角三角板ABC（∠A=60°）按如图所示放置．若∠1=55°，则∠2的度数为（）A．105°B． 110°C． 115°D．120°3、【基础题】（2015）如右图，在△A BC中，∠C=31°，∠A BC的平分线BD交A C于点D，如果DE垂直平分BC，那么∠A= °．4、【综合Ⅰ】在△ABC中，∠A：∠B：∠C＝1：2：3，求△ABC各角的度数.5、【综合Ⅰ】（2015）如左下图，在△ABC中，AB=AC，∠A＝30°，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，则∠D的度数为（）A. 15°B. 17.5°C. 20°D. 22.5°6、【综合Ⅱ】（2015）如右上图，△ABC中，CD是边AB上的高，且AD CD CD BD．（1）求证：△ACD ∽△CBD；（2）求∠ACB的大小．7、【综合Ⅲ】如左下图，点O是△ABC一点，∠A＝80°，∠1＝15°，∠2＝40°，则∠BOC等于_______8、【基础题】（2015）右上图是由射线AB、BC、CD、DE、EA，组成的平面图形，则∠1+∠2+∠3+∠4+∠5=_____．9、【综合Ⅱ】（2015）如左下图，平面上，将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起，则∠3+∠1－∠2=°10、【基础题】（2015）如右上图，□ABCD中，对角线AC与BD交于点O，∠DAC=42º，∠CBD=23º，则∠COD的度数是（）A．61º B．63º C．65º D．67º11、【综合Ⅱ】如右图，在菱形ABCD中，∠BAD＝80°，AB的垂直平分线交对角线AC于点F，E为垂足，连接DF，则∠CDF的度数为．12、【综合Ⅱ】（2010襄阳）菱形的周长为8cm，高为1cm，则该菱形两邻角度数比为（）A．3：1 B．4：1 C．5：1 D．6：113、【综合Ⅲ】如左下图，在矩形ABCD中，AC与BD相交于一点O，AE平分∠BAD，若∠EAO＝15°，求∠BOE的度数．14、【综合Ⅱ】（2015）如右上图，已知点E是正方形ABCD的对角线AC上一点，AE＝AD，过点E作AC的垂线，交边CD于点F，那么∠FAD＝______度．15、【综合Ⅱ】（2015黄冈）如左下图，在正方形ABCD中，点F为CD上一点，BF与AC交于点E．若∠CBF=20°，则∠AED等于度．16、【综合Ⅲ】（2015）如右上图，等腰直角三角形BDC的顶点D在等边三角形ABC的部，∠BDC=90°，连接AD，过点D作一条直线将△ABD分割成两个等腰三角形，则分割出的这两个等腰三角形的顶角分别是度．17、【综合Ⅲ】（2014）如图，在△ABC 中，AB ＝AC ，且D 为BC 上一点，CD ＝AD ，AB ＝BD ，则∠B 的度数为（ ）A ．30°B ．36°C ．40°D ．45°18、【综合Ⅲ】（2015襄阳）在□ABCD 中，AD=BD ，BE 是AD 边上的高，∠EBD=20°，则∠A 的度数为 ．19、【提高题】如左下图，等边△ABC 中，BD ＝CE ，AD 与BE 相交于点P ，则∠APE 的度数是 （ ）A. 45°B. 60°C. 75°D. 80°20、【提高题】（2015）如右上图，在△ABC 中，∠B＝40°，三角形的外角∠DAC 和∠ACF 的平分线交于点E ，则∠AEC＝ 度。

中考数学复习考点题型专题练习 专题21 与三角形、四边形相关的压轴题解答题1．（2022·黑龙江）如图，在平面直角坐标系中，平行四边形ABCD 的边AB 在x 轴上，顶点D 在y 轴的正半轴上，M 为BC 的中点，OA 、OB 的长分别是一元二次方程27120x x -+=的两个根()OA OB <，4tan 3DAB ∠=，动点P 从点D 出发以每秒1个单位长度的速度沿折线DC CB -向点B 运动，到达B 点停止．设运动时间为t 秒，APC △的面积为S ．(1)求点C的坐标；(2)求S 关于t 的函数关系式，并写出自变量t 的取值范围；(3)在点P 的运动过程中，是否存在点P ，使CMP 是等腰三角形？若存在，请直接写出点P 的坐标；若不存在，请说明理由．2．（2022·贵州黔东南）阅读材料：小明喜欢探究数学问题，一天杨老师给他这样一个几何问题：如图，ABC 和BDE 都是等边三角形，点A 在DE 上．求证：以AE 、AD 、AC 为边的三角形是钝角三角形．(1)【探究发现】小明通过探究发现：连接DC ，根据已知条件，可以证明DC AE =，120ADC =∠︒，从而得出ADC 为钝角三角形，故以AE 、AD 、AC 为边的三角形是钝角三角形．请你根据小明的思路，写出完整的证明过程．(2)【拓展迁移】如图，四边形ABCD 和四边形BGFE 都是正方形，点A 在EG 上．①试猜想：以AE 、AG 、AC 为边的三角形的形状，并说明理由． ②若2210AE AG +=，试求出正方形ABCD 的面积．3．（2022·海南）如图1，矩形ABCD 中，6,8AB AD ==，点P 在边BC 上，且不与点B 、C重合，直线AP 与DC 的延长线交于点E ．(1)当点P 是BC 的中点时，求证：ABP ECP △≌△；(2)将APB △沿直线AP 折叠得到APB '，点B '落在矩形ABCD 的内部，延长PB '交直线AD 于点F ．①证明FA FP =，并求出在（1）条件下AF 的值；②连接B C '，求PCB '△周长的最小值；③如图2，BB '交AE 于点H ，点G 是AE 的中点，当2EAB AEB ∠=∠''时，请判断AB 与HG 的数量关系，并说明理由．4．（2022·吉林）如图，在ABC 中，90ACB ∠=︒，30A ∠=︒，6cm =AB ．动点P 从点A 出发，以2cm/s 的速度沿边AB 向终点B 匀速运动．以PA 为一边作120APQ ∠=︒，另一边PQ 与折线AC CB -相交于点Q ，以PQ 为边作菱形PQMN ，点N 在线段PB 上．设点P 的运动时间为(s)x ，菱形PQMN 与ABC 重叠部分图形的面积为2()cm y ．(1)当点Q 在边AC 上时，PQ 的长为cm ；（用含x 的代数式表示）(2)当点M 落在边BC 上时，求x 的值；(3)求y 关于x 的函数解析式，并写出自变量x 的取值范围．5．（2022·黑龙江牡丹江）在菱形ABCD和正三角形BGF中，60∠=︒，P是DF的中ABC点，连接PG、PC．(1)如图1，当点G在BC边上时，写出PG与PC的数量关系．（不必证明）(2)如图2，当点F在AB的延长线上时，线段PC、PG有怎样的数量关系，写出你的猜想，并给予证明；(3)如图3，当点F 在CB 的延长线上时，线段PC 、PG 又有怎样的数量关系，写出你的猜想（不必证明）．6．（2022·内蒙古呼和浩特）下面图片是八年级教科书中的一道题：如图，四边形ABCD 是正方形，点E 是边BC 的中点，90AEF ∠=︒，且EF 交正方形外角的平分线CF 于点F ．求证AE EF =．（提示：取AB 的中点G ，连接EG ．）(1)请你思考题中“提示”，这样添加辅助线的意图是得到条件：；(2)如图1，若点E 是BC 边上任意一点（不与B 、C 重合），其他条件不变．求证：AE EF =；(3)在（2）的条件下，连接AC ，过点E 作EP ⊥AC ，垂足为P ．设=BEk BC，当k 为何值时，四边形ECFP 是平行四边形，并给予证明．7．（2022·福建）已知ABC DEC ≌△△，AB ＝AC ，AB ＞BC ．(1)如图1，CB 平分∠ACD ，求证：四边形ABDC 是菱形；(2)如图2，将（1）中的△CDE 绕点C 逆时针旋转（旋转角小于∠BAC ），BC ，DE 的延长线相交于点F ，用等式表示∠ACE 与∠EFC 之间的数量关系，并证明；(3)如图3，将（1）中的△CDE 绕点C 顺时针旋转（旋转角小于∠ABC ），若BAD BCD ∠=∠，求∠ADB 的度数．8．（2022·湖南衡阳）如图，在菱形ABCD 中，4AB =，60BAD ∠=︒，点P 从点A 出发，沿线段AD 以每秒1个单位长度的速度向终点D 运动，过点P 作PQ AB ⊥于点Q ，作PM AD ⊥交直线AB 于点M ，交直线BC 于点F ，设PQM 与菱形ABCD 重叠部分图形的面积为S （平方单位），点P 运动时间为t （秒）．(1)当点M 与点B 重合时，求t 的值；(2)当t 为何值时，APQ 与BMF 全等；(3)求S 与t 的函数关系式；(4)以线段PQ 为边，在PQ 右侧作等边三角形PQE ，当24t ≤≤时，求点E 运动路径的长．9．（2022·浙江金华）如图，在菱形ABCD中，310,sin5AB B==，点E从点B出发沿折线B C D--向终点D运动．过点E作点E所在的边（BC或CD）的垂线，交菱形其它的边于点F，在EF的右侧作矩形EFGH．(1)如图1，点G在AC上．求证：FA FG=．(2)若EF FG=，当EF过AC中点时，求AG的长．(3)已知8FG=，设点E的运动路程为s．当s满足什么条件时，以G，C，H为顶点的三角形与BEF相似（包括全等）？10．（2022·四川南充）如图，在矩形ABCD 中，点O 是AB 的中点，点M 是射线DC 上动点，点P 在线段AM 上（不与点A 重合），12OP AB =．(1)判断ABP △的形状，并说明理由．(2)当点M 为边DC 中点时，连接CP 并延长交AD 于点N ．求证：PN AN =．(3)点Q 在边AD 上，85,4,5AB AD DQ ===，当90CPQ ∠=︒时，求DM 的长．11．（2022·湖北武汉）已知CD 是ABC 的角平分线，点E ，F 分别在边AC ，BC 上，AD m =，BD n =，ADE 与BDF 的面积之和为S ．(1)填空：当90ACB ∠=︒，DE AC ⊥，DF BC ⊥时，①如图1，若45B ∠=︒，m =n =_____________，S =_____________；②如图2，若60∠=︒，m=n=_____________，S=_____________；B(2)如图3，当90∠=∠=︒时，探究S与m、n的数量关系，并说明理由：ACB EDF(3)如图4，当60n=时，请直接写出S的大小．ACB∠=︒，120∠=︒，6EDFm=，412．（2022·山东临沂）已知ABC是等边三角形，点B，D关于直线AC对称，连接AD，CD．(1)求证：四边形ABCD是菱形；(2)在线段AC上任取一点Р（端点除外），连接PD．将线段PD绕点Р逆时针旋转，使点D落在BA延长线上的点Q处．请探究：当点Р在线∠的大小是否发生变化？说明理由．(3)在满足（2）的段AC上的位置发生变化时，DPQ条件下，探究线段AQ与CP之间的数量关系，并加以证明．13．（2022·江西）问题提出：某兴趣小组在一次综合与实践活动中提出这样一个问题：将足够大的直角三角板()90,60PEF P F ∠=︒∠=︒的一个顶点放在正方形中心O 处，并绕点O 逆时针旋转，探究直角三角板PEF 与正方形ABCD 重叠部分的面积变化情况（已知正方形边长为2）．(1)操作发现：如图1，若将三角板的顶点P 放在点O 处，在旋转过程中，当OF 与OB 重合时，重叠部分的面积为__________；当OF 与BC 垂直时，重叠部分的面积为__________；一般地，若正方形面积为S ，在旋转过程中，重叠部分的面积1S 与S 的关系为__________； (2)类比探究：若将三角板的顶点F 放在点O 处，在旋转过程中，,OE OP 分别与正方形的边相交于点M ，N ．①如图2，当BM CN =时，试判断重叠部分OMN 的形状，并说明理由； ②如图3，当CM CN =时，求重叠部分四边形OMCN 的面积（结果保留根号）； (3)拓展应用：若将任意一个锐角的顶点放在正方形中心O 处，该锐角记为GOH ∠（设GOH α∠=），将GOH ∠绕点O 逆时针旋转，在旋转过程中，GOH ∠的两边与正方形ABCD的边所围成的图形的面积为2S ，请直接写出2S 的最小值与最大值（分别用含α的式子表示），（参考数据：sin15tan152︒=︒=︒=-14．（2022·贵州贵阳）小红根据学习轴对称的经验，对线段之间、角之间的关系进行了拓展探究．如图，在ABCD □中，AN 为BC 边上的高，AD m AN=，点M 在AD 边上，且BA BM =，点E 是线段AM 上任意一点，连接BE ，将ABE △沿BE 翻折得FBE ．(1)问题解决：如图①，当60BAD ∠=︒，将ABE △沿BE 翻折后，使点F 与点M 重合，则AM AN=______；(2)问题探究：如图②，当45BAD ∠=︒，将ABE △沿BE 翻折后，使EF BM ∥，求ABE ∠的度数，并求出此时m 的最小值；(3)拓展延伸：当30BAD ∠=︒，将ABE △沿BE 翻折后，若EF AD ⊥，且AE MD =，根据题意在备用图中画出图形，并求出m 的值．15．（2022·吉林长春）【探索发现】在一次折纸活动中，小亮同学选用了常见的A 4纸，如图①，矩形ABCD 为它的示意图．他查找了A 4纸的相关资料，根据资料显示得出图①中AD =．他先将A 4纸沿过点A 的直线折叠，使点B 落在AD 上，点B 的对应点为点E ，折痕为AF ；再沿过点F 的直线折叠，使点C 落在EF 上，点C 的对应点为点H ，折痕为FG ；然后连结AG ，沿AG 所在的直线再次折叠，发现点D 与点F 重合，进而猜想ADG AFG △≌△．【问题解决】(1)小亮对上面ADG AFG △≌△的猜想进行了证明，下面是部分证明过程： 证明：四边形ABCD 是矩形，∴90BAD B C D ∠=∠=∠=∠=︒． 由折叠可知，1452BAF BAD ∠=∠=︒，BFA EFA ∠=∠．∴45EFA BFA ∠=∠=︒． ∴AF AD ==．请你补全余下的证明过程．【结论应用】(2)DAG ∠的度数为________度，FG AF的值为_________； (3)在图①的条件下，点P 在线段AF 上，且12AP AB =，点Q 在线段AG 上，连结FQ 、PQ ，如图②，设AB a ，则FQ PQ +的最小值为_________．（用含a 的代数式表示）16．（2022·广东深圳）（1）【探究发现】如图①所示，在正方形ABCD 中，E 为AD 边上一点，将AEB △沿BE 翻折到BEF 处，延长EF 交CD 边于G 点．求证：BFG BCG △≌△（2）【类比迁移】如图②，在矩形ABCD 中，E 为AD 边上一点，且8,6,AD AB ==将AEB △沿BE 翻折到BEF 处，延长EF 交BC 边于点,G 延长BF 交CD 边于点,H 且,FH CH =求AE 的长．（3）【拓展应用】如图③，在菱形ABCD 中，E 为CD 边上的三等分点，60,D ∠=︒将ADE 沿AE 翻折得到AFE △，直线EF 交BC 于点,P 求CP 的长．17．（2022·黑龙江）ABC和ADE都是等边三角形．(1)将ADE绕点A旋转到图①的位置时，连接BD，CE并延长相交于点P（点P与点A重合），有PA PB PC+=）成立；请证明．(2)将ADE绕点A旋转到图②的位+=（或PA PC PB置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？并加以证明；(3)将ADE绕点A旋转到图③的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？直接写出结论，不需要证明．18．（2022·辽宁锦州）在ABC中，AC BC=，点D在线段AB上，连接CD并延长至点E，使DE CD=，过点E作EF AB⊥，交直线AB于点F．(1)如图1，若120ACB ∠=︒，请用等式表示AC 与EF 的数量关系：____________．(2)如图2．若90ACB ∠=︒，完成以下问题：①当点D ，点F 位于点A 的异侧时，请用等式表示,,AC AD DF 之间的数量关系，并说明理由；②当点D ，点F 位于点A 的同侧时，若1,3DF AD ==，请直接写出AC 的长．19．（2022·广西）已知MON α∠=，点A ，B 分别在射线,OM ON 上运动，6AB =．(1)如图①，若90α=︒，取AB 中点D ，点A ，B 运动时，点D 也随之运动，点A ，B ，D 的对应点分别为,,A B D '''，连接,OD OD '．判断OD 与OD '有什么数量关系?证明你的结论：(2)如图②，若60α=︒，以AB 为斜边在其右侧作等腰直角三角形ABC ，求点O 与点C 的最大距离：(3)如图③，若45α=︒，当点A ，B 运动到什么位置时，AOB 的面积最大?请说明理由，并求出AOB 面积的最大值．20．（2022·湖北十堰）【阅读材料】如图①，四边形ABCD 中，AB AD =，180B D ∠+∠=︒，点E ，F 分别在BC ，CD 上，若2BAD EAF ∠∠=，则EF BE DF =+．【解决问题】如图②，在某公园的同一水平面上，四条道路围成四边形ABCD ．已知100m CD CB ==，60D ∠=︒，120ABC ∠=︒，150BCD ∠=︒，道路AD ，AB 上分别有景点M ，N ，且100m DM =，)501m BN =，若在M ，N 之间修一条直路，则路线M N →的长比路线M A N →→的长少_________m 1.7≈）．21．（2022·陕西）问题提出(1)如图1，AD 是等边ABC 的中线，点P 在AD 的延长线上，且AP AC =，则APC ∠的度数为__________． 问题探究(2)如图2，在ABC 中，6,120CA CB C ==∠=︒．过点A 作AP BC ∥，且AP BC =，过点P 作直线l BC ⊥，分别交AB BC 、于点O 、E ，求四边形OECA 的面积． 问题解决(3)如图3，现有一块ABC 型板材，ACB ∠为钝角，45BAC ∠=︒．工人师傅想用这块板材裁出一个ABP △型部件，并要求15,BAP AP AC ∠=︒=．工人师傅在这块板材上的作法如下：①以点C 为圆心，以CA 长为半径画弧，交AB 于点D ，连接CD ； ②作CD 的垂直平分线l ，与CD 于点E ； ③以点A 为圆心，以AC 长为半径画弧，交直线l 于点P ，连接AP BP 、，得ABP △． 请问，若按上述作法，裁得的ABP △型部件是否符合要求？请证明你的结论．。

专题七 三角形、四边形实践探究(旋转、动点、折叠问题)1．将矩形ABCD 绕点A 按顺时针方向旋转α(0°＜α＜360°)，得到矩形AEFG.(1)如图，当点E 在BD 上时．求证：FD ＝CD ；(2)当α为何值时，GC ＝GB ？画出图形，并说明理由．(1)证明：由旋转可得AE ＝AB ，∠AEF ＝∠ABC ＝∠DAB ＝90°，EF ＝BC ＝AD.∴∠AEB ＝∠ABE.又∵∠ABE ＋∠EDA ＝90°＝∠AEB ＋∠DEF ，∴∠EDA ＝∠DEF.又∵DE ＝ED ，∴△AED ≌△FDE(SAS )．∴FD ＝AE.又∵AE ＝AB ＝CD ，∴FD ＝CD ；(2)解：当α为60°或300°时，GC ＝GB.理由：如图，当GB ＝GC 时，点G 在BC 的垂直平分线上，分两种情况讨论：①当点G 在AD 右侧时，GH 垂直平分BC ，AG ＝AD.又∵AD ∥BC ，∴GH ⊥AD.∴四边形ABHM 是矩形．∴AM ＝BH ＝12AD. ∴GM 垂直平分AD ，∴GD ＝GA ＝DA.∴△ADG 是等边三角形．∴∠DAG ＝60°.∴旋转角α＝60°；②当点G 在AD 左侧时，同理可得△ADG 是等边三角形，∴∠DAG ＝60°.∴旋转角α＝360°－60°＝300°.2．(2019·唐山路北区三模)如图，在△ABC 中，AB ＝5，AC ＝9，S △ABC ＝272，动点P 从点A 出发，沿射线AB 方向以每秒5个单位长度的速度运动，动点Q 从点C 出发，以相同的速度在线段AC 上由C 向A 运动，当点Q 运动到点A 时，P ，Q 两点同时停止运动，以PQ 为边作正方形PQEF(P ，Q ，E ，F 按逆时针排序)，以CQ 为边在AC 上方作正方形QCGH.(1)tan A ＝________；(2)设点P 运动时间为t s ，正方形PQEF 的面积为S ，请探究S 是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由；(3)当t 为何值时，正方形PQEF 的某个顶点(点Q 除外)落在正方形QCGH 的边HG 上？请直接写出t 的值．解：(1)34；[过点B 作BM ⊥AC 于点M.∵AC ＝9，S △ABC ＝272，∴12AC·BM ＝272，即12×9BM ＝272，解得BM ＝3.由勾股定理，得AM ＝52－32＝4，则tan A ＝BM AM ＝34.](2)存在．过点P 作PN ⊥AC 于点N.依题意，得AP ＝CQ ＝5t.∵tan A ＝34，∴AN ＝4t ，PN ＝3t.∴QN ＝AC －AN －CQ ＝9－9t.根据勾股定理得PN 2＋QN 2＝PQ 2.∴S ＝PQ 2＝(3t)2＋(9－9t)2＝90t 2－162t ＋81⎝⎛⎭⎫0＜t ≤95.∵－b 2a ＝1622×90＝910＜95，∴S 最小＝4ac －b 24a ＝4×90×81－16224×90＝8110；(3)①如图1，当点E 在边HG 上时，t 1＝914；图1图29②如图2，当点F在边HG上时，t2＝11.。

中考复习之——三角形与四边形1、三角形与平行四边形联手例1、如图1，在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB 于点F.试判断AF与CE是否相等，并说明理由.解：∵四边形ABCD为平行四边形∴AB=CD，∠A=∠C，∠ADC=∠CBA∵DF平分∠ADC，BE平分∠CBA∴∠ADF=1/2∠ADC=1/2∠CBA=∠CBE在△ADF和△CBE中∠A=∠CAD=BC∠ADF=∠CBE∴△ADF≌△CBE（ASA）∴AF=CE2、三角形与矩形联手例2、如图5，矩形ABCD中，点E是BC上一点，AE＝AD，DF⊥AE于F，连结DE，求证：DF＝DC．证明：∵AE=AD∴∠AED=∠ADE∵AD ‖BC ∴∠CED=∠ADE∴∠CED=∠AED∵∠DFE=∠C=90∠CED=∠AED （已证）DE=DE （公共边）∴△DFE ≌△DCE （AAS ）∴DF=DC例3、如图4所示，四边形ABCD 是矩形，E 是AB 上一点，且DE =AB ，过C 作CF ⊥DE ，垂足为F.（1）猜想：AD 与CF 的大小关系；（2）请证明上面的结论.解： ∵AB 平行DC ∴∠AED=∠EDC∵CF ⊥DE ∴∠DFC=∠DAE又∵DE=AB 且AB=DC ∴DE=DC∵∠AED=∠EDC ∠DAE=∠DFC DE=DC∴△AED 全等于△FCD∴AD=CF例4、如图6，矩形ABCD 中，O 是AC 与BD 的交点，过O 点的直线EF与AB CD ，的延长线分别交于E F ，．△≌△；（1）求证：BOE DOF，，，为顶点的四边形是菱形？证明你（2）当EF与AC满足什么关系时，以A E C F的结论．证明：1、证明：∵矩形ABCD∴OA＝OC，AB∥CD∴∠E＝∠F，∠EBO＝∠FDO∴△BOE≌△DOF （AAS）2、EF⊥AC时，四边形AECF为菱形∵△BOE≌△DOF∴OE＝OF又∵OA＝OC∴平行四边形AECF∵EF⊥AC∴菱形AECF （对角线互相垂直平分的四边形是菱形）例5、在矩形ABCD中，AB=2，AD=3．（1）在边CD上找．一点E，使EB平分∠AEC，并加以说明；（2）若P为BC边上一点，且BP=2CP，连接EP并延长交AB的延长线于F．①求证：点B平分线段AF；②△PAE能否由△PFB绕P点按顺时针方向旋转而得到，若能，加以证明，并求出旋转度数；若不能，请说明理由．解：（1）∵∠AEB=∠BEC=∠ABE∴∠AEB=∠ABEAB=AE=2DE=1(勾股定理计算)∴DE=EC=1E 是DC 的中点（2）∵⊿ECP∽⊿FBP∴EC/BF=PC/PB=1/2∴BF=2点B平分线段AF②由（1）知⊿AED≌⊿BEC⊿ABE 是等边三角形在⊿PEC 中tan∠PEC=√3/3∴∠PEC=30º=∠F∴⊿AEF 是直角三角形∴AF=2AE=2AB3、三角形与正方形联手例6、如图8所示，四边形ABCD是正方形，G是CD边上的一个动点(点G与C、D不重合)，以CG为一边在正方形ABCD外作正方形CEFG，连结BG，DE．我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系：（1）①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系；②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α，得到如图2、如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断．（2）将原题中正方形改为矩形（如图4—6），且AB=a，BC=b，CE=ka，CG=kb (a≠b，k>0)，第(1)题①中得到的结论哪些成立，哪些不成立？若成立，以图5为例简要说明理由．（08年义乌市）（3）在第(2)题图5中，连结DG、BE，且a=3，b=2，k=12，求22BE DG+的值．解：（1）①BG⊥DE，BG=DE；②∵四边形ABCD和四边形CEFG是正方形，∴BC=DC，CG=CE，∠BCD=∠ECG=90°，∴∠BCG=∠DCE，∴△BCG≌△DCE，∴BG=DE，∠CBG=∠CDE，又∵∠CBG+∠BHC=90°，∴∠CDE+∠DHG=90°，∴BG⊥DE．（2）∵AB=a，BC=b，CE=ka，CG=kb，∴BC/DC ＝CG/CE =b/a ，又∵∠BCG=∠DCE，∴△BCG∽△DCE，∴∠CBG=∠CDE，又∵∠CBG+∠BHC=90°，∴∠CDE+∠DHG=90°，∴BG⊥DE．（3）连接BE、DG．根据题意，得AB=3，BC=2，CE=1.5，CG=1，∵BG⊥DE，∠BCD=∠ECG=90°∴BE2+DG2=BO2+OE2+DO2+OG2=BC2+CD2+CE2+CG2=9+4+2.25+ 1=16.25例7、如图9-甲，在△ABC中，∠ACB为锐角．点D为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．解答下列问题：（1）如果AB=AC，∠BAC=90º．①当点D在线段BC上时（与点B不重合），如图9-乙，线段CF、BD之间的位置关系为▲，数量关系为▲．②当点D在线段BC的延长线上时，如图9-丙，①中的结论是否仍然成立，为什么？（2）如果AB≠AC，∠BAC≠90º，点D在线段BC上运动．试探究：当△ABC满足一个什么条件时，CF⊥BC（点C、F重合除外）？画出相应图形，并说明理由．（画图不写作法）（3）若AC＝42BC=3，在（2）的条件下，设正方形ADEF的边DE与线段CF相交于点P，求线段CP长的最大值．解：（1）①CF与BD位置关系是垂直、数量关系是相等；②当点D在BC的延长线上时①的结论仍成立．由正方形ADEF得AD=AF ，∠DAF=90º．∵∠BAC=90º，∴∠DAF=∠BAC ，∴∠DAB=∠FAC，又AB=AC ，∴△DAB≌△FAC ，∴CF=BD∠ACF=∠ABD．∵∠BAC=90º，AB=AC ，∴∠ABC=45º，∴∠ACF=45º，∴∠BCF=∠ACB+∠ACF= 90º．即CF⊥BD（2）画图正确当∠BCA=45º时，CF⊥BD（如图丁）．理由是：过点A作AG⊥AC交BC于点G，∴AC=AG 可证：△GAD≌△CAF ∴∠ACF=∠AGD=45º∠BCF=∠ACB+∠ACF= 90º．即CF⊥BD（3）当具备∠BCA=45º时，过点A作AQ⊥BC交BC的延长线于点Q，（如图戊）∵DE与CF交于点P时，∴此时点D位于线段CQ上，∵∠BCA=45º，可求出AQ= CQ=4．设CD=x ，∴DQ=4―x，容易说明△AQD∽△DCP，∴，∴，．∵0＜x ≤3 ∴当x=2时，CP 有最大值1．4三角形与梯形联手例8、已知：如图11，梯形ABCD 中，AD BC ∥，点E 是CD 的中点，BE 的延长线与AD 的延长线相交于点F ．（1）求证： BCE △和FDE △全等（2）连结BD CF ，，判断四边形BCFD 的形状，并证明你的结论．1、证明：∵AD ∥BC∴∠CFE ＝∠BAE ，∠FCE ＝∠ABE∵E 是BC 的中点∴BE ＝CE∴△ABE ≌△FCE （AAS ）∴AB ＝CF2、菱形ABFC证明：∵AD ∥BC ，AB ＝CF∴平行四边形ABFC∵△ADC 沿AE 折叠至△AEC ，∠D ＝90∴∠AEC ＝∠D ＝90∴AF ⊥BC∴菱形ABFC例9、如图12，在等腰梯形ABCD 中，AD BC ∥，M 是AD 的中点，求证：MB MC ．（1）证明：∵四边形ABCD 是等腰梯形，∴AB=DC ，∠A=∠D ．∵M 是AD 的中点，∴AM=DM ．在△ABM 和△DCM 中，AB ＝DC ∠A ＝∠D AM ＝DM ∴△ABM ≌△DCM （SAS ）．∴MB=MC．例10、如图13所示，已知等腰梯形ABCD中，AD∥BC，AB=DC，AC与BD相交于点O．请在图中找出一对全等的三角形，并加以证明．解：∵ABCD是等腰梯形∴AB=DC ∠ABC=∠DCBBC是公共边∴△ABC≌△DCB(SAS)还有△ABD≌△DCA(SAS)∵AD‖BC ∠ABC=∠DCB∴∠BAD=∠CDAAD是公共边且AB=DC∴△ABD≌△DCA(SAS)例11、已知：如图14，在梯形ABCD中，AD∥BC，BC=DC，CF平分∠BCD，DF∥AB，BF的延长线交DC于点E。