2020高考文科数学 专题5 第3讲 圆锥曲线中的综合问题
- 格式:ppt
- 大小:9.17 MB
- 文档页数:48



高考必考题突破讲座(五)2 21 .已知双曲线C i 与椭圆2x5+y9 = i 有相同的焦点,并且经过点 (1) 求C i 的标准方程;(2) 直线I : y = kx - 1与C i 的左支有两个相异的公共点,求k 的取值范围.2x解析(1)依题意,双曲线C i 的焦点坐标为F i (-4,0), F 2(4,0),设双曲线的标准方程为-2a—y 2=1(a>0,b>0),则 2a =—寸-4]2+〔—= 4,即a = 2,2 2又因为c = 4,所以b 2= c 2— a 2= 12•故双曲线的标准方程为 X4 —占=1.I y = kx — 1, (2)由x 2 y 2得(3 — k 2)x 2 + 2kx — 13= 0,设该方程的两根分别为 x i , X 2,则—L= 1412■ 3— k 2 丰 0,2 2 2△= 4k + 52 3— k = 156 — 48k >0, _ — 2kX i + x2 =2<0 ,3— k—13 x i x 2= 2>0 ,L 3— k椭圆C 交于Eg y i ), Fg y 2)两点. (1)求椭圆C 的标准方程;⑵若直线AE , AF 分别与x 轴正半轴交于 P , Q 两点,求证:|OP|+ |OQ|为定值.解得一冷3<« — 3,故k 的取值范围是2.已知椭圆 C :2 2x y 孑+ J= 1(a>b>0)过点A(2,1),离心率为于,直线y =|x + t (t z 0)与1.-于[汽,解析(1)由题意知a2= b2+ c2, 4尹1= 1,a= 2 . 2,解得b= 2,-c= , 6,2 2所以椭圆C的方程为x+y=8 2y i 一 1 y 2 — 1(2)证明:由题意知,直线 AE : y — 1= (x — 2),直线AF : y — 1 = (x — 2),所以x i — 2X 2 — 2x 2 + 2tx + 2t 2— 4 = 0.当△>0 时,X 1 + X 2=— 2t ,禺比=2t 2— 4,2丿X 1 — 2 X 2 — 2|0P|= 2 — , |OQ|= 2 — ,因为直线y 1— 1 y 2 — 1EF : y = gx + t(t 工 0),联立 2 22 + 与=1,1 1 y = *+1,1 运 X 1+ t -22~X2 + t — 1X 1 —2 所以 |OP|+0Q|= 4 —X 2— 2X 1X 2 + (t — 2]X 1+ X 2 一 4(t — 1)=4 —1 1 2JX 1X 2 + t — 1 X 1 + X 2 + t — 122t — 4+(t — 2\ — 2t 一 4(t — 1)=4— -------------------------------- = 4.4(2『—4 ” *— 1 •一2t )+(t —12故|0P|+ |0Q|为定值.(1) 说明点M 的轨迹是什么曲线并求出它的轨迹方程;(2) 0是坐标原点,直线I : y = kx + 2与点M 的轨迹交于不同的两点 A , B ,求△ A0B 面积的最大值.解析(1p ' x — .2 2+ y 2+" ' x + .2 2+ y 2= 2 , 3 可表示(x , y)与(.2, 0), (—■, 2, 0)的距 离之和等于常数 2 3,由椭圆的定义,可知此点的轨迹为焦点在x 轴上的椭圆,且 a = ,3,2 —X 2c = .2,故轨迹方程为—+ y = 1.3.如果点M(x , y)在运动过程中总满足关系式 (x —』2)2+ y 2+ (x + 2)2+ y2 = 2 3.-2舒 y 2= 1,⑵由y = kx + 2得(1 + 3k 2)x 2 + 12kx + 9 = 0.因为 △= (12k)2 — 36(1 + 3k 2) = 36k 2 —36>0, 2— 12kk >1, X 1 + X 2= 2,1 + 3k9X1X 2= 21 + 3k且点O 到直线l 的距离为d =,|AB| =寸k 2+ 1 凶一X 2|,所以 S = ^|AB| d =舟 x2|x1 — X 2|=寸(X 1 + X 2 j — 4X 1X 2 = ^2 .令 t = p k 2— 1由①②可解得a 2= 4, b 2= 3, 2 2所以椭圆C 的标准方程为X +二=1.y = kx + 2,(2)设直线 l 的方程为 y = kx + 2, A(X 1, y) B(x 2, y 2),由 〔4 1 —16k16kx + 4= 0,因为 △= 16(12k - 3)> 0,所以 k >4,贝U * + x =AOB 为锐角,所以 OA OB >0,即 X 1X 2 + y 『2> 0,所以 X 1X 2 + (k*+ 2)(kX 2+ 2) >0,所以(1 +224 — 16k 2 4 2 1 1k )X 1X 2+ 2k(X 1 + X 2)+ 4> 0,即(1 + k ) + 2k — + 4> 0,解得 k <~.又 k >,所以;4k + 3 4k + 3 3 44< k 2< 3,解得一于< k < —寸或寸< k < 乎所以直线I 的斜率k 的取值范围为 一晋,一12, 3 •5.在平面直角坐标系 XOy 中,过点C(2,0)的直线与抛物线y 2= 4X 相交于A , B 两点, 设 A(X 1, y 1), B(X 2, y 2).(t>0),则 k 2= t 2 + 1,所以 $=寻7 =-6^^23,当且仅当 t =竽,即 k = ±31时,23t纶口成立,此时S 取最大值-^3.4. (2019汕头期中)已知椭圆C: 02 +器=1(a >b >0)的右焦点为 F(1,0),且点P 1, 椭圆C 上,O 为坐标原点.(1)求椭圆C 的标准方程;⑵设过定点T(0,2)的直线I 与椭圆C 交于不同的两点 A , B ,且/ AOB 为锐角,求直线 I 的斜率k 的取值范围.解析⑴由题意得c = 1,所以a 2= b 2 + 1,① 1 9椭圆C 上,所以孑+届=1,②22得(4 k + 3)x +2 2x y+ = 1 ,X 1X 2= —2 •因为/4k + 3 4k + 3又点P(1)求证:y1y2为定值;(2)是否存在平行于y 轴的定直线被以AC 为直径的圆截得的弦长为定值?如果存在, 出该直线方程和弦长;如果不存在,说明理由.my =x — 2,解析 ⑴证明:设直线AB 的方程为my = x — 2,由得y 2— 4my — 8 = 0,所y 2= 4x以y i y 2 = — 8为定值.A 在抛物线上,所以 y 2 = 4x 1,因此以AC 为直径的圆的半径 r = *|AC|= ^^(X 1— 2『+ y 2=g⑵存在定点 D(4,0)满足条件.设 D(t,0), A(X 1, y 1), B(X 2, y 2).则E(x 2,— y 2),设直线x = my + t ,—6mty 1+ y 2= —2 ,3m + 4 T T2且△>0.因为 FE = (X 2 — 1 , — y 2), FA = (X 1— 1 , y”,则由 A , F , E3t 二12y 1y 2= 2 ,⑵设存在直线I : x = a 满足条件,则 AC 的中点E X 1 + 22 ,|AC |=工[X1 - 2 2+ y 1.点V x 2 + 4,又点E 到直线x = a 的距离d =X 1 + 2—a.故i 被圆截得的弦长为2\.■- r— d=2 4x 1+4 -x 2+ 4 — X 1+ 2 — 2a 2= ' — 4 1 — a X 1+ 8a — 4a 2.当 1 — a = 0, 即a = 1时,弦长为定值 2,这时直线方程为 x = 1.6.已知长轴长为4的椭圆* +器=1(a >b >0)过点P%61 ,点F 是椭圆的右焦点. (1)求椭圆方程;(2)是否存在x 轴上的定点 关于x 轴的对称点,且 A , F , D ,使得过D 的直线I由解析(1)由题意知2a = 4,2 2所以a = 2•把点P 的坐标代入 牛+ bj 2= 1,得|+ p= 1,解得b 2= 3•所以椭圆的方程为2 2x y_+ —= 1 4十3l 的方程为 x = my + t ,联立消去 x , 得 (3m 2+ 4)y 2+ 6mt y + 3t 2— 12= 0,所以X 1+ 22 — a2 2、3m + 4三点共线,得(X2—1)y1 + (X1 —1)y2= 0,即(my2+1—1)y1+ (my1 +1—1)y2= 0,即2my1y2 + (t —23t —12 —6mt1)(y i + y2)= 0,所以2m — + (t —1) —r—= 0,解得t= 4,所以存在定点D(4,0)满足条3m3+ 4 3m2+ 4件.2X7.如图,已知椭圆C: y2= 1(a> 1)的上顶点为A,右焦点为F,直线AF与圆M :ax2+ y2—6x—2y+ 7= 0 相切.(1)求椭圆C的方程;⑵若不过点A的动直线I与椭圆C相交于P, Q两点,且APAQ = 0,求证:直线I过定点,并求出该定点N的坐标.A z薦解析(1)将圆M的一般方程x2+ y2—6x—2y+ 7 = 0化为标准方程为(x—3)2+ (y —1)2= 3, 圆M 的圆心为M(3,1),半径为r = .3•由A(0,1), F(c,0)(c=" a2—1)得直线AF : '+ y= 1,即c|3+ c—c|x+ cy—c= 0.由直线AF与圆M相切得一= ' 3.所以c= .2或c=—2(舍去).所以a彳c2+ 12=,3所以椭圆C的方程为% + y2= 1.3f f⑵证明:由AP AQ = 0知AP1AQ,从而直线AP与坐标轴不垂直,由A(0,1)可设直线AP1 x23 26k得(1 + 3k )x + 6kx = 0 ,解得x = 0 或x = — 2 ,1 + 3k的方程为y= kx+ 1,直线AQ的方程为y=—*x+ 1(k^0),将y= kx+ 1代入椭圆C的方程-+ y2= 1并整理, P的坐标为6k2, 1 + 3k6k21 + 3k2+ 1 h- 6k2,1 + 3k2 \1 —3k1 + 3k2,1将上式中的k换成一°得Q6kk2+ 3所以直线I2 2k —3 1 —3k2k + 3 1 + 3k的方程为y=的方程为y 6k +6k6k、k2—3x—k2+3 +兀,化简得直线1的方程为『=k2— 14k x2■.因此直线I过定点N 0,-2.的顶点在圆M : x 4+ y 十 2 上-⑴求椭圆C 的方程;⑵过椭圆的上焦点作相互垂直的弦AB , CD ,求|AB|+|CD|的最小值.解析(1)由题意可知2b = 2, b = 1•又椭圆C 的顶点在圆 M 上,贝U a =■ 2,故椭圆C 的 方程为y + x 2= 1.(2)当直线AB 的斜率不存在或为零时,|AB|+ |CD|= 3 . 2;当直线AB 的斜率存在,且不y = kx + 1,为零时,设直线 AB 的方程为y = kx + 1, A(x 1, y) B(x 2, y 2),联立*;y 52消去y ,总 + x= 1,k 1 整理得(k + 2) x + 2kx — 1 = 0 ,贝U X 1 + x 2 =-匚一 ,=— 一 ,故 |AB| =2k + 1 k彳 9,当 0v * v 1 时,2v — 1— 2 2+ 9 < 所以晋 w |AB|+ |CD|v 32,综上|AB|+ |CD|< 3 2,所以 |AB|+ |CD|的最小值为 8—25& (2019湖南师大附中期中)已知椭圆 k + 2k + 2|CD| =|AB|+ |CD可知,。

2020年高考数学选择、填空压轴题考法深度揭秘专题五、圆锥曲线圆锥曲线的几何性质是圆锥曲线的灵魂,主要包括离心率、范围、对称性、渐近线、准线等性质.这些性质往往与三角形、四边形等几何图形的有关几何性质、几何量结合在一起,是高考命制选择、填空题压轴题的热点,主要考查根据圆锥曲线中的位置、数量关系,确定其标准方程或某些几何性质.考法10 根据位置、数量关系确定方程、几何性质(2012·湖北理,14)如图,双曲线x 2a 2-y 2b 2=1(a ,b >0)的两顶点为A 1,A 2,虚轴两端点为B 1,B 2,两焦点为F 1,F 2.若以A 1A 2为直径的圆内切于菱形F 1B 1F 2B 2,切点分别为A ,B ,C ,D .则(1)双曲线的离心率e =________;(2)菱形F 1B 1F 2B 2的面积S 1与矩形ABCD 的面积S 2的比值S 1S 2=________.【知识揭秘】 揭秘1:计算△OF 1B 2的面积的方式有两种,12|OB 2|·|OF 1|和12|F 1B 2|·d ,由等面积法得a ,c 的关系式;揭秘2:设∠B 2OB =θ,则AB =2a sin θ,BC =2a cos θ,代入sin θ,cos θ求出S 2.【思维揭秘】 解答题(1)可利用△OF 1B 2的面积求解;本题(2)中可将所求面积的比值转化成离心率的关系.【解析揭秘】 (1)由题意知,在Rt △F 1OB 2中,OB ⊥F 1B 2且OF 1=c ,OB 2=b ,OB =a .∵|F 1B 2|·|OB |=|OF 1|·|OB 2|,∴a b 2+c 2=bc ,∴a 2(b 2+c 2)=b 2c 2, ∴b 2a 2+c 2a 2=b 2a 2·c 2a 2, ∴e 2-1+e 2=(e 2-1)e 2, 即e 4-3e 2+1=0, ∴e 2=3±52,∴e =5±12.∵e >1,∴e =5+12.(2)记∠B 2OB =θ,则AB =2a sin θ,BC =2a cos θ,其中sin θ=a c ,cos θ=ab ,∴S 2=|AB ||BC |=4a 4bc .又∵S 1=2bc , ∴S 1S 2=2bc 4a 4bc=12⎝ ⎛⎭⎪⎫b a 2·⎝ ⎛⎭⎪⎫c a 2=12(e 2-1)e 2=12×⎝ ⎛⎭⎪⎫3+52-1×3+52=5+22.【答案】 (1)1+52 (2)2+521.(2016·四川成都高三一模,10)过双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左顶点A 作斜率为1的直线,该直线与双曲线的两条渐近线的交点分别为B ,C .若AB→=12BC →,则双曲线的离心率是( ) A. 2 B. 3 C. 5 D.101.C 直线l :y =x +a 与渐近线l 1:bx -ay =0交于C ⎝ ⎛⎭⎪⎫a 2b -a ,ab b -a ,l 与渐近线l 2:bx +ay =0交于B ⎝ ⎛⎭⎪⎫-a 2b +a ,ab b +a .∵A (-a ,0),AB→=12BC →,∴⎝ ⎛⎭⎪⎫-a 2b +a +a ,ab b +a =12⎝ ⎛⎭⎪⎫a 2b -a +a 2b +a ,ab b -a -ab b +a , ∴ab b +a =12⎝ ⎛⎭⎪⎫abb -a -ab b +a . ∴b =2a ,∴c 2-a 2=4a 2,即c 2=5a 2, ∴e 2=5,∴e = 5.2.(2015·重庆理,10)设双曲线x 2a 2-y 2b 2=1(a >0,b >0)的右焦点为F ,右顶点为A ,过F 作AF 的垂线,垂线与双曲线交于B ,C 两点,过B ,C 分别作AC ,AB 的垂线交于点D .若D 到直线BC 的距离小于a +a 2+b 2,则该双曲线的渐近线斜率的取值范围是( )A .(-1,0)∪(0,1)B .(-∞,-1)∪(1,+∞)C .(-2,0)∪(0,2)D .(-∞,-2)∪(2,+∞)2.A 方法一:由题意得A (a ,0),B ⎝ ⎛⎭⎪⎫c ,b 2a ,C ⎝ ⎛⎭⎪⎫c ,-b 2a ,由双曲线的对称性知D 在x 轴上,设D (x ,0),由BD ⊥AC 得b 2a -0c -x ·b 2aa -c =-1,解得c -x =b 4a 2(c -a ).画图可知x <0,所以D 到BC 的距离为c -x =b 4a 2(c -a )<a +a 2+b 2=a +c ,所以b 4a 2<c 2-a 2=b 2⇒b 2a 2<1⇒0<b a <1或-1<ba <0,因此渐近线斜率的取值范围是(-1,0)∪(0,1),选A.方法二:如图,由x 2a 2-y 2b 2=1可知A (a ,0),F (c ,0).易得B ⎝ ⎛⎭⎪⎫c ,b 2a ,C ⎝ ⎛⎭⎪⎫c ,-b 2a .∵k AB =b 2a c -a =b 2a (c -a ),∴k CD =a (a -c )b 2.∵k AC =b 2a a -c =b 2a (a -c ),∴k BD =-a (a -c )b 2.∴l BD :y -b 2a =-a (a -c )b 2(x -c ),即y =-a (a -c )b 2x +ac (a -c )b 2+b 2a ,l CD :y +b 2a =a (a -c )b 2 (x -c ),即y =a (a -c )b 2x x -ac (a -c )b 2-b 2a ,∴x D =c +b 4a 2(a -c ).∴点D 到BC 的距离为⎪⎪⎪⎪⎪⎪b 4a 2(a -c ).∴b 4a 2(c -a )<a +a 2+b 2=a +c , ∴b 4<a 2(c 2-a 2)=a 2b 2,∴a 2>b 2, ∴0<b 2a 2<1, ∴0<b a <1或-1<b a <0.因此渐近线斜率的取值范围是(-1,0)∪(0,1).3.(2016·江西南昌二模,16)过原点的直线l 与双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右两支分别相交于A ,B 两点,F (-3,0)是双曲线C 的左焦点.若|F A |+|FB |=4,F A →·FB→=0,则双曲线C 的方程是________.3.【解析】 如图所示,设双曲线的右焦点为F 2(3,0),连接F 2A ,F 2B ,由双曲线的对称性和F A →·FB →=0知四边形AFBF 2为矩形.由|F A |+|FB |=4得|F A |+|F 2A |=4,又因为|F A |-|F 2A |=2a ,所以|F A |=2+a ,|F 2A |=2-a .由|F 2A |2+|F A |2=|FF 2|2得(2-a )2+(2+a )2=(23)2,解得a 2=2,b 2=1,所以双曲线的方程为x22-y 2=1.【答案】 x 22-y 2=1考法11 根据几何性质求某些量的值、范围(最值)(2014·四川理,10)已知F 是抛物线y 2=x 的焦点,点A ,B 在该抛物线上且位于x 轴的两侧,OA →·OB →=2(其中O 为坐标原点),则△ABO 与△AFO 面积之和的最小值是( )A .2B .3 C.1728 D.10【知识揭秘】 揭秘1:由OA →·OB →=2得x 1x 2+y 1y 2=2;揭秘2:直线AB 的方程为x =ny +2,可得直线AB 过点(2,0);揭秘3:△ABO 的面积为y 1-y 2,△AFO 的面积为18y 1.【思维揭秘】 设出直线AB 的方程及点A ,B 的坐标(x 1,y 1),(x 2,y 2),由OA →·OB →=2结合抛物线方程得y 1y 2=-2,用分割法表示出△ABO 的面积,将S △ABO +S △AFO 表示为某一变量的函数,选择适当方法求其最值.【解析揭秘】 设直线AB 的方程为x =ny +m (如图), A (x 1,y 1),B (x 2,y 2).∵OA →·OB →=2,∴x 1x 2+y 1y 2=2.又y 21=x 1,y 22=x 2,∴y 1y 2=-2.联立⎩⎨⎧y 2=x ,x =ny +m 得y 2-ny -m =0,∴y 1y 2=-m =-2,∴m =2,即AB 与x 轴的交点M (2,0).又S △ABO =S △AMO +S △BMO =12|OM ||y 1|+12|OM ||y 2|=y 1-y 2, S △AFO =12|OF |·|y 1|=18y 1, ∴S △ABO +S △AFO =y 1-y 2+18y 1 =98y 1+2y 1≥298y 1·2y 1=3,当且仅当y 1=43时,等号成立. 【答案】 B1.(2016·河北石家庄二模,12)设抛物线C :y 2=4x 的焦点为F ,过F 的直线l 与抛物线交于A ,B 两点,M 为抛物线C 的准线与x 轴的交点,若tan ∠AMB =22,则|AB |=( )A .4B .8C .3 2D .101.B 如图所示,设l :x =my +1,A (x 1,y 1),B (x 2,y 2).由⎩⎨⎧y 2=4x ,x =my +1,得y 2-4my -4=0,∴y 1+y 2=4m ,y 1y 2=-4,x 1x 2=y 214·y 224=1,x 1+x 2=m (y 1+y 2)+2=4m 2+2.又tan ∠AMB =tan(∠AMF +∠BMF )=22,∴y 1x 1+1+-y 2x 2+11-y 1x 1+1·-y 2x 2+1=22,即y 1(my 2+2)-y 2(my 1+2)(x 1+1)(x 2+1)+y 1y 2=22,得y 1-y 2=42m 2,∴4m 2+1=42m 2,解得m 2=1,∴|AB |=|AF |+|BF |=x 1+1+x 2+1=4m 2+4=8,故选B.思路点拨:利用抛物线的定义可解决两类问题:(1)轨迹问题,用抛物线的定义可以确定动点与定点、定直线的距离有关的轨迹是否为抛物线;(2)距离问题,涉及抛物线上的点到焦点的距离、到准线的距离问题时,注意两者之间的转化在解题中的应用.2.(2016·河南洛阳三模,11)设P 是双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)右支上的任意一点,已知A (a ,b )和B (a ,-b ).若OP →=λOA →+μOB →(O 为坐标原点),则λ2+μ2的最小值为( )A.14abB.14C.12abD.122.D 利用坐标运算求解点P 的坐标,结合基本不等式求解.由题意可得OP →=(aλ+aμ,bλ-bμ),又点P (aλ+aμ,bλ-bμ)在双曲线C 上,得(λ+μ)2-(λ-μ)2=1,4λμ=1,λμ=14,则λ2+μ2=≥2λμ=12,当且仅当λ=μ=12时取等号,所以λ2+μ2的最小值为12,故选D.。
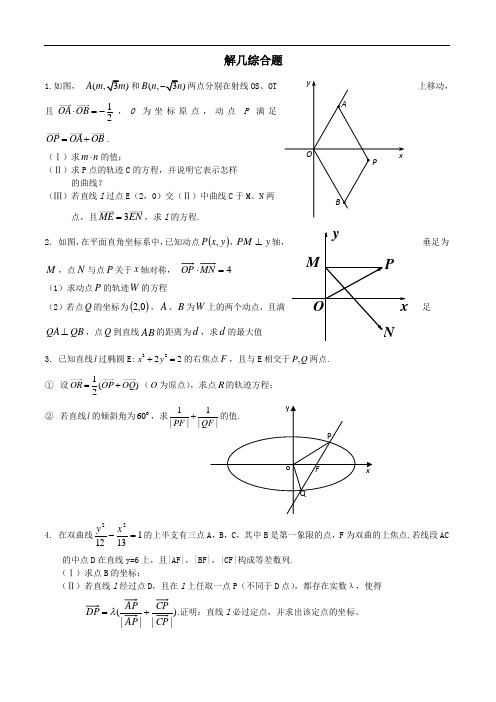
解几综合题1.如图,()A m 和(,)B n 两点分别在射线OS 、OT 上移动,且12OA OB ⋅=-,O 为坐标原点,动点P 满足OP OA OB =+.(Ⅰ)求m n ⋅的值;(Ⅱ)求P 点的轨迹C 的方程,并说明它表示怎样的曲线?(Ⅲ)若直线l 过点E (2,0)交(Ⅱ)中曲线C 于M 、N 两点,且3ME EN =,求l 的方程.2. 如图,在平面直角坐标系中,已知动点()y x P ,,y PM ⊥轴,垂足为M ,点N 与点P 关于x 轴对称, 4=⋅MN OP(1)求动点P 的轨迹W 的方程(2)若点Q 的坐标为()0,2,A 、B 为W 上的两个动点,且满足QB QA ⊥,点Q 到直线AB 的距离为d ,求d 的最大值3. 已知直线l 过椭圆E:2222x y +=的右焦点F ,且与E 相交于,P Q 两点. ① 设1()2OR OP OQ =+(O 为原点),求点R 的轨迹方程;② 若直线l 的倾斜角为060,求1||PF4. 在双曲线1131222=-x y 的上半支有三点A ,B ,C ,其中B 是第一象限的点,F 为双曲的上焦点.若线段AC 的中点D 在直线y=6上,且|AF|,|BF|,|CF|构成等差数列. (Ⅰ)求点B 的坐标;(Ⅱ)若直线l 经过点D ,且在l 上任取一点P (不同于D 点),都存在实数λ,使得 ||||(CP AP +=λ证明:直线l 必过定点,并求出该定点的坐标。
5. 如图,椭圆两焦点F 1、F 2与短轴两端B 1、B 2正好是正方形的四个顶点,且焦点到椭圆上一点最近距离为.12-(I )求椭圆的标准方程;(II )过D(0,2)的直线与椭圆交于不同的两点M 、N ,且M 在D 、N 之间,设λ=||DN DM ,求λ的取值范围.6. 已知F 1、F 2分别是椭圆)0,0(12222>>=+b a by a x 的左、右焦点,其左准线与x 轴相交于点N ,并且满足,.2||,221121==F F NF F F (1)求此椭圆的方程;(2)设A 、B 是这个椭圆上的两点,并且满足]31,51[,∈=λλ当NB NA 时,求直线AB 的斜率的取值范围.7. 已知O 为坐标原点,点E 、F 的坐标分别为(-1,0)、(1,0),动点A 、M 、N 满足||||AE m EF =(1m >),0MN AF =⋅,1()2ON OA OF =+,//AM ME .(Ⅰ)求点M 的轨迹W 的方程; (Ⅱ)点0(,)2mP y 在轨迹W 上,直线PF 交轨迹W 于点Q ,且PF FQ λ=,若12λ≤≤,求实数m 的范围.8. 已知点A (-1,0),B (1,-1)和抛物线.x y C 4:2=,O 为坐标原点,过点A 的动直线l 交抛物线C 于M 、P ,直线MB 交抛物线C 于另一点Q ,如图.(I )若△POM 的面积为25,求向量OM 与OP 的夹角; (II )试探求点O 到直线PQ 的距离是否存在最大值?若存在,求出这个最大值;若不存在,说明理由.9. 设不等式组⎩⎨⎧x +y >0,x -y >0表示的平面区域为D .区域D 内的动点P 到直线x +y =0和直线x -y =0的距离之积为1.记点P 的轨迹为曲线C . (Ⅰ)求曲线C 的方程;(Ⅱ)过点F (2,0)的直线与曲线C 交于A ,B 两点.若以线段AB 为直径的圆与y 轴相切,求线段AB 的长.10. 如图,在△OSF 中,c OF a OS OSF ==︒=∠,,90(c a ,均为正常数),E 、P 是平面OSF内的动点,且满足0=⋅OF SE ,),(R ∈=λλ向量PE c PF a +与PE c PF a -垂 直。

2020年高考文科数学一轮复习大题篇—圆锥曲线综合问题【归类解析】题型一 范围问题【解题指导】 解决圆锥曲线中的取值范围问题应考虑的五个方面(1)利用圆锥曲线的几何性质或判别式构造不等关系,从而确定参数的取值范围.(2)利用已知参数的范围,求新参数的范围,解这类问题的核心是建立两个参数之间的等量关系.(3)利用隐含的不等关系建立不等式,从而求出参数的取值范围.(4)利用已知的不等关系构造不等式,从而求出参数的取值范围.(5)利用求函数的值域的方法将待求量表示为其他变量的函数,求其值域,从而确定参数的取值范围.【例】已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)与双曲线x 23-y 2=1的离心率互为倒数,且直线x -y -2=0经过椭圆的右顶点.(1)求椭圆C 的标准方程;(2)设不过原点O 的直线与椭圆C 交于M ,N 两点,且直线OM ,MN ,ON 的斜率依次成等比数列,求△OMN 面积的取值范围.【解】 (1)∵双曲线的离心率为233, ∴椭圆的离心率e =c a =32. 又∵直线x -y -2=0经过椭圆的右顶点,∴右顶点为点(2,0),即a =2,c =3,b =1,∴椭圆方程为x 24+y 2=1. (2)由题意可设直线的方程为y =kx +m (k ≠0,m ≠0),M (x 1,y 1),N (x 2,y 2).联立⎩⎪⎨⎪⎧y =kx +m ,x 24+y 2=1, 消去y ,并整理得(1+4k 2)x 2+8kmx +4(m 2-1)=0,则x 1+x 2=-8km 1+4k 2,x 1x 2=4m 2-11+4k 2, 于是y 1y 2=(kx 1+m )(kx 2+m )=k 2x 1x 2+km (x 1+x 2)+m 2.又直线OM ,MN ,ON 的斜率依次成等比数列,故y 1x 1·y 2x 2=k 2x 1x 2+km x 1+x 2+m 2x 1x 2=k 2, 则-8k 2m 21+4k 2+m 2=0. 由m ≠0得k 2=14,解得k =±12. 又由Δ=64k 2m 2-16(1+4k 2)(m 2-1)=16(4k 2-m 2+1)>0,得0<m 2<2,显然m 2≠1(否则x 1x 2=0,x 1,x 2中至少有一个为0,直线OM ,ON 中至少有一个斜率不存在,与已知矛盾).设原点O 到直线的距离为d ,则S △OMN =12|MN |d =12·1+k 2·|x 1-x 2|·|m |1+k 2故由m 的取值范围可得△OMN 面积的取值范围为(0,1).【训练】如图,已知点P 是y 轴左侧(不含y 轴)一点,抛物线C :y 2=4x 上存在不同的两点A ,B 满足P A ,PB 的中点均在C 上.(1)设AB 中点为M ,证明:PM 垂直于y 轴; (2)若P 是半椭圆x 2+y 24=1(x <0)上的动点,求△P AB 面积的取值范围. (1)【证明】 设P (x 0,y 0),A ⎝⎛⎭⎫14y 21,y 1,B ⎝⎛⎭⎫14y 22,y 2. 因为P A ,PB 的中点在抛物线上,所以y 1,y 2为方程⎝⎛⎭⎫y +y 022=4·14y 2+x 02,即y 2-2y 0y +8x 0-y 20=0的两个不同的实根.所以y 1+y 2=2y 0,所以PM 垂直于y 轴.(2)【解】 由(1)可知⎩⎪⎨⎪⎧y 1+y 2=2y 0,y 1y 2=8x 0-y 20,所以|PM |=18(y 21+y 22)-x 0=34y 20-3x 0, |y 1-y 2|=22y 20-4x 0. 所以△P AB 的面积S △P AB =12|PM |·|y 1-y 2|)322004y x -.因为x 20+y 204=1(-1≤x 0<0), 所以y 20-4x 0=-4x 20-4x 0+4∈[4,5],所以△P AB 面积的取值范围是⎣⎡⎦⎤62,15104. 题型二 最值问题1 利用三角函数有界性求最值【解题指导】 处理圆锥曲线最值问题的求解方法圆锥曲线中的最值问题类型较多,解法灵活多变,但总体上主要有两种方法:一是利用几何法,即通过利用曲线的定义、几何性质以及平面几何中的定理、性质等进行求解;二是利用代数法,即把要求最值的几何量或代数表达式表示为某个(些)参数的函数(解析式),然后利用函数方法、不等式方法等进行求解.【例】过抛物线y 2=4x 的焦点F 的直线交抛物线于A ,B 两点,点O 是坐标原点,则|AF |·|BF |的最小值是【解】 设直线AB 的倾斜角为θ,可得|AF |=21-cos θ,|BF |=21+cos θ, 则|AF |·|BF |=21-cos θ×21+cos θ=4sin 2θ≥4. 2 数形结合利用几何性质求最值【例】在平面直角坐标系xOy 中,P 为双曲线x 2-y 2=1右支上的一个动点.若点P 到直线x -y +1=0的距离大于c 恒成立,求实数c 的最大值为。
【2020届】高考数学圆锥曲线专题复习:圆锥曲线综合题答案解几综合题答案1.解:(Ⅰ)由已知得()(,) 11 22OA OB m n mn ?=?=-=-分14m n ∴?= …………4分(Ⅱ)设P 点坐标为(x ,y )(x >0),由OP OA OB =+得(,)()(,)x y m n =+())m n m n =+- …………5分∴)x m ny m n =+=-?? 消去m ,n 可得2243y x mn -=,又因14mn = 8分∴ P 点的轨迹方程为221(0)3y x x -=>它表示以坐标原点为中心,焦点在x 轴上,且实轴长为2,焦距为4的双曲线2213y x -=的右支…………9分(Ⅲ)设直线l 的方程为2x ty =+,将其代入C 的方程得 223(2)3ty y +-=即 22(31)1290t y ty -++=易知2(31)0t -≠(否则,直线l的斜率为,它与渐近线平行,不符合题意)又22214436(31)36(1)0t t t ?=--=+>设1122(,),(,)M x y N x y ,则121222129,3131t y y y y t t -+==--∵ l 与C 的两个交点,M N 在y 轴的右侧12122121222222(2)(2)2()491224313134031x x ty ty t y y t y y t t t t t t t =++=+++-=?+?+--+=->-∴ 2310t -<,即2103t <<又由 120x x +>同理可得 2103t << …………11分由3ME EN =得1122(2,)3(2,)x y x y --=- ∴121223(2)3x x y y -=-??-=?由122222123231t y y y y y t +=-+=-=--得 22631t y t =-由21222229(3)331y y y y y t =-=-=-得 222331y t =--消去2y 得2222363(31)31t t t =--- 解之得:2115t = ,满足2103t << …………13分故所求直线l 存在,其方程为:15250x y --=或15250x y +-= 2. (I )由已知()y M ,0,()y x N -, 2分则()()422,,22=-=-?=?y x y x y x MN OP ,即12422=-y x 4分(II )设()11,y x A ,()22,y x B ,如图,由QB QA ⊥可得()()()()022,2,221212211=+--=-?-=?y y x x y x y x QB QA 5分①若直线x AB ⊥轴,则21x x =,24||||2121-==x y y此时()()()02422221212121=---=+--x x y y x x ,则0128121=+-x x ,解之得,61=x 或21=x但是若21=x ,则直线AB 过Q 点,不可能有QB QA ⊥所以61=x ,此时Q 点到直线AB 的距离为4 7分②若直线AB 斜率存在,设直线AB 的方程为m kx y +=,则=-+=4222y x m kx y ()042412222=+++-m kmx x k 则()()>+--=?≠-0421241601222222m k m k k ,即>+-≠-024012222k m k又124221--=+k km x x ,12422221-+=k m x x 9分∴()()()22121m x x km x x k m kx m kx y y +++=++=124122124124222222222222222--=--+---+=k m k k m m k k m k k k m k∴()()()()2121221122,2,2y y x x y x y x +--=-?-=?()=+++-=21212142y y x x x x 01241248128124222222222=--+--+-+-+k m k k k k km k m 则012822=++k km m ,可得k m 6-=或k m 2-=若k m 2-=,则直线AB 的方程为()2-=x k y ,此直线过点Q ,这与QB QA ⊥矛盾,舍若k m 6-=,则直线AB 的方程为k kx y 6-=,即06=--k y kx 12分此时若0=k ,则直线AB 的方程为0=y ,显然与QB QA ⊥矛盾,故0≠k ∴41141|4|22<+=+-=k k k d 13分由①②可得,4max =d 14分3. 解:① 设1122(,),(,),(,)P x y Q x y R x y112211()(,)[(,)(,)]22OR OP OQ x y x y x y =+?=+121222x x x y y y +?=+?=??..........1’由222x x y y +=?+=,易得右焦点(1,0)F ......................2’ 当直线l x ⊥轴时,直线l 的方程是:1x =,根据对称性可知(1,0)R ........3’ 当直线l 的斜率存在时,可设直线l 的方程为(1)y k x =-代入E 有2222(21)4220k x k x k +-+-=2880k ?=+>2122421k x x k +=+....................................................5’于是(,):R x y x =21222221x x k k +=+ (1)y k x =-消去参数k 得2220x y x +-=而(1,0)R 也适上式,故R 的轨迹方程是2220x y x +-=..................8’②设椭圆另一个焦点为'F ,在'PF F ?中0'120,|'|2,PFF F F ∠==设||PF m =,则|'|PF m = 由余弦定理得2220)222cos120m m m =+-??m ?=.............10’同理,在'QF F ?,设||QF n =,则|'|QF m = 也由余弦定理得2220)222cos60n n n =+-??n ?=’于是1111||||PF QF m n +=+=+=..........................14’ 4. 解:(I )设B(x 0,y 0),A(x 1,y 1),C(x 2,y 2)∵双曲线1131222=-x y 的离心率为125,∴F 对应的准线方程为512=y ,由双曲线的定义得|,512|125||,125|512|||11-=∴=-y AF y AF …………(12分)又A 在双曲线的上半支,∴y 1≥12,)4().512(125||),512(125||)3().512(125||201分分 -=-=-=∴y CF y BF y AF∵|AF|,|BF|,|CF|构成等差数列,∴2|BF|=|AF|+|CF|,∴26113126)(21022210==-=+=x x y y y y 得代入,∴点B 的坐标为)6,26(.…………………………(6分)(II )∵在l 上任取一点P (不同于D 点),都存在实数λ,使得(+=λ,∴在∠APC 的角平分线上,………………………………(7分)∵线段AC 的中点为D 点,∴△APC 是等腰三角形,PD 是线段AC 的垂直平分线,………………(8分)∴设直线l 的方程为),2(6212121x x x y y x x y +----=-),(13,11312,11312,)(2621222122221212122212121y y x x x y x y y y x x x y y x x y -=-∴=-=---+---=-∴作差得又,21362121+---=-∴x y y x x y l 的方程为直线………………(11分)故直线l 恒过点(0,225).…………………………(12分) 5. 解:(I )设椭圆的标准方程为12222=+by a x ,因B 1F 1B 2F 2是正方形,所以b=c ,又a 2= b 2+ c 2,所以b a 2=,…………①由于椭圆上的左(右)顶点到左(右)焦点的距离最近,所以12-=-c a ,②由①②知1,2===c b a ,∴椭圆的标准方程为:.1222=+y x (II )当直线的斜率存在,设直线MN 的方程为2+=kx y 解方程组=++=122y x kx y消去.230,034)21(222>>?=+++k kx x k y 得由得设),(),,(2211y x N y x M ,则221214k k x x +-=+……………… ③ .213221k x x +=………………④又因M 在DN 之间,所以DN DM λ=,即212211),2,()2,(x x y x y x λλ=∴-=-,于是λλλλ212212212221)1(,)1(,x x x x x x x x x x =+++=+=,……………⑤ 将③④代入⑤得λλ2222213)1()214(k k k +=++-,整理得.)1(316121,)1(3121162222λλλλ++=+∴+=+k k …………………………8分 .331,34)1(3161,341211,23222<<<+<∴<+<∴>λλλ由此解得kk又.131,10<<∴<<λλ …………………………………………………………10分当直线的斜率不存在时,直线MN 的方程为x 31,0==这时,.31=∴λ ……………………………………………………………………………11分综上所述,λ的取值范围是.1,31??∈λ …………………………………………12分 6. 解:(1)由于2||,221121==F F NF F F ,+===-==∴.,1||1,2||22221221c b a NF caF F c 解得==1222b a ,从而所求椭圆的方程为.1222=+y x (4分)(2)N B A NB NA ,,,∴=λ 三点共线,而点N 的坐标为(-2,0).设直线AB 的方程为)2(+=x k y ,其中k 为直线AB 的斜率,依条件知k ≠0.由=++=12),2(22y x x k y 消去x 得22)21(22=+-y y k ,即.02412222=+-+y k y kk 根据条件可知??≠<+?-=?.0,0128)4(222k kk k 解得.22||0<<="">设),(),,(2211y x B y x A ,则根据韦达定理,得+=+=+.122,1242221221k k y y k k y y 又由),2(),2(,2211y x y x +=+=λλ得=+=+∴.),2(22121y y x x λλ 从而+=+=+.122,124)1(222222k k y k k y λλ 消去.128)1(222+=+k y λλ得(8分)令3151],31,51[,)1()(212≤<≤∈+=λλλλλλφ任取,则22212121)1()1()()(λλλλλφλφ+-+=-.0)11)((2121>--=λλλλ(10分)]31,51[)(是区间λφ∴上的减函数,从而)51()()31(φλφφ≤≤,即536)(316≤≤λφ, 5361283162≤+≤∴k ,解得.22||0,21626221<<≤≤-≤≤-k k k 适合或因此直线AB 的斜率的取值范围是].2 1,62[]62,21[ -- (12分)7. 解:(Ⅰ)∵0MN AF ?=,1()2ON OA OF =+,∴ MN 垂直平分AF .又//AM ME ,∴ 点M 在AE 上,∴ ||||||||2AM ME AE m EF m +===,||||MA MF =,∴ ||||2||ME MF m EF +=>, (4)分∴ 点M 的轨迹W 是以E 、F 为焦点的椭圆,且半长轴a m =,半焦距1c =,∴ 22221b a c m =-=-.∴ 点M 的轨迹W 的方程为222211x y m m +=-(1m >).……………………………6分(Ⅱ)设11(,)Q x y ∵ 0(,)2mP y ,PF FQ λ=,∴ 1011(1),2.m x y y λλ?-=--=? ∴ 1101(1),21.m x y y λλλ?=+-=-??……………………………8分由点P 、Q 均在椭圆W 上,∴ 22220222211,411(1) 1.2(1)y m y m m m λλλ?+=?-+-+=?-?……………………………10分消去0y 并整理,得2211m m m λ-+=-,由221121m m m -+-≤≤及1m >,解得12m <≤.……………………………14分8. 解:(I )设点P y y P y y M ),,4(),,4(222121、M 、A 三点共线,,4,14,4414,2121211222121211=∴+=+--=+=∴y y y y y y y y y y y y k k DM A M 即即………(2分).544212221=+?=?∴y y y y OM …………………………………………………(3分)设∠POM =α,则.5cos ||||=??α.5sin ||||,25=??∴=αS ROM 由此可得tanα=1.……………………(5分)又.45,45),,0(??=∴∈与故向量απα……………………(6分)(II )设点M y y Q ),,4(323、B 、Q 三点共线,,QM BQ k k =∴)9(.04,4))(1(,141,441431312331331233232131233分即即即=+++-=++∴+=-+--=+y y y y y y y y y y y y y y y y y y,0444,4,432322121=+++?∴==y y y y y y y y 即即.(*)04)(43232=+++y y y y ……………………………………(10分))4(4,4442232232232232y x y y y y PQ y y y y y y k PQ-+=-∴+=--=的方程是直线即.4)(,4))((323222322x y y y y y y x y y y y =-+-=+-即……………………(12分)由(*)式,,4)(43232++=-y y y y 代入上式,得).1(4))(4(32-=++x y y y 由此可知直线PQ 过定点E (1,-4).故存在定一点 E (1,-4),使PE ∥.QF …………………………………………(14分)9. (Ⅰ)解:由题意可知,平面区域D 如图阴影所示.设动点P (x ,y ),则|x +y |2?|x -y |2=1,即|x 2-y 2|=2.………………………………4分∵P ∈D .∴x +y >0,x -y >0,即x 2-y 2>0.∴x 2-y 2=2(x >0).即曲线C 的方程为x 22-y 22=1(x >0).…………6分(Ⅱ)解法一:设A (x 1,y 1),B (x 2,y 2),∴以线段AB 为直径的圆的圆心Q (x 1+x 22,y 1+y 22),∵以线段AB 为直径的圆与y 轴相切,∴半径r =12|AB |=x 1+x 22.即|AB |=x 1+x 2.①……………………………………………………………………8分∵曲线C 的方程为x 22-y 22=1(x >0),∴F (2,0)为其焦点,相应的准线方程为x =1,离心率e =2.根据双曲线的定义可得, |AF |x 1-1=|BF |x 2-1=2,∴|AB |=|AF |+|BF |=2(x 1-1)+2(x 2-1)=2(x 1+x 2)-22.②…………………12分由①,②可得,x 1+x 2=2(x 1+x 2)-22.由此可得x 1+x 2=4+22.∴线段AB 的长为4+22.……………………………………………………………14分(Ⅱ)解法二:∵曲线C 的方程为x 22-y 2=1(x >0),∴F (2,0)为其焦点,相应的准线为l :x =1,离心率e =2.分别过A ,B 作AA '⊥l ,BB '⊥l ,垂足分别为A ',B '.设AB 中点Q ,过Q 点作QQ '⊥y 轴,垂足为Q '.由双曲线的定义可得,|AF ||AA '|=|BF ||BB '|=2,∴|AF |=2|AA '|,|BF |=2|BB '|.…………………10分 |AB |=|AF |+|BF |=2(|AA '|+|BB '|) 根据梯形中位线性质可得 |AA '|+|BB '|=2(|QQ '|-1).∴|AB |=2?2(|QQ '|-1).①…………………………12分∵以线段AB 为直径的圆与y 轴相切,∴|QQ '|=12|AB |.②把②代入①得|AB |=22(12|AB |-1),解得|AB |=4+22.……………………………………………………………………14分(Ⅱ)解法三:设A (x 1,y 1),B (x 2,y 2).∵直线AB 过点F (2,0),当AB ⊥x 轴时,|AB |=22,以线段AB 为直径的圆与y 轴相离,不合题意.∴设直线AB 的方程为y =k (x -2).代入双曲线方程x 2-y 2=2得,x 2-k 2(x -2)2=2,即(1-k 2)x 2+4k 2x -(4k 2+2)=0,∵直线与双曲线交于A ,B 两点,∴k ≠±1.∴x 1+x 2=4k 2k 2-1,x 1x 2=4k 2k 2-1.∴|AB |=(x 1-x 2)2+(y 1-y 2)2=(1+k 2)[(x 1+x 2)2-4x 1x 2] =(1+k 2)[? ??4k 2k 2-12-4?4k 2+2k 2-1]……………………………………………………9分∵以线段AB 为直径的圆与y 轴相切,∴圆的半径12|AB |与圆心到y 轴的距离12(x 1+x 2)相等.即12(1+k 2)[? ??4k 2k 2-12-4?4k 2+2k 2-1]=12(x 1+x 2).∴12(1+k 2)[? ??4k 2k 2-12-4?4k 2+2k 2-1]=12?4k 2k 2-1.………………………………………12分化简得k 4 -2k 2-1=0,解得k 2=1+2(k 2=1-2不合,舍去).经检验,当k 2=1+2时,直线与曲线C 有两个不同的交点。
第3讲圆锥曲线中的综合问题求圆锥曲线中的最值范围问题(5年2考)考向1 构造不等式求最值或范围[高考解读]以直线与圆锥曲线的位置关系为载体,融函数与方程,均值不等式、导数于一体,重在考查学生的数学建模、数学运算能力和逻辑推理及等价转化能力.(2019·全国卷Ⅱ)已知点A(-2,0),B(2,0),动点M(x,y)满足直线AM与BM的斜率之积为-错误!.记M的轨迹为曲线C.(1)求C的方程,并说明C是什么曲线;(2)过坐标原点的直线交C于P,Q两点,点P在第一象限,PE⊥x 轴,垂足为E,连接QE并延长交C于点G。
①证明:△PQG是直角三角形;②求△PQG面积的最大值.切入点:(1)由k AM·k BM=-错误!求C的方程,并注意x的范围.(2)①证明k PQ·k PG=-1即可;②建立面积函数,借助不等式求解.[解](1)由题设得错误!·错误!=-错误!,化简得错误!+错误!=1(|x|≠2),所以C为中心在坐标原点,焦点在x轴上的椭圆,不含左、右顶点.(2)①设直线PQ的斜率为k,则其方程为y=kx(k>0).由错误!得x=±错误!。
记u=错误!,则P(u,uk),Q(-u,-uk),E(u,0).于是直线QG的斜率为错误!,方程为y=错误!(x-u).由错误!得(2+k2)x2-2uk2x+k2u2-8=0.设G(x G,y G),则-u和x G是方程①的解,故x G=错误!,由此得y G =错误!。
从而直线PG的斜率为错误!=-错误!。
所以PQ⊥PG,即△PQG是直角三角形.②由①得|PQ|=2u错误!,|PG|=错误!,所以△PQG的面积S=错误!|PQ||PG|=错误!=错误!。
设t=k+错误!,则由k>0得t≥2,当且仅当k=1时取等号.因为S=错误!在[2,+∞)单调递减,所以当t=2,即k=1时,S 取得最大值,最大值为错误!.因此,△PQG面积的最大值为错误!。