图的存储结构算法

数据结构在社交网络分析中的应用社交网络已经成为现代人生活的一部分，人们通过社交网络平台进行交流、分享和获取信息。

这些社交网络平台积累了海量的数据，这些数据需要进行分析来提取有价值的信息，帮助我们更好地理解社交网络中的关系和行为。

数据结构在社交网络分析中起着重要的作用，它提供了一种组织和管理这些数据的方式，使得我们可以更高效地进行分析和挖掘。

一、图（Graph）数据结构：社交网络可以用一个图结构来表示，图由节点和边组成，节点表示社交网络中的个体，边表示个体之间的关系。

在社交网络中，节点可以表示一个人或者一个组织，边表示人与人之间的朋友关系或者组织之间的合作关系。

图数据结构能够帮助我们更好地理解和分析社交网络中的个体和关系。

例如，我们可以使用图算法来发现社交网络中的社群结构，识别核心人物，寻找影响力较大的节点等。

二、栈（Stack）和队列（Queue）数据结构：在社交网络分析中，我们常常需要处理某些社交网络中的事件或行为序列。

栈和队列这两种数据结构能够帮助我们有效地处理这些序列。

例如，我们可以使用栈来保存用户在社交网络中发布的动态，以便进行回溯分析。

队列可以用于管理社交网络中的消息队列，保证消息的顺序性。

三、散列表（Hash Table）数据结构：社交网络中用户的属性和行为丰富多样，例如年龄、性别、兴趣爱好、关注的话题等。

为了高效地找到某个用户的属性信息，我们可以使用散列表这种数据结构。

通过将用户的唯一标识作为键，将属性信息存储在散列表中，可以快速地根据用户标识进行查找和获取。

四、链表（Linked List）数据结构：在社交网络中，我们常常需要处理不同个体之间的关系，例如两个用户之间的好友关系。

链表这种数据结构可以帮助我们有效地存储和管理这些关系。

通过在链表节点中存储关系的相关信息，我们可以轻松地进行关系的添加、删除和修改操作。

五、树（Tree）和堆（Heap）数据结构：社交网络中的一些分析问题可以使用树和堆这两种数据结构解决。

《数据结构》期末考试试卷试题及答案一、选择题（每题5分，共20分）1. 下列哪个不是线性结构？A. 栈B. 队列C. 图D. 数组2. 下列哪个不是栈的基本操作？A. 入栈B. 出栈C. 查找D. 判断栈空3. 下列哪个不是队列的基本操作？A. 入队B. 出队C. 查找D. 判断队列空4. 下列哪个不是图的基本概念？A. 顶点B. 边C. 路径D. 环二、填空题（每题5分，共20分）5. 栈是一种______结构的线性表，队列是一种______结构的线性表。

6. 图的顶点集记为V(G)，边集记为E(G)，则无向图G=(V(G),E(G))，有向图G=(______，______)。

7. 树的根结点的度为______，度为0的结点称为______。

8. 在二叉树中，一个结点的左子结点是指______的结点，右子结点是指______的结点。

三、简答题（每题10分，共30分）9. 简述线性表、栈、队列、图、树、二叉树的基本概念。

10. 简述二叉树的遍历方法。

11. 简述图的存储结构及其特点。

四、算法题（每题15分，共30分）12. 编写一个算法，实现栈的入栈操作。

13. 编写一个算法，实现队列的出队操作。

五、综合题（每题20分，共40分）14. 已知一个无向图G=(V,E)，其中V={1,2,3,4,5}，E={<1,2>,<1,3>,<2,4>,<3,4>,<4,5>}，画出图G，并给出图G的邻接矩阵。

15. 已知一个二叉树，其前序遍历序列为ABDCE，中序遍历序列为DBACE，请画出该二叉树，并给出其后序遍历序列。

答案部分一、选择题答案1. C2. C3. C4. D二、填空题答案5. 后进先出先进先出6. V(G),E(G)7. 0 叶结点8. 左孩子右孩子三、简答题答案9. （1）线性表：一个线性结构，其特点是数据元素之间存在一对一的线性关系。

数据结构的定义数据结构是计算机中存储、组织数据的方式，它定义了数据元素之间的逻辑关系以及如何在计算机中表示这些关系。

提高算法效率合适的数据结构可以显著提高算法的执行效率，降低时间复杂度和空间复杂度。

简化程序设计数据结构为程序设计提供了统一的抽象层，使得程序员可以更加专注于问题本身，而不是底层的数据表示和访问细节。

便于数据管理和维护良好的数据结构设计可以使得数据的管理和维护变得更加方便和高效。

数据结构的定义与重要性线性数据结构中的元素之间存在一对一的关系，如数组、链表、栈和队列等。

线性数据结构非线性数据结构中的元素之间存在一对多或多对多的关系，如树、图等。

非线性数据结构静态数据结构在程序运行期间不会发生改变，如数组、静态链表等。

静态数据结构动态数据结构在程序运行期间可以动态地添加或删除元素，如链表、动态数组等。

动态数据结构数据结构的分类01020304在计算机科学中，数据结构是算法设计和分析的基础，广泛应用于操作系统、编译原理、数据库等领域。

计算机科学在软件工程中，数据结构是软件设计和开发的重要组成部分，用于实现各种软件功能和性能优化。

软件工程在人工智能中，数据结构用于表示和处理各种复杂的数据和知识，如神经网络、决策树等。

人工智能在大数据处理中，数据结构用于高效地存储、管理和分析海量数据，如分布式文件系统、NoSQL 数据库等。

大数据处理数据结构的应用领域0102线性表是具有n个数据元素的有限序列创建、销毁、清空、判空、求长度、获取元素、修改元素、插入元素、删除元素等线性表的定义线性表的基本操作线性表的定义与基本操作03用一段地址连续的存储单元依次存储线性表的数据元素顺序存储结构的定义可以随机存取，即可以直接通过下标访问任意元素；存储密度高，每个节点只存储数据元素顺序存储结构的优点插入和删除操作需要移动大量元素；空间利用率不高，需要提前分配存储空间顺序存储结构的缺点链式存储结构的定义01用一组任意的存储单元存储线性表的数据元素，这组存储单元可以是连续的，也可以是不连续的链式存储结构的优点02插入和删除操作不需要移动大量元素，只需要修改指针；空间利用率高，不需要提前分配存储空间链式存储结构的缺点03不能随机存取，只能通过从头节点开始遍历的方式访问元素；存储密度低，每个节点除了存储数据元素外，还需要存储指向下一个节点的指针0102定义栈（Stack）是一种特殊的线性数据结构，其操作只能在一端（称为栈顶）进行，遵循后进先出（LIFO）的原则。

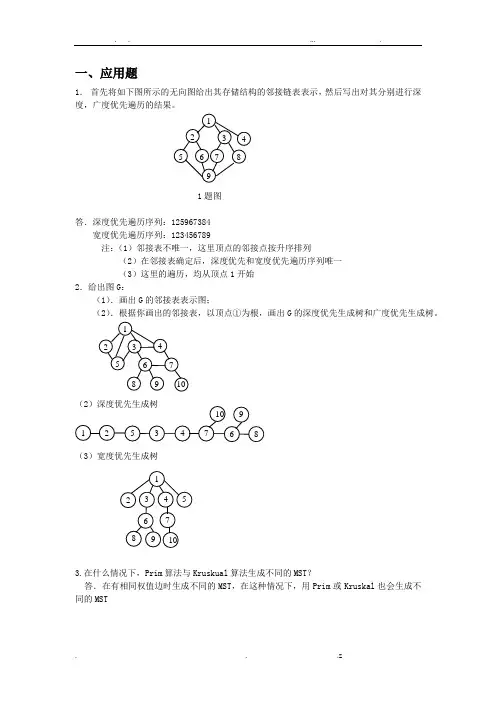
一、应用题1．首先将如下图所示的无向图给出其存储结构的邻接链表表示，然后写出对其分别进行深度，广度优先遍历的结果。

1题图答．深度优先遍历序列：125967384宽度优先遍历序列：123456789注：（1）邻接表不唯一，这里顶点的邻接点按升序排列（2）在邻接表确定后，深度优先和宽度优先遍历序列唯一（3）这里的遍历，均从顶点1开始2．给出图G：（1）．画出G的邻接表表示图；（2）．根据你画出的邻接表，以顶点①为根，画出G的深度优先生成树和广度优先生成树。

（3）宽度优先生成树3.在什么情况下，Prim算法与Kruskual算法生成不同的MST？答．在有相同权值边时生成不同的MST，在这种情况下，用Prim或Kruskal也会生成不同的MST4．已知一个无向图如下图所示，要求分别用Prim 和Kruskal 算法生成最小树（假设以①为起点，试画出构造过程）。

答．Prim 算法构造最小生成树的步骤如24题所示，为节省篇幅，这里仅用Kruskal 算法，构造最小生成树过程如下：（下图也可选(2,4)代替(3,4),(5,6)代替(1,5)）5．G=(V,E)是一个带有权的连通图,则：（1）．请回答什么是G 的最小生成树； （2）．G 为下图所示,请找出G 的所有最小生成树。

28题图答．（1）最小生成树的定义见上面26题 （2）最小生成树有两棵。

（限于篇幅，下面的生成树只给出顶点集合和边集合，边以三元组（Vi,Vj,W ）形式），其中W 代表权值。

V （G ）={1，2，3，4，5} E1(G)={(4，5，2)，（2，5，4），（2，3，5），（1，2，7）}；E2(G)={(4，5，2），（2，4，4），（2，3，5），（1，2，7）}6．请看下边的无向加权图。

（1）．写出它的邻接矩阵。

（2）．按Prim 算法求其最小生成树，并给出构造最小生成树过程中辅助数组的各分量值。

辅助数组各分量值：7．已知世界六大城市为:(Pe)、纽约(N)、巴黎(Pa)、伦敦(L) 、东京(T) 、墨西哥(M),下表给定了这六大城市之间的交通里程:世界六大城市交通里程表(单位:百公里)（1）．画出这六大城市的交通网络图;（2）．画出该图的邻接表表示法;（3）．画出该图按权值递增的顺序来构造的最小(代价)生成树.8．已知顶点1-6和输入边与权值的序列（如右图所示）：每行三个数表示一条边的两个端点和其权值，共11行。

2024年南邮811数据结构考试大纲数据结构是计算机科学中的重要基础课程，它涉及到存储和组织数据的方法，以及在这些数据上进行操作的算法。

南京邮电大学的811数据结构课程旨在培养学生对数据结构的理解和应用能力。

以下是2024年南邮811数据结构考试大纲的详细内容。

一、课程概述1. 课程目标：培养学生掌握数据结构的基本概念、原理和常用算法，能够运用所学知识解决实际问题。

2. 课程内容：线性表、栈和队列、树和二叉树、图、排序算法、查找算法、高级数据结构等。

二、知识要点1. 线性表：顺序表、链表、循环链表、双向链表，线性表的插入、删除、查找等操作。

2. 栈和队列：顺序栈、链栈、顺序队列、链队列，栈和队列的应用、特性及相关算法。

3. 树和二叉树：二叉树的存储结构、遍历算法、线索二叉树、树的遍历和操作等。

4. 图：图的存储结构、图的遍历算法、最小生成树、最短路径等。

5. 排序算法：冒泡排序、选择排序、插入排序、希尔排序、快速排序、归并排序等。

6. 查找算法：顺序查找、二分查找、插值查找、哈希查找、二叉排序树等。

7. 高级数据结构：堆、图的应用、树的应用、哈希表、查找树、红黑树等。

三、能力要求1. 理解数据结构的基本概念、原理和特性，能够分析和解决实际问题。

2. 能够选择合适的数据结构和算法来解决特定的问题，能够评估和比较不同算法的效率。

3. 能够熟练运用编程语言实现各种数据结构和算法。

4. 具备良好的团队合作能力和沟通能力，能够与他人合作解决复杂问题。

四、考试形式1. 笔试：占总成绩的70%，包括选择题、填空题、简答题和编程题。

2. 实验：占总成绩的30%，包括设计和实现一个复杂的数据结构或算法，并进行实验验证和性能分析。

五、参考教材1. 《数据结构（C语言版）》严蔚敏、吴伟民2. 《算法导论》Thomas H. Cormen等六、备考建议1. 认真学习课堂讲授的内容，理解各种数据结构的原理和应用场景。

2. 多做习题和编程实践，加深对知识的理解和掌握。

数据结构与算法实践作业指导书第一章基本概念与算法效率分析 (2)1.1 算法基本概念 (2)1.2 算法效率评价 (2)1.3 时间复杂度分析 (2)1.4 空间复杂度分析 (3)第二章线性表 (3)2.1 线性表的定义与基本操作 (3)2.2 顺序存储结构 (4)2.3 链式存储结构 (4)2.4 线性表的应用实例 (4)第三章栈与队列 (5)3.1 栈的定义与基本操作 (5)3.2 栈的顺序存储结构 (5)3.3 栈的链式存储结构 (5)3.4 队列的定义与基本操作 (6)第四章树与二叉树 (6)4.1 树的定义与基本操作 (6)4.2 二叉树的定义与性质 (6)4.3 二叉树的遍历算法 (7)4.4 线索二叉树 (7)第五章图 (8)5.1 图的定义与基本概念 (8)5.2 图的存储结构 (8)5.3 图的遍历算法 (8)5.4 最短路径算法 (8)第六章排序算法 (9)6.1 排序算法概述 (9)6.2 冒泡排序 (9)6.3 选择排序 (9)6.4 插入排序 (10)第七章查找算法 (10)7.1 查找算法概述 (10)7.2 顺序查找 (10)7.3 二分查找 (11)7.4 哈希查找 (11)第八章动态规划 (12)8.1 动态规划概述 (12)8.2 最长公共子序列 (12)8.3 最小路径和 (12)8.4 最大子段和 (12)第九章贪心算法 (12)9.1 贪心算法概述 (12)9.2 活动选择问题 (13)9.3 背包问题 (13)9.4 最小树问题 (13)第十章分治算法 (13)10.1 分治算法概述 (13)10.2 快速排序 (13)10.2.1 快速排序算法描述 (14)10.2.2 快速排序算法实现 (14)10.3 归并排序 (14)10.3.1 归并排序算法描述 (14)10.3.2 归并排序算法实现 (14)10.4 最大子数组和问题 (15)10.4.1 分治算法求解最大子数组和问题 (15)10.4.2 最大子数组和问题的分治算法实现 (15)第一章基本概念与算法效率分析1.1 算法基本概念算法是计算机科学中一个核心概念，指的是解决问题的一系列明确且有效的步骤。

图1. 填空题⑴设无向图G中顶点数为n，则图G至少有（）条边，至多有（）条边；若G为有向图，则至少有（）条边，至多有（）条边。

【解答】0，n(n-1)/2，0，n(n-1)【分析】图的顶点集合是有穷非空的，而边集可以是空集；边数达到最多的图称为完全图，在完全图中，任意两个顶点之间都存在边。

⑵任何连通图的连通分量只有一个，即是（）。

【解答】其自身⑶图的存储结构主要有两种，分别是（）和（）。

【解答】邻接矩阵，邻接表【分析】这是最常用的两种存储结构，此外，还有十字链表、邻接多重表、边集数组等。

⑷已知无向图G的顶点数为n，边数为e，其邻接表表示的空间复杂度为（）。

【解答】Ｏ(n+e)【分析】在无向图的邻接表中，顶点表有n个结点，边表有2e个结点，共有n+2e个结点，其空间复杂度为Ｏ(n+2e)=Ｏ(n+e)。

⑸已知一个有向图的邻接矩阵表示，计算第j个顶点的入度的方法是（）。

【解答】求第j列的所有元素之和⑹有向图G用邻接矩阵A[n][n]存储，其第i行的所有元素之和等于顶点i的（）。

【解答】出度⑺图的深度优先遍历类似于树的（）遍历，它所用到的数据结构是（）；图的广度优先遍历类似于树的（）遍历，它所用到的数据结构是（）。

【解答】前序，栈，层序，队列⑻对于含有n个顶点e条边的连通图，利用Prim算法求最小生成树的时间复杂度为（），利用Kruskal 算法求最小生成树的时间复杂度为（）。

【解答】Ｏ(n2)，Ｏ(elog2e)【分析】Prim算法采用邻接矩阵做存储结构，适合于求稠密图的最小生成树；Kruskal算法采用边集数组做存储结构，适合于求稀疏图的最小生成树。

⑼如果一个有向图不存在（），则该图的全部顶点可以排列成一个拓扑序列。

【解答】回路⑽在一个有向图中，若存在弧、、，则在其拓扑序列中，顶点vi, vj, vk的相对次序为（）。

【解答】vi, vj, vk【分析】对由顶点vi, vj, vk组成的图进行拓扑排序。

南京信息工程大学2023考研大纲：F18数据结构1500字南京信息工程大学2023考研大纲：F18数据结构1500字南京信息工程大学2023考研大纲中对于F18数据结构的部分，主要包括以下几个方面：线性表、栈和队列、树和二叉树、图、查找和排序。

一、线性表1. 线性表的定义和基本操作：插入、删除、查找、修改2. 顺序存储结构和链式存储结构的实现和应用3. 线性表的应用：串、数组、广义表等二、栈和队列1. 栈的定义和基本操作：进栈、出栈、取栈顶元素2. 栈的应用：表达式求值、递归调用等3. 队列的定义和基本操作：进队列、出队列、取队头元素4. 队列的应用：模拟排队问题、操作系统进程管理等三、树和二叉树1. 树的定义和基本术语：根节点、子节点、叶节点等2. 二叉树的定义和基本操作：插入、删除、遍历（先序、中序、后序）3. 二叉树的表示法：链式存储和顺序存储4. 二叉树的应用：赫夫曼树、AVL树等四、图1. 图的基本概念：顶点、边、度，连通性等2. 图的存储结构：邻接矩阵和邻接表3. 图的遍历：深度优先搜索（DFS）和广度优先搜索（BFS）4. 最小生成树和最短路径算法：Prim算法、Kruskal算法、Dijkstra算法五、查找和排序1. 查找算法：顺序查找、折半查找、哈希查找等2. 排序算法：冒泡排序、选择排序、插入排序、快速排序、归并排序等3. 算法的时间复杂度和空间复杂度分析以上内容是南京信息工程大学2023考研大纲中对于F18数据结构的要求，考生可以按照大纲中的内容进行学习和准备。

对于每个部分，要掌握其基本概念和原理，并能进行相应的实现和应用。

同时，也需要了解算法的时间复杂度和空间复杂度的分析，以便在实际应用中选择合适的算法。

软考⾃查：数据结构与算法基础数据结构与算法基础内容提要数组与矩阵线性表⼴义表树与⼆叉树图排序与查找算法基础及常见的算法数组1. 数组类型：存储地址计算2. ⼀维数组a[n]：a[i]的存储地址为：a+i*len3. ⼆维数组a[m][n]：a[i][j]的存储地址（按⾏存储）为：a+(i*n+j)*lena[i][j]的存储地址（按列存储）为：a+(j*n+i)*len稀疏矩阵例题设有如下所⽰的三⾓矩阵A[0..8,1..8]，将该三⾓矩阵的⾮零元素（即⾏下标不⼩于列下标的所有元素）按⾏优先压缩存储在数组M[1..m]中，则元素A[i,j](0<=i，j<=i)存储在数组M的（A）中。

数据结构的定义1.数据结构的概念2.数据逻辑结构线性结构⾮线性结构（树形结构：⽆环路，图：有环路）线性表的定义1、线性表的概念（a1,a2,...,a3)2、线性表常见的两种存储结构顺序存储结构（顺序表）链式存储结构（链表）线性表顺序表链表单链表循环链表双向链表链表的基本操作单链表删除结点单链表插⼊结点双向链表删除结点双向链表插⼊结点线性表-顺序存储与链式存储对⽐线性表-队列与栈例题输出受限的双端队列是指元素可以从队列的两端输⼊，但只能从队列的⼀端输出，如下图所⽰，若有e1,e2,e3,e4依次进⼊输出受限的双端队列，则得不到输出序列（D）A:e4,e3,e2,e1B:e4,e2,e1.e3C:e4,e3,e1,e2D:e4,e2,e3,e1⼴义表⼴义表是n个表元素组成的有限序列,是线性表的推⼴。

通常⽤递归的形式进⾏定义，记做:LS (a0，a1，....，an)。

注:其中LS是表名，ai是表元素，它可以是表(称做⼦表),也可以是数据元素(称为原⼦)。

其中n是⼴义表的长度(也就是最外层包含的元素个数),n=0的⼴义表为空表;⽽递归定义的重数就是⼴义表的深度,直观地说，就是定义中所含括号的基本运算:取表头head(Ls)和取表尾tail(Ls)。

２００７年６月　Ｊｕｎ．２００７　桂林师范高等专科学校学报　

Ｊｏｕｒｎａｌ　ｏｆ　Ｇｕｉｌｉｎ　Ｎｏｒｍａｌ　Ｃｏｌｌｅｇｅ　第２１卷第２期（总第７０期）　

Ｖｏ１．２１　Ｎｏ．２（Ｓｕｍ　Ｎｏ．７０）　

基于存储结构的Ｄｉｊｋｓｔｒａ算法优化　李　政　（桂林师范高等专科学校数学与计算机科学系，广西桂林５４１００１）　

［摘要］在求解最短路径时经常使用经典的Ｄｉｊｋｓｔｒａ算法，但在实际应用中在计算最短路径长　度时需要进行大量的数据比较，而＇－３图中两顶点之间的距离是ｏ。时，是没有必要进行比较的。本文　从存储结构上讨论如何对Ｄｉｊｋｓｔｒａ算法进行优化，尽量减少数据比较次数。　［关键词］　图；最短路径￣Ｄｉｊｋｓｔｒａ算法；链式存储结构　［中图分类号］Ｏ１５７．６［文献标识码］Ａ［文章编号］１００１—７０７０（２００７）０２－－０１２９—０３　

最短路径算法在电子导航、运输科学、交通旅游　以及电力、通讯等领域有着广泛的应用。Ｄｉｊｋｓｔｒａ算　法是１９５９年由Ｅ．Ｗ．Ｄｉｊｋｓｔｒａ提出的图论中求最短　路径的一个著名的算法，使用其可以求得图中一点到　其他各顶点的最短路径，但在实际应用当中，使用　Ｄｉｊｋｓｔｒａ算法查找最短路径时耗费大量的时间进行　数据的比较，本文对Ｄｉｊｋｓｔｒａ算法进行分析，通过改　变图的存储结构实现减少数据比较的时间，提高算法　的效率达到对其进行优化。　１经典Ｄｉｊｋｓｔｒａ算法简介　１．１　Ｄｉｊｋｓｔｒａ算法的基本思想　首先从起点求出长度最短的一条路径，然后参照　它求出长度次短的一条最短路径，依次类推，直到到　达终点为止。　１．２　Ｄｉｊｋｓｔｒａ算法基本方法　把图中顶点集合Ｖ分成两组，第一组为已求出最　短路径的顶点集合（用Ｓ表示），第二组为其余未确定　最短路径的顶点的集合（用Ｕ表示），按最短路径长　度的递增次序依次把第二组的顶点加入到ｓ中。　具体的算法如下：　（１）初始时，Ｓ只包含出源点，即Ｓ一（ｖ），ｖ的距　离为０。Ｕ包含除Ｖ外的其它顶点，Ｕ中顶点ｕ距离　为：边上的权（若ｖ与ｕ有边＜ｖ，ｕ＞）或ＯＯ（ｕ不是ｖ　的出边邻接点）。　（２）从ｕ中选取一个距离最小的顶点ｋ，把ｋ加入　Ｓ中（该选定的距离就是ｖ到ｋ的最短距离长度）。　（３）以ｋ作为新考虑的中间点，修改ｕ中各顶点　的距离：若从源点ｖ到顶点Ｕ（ｕ∈Ｕ）的距离（经过顶　点ｋ）比原来距离（不经过顶点ｋ）短，则修改顶点ｕ的　距离值，修改后的距离值为顶点ｋ的距离加边＜ｋ，ｕ　＞的权之和。　（４）重复步骤（２）和（３）直到所有的顶点都包在ｓ中。　１．３　Ｄｉｊｋｓｔｒａ算法的缺陷　下ｉｇＮａ３：－个例子说明Ｄｉｊｋｓｔｒａ算法存在的缺陷。　例如：图１所示为一带权图Ｇ一（Ｖ，Ｅ，Ｗ），求从　ｖ　出发到其它各个顶点的最短路径长度。．　

819数据结构考研大纲简介数据结构是计算机科学中非常重要的一门课程，它主要研究数据的存储和组织方式，以及高效地操作和管理数据的算法。

对于考研的计算机科学专业的学生来说，掌握并理解数据结构是非常关键的。

本文将基于819数据结构考研大纲，详细介绍考研所涉及的内容和要求。

1.线性表-顺序存储结构-链式存储结构-线性表的基本操作：插入、删除、查找-线性表的高级操作：合并、拆分-线性表的应用：栈、队列2.树-树的基本概念和术语-二叉树及其性质-遍历二叉树：前序、中序、后序-线索二叉树-树和森林3.图-图的基本概念和术语-图的存储结构：邻接矩阵、邻接表-图的遍历：深度优先搜索、广度优先搜索-最小生成树-最短路径4.排序与查找-内部排序和外部排序-插入排序：直接插入排序、希尔排序-选择排序：简单选择排序、堆排序-交换排序：冒泡排序、快速排序-归并排序-基数排序-顺序查找和二分查找-索引结构和散列表5.动态存储管理-顺序存储管理-链式存储管理-可变长记录的表示和实现-动态存储分配和回收-动态存储管理的应用6.算法设计与分析-算法的基本概念和特性-递归算法-贪心算法-动态规划算法-回溯算法-分支限界算法7.数据结构在算法设计中的应用-栈的应用-队列的应用-树的应用-图的应用-排序和查找的应用8.数据结构的应用领域-数据库系统-操作系统-编译原理-图形图像处理-网络通信总结数据结构是计算机科学中的一门基础课程，通过本文对819数据结构考研大纲进行详细介绍，我们了解到了数据结构的基本概念以及在算法设计和各个应用领域中的重要性。

掌握并深入理解数据结构将对我们的计算机科学研究和实践带来巨大的帮助。

希望本文的内容能帮助考研学生更好地准备数据结构的考试。

数据结构与算法1. 数据结构数据结构是带结构的数据元素的集合。

（结构是指数据元素之间的关系）数据结构包含：逻辑结构：数据之间的逻辑关系物理结构（存储结构）：数据元素及其关系在计算机内部的表示数据的运算和实现2. 逻辑结构线性结构：有且只有一个开始和一个终端结点，并且所有结点最多只有一个直接前驱和一个直接后继。

非线性结构：一个结点可能有多个直接前驱和直接后继；具体有集合结构，树形结构，图状结构。

3. 存储结构顺序存储结构：用一组连续的存储单元依次存储数据元素，数据元素之间的逻辑关系由元素的存储位置来表示。

优点：随机存取；缺点：只能使用相邻的一整块存储单元，可能产生较多外部水片。

链式存储结构：用一组任意的存储单元存储数据元素，数据元素之间的逻辑关系用指针来表示。

优点：不会产生碎片现象，能充分利用所有存储单元；缺点：每个元素因指针而占用额外的存储空间，只能实现顺序存储。

索引存储结构：在存储元素信息的同时，还建立附加的索引表。

优点：检索速度快；缺点：索引表占用额外的存储空间，增加和删除数据会修改索引表，耗时较多。

散列存储结构：根据元素的关键字直接计算出该元素的存储地址。

优点：检索、增加、删除结点操作很快；缺点：可能出现冲突，解决冲突会增加时间和空间开销。

4. 数据类型数据类型是一组性质相同的值的集合，以及定义于这个集合上的一组操作的总称。

在C语言中，声明了某个数据类型的变量，意味着规定了该变量的存储空间大小，以及能够执行的运算。

5. 抽象数据类型（A bstract D ata T ype, ADT）三要素<D, S, P>数据对象数据对象的关系集数据对象的操作集6. 算法算法是对特定问题求解步骤的一种描述，它是指令的有限序列，其中每条指令表示一个或多个操作。

此外算法具有如下5个重要特性：有穷性：一个算法必须总在执行有穷不之后结束，且每一步都可在有穷时间内完成；确定性：算法中每条指令必须有确切的含义，对于相同的输入只得得到相同的输出；可行性：算法中描述的操作都可以通过已经实现的基本运算执行有限次来实现；输入输出7. 算法效率的度量时间复杂度时间复杂度是指算法中基本运算的执行次数的数量级。

图形结构与知识点总结一、引言图形结构是计算机科学中一种重要的数据结构，它是一种通过连接各种数据项来表示抽象实体之间关系的数据结构。

图形结构广泛应用于计算机网络、社交网络、路由算法、图像处理、计算机图形学、人工智能等领域。

在本次总结中，我们将深入探讨图形结构的基本概念、存储表示、图的遍历、最短路径算法、最小生成树算法等知识点，并对相关知识进行系统总结。

二、基本概念1.图形结构的定义图形是一个由结点和边组成的数学模型，它表示了一些对象之间的二元关系。

其中，结点表示对象，边表示对象之间的关系。

图形结构可以分为有向图和无向图。

2.图的术语图的术语包括结点、边、度、路径、环、连通图等。

结点是图形中的基本单位，边表示结点之间的关系，度是结点所连接的边的数量，路径是从一个结点到另一个结点的边的序列，环是起点和终点相同的路径，连通图是图中任意两个结点之间都存在路径的图。

三、存储表示1.邻接矩阵邻接矩阵是一种常用的图形结构存储表示方法。

它使用一个二维数组来表示结点之间的边的关系，其中数组的值表示边的权重或是否存在边。

邻接矩阵适合表示稠密图，但对于稀疏图来说，它会浪费大量的空间。

2.邻接表邻接表是另一种常用的图形结构存储表示方法。

它使用一个数组和一个链表来表示结点之间的边的关系，数组中的元素表示结点，链表中的元素表示结点的邻接结点。

邻接表适合表示稀疏图，但对于稠密图来说，查找邻接结点会消耗较多的时间。

3.其他存储表示方法除了邻接矩阵和邻接表之外，还有其他存储表示方法，如邻接多重表、十字链表等。

这些方法适用于特定类型的图，可以根据具体情况选择合适的存储表示方法。

四、图的遍历1.深度优先搜索（DFS）深度优先搜索是一种图的遍历算法，它从起始结点开始，沿着一条路径一直向下搜索，直到遇到已访问过的结点或者死路为止，然后回溯到最近的一个分支结点继续搜索。

DFS可以用递归或者栈来实现。

2.广度优先搜索（BFS）广度优先搜索是另一种图的遍历算法，它从起始结点开始，一层一层地往外扩展，直到遍历完所有结点。