图形找规律

4-1-2.图形找规律知识点拨找规律是解决数学问题的一种重要的手段，而规律的找寻既需要敏锐的观察力，又需要严密的逻辑推理能力.一般地说，在观察图形变化规律时，应抓住一下几点来考虑问题：⑴图形数量的变化；⑵图形形状的变化；⑶图形大小的变化；⑷图形颜色的变化；⑸图形位置的变化；⑹图形繁简的变化.对于较复杂的图形，也可分为几部分来分别考虑，总而言之，只要全面观察，勤于思考就一定能抓住规律，解决问题.例题精讲模块一、图形规律——数量规律【例1】观察这几个图形的变化规律，在横线上画出适当的图形．【考点】图形找规律【难度】1星【题型】填空【解析】几个图形的边数依次增加，因此横线上应为一个七边形．【答案】七边形【例2】请找出下面哪个图形与其他图形不一样.【考点】图形找规律【难度】1星【题型】填空【解析】这组图形的共同特征是，连接各边上一点，组成一个复合图形.所不同的是，第四个图形是一个六边形，而其它几个都是四边形，这样，只有（4）与其它不一样【答案】（4）【例3】观察图形变化规律，在右边补上一幅，使它成为一个完整系列。

【考点】图形找规律【难度】2星【题型】填空【解析】观察发现，乌龟的顺序是：头、身→一只脚、背上一个点→两只脚、背上两个点→两只脚、一条尾、背上三个点→三只脚、一条尾、背上四个点，根据这个规律，最后一幅图应该是：→四只脚、一条尾、背上五个点.即：【答案】【例4】观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？【考点】图形找规律【难度】2星【题型】填空【解析】横着看，每行圆形的个数一次减少，而三角形的个数依次增加，但每行图形的总个数不变.因为圆形的个数是按4、3、？、1的顺序变化的，显然“？”处应填一个圆形。

【答案】圆形【巩固】观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？【考点】图形找规律【难度】2星【题型】填空【解析】（方法一）横着看，每行圆形的个数一次减少，而三角形的个数依次增加，但每行图形的总个数不变.因为圆形的个数是按5、4、3、？、1的顺序变化的，显然“？”处应填一个圆形.(方法二)竖着看，圆形由左而右依次减少，而三角形由左而右依次增加，圆形按照5、4、？、2、1的顺序变化，也可以看出“？”处应是圆形.【答案】圆形【巩固】观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？？【考点】图形找规律【难度】2星【题型】填空【解析】（方法一）横着看，每行三角形的个数依次减少，而正方形的个数依次增加，但每行图形的总个数不变.因为三角形的个数是按4、3、？、1的顺序变化的，显然“？”处应填一个三角形△.(方法二)竖着看，三角形由左而右依次减少，而正方形由左而右依次增加，三角形按照4、？、2、1的顺序变化，也可以看出“？”处应是三角形△.【答案】△【例5】观察下面的图形，按规律在“？”处填上适当的图形.【考点】图形找规律【难度】2星【题型】填空【解析】本题中，几何图形的变化表现在数量关系上，图中黑三角形的个数从左到右依次增多，从（2）起，每一个格比前面一个格多两个黑三角形，所以，第（4）个方框中应填七个黑三角形.【答案】七个黑三角形【例6】观察图形变化规律，在右边再补上一幅，使它们成为一个完整的系列.【考点】图形找规律【难度】2星【题型】填空【解析】第一格有8个圆圈，第二格有4个圆圈，第三格有2个圆圈，第四格有1个圆圈，第五格有半个圆圈.由此发现，前一格中的图减少一般，正好是后一格的图.所以第六格的图应该是第五格图的一半，即：【答案】【例7】观察下图中的点群，请回答：(1)方框内的点群包含个点；(2)推测第10个点群中包含个点；(3)前10个点群中，所有点的总数是。

幼儿教育图形找规律一、教学内容本节课的教学内容选自幼儿教育教材《图形找规律》一章。

本节课主要通过各种有趣的图形和图案，引导幼儿发现图形的规律，培养幼儿的观察力、想象力和逻辑思维能力。

具体内容包括：1. 基本图形的认识；2. 图形的分类和归纳；3. 图形规律的寻找和应用。

二、教学目标1. 帮助幼儿认识和掌握基本图形，提高幼儿的观察力和识别能力。

2. 培养幼儿通过观察、比较、归纳等方法找出图形规律的能力。

3. 激发幼儿对数学的兴趣，培养幼儿的逻辑思维和创新思维。

三、教学难点与重点重点：1. 幼儿能正确识别和命名基本图形；2. 幼儿能通过观察找出图形的规律。

难点：1. 幼儿对图形规律的理解和应用；2. 幼儿的观察力和逻辑思维能力的培养。

四、教具与学具准备教具：1. 各种形状的卡片；2. 图形规律的示例图；3. 作业纸。

学具：1. 幼儿的画笔和颜料；2. 图形卡片；3. 作业本。

五、教学过程1. 实践情景引入：让幼儿观察教室里的物品，找出形状相同的物品。

2. 基本图形认识：通过展示各种形状的卡片，让幼儿认识和命名基本图形。

3. 图形分类和归纳：让幼儿将图形卡片按照形状分类，并归纳出每种图形的特征。

4. 图形规律寻找：展示图形规律的示例图，引导幼儿观察并找出图形的规律。

5. 随堂练习：让幼儿根据找到的图形规律，自己画出类似的图形。

6. 作业布置：让幼儿根据图形规律，完成作业纸上的题目。

六、板书设计1. 基本图形的名称和特征。

2. 图形规律的示例图。

3. 作业纸上的题目和答案。

七、作业设计作业题目：1. 找出下列图形中，形状相同的一组。

答案：1. 正方形组。

八、课后反思及拓展延伸课后反思：在本节课中，幼儿们对基本图形的认识和图形规律的寻找有了初步的了解。

但在观察力和逻辑思维能力的培养方面，还需要进一步加强。

拓展延伸：可以让幼儿们在家中和家长一起寻找生活中的图形规律，提高幼儿的观察力和逻辑思维能力。

同时，也可以通过阅读相关的数学绘本，让幼儿对图形和规律有更深入的了解。

找规律是解决数学问题的一种重要的手段，而规律的找寻既需要敏锐的观察力，又需要严密的逻辑推理能力.一般地说，在观察图形变化规律时，应抓住一下几点来考虑问题：⑴图形数量的变化； ⑵图形形状的变化； ⑶图形大小的变化； ⑷图形颜色的变化； ⑸图形位置的变化； ⑹图形繁简的变化.对于较复杂的图形，也可分为几部分来分别考虑，总而言之，只要全面观察，勤于思考就一定能抓住规律，解决问题.模块一、图形规律——数量规律【例 1】 观察这几个图形的变化规律，在横线上画出适当的图形．【考点】图形找规律 【难度】1星 【题型】填空【解析】 几个图形的边数依次增加，因此横线上应为一个七边形． 【答案】七边形【例 2】 请找出下面哪个图形与其他图形不一样.（1）（2）（3）（4）（5）【考点】图形找规律 【难度】1星 【题型】填空【解析】 这组图形的共同特征是，连接各边上一点，组成一个复合图形.所不同的是，第四个图形是一个六边形，而其它几个都是四边形，这样，只有（4）与其它不一样【答案】（4）【例 3】 观察图形变化规律，在右边补上一幅，使它成为一个完整系列。

【考点】图形找规律 【难度】2星 【题型】填空例题精讲知识点拨4-1-2.图形找规律【解析】观察发现，乌龟的顺序是：头、身→一只脚、背上一个点→两只脚、背上两个点→两只脚、一条尾、背上三个点→三只脚、一条尾、背上四个点，根据这个规律，最后一幅图应该是：→四只脚、一条尾、背上五个点.即：【答案】【例4】观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？【考点】图形找规律【难度】2星【题型】填空【解析】横着看，每行圆形的个数一次减少，而三角形的个数依次增加，但每行图形的总个数不变.因为圆形的个数是按4、3、？、1的顺序变化的，显然“？”处应填一个圆形。

【答案】圆形【巩固】观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？【考点】图形找规律【难度】2星【题型】填空【解析】（方法一）横着看，每行圆形的个数一次减少，而三角形的个数依次增加，但每行图形的总个数不变.因为圆形的个数是按5、4、3、？、1的顺序变化的，显然“？”处应填一个圆形.(方法二)竖着看，圆形由左而右依次减少，而三角形由左而右依次增加，圆形按照5、4、？、2、1的顺序变化，也可以看出“？”处应是圆形.【答案】圆形【巩固】观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？？【考点】图形找规律【难度】2星【题型】填空【解析】（方法一）横着看，每行三角形的个数依次减少，而正方形的个数依次增加，但每行图形的总个数不变.因为三角形的个数是按4、3、？、1的顺序变化的，显然“？”处应填一个三角形△.(方法二)竖着看，三角形由左而右依次减少，而正方形由左而右依次增加，三角形按照4、？、2、1的顺序变化，也可以看出“？”处应是三角形△.【答案】△【例5】观察下面的图形，按规律在“？”处填上适当的图形.（4）？【考点】图形找规律 【难度】2星 【题型】填空【解析】 本题中，几何图形的变化表现在数量关系上，图中黑三角形的个数从左到右依次增多，从（2）起，每一个格比前面一个格多两个黑三角形，所以，第（4）个方框中应填七个黑三角形.【答案】七个黑三角形【例 6】 观察图形变化规律，在右边再补上一幅，使它们成为一个完整的系列.【考点】图形找规律 【难度】2星 【题型】填空【解析】 第一格有8个圆圈，第二格有4个圆圈，第三格有2个圆圈，第四格有1个圆圈，第五格有半个圆圈.由此发现，前一格中的图减少一般，正好是后一格的图.所以第六格的图应该是第五格图的一半，即：【答案】【例 7】 观察下图中的点群，请回答：(1) 方框内的点群包含 个点；(2) 推测第10个点群中包含 个点；(3)前10个点群中，所有点的总数是 。

【例1】观察下面由点组成的图形（点群），请回答：
（1）方框内的点群包含多少个点？
（2）第（n ）个点群中包含多少个点？
（3）前十个点群中，所有点的总数是多少？
解：（1）前四个点群中包含的点数分别是：1，4，7，10.可以看出，在每相邻的两个数中，后一个数都比前一个数大3。

因为方框内应是第（5）个点群，它的点数应该是10+3=13（个）。

（2）1+3（n -1）=3n -2
（3）前十个点群，所有点的总数是：1+4+7+10+13+16+19+22+25+28=145（个）。

【练习1】（1）如图，是用棋子摆成的图案，摆第1个图案需要7枚棋子，摆第2个图案需要19枚棋子，摆第3个图案需要37枚棋子，按照这样的方式摆下去，则摆第10个图案需要（ ）枚棋子．
（2）为庆祝“六一”儿童节，某幼儿园举行用火柴棒摆“金鱼”比赛．如图所示：
按照上面的规律，摆n 个“金鱼”需用火柴棒的根数为（ A ）
A ．26n +
B ．86n +
C ．44n +
D ．8n
【例2】1=12；1+3=4=22；1+3+5=9=32；1+3+5+7=16=42；…按规律填空：（1）1+3+5+7+9+…+2011= 10062
【练习2】观察下列各式：
22
=⨯+⨯+=
151(11)1005225 22
=⨯+⨯+= 252(21)1005625 22
=⨯+⨯+= 353(31)10051225……。

形状找规律游戏在这个形状找规律游戏中，我们将通过观察图形的变化，寻找出隐藏在背后的规律。

这个游戏既能够增强我们的观察能力，也能锻炼我们的逻辑思维能力。

让我们一起进入这个有趣的世界，寻找规律吧！1. 图形一：△2. 图形二：△ □3. 图形三：△ □ △4. 图形四：△ □ △ □通过观察以上的图形序列，我们可以发现存在以下规律：图形序列中的每个新图形都在上一个图形的基础上添加了一个新的元素。

利用这个规律，我们可以推测下一个图形序列为：5. 图形五：△ □ △ □ △接着观察刚刚推测的图形五，我们可以发现还存在另一种规律：图形序列中的每个新图形都在上一个图形的基础上以相同的方式添加新的元素。

换句话说，新的元素是由之前的元素组成的。

基于这个规律，我们可以继续推测下一个图形序列为：6. 图形六：△ □ △ □ △ □同样地，通过观察图形六，我们可以进一步总结出下一个图形序列的规律为：每个新图形在上一个图形的基础上添加一个新的元素，且新的元素是由之前的元素组成的。

那么，下一个图形序列应该是：7. 图形七：△ □ △ □ △ □ △通过以上的推理过程，可以看出这个形状找规律游戏中的规律是每个新图形在上一个图形的基础上按照一定的模式添加新的元素。

我们可以不断观察并总结规律，进一步推测后续的图形序列。

在这个游戏中，观察能力和逻辑思维是非常重要的。

通过不断观察和总结，我们可以不断提高自己的思考能力，培养出良好的逻辑思维习惯。

同时，这个游戏也可以让我们在娱乐中学习。

通过观察图形的变化，我们能够培养出敏锐的洞察力，从而更好地理解数学等相关科目。

这种将教育和娱乐相结合的方式，可以让学习变得更加有趣和富有成就感。

通过这个形状找规律游戏，我们不仅可以锻炼自己的观察能力和逻辑思维能力，还可以提高自己的数学思维能力。

在日常生活中，我们会面临各种各样的问题，但只要我们能积极思考，利用观察和总结的能力，就能够寻找到解决问题的方法。

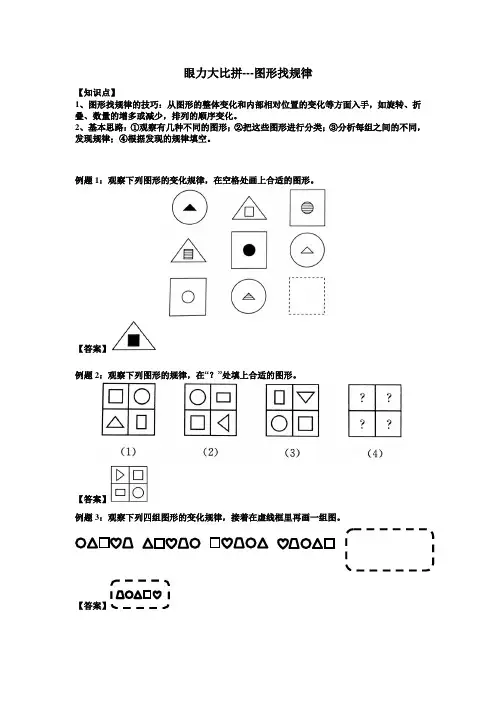
眼力大比拼---图形找规律
【知识点】
1、图形找规律的技巧：从图形的整体变化和内部相对位置的变化等方面入手，如旋转、折叠、数量的增多或减少，排列的顺序变化。

2、基本思路：①观察有几种不同的图形；②把这些图形进行分类；③分析每组之间的不同，发现规律；④根据发现的规律填空。

例题1：观察下列图形的变化规律，在空格处画上合适的图形。

【答案】
例题2：观察下列图形的规律，在“？”处填上合适的图形。

【答案】
例题3：观察下列四组图形的变化规律，接着在虚线框里再画一组图。

【答案】
例题4：找规律，填出“？
变作
变作？
【答案】
【分析】图形的变化规律是，左半部分整体旋转180度到右半部分，右半部分整体翻转到左半部分。

练习1：仔细观察下图的变化规律，请在“？”处添上合适的图形。

【答案】
练习2：观察下图（1）、（2）、（3）的变化规律，画出图（4）。

【答案】（1）（2）（3）（4）
【答案】
练习4：按规律填图。

（1）
☆☆☆
☆☆☆
＃＃☆☆☆
☆☆☆
☆☆＃＃
【答案】（1）（2）☆☆
☆☆＃＃。

【分析】（1）观察这些图形，从左到右，分别是三角形、四边形、五边形，即边数呈递增趋势，每次递增一条边，而且每个图形的每一个角上都有一个点，所以后面一个图形应为六边形，并且六个角上分别有一个黑点；（2）间隔着去看，☆的个数依次减少2个，#的个数始终是2个不变。

数图形—找规律
数出某种图形的个数是一类有趣的图形问题。

由于图形千变万化，错综复杂，所以要想准确地数出其中包含的某种图形的个数，还真需要动点脑筋。

要想有条理、不重复、不遗漏地数出所要图形的个数，最常用的方法就是分类数。

例1数出下图中共有多少条线段。

例2 下列各图形中，三角形的个数各是多少？
例3下列图形中各有多少个三角形？
例4右图中有多少个三角形？
例5数出下页左上图中锐角的个数。

例6在下图中，包含“*”号的长方形和正方形共有多少个？
练习
1.下列图形中各有多少条线段？
2.下列图形中各有多少个三角形？
（3）
3.下列图形中，各有多少个小于180°的角？
（3）
4.下列图形中各有多少个三角形？
A
B
C
D
E
F
A
B
C
D
E
F
F G
H I A
B
C
E
F
D
E
F
D A
B
C O
5.下列图形中各有多少个长方形？
（3）6.下列图形中，包含“*”号的三角形或长方形各有多少？
7.下列图形中，不含“*”号的三角形或长方形各有几个？
8、下图中有多少个正方形？
（1）（2）（3）9、数一数图中有多少个三角形？。

找规律（图形）教学目标1．让学生发现、经历、探究图形和数字简单的排列规律，通过比较，从而理解并掌握找规律的方法，培养学生初步的观察、操作、推理能力。

2．在教学过程中，发展合理推理能力，并合理、清晰的阐述自己的观点。

3．合作中逐步形成评价与反思的意识。

4．培养学生发现和欣赏数学美的意识。

教学内容教科书第88页～89页。

教学设计创设情境，体会规律1．设情引课。

师：你们知道吗，快要过年了，喜欢过六一节吗？小博士班的同学们也在高兴地期盼六一节，他们还要开联欢会呢，这不已经忙着布置开了教室，连小青蛙呱呱和小猪哼哼都赶来帮忙。

（电脑分别出示小猪和小青蛙布置的教室。

）师：他们俩都认为自己布置的漂亮，于是就争吵起来，小朋友，你们认为谁布置的漂亮呢？为什么呢？2．学生讨论。

以四人小组为单位，请小组长领导各组进行讨论，各自发表不同的意见。

3．汇报结果。

请各组派代表来汇报各自不同的想法。

生1：我们认为小青蛙布置的漂亮，因为这样看起来很整齐。

生2：我们认为小猪布置的好，因为花和灯笼放在一起好看。

生3：小青蛙布置的漂亮，因为它的布置是花和花，小旗和小旗，我觉得这样的好。

生4：我们认为小青蛙布置的漂亮，因为小旗是一红一黄，灯笼是一紫一黄，很有顺序。

师：大家有各种不同的意见，那么你们喜欢哪一种就可以选择哪一种。

刚才有人说到小青蛙的布置中小旗是一红一黄一红一黄排列的，像小旗这样一红一黄一红一黄的重复出现，我们就说小旗的排列是有规律的。

4．引入生活。

师：其实规律在我们的日常生活中是会经常遇到的（随着教师的语言电脑出示四幅生活中有规律的图片）。

比如，树枝上叶子的排列，妈妈买的花布上花纹的排列，地面上地板砖的排列以及旅行家旅行时用的热气球上颜色的排列等等都是有规律的。

5．揭示课题。

师：看来规律的用处非常大，今天我们就来学习找规律。

（板书：找规律）引导探究，认识规律1．观察主题图。

师：其实小博士班的同学也比较喜欢小青蛙呱呱布置的教室，请仔细观察（电脑出示书上主题图），说说哪些东西的排列是有规律的？分别是按什么规律排列的？并想个办法让我们一眼就看出这个规律。