下载文档原格式
7.1 磁感应强度、毕奥-萨伐尔定律
一、基本磁现象和本质
1、地球磁场
磁极
磁极
中性区2、磁铁
1820年丹麦奥斯特（1）电流对磁针有作用力
I
（2）磁铁对电流有作用力
（3）电流与电流之间也有相互作用
3、电流的磁效应
总结：磁铁和电流在本质上是否一致？
运动电荷产生磁场
二、毕奥－萨伐尔定律
电流产生磁场，而人体能承受的磁场是有限制的，现实生活中的一些电流产生的磁场：
1.高压线
2.家里的电暖
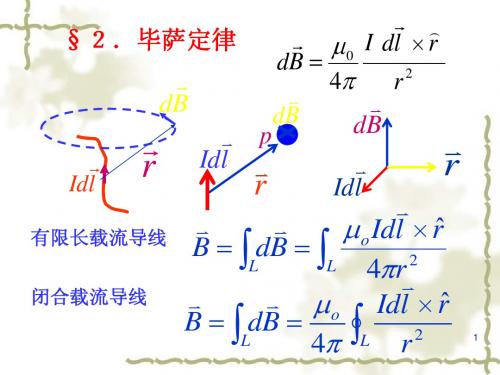
毕奥－萨定律
三、毕奥－萨伐尔定律的运用
B
d r θ P a y 2
θ1
θo l 例 求直线电流外一点的磁场 02d d 4r I l e B r
μπ⨯=取电流元 磁感强度
θπμsin d 4d 20r l I B =大小 方向 ⎰=B B d ⎰=θπμsin d 420r
l I 同向叠加 d I l
θ
sin a r =θactg l -=θ
θ2sin d d a l =⎰=214d sin 0θθπθθμa I B ()210cos cos 4θθπμ-=a I B d r θ P a l I d y 2θ1
θo l ⎰=θπμsin d 4B 20r
l I
()210cos cos 4θθπμ-=a
I B 讨论：1）无限长直电流 a << L 2）半无限长直电流 01=θa
I B πμ20=π
θ=221πθ=π
θ=2a I B πμ40= 3) 延长线上一点 I
P 0ˆd =⨯r l I 0=B r θ P a l I d y 2
θ1θo B
毕奥－萨伐尔定律求解电流磁场的解题思路。
我的电磁学讲义10：磁感应强度毕奥-萨伐尔定律磁感应强度为了描述电场的分布，我们引⼊电场强度⽮量\vec{E}，同样，为了描述磁场的分布，我们也需要引⼊⼀个新的⽮量，这个⽮量就是磁感应强度\vec{B}。
两个电流元的磁相互作⽤⼒满⾜安培定律\begin{equation*} \mathrm d\vec{F}_{12}=k\frac{I_2\mathrm d\vec{l}_2\times (I_1\mathrm d\vec{l}_1\times \hat{r_{12}})}{r_{12}^2}=\frac{\mu_0}{4\pi}\frac{I_2\mathrm d\vec{l}_2\times (I_1\mathrm d\vec{l}_1\times \hat{r_{12}})}{r_{12}^2} \end{equation*}在国际单位制中，\frac{\mu_0}{4\pi}=10^{-7}\mathrm {N/A^2}。
元电流之间的安培⼒的表达式分成两项：\begin{equation*} \mathrm d\vec{F}_{12}=I_2\mathrm d\vec{l}_2\times \mathrm d\vec{B} \end{equation*}\begin{equation*} \mathrm d\vec{B}=\frac{\mu_0}{4\pi}\frac{I_1\mathrm d\vec{l}_1\times \hat{r_{12}}}{r_{12}^2} \end{equation*}把电流元I_2 \mathrm d\vec{l} \_2看做试探电流元，则\mathrm d \vec{B}则为电流元I_1\mathrm d\vec{l} \_1的磁场在电流元I_2\mathrmd\vec{l} \_2所在位置处的磁感应强度。
整个回路1对电流元I_2\mathrm d\vec{l}_2的作⽤⼒为\begin{equation*} \begin{split} \mathrm d\vec{F}_{2}=&\frac{\mu_0}{4\pi}\oint_{L_1}\frac{I_2\mathrm d\vec{l}_2\times (I_1\mathrmd\vec{l}_1\times \hat{r_{12}})}{r_{12}^2}=\frac{\mu_0}{4\pi}I_2d\vec{l}_2\times\mathrm \oint_{L_1}\frac{ I_1\mathrm d\vec{l}_1\times\hat{r_{12}}}{r_{12}^2} \\ =&I_2d\vec{l}_2\times \vec{B} \end{split} \end{equation*}上式中\begin{equation*} \vec{B}=\frac{\mu_0}{4\pi}\oint_{L_1}\frac{I_1\mathrm d\vec{l}_1\times \hat{r_{12}}}{r_{12}^2} \end{equation*}即为闭合回路L_1的磁场在电流元I_2\mathrm d\vec{l}_2所在位置处的磁感应强度。
