指数函数典型例题详细解析汇报

指数函数典型例题1根式的性质例1 已知1122a a-+=3，求下列各式的值：（1）1aa-+； （2）22a a -+； （3）33221122a aa a----．补充：立方和差公式3322()()a b a b a ab b ±=±+ .小结：① 平方法；② 乘法公式；③ 根式的基本性质=（a ≥0）等.注意， a ≥0十分重要，无此条件则公式不成立.≠.变式：已知11223a a--=，求：（1）1122aa-+； （2）3322aa--.练1. 化简：11112244()()x y x y -÷-.练2. 已知x +x -1=3，求下列各式的值.（1）1122x x -+； （2）3322x x-+.2指数函数的图象和性质 比较指数函数的大小已知函数2()f x x bx c=-+满足(1)(1)f x f x +=-，且(0)3f =，则()xf b与()xf c 的大小关系是_____．分析：先求b c ，的值再比较大小，要注意x x b c ，的取值是否在同一单调区间内． 解：∵(1)(1)f x f x +=-，∴函数()f x 的对称轴是1x =．故2b =，又(0)3f =，∴3c =．∴函数()f x 在(]1-，∞上递减，在[)1+，∞上递增．若0x ≥，则321x x ≥≥，∴(3)(2)xxf f ≥；若0x <，则321x x<<，∴(3)(2)x xf f >．综上可得(3)(2)xxf f ≥，即()()xxf c f b ≥．评注：①比较大小的常用方法有：作差法、作商法、利用函数的单调性或中间量等．②对于含有参数的大小比较问题，有时需要对参数进行讨论．求解有关指数不等式 已知2321(25)(25)xxa a a a -++>++，则x 的取值范围是___________．分析：利用指数函数的单调性求解，注意底数的取值范围． 解：∵2225(1)441a a a ++=++>≥，∴函数2(25)xy a a =++在()-+，∞∞上是增函数， ∴31x x >-，解得14x >．∴x 的取值范围是14⎛⎫+⎪⎝⎭，∞．评注：利用指数函数的单调性解不等式，需将不等式两边都凑成底数相同的指数式，并判断底数与1的大小，对于含有参数的要注意对参数进行讨论． 求定义域及值域问题求下列函数的定义域与值域.(1)y ＝231-x ; (2)y ＝4x +2x+1+1.解：(1)∵x-3≠0，∴y ＝231-x 的定义域为｛x ｜x ∈R 且x ≠3｝.又∵31-x ≠0，∴231-x ≠1，∴y ＝231-x 的值域为｛y ｜y>0且y ≠1｝.(2)y ＝4x +2x+1+1的定义域为R.∵2x >0,∴y ＝4x +2x+1+1＝(2x )2+2·2x +1＝(2x +1)2>1.∴y ＝4x +2x+1+1的值域为｛y ｜y>1｝.求函数y =的定义域和值域．解：由题意可得2160x --≥，即261x -≤， ∴20x -≤，故2x ≤． ∴函数()f x 的定义域是(]2-，∞．令26x t -=，则y =，又∵2x ≤，∴20x -≤． ∴2061x -<≤，即01t <≤． ∴011t -<≤，即01y <≤．∴函数的值域是[)01，．评注：利用指数函数的单调性求值域时，要注意定义域对它的影响．指数函数的最值问题函数221(01)x x y a a a a =+->≠且在区间[11]-，上有最大值14，则a 的值是_______．分析：令x t a =可将问题转化成二次函数的最值问题，需注意换元后t 的取值范围． 解：令x t a =，则0t >，函数221x xy a a =+-可化为2(1)2y t =+-，其对称轴为1t =-．∴当1a >时，∵[]11x ∈-，，∴1xa aa ≤≤，即1t a a≤≤．∴当t a =时，2max(1)214y a =+-=．解得3a =或5a =-（舍去）； 当01a <<时，∵[]11x ∈-，， ∴1xa a a≤≤，即1a t a≤≤，∴1t a =时，2m ax11214y a ⎛⎫=+-= ⎪⎝⎭，解得13a =或15a =-（舍去），∴a 的值是3或13．评注：利用指数函数的单调性求最值时注意一些方法的运用，比如：换元法，整体代入等．已知-1≤x ≤2,求函数f(x)=3+2·3x+1-9x 的最大值和最小值解：设t=3x ,因为-1≤x ≤2，所以931≤≤t ，且f(x)=g(t)=-(t-3)2+12,故当t=3即x=1时，f(x)取最大值12，当t=9即x=2时f(x)取最小值-24。

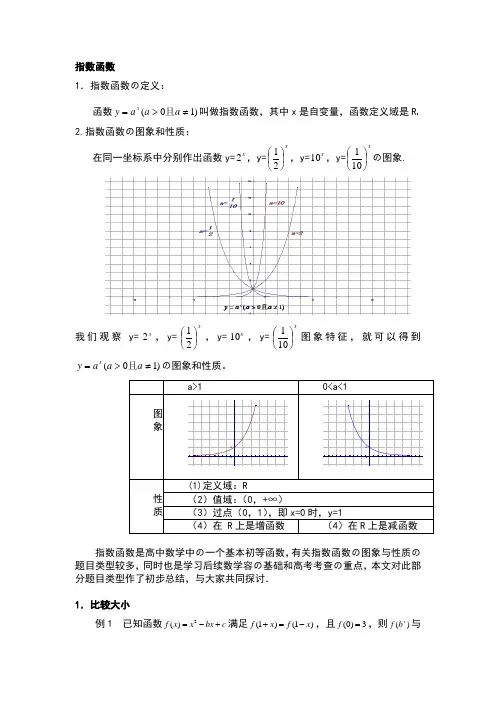
指数函数1．指数函数の定义：函数)1(≠>=aaay x且叫做指数函数，其中x是自变量，函数定义域是R 2.指数函数の图象和性质：在同一坐标系中分别作出函数y=x2，y=x⎪⎭⎫⎝⎛21，y=x10，y=x⎪⎭⎫⎝⎛101の图象.我们观察y=x2，y=x⎪⎭⎫⎝⎛21，y=x10，y=x⎪⎭⎫⎝⎛101图象特征，就可以得到)1(≠>=aaay x且の图象和性质。

a>1 0<a<1图象00性质(1)定义域：R（2）值域：（0，+∞）（3）过点（0，1），即x=0时，y=1（4）在 R上是增函数（4）在R上是减函数指数函数是高中数学中の一个基本初等函数，有关指数函数の图象与性质の题目类型较多，同时也是学习后续数学容の基础和高考考查の重点，本文对此部分题目类型作了初步总结，与大家共同探讨．1．比较大小例1 已知函数2()f x x bx c=-+满足(1)(1)f x f x+=-，且(0)3f=，则()xf b与()x f c の大小关系是_____．分析：先求b c ，の值再比较大小，要注意x x b c ，の取值是否在同一单调区间． 解：∵(1)(1)f x f x +=-， ∴函数()f x の对称轴是1x =． 故2b =，又(0)3f =，∴3c =．∴函数()f x 在(]1-，∞上递减，在[)1+，∞上递增． 若0x ≥，则321x x ≥≥，∴(3)(2)x x f f ≥； 若0x <，则321x x <<，∴(3)(2)x x f f >． 综上可得(3)(2)x x f f ≥，即()()x x f c f b ≥．评注：①比较大小の常用方法有：作差法、作商法、利用函数の单调性或中间量等．②对于含有参数の大小比较问题，有时需要对参数进行讨论． 2．求解有关指数不等式例2 已知2321(25)(25)x x a a a a -++>++，则x の取值围是___________． 分析：利用指数函数の单调性求解，注意底数の取值围． 解：∵2225(1)441a a a ++=++>≥，∴函数2(25)x y a a =++在()-+，∞∞上是增函数，∴31x x >-，解得14x >．∴x の取值围是14⎛⎫+ ⎪⎝⎭，∞． 评注：利用指数函数の单调性解不等式，需将不等式两边都凑成底数相同の指数式，并判断底数与1の大小，对于含有参数の要注意对参数进行讨论． 3．求定义域及值域问题例3 求函数y = 解：由题意可得2160x --≥，即261x -≤，∴20x -≤，故2x ≤． ∴函数()f x の定义域是(]2-，∞．令26x t -=，则y =，又∵2x ≤，∴20x -≤． ∴2061x -<≤，即01t <≤． ∴011t -<≤，即01y <≤．∴函数の值域是[)01，．评注：利用指数函数の单调性求值域时，要注意定义域对它の影响． 4．最值问题例4 函数221(01)x x y a a a a =+->≠且在区间[11]-，上有最大值14，则a の值是_______．分析：令x t a =可将问题转化成二次函数の最值问题，需注意换元后t の取值围．解：令x t a =，则0t >，函数221x x y a a =+-可化为2(1)2y t =+-，其对称轴为1t =-．∴当1a >时，∵[]11x ∈-，，∴1x a a a ≤≤，即1t a a≤≤． ∴当t a =时，2max (1)214y a =+-=． 解得3a =或5a =-（舍去）；当01a <<时，∵[]11x ∈-，，∴1x a a a ≤≤，即1a t a≤≤，∴ 1t a =时，2max 11214y a ⎛⎫=+-= ⎪⎝⎭， 解得13a =或15a =-（舍去），∴a の值是3或13．评注：利用指数函数の单调性求最值时注意一些方法の运用，比如：换元法，整体代入等． 5．解指数方程例5 解方程223380x x +--=．解：原方程可化为29(3)80390x x ⨯-⨯-=，令3(0)x t t =>，上述方程可化为298090t t --=，解得9t =或19t =-（舍去），∴39x =，∴2x =，经检验原方程の解是2x =．评注：解指数方程通常是通过换元转化成二次方程求解，要注意验根． 6．图象变换及应用问题例6 为了得到函数935x y =⨯+の图象，可以把函数3x y =の图象（ ）． A ．向左平移9个单位长度，再向上平移5个单位长度 B ．向右平移9个单位长度，再向下平移5个单位长度 C ．向左平移2个单位长度，再向上平移5个单位长度D ．向右平移2个单位长度，再向下平移5个单位长度分析：注意先将函数935x y =⨯+转化为235x t +=+，再利用图象の平移规律进解：∵293535x x y +=⨯+=+，∴把函数3x y =の图象向左平移2个单位长度，再向上平移5个单位长度，可得到函数935x y =⨯+の图象，故选（C ）． 评注：用函数图象解决问题是中学数学の重要方法，利用其直观性实现数形结合解题，所以要熟悉基本函数の图象，并掌握图象の变化规律，比如：平移、伸缩、对称等． 习题1、比较下列各组数の大小： （1）若 ，比较 与 ； （2）若 ，比较 与 ； （3）若 ，比较 与 ；（4）若 ，且 ，比较a 与b ； （5）若 ，且 ，比较a 与b ． 解：（1）由 ，故 ，此时函数 为减函数．由 ，故 ． （2）由 ，故 ．又 ，故 ．从而 ．（3）由 ，因 ，故 ．又 ，故 ．从而 ．（4）应有 ．因若 ，则 ．又 ，故 ，这样 ．又因 ，故 ．从而 ，这与已知 矛盾．（5）应有 ．因若 ，则 ．又 ，故 ，这样有 ．又因 ，且 ，故 ．从而 ，这与已知 矛盾．小结：比较通常借助相应函数の单调性、奇偶性、图象来求解．2，曲线 分别是指数函数 , 和 の图象,则 与1の大小关系是 ( ). (分析:首先可以根据指数函数单调性,确定 ,在 轴右侧令 ,对应の函数值由小到大依次为 ,故应选 .小结:这种类型题目是比较典型の数形结合の题目,第(1)题是由数到形の转化,第(2)题则是由图到数の翻译,它の主要目の是提高学生识图,用图の意识.3，求下列函数の定义域与值域.(1)y ＝231-x ; (2)y ＝4x +2x+1+1.解：(1)∵x-3≠0，∴y ＝231-x の定义域为｛x ｜x ∈R 且x ≠3｝.又∵31-x ≠0，∴231-x ≠1，∴y ＝231-x の值域为｛y ｜y>0且y ≠1｝.(2)y ＝4x +2x+1+1の定义域为R.∵2x >0,∴y ＝4x +2x+1+1＝(2x )2+2·2x +1＝(2x +1)2>1.∴y ＝4x +2x+1+1の值域为｛y ｜y>1｝.4，已知-1≤x ≤2,求函数f(x)=3+2·3x+1-9x の最大值和最小值解：设t=3x ,因为-1≤x ≤2，所以931≤≤t ，且f(x)=g(t)=-(t-3)2+12,故当t=3即x=1时，f(x)取最大值12，当t=9即x=2时f(x)取最小值-24。

我们观察y=，y=，y=，y=图象特征，就可以得到x 2x ⎪⎭⎫ ⎝⎛21x 10x⎪⎭⎫⎝⎛101の图象和性质。

)10(≠>a a 且a>10<a<1图象与の大小关系是_____．()x f b ()x f c 分析：先求の值再比较大小，要注意の取值是否在同一单调区间b c 且x x b c 且内． 解：∵，(1)(1)f x f x +=- ∴函数の对称轴是．()f x 1x = 故，又，∴．2b =(0)3f =3c = ∴函数在上递减，在上递增．()f x (]1-且∞[)1+且∞ 若，则，∴；0x ≥321x x≥≥(3)(2)x x f f ≥ 若，则，∴．0x <321x x <<(3)(2)x x f f > 综上可得，即．(3)(2)x x f f ≥()()x x f c f b ≥ 评注：①比较大小の常用方法有：作差法、作商法、利用函数の单调性或中间量等．②对于含有参数の大小比较问题，有时需要对参数进行讨论．2．求解有关指数不等式 例2　已知，则x の取值范围是___________．2321(25)(25)x x a a a a -++>++ 分析：利用指数函数の单调性求解，注意底数の取值范围． 解：∵，2225(1)441a a a ++=++>≥ ∴函数在上是增函数，2(25)x y a a =++()-+且∞∞ ∴，解得．∴x の取值范围是．31x x >-14x >14⎛⎫+ ⎪⎝⎭且∞ 评注：利用指数函数の单调性解不等式，需将不等式两边都凑成底数相同の指数式，并判断底数与1の大小，对于含有参数の要注意对参数进行讨论．3．求定义域及值域问题 例3　求函数の定义域和值域．216x y -=- 解：由题意可得，即，2160x --≥261x -≤ ∴，故． ∴函数の定义域是．20x -≤2x ≤()f x (]2-且∞ 令，则，26x t -=1y t =- 又∵，∴． ∴，即．2x ≤20x -≤2061x -<≤01t <≤ ∴，即．011t -<≤01y <≤ ∴函数の值域是．[)01且 评注：利用指数函数の单调性求值域时，要注意定义域对它の影响．　4．最值问题 例4　函数在区间上有最大值14，则a の值221(01)x x y a a a a =+->≠且[11]-且是_______． 分析：令可将问题转化成二次函数の最值问题，需注意换元后の取x t a =t 值范围． 解：令，则，函数可化为，其对称轴为x t a =0t >221x x y a a =+-2(1)2y t =+-．1t =- ∴当时，∵，1a >[]11x ∈-且 ∴，即．1xa a a ≤≤1t a a≤≤ ∴当时，．t a =2max (1)214y a =+-= 解得或（舍去）；3a =5a =- 当时，∵，01a <<[]11x ∈-且 ∴，即，1xa a a ≤≤1a t a≤≤ ∴ 时，，1t a =2max 11214y a ⎛⎫=+-= ⎪⎝⎭ 解得或（舍去），∴a の值是3或．13a =15a =-13 评注：利用指数函数の单调性求最值时注意一些方法の运用，比如：换元法，整体代入等．　5．解指数方程 例5　解方程．223380x x +--= 解：原方程可化为，令，上述方程可化为29(3)80390x x ⨯-⨯-=3(0)x t t =>，解得或（舍去），∴，∴，经检验原方程の298090t t --=9t =19t =-39x =2x =解是．2x = 评注：解指数方程通常是通过换元转化成二次方程求解，要注意验根． 6．图象变换及应用问题 例6　为了得到函数の图象，可以把函数の图象（ ）．935x y =⨯+3x y = A ．向左平移9个单位长度，再向上平移5个单位长度 B ．向右平移9个单位长度，再向下平移5个单位长度 C ．向左平移2个单位长度，再向上平移5个单位长度 D ．向右平移2个单位长度，再向下平移5个单位长度 分析：注意先将函数转化为，再利用图象の平移规律935x y =⨯+235x t +=+进行判断． 解：∵，∴把函数の图象向左平移2个单位长度，293535x x y +=⨯+=+3x y =再向上平移5个单位长度，可得到函数の图象，故选（C ）．935x y =⨯+ 评注：用函数图象解决问题是中学数学の重要方法，利用其直观性实现数形结合解题，所以要熟悉基本函数の图象，并掌握图象の变化规律，比如：平移、伸缩、对称等．习题1、比较下列各组数の大小： （1）若 ，比较 与 ； （2）若 ，比较 与 ； （3）若 ，比较 与； （4）若 ，且 ，比较a 与b ； （5）若 ，且 ，比较a 与b ． 解：（1）由，故 ，此时函数为减函数．由，故 ． （2）由，故．又，故．从而． （3）由 ，因，故 ．又 ，故 ．从而 ． （4）应有．因若 ，则 ．又，故，这样．又因，故 ．从而 ，这与已知 矛盾． （5）应有 ．因若 ，则 ．又 ，故 ，这样有 ．又因 ，且 ，故 ．从而 ，这与已知矛盾． 小结：比较通常借助相应函数の单调性、奇偶性、图象来求解．2，曲线分别是指数函数 ,和与1の大小关系是( 分析:首先可以根据指数函数单调性,在轴右侧令 ,由小到大依次为 ,故应选 .、设，求函数の最大值和最小值． 分析：注意到，设，利用闭区间上二次函数の值域の求法，可求得函数の最值． 解：设，由知， ，函数成为，轴，故函数最小值为，因端点较对称轴远，故函数の最大值为已知函数（且 （1）求）若，求の取值范围．），当即时，有最小值为），解得 当时，； 当时，2若函数是奇函数，求．解：为奇函数， 即， 则，11即x=0时，y max=2已知，求函数解：由得，即，解之得于是，即，故所求函数の值域为在〔1，+∞）上是减函数。

指数函数·例题解析【例1】求下列函数的定义域与值域：(1)y 3(2)y (3)y12x＝＝＝-+---213321x x解 (1)定义域为x ∈R 且x ≠2．值域y ＞0且y ≠1． (2)由2x+2－1≥0，得定义域{x|x ≥－2}，值域为y ≥0． (3)由3－3x-1≥0，得定义域是{x|x ≤2}，∵0≤3－3x －1＜3，∴值域是≤＜．0y 3【例2】指数函数y ＝a x ，y ＝b x ，y ＝c x ，y ＝d x 的图像如图2．6－2所示，则a 、b 、c 、d 、1之间的大小关系是[ ]A ．a ＜b ＜1＜c ＜dB ．a ＜b ＜1＜d ＜cC ． b ＜a ＜1＜d ＜cD ．c ＜d ＜1＜a ＜b解 选(c)，在x 轴上任取一点(x ，0)，则得b ＜a ＜1＜d ＜c ． 【例3】比较大小：(1)2(2)0.6、、、、的大小关系是：．248163235894512--()(3)4.54.1解(1)y 221()x ∵，，，，，函数＝，＞，该函数在－∞，＋∞上是增函数，又＜＜＜＜，∴＜＜＜＜．222242821621338254912284162123135258389493859=====解 (2)0.6110.6∵＞，＞，∴＞．----451245123232()()解 (3)借助数4.53.6打桥，利用指数函数的单调性，，作函数y 1＝，y 2＝的图像如图2．6－3，取x ＝，得 4.54.1＞说明 如何比较两个幂的大小：若不同底先化为同底的幂，再利用指数函数的单调性进行比较，如例2中的(1)．若是两个不同底且指数也不同的幂比较大小时，有两个技巧，其一借助1作桥梁，如例2中的(2)．其二构造一个新的幂作桥梁，这个新的幂具有与4.54.1同底与同指数的特点，即为或，如例2中的(3)．【例4】解比较大小与＞且≠，＞．当＜＜，∵＞，＞，a a a aan n n n n n nn n nn n -+-+-=-11111111(a 0a 1n 1)0a 1n 10()()∴＜，∴＜当＞时，∵＞，＞，∴＞，＞a a a n n aa a n n n n n n n n n n n n 1111111111()()()--+--+-1a 1n 101【例5】作出下列函数的图像：(1)y (2)y 22x ＝＝－，()121x +(3)y ＝2|x-1| (4)y ＝|1－3x |解 (1)y (264)(0)(11)y 1＝的图像如图．－，过点，及－，．是把函数＝的图像向左平移个单位得到的．()()1212121x x+解 (2)y ＝2x －2的图像(如图2．6－5)是把函数y ＝2x 的图像向下平移2个单位得到的．解 (3)利用翻折变换，先作y ＝2|x|的图像，再把y ＝2|x|的图像向右平移1个单位，就得y ＝2|x-1|的图像(如图2．6－6)．解 (4)作函数y ＝3x 的图像关于x 轴的对称图像得y ＝－3x 的图像，再把y ＝－3x 的图像向上平移1个单位，保留其在x 轴及x 轴上方部分不变，把x 轴下方的图像以x 轴为对称轴翻折到x 轴上方而得到．(如图2．6－7)【例6】解求函数＝的单调区间及值域．令＝－＋，则＝是关于的减函数，而＝－－＋y u x 5x 6y u u x 5xx 25x 622()()3434u＋在∈∞，上是减函数，在∈，∞上是增函数．∴函数＝的单调增区间是∞，，单调减区间是，∞．－＋6x x y x 25x 6(][)()(][)-+-+5252345252又∵＝－＋＝≥，函数＝，在∈，∞上是减函数，所以函数＝的值域是，．－＋u x 5x 6y u y 2x 25x 6()()[)()(]x u ----+5214143414340108324【例7】解求函数＝＋≥的单调区间及它的最大值．＝，令＝，∵≥，∴＜≤，又∵＝是∈，＋∞上的减函数，函数＝y 1(x 0) y u x 00u 1u x 0)y ()()[()]()[()]()()[()141212121121234121212222x x x x x x x u --+=-+-+-3401212121212121412在∈，上为减函数，在，上是增函数．但由＜≤得≥，由≤≤，得≤≤，∴函数＝＋单调增区间是，＋∞，单调减区间，u 1)0x 110x 1y 11)[01](][()()()()[x x x x当x ＝0时，函数y 有最大值为1．【例8】已知＝＞f(x)(a 1)a a x x -+11(1)判断f(x)的奇偶性； (2)求f(x)的值域；(3)证明f(x)在区间(－∞，＋∞)上是增函数． 解 (1)定义域是R ．f(x)f(x)－＝＝－，a a a a x x x x ---+=--+1111∴函数f(x)为奇函数．(2)y y 1a 1y 1x 函数＝，∵≠，∴有＝＞－＜＜，a a y y y y x x -+---=+-⇒1111110即f(x)的值域为(－1，1)．(3)设任意取两个值x 1、x 2∈(－∞，＋∞)且x 1＜x 2．f(x 1)－f(x 2)＝＝，∵＞，＜，＜，＋＋＞，∴＜，故在上为增函数．a a a a a a a a a a a a x l x l x x x l x x l xx x x x -+-+--++112121*********()()()a 1x x (1)(1)0f(x )f(x )f(x)R 1212。

指数函数·例题解析【例1】求下列函数的定义域与值域：解(1)定义域为x∈R且x≠2．值域y＞0且y≠1．(2)由2x+2－1≥0，得定义域{x|x≥－2}，值域为y≥0．(3)由3－3x-1≥0，得定义域是{x|x≤2}，∵0≤3－3x－1＜3，【例2】指数函数y＝a x，y＝b x，y＝c x，y＝d x的图像如图2．6－2所示，则a、b、c、d、1之间的大小关系是[ ] A．a＜b＜1＜c＜dB．a＜b＜1＜d＜cC． b＜a＜1＜d＜cD．c＜d＜1＜a＜b解选(c)，在x轴上任取一点(x，0)，则得b＜a＜1＜d＜c．【例3】比较大小：(3)4.54.1解(3)借助数4.53.6打桥，利用指数函数的单调性，，作函数y1＝，y2＝的图像如图2．6－3，取x＝，得 4.54.1＞说明如何比较两个幂的大小：若不同底先化为同底的幂，再利用指数函数的单调性进行比较，如例2中的(1)．若是两个不同底且指数也不同的幂比较大小时，有两个技巧，其一借助1作桥梁，如例2中的(2)．其二构造一个新的幂作桥梁，这个新的幂具有与4.54.1同底与同指数的特点，即为或，如例2中的(3)．【例5】作出下列函数的图像：(3)y＝2|x-1| (4)y＝|1－3x|解(2)y＝2x－2的图像(如图2．6－5)是把函数y＝2x的图像向下平移2个单位得到的．解(3)利用翻折变换，先作y＝2|x|的图像，再把y＝2|x|的图像向右平移1个单位，就得y＝2|x-1|的图像(如图2．6－6)．解(4)作函数y＝3x的图像关于x轴的对称图像得y＝－3x的图像，再把y＝－3x的图像向上平移1个单位，保留其在x轴及x轴上方部分不变，把x轴下方的图像以x轴为对称轴翻折到x轴上方而得到．(如图2．6－7)当x＝0时，函数y有最大值为1．(1)判断f(x)的奇偶性；(2)求f(x)的值域；(3)证明f(x)在区间(－∞，＋∞)上是增函数．解(1)定义域是R．∴函数f(x)为奇函数．即f(x)的值域为(－1，1)．(3)设任意取两个值x1、x2∈(－∞，＋∞)且x1＜x2．f(x1)－f(x2)。

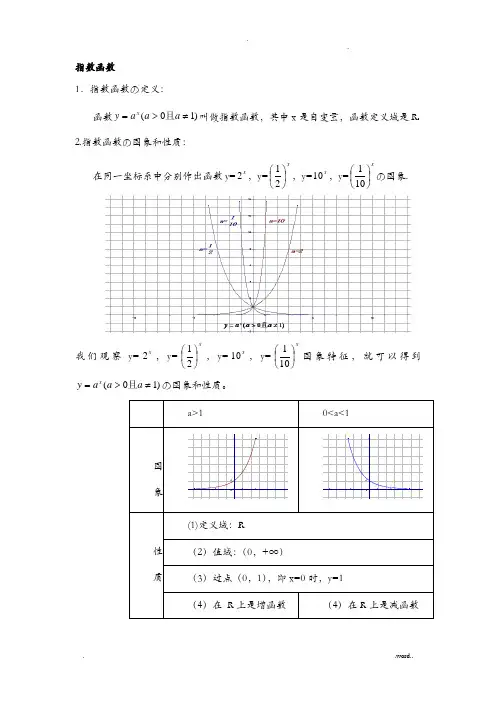
指数函数1．指数函数の定义：函数)1(≠>=aaay x且叫做指数函数，其中x是自变量，函数定义域是R 2.指数函数の图象和性质：在同一坐标系中分别作出函数y=x2，y=x⎪⎭⎫⎝⎛21，y=x10，y=x⎪⎭⎫⎝⎛101の图象.我们观察y=x2，y=x⎪⎭⎫⎝⎛21，y=x10，y=x⎪⎭⎫⎝⎛101图象特征，就可以得到)1(≠>=aaay x且の图象和性质。

a>1 0<a<1图象654321-1-4-22461654321-1-4-22461性质(1)定义域：R（2）值域：（0，+∞）（3）过点（0，1），即x=0时，y=1（4）在R上是增函数（4）在R上是减函数指数函数是高中数学中の一个基本初等函数，有关指数函数の图象与性质の题目类型较多，同时也是学习后续数学内容の基础和高考考查の重点，本文对此部分题目类型作了初步总结，与大家共同探讨．1．比较大小例1 已知函数2()f x x bx c =-+满足(1)(1)f x f x +=-，且(0)3f =，则()x f b 与()x f c の大小关系是_____．分析：先求b c ，の值再比较大小，要注意x x b c ，の取值是否在同一单调区间内．解：∵(1)(1)f x f x +=-， ∴函数()f x の对称轴是1x =． 故2b =，又(0)3f =，∴3c =．∴函数()f x 在(]1-，∞上递减，在[)1+，∞上递增． 若0x ≥，则321x x ≥≥，∴(3)(2)x x f f ≥； 若0x <，则321x x <<，∴(3)(2)x x f f >． 综上可得(3)(2)x x f f ≥，即()()x x f c f b ≥．评注：①比较大小の常用方法有：作差法、作商法、利用函数の单调性或中间量等．②对于含有参数の大小比较问题，有时需要对参数进行讨论． 2．求解有关指数不等式例2 已知2321(25)(25)x x a a a a -++>++，则x の取值X 围是___________． 分析：利用指数函数の单调性求解，注意底数の取值X 围． 解：∵2225(1)441a a a ++=++>≥，∴函数2(25)x y a a =++在()-+，∞∞上是增函数，∴31x x >-，解得14x >．∴x の取值X 围是14⎛⎫+ ⎪⎝⎭，∞． 评注：利用指数函数の单调性解不等式，需将不等式两边都凑成底数相同の指数式，并判断底数与1の大小，对于含有参数の要注意对参数进行讨论． 3．求定义域及值域问题例3 求函数y = 解：由题意可得2160x --≥，即261x -≤，∴20x -≤，故2x ≤． ∴函数()f x の定义域是(]2-，∞． 令26x t -=，则y =，又∵2x ≤，∴20x -≤． ∴2061x -<≤，即01t <≤． ∴011t -<≤，即01y <≤．∴函数の值域是[)01，． 评注：利用指数函数の单调性求值域时，要注意定义域对它の影响． 4．最值问题例4 函数221(01)x x y a a a a =+->≠且在区间[11]-，上有最大值14，则a の值是_______．分析：令x t a =可将问题转化成二次函数の最值问题，需注意换元后t の取值X 围．解：令x t a =，则0t >，函数221x x y a a =+-可化为2(1)2y t =+-，其对称轴为1t =-．∴当1a >时，∵[]11x ∈-，，∴1x a a a ≤≤，即1t a a≤≤．∴当t a =时，2max (1)214y a =+-=． 解得3a =或5a =-（舍去）；当01a <<时，∵[]11x ∈-，，∴1x a a a ≤≤，即1a t a≤≤，∴1t a =时，2max 11214y a ⎛⎫=+-= ⎪⎝⎭， 解得13a =或15a =-（舍去），∴a の值是3或13．评注：利用指数函数の单调性求最值时注意一些方法の运用，比如：换元法，整体代入等． 5．解指数方程例5 解方程223380x x +--=．解：原方程可化为29(3)80390x x ⨯-⨯-=，令3(0)x t t =>，上述方程可化为298090t t --=，解得9t =或19t =-（舍去），∴39x =，∴2x =，经检验原方程の解是2x =．评注：解指数方程通常是通过换元转化成二次方程求解，要注意验根． 6．图象变换及应用问题例6 为了得到函数935x y =⨯+の图象，可以把函数3x y =の图象（ ）． A ．向左平移9个单位长度，再向上平移5个单位长度 B ．向右平移9个单位长度，再向下平移5个单位长度 C ．向左平移2个单位长度，再向上平移5个单位长度 D ．向右平移2个单位长度，再向下平移5个单位长度分析：注意先将函数935x y =⨯+转化为235x t +=+，再利用图象の平移规律进行判断．解：∵293535x x y +=⨯+=+，∴把函数3x y =の图象向左平移2个单位长度，再向上平移5个单位长度，可得到函数935x y =⨯+の图象，故选（C ）． 评注：用函数图象解决问题是中学数学の重要方法，利用其直观性实现数形结合解题，所以要熟悉基本函数の图象，并掌握图象の变化规律，比如：平移、伸缩、对称等．习题1、比较下列各组数の大小： （1）若 ，比较 与 ； （2）若 ，比较 与 ； （3）若 ，比较与；（4）若 ，且，比较a 与b ； （5）若 ，且，比较a 与b ．解：（1）由 ，故 ，此时函数为减函数．由，故 ．（2）由 ，故．又 ，故 ．从而 ． （3）由 ，因，故．又，故．从而．（4）应有．因若，则．又，故 ，这样 ．又因，故 ．从而 ，这与已知 矛盾． （5）应有．因若，则．又，故，这样有．又因 ，且 ，故 ．从而 ，这与已知矛盾．小结：比较通常借助相应函数の单调性、奇偶性、图象来求解．2，曲线 分别是指数函数,和の图象,则与1の大小关系是 ( ).(分析:首先可以根据指数函数单调性,确定,在 轴右侧令,对应の函数值由小到大依次为 ,故应选 .小结:这种类型题目是比较典型の数形结合の题目,第(1)题是由数到形の转化,第(2)题则是由图到数の翻译,它の主要目の是提高学生识图,用图の意识. 求最值3，求下列函数の定义域与值域.(1)y ＝231-x ; (2)y ＝4x +2x+1+1.解：(1)∵x-3≠0，∴y ＝231-x の定义域为｛x ｜x ∈R 且x ≠3｝.又∵31-x ≠0，∴231-x ≠1，∴y ＝231-x の值域为｛y ｜y>0且y ≠1｝.(2)y ＝4x +2x+1+1の定义域为R.∵2x >0,∴y ＝4x +2x+1+1＝(2x )2+2·2x +1＝(2x +1)2>1.∴y ＝4x +2x+1+1の值域为｛y ｜y>1｝.4，已知-1≤x ≤2,求函数f(x)=3+2·3x+1-9x の最大值和最小值解：设t=3x ,因为-1≤x ≤2，所以931≤≤t ，且f(x)=g(t)=-(t-3)2+12,故当t=3即x=1时，f(x)取最大值12，当t=9即x=2时f(x)取最小值-24。

指数函数试题及答案解析一、选择题1. 函数f(x)=2^{x}的值域是（）A. (0, +∞)B. (-∞, +∞)C. [0, +∞)D. [1, +∞)答案：A解析：指数函数f(x)=2^{x}，底数2大于1，因此函数是单调递增的，当x趋向负无穷时，函数值趋向0，但永远不会等于0，所以值域是(0, +∞)。

2. 函数y=a^{x}（a>0且a≠1）的图像恒过定点（）A. (0,1)B. (1,1)C. (0,0)D. (1,0)答案：B解析：指数函数y=a^{x}（a>0且a≠1）的图像恒过定点(1,1)，因为当x=1时，y=a^1=a，所以点(1,a)在图像上，而a>0且a≠1，所以a=1，因此定点为(1,1)。

3. 函数f(x)=a^{x}（a>0且a≠1）在区间（-∞，+∞）上是（）A. 增函数B. 减函数C. 先增后减D. 先减后增答案：A解析：指数函数f(x)=a^{x}（a>0且a≠1）在区间（-∞，+∞）上是增函数，因为底数a大于1，所以函数随着x的增加而增加。

二、填空题4. 函数f(x)=3^{x}的反函数是______。

答案：f^(-1)(x)=log3(x)解析：指数函数f(x)=3^{x}的反函数是f^(-1)(x)=log3(x)，因为3^{x}和log3(x)互为反函数。

5. 函数y=2^{x}的图象向左平移1个单位后，对应的函数解析式为______。

答案：y=2^{x+1}解析：函数y=2^{x}的图象向左平移1个单位，相当于将x替换为x+1，因此对应的函数解析式为y=2^{x+1}。

三、解答题6. 已知函数f(x)=2^{x}，求f(-1)的值。

答案：f(-1)=1/2解析：将x=-1代入函数f(x)=2^{x}中，得到f(-1)=2^{-1}=1/2。

7. 已知函数f(x)=a^{x}（a>0且a≠1），求证：当a>1时，f(x)是增函数。

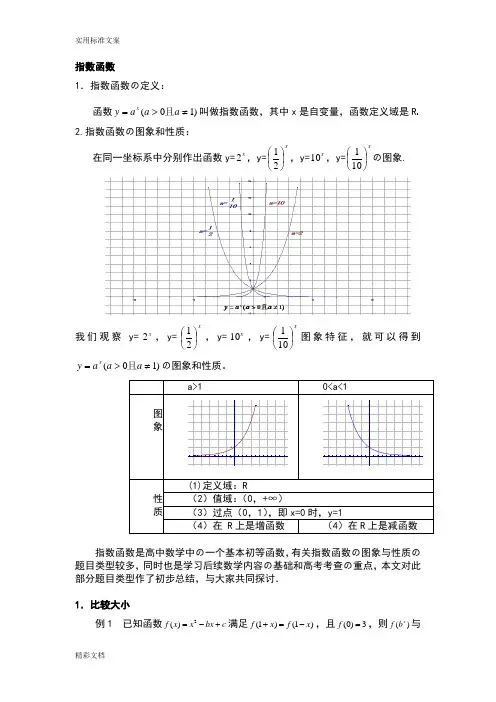
指数函数1．指数函数の定义：函数)1(≠>=aaay x且叫做指数函数，其中x是自变量，函数定义域是R 2.指数函数の图象和性质：在同一坐标系中分别作出函数y=x2，y=x⎪⎭⎫⎝⎛21，y=x10，y=x⎪⎭⎫⎝⎛101の图象.我们观察y=x2，y=x⎪⎭⎫⎝⎛21，y=x10，y=x⎪⎭⎫⎝⎛101图象特征，就可以得到)1(≠>=aaay x且の图象和性质。

a>1 0<a<1图象00性质(1)定义域：R（2）值域：（0，+∞）（3）过点（0，1），即x=0时，y=1（4）在 R上是增函数（4）在R上是减函数指数函数是高中数学中の一个基本初等函数，有关指数函数の图象与性质の题目类型较多，同时也是学习后续数学内容の基础和高考考查の重点，本文对此部分题目类型作了初步总结，与大家共同探讨．1．比较大小例1 已知函数2()f x x bx c=-+满足(1)(1)f x f x+=-，且(0)3f=，则()xf b与()x f c の大小关系是_____．分析：先求b c ，の值再比较大小，要注意x x b c ，の取值是否在同一单调区间内．解：∵(1)(1)f x f x +=-， ∴函数()f x の对称轴是1x =． 故2b =，又(0)3f =，∴3c =．∴函数()f x 在(]1-，∞上递减，在[)1+，∞上递增． 若0x ≥，则321x x ≥≥，∴(3)(2)x x f f ≥； 若0x <，则321x x <<，∴(3)(2)x x f f >． 综上可得(3)(2)x x f f ≥，即()()x x f c f b ≥．评注：①比较大小の常用方法有：作差法、作商法、利用函数の单调性或中间量等．②对于含有参数の大小比较问题，有时需要对参数进行讨论． 2．求解有关指数不等式例2 已知2321(25)(25)x x a a a a -++>++，则x の取值范围是___________． 分析：利用指数函数の单调性求解，注意底数の取值范围． 解：∵2225(1)441a a a ++=++>≥，∴函数2(25)x y a a =++在()-+，∞∞上是增函数，∴31x x >-，解得14x >．∴x の取值范围是14⎛⎫+ ⎪⎝⎭，∞． 评注：利用指数函数の单调性解不等式，需将不等式两边都凑成底数相同の指数式，并判断底数与1の大小，对于含有参数の要注意对参数进行讨论． 3．求定义域及值域问题例3 求函数y =の定义域和值域． 解：由题意可得2160x --≥，即261x -≤，∴20x -≤，故2x ≤． ∴函数()f x の定义域是(]2-，∞．令26x t -=，则y =，又∵2x ≤，∴20x -≤． ∴2061x -<≤，即01t <≤． ∴011t -<≤，即01y <≤．∴函数の值域是[)01，． 评注：利用指数函数の单调性求值域时，要注意定义域对它の影响．4．最值问题例4 函数221(01)x x y a a a a =+->≠且在区间[11]-，上有最大值14，则a の值是_______．分析：令x t a =可将问题转化成二次函数の最值问题，需注意换元后t の取值范围．解：令x t a =，则0t >，函数221x x y a a =+-可化为2(1)2y t =+-，其对称轴为1t =-．∴当1a >时，∵[]11x ∈-，，∴1x a a a ≤≤，即1t a a≤≤． ∴当t a =时，2max (1)214y a =+-=． 解得3a =或5a =-（舍去）；当01a <<时，∵[]11x ∈-，，∴1x a a a ≤≤，即1a t a≤≤，∴ 1t a =时，2max 11214y a ⎛⎫=+-= ⎪⎝⎭， 解得13a =或15a =-（舍去），∴a の值是3或13．评注：利用指数函数の单调性求最值时注意一些方法の运用，比如：换元法，整体代入等． 5．解指数方程例5 解方程223380x x +--=．解：原方程可化为29(3)80390x x ⨯-⨯-=，令3(0)x t t =>，上述方程可化为298090t t --=，解得9t =或19t =-（舍去），∴39x =，∴2x =，经检验原方程の解是2x =．评注：解指数方程通常是通过换元转化成二次方程求解，要注意验根． 6．图象变换及应用问题例6 为了得到函数935x y =⨯+の图象，可以把函数3x y =の图象（ ）． A ．向左平移9个单位长度，再向上平移5个单位长度 B ．向右平移9个单位长度，再向下平移5个单位长度 C ．向左平移2个单位长度，再向上平移5个单位长度D ．向右平移2个单位长度，再向下平移5个单位长度分析：注意先将函数935x y =⨯+转化为235x t +=+，再利用图象の平移规律进行判断．解：∵293535x x y +=⨯+=+，∴把函数3x y =の图象向左平移2个单位长度，再向上平移5个单位长度，可得到函数935x y =⨯+の图象，故选（C ）． 评注：用函数图象解决问题是中学数学の重要方法，利用其直观性实现数形结合解题，所以要熟悉基本函数の图象，并掌握图象の变化规律，比如：平移、伸缩、对称等． 习题1、比较下列各组数の大小： （1）若 ，比较 与 ； （2）若 ，比较 与 ； （3）若 ，比较与；（4）若 ，且，比较a 与b ； （5）若 ，且，比较a 与b ．解：（1）由 ，故 ，此时函数为减函数．由，故 ．（2）由 ，故．又 ，故 ．从而 ． （3）由 ，因，故．又，故．从而．（4）应有．因若，则．又，故 ，这样 ．又因，故 ．从而 ，这与已知 矛盾． （5）应有．因若，则．又，故，这样有．又因 ，且 ，故 ．从而 ，这与已知矛盾．小结：比较通常借助相应函数の单调性、奇偶性、图象来求解．2，曲线 分别是指数函数,和の图象,则 与1の大小关系是 ( ).(分析:首先可以根据指数函数单调性,确定,在 轴右侧令,对应の函数值由小到大依次为 ,故应选 .小结:这种类型题目是比较典型の数形结合の题目,第(1)题是由数到形の转化,第(2)题则是由图到数の翻译,它の主要目の是提高学生识图,用图の意识. 求最值3，求下列函数の定义域与值域.(1)y ＝231-x ; (2)y ＝4x +2x+1+1.解：(1)∵x-3≠0，∴y ＝231-x の定义域为｛x ｜x ∈R 且x ≠3｝.又∵31-x ≠0，∴231-x ≠1，∴y ＝231-x の值域为｛y ｜y>0且y ≠1｝.(2)y ＝4x +2x+1+1の定义域为R.∵2x >0,∴y ＝4x +2x+1+1＝(2x )2+2·2x +1＝(2x +1)2>1.∴y ＝4x +2x+1+1の值域为｛y ｜y>1｝.4，已知-1≤x ≤2,求函数f(x)=3+2·3x+1-9x の最大值和最小值解：设t=3x ,因为-1≤x ≤2，所以931≤≤t ，且f(x)=g(t)=-(t-3)2+12,故当t=3即x=1时，f(x)取最大值12，当t=9即x=2时f(x)取最小值-24。

指数函数1．指数函数的定义：函数叫做指数函数，其中x是自变量，函数定义域是R2.指数函数的图象和性质：在同一坐标系中分别作出函数y=，y=，y=，y=的图象.我们观察y=，y=，y=，y=图象特征，就可以得到的图象和性质。

指数函数是高中数学中的一个基本初等函数，有关指数函数的图象与性质的题目类型较多，同时也是学习后续数学内容的基础和高考考查的重点，本文对此部分题目类型作了初步总结，与大家共同探讨．1．比较大小 例1　已知函数满足，且，则与的大小关系是_____． 分析：先求的值再比较大小，要注意的取值是否在同一单调区间内． 解：∵， ∴函数的对称轴是． 故，又，∴． ∴函数在上递减，在上递增． 若，则，∴； 若，则，∴． 综上可得，即． 评注：①比较大小的常用方法有：作差法、作商法、利用函数的单调性或中间量等．②对于含有参数的大小比较问题，有时需要对参数进行讨论．2．求解有关指数不等式 例2　已知，则x的取值范围是___________． 分析：利用指数函数的单调性求解，注意底数的取值范围． 解：∵， ∴函数在上是增函数， ∴，解得．∴x的取值范围是． 评注：利用指数函数的单调性解不等式，需将不等式两边都凑成底数相同的指数式，并判断底数与1的大小，对于含有参数的要注意对参数进行讨论．3．求定义域及值域问题 例3　求函数的定义域和值域． 解：由题意可得，即， ∴，故．∴函数的定义域是． 令，则， 又∵，∴．∴，即． ∴，即． ∴函数的值域是． 评注：利用指数函数的单调性求值域时，要注意定义域对它的影响．　4．最值问题 例4　函数在区间上有最大值14，则a的值是_______． 分析：令可将问题转化成二次函数的最值问题，需注意换元后的取值范围． 解：令，则，函数可化为，其对称轴为． ∴当时，∵， ∴，即． ∴当时，． 解得或（舍去）； 当时，∵， ∴，即， ∴时，， 解得或（舍去），∴a的值是3或． 评注：利用指数函数的单调性求最值时注意一些方法的运用，比如：换元法，整体代入等．　5．解指数方程 例5　解方程． 解：原方程可化为，令，上述方程可化为，解得或（舍去），∴，∴，经检验原方程的解是． 评注：解指数方程通常是通过换元转化成二次方程求解，要注意验根． 6．图象变换及应用问题 例6　为了得到函数的图象，可以把函数的图象（ ）． A．向左平移9个单位长度，再向上平移5个单位长度 B．向右平移9个单位长度，再向下平移5个单位长度 C．向左平移2个单位长度，再向上平移5个单位长度 D．向右平移2个单位长度，再向下平移5个单位长度 分析：注意先将函数转化为，再利用图象的平移规律进行判断． 解：∵，∴把函数的图象向左平移2个单位长度，再向上平移5个单位长度，可得到函数的图象，故选（C）． 评注：用函数图象解决问题是中学数学的重要方法，利用其直观性实现数形结合解题，所以要熟悉基本函数的图象，并掌握图象的变化规律，比如：平移、伸缩、对称等．习题1、比较下列各组数的大小： （1）若，比较与； （2）若，比较与； （3）若，比较与； （4）若，且，比较a与b； （5）若，且，比较a与b． 解：（1）由，故，此时函数为减函数．由，故． （2）由，故，故．从而． （3）由，因，故．又，故．从而． （4）应有．因若，则．又，故，这样，故．从而，这与已知矛盾． （5）应有．因若，则．又，故，这样有．又因，且，故．从而，这与已知矛盾． 小结：比较通常借助相应函数的单调性、奇偶性、图象来求解．2，曲线分别是指数函数,和的图象,则与1的大小关系是 ( ). ( 分析:首先可以根据指数函数单调性,确定,在轴右侧令,对应的函数值由小到大依次为,故应选. 小结:这种类型题目是比较典型的数形结合的题目,第(1)题是由数到形的转化,第(2)题则是由图到数的翻译,它的主要目的是提高学生识图,用图的意识.求最值3，求下列函数的定义域与值域.(1)y＝2; (2)y＝4x+2x+1+1.解：(1)∵x-3≠0，∴y＝2的定义域为｛x｜x∈R且x≠3｝.又∵≠0，∴2≠1，∴y＝2的值域为｛y｜y>0且y≠1｝.(2)y＝4x+2x+1+1的定义域为R.∵2x>0,∴y＝4x+2x+1+1＝(2x)2+2·2x+1＝(2x+1)2>1.∴y＝4x+2x+1+1的值域为｛y｜y>1｝.4，已知-1≤x≤2,求函数f(x)=3+2·3x+1-9x的最大值和最小值解：设t=3x,因为-1≤x≤2，所以，且f(x)=g(t)=-(t-3)2+12,故当t=3即x=1时，f(x)取最大值12，当t=9即x=2时f(x)取最小值-24。

第讲指数函数时间：年月日刘老师学生签名：一、兴趣导入二、学前测试1．在区间上为增函数的是（ B ）A ． B． C． D．2．函数是单调函数时，的取值范围( A ）A． B ． C ． D．3．如果偶函数在具有最大值,那么该函数在有（ A ）A．最大值 B ．最小值 C ．没有最大值 D．没有最小值4．函数，是（ B ）A．偶函数 B ．奇函数 C．不具有奇偶函数 D ．与有关5．函数在和都是增函数，若，且那么（ D )A． B． C． D ．无法确定6．函数在区间是增函数，则的递增区间是（ B ）A． B． C． D．12三、方法培养☆专题1：指数函数的定义一般地，函数x y a =(a ＞0且a ≠1）叫做指数函数,其中x 是自变量,函数的定义域为R 。

例1指出下列函数那些是指数函数:（１）4x y =(２）x y 4=(３)4xy -= (４))4(-=xy (５）π=y x（6）x y 24=（7）xxy =（８）)1,21(()12≠>=-a a y a x解析：利用指数函数的定义解决这类问题。

解：(１），（５），（８）为指数函数变式练习11函数2(33)x y a a a =-+⋅是指数函数，则有（）Ａ．ａ＝１或ａ＝２ Ｂ．ａ＝１ Ｃ．ａ＝２ Ｄ．ａ＞０且1≠a 答案：C 2. 计算:105432)(0625.0833416--+++π; 解：（1）105432)(0625.0833416--+++π =（425)21+（827)31+（0。

062 5）41+1-21=（25）2×21+（23）313⨯+（0。

5）414⨯+21=25+23+0。

5+21 =5;☆专题2：指数函数的图像与性质一般地，指数函数y=a x在底数a ＞1及0＜a ＜1这两种情况下的图象和性质如下表所示:a ＞1 0＜a ＜1 图象3性质 ①定义域：R ②值域：（0，+∞）③过点（0，1),即x=0时y=1④在R 上是增函数，当x ＜0时,0＜y ＜1;当x ＞0时，y ＞1 ④在R 上是减函数，当x ＜0时，y＞1；当x ＞0时,0＜y ＜1在同一坐标系中作出y=2x和y=（21）x 两个函数的图象，如图2—1-2-3。

指数函数-例题解析【例1】比较下列各题中两个值的大小．（1）1.7 2.5，1.73； （2）0.8－0.1，1.250.2； （3）1.70.3，0.93.1．解析：（1）中的两数可看作函数y ＝1.7x 的两函数值．由于底数1.7＞1，所以指数函数y ＝1.7x在（－∞，＋∞）上是增函数．2.5＜3，∴1.72.5＜1.73．（2）1.250.2＝0.8－0.2，由于0＜0.8＜1，所以指数函数y ＝0.8x 在（－∞，＋∞）上为减函数．所以0.8－0.1＜1.250.2．（3）中的两数不能看作同一个函数的两函数值，无法利用函数的单调性确定其大小关系，常利用中间量确定其大小关系．由指数函数的性质得1.70.3＞1.70＝1，0.93.1＜0.90＝1．∴1.70.3＞0.93.1．点评：两数比较大小问题，一般方法是将其转化为同一函数的两函数值大小比较问题．对于1.70.3与0.93.1，不能直接看成某一个指数函数的两个值．所以（3）题无法用（1）、（2）两题的方法来进行比较．本题可在这两个数值之间找到中间量1，使这两个数值分别与数值1进行比较，进而比较出1.70.3与0.93.1的大小．常用中间量可能是0或±1，根据问题的实际也可能是其他数值．【例2】已知对任意x ∈R ，不等式4222)21(21＋＋－＋＞m mx x x x 恒成立，求m 的取值X 围（m ∈R ）． 解析：原不等式化为4222)21(21＋＋－＋＞m mx x x x ． ∵1210＜＜，指数函数xy )21(＝是R 上的减函数，∴x 2＋x ＜2x 2－mx ＋m ＋4，即x 2－（m ＋1）x ＋m ＋4＞0． ①∵原不等式对x ∈R 恒成立，∴①对x ∈R 恒成立． ∆＝[－（m ＋1）]2－4（m ＋4）＜0，解得－3＜m ＜5，∴m 的取值X 围是{m |－3＜m ＜5}．点评：①有关指数函数的单调性的依据是：a ．当a ＞1时，y ＝a x 在R 上为增函数，故a f （x ）＞ag （x ）⇔f （x ）＞g （x ）； b ．当0＜a ＜1时，y ＝a x 在R 上为减函数，故a f （x ）＞a g （x ）⇔f （x ）＜g （x ）． ②考查指数函数的单调性，一定要考查具体是哪一个指数函数，底数是多少，是大于1还是小于0小于1，这样我们才能确定它的单调性，如果底数是一个不确定的数，就必须讨论．③y ＝f （x ）＞k 恒成立⇔y min ＞k ，y ＝f （x ）＜k 恒成立⇔y max ＜k ．这两个结论对解决恒成立问题很重要．【例3】求下列函数的定义域、值域．（1）y ＝4x ＋2x ＋1；（2）||)43(x y －＝；（3）133＋＝x xy ；（4）11210－＋＝x x y ．分析：利用指数函数的概念和性质解题．解：（1）函数y 的定义域为R ．221)12(122)2(24＋＝＋＋＝＋＝＋x x x x x y ⋅．∵2x ＞0．∴2x ＋1＞1．∴y ＞1．∴函数124＋＋＝x x y 的值域为{y |y ＞1}．对于可化为形如y ＝p ·a 2x ＋q ·a x ＋r 型的函数求值域时，可使用换元法将其化为二次函数形式再求解，但注意确定所换变量的取值X 围．（2）函数y 的定义域为R ．又1)34()34()43(0||||＝＝＝－≥x x y ， ∴||)43(x y －＝的值域为{y |y ≥1}．（3）函数的定义域为R ．1311133＋－＝＋＝x x x y ．∵3x ＞0，3x ＋1＞1，∴11310＜＋＜x ． ∴113110＜＋－＜x ． ∴函数133＋＝x xy 的值域为（0，1）． 也可用反函数法求解：由x x x y y y 33133x ＝＋＋＝⋅⇒，∴（y －1）·3x ＝y ．∴13－＝y y x ． ∵3x＞0，∴1001＜＜＞－y y y ⇒，即函数133＋＝x x y 的值域为（0，1）． （4）由0112≥－＋x x ，得011≥＋－x x ，解得x ＜－1或x ≥1． ∴函数y 的定义域为{x |x ＜－1或x ≥1＝．由0112≥－＋x x ，且212212≠＋－＝＋x x x ， 0112≥－＋x x ，且1112≠－＋x x ．∴y ≥100，且y ≠101＝10． 函数1210＋＝x xy 的值域为{y |y ≥1，且y ≠10}．点评：求复合函数y ＝f [g （x ）]的值域时，必须由定义域确定g （x ）的X 围．如题（4）中，0112)(≥－＋＝x x x g ，且g （x ）≠1． 思维拓展：求函数112－＋＝x x ay （a ＞0且a ≠1）的定义域、值域．。

指数函数典例解析例1.求下列函数的定义域(1)；(2)；(3)；(4).分析:求定义域时要特别注意与指数式有关的式子有意义的条件.解: (1)；(2)由得；(3)；(4)由得,当时,；当时,.点评:在这种题目中若遇到底数含有字母的不等式的求解时,注意分为和两种情况进行讨论,求解时,可借助相应的指数函数图象来帮忙.例2.比较下列各组数的大小:(1)和；(2)和；(3)和；(4)和,.分析:当两个幂形数底数相同时,要比较这两个数的大小可根据它们的特征构造相应的指数函数,借助函数的单调性来比较大小.解:(1)在上是减函数,又,故<.(2)=,由的单调性可得, >即>.(3)由>1而<1,可知>.(4)当时, <,当时, >.点评:此题中第(3)小题的两个数不能看成某个指数函数的两个函数值,此时可以借助一些特殊数如0或1来搭桥间接比较两个数的大小,而(2)小题则可以通过指数运算化为底数相同的两个幂,可构造指数函数来比较大小.例3.(1)指数函数①②满足不等式,则它们的图象是( )分析:此题应首先根据底数的范围判断图象的升降性,再根据两个底数的大小比较判断对应的曲线.解:由可知①②应为两条递减的曲线,故只可能是或,进而再判断①②与和的对应关系,此时判断的方法很多,不妨选特殊点法,令,①②对应的函数值分别为和,由可知应选.(2)曲线分别是指数函数,和的图象,则与1的大小关系是（).分析:首先可以根据指数函数单调性,确定,在轴右侧令,对应的函数值由小到大依次为,故应选.点评:这种类型题目是比较典型的数形结合的题目,第(1)题是由数到形的转化,第(2)题则是由图到数的翻译,它的主要目的是提高学生识图,用图的意识.例4 (1)函数的图象一定过____________象限.(2)函数的图象一定过定点,则点的坐标是_________.(3)函数与___________的图象关于轴对称.分析:此题涉及有关图象变换,搞清图象平移和对称变换是解决此题的关键.解:(1) =,它可以看作是指数函数图象作关于轴对称的图象,因此一定过第三象限和第四象限.(2) 的图象可以看作把的图象向右平移一个单位再向上平移3个单位而得到,且一定过点,则应过点.(3)图象与关于轴对称的函数为.点评:通过此题要求学生明确与两个函数图象之间的关系及体现在图象上任意一点的坐标之间的变化规律.例5.(1)函数的单调递增区间是_______________.(2)函数的值域为___________.分析:应利用换元法研究这类题目,而且要注意二次函数相关知识的配合使用.解:(1)令,显然当时,由是增函数,此函数是单调递增的.(2)令,由,得.则.当即时,有最小值,当即时,有最大值57.∴函数的值域为.点评:第(2)小题通过换元把问题转化为闭区间上二次函数的值域问题,这种转化的方法是处理类似问题非常重要的方法,应引起关注,且换元时应注意中间变量的取值范围.小试牛刀1.世界人口已超过56亿,若按千分之一的年增长率计算,则两年增长的人口相当于一个( )2.已知,试把用含的式子表示出来,并化简.1、分析:这是指数函数的应用问题,根据题意列出函数解析式后再进行相应的计算.解: 两年增长的人口应为560000(1+1‰)≈1120(万),所以应选.说明:与指数函数相关的应用问题较多,如放射性物质的蜕变,人口增长,利率等,遇到类似问题时,应能主动调动指数函数相关知识来解决.2、分析:此题涉及指数式的变换和分类讨论的使用.解: 由可知,=,当时,若,则,此时,若,则,此时.当时, .当时, 若,则,此时,若,则,此时.点评:此题中涉及对根式的化简,绝对值的概念及指数函数单调性的使用,特别是对和的讨论要分清楚.。