3.5.3 扰动稳态误差

稳态误差的总结分析和例解控制系统稳态误差是系统控制准确度的一种度量，通常称为稳态性能。

只有当系统稳定时，研究稳态误差才有意义，对不能稳定的系统，根本不存在研究稳态误差的可能性。

一、 误差与稳态误差1、输入端的定义：对图一，比较输出得到：E(s)=R(s)-H(s)*Y(s)称E(s)为误差信号，简称误差图一2、输出端的定义：将图一转换为图二，便可定义输出端的稳态误差，并且与输入端的稳态误差有如下关系：E ’(s)=E(s)/H(s)输入端定义法可测量实现，输出端定义法常无法测量，因此只有数学意义，以后在不做特别说明时，系统误差总是指输入端定义误差。

图二再有误差的时域表达式：也有：e(t)= [E(S)]= [Φe (s)*R(S)]其中Φe (s)是误差传递函数，定义为：Φe (s)==根据拉氏变换终值定理，由上式求出稳态误差：(T j s+1)e ss (∞)= =二、 系统类型一般的，定义一个分子为m 阶次，分母为n 阶次的开环传递函数为：[]1()()()()ts ss e t L E s e t e t -==+G(S)H(S)=K为开环增益，ν表示系统类型数，ν=0，表示0型系统；ν=1表示Ⅰ型系统；当ν大于等于2时，除了符合系统外，想使得系统稳定相当困难。

四、阶跃输入下的ess(∞)与静态位置误差系数Kpr(t)=R*1(t),则有：ess (∞)=νν用Kp表示静态位置误差系数：ess(∞)==其中： Kp=且有一般式子：Kp=ν∞ν五、斜坡输入下的ess(∞)与静态速度误差系数Kvr(t)=Rt,则有：ess (∞)=ν用Kv表示静态速度误差系数：ess(∞)==其中： Kv=六、加速度输入下的ess(∞)与静态加速度误差系数Kar(t)=Rt2/2,则有： ess (∞)=ν、用Kv表示静态速度误差系数： ess(∞)==其中： Kv=且有： Ka=、七、扰动状况下的稳态误差系统的模型如图三所示对扰动状况下的稳态误差仍然有输入端与输出端的两种定义：图三1、输入端定义法：扰动状况下的系统的稳态误差传递函数：由拉氏变换终值定理，求得扰动状况下的稳态误差为：2、输出端定义法：212()'()0()()1()()()G s E s Y s N s G s G s H s =-=-+记Φe (s) =为误差传递函数，其中G(s)为：G(s)=G 1(s)*G 2(s)*H(s)八、减小或者消除稳态误差的措施： （1）保证系统中各个环节（或元件），特别是反馈回路中元件的参数具有一定的精度和恒定性；（2）对输入信号而言，增大开环放大系数（开环增益），以提高系统对给定输入的跟踪能力；（3）对干扰信号而言，增大输入和干扰作用点之间环节的放大系数（扰动点之前的前向通道增益），有利于减小稳态误差；（4）增加系统前向通道中积分环节数目，使系统型号提高，可以消除不同输入信号时的稳态误差。

稳态误差公式稳态误差公式是控制系统中常用的一个概念，用于评估系统输出与期望输出之间的偏差。

在控制系统设计和分析中，稳态误差公式被广泛应用，能够帮助工程师评估系统的性能和稳定性。

稳态误差公式的含义稳态误差公式指的是控制系统在稳态下输出与期望输出之间的偏差。

稳态是指系统已经达到恒定状态，即输入信号已经稳定，系统没有改变时的状态。

稳态误差是输出与期望输出之间的差值，通常用e表示。

稳态误差公式可以用以下公式表示：e(t) = y(t) - r(t)其中e(t)表示在时间t时刻的稳态误差，y(t)表示系统输出在时间t时的值，r(t)表示期望输出在时间t时的值。

稳态误差公式的应用稳态误差公式在控制系统中具有广泛的应用，通常被用于以下几个方面：1. 系统性能分析稳态误差公式可以用于分析系统的性能，帮助工程师评估系统输出与期望输出之间的差距。

通过分析稳态误差，可以明确系统的性能限制，从而确定是否需要改进系统的设计。

2. 系统稳定性分析稳态误差公式也可以用于系统稳定性分析。

稳态误差越小，系统的稳定性越好。

因此，通过分析稳态误差的大小可以评估系统的稳定性。

3. 控制系统设计在控制系统设计中，稳态误差公式是一个非常重要的工具。

通过控制系统的参数设置，可以调整系统的稳态误差。

因此，稳态误差公式可以帮助工程师设计出性能更好、稳定性更高的控制系统。

稳态误差公式的限制稳态误差公式虽然在控制系统中具有广泛的应用，但也存在一些限制。

其中最重要的一个限制是，稳态误差公式只适用于稳态下的系统。

如果系统还没有进入稳态，稳态误差公式将无法提供准确的结果。

此外，稳态误差公式还有一个限制，那就是它不能完全反映系统的动态响应。

稳态误差公式只考虑了系统输出与期望输出之间的偏差，而没有考虑系统响应的速度、振荡等因素。

因此，在分析系统性能时，需要同时考虑系统的稳态误差和动态响应。

稳态误差公式的应用示例为了更好地理解稳态误差公式的应用，下面以比例控制系统为例进行说明。

自动控制原理稳态误差相关的基本原理引言自动控制原理是研究如何通过对被控对象进行测量和调节，使其输出达到期望值的一门学科。

在实际应用中，我们往往希望被控对象能够快速、准确地达到期望值，并且能够稳定在该期望值附近。

然而，由于各种因素的影响，被控对象在实际操作中往往会存在一定的误差。

稳态误差就是描述系统输出与期望值之间的偏差。

稳态误差的定义稳态误差是指系统在长时间运行后，输出与期望值之间的持续偏差。

通常使用误差函数来描述稳态误差，常见的有积分误差、百分比偏差等。

稳态误差分类根据系统输入信号和输出响应之间的关系，稳态误差可以分为以下几种类型：阶跃输入信号下的稳态误差当输入信号为阶跃函数时，系统响应过程中存在一个阶段性变化。

根据输出与期望值之间的偏差大小和持续时间的不同，可以将阶跃输入信号下的稳态误差分为零稳态误差、常数稳态误差和无限稳态误差三种情况。

零稳态误差当系统输出在长时间运行后与期望值完全一致时，称系统具有零稳态误差。

这意味着系统能够快速、准确地响应输入信号，并最终达到期望值。

常数稳态误差当系统输出在长时间运行后与期望值存在一个固定的偏差时，称系统具有常数稳态误差。

虽然系统能够达到期望值附近，但始终存在一个固定的偏差。

无限稳态误差当系统输出在长时间运行后与期望值之间的偏差持续增大，并且无法消除时，称系统具有无限稳态误差。

这种情况下，系统无法达到期望值。

正弦输入信号下的稳态误差当输入信号为正弦函数时，系统响应过程中存在周期性变化。

对于正弦输入信号下的稳态误差，我们通常关注其幅频特性和相频特性。

幅频特性描述了输出信号的幅值与输入信号频率之间的关系。

对于稳定系统，幅频特性通常是一个函数，它可以用来衡量系统对不同频率的正弦输入信号的响应能力。

当幅频特性在某个频率处衰减到0时，称该频率为系统的截止频率。

相频特性相频特性描述了输出信号与输入信号相位之间的关系。

对于稳定系统，相频特性通常是一个函数，它可以用来衡量系统对不同相位的正弦输入信号的响应能力。

稳态误差计算稳态误差是指控制系统在稳定状态下输出与期望输出之间的差异。

在控制系统中，我们希望输出能够尽量接近期望输出，从而实现优化和准确的控制。

稳态误差的大小直接影响到控制系统的性能和精确度。

本文将介绍稳态误差的计算方法及其普通解法。

稳态误差的计算可以通过以下步骤进行：1.确定系统的开环传递函数系统的开环传递函数是控制系统的输入与输出之间的关系。

它描述了控制系统的动态特性。

通常，开环传递函数可以由系统的物理方程或实验数据拟合得出。

2.确定系统的期望输入信号期望输入信号是控制系统的期望输出值。

它可以是一个固定值或者一个随时间变化的函数。

期望输入信号决定了控制系统的目标。

3.计算系统的闭环传递函数闭环传递函数描述了控制系统的反馈路径对输出的影响。

它是开环传递函数与控制器传递函数的乘积。

4.计算系统的稳态误差在进行稳态误差计算之前，需要确定系统的类型。

根据系统是否包含积分环节，可以将系统分为4种类型：类型0系统、类型1系统、类型2系统和类型3系统。

-类型0系统：开环传递函数中不包含积分环节。

例如，开环传递函数为G(s)=K/(s+a)。

类型0系统的稳态误差可以通过输入信号的阶数来确定。

对于阶数为n的输入信号，稳态误差为0。

-类型1系统：开环传递函数中包含一个积分环节。

例如，开环传递函数为G(s)=K/(s*(s+a))。

类型1系统的稳态误差可以通过输入信号的阶数来确定。

对于阶数为n的输入信号，稳态误差为1/((n+1)*K)。

-类型2系统：开环传递函数中包含两个积分环节。

例如，开环传递函数为G(s)=K/(s^2*(s+a))。

类型2系统的稳态误差可以通过输入信号的阶数来确定。

对于阶数为n的输入信号，稳态误差为1/(n*K)。

-类型3系统：开环传递函数中包含三个积分环节。

例如，开环传递函数为G(s)=K/(s^3*(s+a))。

类型3系统的稳态误差可以通过输入信号的阶数来确定。

对于阶数为n的输入信号，稳态误差为1/((n-1)*K)。

单位负反馈控制系统稳态误差的计算公式（原创实用版）目录1.引言2.稳态误差的定义及分类3.稳态误差的计算公式4.示例：单位负反馈控制系统的稳态误差计算5.结论正文一、引言在工程技术领域，控制系统的稳定性和精度是评价一个系统性能的重要指标。

稳态误差是衡量系统稳定性和精度的一个重要参数，它反映了系统在稳态条件下，输出与期望值之间的偏差。

对于单位负反馈控制系统，稳态误差的计算公式是一个重要的研究课题。

本文将从稳态误差的定义及分类入手，介绍稳态误差的计算公式，并通过一个示例来说明如何计算单位负反馈控制系统的稳态误差。

二、稳态误差的定义及分类稳态误差（Steady-State Error, ess）是指系统在稳态条件下，输出与期望值之间的偏差。

稳态误差按照产生的原因分为原理性误差和实际性误差两类。

原理性误差是由于系统结构和参数设计不合理导致的，而实际性误差是由于实际工作中存在的各种干扰和非线性因素引起的。

三、稳态误差的计算公式稳态误差的计算公式为：ess = lim(s→0) [E(s)] / R(s)其中，E(s) 表示系统输出的稳态误差，R(s) 表示系统的稳态增益。

四、示例：单位负反馈控制系统的稳态误差计算假设有一个单位负反馈控制系统，其单位阶跃响应的稳态误差为 0.1，求该系统的类型。

根据稳态误差的计算公式，我们可以得到：ess = lim(s→0) [E(s)] / R(s) = 0.1由于该系统的单位阶跃响应的稳态误差为 0.1，因此可以判断该系统为二型系统。

五、结论本文从稳态误差的定义及分类入手，介绍了稳态误差的计算公式，并结合一个单位负反馈控制系统的示例，详细说明了如何计算稳态误差。

3.6.7、扰动稳态误差终值的计算根据终值定理及式(3-81)、式(3-82)，式(3-84)、式(3-86), 扰动稳态误差的终值e sn 可由下式计算：)()(lim )(lim )(lim 0s s sN s sE t e e en s n s sn t sn φ-===→→∞→∏∏∏∏=--=++==→+++++-=mj jv n i iv ml j jq i ivs s K s s s s sK s sN 111120)1()1()1()1()(lim ττττμμ(3-105)比较式(3-105)及(3-87)可见，)(s en φ的分母多项式与)(s ex φ一样，但)(s en φ的分子多项式中只有vs 项，不象)(s ex φ的分子多项式中有μ+v s 项。

它说明只是控制环节传递函数)(1s G 中串联积分环节的数目v 对系统扰动稳态误差有决定性影响。

一 阶跃扰动作用下的稳态误差在单位阶跃扰动作用下 n t N s s(),()==11这时扰动稳态误差终值为)(lim 0s e en s sn φ→= (3-106)二 斜坡扰动作用下的稳态误差在单位斜坡扰动作用下n t t N s s (),()==12这时扰动稳态误差终值为e ss sn s n =→lim ()01φ (3-107)三 加速度扰动作用下的稳态误差在单位加速度扰动作用下n t t ()=122 N s s()=13 这时扰动稳态误差终值为e s s sn s n =→lim()021φ (3-108)按式(3-105)、(3-106)、(3-107)及(3-108)计算求得的各型系统在不同扰动作用下的稳态误差终值汇总列于表3-2中。

表3-2 不同系统中扰动稳态误差的终值扰 动 稳 态 误 差 的 终 值 扰 动 输 入 ν=0 系 统 ν=1系 统 ν=2系 统K K 210+=()μ )(t u1013K K ()μ≠ 0 0 t ∞ 113K K 0122t ∞ ∞ 113K K由表3-2可见，系统扰动稳态误差终值有可能为零、常数及无穷大三种情况。

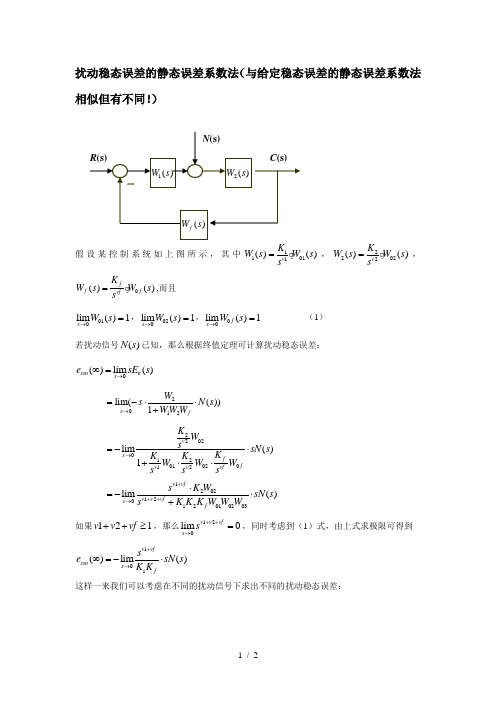
扰动稳态误差的静态误差系数法（与给定稳态误差的静态误差系数法相似但有不同！）假设某控制系统如上图所示，其中11011()()v K W s W s s =g ，22022()()v K W s W s s =g ，0()()ff f vf K W s W s s =g ,而且010lim ()1s W s →=，020lim ()1s W s →=，00lim ()1f s W s →= （1） 若扰动信号()N s 已知，那么根据终值定理可计算扰动稳态误差：()lim ()ssn n s e sE s →∞= 2012lim(())1s fW s N s WW W →=-⋅⋅+ 20220120102012lim ()1v s f f v v vf K W s sN s K K K W W W s s s→=-⋅+⋅⋅ 120212012010203lim ()v vf v v vf s f s K W sN s s K K K W W W +++→⋅=-⋅+ 如果121v v vf ++≥，那么120lim 0v v vfs s ++→=，同时考虑到（1）式，由上式求极限可得到101()lim ()v vfssn s fs e sN s K K +→∞=-⋅ 这样一来我们可以考虑在不同的扰动信号下求出不同的扰动稳态误差：从上面这个表格我们可看出用静态误差系数法求扰动稳态误差时与求给定稳态误差时很相似，但是又有很大不同：用静态误差系数法求扰动稳态误差判定系统的型号和开环放大系数时，只需考虑1()W s 和()f W s ，即只考虑原系统扰动作用点之前的前向通道传函以及反馈通道传函，至于系统扰动作用点之后的前向通道传函2()W s 与扰动稳态误差无关（而求给定稳态误差时所有的环节都要考虑）。

因此要减小扰动稳态误差的话只需改变扰动作用点之前的前向通道传函以及反馈通道传函，改变扰动作用点之后的前向通道传函是无效的。