当前位置：文档之家 › 2解方程(二)

2解方程(二)

  • 格式：ppt
  • 大小：1001.50 KB
  • 文档页数：17

下载文档原格式

  / 17

合集下载

五年级上数学解方程(2)

五年级上数学解方程(2)

等式两边除以同一个不为 0 数，左右两边仍然相等。
想一想：你能运用等式的性质解方程吗？
你能借助天平解释一下解方程的过程吗？
3x＝18 解：3x÷3＝18÷3
x＝6
x＝6是方程3x＝18的解吗？
方程左边＝3x ＝3×6 ＝18 ＝方程右边
所以，x＝6是方程的解。
知识提炼
知识点：形如ax＝b（a≠0）的方程的解法：
第5单元 简易方程
第7课时 解方程（2）
1.应用等式的性质，能较熟练地解形如ax＝b（a≠0）、 a－x＝b的方程。（重点）
2.理解运用等式的性质解方程的算理。（难点）
解：x＋4－4＝12－4 解：x－5＋5＝6.8＋5
x＝8
x＝11.8
解方程3x＝18
3x＝18 解：3x÷3＝18÷3
x＝6
所以，x＝11是方程的解。
知识提炼
知识点：解形如a－x＝b的方程时，可以根据等式的性质把它转
化成形如a＋x＝b的方程，再求x的值。解法如下： a－x＝b
解：a－x＋x＝b＋x a＝b＋x
x＋b＝a x＋b－b＝a－b
x＝a－b
Байду номын сангаас
小试牛刀
解方程并检验。 15－x＝6
解：15－x ＋x＝6＋x 15＝6＋x
解方程20－x＝9 想一想：你能运用等式的性质解方程吗？
等式两边同时减去20可以吗？
今天学的解方程与以前解决的方 程进行比较，有什么不同？
20－x＝9
解：20－x ＋ ＝9 ＋ x 20＝9＋x x 9＋x＝20
9＋x－9＝20－9 x＝11
检验：
方程左边＝20－x ＝20－11 ＝9 ＝方程右边
6＋x＝15 6＋x－6＝15－6

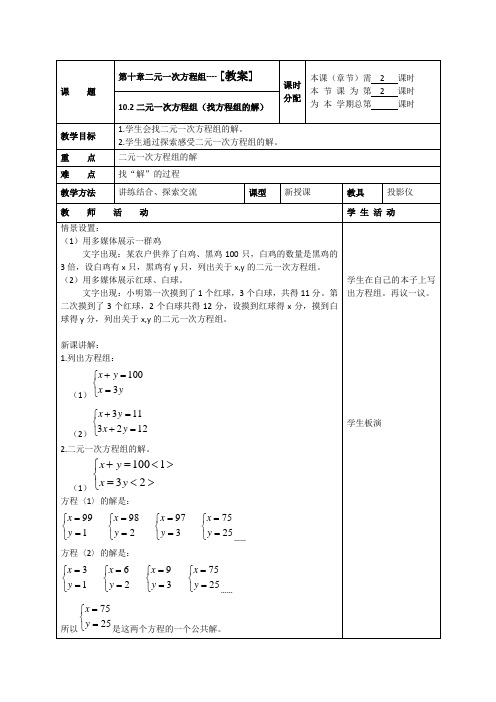
10.2二元一次方程组的解(2)(找方程组的解)

10.2二元一次方程组的解(2)(找方程组的解)

学生在自己的本子上写 出方程组。再议一议。
x y 100 x 3y （1） x 3 y 11 3x 2 y 12 （2）
2.二元一次方程组的解。 学生板演
x y 100 1 x 3y 2 （1）
方程〈1〉的解是：
x 75 y 25 是这两个方程的一个公共解。 所以
x 3 y 11 1 3x 2 y 12 2 （2）
方程〈1〉的解是：
x 2 y 3 x 0 y 6
x 5 y 2 x 2 y 3
x 0 y 2
x 2 y 3
x 1 y 5
(1) 哪几对是方程 2x-y=7 的解； (2) 哪几对是方程 x+2y=-4 的解？ 2．下面三对数值：
x 1 y 1
x 2 y 1
x 4 y 5 y 2x 3 4x 3y 1 （2）
课时 课时 课时
教学方法 教 师
新授课
教具
投影仪
学 生 活 动
情景设置： （1）用多媒体展示一群鸡 文字出现：某农户供养了白鸡、黑鸡 100 只，白鸡的数量是黑鸡的 3 倍，设白鸡有 x 只，黑鸡有 y 只，列出关于 x,y 的二元一次方程组。 （2）用多媒体展示红球、白球。 文字出现：小明第一次摸到了 1 个红球，3 个白球，共得 11 分。第 二次摸到了 3 个红球，2 个白球共得 12 分，设摸到红球得 x 分，摸到白 球得 y 分，列出关于 x,y 的二元一次方程组。 新课讲解： 1.列出方程组：
x 8 y 1 …… x 4 y 0 ……

北师大版数学四年级下册 第5单元解方程(二) 教案

北师大版数学四年级下册 第5单元解方程(二) 教案

《解方程（二）》教学设计教学目标：1、通过观察天平称重的具体情境，类比等式变形的过程，抽象出等式性质，即等式两边都乘同一个数（或除以同一个不为零的数），等式仍然成立；进一步了解等式性质是解方程的根据。

2、会用等式的性质解形如2X=10的简单方程。

教学过程：一、谈话导入，引发猜想。

1、同学们，上一节课我们已经学习了"等式两边都加上(或减去)同一个数，等式仍然成立"，受这个规律的启发，你有什么新的猜想呢？2、对于他的猜想，谁还有补充？为什么？3、谁能把大家的猜想用一句话来概括一下？4、我们的猜想是否正确呢？（ppt出示？）今天我们就来一起走进《解方程二》，验证大家的猜想。

板书课题。

二、合作交流，尝试验证怎样验证我们的猜想呢？（举例子、用天平）（这个同学给大家的建议不错）有请我们的老朋友“天平”闪亮登场！1、出示合作学习要求2、组长组织组员合作探究3、小组代表展示汇报（选一组天平展讲）4、师过渡语：一个数学规律的探究只做一次实验往往是不够的，数学家门经常要经过很多次的探究论证才能得出，那我们就再请一组同学来验证一下吧。

5、现在请大家一起自豪大声的读出我们探究的规律。

6、这就是等式的又一个性质，你认为哪些词最重要？为什么？7、规律探究出来了，你会用规律吗？8、出示4y=2000，集体解方程，根据昨天《解方程一》的经验，你觉得这个方程该怎么解呢？（师提醒解方程的格式：先写“解：”，等号对齐，未知数一般写在等号左边）10、师：关于刚才解方程的过程，大家有什么疑问吗？ 11、y=500对吗？怎么验证呢？（生口答，师板演） 12、还有疑问吗？为什么非要除以4呢？两边都除以别的不为0的数也可以呀？ 13、师小结：等式两边到底选择怎样的乘除运算，其本质就是依据等式性质，通过乘除的相互抵消，得出未知数的值。

14、师：淘气给大家刚才解方程的过程配了一副图，谁能看懂，给大家分享一下自己的想法。

三、学以致用，小试牛刀。

2022年人教版五年级上册数学第五单元教案2 解简易方程 第3课时

2022年人教版五年级上册数学第五单元教案2 解简易方程 第3课时

第三课时教学内容解方程(二)。

(教材第69页)教学目标1.使学生会用等式的性质解形如ax±b=c类型的方程，并会用方程的解进行验算。

2.使学生会把小括号内的式子看作一个“整体”，来解形如(x+b)a=c类型的方程，体会“整体”思想在教学中的运用。

重点难点重点：连续两次运用等式的性质，解形如ax±b=c、(x+b)a=c类型的方程。

难点：体会“整体”思想在教学中的运用。

教具学具多媒体课件。

教学过程一导入1.请学生默写或者默背等式的性质，然后指名回答。

(1)等式两边同时加上或减去同一个数，等式两边仍然相等。

(2)等式两边同时乘同一个数，或除以同一个不为0的数，左右两边仍然相等。

2.说说解下面方程的根据。

x+3.5=79.41.5x=7.5x÷5=4.23-x=2.5二教学实施教学教材第69页例4。

1.投影出示。

师：图中左边有几盒水彩笔，每盒多少支?右边散放着几支?整盒的水彩笔有多少支?一共有多少支?生：从图中可以看出，有3盒水彩笔，每盒x支，所以整盒的水彩笔应该有x+x+x=3x(支)，散放着4支，一共有(3x+4)支水彩笔。

师：大括号表示什么意思?40支和大括号有什么关系?生：上图中的大括号表示把整盒的和散放着的加在一起是40支。

师：你能根据图列方程吗?生：根据图中给出的信息可以得出，3盒水彩笔的支数+4=40，所以可以列出方程3x+4=40。

2.探索3x+4=40的解法。

师：观察这个方程的形式和前面学习过的方程有什么不同?你会计算吗?(学生独立思考)追问：能否用等式的性质解这种形式的方程?怎样算?根据学习解方程的经验，尝试解这个方程。

学生独立完成，集体订正。

师：解方程3x+4=40时，一般把“3x”看作“整体”，根据等式的性质1先在方程的两边都减去4，把方程转化为3x=36，然后再根据等式的性质2求出方程的解。

学生汇报交流算法。

先把3x看作一个数，把这题看成是x+b=c形式的方程，运用等式性质1：等式两边同时减去同一个数，等式两边仍然相等来解方程。

小学数学《解方程(2)》教学课件

小学数学《解方程(2)》教学课件
3x÷3=2.1÷3 x=0.7
巩固提高
2.列方程并解答。[教材P68 做一做 第2题 ]
x元
1.2元
4元
x+1.2＝4 解：x+1.2-1.2＝4-1.2
x＝2.8
2.列方程并解答。[教材P68 做一做 第2题 ]
x元
x元 x元
8.4元
3x＝8.4 解：3x÷3＝8.4÷3
x＝2.8
巩固提高
方程左边＝20－x ＝20－11 ＝9 ＝方程右边
所以，x＝11是方程的解。
巩固提高
1.解下列方程。[教材P68 做一做 第1题 ]
x+3.2=4.6
x-1.8=4
解：x+3.2-3.2=4.6-3.2 x=1.4
解：x-1.8+1.8=4+1.8 x=5.8
巩固提高
1.解下列方程。[教材P68 做一做 第1题 ]
（等式的性质1）
（等式左右两边交换位置） （加法交换律，等式性质1）
探索新知
解方程 20－x＝9 。
[教材P68 例3]
解：20－x＋x＝9＋x 20＝9＋x
9＋x＝20 9＋x－9＝20－9
x＝11
你学会解方程了吗？和同学讨论 一下，解方程需要注意什么？
等式两边加上相同的式子， 左右两边仍然相等。
R·五年级上册
解方程（2）
探索新知
解方程 3x=18 。[教材P68 例2]
x xx
看图列方程： 3x=18
等式两边除以同一个不等于0 的数，左右两边仍然相等。
解：3x÷（ 3 ）=18÷（ 3 ） x=（ 6 ）
请你检验一下。
探索新知
解方程 3x=18 。[教材P68 例2]

人教五年级数学上册解方程(二)

人教五年级数学上册解方程(二)

?[选自《创优作业100分》P45] 1.解：设这个数是x。
2.解：设这个数是x。
5x－6.8=12.7
1.4x+3.2×3=23.6
x=3.9
x=10
答：这个数是3.9。
答：这个数是10。
六、如果x+x+x+y+y=54，x +x +y +y=46，那么x和y 各是多[少选自?《创优作业100分》P45]
x=4.2
解： x-45=128 x-45+45=128+45 x=173
解： 9x=18 9x÷9=18÷9
x=2
解： x÷4=75 x÷4×4=75×4
x=300
2.看图列方程并求解。 [教材P72 练习十五 第11题 ]
周长36m
xm
2(x+5)=36
5m 解：
2(x+5)÷2=36÷2
＝8 ＝方程右边
8 2x－32＋32＝8＋32所以，x＝20是方程的解。
2x＝40 2x÷2＝40÷2
x＝20
三、巩固练习
1.看图列方程，并求出方程的解。[教材P69 做一做 第1题 ]
x元/本
7.5元 5x+1.5＝7.5 解： 5x＋1.5－1.5＝7.5－1.5
5x＝6 5x÷5＝6÷5
x＝1.2
0.4=1.7
x=37
x－
*3x－4×0.6=5.4
0.4+0.4=1.7＋0.4
解：3x－2.4=5.4 方程左边=3×2.6－4×0.6
3x－2.4+2.4=5.4+2.4
x==27..81-2.4
3x=7.8

解方程(2)

等式两边同时加上x，方程会变成我 们学过的20=9+x。
新教课学讲目解
解方程
20-x=9 解： 20-x+x=9+x
20=9+x 9+x=20 9+x-9=20-9
x=11
方程两边同时加 上相同的式子，等式 仍然相等。
检验：方程左边=20-x =20-11 =9 =方程右边
所以，x=11是方程的解。
解方程2
数学人教版 五年级上
导入新课
解方程
x+30=49 解：x+30-30=49-30
x=19
x-30=49 解：x-30+30=49+30
x=79
解这两个方程的依据是什么？
依据等式的性质1,：等式的两边同时加上 或者减去同一个数，等式两边仍然相等。
导入新课
等式的另一个性质是什么？
等式的两边同时乘以或者除以一个相同 的数（这个数不能是0），等式仍然成立。
38=5+x 5+x=38 5+x-5=38-5
x=33
巩教固学提目升
列方程解决问题
500kg
xkg
已知牛的体重是狗的20 倍，狗的体重是多少千克？
500÷X=20 解：500÷X×X =20×X
500=20X 20X=500 20X÷20=500÷20
x=25
课教堂学小目结
本课你有什么收获？
1、利用等式的性质2解方程。 2、学会了解形如3x=18和20-x=9方程。
什么情况下用这个性质解方程呢？
新课讲解
解方程
3x = 18
等式的两边同时除以一个不为0的数， 等式仍然成立。 3x÷3 = 18÷3 x =6

解方程例2

所以，x=3.3是方程来自解。3. 解下列方程并检验。
0.2x=6 解：0.2x÷0.2=6÷0.2
x=30 检验 方程左边=0.2×30
=6 =方程右边 所以，x=30是方程的解。
4. 看图列方程，并求出方程的解。
xm
2.7 m 6.9 m
原价：x 元 降价：45 元 现价：128元
x+2.7 = 6.9
ɑx= b
解：ax÷a = b÷ɑ
x = b÷ɑ
x÷a =b 解：x÷a×a = b×ɑ
x = b×ɑ
利用等式的性质2解类似于上面的方程时，方程左边乘几，两边就同时除以 几；方程左边除以几，两边就同时乘几。
巩固提高
2.列方程并解答。[教材P68 做一做 第2题 ]
x元
1.2元
4元
x+1.2＝4 解：x+1.2-1.2＝4-1.2
这个方程与乘法有关，我觉得可以根据等式 的性质2来解方程。
（教材第68页例2）
2 解方程 3x = 18。
x xx
3x = 18
等式两边除以同一个不等于 0的数，左右两边仍然相等。
3x÷( 3 )= 18÷( 3 )
方程左边有×3，两 边要“÷3” 是为了 消去左边的×3。
为什么要÷3？
2 解方程 3x = 18。
ɑx= b
解：ax÷a = b÷ɑ
x = b÷ɑ
x÷a =b 解：x÷a×a = b×ɑ
x = b×ɑ
解： 4.6+x = 7.5 4.6+x-4.6 = 7.5-4.6
x = 2.9
将x=2.9代入方程ax=5.8
2.9a = 5.8 2.9a÷2.9 = 5.8÷2.9

5.2《解方程(2)》练习

5.2《解方程(2)》练习
一、基础过关
1.解下列方程：
(1)66)1(3=--x (2)x x 4853-=-
(3)4)3(2-=--x (4)26)5.1(4=++x x
(5))12(4113+=-x x (6)3)20(34=--x x
(7)86)24(12+=-x x (8)2)32(68-=+-x
(9)3)1()63(2=--+x x (10))23(5)1(36)8(8x x x ---=+-
2.若代数式3-x 与2
1互为倒数，则x 的值是_________. 3.代数式43-x 和)3(2+x 互为相反数，则=x _______.
二、能力提升
4.代数式)42(4)36(31x x x ----的值等于2，求x 的值.
5.关于x 的方程x a x a )13(6--=+的解为1=x ，求32-a 的值.
6.代数式4)5(38y x
m --与1)3(221+--n m y x 为同类项，求n m 3-的值.
7.若关于x 的方程063=-a x 与方程a x -=9有相同的解,求a 的值.
8.在一次美化校园的活动中，先安排31人去拔草，18人去植树，后又增派20人去支援他们，结果拔草的人数是植树人数的2倍，问支援拔草和植树的分别有多少人？
三、聚沙成塔
有一旅客携带30千克的行李，从国际机场乘飞机去某市，按民航规定，旅客最多可免费带20千克行李，超重部分每千克按飞机票价格的1.5%购买行李票，若行李票价为120元，求他的飞机票的价格应是多少？。

人教新课标五年级上册数学教案：5.5《解方程2》

标题：人教新课标五年级上册数学教案：5.5《解方程2》一、教学目标1. 让学生掌握解方程的基本方法，能够解一元一次方程。

2. 培养学生的逻辑思维能力和解决问题的能力。

3. 通过解方程的过程，让学生体验数学的奥妙，激发学生学习数学的兴趣。

二、教学内容1. 解方程的基本方法：等式两边同时加上或减去相同的数，等式仍然成立；等式两边同时乘以或除以相同的数（不为0），等式仍然成立。

2. 解一元一次方程的步骤：去分母、去括号、移项、合并同类项、系数化为1。

三、教学重点与难点1. 教学重点：解方程的基本方法和步骤。

2. 教学难点：解方程时如何灵活运用等式的基本性质，以及如何处理各种复杂情况。

四、教学过程1. 导入：通过回顾上一节课的内容，引导学生思考如何解方程。

2. 探究：让学生尝试解一些简单的一元一次方程，如2x 3=7，3x-4=2等。

在此过程中，引导学生发现解方程的基本方法，即等式两边同时加上或减去相同的数，等式仍然成立；等式两边同时乘以或除以相同的数（不为0），等式仍然成立。

3. 讲解：讲解解一元一次方程的步骤，如去分母、去括号、移项、合并同类项、系数化为1等。

通过示例演示，让学生理解并掌握这些步骤。

4. 练习：让学生独立完成一些练习题，巩固解方程的方法和步骤。

在此过程中，教师巡视课堂，及时解答学生的问题。

5. 小结：通过提问方式，让学生回顾本节课所学内容，总结解方程的方法和步骤。

6. 作业：布置一些课后作业，让学生在课后巩固所学知识。

五、教学评价1. 课堂表现：观察学生在课堂上的参与程度、积极性和解题能力。

2. 练习完成情况：检查学生练习题的完成情况，了解学生对解方程方法和步骤的掌握程度。

3. 作业完成情况：批改学生的课后作业，评估学生对本节课知识的掌握程度。

六、教学反思本节课结束后，教师应认真反思教学过程中的优点和不足，以便在今后的教学中不断改进，提高教学质量。

同时，关注学生的学习情况，针对学生的实际情况进行教学调整，使每个学生都能在数学课堂上获得更好的学习效果。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
返回

方程两边同除以5, 方程两边同除以5, 得 x=3
下列方程的求解过程是否正确
（1） 5（x-1）=4 (2） (2） 2-（1-x）=-2+2x 1+x=去括号, 去括号,得 2-1+x=-2+2x 移项, 移项,得 化简, 化简,得 x-2x=-2-2+1 2;x=20-3 4(x+0.5)+x=20-

学习目标
1、学习含有括号的一元一次方程的解法. 学习含有括号的一元一次方程的解法. 2、进一步体会解方程是运用方程解决实际问 题重要环节. 题重要环节.

自学提示:请同学们阅读教材174页想一想 回答： 自学提示:请同学们阅读教材174页想一想，回答： 页想一想，
（1）这个方程列得对吗？ 这个方程列得对吗？ （2）怎样解所列的方程呢？ 怎样解所列的方程呢？ （3）你还有什么疑问吗？ 你还有什么疑问吗？
继续


1.学习了含有括号的一元一次方 1.学习了含有括号的一元一次方 程的解法. 程的解法. 2.学习了利用整体思想解一元一 2.学习了利用整体思想解一元一 次方程

A 组:课本习题 课本习题5.4 1 2 3 课本习题 B组 : 176页 问题解决 组 页
解方程:4(x+0.5)+x=17 解方程:4(x+0.5)+x=17
须先去 括号
去括号有什么 注意事项呢? 注意事项呢

注意：括号前面的数要和括号里的每一项都 注意： 相乘
解方程: 4(x+0.5)+x=17 解方程: 4(x+0.5)+x=17 解:去括号, 得 去括号, 4x+2+x=17 移项, 移项, 得 合并同类项, 合并同类项, 得 4x+x=174x+x=17-2 5x=15
解方程解方程-2（X-1）=4
方法一：先去括号 方法一： 方法二：整体思想 方法二：
你有几种 方法呢？ 方法呢？

解法一： 解法一： -2（x-1）=4 去括号，得 去括号， 移项，得 移项， 化简，得 化简， 方程两边同除以方程两边同除以-2，得 -2x+2=4 -2x=4-2 2x=4-2x=2 x=-1 x=返回
X=-11 X=X=-4 X=-

一个两位数,十位数字是个位数字的两倍, 一个两位数,十位数字是个位数字的两倍,将两个 数字对调后得到的两位数比原来的两位数小36, 数字对调后得到的两位数比原来的两位数小36, 求这个两位数. 求这个两位数.
解：设这个两位数的个位数字为x,十位数字为2x, 设这个两位数的个位数字为x,十位数字为 十位数字为2x, (10 *2x+x)-(10x+2x)=36 *2x+x)解得 x=4 则这个两位数为10*2x+x=10*2*4+4=84 则这个两位数为10*2x+x=10*2*4+4=84 答：这个两位数是84. 这个两位数是84.



解法二 -2（x-1）=4 方程两边同除以方程两边同除以-2，得 x-1=-2 1=移项，得 移项， 即 x=-2+1 x=x=-1 x=-
返回

(1) -3(x+3)=24 (2) -2(x-2)=12 2(x-
解:去括号,得 5x-1=4 去括号, 5x移项, 移项,得 化简, 化简,得 5x=4+1 5x=5
方程两边同除以5, 方程两边同除以5,得 5,得 x=1

解下列方程
(1)11x+1=5(2x+1) x=4 (1)11x+1=5(2x+1) (2)4x-3(20-x)=3 (2)4x-3(20(3)5(x+8)-5=0 (3)5(x+8)(4)2(3-x)=9 (4)2(3x=9 x=-7 x=x=-1.5 x=
第五章 一元一次方程

一听可乐比 一听果奶多 0.5元 元
我要一听果奶和4听可 我要一听果奶和 听可 乐
一听果奶多 少钱？ 少钱？你能 列出方程吗？ 列出方程吗？
找你3 找你3 元
给 您 20 元

如果设一听果奶X 如果设一听果奶X元，那么可列出方程