工程力学讲义
- 格式:doc
- 大小:303.32 KB
- 文档页数:6



课题第1讲——第一章绪论学时2学时教学目的要求1、掌握工程力学的任务、地位、作用和学习方法,可变形固体的基本假设,工程力学的研究对象(杆件),杆件变形的形的形式。
2.理解工程力学的研究对象(杆件)的几何特征,使学生对工程力学这门课程的任务、研究对象有一个全面的概念。
3.了解工程的发展简史和学习本课程的方法。
主要内容1、简单介绍四种基本变形重点难点变形固体及其基本假设教学方法和手段以讲授为主,使用电子教案课后作业练习预习:第二章本次讲稿第一章绪论第一节工程力学的研究对象建筑物中承受荷载而起骨架作用的部分称为结构。
结构是由若干构件按一定方式组合而成的。
组成结构的各单独部分称为构件。
例如:支承渡槽槽身的排架是由立柱和横梁组成的刚架结构,如图1-1a所示;单层厂房结构由屋顶、楼板和吊车梁、柱等构件组成,如图1-1b所示。
结构受荷载作用时,如不考虑建筑材料的变形,其几何形状和位置不会发生改变。
图1-1ab结构按其几何特征分为三种类型:(1)杆系结构:由杆件组成的结构。
杆件的几何特征是其长度远远大于横截面的宽度和高度。
(2)薄壁结构:由薄板或薄壳组成。
薄板或薄壳的几何特征是其厚度远远小于另两个方向的尺寸。
(3)实体结构:由块体构成。
其几何特征是三个方向的尺寸基本为同一数量级。
工程力学的研究对象主要是杆系结构。
第二节工程力学的研究内容和任务工程力学的任务是研究结构的几何组成规律,以及在荷载的作用下结构和构件的强度、刚度和稳定性问题。
研究平面杆系结构的计算原理和方法,为结构设计合理的形式,其目的是保证结构按设计要求正常工作,并充分发挥材料的性能,使设计的结构既安全可靠又经济合理。
进行结构设计时,要求在受力分析基础上,进行结构的几何组成分析,使各构件按一定的规律组成结构,以确保在荷载的作用下结构几何形状不发生发变。
结构正常工作必须满足强度、刚度和稳定性的要求。
强度是指抵抗破坏的能力。
满足强度要求就是要求结构的构件在正常工作时不发生破坏。


《工程力学》(陈传尧,高等教育出版社)§1 绪论§1.1什么是力学力学是物质机械运动规律的科学。
工程力学(应用力学)是将力学原理应用于实际意义的工程系统的科学。
目的:了解工程系统的性态并为其设计合理的规则。
§1.2力学发展史力学发展史就是人类从自然现象和生产活动中认识和应用物体机械运动规律的历史。
春秋墨翟及其弟子《墨经》;古希腊亚里士多德杠杆、运动;古希腊阿基米德静力学;牛顿《自然哲学的数学原理》牛顿以后力学研究的四个时期:1、17世纪初-18世纪末经典力学伽利略惠更斯牛顿莱布尼茨伯努利拉格朗日达朗贝尔2、19世纪力学各主要分支的建立材料力学结构力学流体力学弹性力学3、1900-1960年近代力学固体力学空气动力学一般力学4、1960年后现代力学计算力学生物力学“善于从错综复杂的自然现象、科学研究结果和工程技术实践中抓住事物的本质,提炼成力学模型,采用合理的数学工具,分析掌握自然现象的规律,进而提出解决工程技术问题的方案,最后再和观察或实验结果反复校核直到接近为止的科学研究方法。
”§1.3力学与工程力学与工程是紧密相连的。
飞行问题§1.4学科分类;静力学+运动学+动力学;一般力学(理论力学、分析力学、振动力学),固体力学(材料力学、结构力学、弹性力学、塑性力学、断裂力学、复合材料力学),流体力学(水力学、空气动力学、环境流体力学);研究手段:理论分析、实验研究、数值计算§1.5基本概念与基本方法1、基本概念力是物体间的相互作用。
运动是整个物体的位置随时间的变化。
变形是物体自身尺寸、形状的改变。
F=m*a 将力与运动联系起来。
2、研究方法选择研究系统;对系统抽象简化,建立力学模型;将力学原理应用于理想模型,分析、推理、得出结论;实验验证或将问题退化至简单情况与已知结论比较;验证后,若结论不满意,建立不同模型,再分析。
3、研究内容力的平衡、变形的几何协调、材料的物理性能是研究工程静力学问题的核心内容和主线。

工程力学基础目录概述 (3)第一章物体的受力分析和静力学平衡方程 (5)第一节静力学基本概念 (5)第二节约束和约束反力 (10)第三节分离体和受力图 (13)第四节力的投影合力投影定理 (16)第五节力矩力偶 (19)第六节力的平移 (22)第七节平面力系的简化合力矩定理 (23)第八节平面力力系的平衡方程 (30)第九节空间平面力系 (38)第二章拉伸、压缩与剪切 (43)第一节轴向拉伸与压缩的概念和实例 (44)第二节轴向拉伸或压缩时横截面上的内力 (45)第三节轴向拉伸或压缩时横截面上的内力 (47)第四节轴向拉伸或压缩时的变形 (50)第五节材料在拉伸与压缩时的力学性能 (54)第六节轴向拉伸或压缩时的强度计算 (59)第七节应力集中的概念 (63)第八节剪切与挤压的实用计算 (64)第三章扭转 (68)第一节扭转的概念和实例 (68)第二节扭转时外力和内力的计算 (69)第三节纯剪切 (71)第四节圆轴扭转时横截面上的应力 (73)第五节圆轴扭转的强度计算 (76)第六节圆轴扭转的变形和刚度计算 (78)第四章弯曲 (79)第一节平面弯曲的概念和实例 (79)第二节梁弯曲时的内力—剪力和弯矩 (81)第三节剪力图和弯矩图 (84)第四节纯弯曲时梁横截面上的正应力 (89)第五节惯性矩和弯曲截面系数 (91)第六节梁的弯曲强度计算 (92)第七节*不作要求* (96)第八节弯曲变形 (96)第五章组合变形构件的强度计算 (101)第一节点的应力状态简介 (101)第二节(第二、三节不讲) (103)第三节(第二、三节不讲) (103)第四节强度理论简介 (103)第五节组合变形的强度计算 (106)第六章交变应力 (113)第一节交变应力及构件的疲劳破坏 (113)第二节循环特征和持久极限(二、三节合并) (115)第四节提高构件疲劳强度的措施 (118)工程力学基础概述工程力学是一门研究物体机械运动及构件强度、刚度和稳定性的科学。

工程力学讲义静力学静力学的基本概念1、平衡——平衡是物体机械运动的特殊形式,是指物体相对地球处于静止或匀速直线运动状态。
2、刚体——在外界的任何作用下形状和大小都始终保持不变的物体。
或者在力的作用下,任意两点间的距离保持不变的物体。
刚体是一种理想化的力学模型。
一个物体能否视为刚体,不仅取决于变形的大小,而且和问题本身的要求有关。
3、力——力是物体相互间的机械作用,其作用结果使物体的形状和运动状态发生改变。
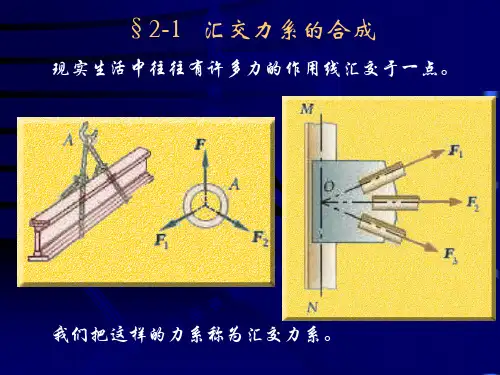
1. 静力学公理基本概念力系——作用于同一物体或物体系上的一群力。
等效力系——对物体的作用效果相同的两个力系。
平衡力系——能使物体维持平衡的力系。
合力——在特殊情况下,能和一个力系等效的一个力。
公理一 (二力平衡公理)要使刚体在两个力作用下维持平衡状态,必须也只须这两个力大小相等、方向相反、沿同一直线作用。
公理二 (加减平衡力系公理)可以在作用于刚体的任何一个力系上加上或去掉几个互成平衡的力,而不改变原力系对刚体的作用。
推论 (力在刚体上的可传性)作用于刚体的力,其作用点可以沿作用线在该刚体内前后任意移动,而不改变它对该刚体的作用。
公理三 (力平行四边形公理)作用于物体上任一点的两个力可合成为作用于同一点的一个力,即合力。
合力的矢由原两力的矢为邻边而作出的力平行四边形的对角矢来表示。
即,合力为原两力的矢量和。
矢量表达式:R= F1+F2推论 (三力汇交定理)当刚体在三个力作用下平衡时,设其中两力的作用线相交于某点,则第三力的作用线必定也通过这个点。
公理四 (作用和反作用公理)任何两个物体间的相互作用的力,总是大小相等,作用线相同,但指向相反,并同时分别作用于这两个物体上。
公理五 (刚化公理)设变形体在已知力系作用下维持平衡状态,则如将这个已变形但平衡的物体变成刚体(刚化),其平衡不受影响。
2. 力对点之矩力矩:表示力使物体绕某点转动效应的量称为力对点之矩简称力矩。
它的大小为力F的大小与力臂d的乘积,它的正负号表示力矩在平面上的转向。

《工程力学》讲义目录绪论0. 1 工程力学的课程内容及其工程意义0. 2 工程力学的研究模型第一篇工程静力学第1章工程静力学基础1.1 力1.1.1 力的概念及其效应1.1.2 力系的概念(分类)1.1.3 力的性质(力的可传性、平行四边形法则)1.2 约束与约束力1.2.1 约束与约束力的概念1.2.2 柔性约束1.2.3 光滑面约束1.2.4 光滑铰链约束1.2.5 滑动轴承与推力轴承1.3 平衡的概念1.3.1 二力平衡与二力构件1.3.2 不平行的三力平衡条件1.3.3 加减平衡力系原理1.4 受力图1.4.1 隔离体和受力分析步骤1.4.2 受力图绘制方法应用举例1.5 力矩1.5.1 力对点之矩1.5.2合力矩定理1.5.3力对轴之矩1.6 力偶及其性质1.6.1 力偶的概念1.6.2 力偶的性质1.6.3 力偶系的合成及其平衡第2章力系的简化2.1 力在坐标轴上的投影2.1.1 力在坐标轴上的投影2.1.2 合力投影定理2.2 力线平移定理2.3 平面任意力系的简化2.3.1 平面力系向已知点的简化——主矢与主矩2.3.2 固定端约束2.3.3 简化结果的讨论2.4 其他力系的简化2.4.1 平面汇交力系的合成结果2.4.2 空间任意力系的简化第3章工程中的静力平衡问题分析3.1 平面力系的平衡条件与平衡方程3.1.1 平面任意力系的平衡条件与平衡方程3.1.2 平面任意力系平衡方程的其他形式3.1.3 平面汇交力系和平面平行力学的平衡(配重问题)3.2 简单的刚体系统平衡问题3.2.1 刚体系统静定与静不定的概念3.2.2 刚体系统的平衡问题的求解3.3 考虑摩擦时的平衡问题3.3.1 滑动摩擦定律3.3.2 考虑摩擦时构件的平衡问题3.3.3 摩擦角与自锁的概念3.4 空间力系平衡问题3.4.1 空间力系平衡条件与平衡方程3.4.2 重心第二篇材料力学第4章材料力学的基本概念4.1 材料力学的基本假设4.1.1 连续性假定4.1.2 均匀性假设4.1.3 各向同性假定4.1.3 小变形假定4.2 弹性杆件的外力与内力4.2.1 外力4.2.2 内力与截面法4.3 正应力与切应力4.4 正应变与切应变4.5 杆件受力与变形的基本形式4.5.1 拉伸或压缩4.5.2 剪切4.5.3 扭转4.5.4 平面弯曲4.5.5 组合受力与变形第5章轴向拉伸、压缩与剪切5.1 工程中的轴向拉伸和压缩问题5.2 轴力与轴力图5.2.1 截面法求轴力5.2.2 轴力图5.3 拉压杆的应力5.3.1 横截面上的应力5.3.2 斜截面上的应力5.3.3 圣维南原理5.4 材料在拉伸与压缩时的力学性能5.4.1 应力应变图5.4.2 低碳钢在拉伸时的力学性能5.4.3 其他材料的拉伸力学性能5.4.4 材料在压缩时的力学性能5.5 拉压杆的强度设计5.5.1 失效与许用应力5.5.2 轴向拉伸与压缩时的强度条件5.5.3 三类强度计算问题5.6 轴向拉伸和压缩时的变形计算5.6.1 轴向变形与虎克定律5.6.2 横向变形与泊松比5.7 简单拉压静不定问题5.8 连接部分的强度计算5.8.1 剪切的实用计算5.8.2 挤压的实用计算第6章圆轴的扭转6.1 工程中的扭转问题6.2 外力偶矩、扭矩与扭矩图6.2.1 外力偶矩6.2.2 扭矩6.2.3 扭矩图6.3 切应力互等定理与剪切虎克定律6.3.1 切应力互等定理6.3.2 剪切虎克定理6.4 圆轴扭转时横截面上的应力6.4.1 圆轴扭转时横截面上的切应力公式6.4.2 极惯性矩与抗扭截面系数6.5 圆轴扭转时的变形6.6 圆轴扭转的强度设计和刚度设计6.6.1 强度条件和强度计算6.6.2 刚度条件和刚度计算6.7 非圆截面轴扭转简介第7章梁的弯曲内力7.1 工程中的弯曲问题7.2 梁的计算简图7.2.1 载荷的简化7.2.2 实际约束的简化7.2.3 梁的类型7.3 剪力与弯矩7.4 剪力方程与弯矩方程、剪力图与弯矩图7.5 载荷集度、剪力、弯矩之间的微分关系第8章梁的应力及强度设计8.1 对称弯曲正应力8.1.1 纯弯梁横截面上的正应力8.1.2 常见界面的惯性矩、抗弯截面系数及组合截面的惯性矩8.2 对称弯曲切应力简介8.3 梁的强度条件及其应用8.4 提高梁强度条件的主要措施8.5 斜弯曲8.6 弯拉(压)组合梁的强度计算第9章平面弯曲梁的变形与刚度设计9.1 弯曲变形概念9.2 挠曲线近似微分方程9.3 计算弯曲变形的积分法9.4 计算弯曲变形的叠加法9.5 梁的刚度条件与合理刚度设计9.5.1 梁的刚度条件9.5.2 刚度的合理设计9.5.3 提高梁的弯曲刚度的措施9.6 简单静不定梁第10章压杆稳定10.1 稳定性概念10.2 临界压力的欧拉公式10.2.1 两端铰支压杆的临界压力10.2.2 其他约束条件下的压杆的临界压力10.2.3 临界应力、柔度、欧拉公式的适用范围10.3 中、小柔度杆的临界应力10.3.1 中柔度杆临界应力的经验公式10.3.2 小柔度杆的临界应力10.3.3 临界应力总图10.4 压杆的稳定计算与合理设计10.4.1 稳定性条件10.4.2 压杆的合理设计10.4.3 提高压杆稳定性的措施0.1 工程力学的课程内容及其工程意义工程力学是一门关于力学学科在工程上的基本应用的课程,它通过研究物体机械运动的一般规律来对工程构件进行相关的力学分析和设计,其包含的内容极其广泛。
静力学
静力学的基本概念
1、平衡——平衡是物体机械运动的特殊形式,是指物体相对地球处于静止或匀速直线运动状态。
2、刚体——在外界的任何作用下形状和大小都始终保持不变的物体。
或者在力的作用下,任意两点间的距离保持不变的物体。
刚体是一种理想化的力学模型。
一个物体能否视为刚体,不仅取决于变形的大小,而且和问题本身的要求有关。
3、力——力是物体相互间的机械作用,其作用结果使物体的形状和运动状态发生改变。
1. 静力学公理
基本概念
力系——作用于同一物体或物体系上的一群力。
等效力系——对物体的作用效果相同的两个力系。
平衡力系——能使物体维持平衡的力系。
合力——在特殊情况下,能和一个力系等效
的一个力。
公理一 (二力平衡公理)
要使刚体在两个力作用下维持平衡状态,必须也只须这两个力大小相等、方向相反、沿同一直线作用。
公理二 (加减平衡力系公理)
可以在作用于刚体的任何一个力系上加上或去掉几个互成平衡的力,而不改变原力系对刚体的作用。
推论 (力在刚体上的可传性)
作用于刚体的力,其作用点可以沿作用线在该刚体内前后任意移动,而不改变它对该刚体的作用。
公理三 (力平行四边形公理)
作用于物体上任一点的两个力可合成为作用于同一点的一个力,即合力。
合力的矢由原两力的矢为邻边而作出的力平行四边形的对角矢来表示。
即,合力为原两力的矢量和。
矢量表达式:R= F1+F2
推论 (三力汇交定理)
当刚体在三个力作用下平衡时,设其中两力的作用线相交于某点,则第三力的作用线必定也通过这个点。
公理四 (作用和反作用公理)
任何两个物体间的相互作用的力,总是大小相等,作用线相同,但指向相反,并同时分别作用于这两个物体上。
公理五 (刚化公理)
设变形体在已知力系作用下维持平衡状态,则如将这个已变形但平衡的物体变成刚体(刚化),其平衡不受影响。
2. 力对点之矩
力矩:表示力使物体绕某点转动效应的量称为力对点之矩简称力矩。
它的大小为力F的大小与力臂d的乘积,它的正负号表示力矩在平面上的转向。
由力矩的定义可知:
a 当力的作用线通过矩心时,力臂值为0,力矩值也为0.
b 力沿其作用线滑移时,不会改变力对点之矩的值,因为此时并未改变力,力臂的大小及力矩的转向。
合力矩定理
平面力系的合理对平面上任一点之矩,等于所有各分力对同一点力矩的代数和。
3 力偶的性质:
1、力偶的第一性质:力偶的作用效果是使刚体发生转动,不能与一个力等效——没有合力,也不能用一个力与之平衡——只有一个反转向的力偶才能与之平衡。
因此力偶和力是静力学的两个基本要素(机械作用量)。
2、力偶的第二性质:力偶对物体的转动效应,用力偶矩来度量,其大小为力偶中力F与力偶臂h的乘积。
同平面力偶的等效定理
3、同一平面内的两个力偶,如果力偶矩相等,则此二力偶相等。
4、力偶可在其作用面内任意移动(或移动到另一平行平面),而不改变对刚体的作用。
5、只要力偶的转向和力偶矩的大小不变(F、h可变),则力偶对刚体的作用效应就不变,
4. 力的平移定理
力的平移定理表明,作用于刚体上的力可以平移到刚体内任意一点,但必须附加一力偶。
此附加力偶的力偶矩等于原力对平移点之矩。
5. 约束和约束反力
基本概念:
1、自由体:可以任意运动(获得任意位移)的物体。
2、非自由体:不可能产生某方向的位移的物体。
3、约束:由周围物体所构成的、限制非自由体位移的条件。
4、约束反力:约束对被约束体的反作用力。
5、主动力:约束力以外的力。
几种常见约束力
(一)光滑接触面约束
性质:光滑支承面对物体的约束力,作用在接触点处,方向沿接触表面的公法线,
并指向被约束的物体,这种约束力称为法向约束力,通常用FN表示,如图。
(a)(b)
光滑接触面约束
(二)柔性体(由绳索、链条或皮带等构成)约束
性质:约束力作用在接触点处,方向沿着柔索背离物体,通常用FT表示,如图。
(a)(b)
柔性约束
(三)光滑铰链约束
1、径向轴承
性质:当轴所受的主动力未确定时,约束力的方向预先不能确定,但无论约束力的作用线必垂直于轴线并通过圆心。
对于这样方向不能预先确定的约束力,通常用通过轴心的两个大小未知的正交分力Fx和Fy来表示,如图。
(a)(b)
(c)(d)
径向轴承及其约束力
2、固定铰支座
性质:将销钉看作是杆的一部分,则销钉受到的支座约束力就是杆的受力。
销钉与支座孔壁的接触点位置随外力而定,与轴承具有相同的性质,同样可以用两个大小未知的正交分力来表示。
(a)(b)
固定铰支座及其约束力
3、圆柱铰链
由销钉将两个钻有同样大小孔的构件连接在一起而成。
性质:通常把销钉固连在其中任意一个构件上,两个构件互为约束,其约束力方向不能预先定出,同样用两个大小未知的正交分力来表示,如图。
(a)(b)(c)
圆柱铰链及其约束力
4、滚动支座
性质:在上述固定铰支座与光滑固定平面之间装有光滑辊轴而成,约束性质与光滑面约束相同,约束力垂直于光滑面,且通过铰链中心,如图18。
(a)(b)
滚动支座及其约束力
5、固定端约束
该约束的特点:固定端约束对物体的作用,是接触面上作用了一群力,即是为一平面任意力系,如图)所示。
通过简化,在固定端A处约束力可简化为两个约束力FAx,FAy和一个矩为MA的约束力偶,如图所示。
(a)
(b )
(c )
6. 受力分析和受力图
画受力图的方法与步骤:
1、取分离体(研究对象)
2、画出研究对象所受的全部主动力(使物体产生
运动或运动趋势的力)
3
、在存在约束的地方,按约束类型逐一画出约束反力(研究对象与周围物体的连接关系)
复习题
外伸梁约束及尺寸如图: 1、试求A 、B 的约束力;2、列出AB 的剪力、弯矩方程; 3、画出该梁的剪力、弯矩图。
解:(1)受力如图所示,列平衡方程
02002230()y By Ay A
By F F F q a P M F F a q a a P a ⎧=+-⋅-=⎪⎨=⋅-⋅⋅-⋅=⎪⎩∑∑ F Ay F By F Ay F By F Ay F By
解得
05.Ay F qa =,25.By F qa =
(2)在AB 段取截面将AB 截开,剪力方程为 05().Ay Q x F qx qa qx =-=-
弯矩方程为
2111222
()Ay M x F x qx x qax qx =⋅-⋅=- (3)该梁的剪力、弯矩图如图所示。