截一个几何体知识点归纳(2020年10月整理).pdf

初一人教版数学上册截一个几何体知识点讲解《截一个几何体》取材于北师大版教材《数学》七年级上册第一章第三节，是初中新课程改革中的新增内容，我们为大家整理的截一个几何体知识点具体如下，希望大家可以认真阅读，在新学期努力学习。

核心知识点截面的定义：用一个平面去截一个几何体，截出的面叫截面。

由前面的知识知道，“面与面相交得到线”，用平面去截几何体,学习规律，所得到的截面就是这个平面与几何体每个面相交所围成的图形。

用平面截一个几何体所得截面的形状：截面的形状多为圆和多边形，也可能是不规则图形，一般与下面两点有关：（1）几何体的形状；（2）切截的方向和角度。

一般的，截面与几何体的几个面相交，就得到几条交线，截面与平面相交就得到几边形；截面与曲面相交，得到曲线，截面是圆或不规则图形。

几种常见几何体的截面：①正方体的截面有：三角形，等腰三角形,等边三角形；正方形，长方形，平行四边形，菱形，梯形五边形，六边形②圆柱的截面：圆，椭圆，长方形，不规则图形;③圆锥的截面：圆，椭圆，等腰三角形，不规则图形课后练习要练说，得练听。

听是说的前提，听得准确，才有条件正确模仿，才能不断地掌握高一级水平的语言。

我在教学中，注意听说结合，训练幼儿听的能力，课堂上，我特别重视教师的语言，我对幼儿说话，注意声音清楚，高低起伏，抑扬有致，富有吸引力，这样能引起幼儿的注意。

当我发现有的幼儿不专心听别人发言时，就随时表扬那些静听的幼儿，或是让他重复别人说过的内容，抓住教育时机，要求他们专心听，用心记。

平时我还通过各种趣味活动，培养幼儿边听边记，边听边想，边听边说的能力，如听词对词，听词句说意思，听句子辩正误，听故事讲述故事，听谜语猜谜底，听智力故事，动脑筋，出主意，听儿歌上句，接儿歌下句等，这样幼儿学得生动活泼，轻松愉快，既训练了听的能力，强化了记忆，又发展了思维，为说打下了基础。

我国古代的读书人,从上学之日起,就日诵不辍,一般在几年内就能识记几千个汉字,熟记几百篇文章,写出的诗文也是字斟句酌,琅琅上口,成为满腹经纶的文人。

1.3截一个几何体新知概览：知识要点课标要求中考考点用平面去截几何体所得截面的形状探索并理解几何体的截面形状。

截面的定义（掌握）几种常见几何体的截面掌握几种常见几何体的截面。

判断一个几何体的截面(应用)本节重、难点1.重点：截面的定义和形状．2.难点：利用截面解决实际问题．知识全解知识点1截面（1）截面的概念：用一个平面去截几何体，截出的面叫做截面．（2）正方体的截面：根据面与面相交可以得到线可知用一个平面去截正方体的三个面，得到的截面是三角形.如果用一个平面去截正方体的四个面，就能得到四边形，除能得到正方形、长方形这样的四边形外，还能得到其他的四边形，如梯形、平行四边形等.知识警示：（1）正方体总共有六个面，用一个平面去截最多只能得到六条交线，从而截面的边数最多只能是六，还可以得到五，但不可能截得七边形.（2）一般地，截面与几何体的几个面相交就得到几条交线，截面就是几边形.因此，若一个几何体有n个面，则截面最多的边数是n．知识拓展正方体的截面主要有三角形、四边形、五边形和六边形，如图1-3-1所示. 【试练例题1 】如图1-3-2所示的一块长方体木头，想象沿虚线所示位置截下去所得到的截面图形是（ ）思路导引：首先根据两组对边平行，可确定为平行四边形；又有一角为直角，故截面图形是长方形．答案：B.长方体的截面，经过长方体四个侧面，长方体中，对边平行，故可确定为平行四边形，一条边垂直于底面，故为长方形． 知识方法：截面的形状既与被截的几何体有关，还与截面的角度和方向有关．对于这类题，最好是动手动脑相结合，亲自动手做一做，从中学会分析和归纳的思想方法．知识点2几种常见几何体的截面（1）如图1-3-3所示，用平面截圆柱体，可能出现以下的几种情况．（2）如图1-3-4所示，用平面去截一个圆锥，能截出以下的几种情况．（3）如图1-3-5所示,用平面去截球体，只能出现一种形状的截面---圆.A图1-3-2 B C D 图1-3-4 图1-3-1知识警示：（1）用一个平面去截一个圆柱所得到的截面有圆、长方形、椭圆、拱形形状和梯形.（2）用一个平面去截圆锥，可得到圆、三角形、拱形形状和椭圆. 【试练例题2】如图1-3-6中几何体的斜截面形状是（ ）思路导引：几何体是一个圆柱体，用一个平面斜截它，得到的截面应该是类似拱形的图形．答案C 用一个平面去截一个圆柱体，过平行于上下底面的面去截可得到圆；圆柱体的轴截面是矩形；过侧面且不平行于上下底面的面去截可得到椭圆；过一底面且不与另一底面相交的面去截可得到类似拱形的截面．方法：平面与平面相交得直线，平面与曲面相交可能得到直线，也可能得到曲线． 图1-3-5 图1-3-6。

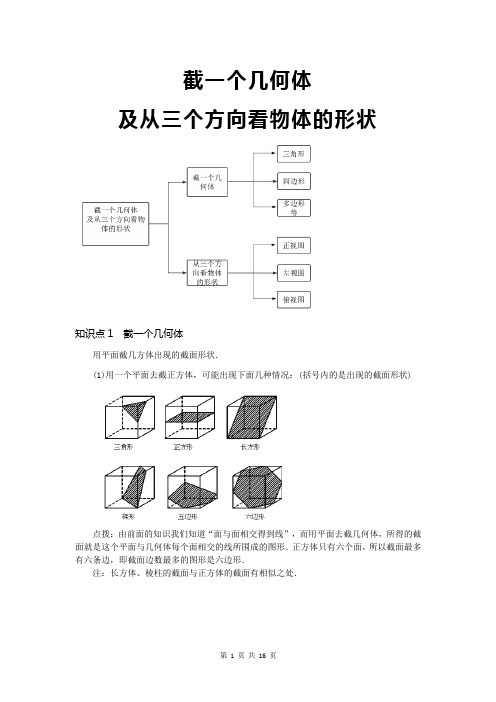
截一个几何体及从三个方向看物体的形状知识点1 截一个几何体用平面截几方体出现的截面形状．(1)用一个平面去截正方体，可能出现下面几种情况：(括号内的是出现的截面形状)点拨：由前面的知识我们知道“面与面相交得到线”，而用平面去截几何体，所得的截面就是这个平面与几何体每个面相交的线所围成的图形．正方体只有六个面，所以截面最多有六条边，即截面边数最多的图形是六边形．注：长方体、棱柱的截面与正方体的截面有相似之处．(2)用平面截圆柱体，可能出现以下的几种情况．分析：用平面去截圆柱体，可以与圆柱的三个面(两个底面，一个侧面)同时相交，由于圆柱侧面为曲面，故相交得到是曲线，无法截出三角形．只能用平面平行和垂直于圆柱的底面截出这几种图形．(3)用平面去截一个圆锥，能截出圆和三角形两种截面(还有其他截面，初中不予研究)(4)用平面去截球体，只能出现一种形状的截面——圆．例1.用一个平面截一个几何体，得到的截面是四边形，则这个几何体可能是（）．A．球体 B．长方体 C．圆锥 D．三棱锥例2.如图，一个有盖．．的圆柱形玻璃杯中装有半杯水，若任意放置这个水杯，则水面的形状不可能是A．B．C．D．例3.用一个平面去截一个正方体，截面不可能是（）A．梯形B．五边形C．六边形D．七边形例4.如图，从边长为10的正方体的一顶点处挖去一个边长为1的小正方体，则剩下图形的表面积为（）A.600B.599C.598D.597知识点2 物体的三视图1．主视图、左视图、俯视图的定义从不同方向观察同一物体，从正面看到的图叫主视图，从左面看到的图叫左视图，从上面看到的图叫做俯视图．2．几种几何体的三视图(1)正方体：三视图都是正方形．(2)球：三视图都是圆．提醒：在所有几何体中，只有正方体与球这两种几何体的三视图是相同的．(3)圆柱体：(4)圆锥体：圆锥的主视图、左视图都是三角形，而俯视图的图中有一个点表示圆锥的顶点，因为从上往下看圆锥时先看到圆锥的顶点，再看到底面的圆．3．如何画三视图当用若干个小正方体搭成新的几何体，如何画这个新的几何体的三视图？由俯视图画主视图、左视图．①主视图与俯视图列数相同，俯视图中每列的方框内的最大数字即为主视图本列的层数．②左视图的列数与俯视图的行数相同，俯视图每一横行的方框内的最大数字，就是这一横行逆时针转90°所成的左视图中的列的层数．需要记住的要点：几何体截面形状正方体三角形、正方形、长方形、梯形、五边形、六边形圆柱圆、长方形、正方形、……圆锥圆、三角形、……球圆例1.如图所示由五个小立方体构成的立体图形,请你分别画出从它的正面、左面、上面三个方向看所得到的平面图形．例2.如图是由几个小立方块所搭几何体的俯视图，小正方形中的数字表示该位置上小立方块的个数，请画出这个几何体的主视图和左视图.（答案图）例3.从不同方向看一只茶壶，你认为是俯视效果图的是（）A．B．C．D．例4.如右图，是由若干个相同的小立方体搭成的几何体的俯视图和左视图，则小立方体的个数有可能是（）．俯视图左视图A．5或6 B．5或7 C．4或5或6 D．5或6或7例5.一个几何体的三视图如图所示，则该几何体的侧面展开图的面积为（）26.cm9.cmDπCπ2Bπ26.cmA24.cm例6在下列几何体中，轴截面是等腰梯形的是（）A.圆锥B.圆台C.圆柱D.球例7.用一个平面去截圆锥，截面图形不可能是（）A. B. C. D.例8.由五个同样大小的立方体组成如图的几何体，则关于此几何体三种视图叙述正确的是（）A．左视图与俯视图相同 B．左视图与主视图相同C．主视图与俯视图相同 D．三种视图都相同例9.由五个同样大小的立方体组成如图的几何体，则关于此几何体三种视图叙述正确的是（）A．左视图与俯视图相同 B．左视图与主视图相同C．主视图与俯视图相同 D．三种视图都相同例10.面几何体中，同一几何体的主视图和俯视图相同的有（）A.1个B.2个C.3个D.4个例11.如图所示的几何体是由5个相同的小正方体组成，其左视图为（）正面A B. C. D.例12.如图所示的一块长方体木头，想象沿虚线所示位置截下去所得到的截面图形是（）A. B. C. D.例13. 如图是由两个小正方体和一个圆锥体组成的立体图形，其主视图是（）A．B．C．D．练习题1.（2020春•南关区校级月考）如图，图①和图②均是由6个相同的小正方体组成的立体图形，则下列说法正确的是（）A．主视图相同B．俯视图相同C．左视图相同D．主视图、俯视图、左视图都不相同2．（2020•上蔡县模拟）如图1、图2、图3所示，下列说法错误的是（）A．图1的主视图和图2的主视图相同B．图2的左视图和图3的主视图相同C．图1的左视图和图2的主视图相同D．图3的左视图和图2的主视图相同3．（2020•吉林）如图，由5个完全相同的小正方体组合成一个立体图形，它的左视图为（）A．B．C．D．4．（2020•哈尔滨模拟）下列立体图形①长方体②圆锥③圆柱④球中，左视图可能是长方形的有（）A．①B．①②C．①③D．①④5．（2019•历下区二模）下列图形的主视图与左视图不相同的是（）A．B．C．D．6．（2016•龙岩）如图，正三棱柱的主视图为（）A．B．C．D．7．（2015•镇江一模）如图所示，下列几何体中主视图与俯视图相同的是（）A．半球B．圆柱C．球D．六棱柱8．下列四个立体图形中，主视图为圆的是（）A．B．C．D．9．下面说法中错误的是（）A．球的主视图是圆B．球的俯视图是圆C．球的任何截面都是圆D．以上说法都不对10．（2019秋•南岗区期末）小圆的半径是4cm，大圆的半径是8cm，小圆面积是大圆面积的（）A．B．C．D．11．（2019秋•南岗区期中）如图，此图形中阴影部分的面积为（）dm2．A．πB．4πC．πD．7π12．如图所示，在一个圆中任意画3条半径，可以把这个圆分成几个扇形（）A．3B．4C．5D．613．（2020秋•太原期末）从如图所示的7个小正方形中剪去一个小正方形，使剩余的6个小正方形折叠后能围成一个正方体，则应剪去标记为（）的小正方形A．祝或考B．你或考C．好或绩D．祝或你或成14．（2020秋•淇滨区校级月考）下列选项中的图形折叠后，能得到如图所示的正方体的是（）A．B．C．D．15．（2020秋•解放区校级月考）下列图形可以围成一个棱柱的是（）A．B．C．D．16．（2020•滨海县二模）下列图形经过折叠不能围成棱柱的是（）A．B．C．D．17．（2018•山西模拟）下列图形通过折叠能围成一个三棱柱的是（）A．B．C．D．18．（2020秋•黄埔区期末）如图，下列图形中，①能折叠成，②能折叠成，③能折叠成．19．（2020秋•辽阳期末）将如图所示的图形剪去一个小正方形，使余下的部分恰好能折成一个正方体，那么应剪去．（填一个字母即可）20．（2018秋•锦江区校级月考）如图所示的平面图形，能折叠成的几何体可能是．21．（2019秋•越秀区期末）如图是一个小正方体的展开图，把展开图折叠成小正方体后，有“守”字一面的相对面上的字是．22．（2019秋•宽城区期末）将正方体的表面沿某些棱剪开，展成如图所示的平面图形，则原正方体中与“我”字所在面相对的面上的汉字是．23．（2019秋•历城区期中）一个立方体的表面展开图如图所示，将其折叠成立方体后，“步”对面的字是．24．（2018秋•芝罘区期末）若要使得图中平面展开图折叠成正方体后，相对面上的两个数之和相等，则a+b+c的值为．25．（2019秋•宁德期中）一个正方体的每个面都有一个汉字，其平面展开图如图所示，则该正方体中与“爱”字相对的面上的字是．26．（2020秋•郫都区校级月考）用一个平面去截一个正方体，得到的截面的形状可能是：①圆，②三角形，③长方形，④五边形，⑤六边形，⑥七边形其中的．27．（2019秋•大邑县期末）在“长方体、圆柱、圆锥”三种几何体中，用一个平面分别去截三种几何体，则截面的形状可以截出长方形也可以截出圆形的几何体是．28．（2019秋•盐田区期末）（多选）下列几何体中，截面可能为圆的是．A．棱柱B．圆柱C．圆锥D．球29．（2018秋•中牟县期中）如图所示的几何体的截面形状分别是：．30．（2012•龙凤区校级模拟）把长方体的八个角切去一个角后，余下的图形有条棱．31．用平面截几何体可得到平面图形，在表示几何体的字母后填上它可截出的平面图形的号码．如A（1，5，6）；则B（）；C（）；D（）；E（）．32．指出下面几何体截面的形状：．33．（2020秋•铁西区校级期末）如图是由几个相同的小正方体分别从上面、左面看到的形状图，这样的几何体最多需要个小立方体块，最少需要个小立方体块．34．（2013秋•信州区校级期末）如图是由一些相同的小正方体构成的几何体从不同方向看得到的平面图形，则在这个几何体中，小正方体的个数是．35．（2009秋•太原期末）下列两个图是由几个相同的小长方体堆成的物体视图，那么堆成这个物体的小长方体最多有个．36.（2020秋•龙岗区校级月考）一个小朋友用五块正方体积木摆成了一件作品[如图]．请你只移动一块积木，使这件作品从正面看是图一，左面是图二，你有几种移动方法，从上面看移动后的作品，请你把看到的平面图形画出来（画出所有情况）．37．（2019秋•平川区校级期中）画出下面几何体的从正面看、从左面看与从上面看的图形．38．（2018秋•宝安区期中）如图是小强用六块相同的小立方体搭成的一个几何体，从正面、左面和上面观察这个几何体，请你在下面相应的位置分别画出你所看到的几何体的形状图（在答题卡上画完图后请用黑色签字笔描图）．39．（2018秋•建宁县期中）（1）按要求将下列几何体进行分类，并将分类后几何体的名称写在对应的括号内．柱体{}锥体{}（2）6个完全相同的正方体组成如图所示的几何体，画出该几何体从正面，左面看到的形状图（用阴影画在所给的方格中）。

1.3截一个几何体新知概览：知识要点课标要求中考考点用平面去截几何体所得截面的形状探索并理解几何体的截面形状。

截面的定义（掌握）几种常见几何体的截面掌握几种常见几何体的截面。

判断一个几何体的截面(应用)本节重、难点1.重点：截面的定义和形状．2.难点：利用截面解决实际问题．知识全解知识点1截面（1）截面的概念：用一个平面去截几何体，截出的面叫做截面．（2）正方体的截面：根据面与面相交可以得到线可知用一个平面去截正方体的三个面，得到的截面是三角形.如果用一个平面去截正方体的四个面，就能得到四边形，除能得到正方形、长方形这样的四边形外，还能得到其他的四边形，如梯形、平行四边形等.知识警示：（1）正方体总共有六个面，用一个平面去截最多只能得到六条交线，从而截面的边数最多只能是六，还可以得到五，但不可能截得七边形.（2）一般地，截面与几何体的几个面相交就得到几条交线，截面就是几边形.因此，若一个几何体有n个面，则截面最多的边数是n．知识拓展正方体的截面主要有三角形、四边形、五边形和六边形，如图1-3-1所示.【试练例题1 】如图1-3-2所示的一块长方体木头，想象沿虚线所示位置截下去所得到的截面图形是（）思路导引：首先根据两组对边平行，可确定为平行四边形；又有一角为直角，故截面图形是长方形．答案：B.长方体的截面，经过长方体四个侧面，长方体中，对边平行，故可确定为平行四边形，交点垂直于底边，故为长方形．知识方法：截面的形状既与被截的几何体有关，还与截面的角度和方向有关．对于这类题，最好是动手动脑相结合，亲自动手做一做，从中学会分析和归纳的思想方法．知识点2几种常见几何体的截面（1）如图1-3-3所示，用平面截圆柱体，可能出现以下的几种情况．（2）如图1-3-4所示，用平面去截一个圆锥，能截出圆和三角形两种截面．图1-3-1A图1-3-2B C D（3）如图1-3-5所示,用平面去截球体，只能出现一种形状的截面---圆.知识警示： (1) 用一个平面去截一个圆柱所得到的截面有圆、长方形、椭圆、拱形形状和梯形.(2) 用一个平面去截圆锥，可得到圆、三角形、拱形形状和椭圆.【试练例题2】如图1-3-6中几何体的斜截面形状是（ ）思路导引：几何体是一个圆柱体，用一个平面斜截它，得到的截面应该是类似拱形的图形．答案C 用一个平面去截一个圆柱体，过平行于上下底面的面去截可得到圆；圆柱体的轴截面是矩形；过侧面且不平行于上下底面的面去截可得到椭圆；过一底面不平行于另一底面的面去截可得到类似拱形的截面．方法：平面与平面相交得直线，平面与曲面相交可能得到直线，也可能得到曲线．图1-3-5图1-3-4 图1-3-6。

截一个几何体
知识点一：截面，用一个平面去截几何体，截出的面叫做截面，截面形状通常为三角形、正方形、长方形、梯形、圆、椭圆等，截面的形状既与被截的几何体有关，还与截面的角度和方向有关。

知识点二：截一个几何体所得截面的形状
1、用平面去截正方体：用一个平面截正方体，
截面的形状可能是三角形、正方形、长方形、梯形、五
边形、六边形等。

2、用平面去截圆柱：常见的截面有长方形、圆、
椭圆、类似于梯形、类似于拱形。

3、用平面去截圆锥：截面的形状可能是三角形、圆、椭圆、类似于拱形。

4、用平面去截球：截面的形状都是圆。

专题1.7截一个几何体（知识梳理与考点分类讲解）一、知识梳理【知识点】几何体的截面如图所示，把一个底面半径是5cm，高是8cm的圆柱放在水平桌面上．(1)若用一个平面沿水平方向去截这个圆柱，所得的截面是；(2)若用一个平面沿竖直方向去截这个圆柱，所得的截面是；(3)若用一个平面去截这个圆柱，使截得的截面是长方形且长方形的截面面积最大，请写出截法，并求出此时截面面积．【答案】(1)圆；(2)长方形；(3)当平面沿竖直方向且经过两个底面的圆心时，截得的长方形面积最大，80cm2【分析】（1）根据截的方向可得截面形状；（2）根据截的方向可得截面形状；（3）当平面沿竖直方向且经过两个底面的圆心时，截得的长方形面积最大，再根据截面形状求面积即可．（1）解：若用一个平面沿水平方向去截这个圆柱，所得的截面是圆；故答案为：圆；（2）若用一个平面沿竖直方向去截这个圆柱，所得的截面是长方形；故答案为：长方形；（3）当平面沿竖直方向且经过两个底面的圆心时，截得的长方形面积最大，此时截面的面积为：5×2×8＝80（cm2）．【点拨】本题考查用一个平面去截几何体，截面的形状既与被截的几何体有关，还与截面的角度和方向有关．【变式】用一个平面截一个几何体，所截出的面出现了如图所示的四种形式，试猜想，该几何体可能是___．【答案】圆柱【分析】根据截面图可知，有圆形和长方形，则该几何体为圆柱．解答：平面倾斜竖截圆柱侧面和底面可得图①，平面倾斜竖截圆柱侧面截圆柱可得图②，平面经过两个底面截圆柱可得图③，平面平行与底面截圆柱可得图④，故该几何体可能是圆柱．【点拨】本题考查了由平面截几何体得到的平面图形猜测几何体的形状，根据截面为长方形和圆得到几何体是圆柱是解题的关键．二、考点分类讲解【题型一】根据截面判断几何体的形状【例1】一个几何体的一个截面是三角形，则原几何体一定不是下列图形中的()A．圆柱和圆锥B．球体和圆锥C．球体和圆柱D．正方体和圆锥【答案】C【分析】观察题目，每个选项中都有圆锥，而圆锥的截面可能是三角形，故可以判断A、B、D；根据圆柱的截面可能是圆，长方形，不会是三角形，球体的截面永远是圆对C选项进行判断.解：圆柱的截面可能是圆，长方形，不会是三角形，球体的截面永远是圆，也不会是三角形.故选C．【点拨】本题主要考查的是几何体的有关知识，熟练掌握常见几何体截面的形状是解答本题的关键.【变式】用一个平面去截一个几何体，能截出如图所示的四种平面图形，则这个几何体可能是（）A．圆柱B．圆锥C．长方体D．球【答案】A【分析】用平面截圆锥，得到的截面是圆、椭圆或者三角形等，不可能是四边形，用平面截球体，得到的截面始终是圆形；用平面截长方体，得到的截面是三角形，长方形等；接下来，用平面截圆柱，对得到的截面进行分析，即可得到答案.解:∵圆柱体的主视图只有矩形或圆，∴圆柱体的主视图符合题意．故选A．【点拨】此题考查截一个几何体，熟练掌握常见几何体的特征是解题的关键.【题型二】根据截面判断几何体的内部结构【例2】一个物体的外形是长方体，其内部构造不详．用一组水平的平面截这个物体时，得到了一组（自下而上）截面，截面形状如图所示，这个长方体的内部构造可能是（）A．圆柱B．棱柱C．棱锥D．圆锥【答案】D【分析】通过观察可以发现：在长方体内部的三角形自下而上由大圆逐渐变成小圆、最后变成点，由此判定即可．解：∵通过观察可以发现：在正方体内部的圆自下而上由大圆逐渐变成小圆、最后变成点，∴这个长方体的内部构造可能是圆锥，故D正确．故选：D．【点拨】由截面形状去想象几何体与给一个几何体想象它的截面是一个互逆的思维过程，要根据所给截面形状仔细分析，展开想象．【变式1】一个物体的外形是长方体，其内部构造不详．用5个水平的平面纵向平均截这个物体时，得到了一组（自下而上）截面，截面形状如图所示，这个长方体的内部构造可能是（）A．球体B．圆柱C．圆锥D．球体或圆锥【答案】C解：选项A,球体截完是圆，由小变大，再变小,A不符合题意；选项B,圆柱截完都是等圆，B不符合题意；选项C,圆锥是由小变大，或者由大变小.C符合题意；选项D，由A可知不符合题意.故选C.【变式2】一个物体的外形是长方体，其内部构造不详．用一组水平的平面截这个物体时，得到了一组（自下而上）截面，截面形状如图所示，这个长方体的内部构造可能是______．【答案】三棱锥【分析】通过观察可以发现：在长方体内部的三角形自下而上由大三角形逐渐变成小三角形、最后变成点，由此判定即可．解：通过观察可以发现：在正方体内部的三角形自下而上由大三角形逐渐变成小三角形、最后变成点，∴这个长方体的内部构造可能是三棱锥，故答案为：三棱锥．【点拨】由截面形状去想象几何体与给一个几何体想象它的截面是一个互逆的思维过程，要根据所给截面形状仔细分析，展开想象．【题型三】判断截后几何体的形状【例3】用一个平面去截圆锥，截面图形不可能是（）A．B．C．D．【答案】C试题分析：根据圆锥的形状特点判断即可，也可用排除法．解：如果用平面取截圆锥，平面过圆锥顶点时得到的截面图形是一个等腰三角形，如果不过顶点，且平面与底面平行，那么得到的截面就是一个圆，如果不与底面平行得到的就是一个椭圆或抛物线与线段组合体，所以不可能是直角形．故选；C．点评：此题主要考查了截一个几何体，截面的形状既与被截的几何体有关，还与截面的角度和方向有关．对于这类题，最好是动手动脑相结合，亲自动手做一做，从中学会分析和归纳的思想方法．【变式】用过正方体上底面的对角线和下底面的一个顶点的平面去截这个正方体，则截面形状是_______．【答案】等边三角形【分析】根据正方体有六个面，用平面去截正方体时最多与六个面相交得六边形，最少与三个面相交得三角形．因此截面的形状可能是：三角形、四边形、五边形、六边形，据此解答即可．解：用过正方体上底面的对角线和下底面一个顶点的平面去截这个正方体，则截面形状是等边三角形，如下图．故答案为：等边三角形．【点拨】本题考查正方体的截面，注意：截面的形状随截法的不同而改变，一般为多边形或圆，也可能是不规则图形，一般的截面与几何体的几个面相交就得到几条交线，截面就是几边形，因此，若一个几何体有几个面，则截面最多为几边形．。

1.3 截一个几何体学习目标1.通过参与对实物的切截活动和观察，了解一些几何体截面的形状。

2.通过经历对几何体切截的实践过程，认识面与体之间的转换。

知识详解1．截面定义：用一个平面去截一个几何体，截出的面叫做截面。

如图所示，阴影部分就是截面。

截面的理解：①由前面的知识我们知道“面与面相交得到线”，而用平面去截几何体，所得的截面就是这个平面与几何体每个面相交的线所围成的图形②截面的形状与所截几何体有关，也与所截角度和方向有关③对于同一个几何体，截面的方向不同，得到的截面形状一般也不相同，同一个几何体可能有多种不同形状的截面。

2.正方体的截面正方体截面的形状：如图所示，正方体的截面的形状可以是：（1）三角形（包括等腰三角形、等边三角形和一般三角形），如图①（2）四边形（包括正方形、长方形、梯形等），如图②③④（3）五边形，如图⑤（4）六边形，如图⑥正方体中不同形状的截面的截法：（1）沿竖直或水平方向截正方体，截面为正方形。

（2）图①中的截面是等边三角形，与该平面平行，能截正方体三条棱的平面，都能截出等边三角形。

（3）过正方体同一个面上不相邻的两个顶点和一条棱上的一点，可截出等腰三角形（如图），且与该面平行的能截正方体三条棱的平面，都能截出等腰三角形。

（4）分别过正方体的上、下底面，且与任何棱都不平行的截面，可截出梯形。

（5）只要截面与五个面相交或与六个面相交，即可截出五边形或六边形。

3．圆柱、圆锥、球的截面（1）圆柱的截面用一个平面去截一个圆柱，可得到的截面形状是长方形、圆、椭圆、椭圆的一部分。

（2）圆锥的截面用一个平面去截圆锥，可得到的截面形状是三角形、圆、椭圆及椭圆的一部分。

（3）球体的截面用一个平面去截球体，可得到的截面形状是圆。

4．根据截面判断几何体（1）常见几何体截面的比较常见几何体主要是棱柱、圆柱、圆锥和球体．棱柱包括正方体、长方体、三棱柱、五棱柱、六棱柱……其中以正方体为代表，各种几何体的截面如下表：（2）根据截面判断原几何体的方法：①截面中有曲线，则原几何体一定有曲面．例如截面形状是圆的几何体可能是圆柱、圆锥、球或圆台。