当前位置：文档之家 › 上海师大固体物理第五章(4)紧束缚近似法分析

上海师大固体物理第五章(4)紧束缚近似法分析

  • 格式：ppt
  • 大小：1.83 MB
  • 文档页数：44

下载文档原格式

  / 44

合集下载

紧束缚近似理论

紧束缚近似理论

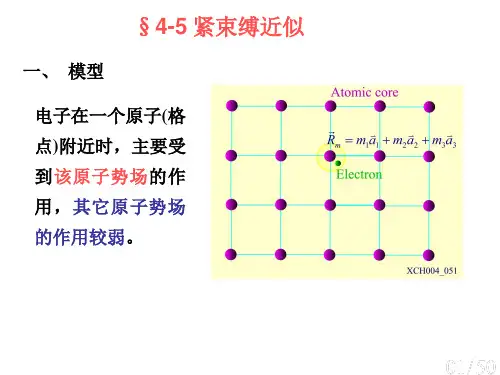
§5-4 紧束缚近似理论原子结合为原子时，电子的状态发生了根本性的变化，电子从孤立原子的束缚态变为晶体中的共有化状态。

电子状态变化的大小取决于电子在某原子附近所受该原子势场的作用与其它诸原子势场作用的相对大小。

若原子所处原子势场的作用较之其它原子势场的作用要大得多，例如对于原子中内层电子，或晶体间距较大时，上面讨论的近自由电子近似就不适用，这时共有化运动状态与束缚态之间有直接联系，即紧束缚近似理论。

紧束缚理论的实质是把原子间相互作用影响看成微扰的简并微扰方法，微扰后的状态是N 个简并态的线性组合，即用原子轨道()i m ϕ-r R 的线性组合来构成晶体中的电子共有化运动的轨道(,)ψk r ，也称原子轨道线性组合法，简写为LCAO 。

5．4．1 原子轨道线性组合设晶体中第m 个原子的位矢为：112233m m m m =++R a a a ……………………………………………………………………………（5-4-1） 若将该原子看作一个孤立原子，则在其附近运动的电子将处于原子的某束缚态()i m ϕ-r R ，该波函数满足方程：22()()()2m i m i i m V m ϕεϕ⎡⎤-∇+--=-⎢⎥⎣⎦h r R r R r R ………………………………………………（5-4-2） 其中()m V -r R 为上述第m 个原子的原子势场，i ε是与束缚态i ϕ相对应的原子能级。

如果晶体为N 个相同的原子构成的布喇菲格子，则在各原子附近将有N 个相同能量i ε的束缚态波函数i ϕ。

因此不考虑原子之间相互作用的条件下，晶体中的这些电子构成一个N 个简并的系统：能量为i ε的N 度简并态()i m ϕ-r R ，m=1，2，…，N 。

实际晶体中的原子并不是真正孤立、完全不受其它原子影响的。

由于晶体中其它诸原子势场的微扰，系统的简并状态将消除，而形成由N 个能级构成的能带。

根据以上的分析和量子力学的微扰理论，我们可以取上述N 个简并态的线性组合(,)()()m i m ma ψϕ=-∑k r k r R ………………………………………………………………………（5-4-3）作为晶体电子共有化运动的波函数，同时把原子间的相互影响当作周期势场的微扰项，于是晶体中电子的薛定谔方程为：22()()()2U E m ψψ⎡⎤-∇+=⎢⎥⎣⎦h r r r …………………………………………………………………（5-4-4） 其中晶体势场U (r )是由原子势场构成的，即()()()n l nU V U =-=+∑r r R r R …………………………………………………………………（5-4-5）5．4．2 微扰计算（5-4-4）式可以转化为如下形式：()()22()()()2m m V U V E m ψψ⎡⎤-∇+-+--=⎢⎥⎣⎦h r R r r R r r 代入（5-4-2）和（5-4-3）后，可得：[()()()]()0m i m i m m aE U V εϕ-+---=∑r r R r R ………………………………………………（5-4-5）在紧束缚近似作用下，可认为原子间距较i ϕ态的轨道大得多，不同原子的i ϕ重叠很小，从而有：()()*i n i m nm d ϕϕδ--=⎰r R r R r …………………………………………………………………（5-4-6） 现以()*i n ϕ-r R 左乘方程（5-4-5），并对整个晶体积分，可以得： *()()[()()]()n i m i m m i m ma E a U V d 0εϕϕ-+---⋅-∑⎰r R r r R r R r =…………………………（5-4-7）首先讨论（5-4-7）式中的积分。

紧束缚近似理论

紧束缚近似理论

§5-4 紧束缚近似理论原子结合为原子时，电子的状态发生了根本性的变化，电子从孤立原子的束缚态变为晶体中的共有化状态。

电子状态变化的大小取决于电子在某原子附近所受该原子势场的作用与其它诸原子势场作用的相对大小。

若原子所处原子势场的作用较之其它原子势场的作用要大得多，例如对于原子中内层电子，或晶体间距较大时，上面讨论的近自由电子近似就不适用，这时共有化运动状态与束缚态之间有直接联系，即紧束缚近似理论。

紧束缚理论的实质是把原子间相互作用影响看成微扰的简并微扰方法，微扰后的状态是N 个简并态的线性组合，即用原子轨道()i m ϕ-r R 的线性组合来构成晶体中的电子共有化运动的轨道(,)ψk r ，也称原子轨道线性组合法，简写为LCAO 。

5．4．1 原子轨道线性组合设晶体中第m 个原子的位矢为：112233m m m m =++R a a a ……………………………………………………………………………（5-4-1）若将该原子看作一个孤立原子，则在其附近运动的电子将处于原子的某束缚态()i m ϕ-r R ，该波函数满足方程：22()()()2m i m i i m V m ϕεϕ⎡⎤-∇+--=-⎢⎥⎣⎦r R r R r R ………………………………………………（5-4-2） 其中()m V -r R 为上述第m 个原子的原子势场，i ε是与束缚态i ϕ相对应的原子能级。

如果晶体为N 个相同的原子构成的布喇菲格子，则在各原子附近将有N 个相同能量i ε的束缚态波函数i ϕ。

因此不考虑原子之间相互作用的条件下，晶体中的这些电子构成一个N 个简并的系统：能量为i ε的N 度简并态()i m ϕ-r R ，m=1，2，…，N 。

实际晶体中的原子并不是真正孤立、完全不受其它原子影响的。

由于晶体中其它诸原子势场的微扰，系统的简并状态将消除，而形成由N 个能级构成的能带。

根据以上的分析和量子力学的微扰理论，我们可以取上述N 个简并态的线性组合(,)()()mi m maψϕ=-∑k r k r R ………………………………………………………………………（5-4-3）作为晶体电子共有化运动的波函数，同时把原子间的相互影响当作周期势场的微扰项，于是晶体中电子的薛定谔方程为：22()()()2U E m ψψ⎡⎤-∇+=⎢⎥⎣⎦r r r …………………………………………………………………（5-4-4） 其中晶体势场U (r )是由原子势场构成的，即 ()()()nl nU V U =-=+∑r r Rr R …………………………………………………………………（5-4-5）5．4．2 微扰计算（5-4-4）式可以转化为如下形式：()()22()()()2m m V U V E m ψψ⎡⎤-∇+-+--=⎢⎥⎣⎦r R r r R r r 代入（5-4-2）和（5-4-3）后，可得：[()()()]()0mi m i m maE U V εϕ-+---=∑r r R r R ………………………………………………（5-4-5）在紧束缚近似作用下，可认为原子间距较i ϕ态的轨道大得多，不同原子的i ϕ重叠很小，从而有：()()*in i m nm d ϕϕδ--=⎰r R r R r …………………………………………………………………（5-4-6）现以()*in ϕ-r R 左乘方程（5-4-5），并对整个晶体积分，可以得： *()()[()()]()n i m i m m i m ma E a U V d 0εϕϕ-+---⋅-∑⎰r R r r R r R r =…………………………（5-4-7）首先讨论（5-4-7）式中的积分。

固体物理Ch4.5 紧束缚近似

固体物理Ch4.5 紧束缚近似

HUBEI UNIVERSITYCh4.5 紧束缚近似——原子轨道线性组合(LCAO)法3孤立原子中电子运动方程i 个束缚态的能级孤立原子中的电子表示所处能级0ˆH (2)晶体中电子运动方程势场⇀Ch4.5 紧束缚近似——原子轨道线性组合(LCAO)法5()+-+∑ mm R V r R V 2()∇+- m V r R (r ψCh4.5 紧束缚近似——原子轨道线性组合(LCAO)法9周期性势场减去原子的势场，仍为负值Ch4.5 紧束缚近似——原子轨道线性组合(LCAO)法11(k rψCh4.5 紧束缚近似——原子轨道线性组合(LCAO)法13Ch4.5 紧束缚近似——原子轨道线性组合(LCAO)法15Ch4.5 紧束缚近似——原子轨道线性组合(LCAO)法17()2(cos cos cos )E k J J k a k a k a =ε--++⇀⋅ ⇀Ch4.5 紧束缚近似——原子轨道线性组合(LCAO)法19Ch4.5 紧束缚近似——原子轨道线性组合(LCAO)法212222min *()()2x y z E k E k k k m=+++能带底部电子的有效质量2*212m J a=在能带顶部 : ⇀, , 在 ⇀, , 附近按泰勒级数展开将 ⇀2 cos cos cos⇀有效质量为正⇀Ch4.5 紧束缚近似——原子轨道线性组合(LCAO)法23max ()E k E =+ ⇀ 内层电子外层电子(2).若考虑p态电子，d态电子，这些状态是简并的，N个原子组成的晶体形成能带比较复杂，一个能带不一定同孤立原子的某个能级对应，可能出现能带交叠.——由于p态是三重简并的，对应的能带发生相互交叠，d态等一些态也有类似能带交叠紧束缚讨论中只考虑不同原子、相同原子态之间的相互作用，不考虑不同原子态之间的作用——对于内层电子能级和能带有一一对应的关系——对于外层电子，能级和能带的对应关系较为复杂Ch4.5 紧束缚近似——原子轨道线性组合(LCAO)法25Ch4.5 紧束缚近似——原子轨道线性组合(LCAO)法27Ch4.5 紧束缚近似——原子轨道线性组合(LCAO)法29()mik R m s me r R ϕτ⋅--∑Ch4.5 紧束缚近似——原子轨道线性组合(LCAO)法33Ch4.5 紧束缚近似——原子轨道线性组合(LCAO)法35。

我们从近自由电子近似(NFE)和紧束缚近似(TB)

我们从近自由电子近似(NFE)和紧束缚近似(TB)


h2 2 − 2m ∇ + U ( r ) ψ k ( r ) = E ( k )ψ k ( r )
只有求出一个原胞中的波函数就可以把整个晶体的问题解决了 （平均地说，每个原胞都被一个传导电子所占据，这些电子往 往有屏蔽离子的作用，从而强烈地消弱了离子势场。）
这是一个近似图，并不准确。
wk = ϕ k + ∑ ai vi
ϕ k 是一个平面波， vi 是一个原子波函数，对 i 求和要遍 其中： 及所有被电子占据的原子壳层，例如 Na 要对 1s,2s,2p壳层 求和，系数 ai 的选择要使代表3s 的 wk 与芯函数 vi 正交。
i
使用OPW 方法很方便的求出了 Li 的价带，求 出了半导体 Si 和 Ge的能带，从上图可以看出； （a）是平面波，（b) 是离子实波，（c）是正交 化平面波。后者本身包括了电子在离子实区的多次 振荡特征，已经十分接近真实波函数了。因此正交 平面波法是描述价带和导带电子波函数（即外层电 子）的好表象，是定量计算能带的重要方法。
V
同样也可求出E0 ,和
h2 2 E (k ) = ψ k − ∇ +V (r) ψ k 2m
Wigner和Seitz 用这种方法得到的能量去计算简单金属的结 合能，其结果令人满意地与实验一致。见陈洗书p340
这是原胞法求出的 ψ 0 曲线（实线），可以看出波函数在离 子实内是振荡的，而一旦离开离子实部分，就基本是常数。波函 数的这个常数部分几乎占原胞体积的90%，因此在晶体中波函数 基本是一个平面波。电子在晶体中的运动基本是自由的，所以Na ψ 0 和原子波函数（虚线）相比，变平是 的导电电子是自由电子。 由于加上边界条件产生的，而不是离子势场有什么特殊的性质， 这个结果对以后的能带计算有启示。
紧束缚近似

紧束缚近似


定义：
i ( r Rm ) 表示位于格点 Rm 上的孤立原子波函数； i (k , r ) 紧束缚下晶体中电子波函数，可表示 为 i ( r Rm )的线性组合，即： (k , r ) am (k ) i (r Rm )
这里：
(k , r ) am (k ) i (r Rm ).......... .......... ......( 3)
m V U ( r ) V ( r Rm )......... .......... .......... .......... ......( 4)
例二、面心立方晶格中由原子s态形成的能带，并分 析其能带宽度；
例三、简立方晶格中由原子p态形成的能带。
13
紧束缚近似微扰计算——例一
例一、简立方晶格中由原子s态形成的能带，并分析其能 带宽度。 求解方法：利用公式计算 E s(k )
E k i J 0
公式中需要解决的是：
*
对应本征值为：
ik E (k ) i J ( Rs )e Rs s
特点：是准连续能级
11
化简J ( Rs ) :
紧束缚近似微扰计算
表示式：
* J ( Rs ) i －Rs U V i d




化简： am i i r Rm am V i r Rm E am i r Rm
m m m
i i r Rm
m
m
7
紧束缚近似微扰计算
继续化简得： am i V i r Rm E am i r Rm
紧束缚近似解析

紧束缚近似解析


波函数代入，晶体波函数为
1
N
2
n eikRn [ 2m 2 V (r Rm ) U (r ) V (r Rm ) E (k)]
at (k, r Rn ) 0
周期性势场减去原子的势场，仍为负值
例子：对于非简并的s态电子，利用关系式
2
[
2m
2
V
(r
Rm
)
Es
(k )]at
(k,
r
Rn
)
[E at s
0,0, a
Es (k) Esat (k) Cs 2Js (cos kxa cos kya cos kza)
Es (k) Esat (k) Cs 6Js 0,0,0
Es (k ) Esat (k ) Cs 6J s
a
,
a
,
a
不同能带计算方法的特征区别在两个方面：
• 采用不同的函数集来展开晶体的波函数 • 根据研究对象的物理性质对晶体势作合理
(k)
Es
(k )]sat
(k,
r
Rn
)
乘以波函数并对晶体积分，将晶体波函数改为
[
E
at
s
(k
)
Es
(k
)]
eikRn
at s
(r )sat
(k
,
r
Rn
)dr
n
N
eikRn
at
N s
(r)[U
(r
)
V
(r
Rm
)]at
(k,
r
Rn
)
0
n
当Rn不等于0时，两个波函数交叠很少
N
at s
(r
复旦固体物理讲义-19紧束缚近似

复旦固体物理讲义-19紧束缚近似

* Bloch定理推论二，Bloch函数也是倒空间周期函数
(k,r) (k K ,r)
* 也可以在实空间作傅立叶展开
• 紧束缚近似的物理
* 零级近似：将每个原子看作与周围原子无相互作 用，其解是N个孤立原子的N重简并的解，孤立原子 的分裂能级即成分裂的N重简并能级
* 微扰法：N重孤立原子的简并解线性组合N重简并 能级在简并微扰作用下打开，形成能带
http://10.45.24.132/~jgche/
紧束缚近似
19
• 积分
* (k , r ) (k , r )dr
1
e ik ( R R ') * (r R ' ) (r R )d r
N R ,R'
1
e ik R " * (r ) (r R " )dr
K
• 近自由电子近似的物理
* K=0相当于V=0的解，对V≠0，逐步加入微扰
* 对K求和，K由小到大，取遍使V(K)≠0的平面波
* (k+K)2动量算符的本征值，k+K不同动量的电子
• 能隙宽度由V(K) 定；那么，能带宽度呢？ 1
本讲目的：紧束缚换个角度看能带
• 看作孤立原子分裂能级在有相互作用时的展宽 • 紧束缚近似的数学
1 N
(r R n )e ikR n
n
http://10.45.24.132/~jgche/
紧束缚近似
18
4、 s电子紧束缚能带
• 先假定只考虑s电子，即组成孤立原子的s电子
的波函数的Bloch和 (k , r ) 1
(r R )eikR
NR
• 注意：孤立原子波函数是局域的，但其Bloch 和却是广域的，在任何原胞内都有相同的几率
紧束缚近似公式(一)

紧束缚近似公式(一)

紧束缚近似公式(一)紧束缚近似公式紧束缚近似（Tight Binding Approximation）是一种描述电子在固体晶格中行为的数学方法。

在紧束缚近似中，电子波函数被表示为原子轨道的线性组合，通过求解薛定谔方程来得到能级结构和电子态密度等信息。

Bloch定理Bloch定理表明在理想晶体中，电子波函数可以表示为平面波和某个周期函数的乘积形式。

根据Bloch定理，电子波函数可以用下式表示：Ψk(r)=e ik⋅r u k(r)其中，e ik⋅r是平面波，u k(r)是周期函数。

紧束缚近似基本公式紧束缚近似基本公式是在Bloch定理的基础上，进一步假设电子波函数由最近邻原子的原子轨道线性组合构成。

根据紧束缚近似，电子在晶体中的波函数可以用下式表示：e ik⋅R n u n(r−R n)Ψk(r)=∑c nn其中，R n是最近邻原子的位置矢量，u n(r−R n)是最近邻原子的原子轨道。

紧束缚近似能带关系根据紧束缚近似基本公式，可以得到能带关系，即能量与波矢之间的关系。

能带关系可以用下式表示：E k=∑c n∗c n e ik⋅(R n−R m)ϵnmn其中，E k是能量，c n∗和c n是电子的系数，e ik⋅(R n−R m)是相位因子，ϵnm是最近邻原子间的相互作用能。

紧束缚近似的应用举例紧束缚近似在描述材料的能带结构和电子态密度等方面有广泛的应用。

以下是一些应用举例：1.能带计算：通过紧束缚近似，可以计算材料的能带结构，进而分析材料的导电性、绝缘性等特性。

2.电子态密度计算：紧束缚近似可以用于计算材料的电子态密度，这对于研究材料的化学反应等方面非常重要。

3.值得注意的是，紧束缚近似也有其局限性，适用于描述弱相互作用体系，如共价键、金属键等。

对于强相互作用系统，如强关联电子体系，紧束缚近似可能不适用。

总之，紧束缚近似是一种重要的描述电子在晶体中行为的方法，在材料科学和凝聚态物理等领域有着广泛的应用。

紧束缚近似实验报告

紧束缚近似实验报告

1. 理解紧束缚近似的基本原理和方法；2. 掌握紧束缚近似在计算电子能带结构中的应用；3. 通过实验验证紧束缚近似在石墨烯材料中的适用性。

二、实验原理紧束缚近似是一种用于研究固体材料电子能带结构的方法。

该方法的基本思想是将晶体中的电子波函数近似为各个原子波函数的线性叠加，即紧束缚近似波函数。

通过求解紧束缚近似下的薛定谔方程，可以得到晶体中电子的能带结构。

三、实验仪器与材料1. 仪器：计算机、计算软件（如MATLAB、Python等）、实验数据；2. 材料：石墨烯样品、石墨烯样品制备设备、测量设备等。

四、实验步骤1. 石墨烯样品制备：制备高质量的石墨烯样品，确保样品表面干净、无杂质；2. 数据测量：使用测量设备对石墨烯样品进行电子能带结构测量；3. 数据处理：将测量得到的电子能带数据输入计算机，利用紧束缚近似方法进行计算；4. 结果分析：比较计算得到的能带结构与实验数据进行对比，验证紧束缚近似的适用性。

五、实验结果与分析1. 石墨烯样品制备：采用机械剥离法，成功制备出高质量的石墨烯样品；2. 数据测量：使用扫描隧道显微镜（STM）对石墨烯样品进行测量，得到其电子能带结构；3. 数据处理：将测量得到的电子能带数据输入计算机，利用紧束缚近似方法进行计算；4. 结果分析：通过比较计算得到的能带结构与实验数据进行对比，发现两者具有较高的吻合度，验证了紧束缚近似在石墨烯材料中的适用性。

1. 紧束缚近似是一种有效的计算电子能带结构的方法，尤其在石墨烯等二维材料中具有较高的适用性；2. 通过实验验证了紧束缚近似在石墨烯材料中的适用性，为后续石墨烯材料的理论研究提供了基础；3. 紧束缚近似在固体物理学、材料科学等领域具有广泛的应用前景。

七、实验讨论1. 紧束缚近似是一种简化的近似方法，其适用性受限于材料类型和晶体结构。

对于某些材料，紧束缚近似可能存在较大的误差；2. 在实际应用中，紧束缚近似可以与其他理论方法相结合，如第一性原理计算、分子动力学模拟等，以提高计算精度；3. 本实验中，紧束缚近似与实验数据具有较高的吻合度，表明该方法在石墨烯材料中具有较高的适用性。

上海师大固体物理第五章(4)紧束缚近似法分析

上海师大固体物理第五章(4)紧束缚近似法分析


0
Rn
E k
Eat J ss
'
e ik Rn
Rs
J
sn
Rn
利用周期性边界条件容易证明波矢在第一布里渊区共有N个值(N为晶体的 原胞个数)，对应N个准连续的能量本征值形成一个能带。亦即，孤立原 子的能级与晶体中的电子能带相对应。如2s、2p等能带。
J与sn表at (示r 相Rs距) 为的R重s 叠R程n 的度两，R个s 格R点n 上重的叠波最函完数全的，重即叠Jss积最分大，，它其依次赖是于最近at (r邻
有N个类似的aat方t ((rr程。RR12
) )
Eat
at
(r
RN
)
这些波函数对应于同样的能量Eat ，是 N重简并的。考虑到微扰后，晶体中电 子运动波函数应为N个原子轨道波函数 的线性组合。
即运用动孤的立波原函子数的 电k,r子，波因函此数紧束k,缚r 近Rn 似的也线称性为组原合子来轨构道成函晶数体线中性电组子合共法有,简化
(1)重叠积分J的大小：取决于近邻原子 波函数间的重叠，重叠越多，形成的 能带就越宽。
原子能级分裂成能带
能量越低，能带就越窄；能量越高，能带就越宽。这是由于能量最低的带对应 最内层的电子，其电子轨道很小，不同原子间波函数的重叠很少，因而能带较 窄；而能量较高的能带对应于外层电子，不同原子间波函数有较多的重叠，因 而形成的能带就较宽。
✓
当
r
Rn
时，
(k ,
r
Rn
)
与孤立原子波函数at
(r
Rn
)
相近。
由描于述 r(偏k,离r 格R点n ) Rn稍能大概时括紧a束t (r缚条Rn件) 是下个波小函量数，的所上以述用两个at特(r点。Rn我) 们来
固体物理学：4-5 紧束缚近似

固体物理学：4-5 紧束缚近似

N个A位原子 形成4个布洛赫和
同一量子数 —— N个3s和N个3p轨道相互杂化 第m个B位原子
N个B位原子 形成4个布洛赫和
A位和B位原子3s和3p轨道杂化形成8个布洛赫和 —— Si的价带和导带是8个布洛赫和的线性组合
1个3s和3个3p轨道相互杂化 —— 4个杂化轨道 单个Si原子轨道杂化
同一量子数 —— N个3s和N个3p轨道相互杂化 A位原子和B位原子的杂化形成成键态和反键态
—— 表示方程中的积分项
—— 积分只取决与相对位置
—— 周期性势场减去原子的势场 —— 仍为负值
方程的解
—— 关于am为未知数的N个齐次线性方程组
—— am只由
来决定
—— 任意常数矢量
能量本征值
（4-58）
—— 最完全的重叠
其次考虑近邻格点的格矢 能量本征值
（4-60）
能带的形成
应用周期性边界条件 K的取值
复式格子 原胞中有l个原子，原子的位置
布洛赫和
—— 原胞中不同原子的相对位移
—— 不同的分格子，i ——不同的原子轨道
具有金刚石结构的Si，原胞有1个A位和4个B位原子 A位原子格子与B位原子格子的相对位移
坐标原点选取在A 位格子 的格点上
同一量子数 —— N个3s和N个3p轨道相互杂化 第m个A位原子
的取值有N个，每一个 值对应波函数和一 个能量本征值，对于准连续的N个k值， E(k)将形成一准连续的能带，因此，形成固 体时原子态将形成一相应的能带。
晶体中电子的波函数具有布洛赫函数形式？？ 对于确定的 ， 晶体中电子的波函数
改写为 —— 晶格周期性函数
— 简约波矢，取值限制在简约布里渊区 晶体中电子的波函数具有布洛赫函数形式

固体物理09-紧束缚近似



ik x a
e
ik x a
e
ik y a
e
e ik z a e ik z a
* i ξ R n R m U ξ V ξ i ξ dξ J R n R m
这表明，积分值仅与两格点的相对位置 (Rn－Rm) 有关。 式中引入负号的原因是：就是周期势场减去在原点的原子势场，
如下图所示，这个场仍为负值。
方程化简为
能带交迭的示意图
4.4 紧束缚近似（TBA）
与近自由电子近似认为原子实对电子的作用很弱相反，本节，我们假
定原子实对电子的束缚作用很强，因此，当电子距某个原子实比较近
时，电子的运动主要受该原子势场的影响，受其它原子势场的影响很 弱。因此固体中电子的行为同孤立原子中电子的行为更为相似。这时 可将孤立原子看成零级近似，而将其他原子势场的影响看成小的微扰， 由此可以给出电子的原子能级和晶体能带之间的相互联系。这种方法 称为紧束缚近似 (Tight Binding Approximation)。 该模型主要适合于晶 体中原子间距较大时，或能带低而窄、壳层半径比晶格常数小的多的 情况，这时的原子轨道只受到其它原子很微弱的作用，如过渡金属中 的3d电子等。
能量本征值 E(k) 的表达式可进一步简化。
J R s i* ξ R s U ξ V ξ i ξ dξ
i* ξ R s 和 i* ξ 表示相距为Rs的格点上的原子波函数。只有它们有
一定重叠时积分值才不为零：
当 Rs ＝0时，两波函数完全重叠。
U r V r R m
m
晶体中电子的本征运动方程为：
2 2 U r r E r 2m

4.5 紧束缚近似、能态密度和费米面

Z N ( E ) lim E
如果在 k 空间中, 根据
E(k ) 常数
作出等能面, 那么在等能面 E 和 E+ΔE 之间的状态 的数目就是 ΔZ , 由于状态在 k 空间分布是均匀的, 密度为 V/(2π)³
V Z (能量为E和E E的等能面之间的体积) 3 (2 )
s k px k py k
代入波动方程, 解出系数和 能量本征值
虚线表示没有计入相互作用, 只是能带发生了明显的交迭
实线表示计入相互作用后的 结果, 可看出能级间的“排 斥作用”, 最下面能带既有 s 能级也有 p 能级的成分
3. 如果是复式晶格，每个原胞中有 l 个原子，原子 的位置为
Rm r m1 a1 m2 a2 m3 a3 r , 1,2,..., l
按照 LCAO 近似, Si 的价带和导带可以看成八个Bloch 和的线性组合
也可以取另外一种看法, 金刚石结构中的硅原子进 行 sp³ 轨道杂化, 形成四个杂化轨道
1 h1 2 1 h 2 2 1 h3 2 1 h 4 2

*
则 Wannier 函数就是各个格点上孤立原子的波 函数。如果某些能带与紧束缚近似模型相差很 远, 这时 Wannier 函数很少保留孤立原子波函数 的信息, 但是它仍然是比较定域的
在讨论电子空间局域性起重要作用问题时, Wannier 函数会是较好的工具
§4-5 紧束缚近似—原子轨道线性组合法 小 结
简单立方晶格 s 能带, p 能带沿 Δ 轴 E(k) 函数
二、原子能级与能带的对应 1. 上面讨论的是最简单的情形, 一个原子能级 εi 对应一个能带, 原子的不同能级, 在固体中将产 生一系列相应的能带

4-5紧束缚近似

* i
(r Rn )
* i
m
—— N种可能选取，方程是N个联立方程中的一个方程
am (r Rn )[U (r ) V (r Rm )] i (r Rm )dr ( E i )an
* i m
变量替换 势场具有周期性 引入函数
ikR E i J ( Rs )e s s
m
Rs Rn Rm
10 / 40
对于确定的 k
波函数 k ( r ) a m i ( r Rm )
m
am Ce
晶体中电子的波函数
ik Rm
1 k (r ) N
2
V (r Rm ) —— Rm 格点的原子在 r 处的势场
i —— 电子第i 个束缚态的能级
i (r Rm ) —— 电子第i 个束缚态的波函数
2. 电子在第m个原子附近运动，其它原子的作用是微扰
则 晶体中电子的波函数 ( r ) 满足的薛定谔方程 2 2 [ U ( r )] ( r ) E ( r ) 2m U ( r ) ——晶体的周期性势场，它是所有原子的势场之和
—— 最完全的重叠 Rs Rn Rm 0
J 0 ( )[U ( ) V ( )] i ( )}d
* i





J 0 i ( ) [U ( ) V ( )]d
其次考虑近邻格点的格矢

2


Rs
Rs Nearest ikR s J ( R ) e s

—— 积分只取决与相对位置 ( Rn Rm )

第三节 紧束缚近似


4、半导体的导电电子及空穴主要占据导带底与价带顶附近的状态 对于锗和硅 价带顶有三支能带发生简并 价带顶处等能面不是椭球面 导带底未发生简并，等能面是椭球面 5、半导体的导带底与价带顶的能量差为禁带宽度Eg
二、金属的能带结构 1、简单金属（如Na、Mg、Al等）的能带结构具有明显的近自由 电子的特征：除了在布里渊区边界附近以外，能带结构与自由电 子能带很接近。 2、过渡金属的能带由 很窄的d带和较宽的s 带交叠在一起形成。
孤立原子波函数是归一化的，因而
r r R d
a s a s n
o,n
1 0
当Rn 0 当Rn 0
于是，方程的左侧成为ES(k)-Esa
方程的右侧分为Rn=0和Rn≠0两项 令
A sa r Vcsa r d Vc r

n
系数
Ck ,n
1 N
1/ 2
e
ik Rn
s,k r
1 N
1/ 2
e
n
ik Rn
r Rn
a s
二、紧束缚近似下晶体中电子能量Es（k）的计算 将上述波函数带入薛定谔方程：
2 2 2 m V r Es K S , K r 0 a 1 2 2 ik Rn e V r E K s s r Rn 0 1/ 2 N n 2m
第四节、实际的能带结构
晶体实际的能带结构，通过理论计算与实验相结合而得到 能带的计算 能带的简并 对于某一给定的波矢k，两个或两个以上的子能带的能量相等,于 是这些子能带在k处简并。 一、半导体Ge、Si等的能带结构 1、能带 结构

紧束缚近似名词解释

紧束缚近似名词解释
紧束缚近似（Tight-Binding Approximation）是一种在固体物理学和材料科学中常用的近似方法，用于描述电子在晶格结构中的行为。

该方法假设电子只在相邻原子之间的相互作用下运动，忽略了更远的相互作用。

这种近似方法特别适用于那些电子波函数重叠较少的材料，因为在这种情况下，电子的波函数主要集中在它们各自的原子附近。

在紧束缚近似下，电子的能量和波函数可以通过一个包含原子轨道和它们之间相互作用的模型来描述。

这种方法的一个优点是它可以处理大规模系统，因为它只需要考虑每个原子周围的有限数量的其他原子。

尽管紧束缚近似有许多优点，但它也有一些局限性。

例如，它不能很好地描述那些电子波函数重叠较大的材料，如金属和半金属。

此外，它也不能描述那些具有强电子关联效应的材料，如某些过渡金属氧化物。

以上信息仅供参考，如有需要，建议您咨询专业人士。

4-3-紧束缚模型

i (r Rn )i (r Rm )dr m,n
以
Rm
i (r Rn )
左乘波动方程并积分
ik Rm ik Rn e ( r R ) U ( r ) V ( r R ) ( r R ) dr E e i n m i m i
s
把近邻格式代入能量表达式，得到s 态形成能带后的能量本征值为：
E (k ) i J 0 e
Rs r r - i k Rs
ky kx
J ( Rs ) e
r r ik aj
i J 0 J 1 (e
r r ik ai
e
r r ik ai
e
r r ik aj
由周期性边界条件限定波矢k有N个准连 续的取值，等于原胞数。
7
举例：简单立方晶格中由原子s态 形成的能带
s 态波函数是球对称的，在各个方向重叠积分相同，因此 （ s r） s r） J(Rs)有相同的值J1。s 态波函数为偶宇称，即 （ ， 在近邻重叠积分中，波函数的贡献为正，所以J1>0。简单立 方晶格每个原子的最近邻原子有6 个： kz (a, 0, 0), (0, a, 0), (0, 0, a) (.a, 0, 0), (0, . a ,r） 0), (0, 0, .a) （
9
环绕不同的 N 个格点，将有 N 个类似的波函数， 它们具有相同的能量 i ，也就是说是N 重简并。微 扰以后的状态是 N 个简并态的线性组合，即用原子 轨道ϕi(r−Rm)的线性组合来构成晶体中电子共有化运 动 的 轨 道 ψ (r ) ， 因 而 也 称 为 原 子 轨 道 线 性 组 合 LCAO。晶体中电子共有化运动的波函数为
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

k
1 ，得到 W
r Rn
at
r Rn
k
k,r
1 N
e ikRn at
r Rn
Rn
---上式称为布洛赫和，它是原子轨道的线性组合。
如果晶体是由N个相同的原子构成的布喇菲晶格，则在各原子附近有N个
相同的能量Eat 的束缚态波函数at ，因此在不考虑原子间相互作用时，应
✓
当
r
Rn
时，
(k ,
r
Rn
)
与孤立原子波函数at
(r
Rn
)
相近。
由描于述 r(偏k,离r 格R点n ) Rn稍能大概时括紧a束t (r缚条Rn件) 是下个波小函量数，的所上以述用两个at特(r点。Rn我) 们来
取：
k, r Rn
k at
r Rn
把上式代入万尼尔函数，
W Rn , r
1 N
k,r
eik Rn
k
布洛赫定理
k,r
eik r
u
(r )
k
1 N
e e u ik Rn ik r
r
k
k
1 N
eikr
Rn
u
k
r Rn
k
1 N
k , r Rn
k
W (r Rn )
W r Rn
的关系
W r Rn
1 N
k , r Rn
k
当晶体中原子间距增大时，电子被束缚在原子附近的几率比它远离原子的
几率大得多，电子在某格点附近的行为同孤立原子中电子的行为相似。紧
束缚条件下电子的波函数具有如下两个特点：
✓
当r偏离格点Rn较大时，波函数
(k ,
r
Rn
)
是一个小量；
W r Rn
1 N
k , r Rn
k
at
r Rn
1
k
N
k
利用万尼尔函数的正交性，得到
N
ΩW
(r
Rn
)W
(r
Rn
)dr
1 N
k
2
at
NΩ
r
Rn
at
r Rn dr
k
1 N
2 k 1
k
我们取
1 N
称 LCAO。
k,r
Cnat
r Rn
Rn
与
k,r
1 N
e ikRn at
r Rn
Rn
相比，Cn
1 eikRn N
5.5.2 模型和微扰计算
1. 模型
晶体中的电子在某个原子附近时主要受该原子势场
V
(r
Rn
)
的作用，
其它原子的作用视为微扰来处理，以孤立原子的电子态作为零级近似
(1) 孤立原子运动方程
Hˆ 0at
(r
Rn
)
Eat at
(r
Rn
)
Eat 表示孤立原子中的电子能级，表示所处能级1s，2s，2p等。
(2) 晶体中电子运动方程
Hˆ
(k ,
r)
E
(k )
(k ,
r)
将电子波函数
(k ,
r)
1 N
e ikRn at
(r
Rn
)
Rn
代入薛定谔方程
Hˆ
(k ,
r)
E
(k )
(k ,
r)
1
N
Rn
eik Rn
2 2 2m
V
at
(r
Rn
)
Rm
'V
at
(r
Rm )
E
(k)at
(r
Rn
)
0
Hˆ
at
0
(r
Rn
)
Hˆ 0
Eat at
(r
Rn
)
eikRn Eat E (k )
'V
at
(r
Rm
)at
。
2. 势场
V
r
V
at
(r
Rn
)
'V
at
(r
Rm
)
V at
r Rn
表示位于Rn
Rm n1a1
n2a2
n3a3
的孤立原子在r 处的势场， '表示求和不
含
Rm
Rn
这一项。
Rm
r r Rn
O
Rn
3. 方程与计算
V
r
V
at
(r
Rn
)
'V
at
(r
Rm
)
Rm
(r
Rn
)
0
Rn
Rm
上式左乘
at
(r
Rs
)，并对整个晶体积分得，
eik Rn Eat E (k ) sn
Rn eik Rn
at
(r
Rs )
'V
at
(r
Rm
)at
(r
Rn
)dr
0
Rn
Rm
令
eik Rn
at
(r
Rs )
V'
at
(r
Rm
第五节 紧束缚近似法
5.5.1 万尼尔函数 5.5.2 模型和微扰计算 5.5.3 原子能级与能带的对应关系 5.5.4 近自由电子近似和紧束缚近似的比 较
5.5.1 万尼尔函数
1. 定义 在周期性势场中运动的波函数一定是布洛赫波函数，而布洛赫波函数在k 空
间具有周期性，即：
(r ) (r )
1 N
k , r Rn
k
变量总是以
(r
Rn
)
出现，即Wannier函数是以R为中心的函数，即处
于R的局域函数，波函数可写成
k,r
1 N
W
r Rn
eik Rn
Rn
不同能带或不同格点的万尼尔函数是正交的，即
N
ΩW
(r
Rn
)W
(r
Rn
)d
nn
N
Ω
W
(r
)at
(r
Rn
)dr
0
J sn
Rn
Rm
eik Rs
k
k Kh
所以可以将 k , r 在波矢空间作傅里叶展开
k,r
1 N
W
(
Rn
,
r
)e
ik Rn
Rn
展开系数 W Rn , r
。
1 N
k,r
eik Rn
k
称为万尼尔（Wannier）函数
(2) 万尼尔函数的性质
Wannier函数是以Rn为中心的波包，为局域函数，具有定域的特性。
有N个类似的aat方t ((rr程。RR12
) )
Eat
at
(r
RN
)
这些波函数对应于同样的能量Eat ，是 N重简并的。考虑到微扰后，晶体中电 子运动波函数应为N个原子轨道波函数 的线性组合。
即运用动孤的立波原函子数的 电k,r子，波因函此数紧束k,缚r 近Rn 似的也线称性为组原合子来轨构道成函晶数体线中性电组子合共法有,简化
Hˆ
2 2 2m
V
at
(r
Rn
)
Rm
'V
at
(r
Rm
)
Hˆ 0
Hˆ
Hˆ 0
2 2m
2
V
at
(r
Rn )
Hˆ
'V
at
(r
Rm
)
Rm
r r Rn
O
Rn
如果不考虑原子间的相互影响，在格点 Rn 附近的电子将以原子束缚
态
at
绕
Rn
点运动。at
(r
Rn
)
表示孤立原子的电子波函数。ຫໍສະໝຸດ Rn)W(r
Rn
)d
1 N
N
k
k,
r
eik Rn
k,r
e d ik Rn
k
1 N
e e ik Rn ik Rn
N
k,r
k , r d
k
1 ik Rn Rn
e
,
Nk
nn
(3)
布洛赫和：
k,r
与 at
r Rn