余数与除数的关系
- 格式:docx
- 大小:1.62 MB
- 文档页数:10

余数和除数的关系
1、在有余数的除法里,余数和除数之间的关系是:商×除数+余数=被除数。
2、余数必然小于除数
例:6÷3=2……0,余数0小于除数3。
余数性质
1、如果a,b除以c的余数相同,那么a与b的差能被c 整除。
例如,17与11除以3的余数都是2,所以17-11能被3整除。
2、a与b的和除以c的余数(a、b两数除以c在没有余数的情况下除外),等于a,b分别除以c的余数之和(或这个和除以c的余数)。
例如,23,16除以5的余数分别是3和1,所以(23+16)除以5的余数等于3+1=4。
注意:当余数之和大于除数时,所求余数等于余数之和再除以c的余数。
3、a与b的乘积除以c的余数,等于a,b分别除以c的余数之积(或这个积除以c的余数)。
例如,23,16除以5
的余数分别是3和1,所以(23×16)除以5的余数等于
3×1=3。
注意:当余数之积大于除数时,所求余数等于余数之积再除以c的余数。

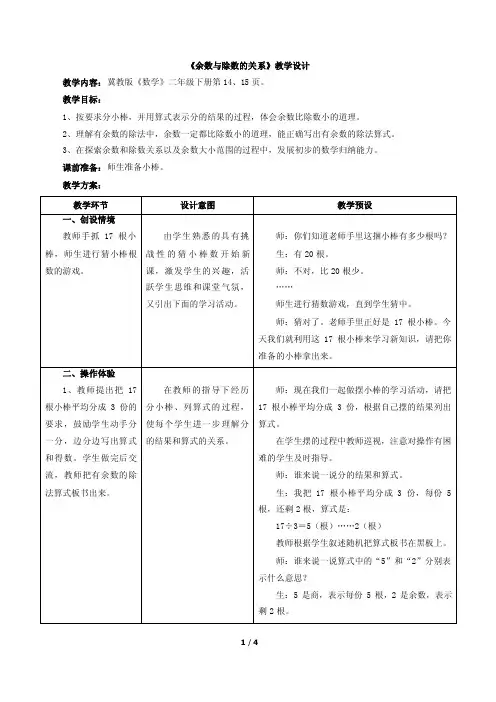
二年级数学下册《余数和除数的关系》教学设计【教学目标】1、知识与技能:知道余数一定要比除数小。
会口算简单的有余数的除法。
2、过程与方法:经历操作、观察、讨论的过程,体会余数比除数小的道理。
3、情感态度与价值观:(1)在探索余数和除数关系的过程中,学习简单的数学思考。
(2)在学习的过程中,对学生渗透《中华人民共和国消费者权益保护法》,让学生知道,作为消费者有哪些权益?在以后的生活中,会用法律的手段来保护自己和他人。
(3)让学生能在具体情境中借助已有的经验和知识展开学习,激发学生的学习热情和兴趣,感受数学学习的价值。
【教学重点】进一步体会有余数除法的意义,认识余数小于除数。
【教学难点】在观察、操作、推理、验证、归纳的过程中发现余数和除数之间的关系,并理解应用其关系。
【教学准备】小棒、课件。
【教学过程】一、复习引入:1、师:同学们,你们爱吃草莓吗?学生可能会说:爱吃。
2、师:老师也爱吃,昨天老师去买草莓的时候遇到了一些问题,同学们愿意帮老师解决吗?(学生可能会说:愿意)课件出示题目及图片。
草莓每斤6元,老师带了20元钱,能买几斤草莓?谁能用除法算式来解决。
学生可能会说:20÷6=3(斤)……2(元)师:这个算式表示什么意思?2表示什么?20、6、3表示什么?指名学生回答。
3、复习除法算式各部分的名称。
师:谢谢同学们帮我解决了这个问题,我还有一个问题想听听同学们的意见,我昨天付了20元钱就走了,忘了拿找回的2元钱了,你们说,我该不该找他去要那2元钱呢?学生可能会说2元钱就算了,也可能有学生说应该去要回2元钱来。
师:同学们,虽然只是2元钱,但那也是我们的财产啊,作为消费者,我们是有权拿回属于我们的东西的,这是受法律保护的,根据《中华人民共和国消费者权益保护法》,第二章消费者的权利第七条消费者在购买、使用商品和接受服务时享有人身、财产安全不受损害的权利。
消费者有权要求经营者提供的商品和服务,符合保障人身、财产安全的要求。

小学三年级数学知识点小学三年级数学知识点有余数的除法知识点:1、余数:在整数的除法中,只有能整除与不能整除两种情况。
当不能整除时,就产生余数,取余数运算:1。
指整数除法中被除数未被除尽部分。
例如27除以6,商数为4,余数为3。
2、余数的性质:余数有如下一些重要性质(a,b,c均为自然数)(1)余数小于除数。
(2)被除数=除数×商+余数除数=(被除数-余数)÷商商=(被除数-余数)÷除数余数=被除数-除数×商。
3、有余数除法的含义:通过平均分一些物体,有时有剩余,就出现了余数。
如:一共有23盆花,每组摆5盆,最多可以摆几组,还多几盆?23÷5=4(组)……3(盆)其中,被除数23,除数5,商4,余数34、余数与除数的关系:在有余数的除法中,每一次除得的余数必须比除数小。
(余数除数)如:23÷5=4……3,其中(余数3除数4)5、除法各部分之间的关系:被除数=商×除数+余数或被除数=商×除数小学三年级数学复习知识点可能性知识点:1、不可能和一定’,都表示确定的现象。
‘可能’,表示不确定的现象。
2、请用“一定、可能、不可能”来说一说。
①一定:太阳一定从东边升起,月亮一定绕着地球转,地球一定每天都在转动,每天一定都有人出生,人一定要喝水……②可能:三天后可能下雨,花可能是香的,明天可能有风,下周可能会考试。
③不可能:太阳不可能从西边升起,地球不可能绕着月亮转,鲤鱼不可能在陆地上生活。
小学三年级数学必背知识点四边形知识点:【正方形】概念:四条边都相等、四个角都是直角的四边形是正方形。
特点:有4个直角,4条边相等。
(正方形既是长方形,也是菱形)周长:正方形的周长=边长×4【长方形】概念:有一个角是直角的平行四边形叫做长方形。
特点:长方形有两条长,两条宽,四个直角,对边相等。
周长:长方形的周长=(长+宽)×2【平行四边形】概念:两组对边互相平行的四边形,它的对边平行且相等,对角相等。




第六单元《余数与除数的关系》教案二年级下册数学人教版一、教学内容本课为《余数与除数的关系》的第一课时,主要是引导学生通过观察、实验、推理、交流等数学活动,发现并理解余数与除数的关系,并能运用到实际生活中。
二、教学目标1. 知识与技能:使学生理解余数与除数的关系,能正确计算有余数的除法。
2. 过程与方法:通过观察、实验、推理、交流等数学活动,培养学生的观察能力、实验能力、推理能力和交流能力。
3. 情感态度与价值观:激发学生学习数学的兴趣,培养学生的团队合作精神和探究精神。
三、教学难点1. 理解余数与除数的关系。
2. 正确计算有余数的除法。
四、教具学具准备1. 教具:PPT、教学卡片、黑板、粉笔等。
2. 学具:练习本、铅笔、橡皮等。
五、教学过程1. 导入:通过PPT展示一些有余数的除法题目,引导学生观察并发现余数与除数的关系。
2. 新课:讲解余数与除数的关系,通过例题和练习题巩固知识。
3. 练习:让学生独立完成练习题,教师巡回指导,及时解答学生的疑问。
4. 小结:总结本节课的主要内容,强调余数与除数的关系。
5. 作业布置:布置课后作业,要求学生按时完成。
六、板书设计1. 余数与除数的关系2. 主要内容:余数与除数的关系、有余数的除法计算方法、练习题等。
七、作业设计1. 基础题:完成课后练习题,巩固余数与除数的关系。
2. 提高题:完成一些有余数的除法题目,提高计算能力。
3. 拓展题:研究一些与余数与除数的关系相关的实际问题,培养学生的解决问题的能力。
八、课后反思本节课通过观察、实验、推理、交流等数学活动,使学生理解了余数与除数的关系,并能正确计算有余数的除法。
但在教学过程中,发现部分学生对有余数的除法计算方法掌握不够熟练,需要在今后的教学中加强练习。
同时,要注意激发学生的学习兴趣,培养学生的团队合作精神和探究精神。
总体来说,本节课达到了预期的教学目标,但也存在一些不足之处,需要在今后的教学中加以改进。



初中余数知识点总结在学习余数的概念时,我们需要了解四则运算、整数的概念、两个整数的相对大小的比较、除法时商和余数的关系等。
这是一系列基本数学概念和技能的纽带,是数学教学中重要的知识点之一。
概述:余数是指一个数被另一个数除后得到的剩余部分。
例如 15除以4等于3余3。
余数的概念:在算术中,除法运算是划分的过程。
除法中划分得到的相等的几份就是商。
而最后剩下的一份就是余数。
当我们用一个数除另一个数时,有时会有余数。
例如,当12 ÷ 5时,商是2,余数是2;而当13 ÷ 4时,商是3,余数是1。
取模运算和余数:取模运算即求余数的运算。
它是计算机领域常用的一种数学运算符号。
如果说 a 除以 b 可以得到商 c 和余数 r,那么 r = a % b。
小数和余数:小数是再除法时出现的一种特殊的余数形式。
例如 7 ÷ 2 = 3.5,其中3是商数,0.5是余数,但是以小数的形式存在。
正整数的除法:当一个正整数(除数)除不尽一个大于零的整数(被除数)时,结果和余数都是一个非负整数。
这就是正整数的除法。
负整数的除法:当一个负整数(除数)除不尽一个大于零的整数(被除数)时,结果和余数都是一个与除数同号的整数。
但是当被除数是负数时,结果和余数可能会有很多种情况。
需要合理的确定符号。
同余关系:同余关系是指两个数的差能整除一个数的性质。
例如13和5模6是同余关系,因为13-5=8,8可以整除6。
余数的性质:(1)余数与除数的关系:不管是正负整数,被除数总能写成“商×除数+余数”的形式。
(2)余数的大小:余数永远小于除数,但可以等于0。
余数运算:余数的运算是对余数进行特定的运算。
例如,对余数做加法、减法、乘法、除法等运算。
余数的应用:余数可以用在取模运算、排列组合、密码学、数据校验等领域。
本文将详细介绍余数相关的概念和运算,以及余数的一些基本性质、应用和相关知识点。
一、余数的概念余数是指一个数被另一个数除后得到的剩余部分。
人教版二年级下册数学《余数和除数的关系》教案一. 教材分析《余数和除数的关系》是人教版二年级下册数学的一章内容,主要让学生理解在除法运算中,除数、被除数和余数之间的关系。
通过本节课的学习,学生将掌握除法的基本概念,并能运用除法解决实际问题。
二. 学情分析二年级的学生已经掌握了加减法的基本运算,但对除法运算的认识尚浅。
本节课需要学生理解除数、被除数和余数之间的关系,具有一定的抽象思维能力。
同时,学生需要通过实例感受除法在实际生活中的应用,提高学习兴趣。
三. 教学目标1.知识与技能:学生能够理解除数、被除数和余数之间的关系,掌握除法的基本运算。
2.过程与方法:学生通过实例探究,培养观察、分析、归纳的能力。
3.情感态度与价值观:学生感受数学与生活的联系,提高学习数学的兴趣。
四. 教学重难点1.重点:学生能够理解除数、被除数和余数之间的关系,进行简单的除法运算。
2.难点:学生能够运用除法解决实际问题,理解除法的本质。
五. 教学方法采用情境教学法、游戏教学法和小组合作学习法,激发学生的学习兴趣,培养学生的主体意识、合作精神和创新能力。
六. 教学准备1.教具:课件、黑板、粉笔、实物等。
2.学具:练习本、铅笔、橡皮等。
七. 教学过程1.导入(5分钟)通过一个生活实例,如分水果,引入除法运算。
引导学生思考:如何分配这些水果才能使每个人得到的数量一样多?从而引出除数、被除数和余数的概念。
2.呈现(10分钟)通过PPT展示除数、被除数和余数之间的关系,让学生观察、思考并总结规律。
如:10 ÷ 3 = 3 … 1,引导学生发现除数乘以商加上余数等于被除数。
3.操练(10分钟)学生分组进行除法运算,教师巡回指导。
要求学生用口头表达和书面形式展示除法运算过程,强化对除数、被除数和余数之间关系的理解。
4.巩固(10分钟)设计一些有趣的游戏,如除法接力、除法拼图等,让学生在游戏中运用除法运算,巩固所学知识。
5.拓展(10分钟)让学生运用除法解决实际问题,如计算购物时的找零、分配物品等。
二年级下册数学《有余数的除法》知识点总结+练习题一、知识点回顾:有余数的除法1、有余数的除法的意义:在平均分一些物体时,有时会有剩余。
2、余数与除数的关系:在有余数的除法中,余数必须比除数小。
最大的余数小于除数1,最小的余数是1。
3、笔算除法的计算方法:(1)先写除号“厂”(2)被除数写在除号里,除数写在除号的左侧。
(3)试商,商写在被除数上面,并要对着被除数的个位。
(4)把商与除数的乘积写在被除数的下面,相同数位要对齐。
(5)用被除数减去商与除数的乘积,如果没有剩余,就表示能除尽。
4、有余数的除法的计算方法可以分四步进行:一商,二乘,三减,四比。
(1)商:即试商,想除数和几相乘最接近被除数且小于被除数,那么商就是几,写在被除数的个位的上面。
(2)乘:把除数和商相乘,将得数写在被除数下面。
(3)减:用被除数减去商与除数的乘积,所得的差写在横线的下面。
(4)比:将余数与除数比一比,余数必须必除数小。
解决问题(1)余数比除数小。
例:43÷7=( )…( ),余数可能是( )或者余数最大是( )(2)至少问题(进一法):商+1例:有27箱菠萝,王叔叔每次最多能运8箱。
至少要运多少次才能运完这些菠萝。
(3)最多问题(去尾法)例:小丽有10元钱,买3元一个的面包,最多能买几个?(4)用有余数除法的知识解决与按规律排列有关的问题。
例:第68页例6.(5)练习十五第8题第11题(特别讲,更要让学生弄懂,很可能会考)二、小试牛刀填一填。
1、计算有余数的除法时,( )一定要比( )小。
2、★★★★★★★★★★★★★★★★★★★★★★★★★★★★(1)把这些★每8个8个的圈,圈()组,还剩()个。
(2)把这些★每6个6个的圈,圈()组,还剩()个。
3、( )里最大能填几?( )×7<36 8×( )<75 42>( )×654>( )×9 4×( )<31 39>( )×54、18朵花平均放在4个花瓶里,每个花瓶里放( )朵,还剩( )朵。
三年级数学知识点归纳三年级数学知识点归纳有余数的除法知识点:1、余数:在整数的除法中,只有能整除与不能整除两种情况。
当不能整除时,就产生余数,取余数运算:1。
指整数除法中被除数未被除尽部分。
例如27除以6,商数为4,余数为3。
2、余数的性质:余数有如下一些重要性质(a,b,c均为自然数)(1)余数小于除数。
(2)被除数=除数×商+余数除数=(被除数-余数)÷商商=(被除数-余数)÷除数余数=被除数-除数×商。
3、有余数除法的含义:通过平均分一些物体,有时有剩余,就出现了余数。
如:一共有23盆花,每组摆5盆,最多可以摆几组,还多几盆?23÷5=4(组)……3(盆)其中,被除数23,除数5,商4,余数34、余数与除数的关系:在有余数的除法中,每一次除得的余数必须比除数小。
(余数除数)如:23÷5=4……3,其中(余数3除数4)5、除法各部分之间的关系:被除数=商×除数+余数或被除数=商×除数三年级数学知识点梳理可能性知识点:1、不可能和一定’,都表示确定的现象。
‘可能’,表示不确定的现象。
2、请用“一定、可能、不可能”来说一说。
①一定:太阳一定从东边升起,月亮一定绕着地球转,地球一定每天都在转动,每天一定都有人出生,人一定要喝水……②可能:三天后可能下雨,花可能是香的,明天可能有风,下周可能会考试。
③不可能:太阳不可能从西边升起,地球不可能绕着月亮转,鲤鱼不可能在陆地上生活。
三年级数学知识点四边形知识点:【正方形】概念:四条边都相等、四个角都是直角的四边形是正方形。
特点:有4个直角,4条边相等。
(正方形既是长方形,也是菱形)周长:正方形的周长=边长×4【长方形】概念:有一个角是直角的平行四边形叫做长方形。
特点:长方形有两条长,两条宽,四个直角,对边相等。
周长:长方形的周长=(长+宽)×2【平行四边形】概念:两组对边互相平行的四边形,它的对边平行且相等,对角相等。
二年级数学《余数和除数的关系》教学设计二年级数学《余数和除数的关系》教学设计作为一名教学工作者,时常要开展教学准备工作,借助教学设计可以更好地组织教学活动。
教学设计应该怎么写呢?以下是小编整理的二年级数学《余数和除数的关系》教学设计,仅供参考,大家一起来看看吧。
二年级数学《余数和除数的关系》教学设计篇1教学目标:1、进一步巩固对有余数除法的认识和理解。
2、通过操作、观察、比较、归纳等数学学习活动,让学生发现并理解余数比除数小,培养学生合情推理能力和动手操作能力。
3、在自主探索、合作交流中经历发现知识的过程,积累数学活动经验,体会探究的乐趣。
教学重难点:自主探究余数与除数的关系。
教学过程:一、创设情景,复习旧知出示修改后人教材59页出题图。
看:他们在干什么?师:这些小朋友啊,在用8根小棒摆正方形、三角形、五边形研究数学问题,想知道这里面的数学问题吗?1、用8根小棒能摆几个正方形?学生摆后指名汇报摆的结果,课件相机展示摆的结果。
师:8根小棒摆正方形的过程可以用什么算式来表示?为什么可以这样表示?学生回答后板书算式。
2、用8根小棒能摆几个三角形?学生摆后指名汇报摆的结果,课件相机展示摆的结果。
8根小棒摆三角形的过程又可以用什么算式来表示?学生回答后板书算式。
谁能说出这个算式各部分的名称?学生回答大屏幕展示。
结合图形,谁能说说各部分表示的含义?3、用8根小棒能摆几个五边形?学生摆后指名汇报摆的结果,课件相机展示摆的结果。
8根小棒摆五边形的过程又可以用什么算式来表示?学生回答后板书算式。
算式中5的名称叫什么?它表示什么?的名称叫什么?它又表示什么?学生回答后大屏幕展示。
4、观察算式,提出问题问:观察我们写出的三个算式,它们哪部分相同?第一个算式和二、三两算式最大的区别是什么?师:被除数相同,写出的除法算式,有的有余数,有的没有,就是有余数,余数也不一样,那么,余数和除法算式中的哪一些部分有关系呢?大胆猜一猜。
一、知识点回顾1、有余数的除法的意义:在平均分一些物体时,有时会有剩余。
2、余数与除数的关系:在有余数的除法中,余数必须比除数小。
最大的余数小于除数1,最小的余数是1。
3、笔算除法的计算方法:(1)先写除号“厂”(2)被除数写在除号里,除数写在除号的左侧。
(3)试商,商写在被除数上面,并要对着被除数的个位。
(4)把商与除数的乘积写在被除数的下面,相同数位要对齐。
(5)用被除数减去商与除数的乘积,如果没有剩余,就表示能除尽。
4、有余数的除法的计算方法可以分四步进行:一商,二乘,三减,四比。
(1)商:即试商,想除数和几相乘最接近被除数且小于被除数,那么商就是几,写在被除数的个位的上面。
(2)乘:把除数和商相乘,将得数写在被除数下面。
(3)减:用被除数减去商与除数的乘积,所得的差写在横线的下面。
(4)比:将余数与除数比一比,余数必须必除数小。
二、解决问题根据除法的意义,解决简单的有余数的除法的问题,要根据实际情况,灵活处理余数。
1.租船问题:运用有余数的除法解决租船问题时,商加1才是最后的结果。
2.周期问题:在实际生活中,有一些事物按照一定的规律循环出现,这样的问题,称为周期问题。
解决周期问题时,可以根据题中循环出现的规律列出除法算式,求出余数,再根据余数得出所求问题的答案。
在有余除法中,要记住:(1)余数<除数;(2)被除数=商×除数+余数三、有余数的除法练习题一、填空1、有余数的除法中,被除数=()×()+()2、20以内能被3整除的数有:3、6、()、()、()、()二、文字题1、一个数除以5商是9余数是2,这个数是多少?2、把77平均分成9份,每份是多少?还余多少?3、从58里面减去3与8的积,得到的差再被4除,商是多少?余多少?三、直接写出得数。
7×8=34÷7=74÷9=48÷6=23÷3=17÷6=58÷6=39÷6=54÷9=19÷2=24÷5=63÷7=82÷9=77÷8=54÷9=36÷7=四、填空。
余数与除数的关系
余数与除数的关系
教学内容:
《义务教育教科书数学二年级下册》第61页例二。
教学目标
知识与能力:
1.进一步巩固对有余数除法的认识和理解;
2.在操作中,发现并归纳出余数与除数的关系。
3.理解并掌握余数和除数的关系,能灵活运用其关系解决实际问题。
过程与方法:
学生通过感知、猜测、验证的过程,发现余数和除数的关系。
情感与态度:
1. 学生在数学探究学习中敢于大胆猜测,并找到恰当的方法验证,以完整的探究过程来培养其良好的学习品质。
2. 激发学生运用所学知识解决实际问题的兴趣。
教学重点、难点:
在猜测、操作、验证的过程中,发现余数和除数的关系,并理解应用其关系。
教学具准备:课件小棒
一、复习导入
以《熊出没》故事引入,从而复习旧知。
(播放音频:一天,小镇的房屋管理员给光头强打来电话说他的木屋太破旧,地震就要来了,住着很不安全,赶紧搬到小镇上去。
光头强舍不得生活了很久的木屋,又担心安全。
善良的熊大和熊二帮光头强修好了小木屋。
为了感谢他们,光头强送来10罐上好的蜂蜜,他们舍不得吃,想储存起来。
如果每3罐分一份,能分成几份?还剩几罐呢?)
(课件出示第一个问题):有10罐蜂蜜,每3罐分一份。
可以分成几份?还剩几罐?
学生列出算式并自主尝试计算结果。
抽生汇报:10÷3=3(份)……1(罐)
提问:这个算式表示的含义是?这里的1表示什么?在除法算式中它们分别叫做什么?
预设:除数,余数。
谈话:孩子们,在除法算式中,余数和除数之间有一种神秘的关系。
你想知道吗?这节课,我们就来研究余数与除数的关系。
(板书课题)(设计意图:通过有趣的故事导入,抓住学生的好奇心和低年级儿童特点。
来激发学生的学习兴趣。
唤起已有知识经验,为新课教学奠定
谈话:同学们的观察很仔细,也都发现了一些秘密。
关于余数与除数的关系,到底谁的猜测准确呢?咱们一起来验证一下。
幻灯片出示例2的主题图。
○1提问:请大家观察这幅图,说说这些小朋友在干什么?
引导学生说出:用小棒摆独立的正方形,每个正方形要用4根小棒。
○2谈话:请大家拿出学具,每4人一个小组,按要求完成学习单。
师巡视指导。
○3小组汇报交流。
(设计意图:以小组合作的方式,给了学生很大的空间,充分调动学生的积极性,通过直观操作,感知发现余数与除数之间的关系。
根据汇报与置疑,让学生在解疑的过程中,突破教学难点。
学生真正担当了小小探索者。
)
3、小结。
谈话:通过操作验证,得出余数与除数之间的关系是:除数>余数(课件出示)。
也可以说:余数<除数(板书)
同桌之间互相说一说余数与除数的关系。
(设计意图:通过总结进一步明确除数与余数之间的关系,加深印
象。
)
三、练习巩固
谈话:孩子们,这么重要的规律你能灵活运用吗?
课件出示。
1、判断对错。
光头强:35÷8=3 (11)
熊大: 81÷9=8 (9)
吉吉: 25÷5=5 0
熊二: 26÷7=3 (5)
谈话:熊二觉得大家真了不起。
现在想邀请大家一起玩游戏。
好吗?
2、熊二在哪里?
○1提示:除数是2,我躲在余数的后面。
□0□1□2□3
○2提示:余数可能是1,2,3,4,5,我躲在除数的后面。
□0□2□4□6
3、熊二找朋友。
他们躲在除数是5时可能出现的余数后面,帮我找到他们吧。
□1□2□3□4□6
4、帮熊二找蜂蜜。
■中最大能填几?
()÷8= 3……■
()÷6= 4……■
★中最小能填几?
()÷★ = 5 (2)
()÷★ = 6 (6)
5.谁是智多星?
()里能填哪些数?
()÷6 = 4……■
(设计意图:习题的设计,有趣而新颖。
题目由浅及深,学生通过不同类型的练习,一方面巩固已学知识,另一方面能拓展思维空间。
通过练习,使不同的学生得到不同的发展。
)
四、总结。
1、学生自主总结:这节课学了什么?你有什么收获?
2、师生共同梳理总结:余数与除数的关系是:余数<除数。
五、板书。
余数与除数的关系
10÷3=3(份)……1(罐)
11÷3=3(份)……2(罐)
12÷3=4(份)
除数>余数
余数<除数
操作单:
用指定根数的小棒摆正方形,再填表。
小棒的根数/根摆出正方形的
个数/个
剩下的小棒根数
/根
算式
8
我发现
9 10 11 12 13 14 15 16
用8根,9根,10根,11根小棒都
能摆出( )个正方形,还分别剩下( )根,( )根,( )根小棒。
列
出除法算式的余数就分别是( 、 、 )。