立体几何——点线面位置关系

空间几何的基本概念点线与面的关系空间几何的基本概念：点、线与面的关系空间几何是研究三维空间中点、线和面之间的关系的数学分支。

点、线和面是空间几何中最基本的概念，它们之间的关系是建立在欧几里得几何基础上的。

本文将介绍空间几何中点、线和面的定义及其之间的关系。

一、点点是空间几何中最基本的对象，它是没有长度、宽度和高度的，仅有一个位置。

点通常用字母标记，如A、B、C等。

在空间中，任意两点可以确定一条线段，而三个非共线的点可以确定一个平面。

二、线线是空间几何中由无数个点组成的集合，它只有长度没有宽度和高度。

线通常用字母表示，如l、m、n等。

线可以分为直线和曲线两种。

直线是在空间中两点之间连续延伸的路径，它有无限个点。

而曲线则是非直线的线，它的形状可以是弯曲或蜿蜒的。

三、面面是空间几何中由无数个直线组成的集合，它有长度和宽度，没有高度。

面通常用字母表示，如α、β、γ等。

面可以分为平面和曲面两种。

平面是由无数个共面的点和一条穿过其中的直线组成的，它没有弯曲的部分。

而曲面则不是平的，它可以弯曲或扭曲。

点、线和面的关系是空间几何中重要的内容。

在空间中，点是构成线和面的基础。

在两个点之间，可以画一条直线，它是连接两个点的最短路径。

多个点可以连成一条折线，折线也是一种线。

线可以在平面内运动、延伸或相交，形成不同的几何形状，而面是由无数条线构成的，它们共面并围成了一个封闭的区域。

点线面之间的关系可以通过以下几个方面进行描述：1. 点与线的关系：一条直线上的任意两点可以确定一条线段，反之，一条线段也可以看作是两个端点之间的直线。

点也可以在一条直线上移动，形成线段的延伸或缩短。

两条相交的直线可以在交点处确定一个新的点。

2. 点与面的关系：一个点可以在平面内，平面也可以通过一个点来确定。

在一个平面上，可以找到无数个点。

3. 线与面的关系：一条线可以在平面内或平面上延伸，两条相交的直线可以确定平面上的一条直线。

一个平面上可以有多条直线，它们可以平行、相交或重合。

点线面的关系在几何学中，点、线和面构成了基本的几何要素，它们之间存在着紧密的关系。

点是最基本的元素，它是没有长度、宽度和高度的，只有位置。

线是由一系列相邻点组成的，它具有长度但没有宽度和高度。

面由若干条线段相交形成的封闭区域，它具有长度和宽度但没有高度。

点、线和面之间的关系可以通过以下几个方面来描述。

1. 点与线的关系点与线之间的关系比较简单。

一条线段由两个端点组成，而一个点可以是一条线段的一个端点。

点可以在线上或者线的延长线上，也可以不在线上。

点的位置相对于线的位置有多种可能：在线的中间、在线的一端或者在线的外部。

点和线之间的关系可以通过点是否在线上来判断。

2. 点与面的关系点和面之间的关系也比较简单。

点可以在面上、在面的边界上或者在面的外部。

如果一个点在面上，则称该点在该面内。

点和面之间的关系可以通过点是否在面上来判断。

3. 线与线的关系线与线之间的关系有多种情况。

两条线可以相交，也可以平行或重合。

线与线之间的关系可以通过它们的位置关系来描述：如果两条线没有任何交点，则它们平行；如果两条线有且仅有一个交点，则它们相交；如果两条线的所有点都重合，则它们重合。

4. 线与面的关系线和面之间的关系也有多种情况。

线可以位于面内、跨越面或者位于面的边界上。

当一条线既在面内又与面相交时，它被称为切线。

线和面之间的关系可以通过它们的位置关系来判断。

5. 面与面的关系面与面之间的关系也有多种情况。

两个面可以平行，也可以相交。

两个相交的面可以有共线的边，也可以没有共线的边。

两个面之间的关系可以通过它们的位置关系来描述。

综上所述，点、线和面之间存在着丰富的关系。

它们相互作用和相互影响，形成了几何学中复杂而有趣的结构。

通过研究点、线和面之间的关系，我们可以深入理解几何学的基本原理，并将其应用于实际问题的解决中。

几何学作为数学的一部分，对于我们认识和探索世界具有重要的意义。

因此，我们应该充分理解和运用点、线和面之间的关系，以拓宽我们的视野和思维方式。

空间向量点线面的位置关系在三维空间中，点、线和面是基本的几何要素。

它们的位置关系在数学和几何学中扮演着重要的角色。

本文将探讨空间向量中点、线和面之间的不同位置关系及其特点。

一、点和线的位置关系在三维空间中，点和线的位置关系主要有以下几种情况。

1. 点在线上：如果一个点位于一条直线上，那么这个点与直线上的任意两点构成的向量都是共线的。

换句话说，点和线的向量共线。

2. 点在线的延长线上：点也可以位于一条线的延长线上，这时点与线上的任意两点构成的向量也是共线的。

3. 点与线相交：在三维空间中，点还可以与一条直线相交。

这时，点与线上的任意两点构成的向量不再共线。

4. 点与线平行：若一点与直线平行，则该点与直线上的任意两点构成的向量平行。

但是，点与线平行并不意味着点在线的延长线上。

二、点和面的位置关系点和面的位置关系也有几种情况，如下所示。

1. 点在面上：如果一个点位于一个平面上，那么这个点与平面上的任意三个点构成的向量都在同一个平面内。

2. 点在面的延长线上：点也可以位于一个平面的延长线上，这时点与平面上的任意三个点构成的向量仍在同一个平面内。

3. 点在平面内但不在平面上：有时，一个点位于一个平面内部但不在平面上。

这时，点与平面上的任意三个点构成的向量不在同一个平面内。

4. 点与平面相交：在三维空间中，点还可以与一个平面相交。

这时，点与平面上的任意三个点构成的向量不在同一个平面内。

三、线和面的位置关系线和面的位置关系主要有以下几种情况。

1. 线在平面上：如果一条直线位于一个平面上，那么直线上的任意两点构成的向量都在同一个平面内。

2. 线与平面相交于一点：一个直线也可以与一个平面相交于一点。

这时，直线上的任意两点构成的向量不在同一个平面内。

3. 线与平面平行：若一条直线与一个平面平行，则直线上的任意两点构成的向量与平面内的向量平行。

但是，直线与平面平行并不意味着直线在平面上。

4. 线在平面的延长线上：一条直线还可以位于一个平面的延长线上，这时直线上的任意两点构成的向量仍在同一个平面内。

点线面的位置关系在几何学中，点、线和面是基本的几何元素。

它们之间的位置关系是我们研究几何学的基础。

本文将详细探讨点线面之间的位置关系，并从几何学的角度解释这些关系。

一、点与线的位置关系在平面几何中，点是最简单的几何元素。

它没有长度、面积和方向。

而线则是由无数个点组成的，具有长度但没有宽度。

点与线之间有以下几种位置关系：1. 点在线上：当一个点正好在一条线上时，我们说这个点在这条线上。

这意味着点与线上的所有点重合。

2. 点在线的两侧：如果一个点不在一条线上，并且离线的两侧距离都不为零，则我们说这个点在这条线的两侧。

3. 点在线的延长线上：如果一个点不在一条线上，并且它在这条线的延长线上，则我们说这个点在线的延长线上。

延长线是指将线无限延长的线段。

二、点与面的位置关系与点与线的位置关系类似，点与面之间也有几种不同的位置关系：1. 点在面上：当一个点正好在一个平面上时，我们说这个点在这个平面上。

这意味着点与面上的所有点重合。

2. 点在面的上方或下方：如果一个点不在一个平面上，并且它在这个平面的上方或下方，则我们说这个点在这个平面的上方或下方。

3. 点在面的边界上：如果一个点在一个平面的边界上，则我们说这个点在这个平面的边界上。

三、线与面的位置关系线与面之间的位置关系也是几何学中重要的内容，它们之间有以下几种位置关系：1. 线在面上：当一条线正好在一个平面上时，我们说这条线在这个平面上。

这意味着线上的所有点都在这个平面上。

2. 线与面相交：如果一条线与平面有一个或多个公共点，则我们说这条线与这个平面相交。

3. 线平行于面：如果一条线与平面上的所有点都不相交，则我们说这条线平行于这个平面。

4. 线垂直于面：如果一条线与平面的交点为一点，并且与平面上的所有其他点都垂直，则我们说这条线垂直于这个平面。

综上所述，点线面之间的位置关系是几何学的重要内容，它们的不同位置关系可以通过几何学的方法进行判断和描述。

通过研究这些位置关系，我们可以更好地理解几何学的基本概念，并应用于实际生活和工作中。

点线面的位置关系和判定方法在几何学中，点、线段和平面是最基本的图形元素，它们之间的位置关系和判定方法对于几何问题的解决至关重要。

本文将探讨点线面的位置关系以及相应的判定方法。

一、点与线段的位置关系和判定方法1. 点在线段上的情况：一个点可以在线段的两端点之间，也可以在线段上，或者在线段外。

要判断一个点是否在线段上，可以使用如下方法：（1）距离判定法：计算点到线段两个端点的距离，如果两个距离之和等于线段长度，那么点就位于线段上。

（2）向量判定法：将线段的两个端点视为向量A和向量B，将点与线段的一个端点视为向量C。

如果向量C可以表示为向量A与向量B的线性组合，且系数的和等于1，那么点就位于线段上。

2. 点在线段的延长线上的情况：当一个点在线段的延长线上时，意味着可以无限延长线段，点位于线段的一侧。

判定方法如下：（1）向量判定法：同样将线段的两个端点视为向量A和向量B，将点与线段的一个端点视为向量C。

如果向量C可以表示为向量A与向量B的线性组合，且系数的和大于1，那么点在线段的延长线上。

3. 点在线段的左侧或右侧的情况：若点位于线段的左侧（或右侧），则该点与线段的两个端点所形成的线段组合为逆时针（或顺时针）方向。

判定方法如下：（1）向量叉积法：将线段的一个端点与点构成的向量记为向量A，将线段的一个端点与线段另一端点构成的向量记为向量B。

计算向量A和向量B的叉积，若叉积大于0，则点在线段的左侧；若叉积小于0，则点在线段的右侧；若叉积等于0，则点在线段上。

二、点与平面的位置关系和判定方法1. 点在平面上的情况：一个点可以位于平面上，也可以位于平面外部。

判定方法如下：（1）向量法：选择平面上的三个非共线点A、B、C，将点与这三个点分别构成向量。

如果点与向量A、B、C共面，那么点就位于平面上。

2. 点在平面的一侧或另一侧的情况：当一个点在平面的一侧时，意味着通过该点可以画出与平面垂直的直线。

判定方法如下：（1）点法向量法：选择平面上的一个点P，计算向量AP与平面的法向量N的点积。

点线面的位置关系知识点在几何学中，点、线和面是三个基本的几何概念，它们之间存在着一系列的位置关系。

这些位置关系的理解对于解决几何问题以及应用几何知识有着重要的意义。

本文将介绍点线面的位置关系的几个重要知识点。

一、点与直线的位置关系1. 在直线上：当一个点恰好位于一条直线上时，我们可以说这个点在直线上。

例如，点A在直线AB上。

2. 在直线的两侧：如果一个点既不在直线上，也不在直线的延长线上，我们可以说这个点在直线的两侧。

例如，点C在直线AB的两侧。

3. 在直线的延长线上：如果一个点不在直线上，但位于直线的延长线上，我们可以说这个点在直线的延长线上。

例如，点D在直线AB的延长线上。

4. 平行于直线：如果一条直线与给定直线没有任何交点，我们可以说这条直线平行于给定直线。

例如，直线CD平行于直线AB。

二、点与平面的位置关系1. 在平面上：当一个点位于一个平面内部时，我们可以说这个点在平面上。

例如，点A在平面P上。

2. 不在平面上：如果一个点既不在平面上，也不在平面的延长线上，我们可以说这个点不在平面上。

例如，点B不在平面P上。

3. 在平面的延长线上：如果一个点不在平面上，但位于平面的延长线上，我们可以说这个点在平面的延长线上。

例如，点C在平面P的延长线上。

4. 垂直于平面：如果一条直线与给定平面的任意一条线都垂直，我们可以说这条直线垂直于给定平面。

例如，直线EF垂直于平面P。

三、直线与平面的位置关系1. 相交于一点：当一条直线与平面有且仅有一个交点时，我们可以说这条直线与平面相交于一点。

例如，直线L与平面P相交于点A。

2. 平行于平面：如果一条直线与给定平面的任意一条线都平行，我们可以说这条直线平行于给定平面。

例如，直线M平行于平面P。

3. 包含于平面：当一条直线上的所有点都位于给定平面上时，我们可以说这条直线被包含于给定平面中。

例如，直线N被包含于平面P 中。

4. 相交于一条线：当一条直线与平面有无穷多个交点时，我们可以说这条直线与平面相交于一条线。

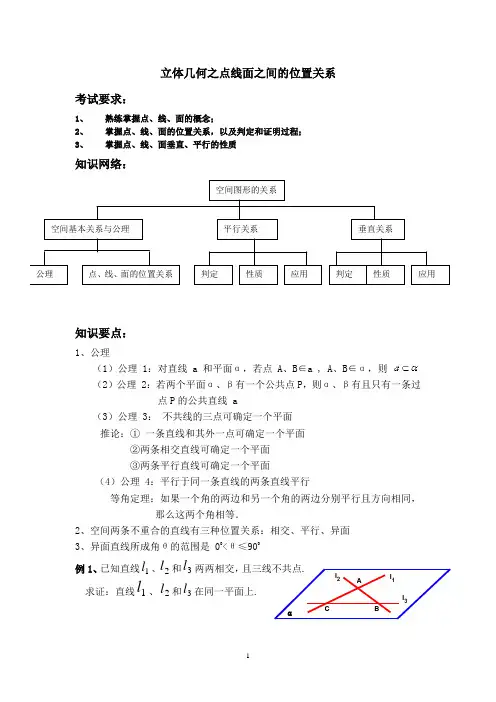
CBAl 3l 2l 1立体几何之点线面之间的位置关系考试要求：1、 熟练掌握点、线、面的概念；2、 掌握点、线、面的位置关系，以及判定和证明过程；3、掌握点、线、面垂直、平行的性质知识网络：知识要点：1、公理（1）公理 1：对直线 a 和平面α，若点 A 、B ∈a , A 、B ∈α，则（2）公理 2：若两个平面α、β有一个公共点P ，则α、β有且只有一条过点P 的公共直线 a（3）公理 3： 不共线的三点可确定一个平面 推论：① 一条直线和其外一点可确定一个平面②两条相交直线可确定一个平面 ③两条平行直线可确定一个平面（4）公理 4：平行于同一条直线的两条直线平行等角定理：如果一个角的两边和另一个角的两边分别平行且方向相同，那么这两个角相等．2、空间两条不重合的直线有三种位置关系：相交、平行、异面3、异面直线所成角θ的范围是 00<θ≤900例1、已知直线1l 、2l 和3l 两两相交，且三线不共点. 求证：直线1l 、2l 和3l 在同一平面上.空间图形的关系空间基本关系与公理 平行关系 垂直关系 公理 点、线、面的位置关系 判定 性质 应用 应用 性质 判定例2、三个平面将空间分成k 个部分,求k 的可能取值. 分析: 可以根据三个平面的位置情况分类讨论，按条件可将三个平面位置情况分为5种:（1）三个平面相互平行（2）两个平面相互平行且与第三个平面相交 （3）三个平面两两相交且交线重合 （4）三个平面两两相交且交线平行 （5）三个平面两两相交且交线共点例3、已知棱长为a 的正方体中，M 、N 分别为CD 、AD 中点。

求证：四边形是梯形。

例4、如图，A 是平面BCD 外的一点,G H 分别是,ABC ACD ∆∆的重心，求证：//GH BD ．例5、如图，已知不共面的直线,,a b c 相交于O 点，,M P 是直线a 上的两点，,N Q 分别是,b c 上的一点求证：MN 和PQ 是异面直线N MH G D C B Aαc b a Q P N MO例6、已知正方体ABCD －A 1B 1C 1D 1的棱长为a ，则棱A 1B 1所在直线与面对角线BC 1所在直线间的距离是直线与平面平行、平面与平面平行1、 直线与平面的位置关系：平行、相交、在平面内2、 直线和平面平行的判定及性质（1） 判定 如果平面外一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行。

点线面的位置关系〔1〕四个公理公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内符号语言：A l,B l,且A ,B l .公理2:过不在一条直线上的三点,有且只有一个平面.三个推论：① 经过一条直线和这条直线外一点,有且只有一个平面②经过两条相交直线,有且只有一个平面_______________________③经过两条平行直线,有且只有一个平面_______________________它给出了确定一个平面的依据.公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线〔两个平面的交线〕.符号语言：P ,且P I l,P 1.公理4:〔平行线的传递性〕平行与同一直线的两条直线互相平行符号语言：a//l,nb//l a//b 0〔2〕空间中直线与直线之间的位置关系1 .概念异面直线及夹角：把不在任何一个平面内的两条直线叫做异面直线.两条异面直线a,b ,经过空间任意一点O作直线a //a,b //b ,我们把a与b所成的角〔或直角〕叫异面直线a, b所成的夹角.〔易知：夹角范围0 90 〕公理4:〔平行线的传递性〕平行与同一直线的两条直线互相平行.符号语言：a〃l,且b//l a//b 0定理：空间中如果一个角的两边分别与另一个角的两边分别平行, 那么这两个角相等或互补.〔注意：会画两个角互补的图形〕小,击〃心相交直线：同一平面内,有且只有一个公共点；u向宜线2 .位置关系：八’ 平行直线：同一平面内,没有公共点；异面直线：不同在任何一个平面内,没有公共点〔3〕空间中直线与平面之间的位置关系直 线 与 平 面 的 位 置 关 系 有 三 种 直线在平面内〔l 〕有无数个公共点〔4〕空间中平面与平面之间的位置关系平面与平面之间的位置关系有两种 两个平面平行〔// 〕没有公共点 两个平面相交〔I 1〕有一条公共直线考点1：点,线,面之间的位置关系例1.〔2021辽宁,4,5分〕m,n 表示两条不同直线,a 表示平面.以下说法正确 的是〔〕A.假设 m// a ,n // a ,那么 m/l nB.假设 a ,n ? a ,那么 nC.假设 a ,m±n, WJ n // aD.假设 mil a ,m±n,那么 n± a［答案］1.B［解析］1.A 选项m n 也可以相交或异面,C 选项也可以n? a ,D 选项也可以n // a 或n 与a 斜交.根据线面垂直的性质可知选 B.例2.〔2021山东青岛高三第一次模拟测试,5〕设"、"是两条不同的直线,空 ,是两个不同的平面,那么以下命题正确的选项是〔〕A.假设 口〃瓦口〃/那么 6"a B .假设 01 人口那么."C .假设 ,, 「那么D .假设・ . . ..那么［答案］2. D［解析］2.A 选项不正确,由于方匚口是可能的;直线在平面外直线与平面相交〔11 直线与平面平行〔1 / / 〕 A 有且只有一个公共点没有公共点B选项不正确,由于以‘产,""靠时,""尸,"仁/都是可能的;C选项不正确,由于我上方,口工户时,可能有m；D选项正确,可由面面垂直的判定定理证实其是正确的.应选D例3. 〔2021广西桂林中学高三2月月考,4〕设小、"是两条不同的直线,以、川是两个不同的平面.以下命题中正确的选项是〔A〕'；：」-•・；〃一/…」「；二.一不〔C〕滂,£©［8―明〃,••曾 = .,・,A［答案］3. D［解析］3. 假设m上R MU E用工'、那么平面"与“垂直或相交或平行,故〔A〕错误；假设“1凤阳1 g//Q,那么直线用与〃相交或平行或异面,故〔B〕错误；假设口L凤仪1.二风雨工,;那么直线片与平面#垂直或相交或平行,故〔C〕错误; 假设那么直线、1M,故©正确.选D.例4. 〔2021周宁、政和一中第四次联考, 示不同的平面,给出以下四个命题：①假设州且EU•那么u〞；②假设州// f,且阳// c.贝〞// 口；③假设Hl…内T = M ",那么'//巾//E ；④假设m D 且打// #,那么f //7〕设L E,H表示不同的直线,小丹「表( )(B) " ’(D)睽C f其中正确命题的个数是〔〕A. 1B. 2C. 3D. 4 ［答案］4. B［解析］4. ①正确；②直线也或£上,错误；③错误,由于正方体有公共端点的三条棱两两垂直；④正确.故真正确的选项是①④,共2个.2.空间几何平行关系转化关系:i I城线平行---------- "线面平行" ------------ "面面平行直线、平面平行的判定及其性质归纳总结证实线线平行的方法:11 (平行线的传递性)平行与同一直线的两条直线互相平行.即公理4(2证实这条两条直线的方向量共线.③如果两个平行平面同时和第三个平面相交,那么它们的交线平行.即面面平行的性质.2 .证实直线和平面相互平行的方法(1证实直线和这个平面内的一条直线相互平行；②证实这条直线的方向量和这个平面内的一个向量相互平行；③证实这条直线的方向量和这个平面的法向量相互垂直.3 .证实两平面平行的方法：(1)利用定义证实.利用反证法,假设两平面不平行,那么它们必相交,再导出矛盾.(2)判定定理：一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行,这个定理可简记为线面平行那么面面平行.用符号表示是：anb, aa , a// e , b// e , WJ a // e.(3)垂直于同一直线的两个平面平行.用符号表示是：a±a , a,B那么a// B.(4)平行于同一个平面的两个平面平行. 〃 ,// //4.两个平面平行的性质有五条：(1)两个平面平行,其中一个平面内的任一直线必平行于另一个平面,这个定理可简记为：〞面面平行,那么线面平行〞.用符号表示是：a // B, aa ,那么a // B.(2)如果两个平行平面同时与第三个平面相交,那么它们的交线平行,这个定理可简记为：〞面面平行,那么线线平行〞.用符号表示是：a//0, aP 丫=a, B C = =b,贝U a// bo(3) 一条直线垂直于两平行平面中的一个平面,它也垂直于另一个平面.这个定理可用于证线面垂直.用符号表示是：a // B , a, a ,那么a, B.(4)夹在两个平行平面间的平行线段相等口(5)过平面外一点只有一个平面与平面平行七3.空间几何垂直关系1 .线线垂直判断线线垂直的方法：所成的角是直角,两直线垂直；垂直于平行线中的一 条,必垂直于另一条.三垂线定理：在平面内的一条直线,如果它和这个平面的一条斜线的射影垂 直,那么它也和这条斜线垂直.三垂线定理的逆定理：在平面内的一条直线,如果和这个平面的一条斜线垂 直,那麽它也和这条斜线的射影垂直.注意：⑴三垂线指PA PQ AO 都垂直a 内的直线a 其实质是：斜线和平 面内一条直线垂直的判定和性质定理.⑵要考虑a 的位置,并注意两定理交替使 用.2 .线面垂直(1)定义：如果一条直线l 和一个平面a 相交,并且和平面a 内的任意一条直 线都垂直,我们就说直线l 和平面a 互相垂直,其中直线l 叫做平面的垂线,平面 a 叫做直线l 的垂面,直线与平面的交点叫做垂足.直线l 与平面a 垂直记作：I ,ob a J /不(2)直线与平面垂直的判定定理：如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面.(3)直线和平面垂直的性质定理：如果两条直线同垂直于一个平面,那么这两条 直线平行. 3 .面面垂直(1)两个平面垂直的定义：相交成直二面角的两个平面叫做互相垂直的平面. (2)两平面垂直的判定定理：(线面垂直 面面垂直)如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.(3)两平面垂直的性质定理：(面面垂直 线面垂直)假设两个平面互相垂直, 那么在一个平面内垂直于它们的交线的直线垂直于另一个平面PO 推理模式：PAI,OA ,a APa AOAOa考点2:证实线面之间的平行与垂直例1 .如图,四边形ABC时正方形,PD,平面ABCD/DPC=30 ,AF,PC于点F,FE // CD,交PD于点E.(1)证实:CFL平面ADF;［解析］1.⑴证实：V PDL平面ABCD/ PDL AD,又CDL AD,Pm CD=D,• ・ADL平面PCD/ ADL PC,又AF, PC,AFA AD=A,「• PC1平面ADF,即CF,平面ADF.例2. (2021江苏,16, 14分)如图,在四棱锥P-ABC时,平面PADL平面ABCD, AB=AD, / BAD=60 , E, F 分别是AP, AD的中点.求证：(I )直线EF//平面PCD;(R)平面BEFL平面PAD.J)［答案］(I )在△ PAD中,由于E, F分别为AP, AD的中点,所以EF// PD.又因为EF?平面PCD, PC?平面PCD,所以直线EF//平面PCD.(n)连结BD.由于AB=AD, /BAD=60 ,所以△ ABM正三角形.由于F是AD 的中点,所以BF±AD.由于平面PADL平面ABCD, BF?平面ABCD,平面PAD? 平面ABCD=AD所以BF,平面PAD.又由于BF?平面BEF,所以平面BEFL平面PAD.例3. (2021 江苏,16, 14 分)如图,在直三棱柱ABC-ABG中,E、F分别是AB、A i C的中点,点D在BC上,A iD± B i C.求证：(I ) EF // 平面ABC;(II)平面AFD1平面BBCC.［答案］3.( I )由于E、F分别是A i B、A i C的中点,所以EF// BC, EF?面ABC, BC ?面ABC.所以EF//平面ABC.(II)由于直三棱柱ABC-AB i C i,所以BBL面A i B i C i, BB iX A i D,又A i DLBC,所以A i DL面BBCC,又AD?面A i FD,所以平面AFDL平面BBCC.例4. (2021江苏,i6, i4 分)如图,在四面体ABCm,CB=CD, ADLBD,点E、F分别是AB BD的中点.求证:(I )直线EF//平面ACD;(n)平面EFd平面BCD.［答案］4.( I )在4ABD中,由于E、F分别是AB BD的中点,所以EF// AD.又AD?平面ACD, EF?平面ACD,所以直线EF//平面ACD.(H)在AABD^ ,由于ADL BD, EF // AD,所以EF, BD.在△BCDt ,由于CD=CB, F为BD的中点,所以CF± BD.由于EF?平面EFC, CF?平面EFC, EF与CF交于点F,所以BDL平面EFC.又由于BD?平面BCD,所以平面EFCL平面BCD.例5. (2021北京海淀区高三三月模拟题,17,14分)在四棱锥P-/3m 中,产,！平面N夙力,匚是正三角形,金.与凡0的交点5/恰好是AC中点,又= ZCTH二120.,点A『在线段PB上,且(H)求证：AN"平面『DC;［答案］7.(1) 由于必出.是正三角形,■是JC'中点,所以m C',即8OLRC.又由于^ 平面HBCD , 80u平面月8CQ,所以以_LHD.又Rin」心=1,所以叨_L平面心C.又尸.仁平面尸〃’,所以皿_LPC.(H)在正三角形月中,3M =2V'3,在AJC.中,由于M为/C中点, DM±AC y所以才口二CD.又2OM = 120 ,所以NCMf = 60..1tan ZCDM = ♦"=々=出DM —二'所以由冈冈,得3 .所以a1九=31在等腰直角三角形尸/E中,2月"/lA",所以PB = 4五. 所以BMNPCA , BN 小)= BY : ,所以MN NPD .又“V之平面"DC , PD仁平面产比,所以W j平面热乂：.。

点线面的位置关系点、线、面是几何学中的基本概念，它们之间存在着重要的位置关系。

通过研究它们的位置关系，我们可以更好地理解和应用几何学知识。

本文将详细探讨点、线、面的位置关系，并对其应用进行讨论。

一、点、线、面的定义1. 点：几何学中最基本的元素，没有大小和形状，只有位置。

可以用坐标表示，例如(x, y)。

2. 线：由无数个点按照一定规律连接而成，具有长度但没有宽度。

可以用两个点的坐标表示，例如(1, 2)和(3, 4)之间的线段。

3. 面：由无数个线按照一定规律连接而成，具有长度和宽度。

可以用多边形的边界来表示，例如三角形、矩形等。

二、点、线、面的位置关系1. 点与线的位置关系：a. 在线上：如果一个点恰好在一条线上，则称该点在线上。

b. 在线内：如果一个点在一条线的两个端点之间，则称该点在线内。

c. 在线外：如果一个点既不在线上，也不在线内，则称该点在线外。

2. 点与面的位置关系：a. 在面上：如果一个点恰好在一个面上，则称该点在面上。

b. 在面内：如果一个点在一个面的边界之内，则称该点在面内。

c. 在面外：如果一个点既不在面上，也不在面内，则称该点在面外。

3. 线与线的位置关系：a. 相交：如果两条线有公共的一个或多个点，则称这两条线相交。

b. 平行：如果两条线的方向相同，但没有公共的点，则称这两条线平行。

c. 重合：如果两条线有无数个公共的点，则称这两条线重合。

4. 线与面的位置关系：a. 相交：如果一条线与一个面有公共的一个或多个点，则称这条线与该面相交。

b. 平行：如果一条线的方向与一个面平行，且线上没有与该面有公共的点，则称这条线与该面平行。

c. 重合：如果一条线与一个面重合，即线上的所有点都在该面上，则称这条线与该面重合。

5. 面与面的位置关系：a. 相交：如果两个面有公共的一条或多条线段，则称这两个面相交。

b. 平行：如果两个面的法向量平行，则称这两个面平行。

c. 重合：如果两个面有无数个公共的点，则称这两个面重合。

空间点、直线、平面之间的位置关系考纲要求1理解空间直线、平面位置关系的定义，并了解如下可以作为推理依据的公理和定理.公理1:如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在此平面内.公理2：过不在同一条直线上的三点，有且只有一个平面.公理3；如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线.公理4：平行于同一条直线的两条直线互相平行.定理：空间中如果一个角的两边与另一个角的两边分别平行，那么这两个角相等或互补.知巩梳理"T"平面的基本性质名称内容图形衣示谄R表不作用公理1如果一条自线上的两点Ae/.be住一个/ILAG G,平而内•册么/〉《?■—/ B e U =>这条n纟戈在lUa此¥面内①判定直线住rifti A ；②判足点在平血内过不在—勒工线I-的三点・右-R只有一个平曲•B•C若A、”、「-：点不同住一条立线L.则A、”、「三点的定一个 fifiJa① a >iz平而；②ill：明点、线共而如果则个不重合的平向冇一个公典点•那么它们冇M貝仃一条过该点的公共宜线P W a • li "j =>a 「14 Z. H.He/①判定两亍半向是杏相交；©ill-明点在（!£线I .；③UF明三点、兵线* ①旺明三线共点S⑤iBlj两个相交平而的交线(3) 等角定理：空间中如果两个角的两边分别对应平 行，则这两个角相等或者互补.(4) 两异面直线所成的角：两条异面直线a, b,经过空 间任一点0作直线a' 〃d,方'lib 、把o' , H 所成的锐角 (或直角)叫异面直线a, 〃所成的角(或夹角).心，Z 所成 的角的大小与点O 的选择无关，为了简便，点O 通常取在异 两直裁的一条上；异,如果两条异面直线所成异面直线垂直，记作心 • 2 •空间直线(1)空间两直线的位置关系；相交直线：有且只有一个公共点; 平行直线：没有公共点：. .. (2)公理4： 空间中的直线4, b, C,如果4〃力，b//c.则0〃0问誠思考►问题1平面的基本性质（1）若点A在直线/上，直线/在平面G内，则点A在平面伉内；（）（2）—条直线与一个点确定一个平面；（）（3）三点确定一个平面；（）（4）两个相交平面只有有限个公共点.（）［答案］⑴对（2）错⑶错（4）错►问题2设平面仅与4UG直线比卩,则点M—定不在直线/上.（）［答案］错［解析1因为《rU=M, uUa, bup,所以』1/在《内，M在〃内.又因为平面a与平面/栩交于人所以M在/上.►问题4 若O4〃0iAi，0B〃0右且Z4O〃=60。

立体几何初步（空间点、线、面的位置关系）一、平面⑴ 平面的概念：（描述性）（描述性）⑵平面的表示：通常用希腊字母a 、β、g 表示，如平面a （通常写在一个锐角内）；也可以用两个相对顶点的字母来表示，如平面A C ⑶点与平面的关系：点A 在平面a 内，记作A a Î；点A 不在平面a 内，记作A a Ï点与直线的关系：点A 的直线l 上，记作A Îl ； 点A 不在直线l 上，记作A Ïl直线与平面的关系：直线l 在平面a 内，记作l Ìa ；直线l 不在平面a 内，记作l Ëa 。

二、几个公理公理1：如果一条直线的两点在一个平面内，那么这条直线上所有的点都在这个平面内。

（即直线在平面内，或者平面经过直线）或者平面经过直线）符号语言：,,,A l B l A B l a a a ÎÎÎÎÞÌ公理2：经过不在同一条直线上的三点，有且只有一个平面。

：经过不在同一条直线上的三点，有且只有一个平面。

推论：推论：⑴一条直线和直线外一点确定一平面；⑴一条直线和直线外一点确定一平面；⑵两条相交直线确定一平面；⑵两条相交直线确定一平面；⑶两条平行直线确定一平面。

⑶两条平行直线确定一平面。

公理3：如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线那么它们有且只有一条过该点的公共直线符号语言：l P l B A B A P Î=ÇÞÇÎ,公理3的作用：①它是判定两个平面相交的方法。

①它是判定两个平面相交的方法。

②它说明两个平面的交线与两个平面公共点之间的关系：交线必过公共点。

②它说明两个平面的交线与两个平面公共点之间的关系：交线必过公共点。

③它可以判断点在直线上，即证若干个点共线的重要依据。

③它可以判断点在直线上，即证若干个点共线的重要依据。

立体几何第二节空间点、直线、平面之间的位置关系本节主要包括2个知识点：1.平面的基本性质；2.空间两直线的位置关系.突破点(一) 平面的基本性质1．公理1～32．公理2的三个推论推论1：经过一条直线和这条直线外一点有且只有一个平面；推论2：经过两条相交直线有且只有一个平面；推论3：经过两条平行直线有且只有一个平面．考点贯通 抓高考命题的“形”与“神”点、线、面的位置关系1．证明点共线问题的常用方法(1)公理法：先找出两个平面，然后证明这些点都是这两个平面的公共点，再根据公理3证明这些点都在交线上；(2)同一法：选择其中两点确定一条直线，然后证明其余点也在该直线上． 2．证明线共点问题的方法先证两条直线交于一点，再证明第三条直线经过该点． 3．证明点、直线共面问题的常用方法(1)纳入平面法：先确定一个平面，再证明有关点、线在此平面内；(2)辅助平面法：先证明有关的点、线确定平面α，再证明其余元素确定平面β，最后证明平面α，β重合．[典例] 已知：空间四边形ABCD (如图所示)，E ，F 分别是AB ，AD 的中点，G ，H 分别是BC ，CD 上的点，且CG ＝13BC ，CH ＝13DC .求证：(1)E ，F ，G ，H 四点共面； (2)三直线FH ，EG ，AC 共点． [方法技巧]平面的基本性质的应用公理1是判断一条直线是否在某个平面内的依据，公理2及其推论是判断或证明点、线共面的依据，公理3是证明三线共点或三点共线的依据．能力练通 抓应用体验的“得”与“失” 1．如图是正方体或四面体，P ，Q ，R ，S 分别是所在棱的中点，则这四个点不共面的一个图是( )2．若空间中n 个不同的点两两距离都相等，则正整数n 的取值( ) A ．至多等于3 B ．至多等于4 C ．等于5D ．大于53．以下四个命题中，正确命题的个数是( ) ①不共面的四点中，其中任意三点不共线；②若点A ，B ，C ，D 共面，点A ，B ，C ，E 共面，则A ，B ，C ，D ，E 共面； ③若直线a ，b 共面，直线a ，c 共面，则直线b ，c 共面； ④依次首尾相接的四条线段必共面． A ．0 B ．1 C ．2D ．34.如图所示，四边形ABEF 和四边形ABCD 都是梯形，BC 綊12AD ，BE 綊12FA ，G ，H 分别为FA ，FD 的中点．(1)证明：四边形BCHG 是平行四边形； (2)C ，D ，F ，E 四点是否共面？为什么？突破点(二) 空间两直线的位置关系1．空间中两直线的位置关系 (1)空间中两直线的位置关系⎩⎨⎧共面直线⎩⎪⎨⎪⎧平行相交异面直线：不同在任何一个平面内(2)公理4和等角定理①公理4：平行于同一条直线的两条直线互相平行．②等角定理：空间中如果两个角的两边分别对应平行，那么这两个角相等或互补． 2．异面直线所成的角(1)定义：设a ，b 是两条异面直线，经过空间任一点O 作直线a ′∥a ，b ′∥b ，把a ′与b ′所成的锐角(或直角)叫做异面直线a 与b 所成的角(或夹角)．(2)范围：⎝⎛⎦⎥⎤0，π2.[例1] (1)下列结论正确的是( )①在空间中，若两条直线不相交，则它们一定平行； ②平行于同一条直线的两条直线平行；③一条直线和两条平行直线中的一条相交，那么它也和另一条相交； ④空间四条直线a ，b ，c ，d ，如果a ∥b ，c ∥d ，且a ∥d ，那么b ∥c . A ．①②③ B ．②④ C ．③④D ．②③(2)在图中，G ，N ，M ，H 分别是正三棱柱的顶点或所在棱的中点，则表示直线GH ，MN 是异面直线的图形有________．(填上所有正确答案的序号)[方法技巧]判断空间两直线位置关系的思路方法(1)判断空间两直线的位置关系一般可借助正方体模型，以正方体为主线直观感知并准确判断．(2)异面直线的判定方法①反证法：先假设两条直线不是异面直线，即两条直线平行或相交，由假设的条件出发，经过严格的推理，导出矛盾，从而否定假设，肯定两条直线异面．②定理法：平面外一点A与平面内一点B的连线和平面内不经过点B的直线是异面直线．异面直线所成的角[例2] 空间四边形ABCD中，AB＝CD且AB与CD所成的角为30°，E，F分别为BC，AD的中点，求EF与AB所成角的大小．[方法技巧]用平移法求异面直线所成的角的步骤(1)一作：即根据定义作平行线，作出异面直线所成的角；(2)二证：即证明作出的角是异面直线所成的角；(3)三求：解三角形，求出作出的角．如果求出的角是锐角或直角，则它就是要求的角；如果求出的角是钝角，则它的补角才是要求的角．能力练通抓应用体验的“得”与“失”1．[考点一]下列说法正确的是( )A．若a⊂α，b⊂β，则a与b是异面直线B．若a与b异面，b与c异面，则a与c异面C．若a，b不同在平面α内，则a与b异面D．若a，b不同在任何一个平面内，则a与b异面2．[考点一]l1，l2，l3是空间三条不同的直线，则下列命题正确的是( ) A．l1⊥l2，l2⊥l3⇒l1∥l3 B．l1⊥l2，l2∥l3⇒l1⊥l3C．l1∥l2∥l3⇒l1，l2，l3共面 D．l1，l2，l3共点⇒l1，l2，l3共面3．[考点二]如图，四边形ABCD和ADPQ均为正方形，它们所在的平面互相垂直，则异面直线AP与BD所成的角为________．4．[考点一、二]如图所示，三棱锥P­ABC中，PA⊥平面ABC，∠BAC＝60°，PA＝AB＝AC＝2，E是PC的中点．(1)求证AE与PB是异面直线；(2)求异面直线AE与PB所成角的余弦值．[全国卷5年真题集中演练——明规律]1.(2016·全国乙卷)平面α过正方体ABCD­A1B1C1D1的顶点A，α∥平面CB1D1，α∩平面ABCD＝m，α∩平面ABB1A1＝n，则m，n所成角的正弦值为( )A.32B.22C.33D.132．(2013·新课标全国卷Ⅱ)已知m，n为异面直线，m⊥平面α，n⊥平面β.直线l满足l⊥m，l⊥n，l⊄α，l⊄β，则( )A．α∥β且l∥αB．α⊥β且l⊥βC．α与β相交，且交线垂直于lD．α与β相交，且交线平行于l3．(2016·全国甲卷)α，β是两个平面，m，n是两条直线，有下列四个命题：①如果m⊥n，m⊥α，n∥β，那么α⊥β.②如果m⊥α，n∥α，那么m⊥n.③如果α∥β，m⊂α，那么m∥β.④如果m∥n，α∥β，那么m与α所成的角和n与β所成的角相等．其中正确的命题有________．(填写所有正确命题的编号)[课时达标检测] 重点保分课时——一练小题夯双基，二练题点过高考[练基础小题——强化运算能力]1．四条线段顺次首尾相连，它们最多可确定的平面有( )A．4个 B．3个 C．2个 D．1个2．已知A，B，C，D是空间四点，命题甲：A，B，C，D四点不共面，命题乙：直线AC 和BD不相交，则甲是乙成立的( )A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件3．若直线a⊥b，且直线a∥平面α，则直线b与平面α的位置关系是( )A．b⊂αB．b∥αC．b⊂α或b∥αD．b与α相交或b⊂α或b∥α4.如图，平行六面体ABCD­A1B1C1D1中既与AB共面又与CC1共面的棱有________条．[练常考题点——检验高考能力]一、选择题1．若直线上有两个点在平面外，则( )A．直线上至少有一个点在平面内 B．直线上有无穷多个点在平面内C．直线上所有点都在平面外 D．直线上至多有一个点在平面内2．空间四边形两对角线的长分别为6和8，所成的角为45°，连接各边中点所得四边形的面积是( )A．6 2 B．12 C．12 2 D．24 23．若空间中四条两两不同的直线l1，l2，l3，l4，满足l1⊥l2，l2⊥l3，l3⊥l4，则下列结论一定正确的是( )A．l1⊥l4 B．l1∥l4C．l1与l4既不垂直也不平行 D．l1与l4的位置关系不确定4．已知直线a和平面α，β，α∩β＝l，a⊄α，a⊄β，且a在α，β内的射影分别为直线b和c，则直线b和c的位置关系是( )A．相交或平行 B．相交或异面C．平行或异面 D．相交、平行或异面5.如图，ABCD ­A 1B 1C 1D 1是长方体，O 是B 1D 1的中点，直线A 1C 交平面AB 1D 1于点M ，则下列结论正确的是( )A ．A ，M ，O 三点共线B ．A ，M ，O ，A 1不共面C ．A ，M ，C ，O 不共面D ．B ，B 1，O ，M 共面6．过正方体ABCD ­A 1B 1C 1D 1的顶点A 作直线l ，使l 与棱AB ，AD ，AA 1所成的角都相等，这样的直线l 可以作( )A ．1条B ．2条C ．3条D ．4条二、填空题7.如图所示，在空间四边形ABCD 中，点E ，H 分别是边AB ，AD 的中点，点F ，G 分别是边BC ，CD 上的点，且CF CB ＝CG CD ＝23，则下列说法正确的是________．(填写所有正确说法的序号)①EF 与GH 平行 ②EF 与GH 异面③EF 与GH 的交点M 可能在直线AC 上，也可能不在直线AC 上 ④EF 与GH 的交点M 一定在直线AC 上8．如图为正方体表面的一种展开图，则图中的AB ，CD ，EF ，GH 在原正方体中互为异面直线的有________对．9．已知a ，b ，c 为三条不同的直线，且a ⊂平面α，b ⊂平面β，α∩β＝c . ①若a 与b 是异面直线，则c 至少与a ，b 中的一条相交； ②若a 不垂直于c ，则a 与b 一定不垂直； ③若a ∥b ，则必有a ∥c ； ④若a ⊥b ，a ⊥c ，则必有α⊥β.其中正确的命题有________．(填写所有正确命题的序号)10.如图，在三棱锥A­BCD中，AB＝AC＝BD＝CD＝3，AD＝BC＝2，点M，N分别为AD，BC的中点，则异面直线AN，CM所成的角的余弦值是________．三、解答题11.如图所示，A是△BCD所在平面外的一点，E，F分别是BC，AD的中点．(1)求证：直线EF与BD是异面直线；(2)若AC⊥BD，AC＝BD，求EF与BD所成的角．12.如图，在三棱锥P ­ABC 中，PA ⊥底面ABC ，D 是PC 的中点．已知∠BAC ＝π2，AB ＝2，AC ＝23，PA ＝2.求：(1)三棱锥P ­ABC 的体积；(2)异面直线BC 与AD 所成角的余弦值．立体几何第二节空间点、直线、平面之间的位置关系本节主要包括2个知识点：1.平面的基本性质；2.空间两直线的位置关系.突破点(一) 平面的基本性质1．公理1～32．公理2的三个推论推论1：经过一条直线和这条直线外一点有且只有一个平面；推论2：经过两条相交直线有且只有一个平面；推论3：经过两条平行直线有且只有一个平面．考点贯通 抓高考命题的“形”与“神”点、线、面的位置关系1．证明点共线问题的常用方法(1)公理法：先找出两个平面，然后证明这些点都是这两个平面的公共点，再根据公理3证明这些点都在交线上；(2)同一法：选择其中两点确定一条直线，然后证明其余点也在该直线上．2．证明线共点问题的方法先证两条直线交于一点，再证明第三条直线经过该点．3．证明点、直线共面问题的常用方法(1)纳入平面法：先确定一个平面，再证明有关点、线在此平面内；(2)辅助平面法：先证明有关的点、线确定平面α，再证明其余元素确定平面β，最后证明平面α，β重合．[典例] 已知：空间四边形ABCD (如图所示)，E ，F 分别是AB ，AD的中点，G ，H 分别是BC ，CD 上的点，且CG ＝13BC ，CH ＝13DC .求证： (1)E ，F ，G ，H 四点共面；(2)三直线FH ，EG ，AC 共点．[证明] (1)连接EF ，GH ，∵E ，F 分别是AB ，AD 的中点，∴EF ∥BD .又∵CG ＝13BC ，CH ＝13DC ， ∴GH ∥BD ，∴EF ∥GH ，∴E ，F ，G ，H 四点共面．(2)易知FH 与直线AC 不平行，但共面，∴设FH ∩AC ＝M ，∴M ∈平面EFHG ，M ∈平面ABC .又∵平面EFHG ∩平面ABC ＝EG ，∴M ∈EG ，∴FH ，EG ，AC 共点．[方法技巧]平面的基本性质的应用公理1是判断一条直线是否在某个平面内的依据，公理2及其推论是判断或证明点、线共面的依据，公理3是证明三线共点或三点共线的依据．能力练通 抓应用体验的“得”与“失”1．如图是正方体或四面体，P ，Q ，R ，S 分别是所在棱的中点，则这四个点不共面的一个图是( )解析：选D A 、B 、C 图中四点一定共面，D 中四点不共面．2．若空间中n 个不同的点两两距离都相等，则正整数n 的取值( )A ．至多等于3B ．至多等于4C ．等于5D ．大于5 解析：选B n ＝2时，可以；n ＝3时，为正三角形，可以；n ＝4时，为正四面体，可以；n ＝5时，为四棱锥，侧面为正三角形，底面为菱形且对角线长与边长相等，这种情况不可能出现，所以正整数n 的取值至多等于4.3．以下四个命题中，正确命题的个数是( )①不共面的四点中，其中任意三点不共线；②若点A ，B ，C ，D 共面，点A ，B ，C ，E 共面，则A ，B ，C ，D ，E 共面；③若直线a ，b 共面，直线a ，c 共面，则直线b ，c 共面；④依次首尾相接的四条线段必共面．A ．0B ．1C ．2D ．3解析：选 B ①显然是正确的，可用反证法证明；②中若A ，B ，C三点共线，则A ，B ，C ，D ，E 五点不一定共面；③构造长方体或正方体，如图显然b ，c 异面，故不正确；④中空间四边形中四条线段不共面．故只有①正确．4.如图所示，四边形ABEF 和四边形ABCD 都是梯形，BC 綊12AD ，BE 綊12FA ，G ，H 分别为FA ，FD 的中点．(1)证明：四边形BCHG 是平行四边形；(2)C ，D ，F ，E 四点是否共面？为什么？解：(1)证明：由已知FG ＝GA ，FH ＝HD ，可得GH 綊12AD .又∵BC 綊12AD ，∴GH 綊BC ，∴四边形BCHG 为平行四边形．(2)C ，D ，F ，E 四点共面，证明如下：由BE 綊12AF ，G 为FA 的中点知BE 綊FG ，∴四边形BEFG 为平行四边形，∴EF ∥BG .由(1)知BG ∥CH ，∴EF ∥CH .∴EF 与CH 共面．又D ∈FH ，∴C ，D ，F ，E 四点共面．突破点(二) 空间两直线的位置关系1．空间中两直线的位置关系(1)空间中两直线的位置关系⎩⎨⎧ 共面直线⎩⎪⎨⎪⎧ 平行相交异面直线：不同在任何一个平面内(2)公理4和等角定理①公理4：平行于同一条直线的两条直线互相平行．②等角定理：空间中如果两个角的两边分别对应平行，那么这两个角相等或互补．2．异面直线所成的角(1)定义：设a ，b 是两条异面直线，经过空间任一点O 作直线a ′∥a ，b ′∥b ，把a ′与b ′所成的锐角(或直角)叫做异面直线a 与b 所成的角(或夹角)．(2)范围：⎝⎛⎦⎥⎤0，π2.[例1] (1)下列结论正确的是( )①在空间中，若两条直线不相交，则它们一定平行；②平行于同一条直线的两条直线平行；③一条直线和两条平行直线中的一条相交，那么它也和另一条相交；④空间四条直线a ，b ，c ，d ，如果a ∥b ，c ∥d ，且a ∥d ，那么b ∥c .A ．①②③B ．②④C ．③④D ．②③(2)在图中，G ，N ，M ，H 分别是正三棱柱的顶点或所在棱的中点，则表示直线GH ，MN 是异面直线的图形有________．(填上所有正确答案的序号)[解析] (1)①错，两条直线不相交，则它们可能平行，也可能异面；②由公理4可知正确；③错，若一条直线和两条平行直线中的一条相交，则它和另一条直线可能相交，也可能异面；④由平行直线的传递性可知正确．故选B.(2)图①中，直线GH ∥MN ；图②中，G ，H ，N 三点共面，但M ∉平面GHN ，因此直线GH 与MN 异面；图③中，连接MG ，GM ∥HN ，因此GH 与MN 共面；图④中，G ，M ，N 共面，但H ∉平面GMN ，因此GH 与MN 异面．所以在图②④中，GH 与MN 异面．[答案] (1)B (2)②④[方法技巧] 判断空间两直线位置关系的思路方法(1)判断空间两直线的位置关系一般可借助正方体模型，以正方体为主线直观感知并准确判断．(2)异面直线的判定方法①反证法：先假设两条直线不是异面直线，即两条直线平行或相交，由假设的条件出发，经过严格的推理，导出矛盾，从而否定假设，肯定两条直线异面．②定理法：平面外一点A 与平面内一点B 的连线和平面内不经过点B 的直线是异面直线．异面直线所成的角[例2] 空间四边形ABCD 中，AB ＝CD 且AB 与CD 所成的角为30°，E ，F 分别为BC ，AD 的中点，求EF 与AB 所成角的大小．[解] 取AC 的中点G ，连接EG ，FG ，则EG 綊12AB ，FG 綊12CD ， 由AB ＝CD 知EG ＝FG ，∴∠GEF (或它的补角)为EF 与AB 所成的角，∠EGF (或它的补角)为AB 与CD 所成的角． ∵AB 与CD 所成的角为30°，∴∠EGF ＝30°或150°.由EG ＝FG 知△EFG 为等腰三角形，当∠EGF ＝30°时，∠GEF ＝75°；当∠EGF ＝150°时，∠GEF ＝15°.故EF 与AB 所成的角为15°或75°.[方法技巧]用平移法求异面直线所成的角的步骤(1)一作：即根据定义作平行线，作出异面直线所成的角；(2)二证：即证明作出的角是异面直线所成的角；(3)三求：解三角形，求出作出的角．如果求出的角是锐角或直角，则它就是要求的角；如果求出的角是钝角，则它的补角才是要求的角．能力练通 抓应用体验的“得”与“失”1．[考点一]下列说法正确的是( )A ．若a ⊂α，b ⊂β，则a 与b 是异面直线B ．若a 与b 异面，b 与c 异面，则a 与c 异面C ．若a ，b 不同在平面α内，则a 与b 异面D ．若a ，b 不同在任何一个平面内，则a 与b 异面解析：选D 由异面直线的定义可知D 正确．2．[考点一]l 1，l 2，l 3是空间三条不同的直线，则下列命题正确的是( )A ．l 1⊥l 2，l 2⊥l 3⇒l 1∥l 3B ．l 1⊥l 2，l 2∥l 3⇒l 1⊥l 3C ．l 1∥l 2∥l 3⇒l 1，l 2，l 3共面D ．l 1，l 2，l 3共点⇒l 1，l 2，l 3共面解析：选B 若l 1⊥l 2，l 2⊥l 3，则l 1，l 3有三种位置关系，可能平行、相交或异面，A 不正确；当l 1∥l 2∥l 3或l 1，l 2，l 3共点时，l 1，l 2，l 3可能共面，也可能不共面，C ，D 不正确；当l 1⊥l 2，l 2∥l 3时，则有l 1⊥l 3，故选B.3．[考点二]如图，四边形ABCD 和ADPQ 均为正方形，它们所在的平面互相垂直，则异面直线AP 与BD 所成的角为________．解析：如图，将原图补成正方体ABCD ­QGHP ，连接GP ，AG ，则GP ∥BD ，所以∠APG 为异面直线AP 与BD 所成的角，在△AGP 中AG ＝GP ＝AP ，所以∠APG ＝π3. 答案：π34．[考点一、二]如图所示，三棱锥P ­ABC 中， PA ⊥平面ABC ，∠BAC ＝60°，PA ＝AB ＝AC ＝2，E 是PC 的中点．(1)求证AE 与PB 是异面直线；(2)求异面直线AE 与PB 所成角的余弦值．解：(1)证明：假设AE 与PB 共面，设平面为α，∵A ∈α，B ∈α，E ∈α，∴平面α即为平面ABE ，∴P ∈平面ABE ，这与P ∉平面ABE 矛盾，所以AE 与PB 是异面直线．(2)取BC 的中点F ，连接EF ，AF ，则EF ∥PB ，所以∠AEF (或其补角)就是异面直线AE 与PB 所成的角．∵∠BAC ＝60°，PA ＝AB ＝AC ＝2，PA ⊥平面ABC ，∴AF ＝3，AE ＝2，EF ＝2，cos ∠AEF ＝AE 2＋EF 2－AF 22·AE ·EF ＝2＋2－32×2×2＝14，故异面直线AE 与PB 所成角的余弦值为14.[全国卷5年真题集中演练——明规律]1.(2016·全国乙卷)平面α过正方体ABCD ­A 1B 1C 1D 1的顶点A ，α∥平面CB 1D 1，α∩平面ABCD ＝m ，α∩平面ABB 1A 1＝n ，则m ，n 所成角的正弦值为( ) A.32 B.22 C.33 D.13解析：选A 如图，在正方体ABCD ­A 1B 1C 1D 1的上方接一个同等大小的正方体ABCD ­A 2B 2C 2D 2，则过A 与平面CB 1D 1平行的是平面AB 2D 2，即平面α就是平面AB 2D 2，平面AB 2D 2∩平面ABB 1A 1＝AB 2，即直线n 就是直线AB 2，由面面平行的性质定理知直线m 平行于直线B 2D 2，故m ，n 所成的角就等于AB 2与B 2D 2所成的角，在等边三角形AB 2D 2中，∠AB 2D 2＝60°，故其正弦值为32.故选A. 2．(2013·新课标全国卷Ⅱ)已知m ，n 为异面直线，m ⊥平面α，n ⊥平面β.直线l 满足l ⊥m ，l ⊥n ，l ⊄α，l ⊄β，则( )A ．α∥β且l ∥αB ．α⊥β且l ⊥βC ．α与β相交，且交线垂直于lD ．α与β相交，且交线平行于l解析：选D 由于m ，n 为异面直线，m ⊥平面α，n ⊥平面β，则平面α与平面β必相交，但未必垂直，且交线垂直于直线m ，n ，又直线l 满足l ⊥m ，l ⊥n ，则交线平行于l ，故选D.3．(2016·全国甲卷)α，β是两个平面，m ，n 是两条直线，有下列四个命题： ①如果m ⊥n ，m ⊥α，n ∥β，那么α⊥β.②如果m ⊥α，n ∥α，那么m ⊥n .③如果α∥β，m ⊂α，那么m ∥β.④如果m ∥n ，α∥β，那么m 与α所成的角和n 与β所成的角相等．其中正确的命题有________．(填写所有正确命题的编号)解析：对于①，α，β可能平行，也可能相交但不垂直，故错误．对于②，由线面平行的性质定理知存在直线l ⊂α，n ∥l ，又m ⊥α，所以m ⊥l ，所以m ⊥n ，故正确．对于③，因为α∥β，所以α，β没有公共点．又m⊂α，所以m，β没有公共点，由线面平行的定义可知m∥β，故正确．对于④，因为m∥n，所以m与α所成的角和n与α所成的角相等．因为α∥β，所以n与α所成的角和n与β所成的角相等，所以m与α所成的角和n与β所成的角相等，故正确．答案：②③④[课时达标检测] 重点保分课时——一练小题夯双基，二练题点过高考[练基础小题——强化运算能力]1．四条线段顺次首尾相连，它们最多可确定的平面有( )A．4个 B．3个 C．2个 D．1个解析：选A 首尾相连的四条线段每相邻两条确定一个平面，所以最多可以确定四个平面．2．已知A，B，C，D是空间四点，命题甲：A，B，C，D四点不共面，命题乙：直线AC 和BD不相交，则甲是乙成立的( )A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件解析：选A 若A，B，C，D四点不共面，则直线AC和BD不共面，所以AC和BD不相交，充分性成立；若直线AC和BD不相交，若直线AC和BD平行，则A，B，C，D四点共面，必要性不成立，所以甲是乙成立的充分不必要条件．3．若直线a⊥b，且直线a∥平面α，则直线b与平面α的位置关系是( )A．b⊂αB．b∥αC．b⊂α或b∥αD．b与α相交或b⊂α或b∥α解析：选D 结合正方体模型可知b与α相交或b⊂α或b∥α都有可能．4.如图，平行六面体ABCD­A1B1C1D1中既与AB共面又与CC1共面的棱有________条．解析：依题意，与AB和CC1都相交的棱有BC；与AB相交且与CC1平行有棱AA1，BB1；与AB平行且与CC1相交的棱有CD，C1D1.故符合条件的棱有5条．答案：5[练常考题点——检验高考能力]一、选择题1．若直线上有两个点在平面外，则( )A．直线上至少有一个点在平面内 B．直线上有无穷多个点在平面内C．直线上所有点都在平面外 D．直线上至多有一个点在平面内解析：选D 根据题意，两点确定一条直线，那么由于直线上有两个点在平面外，则直线在平面外，只能是直线与平面相交，或者直线与平面平行，那么可知直线上至多有一个点在平面内．2．空间四边形两对角线的长分别为6和8，所成的角为45°，连接各边中点所得四边形的面积是( )A．6 2 B．12 C．12 2 D．24 2解析：选A 如图，已知空间四边形ABCD，对角线AC＝6，BD＝8，易证四边形EFGH为平行四边形，∠EFG或∠FGH为AC与BD所成的角，大小为45°，故S四边形EFGH＝3×4×sin 45°＝62，故选A.3．若空间中四条两两不同的直线l1，l2，l3，l4，满足l1⊥l2，l2⊥l3，l3⊥l4，则下列结论一定正确的是( )A．l1⊥l4 B．l1∥l4C．l1与l4既不垂直也不平行 D．l1与l4的位置关系不确定解析：选D 构造如图所示的正方体ABCD­A1B1C1D1，取l1为AD，l2为AA1，l3为A1B1，当取l4为B1C1时，l1∥l4，当取l4为BB1时，l1⊥l4，故排除A、B、C，选D.4．已知直线a和平面α，β，α∩β＝l，a⊄α，a⊄β，且a在α，β内的射影分别为直线b和c，则直线b和c的位置关系是( )A．相交或平行 B．相交或异面C．平行或异面 D．相交、平行或异面解析：选D 依题意，直线b和c的位置关系可能是相交、平行或异面．5.如图，ABCD­A1B1C1D1是长方体，O是B1D1的中点，直线A1C交平面AB1D1于点M，则下列结论正确的是( )A ．A ，M ，O 三点共线B ．A ，M ，O ，A 1不共面C ．A ，M ，C ，O 不共面D ．B ，B 1，O ，M 共面解析：选A 连接A 1C 1，AC ，则A 1C 1∥AC ，所以A 1，C 1，C ，A 四点共面，所以A 1C ⊂平面ACC 1A 1，因为M ∈A 1C ，所以M ∈平面ACC 1A 1，又M∈平面AB 1D 1，所以M 在平面ACC 1A 1与平面AB 1D 1的交线上，同理O 在平面ACC 1A 1与平面AB 1D 1的交线上，所以A ，M ，O 三点共线．6．过正方体ABCD ­A 1B 1C 1D 1的顶点A 作直线l ，使l 与棱AB ，AD ，AA 1所成的角都相等，这样的直线l 可以作( )A ．1条B ．2条C ．3条D ．4条解析：选D 如图，连接体对角线AC 1，显然AC 1与棱AB ，AD ，AA 1所成的角都相等，所成角的正切值都为 2.联想正方体的其他体对角线，如连接BD 1，则BD 1与棱BC ，BA ，BB 1所成的角都相等，∵BB 1∥AA 1，BC∥AD ，∴体对角线BD 1与棱AB ，AD ，AA 1所成的角都相等，同理，体对角线A 1C ，DB 1也与棱AB ，AD ，AA 1所成的角都相等，过A 点分别作BD 1，A 1C ，DB 1的平行线都满足题意，故这样的直线l 可以作4条．二、填空题7.如图所示，在空间四边形ABCD 中，点E ，H 分别是边AB ，AD 的中点，点F ，G 分别是边BC ，CD 上的点，且CF CB ＝CG CD ＝23，则下列说法正确的是________．(填写所有正确说法的序号)①EF 与GH 平行 ②EF 与GH 异面③EF 与GH 的交点M 可能在直线AC 上，也可能不在直线AC 上④EF 与GH 的交点M 一定在直线AC 上解析：连接EH ，FG (图略)，依题意，可得EH ∥BD ，FG ∥BD ，故EH ∥FG ，所以E ，F ，G ，H 共面．因为EH ＝12BD ，FG ＝23BD ，故EH ≠FG ，所以EFGH 是梯形，EF 与GH 必相交，设交点为M .因为点M 在EF 上，故点M 在平面ACB 上．同理，点M 在平面ACD 上， ∴点M 是平面ACB 与平面ACD 的交点，又AC 是这两个平面的交线， 所以点M 一定在直线AC 上．答案：④8．如图为正方体表面的一种展开图，则图中的AB ，CD ，EF ，GH 在原正方体中互为异面直线的有________对．解析：平面图形的翻折应注意翻折前后相对位置的变化，则AB ，CD ，EF 和GH 在原正方体中，显然AB 与CD ，EF 与GH ，AB 与GH 都是异面直线，而AB 与EF 相交，CD 与GH 相交，CD 与EF 平行．故互为异面直线的有3对．答案：39．已知a ，b ，c 为三条不同的直线，且a ⊂平面α，b ⊂平面β，α∩β＝c .①若a 与b 是异面直线，则c 至少与a ，b 中的一条相交；②若a 不垂直于c ，则a 与b 一定不垂直；③若a ∥b ，则必有a ∥c ；④若a ⊥b ，a ⊥c ，则必有α⊥β.其中正确的命题有________．(填写所有正确命题的序号)解析：①中若a 与b 是异面直线，则c 至少与a ，b 中的一条相交，故①正确；②中平面α⊥平面β时，若b ⊥c ，则b ⊥平面α，此时不论a ，c 是否垂直，均有a ⊥b ，故②错误；③中当a ∥b 时，则a ∥平面β，由线面平行的性质定理可得a ∥c ，故③正确；④中若b ∥c ，则a ⊥b ，a ⊥c 时，a 与平面β不一定垂直，此时平面α与平面β也不一定垂直，故④错误．答案：①③10.如图，在三棱锥A ­BCD 中，AB ＝AC ＝BD ＝CD ＝3，AD ＝BC ＝2，点M ，N 分别为AD ，BC 的中点，则异面直线AN ，CM 所成的角的余弦值是________．解析：如图所示，连接DN ，取线段DN 的中点K ，连接MK ，CK .∵M为AD 的中点，∴MK ∥AN ，∴∠KMC (或其补角)为异面直线AN ，CM 所成的角．∵AB ＝AC ＝BD ＝CD ＝3，AD ＝BC ＝2，N 为BC 的中点，由勾股定理易求得AN ＝DN ＝CM ＝22，∴MK ＝ 2.在Rt △CKN 中，CK ＝ 22＋12＝ 3.在△CKM 中，由余弦定理，得cos ∠KMC ＝22＋222－322×2×22＝78，所以异面直线AN ，CM 所成的角的余弦值是78. 答案：78三、解答题11.如图所示，A 是△BCD 所在平面外的一点，E ，F 分别是BC ，AD的中点．(1)求证：直线EF 与BD 是异面直线；(2)若AC ⊥BD ，AC ＝BD ，求EF 与BD 所成的角．解：(1)证明：假设EF 与BD 不是异面直线，则EF 与BD 共面，从而DF 与BE 共面，即AD 与BC 共面，所以A ，B ，C ，D 在同一平面内，这与A 是△BCD 所在平面外的一点相矛盾．故直线EF 与BD 是异面直线．(2)取CD 的中点G ，连接EG ，FG ，则AC ∥FG ，EG ∥BD ，所以相交直线EF 与EG 所成的角，即为异面直线EF 与BD 所成的角．又因为AC ⊥BD ，则FG ⊥EG .在Rt △EGF 中，由EG ＝FG ＝12AC ，求得∠FEG ＝45°，即异面直线EF 与BD 所成的角为45°.12.如图，在三棱锥P ­ABC 中，PA ⊥底面ABC ，D 是PC 的中点．已知∠BAC ＝π2，AB ＝2，AC ＝23，PA ＝2.求： (1)三棱锥P ­ABC 的体积；(2)异面直线BC 与AD 所成角的余弦值．解：(1)S △ABC ＝12×2×23＝23，三棱锥P ­ABC 的体积为V ＝13S △ABC ·PA ＝13×23×2＝433. (2)如图，取PB 的中点E ，连接DE ，AE ，则ED ∥BC ，所以∠ADE (或其补角)是异面直线BC 与AD 所成的角．在△ADE 中，DE ＝2，AE ＝2，AD ＝2，cos ∠ADE ＝22＋22－22×2×2＝34. 故异面直线BC 与AD 所成角的余弦值为34.。

第二部分点、线、平面之间的位置关系第一讲空间点、直线、平面之间的位置关系一、导入1. 正确理解平面的儿何概念，掌握平面的基本性质；2 .熟练掌握三种数学语言的转换与翻译，熟练点线面关系符号语言的书写:;3. 结合图形理解空间中直线与平面、平面与平面之间的位置关系；4 .进一步熟悉文字语言、图形语言、符号语言的相互转换；5 .进一步培养学生的空间想象和全面思考问题的能力.二、知识点梳理（一）平面的表示方法1. 平面是无限延伸的，但常用平面的一部分来表示平面.2.画法:常用平彳二四边形3.1 • （标记在角上）②平面A BCD ③平面A C或平面BD注意：（1）平面的两个特征:①无限延伸②平的（没有厚度）（2）一条直线把平面分成两部分，一个平面把空间分成两部分（二）点、线、面的基本位置关系（1）符号表示：点A、线a、面a(2)集合关系:A e a, A e a,a u a例1判断下列各题的说法正确与否，在正确的说法的题号后打否则打X1、一个平面长4米，宽2米；（）2、平面有边界；（）3、一个平面的面积是2 5 cnr :4、一个平面可以把空间分成两部分・（）例2如图，用符号表示以下各概念：①点力、B在直线*上；②直线a在平面a内；点C在平面01内；③点O不在平面0C内；直线b不在平面a内.变式训练一1 •将下列符号语言转化为图形语言:(1) B 已卩、A el, Bel(2 ) a u a、b u 卩、ar\ 卩= c y a // c, b cc = p2. 将下列文字语言转化为符号语言：（I ）点八在平面&内，但不在平面0内（2）直线d经过平面&外一点M（3）直线/在平面a内，乂在平面0内（即平面和平面相交于直线）（三）平面的基本性质1. 公理1若一条直线在一个平面内，则这条直线上所有的点都在这个平面内三条推论：1. 经过一条直线和这条直线外一点，有且只有一个平面2. 经过两条相交直线，有且只有一个平面3. 经过两条平行直线，有且只有一个平面3. 公理3若两个不重合的平面有一个公共点，那么它们有且只有一条过该点的 公共直线.即：P 已a 、P 已卩、ac/3 = l n P 已I例3已知长方体/WCD — A5G®中川.N 分别是和BC 的中点,AB= 4 , AD = 2,BB 、=2届,求异而直线dD 与MN 所成角的余弦值。

第2讲 立体几何之点线面之间的位置关系一、知识点： （一）三种关系：1、线线关系：相交（特殊垂直）、平行、异面（既不平行也不相交） ①异面直线夹角]90,0(︒︒∈θ（平移构造)；2、线面关系：线在面内、线面平行、线面相交（特殊垂直）；3、面面关系：面面平行、面面相交（特殊垂直）； （二）重要关系——平行、垂直(I )、线面平行：判定：线和面内直线平行，则线面平行； 性质：线面平行，则线平行于面面交线；(II )、面面平行：判定：α内两交线分别与β平行，则α∥β；性质1：γ穿过平行平面α、β，则交线平行；性质2：面面平行，则面内直线平行于另一面；（III ）、线面垂直: 判定：线和面内两相交直线垂直，则线面垂直； 性质：垂直于同一面的直线平行； （IV ）、面面垂直：判定：α经过β的垂线，则α⊥β；性质：α⊥β，则α内垂直于交线的线垂直于β； （三）、高频考点+做题技巧： 1、证明线线平行：中位线法【有中点、中位线】；平行四边形法【证//AB CD ，只需证//AC BD 】；传递性； 角度法【内错角、同位角、同旁内角】；面面平行性质【γ穿过平行平面α、β，则交线平行】 2、判断线面关系——辅助正（长）方体； 二、典型题目1、 平面l =⋂βα，点βαα∈∈∈C B A ,,，且l C ∈，又R l AB =⋂，过A 、B 、C 三点确定的平面记作γ，则γβ⋂是（ ） A ．直线AC B ．直线BC C ．直线CR D ．以上都不对 2、空间不共线的四点，可以确定平面的个数是（ ）A ．0B ．1C ．1或4D ．无法确定4、正方体1111D C B A ABCD -中，P 、Q 分别为11,CC AA 的中点，则四边形PBQ D 1是（ ） A ．正方形 B ．菱形 C ．矩形 D ．空间四边形5、在空间四边形ABCD 中，点E 、F 、G 、H 分别为AB 、BC 、CD 、DA 的中点，若AC=BD ， 且BD AC ⊥，则四边形EFGH 为6、下列命题正确的是（ ）A 若βα⊂⊂b a ,，则直线b a ,为异面直线B 若βα⊄⊂b a ,，则直线b a ,为异面直线C 若∅=⋂b a ，则直线b a ,为异面直线D 不同在任何一个平面内的两条直线叫异面直线 7、如果两直线b a //，且//a 平面α，则b 与平面α的位置关系是（ ）A ．相交B ．α//bC ．α⊂bD ．α//b 或α⊂b8、若直线a 与直线b 是异面直线，且//a 平面α，则b 与平面α的位置关系是（ ）A ．α//bB ．b 与平面α相交C ．α⊂bD ．不能确定 9、已知//a 平面α，直线α⊂b ，则直线a 与直线b 的关系是（ ） A ．相交 B ．平行 C ．异面 D ．平行或异面 10、b a ,是异面直线，则过a 且与b 平行的平面有____个11.对于平面α和直线m 、n ，下列命题中假命题是 （填序号）. ①若m ∥n ,n ⊂α,则m ∥α;②若m ∥α，n ∥α，则m ∥n③若m ⊂α，n ∥α，则m ∥n ；④若m ⊂α，n ⊂α,m ∥β,n ∥β,则α∥β12.若m 、n 是两条不同的直线，α、β、γ是三个不同的平面，则下列命题中的真命题是( )A.若m ⊂β，α⊥β，则m ⊥αB.若α∩γ＝m ，β∩γ＝n ，m ∥n ，则α∥βC.若m ⊥β，m ∥α，则α⊥βD.若α⊥γ，α⊥β，则β⊥γ13．设正四棱锥S —ABCD 的侧棱长为2，底面边长为3，E 是SA 的中点，则异面直线BE 与SC 所成的角是（ ）A ．30° B ．45° C ．60° D ．90°14设M 表示平面，a 、b 表示直线，给出下列四个命题：①M b M a b a ⊥⇒⎭⎬⎫⊥// ②b a M b M a //⇒⎭⎬⎫⊥⊥ ③⇒⎭⎬⎫⊥⊥b a M a b ∥M ④⇒⎭⎬⎫⊥b a M a //b ⊥M . 其中正确的命题是 ( ) A.①② B.①②③ C.②③④ D.①②④15、把正方形ABCD 沿对角线AC 折起，当点D 到平面ABC 的距离最大时，直线BD 和平面ABC 所成角的大小为 （ ）A ． 90B ． 60C ． 45D ．3016．在正方体1111ABCD A B C D -中，若E 是11AC 的中点，则直线CE 垂直于（ ） A ．AC B ． BD C ．1A D D ．11A D17．四面体S ABC -中，各个侧面都是边长为a 的正三角形，,E F 分别是SC 和AB 的中点，则异面直线EF 与SA 所成的角等于（ ）A ．090 B ．060 C ．045 D ．03018、到空间不共面四点距离相等的平面的个数为（ ） A ． 1 B ． 2 C ． 4 D ． 719.空间四边形ABCD 中，线段AB 、BC 、CD 、DA 的中点分别为P 、Q 、R 、S ，则在下面的命题中： （1）P 、Q 、R 、S 四点共面；（2）PR 与QS 不相交； （3）当AC=BD 时，四边形PQRS 是菱形；（4）当AC ⊥BD 时，四边形PQRS 是矩形． 正确命题的个数为（ ）A. 1 B ． 2 C ． 4 D ． 720、已知a ，b 是两条异面直线，直线c ∥a ，那么c 与b 的位置关系是 21、空间三条直线a 、b 、c ，若a ⊥b ，b ⊥c ，则a 、c 的位置关系是22、过已知直线外一点可作 条直线与已知直线平行；可以作 条直线与已知直线垂直23、如图，A 是平面BCD 外的一点,G H 分别是,ABC ACD ∆∆的重心，求证：//GH BD ．24、如图，在三棱锥P-ABC 中，点Ο、D 分别是AC 、PC 的中点，求证： OD//平面PAB 。