能量衡算方程式

化工中物料衡算和热量衡算公式一、物料衡算公式1.物料总量计算公式物料总量计算公式可以根据物质的密度（ρ）和体积（V）来计算。

公式如下：物料总量=密度×体积2.物料质量计算公式物料质量计算公式可以根据物质的密度（ρ）、体积（V）和物质的质量（m）之间的关系得出。

公式如下：质量=密度×体积3.物料浓度计算公式物料浓度计算公式可以根据溶质的质量（m）和溶液的体积（V）来计算。

公式如下：浓度=质量/体积4.溶液的重量和体积之间的关系溶液的重量可以根据溶液的密度（ρ）和溶液的体积（V）相乘得到。

公式如下：重量=密度×体积1.热量传递计算公式热量传递计算公式可以用于计算传热功率（Q）和传热面积（A）之间的关系。

公式如下：Q=h×A×ΔT其中，h为传热系数，ΔT为温差。

2.物料的热量计算公式物料的热量计算公式可以根据物料的质量（m）、比热容（Cp）和温度变化（ΔT）来计算。

公式如下：热量=质量×比热容×温度变化3.水的蒸发热计算公式水的蒸发热计算公式可以根据水的质量（m）和蒸发热（ΔHvap）来计算。

热量=质量×蒸发热三、补充说明1. 密度（ρ）是物质单位体积的质量，常用的单位有千克/立方米（kg/m^3）或克/立方厘米（g/cm^3）。

2. 比热容（Cp）是物质单位质量的热容量，表示单位质量物质温度升高1℃所需的热量，常用的单位是千焦/千克·℃（kJ/kg·°C）或焦/克·℃（J/g·°C）。

3.传热系数（h）是衡量热传导性能的参数，表示单位面积上的热量流入或流出的速率，常用的单位是瓦特/平方米·℃（W/m^2·°C）。

4.温度变化（ΔT）是物质的温度差，常用的单位是摄氏度（℃）或开尔文（K）。

5. 蒸发热（ΔHvap）是物质从液态转变为气态所需的热量，常用的单位是焦耳/克（J/g）或千焦/千克（kJ/kg）。

化工计算能量衡算引言化工过程中，能量的衡算是一个重要的步骤。

能量衡算可以帮助工程师了解化工过程中的能量转化和能量损失情况，从而优化工艺和提高能源利用效率。

本文将介绍化工计算能量衡算的基本原理和方法，并以实际案例进行说明。

一、能量的基本概念在进行能量的衡算之前，我们需要先了解能量的基本概念和单位。

能量是物体或系统所具有的做功能力，它是物质存在的一种属性。

能量的单位通常用焦耳（J）表示。

以下是一些常见的能量单位：•千焦（kJ）= 10^3 J•兆焦（MJ）= 10^6 J•吉焦（GJ）= 10^9 J此外，化学工程中经常使用的能量单位还有千卡（kcal）和英尺磅（ft-lbf）等。

二、能量转化和传递能量在化工过程中会发生转化和传递。

常见的能量转化包括热能转化为机械能、化学能转化为热能等。

能量传递则是指能量从一个物体传递到另一个物体。

能量转化和传递的过程可以通过能量平衡方程表示。

能量平衡方程的一般形式为：$$E_{in} - E_{out} = \\Delta E_{sys}$$其中，E in表示系统收入的能量，E out表示系统输出的能量，$\\Delta E_{sys}$表示系统内能的变化。

能量平衡方程是能量衡算的基础，通过对各个能量项进行计算和衡量，可以得到系统能量的全面情况。

三、能量衡算的方法能量衡算的方法包括物料平衡法、焓平衡法和热力学计算法等。

下面分别介绍这些方法的主要原理和应用。

3.1 物料平衡法物料平衡法是一种根据物料的进出量来计算能量收支的方法。

它基于质量守恒定律，假设在化工过程中物料是不可压缩和不可消失的。

使用物料平衡法进行能量衡算的一般步骤如下：1.确定系统边界，包括进出口和反应器等；2.收集进出口的物料信息，包括物料的质量、温度、压力等；3.列出物料平衡方程，根据质量守恒定律得到进出口物质量的关系；4.根据进出口物料的属性，计算出相应的能量。

物料平衡法可以应用于各种化工过程，包括反应器、蒸馏塔、萃取塔等。

能量衡算方程式在图1-9所示的定态流动系统中，流体从截面1-1′流入，经粗细不同的管道，从截面2-2′流出。

管路上装有对流体作功的泵2及向流体输入或从流体取出热量的换热器1。

衡算范围：内壁面、1-1′与2-2′截面间。

衡算基准：1kg流体。

基准水平面：o-o′设u1、u2分别为流体在截面1-1′与2-2′处的流速，m/s；p1、p2分别为流体在截面1-1′与2-2′处的压强，Pa。

1kg流体进、出系统时输入和输出的能量有下面各项：（1）内能物质内部能量的总和称为内能。

1kg流体输入与输出的内能分别以U1和U2表示，其单位为J/kg。

（2）位能流体因受重力的作用，在不同的高度处具有不同的位能，相当于质量为m的流体自基准水平面升举到某高度Z所作功，即：位能=mgZ位能的单位是N·m或者J。

1kg流体输入与输出的位能分别为gZ1与gZ2，其单位为J/kg。

位能是个相对值，随所选的基准水平面位置而定，在基准水平面以上的位能为正值，以下的为负值。

（3）动能流体以一定的速度运动时，便具有一定的动能．质量为m，流速为u的流体所具有的动能为：动能=mu2/2 动能的单位是N·m或J1kg流体输入与输出的动能分别为u12/2与u22/2，其单位为J/kg。

（4）静压能(压强能) 静止流体内部任一处都有一定的静压强。

流动着的流体内部任何位置也都有一定的静压强。

如果在内部有液体流动的管壁上开孔，并与一根垂直的玻璃管相接，液体便会在玻璃管内上升，上升的液柱高度便是运动着流体在该截面处的静压强的表现。

对于图1-9所示的流动系统，流体通过截面1-1′时，由于该截面处流体具有一定的压力，这就需要对流体作相应的功，以克服这个压力，才能把流体推进系统里去。

于是通过截面1-1′，的流体必定要带着与所需的功相当的能量进入系统，流体所具有的这种能量称为静压能或流动功。

设质量为m、体积为Vl的流体通过截面1-1′，把该流体推进此截面所需的作用力为p1A1，而流体通过此截面所走的距离为V1/A1，则流体带入系统的静压能为：对1kg流体，则：同理，1kg流体离开系统时输出的静压能为p2v2，其单位为J/kg。

化工计算中的能量衡算是根据热力学第一定律，即能量守恒与转化定律，对化工过程进行能量计算。

化工生产中消耗的能量形式有机械能，电能和热能等等，其中以热能为主要形式，因此化工过程中的能量衡算重点是热量衡算。

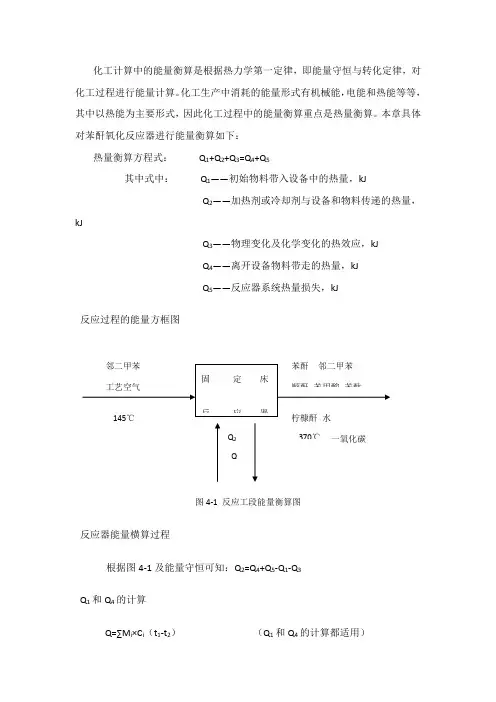
本章具体对苯酐氧化反应器进行能量衡算如下：热量衡算方程式：Q1+Q2+Q3=Q4+Q5其中式中：Q1——初始物料带入设备中的热量，kJQ2——加热剂或冷却剂与设备和物料传递的热量，kJQ3——物理变化及化学变化的热效应，kJQ4——离开设备物料带走的热量，kJQ5——反应器系统热量损失，kJ反应过程的能量方框图图4-1 反应工段能量衡算图反应器能量横算过程根据图4-1及能量守恒可知：Q2=Q4+Q5-Q1-Q3Q1和Q4的计算Q=∑M i×C i（t1-t2）（Q1和Q4的计算都适用）式中：M i ——反应物体系中组分的质量，kg ； C i ——组分i 在0-T ℃时的平均比热容，KJ/； t 1，t 2——反应物系在反应前后的温度，℃。

物料进入设备时的温度为145℃，热量衡算的基准为145℃，△T=0,则： Q 1=0查得各物项平均比热容数据： （kJ/kg.℃）表4-1 各物相平均比热容所以： ()21i i 4t C M Q t -=∑=××(370-145)+××225+××225+××225+××225+××225+××225+××225+××225+××225+××225= 过程Q 3的计算过程热效率可以分为两类：一类是化学过程的热效率即化学反应速率；另一类是物理过程热效率。

物料化学变化过程，除化学反应外，往往伴随着物料状态变化热效率，但本工艺流程中物理过程热效率较低，可以忽略不计，该过程皆为放热反应，则过程热效率可以由下式计算：主反应：C 8H 10+3O 2→C 8H 4O 3+3H 2O + Q 3-1=×103×=×103kJ/h副反应：CH 3C 6H 4CH 3+→C 4H 2O 3（顺酐）+4CO 2+4H 2O + Q 3-2=×103×=×103kJ/hCH3C6H4CH3+3O2→C6H5COOH（苯甲酸）+CO2+2H2O +Q3-3=×103×=×103kJ/hCH3C6H4CH3+2O2→C8H6O2（苯酞）+2H2O +Q3-4=×103×=×103kJ/hCH3C6H4CH3+→C5H5O3（柠槺酐）+3CO+3H2O +Q3-5=×103×=×103kJ/hCH3C6H4CH3+→8CO+5H2O +Q3-6=×103×=×103kJ/hCH3C6H4CH3+→8CO2+5H2O +Q3-7=×103×=×103kJ/h继而得到：Q3 = Q3-1+Q3-2+Q3-3+Q3-4+Q3-5+Q3-6+Q3-7=×103kJ/hQ5的计算该反应中的热损失按5%计算，即：Q5=5%×（Q1+Q3）=5%×（0+×103）=×103kJ/hQ2的计算Q2为熔岩移出反应器的热量，由反应器热量守恒可知：Q2=Q4+Q5-Q1-Q3=h反应器能量衡算表根据以上计算列出氧化反应工段能量衡算表格如下：表4-2 反应工段能量衡算表（吸收热量为“+”，释放热量为“-”）。

物料衡算和热量衡算物料衡算根据质量守恒定律，以生产过程或生产单元设备为研究对象，对其进出口处进行定量计算，称为物料衡算。

通过物料衡算可以计算原料与产品间的定量转变关系，以及计算各种原料的消耗量，各种中间产品、副产品的产量、损耗量及组成。

物料衡算的基础物料衡算的基础是物质的质量守恒定律，即进入一个系统的全部物料量必等于离开系统的全部物料量，再加上过程中的损失量和在系统中的积累量。

∑G1=∑G2+∑G3+∑G4∑G2：——输人物料量总和；∑G3：——输出物料量总和；∑G4：——物料损失量总和；∑G5：——物料积累量总和。

当系统内物料积累量为零时，上式可以写成：∑G1=∑G2+∑G3物料衡算是所有工艺计算的基础，通过物料衡算可确定设备容积、台数、主要尺寸，同时可进行热量衡算、管路尺寸计算等。

物料衡算的基准(1)对于间歇式操作的过程，常采用一批原料为基准进行计算。

(2)对于连续式操作的过程，可以采用单位时间产品数量或原料量为基准进行计算。

物料衡算的结果应列成原材料消耗定额及消耗量表。

消耗定额是指每吨产品或以一定量的产品(如每千克针剂、每万片药片等)所消耗的原材料量；而消耗量是指以每年或每日等时间所消耗的原材料量。

制剂车间的消耗定额及消耗量计算时应把原料、辅料及主要包装材料一起算入。

热量衡算制药生产过程中包含有化学过程和物理过程，往往伴随着能量变化，因此必须进行能量衡算。

又因生产中一般无轴功存在或轴功相对来讲影响较小，因此能量衡算实质上是热量衡算。

生产过程中产生的热量或冷量会使物料温度上升或下降，为了保证生产过程在一定温度下进行，则外界须对生产系统有热量的加入或排除。

通过热量衡算，对需加热或冷却设备进行热量计算，可以确定加热或冷却介质的用量，以及设备所需传递的热量。

热量衡算的基础热量衡算按能量守恒定律“在无轴功条件下，进入系统的热量与离开热量应该平衡”，在实际中对传热设备的衡算可由下式表示Q1+Q2+Q3=Q4+Q5+Q6（1—1）式中： Q1—所处理的物料带入设备总的热量，KJ;Q2—加热剂或冷却剂与设备和物料传递的热量（符号规定加热剂加入热量为“+”，冷却剂吸收热量为“-”），KJ;Q3—过程的热效率，（符号规定过程放热为“+”；过程吸热为“-”）Q4—反应终了时物料的焓（输出反应器的物料的焓）Q5—设备部件所消耗的热量，KJ;Q6—设备向四周散失的热量，又称热损失,KJ;热量衡算的基准可与物料衡算相同，即对间歇生产可以以每日或每批处理物料基准。