用直方图描述数据-初中二年级数学试题练习、期中期末试卷-初中数学试卷

12.2.2用直方图描述数据［要点再现］1．用直方图描述数据的一般步骤是：（1）收集数据；（2）求出数据中的最大值与最小值的，即求出数据的变化范围（3）按这个变化范围确定组距并把数据进行分组；（4）列频数分布表；（5）画出直方图。

2．组距和组数的确定没有固定的标准，要根据经验和研究的具体问题来决定，通常数据越多，分成的组数也越多，当数据在100个以内时，根据数据的多少通常分成个组。

［基础闯关］1．某中学举行了一次演讲比赛，分段统计参赛同学的成绩，结果（1）参加这次演讲比赛的同学有人；（2）已知成绩在91～100分的同学为优胜者，那么优胜率为；（3）将成绩频数分布直方图补充完整（4）画出频数折线图，分析数据分布情况。

2.人们常用人均教育经费来反映一个地区对教育投入的情况，我国30个城市2001年人均教育经费的统计数据如下。

（单位：元）北京731南宁100长春101重庆102乌鲁木齐171青岛425深圳584合肥192武汉184上海790 兰州170呼和浩特206广州483天津440郑州197 南京292福州349洛阳127南昌117贵阳166 吉林76海口183济南205昆明234西安126 成都160哈尔滨249石家庄228长沙155沈阳237（2）画出分布直方图和折线图。

［能力提升］1．为了解某地初中三年级男生的身高情况，从该地的一所中学选取容量为60的样本（60名学生的身高.单位：厘米），分组情况如下表（表1）：表1(1)求出表中a、m的值；(2)画出频数分布直方图和频数折线图，分析数据分布情况.12．2．1用直方图描述数据［要点再现］1．，2．［基础闯关］1、（1）20 ；（2）20% ；（3）71～80（4）（图略）（2）图略［能力提升］1．解：（1）6，0.1（2）图略。

讲直方图练习题直方图是一种用来表示数据分布的图表形式，通过图形的高度和宽度来表示数据的频数或频率。

它通常用于描述连续数据的分布情况，可以直观地显示数据的集中程度、偏态和峰态等统计特征。

在解答直方图练习题时，我们需要了解如何构建直方图、读取直方图中的信息以及进行数据分析和解释。

本文将通过几个具体的练习题，来帮助读者掌握直方图的应用技巧。

练习题一：某班级在一次考试中，统计了学生们的成绩分布情况，得到了以下数据：分数范围频数60-70 670-80 1080-90 890-100 4请根据上述数据绘制出该班级学生考试成绩的直方图，并分析该班级学生在该次考试中的成绩分布情况。

解答：根据给定的数据，我们可以首先确定横坐标的分组区间，即分数范围。

在本题中，分数范围可取60-70、70-80、80-90和90-100四个区间。

然后，我们可以根据每个区间的频数绘制出相应的矩形条，并计算出每个矩形条的高度。

练习题二：一家电视台在某个时间段内进行了一项调查，统计了观众对于一档综艺节目的评分情况，得到了以下数据：评分区间频数5-6 106-7 157-8 208-9 309-10 25请根据上述数据绘制出该综艺节目观众评分情况的直方图，并分析观众对于该节目的评价。

解答：根据给定的数据，我们可以确定评分区间的分组范围为5-6、6-7、7-8、8-9和9-10。

然后，根据每个区间的频数绘制出相应的矩形条，并计算出每个矩形条的高度。

练习题三：某城市在连续10天内的降雨量进行了统计，得到了以下数据（单位：毫米）：降雨量区间频数0-10 410-20 620-30 830-40 540-50 2请根据上述数据绘制出该城市连续10天内的降雨量分布的直方图，并分析该城市的降雨情况。

解答：根据给定的数据，我们可以确定降雨量区间的分组范围为0-10、10-20、20-30、30-40和40-50。

然后，根据每个区间的频数绘制出相应的矩形条，并计算出每个矩形条的高度。

直方图统计练习题在统计学中，直方图是一种用来表示数据分布情况的图表。

它将数据划分成一系列等宽的区间，并在横轴上绘制出这些区间的范围，纵轴表示数据在该区间内的频数或频率。

通过直方图，我们可以直观地观察到数据的分布形态、集中程度以及异常值等信息。

为了更好地理解和练习直方图的统计分析，下面将给出一些直方图统计练习题。

练习题1：某班级的学生体重数据如下（单位：kg）：56 54 59 62 63 65 60 65 57 58 70 65 58 63 64请根据这组数据绘制出直方图，并回答以下问题：1. 该班级学生的体重数据大致呈什么样的分布形态？2. 最常见的体重区间是多少至多少kg？3. 体重在50kg至60kg之间的学生人数占总人数的百分比是多少？练习题2：一份调查统计了某国家不同年龄段的人口数量数据如下（单位：百万）：0-18岁：250 18-35岁：320 35-50岁：280 50岁以上：220请根据这组数据绘制出直方图，并回答以下问题：1. 该国家人口数量在不同年龄段上的分布情况如何？2. 在哪个年龄段上，人口数量最多？3. 50岁以上的人口数量占总人口数量的百分比是多少？练习题3：一份统计调查了某公司员工的工作经验数据如下（单位：年）：0-2年：20 2-5年：30 5-10年：40 10年以上：10请根据这组数据绘制出直方图，并回答以下问题：1. 该公司员工的工作经验分布情况如何？2. 在哪个工作经验区间上，员工数量最多？3. 具有5年以上工作经验的员工占总员工数量的百分比是多少？练习题4：一份调查记录了某城市不同民族的人口数量数据如下（单位：千人）：汉族：900 苗族：120 壮族：300 回族：100请根据这组数据绘制出直方图，并回答以下问题：1. 该城市不同民族的人口分布情况如何？2. 哪个民族的人口数量最多？3. 除汉族外，其他民族的人口数量总和占该城市总人口数量的百分比是多少？通过以上的练习题，我们可以巩固对直方图及其统计分析的理解。

直方图练习题直方图是一种用长方形的面积表示数据分布情况的统计图表。

它由一系列的纵向条纹或矩形组成，其中每个条纹的宽度相等，但高度表示相应数据值的频次或对应的百分比。

直方图可以帮助我们直观地理解数据的分布情况。

本文将通过一些练习题来帮助读者更好地理解和应用直方图。

练习一：某班级学生的考试成绩分布情况如下：60 65 70 75 80 80 85 85 90 90 90 95 100请根据以上数据绘制对应的直方图并分析成绩分布情况。

解答一：根据给定的数据，我们可以首先统计各个分数段的频次，然后绘制直方图。

分数段频次60-64 165-69 170-74 175-79 180-84 285-89 290-94 395-100 1绘制直方图如下：3 | #2 | # #1 | # # # #----------------------60 65 70 75 80 85 90 95 100从直方图中我们可以看出，成绩主要集中在80-90分之间，而90分以上和80分以下的分数频次较少。

练习二：一家餐厅在一周内的每天记录了进店的人数：星期一：30星期二：40星期三：50星期四：45星期五：60星期六：55星期日：50请根据以上数据绘制对应的直方图并分析人数分布情况。

解答二：根据给定的数据，我们可以首先统计每天进店人数的频次，然后绘制直方图。

进店人数频次30-39 140-49 250-59 360-69 1绘制直方图如下：3 | #2 | # #1 | # # #-----------------30 40 50 60从直方图中我们可以看出，进店人数主要集中在40-59人之间，而少数时候会有超过60人的情况。

练习三：某城市在一年内每个月的降雨量（单位：毫米）如下：1月：502月：453月：354月：605月：706月：907月：808月：1009月：7510月：5511月：4012月：30请根据以上数据绘制对应的直方图并分析降雨情况。

人教版七年级数学下册第十章数据的收集、整理与描述第二节直方图复习试题（含答案)一、单选题1．一组数据的最大值是97，最小值76，若组距为4，则可分为几组（）A．4 B．5 C．6 D．7【答案】B【解析】根据题意，一组数据的最大值是97，最小值76，最大值与最小值的差为=5.25；则可分为6组.21；若组距为4，有214故选C．点睛：本题考查组数的确定方法，注意极差的计算与最后组数的确定，组数不要太少，也不能太多．2．小明在选举班委时得了28票，下列说法错误的是（）A．不管小明所在的班级有多少学生，所有选票中选小明的选票频率不变B．不管小明所在的班级有多少学生，所有选票中选小明的选票频数不变C．小明所在班级的学生人数不少于28人D．小明的选票的频率不能大于1【答案】A【解析】【分析】根据频率=频数，即可解答．数据总和【详解】解：频率=频数数据总和，当全班人数变化时，所有选票中选小明的选票频率也随着变化；根据各小组频数之和等于数据总和，各小组频率之和等于1；可得B，C，D，都正确，A错误．故选A．【点睛】本题是对频率、频数灵活运用的综合考查，各小组频数之和等于数据总和，各小组频率之和等于1．频率、频数的关系：频率=频数数据总和．3．小亮把全班50名同学的期中数学测试成绩，绘成如图所示的条形图，其中从左起第一、二、三、四个小长方形高的比是1∶3∶5∶1．从中同时抽一份最低分数段和一份最高分数段的成绩的概率分别是（）．A．110、110B．110、12C．12、110D．12、12【答案】A【解析】试题分析：设第一个长方形的高为x，则第二、三、四个小长方形高分别为3x，5x，x，由题意得x＋3x＋5x＋x＝50，解得x＝5，即最低分为5人，最高分为5人，根据概率公式从中同时抽一份最低分数段和一份最高分数段的成绩的概率分别是550＝110、550＝110．故选A．点睛：本题考查频率分布直方图的知识和概率公式，难度不大，注意掌握如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）＝mn．4．在全班45人中进行了你最喜爱的电视节目的调查活动，喜爱的电视剧有人数为18人，喜爱动画片有人数为15人，喜爱体育节目有人数为10人，则下列说法正确的是（）A．喜爱的电视剧的人数的频率是1818+15+10B．喜爱的电视剧的人数的频率是1845C．喜爱的动画片的人数的频率是1818+10D．喜爱的体育节目的人数的频率是181514545--【答案】B【解析】试题分析：频率应为频数除以总数，所以喜欢看电视剧、动画片和体育节目的频率分别是1845、1545、1045，故选B.5．在-（-3），（-3）2，（-3）3，︱-3︱中，负数出现的频率为（）A．25％B．50％C．75％D．100％【答案】A【解析】试题分析：-（-3）=3，（-3）2=9，（-3）3=-27，︱-3︱=3，所以负数出现的频率为25％，故选A.6．小文同学统计了他所在小区居民每天微信阅读的时间，并绘制了直方图．有以下说法：①小文同学一共统计了60人；②每天微信阅读不足20分钟的人数有8人；③每天微信阅读30～40分钟的人数最多；④每天微信阅读0－10分钟的人数最少．根据图中信息，上述说法中正确的是( )A．①②③④B．①②③C．②③④D．③④【答案】D【解析】①小文同学一共统计了4+8+14+20+16+12=74(人)，则命题错误；②每天微信阅读不足20分钟的人数有4+8=12(人)，故命题错误；③每天微信阅读30−40分钟的人数最多，正确；④每天微信阅读0−10分钟的人数最少，正确．故选D.点睛: 本题考查读频数分布直方图的能力和利用统计图获取信息的能力．利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．7．要反映一个家庭在教育方面支出占总收入的比，宜采用（）A．条形统计图B．扇形统计图C．折线统计图D．频数分布直方图【答案】B【解析】根据统计图的特点进行分析可得：扇形统计图表示的是部分在总体中所占的百分比，但一般不能直接从图中得到具体的数据；折线统计图表示的是事物的变化情况；条形统计图能清楚地表示出每个项目的具体数目．【解答】解：由统计图的特点，知要反映一个家庭在教育方面支出占总收入的比，宜采用扇形统计图．故选B．8．某班将安全知识竞赛成绩整理后绘制成直方图，图中从左至右前四组的百分比分别是4%、12%、40%、28%，第五组的频数是8，下列结论错误的是（）A．该班有50名同学参赛B．第五组的百分比为16%C．成绩在70～80分的人数最多D．80分以上的学生有14名【答案】D【解析】A.8÷（1-4 %-12 %-40 %-28 %）=50（人），故正确；B. 1-4 %-12 %-40 %-28 %=16%，故正确；C.由图可知，成绩在70～80分的人数最多，故正确；D.50×（28 %+16 %）=22（人），故不正确；9．单位在植树节派出50名员工植树造林，统计每个人植树的棵树之后，绘制出如图所示的频数分布直方图（图中分组含最低值，不含最高值），则植树7棵及以上的人数占总人数的（ ）A ．40%B ．70%C ．76%D ．96%【答案】C【解析】 由图可得，植树7棵及以上的人数占总人数的5029650-=％ ，故选D. 10．下列关于统计图的说法中，错误的是（ ）A ．条形图能够显示每组中的具体数据B ．折线图能够显示数据的变化趋势C ．扇形图能够显示数据的分布情况D ．直方图能够显示数据的分布情况【答案】C【解析】A. ∵条形图能够显示每组中的具体数据，故正确；B. ∵折线图能够显示数据的变化趋势，故正确；C. ∵扇形图能够显示部分与总体的关系，故不正确；D. ∵直方图能够显示数据的分布情况，故正确；。

10.2《直方图》同步练习知识点：频数分布直方图①组距：每个小组两个端点之间的距离②组数：组数②频数：数据出现的次数③频率：频数与数据总数的比同步练习1．下表是对某班50名学生如何到校问题进行的一次调查结果，根据表中已知数据填表：频数所占比步行9骑自行车28坐公共汽车20%其他 32．下表是某班学生在一次身高测量中得到的统计结果请回答：（1）这个班总人数是_____人；身高为______m 的人数最多，有____人.（2）身高最高、最低的分别是_____m 、_____m ，他们分别有____人，_____人；最高的与最低的相身高/m 1.40 1.45 1.49 1.54 1.57 1.60 1.62 1.68 1.72 1.78人数/人 1 3 4 6 11 15 96 3 2差______m.3．（25分）七年级13班其中40个同学某次数学测验成绩（单位：分）：63 84 91 53 69 81 61 69 91 78 75 81 80 67 76 81 79 94 61 69 89 70 70 87 81 86 90 88 85 67 71 82 87 75 87 95 53 65 74 77 数学老师按10分的组距分段，进行统计分析：解：1、求极差：最高分，最低分。

极差： d2、列频率分布表:分组6050<≤x7060<≤x8070<≤x9080<≤x10090<≤x频数记录正正正频数2 9 14 5所占比例5% 35%4题图（每组含最低分数，但不含最高分数）120人数/人01234567860708090110100分数/分（1）请把频数分布表及频数分布直方图补充完整；（2）绘制频数折线图.4．某中学部分同学参加全国初中数学竞赛，取得了优异的成绩.指导老师统计了所有参赛同学的成绩（成绩都是整数，试题满分为120分），并且绘制了频率分布直方图（如图）.请回答：（1）该中学参加本次数学竞赛的有多少名同学？（2）如果成绩在90分以上（含90分）的同学获奖，那么该中学参赛同学的获奖率是多少？（3）图中还提供了其他信息，例如该中学没有获得满分的同学等.请再写出两条信息.10.2《直方图》同步练习题（1）答案：1.10 ；18％；56％； 6 ％2.（1）60 ；1.60 ；15 ；（2）1.78 ；1.40 ；2 ； 1 ；0.383. 94 ；53 ；41 ；略4.32 ；43.75％；80到90分的人数最多；80到90分的人数的百分比为25％。

人教版七年级数学下册第十章数据的收集、整理与描述第二节直方图复习试题（含答案)某校未为了解学生每天参加体育锻炼的时间情况，随机选取该校的部分学生进行调查．以下是根据调查结果绘制的统计图表的一部分．根据以上信息，解答下列问题：（1）被调查的学生中，每天参加体育锻炼的时间不少于90min的有_____人，这些学生数占被调查总人数的百分比为_____%，每天参加体育锻炼的时间不足60min的有_____人；（2）被调查的学生总数为_____人，统计表中m的值为_____，统计图中n 的值为_____，被调查学生每天参加体育锻炼时间的中位数落在_____组；（3）该校共有960名学生，根据调查结果，估计该校每天参加体育锻炼的时间不少于60min的学生数．【答案】（1）18，15，30（2）120，42，25，C（3）720【解析】【分析】（1）根据统计图表中的信息即可得到结论；（2）根据统计图表中的信息列式计算即可；（3）根据题意列式计算即可得到结论．【详解】解：（1）被调查的学生中，每天参加体育锻炼的时间不少于90min的有18人，这些学生数占被调查总人数的百分比为15%，每天参加体育锻炼的时间不足60min的有12＋18=30人；故答案为18，15，30；（2）被调查的学生总数为18÷15%=120人，统计表中m的值为120﹣12﹣18﹣30﹣18=42，统计图中n的值为×100%×100=25，被调查学生每天参加体育锻炼时间的中位数落在C组；故答案为120，42，25，C；（3）960×=720，答：估计该校每天参加体育锻炼的时间不少于60min的学生数为720人．【点睛】本题考查了频（数）率分布直方图：频率分布表列出的是在各个不同区间内取值的频率，频率分布直方图是用小长方形面积的大小来表示在各个区间内取值的频率．直角坐标系中的纵轴表示频率与组距的比值，即小长方形面积=组距×频数组距=频率．②各组频率的和等于1，即所有长方形面积的和等于1．也考查了用样本估计总体．32．为了提高学生书写汉字的能力，增强保护汉字的意识，我市举办了首届“汉字听写大赛”，经选拔后有50名学生参加决赛，这50名学生同时听写50个汉字，若每正确听写出一个汉字得1分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：请结合图表完成下列各题：（1）求表中a的值；（2）请把频数分布直方图补充完整；（3）若测试成绩不低于40分为优秀，则本次测试的优秀率是多少？（4）第5组10名同学中，有4名男同学，现将这10名同学平均分成两组进行对抗练习，且4名男同学每组分两人，求小宇与小强两名男同学能分在同一组的概率．【答案】（1）12；（2）补充频数分布直方图见解析； （3）本次测试的优秀率是0.44；（4）小宇与小强两名男同学分在同一组的概率是16．【解析】试题分析：（1）用总人数减去第1、2、3、5组的人数，即可求出a 的值； （2）根据（1）得出的a 的值，补全统计图；（3）用成绩不低于40分的频数乘以总数，即可得出本次测试的优秀率； （4）用A 表示小宇，B 表示小强，C 、D 表示其他两名同学，画出树状图，再根据概率公式列式计算即可．试题解析：（1）表中a 的值是：a=50-4-8-16-10=12； （2）根据题意画图如下：（3）本次测试的优秀率是12100.4450+=．答：本次测试的优秀率是0．44；（4）用A表示小宇，B表示小强，C、D表示其他两名同学，根据题意画树状图如下：共有12种情况，小宇与小强两名男同学分在同一组的情况有4种，则小宇与小强两名男同学分在同一组的概率是41．123考点：1．频数（率）分布直方图；2．频数（率）分布表；3．列表法与树状图法．33．为积极创建全国文明城市，某市对某路口的行人交通违章情况进行了20天的调查，将所得数据绘制成如下统计图（图2不完整）：请根据所给信息，解答下列问题：（1）第7天，这一路口的行人交通违章次数是多少次；这20天中，行人交通违章6次的有多少天；（2）请把图2中的频数直方图补充完整；（温馨提示：请画在答题卷相对应的图上）（3）通过宣传教育后，行人的交通违章次数明显减少．经对这一路口的再次调查发现，平均每天的行人交通违章次数比第一次调查时减少了4次，求通过宣传教育后，这一路口平均每天还出现多少次行人的交通违章．【答案】（1）8，5；（2）图像见解析；（3）3次． 【解析】 【分析】（1）直接根据折线统计图可读出数据； （2）求出8次的天数，补全图形即可；（3）求出这20天的平均数，然后再算出交通违章次数即可． 【详解】解：（1）第7天，这一路口的行人交通违章次数是8次； 这20天中，行人交通违章6次的有5天； （2）补全的频数直方图如图所示：（3）第一次调查，平均每天行人的交通违章次数为：536574859320⨯+⨯+⨯+⨯+⨯=7（次）∵7-4=3（次）∵通过宣传教育后，这一路口平均每天还出现3次行人的交通违章． 【点睛】本题考查折线统计图，频数分布直方图．34．现今“微信运动”被越来越多的人关注和喜爱，某兴趣小组随机调查了我市名教师某日“微信运动”中的步数情况进行统计整理，绘制了如下的统计图表（不完整）：请根据以上信息，解答下列问题：（1）写出的值并补全频数分布直方图；（2）本市约有名教师，用调查的样本数据估计日行走步数超过步（包含步）的教师有多少名？（3）若在名被调查的教师中，选取日行走步数超过步（包含步的两名教师与大家分享心得，求被选取的两名教师恰好都在步（包含步）以上的概率.【答案】（1）0.16，0.24，10，2；补图见解析；（2）11340；（3）【解析】试题分析：（1）根据频率=频数÷总数可得答案；（2）用样本中超过12000步（包含12000步）的频率之和乘以总人数可得答案；（3）画树状图列出所有等可能结果，根据概率公式求解可得．试题解析：（1）a=8÷50=0.16，b=12÷50=0.24，c=50×0.2=10，d=50×0.04=2，补全频数分布直方图如下：（2）37800×（0.2+0.06+0.04）=11340，答：估计日行走步数超过12000步（包含12000步）的教师有11340名；（3）设16000≤x＜20000的3名教师分别为A、B、C，20000≤x＜24000的2名教师分别为X、Y，画树状图如下：由树状图可知，被选取的两名教师恰好都在20000步（包含20000步）以上的概率为．考点：列表法与树状图法；用样本估计总体；频数（率）分布表；频数（率）分布直方图．35．养成良好的早锻炼习惯，对学生的学习和生活都非常有益，某中学为了了解七年级学生的早锻炼情况，校政教处在七年级随机抽取了部分学生，并对这些学生通常情况下一天的早锻炼时间x（分钟）进行了调查．现把调查结果分成A、B、C、D四组，如下表所示，同时，将调查结果绘制成下面两幅不完整的统计图．请你根据以上提供的信息，解答下列问题：（1）补全频数分布直方图和扇形统计图；（2）所抽取的七年级学生早锻炼时间的中位数落在区间内；（3）已知该校七年级共有1200名学生，请你估计这个年级学生中约有多少人一天早锻炼的时间不少于20分钟．（早锻炼：指学生在早晨7：00～7：40之间的锻炼）【答案】（1）作图见解析；（2）C；（3）1020．【解析】试题分析：（1）先根据A区间人数及其百分比求得总人数，再根据各区间人数之和等于总人数、百分比之和为1求得C区间人数及D区间百分比可得答案；（2）根据中位数的定义求解可得；（3）利用样本估计总体思想求解可得．试题解析：（1）本次调查的总人数为10÷5%=200，则20～30分钟的人数为200×65%=130（人），D项目的百分比为1﹣（5%+10%+65%）=20%，补全图形如下：（2）由于共有200个数据，其中位数是第100、101个数据的平均数，则其中位数位于C区间内，故答案为：C；（3）1200×（65%+20%）=1020（人）．答：估计这个年级学生中约有1020人一天早锻炼的时间不少于20分钟．考点：频数（率）分布直方图；用样本估计总体；扇形统计图；中位数．36．随若移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项：A .和同学亲友聊天；B．学习；C．购物；D．游戏；E.其它）,端午节后某中学在全校范围内随机抽取了若干名学生进行调査,得到如下图表（部分信息未给出）:根据以上信息解答下列问题:（1）这次被调查的学生有多少人？（2）求表中m，n，p的值，并补全条形统计图；（3）若该中学约有名学生，估计全校学生中利用手机购物或玩游戏的共有多少人？并根据以上调査结果，就中学生如何合理使用手机给出你的一条建议.【答案】（1）50人；（2）0.2；10；20.补图见解析；（3）400人.【解析】【分析】【详解】（1）从C可以看出：5÷0.1=50（人）答：这次被调查的学生有50人；=0.2，n=0.2×50=10，p=0.4×50=20（2）m=1050补全图形如图所示：（3）800×（0.1+0.4）=800×0.5=400（人）答：全校学生中利用手机购物或玩游戏的共有400人建议：中学生使用手机要多用于学习.考点：频数、频率、统计图实际应用37．为了解某个某个季度的气温情况，用适当的抽样方法从该地这个季度中抽取30天，对每天的最高气温（单位：）进行调查，并将所得的数据按照，，，，分成五组，得到如图频率分布直方图．（1）求这30天最高气温的平均数和中位数（各组的实际数据用该组的组中值代表）；（2）每月按30天计算，各组的实际数据用该组的组中值代表，估计该地这个季度中最高气温超过（1）中平均数的天数；（3）如果从最高气温不低于的两组内随机选取两天，请你直接写出这两天都在气温最高一组内的概率．【答案】（1）这30天最高气温的平均数为20.4℃；中位数为22℃；（2）该地这个季度中最高气温超过（1）中平均数的天数为48天；（3）这两天都在气温最高一组内的概率为．【解析】试题分析：（1）根据30天的最高气温总和除以总天数，即可得到这30天最高气温的平均数，再根据第15和16个数据的位置，判断中位数；（2）根据30天中，最高气温超过（1）中平均数的天数，即可估计这个季度中最高气温超过（1）中平均数的天数；（3）从6天中任选2天，共有15种等可能的结果，其中两天都在气温最高一组内的情况有6种，据此可得这两天都在气温最高一组内的概率．试题解析：（1）这30天最高气温的平均数为：=20.4℃；℃中位数落在第三组内，℃中位数为22℃；（2）℃30天中，最高气温超过（1）中平均数的天数为16天，℃该地这个季度中最高气温超过（1）中平均数的天数为×90=48（天）；（3）从6天中任选2天，共有15种等可能的结果，其中两天都在气温最高一组内的情况有6种，故这两天都在气温最高一组内的概率为=．考点：1.列表法与树状图法；2.用样本估计总体；3.频数（率）分布直方图；4.加权平均数；5.中位数．38．为了加强学生课外阅读，开阔视野，某校开展了“书香校园，从我做起”的主题活动，学校随机抽取了部分学生，对他们一周的课外阅读时间进行调查，绘制出频数分布表和频数分布直方图的一部分如下：请根据图表信息回答下列问题：（1）频数分布表中的a= ，b= ；（2）将频数分布直方图补充完整；（3）学校将每周课外阅读时间在8小时以上的学生评为“阅读之星”，请你估计该校2000名学生中评为“阅读之星”的有多少人？【答案】（1）25；0.10；（2）补图见解析；（3）200人．【解析】【分析】（1）由阅读时间为0＜t≤2的频数除以频率求出总人数，确定出a与b的值即可；（2）补全条形统计图即可；（3）由阅读时间在8小时以上的百分比乘以2000即可得到结果．【详解】解：（1）根据题意得：2÷0.04=50（人），则a=50﹣（2+3+15+5）=25；b=5÷50=0.10；故答案为25；0.10；（2）阅读时间为6＜t≤8的学生有25人，补全条形统计图，如图所示：（3）根据题意得：2000×0.10=200（人），则该校2000名学生中评为“阅读之星”的有200人．【点睛】此题考查了频率（数）分布表，条形统计图，以及用样本估计总体，弄清题中的数据是解本题的关键．39．随着社会的发展，私家车变得越来越普及，使用节能低油耗汽车，对环保有着非常积极的意义，某市有关部门对本市的某一型号的若干辆汽车，进行了一项油耗抽样实验：即在同一条件下，被抽样的该型号汽车，在油耗1L的情况下，所行驶的路程（单位：km）进行统计分析，结果如图所示：（注：记A为12～12.5，B为12.5～13，C为13～13.5，D为13.5～14，E为14～14.5）请依据统计结果回答以下问题：（1）试求进行该试验的车辆数；（2）请补全频数分布直方图；（3）若该市有这种型号的汽车约900辆（不考虑其他因素），请利用上述统计数据初步预测，该市约有多少辆该型号的汽车，在耗油1L的情况下可以行驶13km以上？【答案】（1）30；（2）作图见解析；（3）660．【解析】试题分析：（1）根据C所占的百分比以及频数，即可得到进行该试验的车辆数；（2）根据B的百分比，计算得到B的频数，进而得到D的频数，据此补全频数分布直方图；（3）根据C，D，E所占的百分比之和乘上该市这种型号的汽车的总数，即可得到结果．试题解析：（1）进行该试验的车辆数为：9÷30%=30（辆）；（2）B：20%×30=6（辆），D：30﹣2﹣6﹣9﹣4=9（辆），补全频数分布直方图如下：（3）900×=660（辆）．答：该市约有660辆该型号的汽车，在耗油1L的情况下可以行驶13km以上．考点：频数（率）分布直方图；用样本估计总体；扇形统计图．40．某体育老师测量了自己任教的甲、乙两班男生的身高，并制作了如下不完整的统计图表．身高分组频数频率152≤x＜155 3 0.06155≤x＜158 7 0.14158≤x＜161 m 0.28161≤x＜164 13 n164≤x＜167 9 0.18167≤x＜170 3 0.06170≤x＜173 1 0.02根据以上统计图表完成下列问题：（1）统计表中m= ，n= ，并将频数分布直方图补充完整；（2）在这次测量中两班男生身高的中位数在：范围内；（3）在身高≥167cm的4人中，甲、乙两班各有2人，现从4人中随机推选2人补充到学校国旗护卫队中，请用列表或画树状图的方法求出这两人都来自相同班级的概率．【答案】(1) 14，0.26．补图见解析；(2) 161≤x＜164．（3）．【解析】试题分析：（1）设总人数为x人，则有=0.06，解得x=50，再根据频率公式求出m，n．画出直方图即可；（2）根据中位数的定义即可判断；（3）画出树状图即可解决问题；试题解析：（1）设总人数为x人，则有=0.06，解得x=50，℃m=50×0.28=14，n==0.26．频数分布直方图：（2）观察表格可知中位数在161≤x＜164内，（3）将甲、乙两班的学生分别记为甲1、甲2、乙1、乙2树状图如图所示：所以P（两学生来自同一所班级）=．考点：列表法与树状图法；频数（率）分布表；频数（率）分布直方图；中位数．。

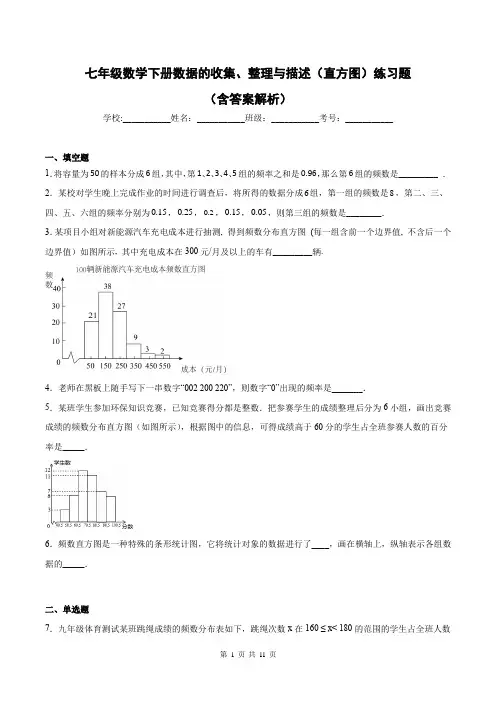
七年级数学下册数据的收集、整理与描述（直方图）练习题（含答案解析）学校:___________姓名：___________班级：___________考号：___________一、填空题1．将容量为50的样本分成6组，其中，第1、2、3、4、5组的频率之和是0.96，那么第6组的频数是_________．2．某校对学生晚上完成作业的时间进行调查后，将所得的数据分成6组，第一组的频数是8，第二、三、四、五、六组的频率分别为0.15，0.25，0.2，0.15，0.05，则第三组的频数是________．3．某项目小组对新能源汽车充电成本进行抽测, 得到频数分布直方图(每一组含前一个边界值, 不含后一个边界值）如图所示, 其中充电成本在300元/月及以上的车有_________辆.4．老师在黑板上随手写下一串数字“002 200 220”，则数字“0”出现的频率是_______．5．某班学生参加环保知识竞赛，已知竞赛得分都是整数．把参赛学生的成绩整理后分为6小组，画出竞赛成绩的频数分布直方图（如图所示），根据图中的信息，可得成绩高于60分的学生占全班参赛人数的百分率是_____．6．频数直方图是一种特殊的条形统计图，它将统计对象的数据进行了____，画在横轴上，纵轴表示各组数据的_____．二、单选题7．九年级体育测试某班跳绳成绩的频数分布表如下，跳绳次数x在160 ≤ x< 180的范围的学生占全班人数的（）A．6%B．12%C．26%D．52%8．一组数据最大值与最小值的差为80，若确定组距为9，则分布的组数为()A．7B．8C．9D．129．某校从初二年级抽出40名女生的身高数据，分组整理出如下频数分布表：表中a，b，c分别是（）A．6，12，0.30B．6，10，0.25C．8，12，0.30 D．6，12，0.2410．为了解学生假期每天帮忙家长做家务活动情况，学校团委随机抽取了部分学生进行线上调查，并将调查结果绘制成频数直方图（不完整，每组含最小值，不含最大值），并且知道80～100分钟占所抽查学生的17.5%，根据提供信息，以下说法不正确的是（）A．本次共随机抽取了40名学生；B．抽取学生中每天做家务时间的中位数落在40～60分钟这一组；C．如果全校有800名学生，那么每天做家务时间超过1小时的大约有300人；D．扇形统计图中0～20分钟这一组的扇形圆心角的度数是30°；11．某面粉厂准备确定面粉包装袋的规格，市场调查员小李随机选择三家超市进行调查，收集三家超市一周的面粉销售情况，并整理数据、做出如图所示的统计图，则该面粉厂应选择面粉包装袋的规格为（）A．2kg/包B．3kg/包C．4kg/包D．5kg/包12．在一个不透明的盒子中装有20个黄、白两种颜色的乒乓球，除颜色外其它都相同，小明进行了多次摸球实验，发现摸到白色乒乓球的频率稳定在0.2左右，由此可知盒子中黄色乒乓球的个数可能是（）A．2个B．4个C．18个D．16个三、解答题13．为了调查本班学生对哪国动画片最喜欢，对班里20名学生进行调查，结果如下所示：(1)请完成表格：(2)根据上表画一张反映频数的条形统计图．14．在信息快速发展的社会，“信息消费”已成为人们生活的重要部分．泰州市的一个社区随机抽取了部分家庭，调查每月用于信息消费的金额，数据整理成如图所示的不完整统计图．已知A、B两组户数直方图的高度比为1：5，请结合图中相关数据回答下列问题．月消费额分组统计表(1)A组的频数是，本次调查样本的容量是；(2)补全直方图（需标明各组频数）；(3)若该社区有3000户住户，请估计月信息消费额不少于200元的户数是多少？15．为了了解学生在2022年3月的学习情况，某校九年级1班组织了一次网上全班数学测试，任科老师从本班中抽取了n个学生的成绩（满分100分，且抽取的学生成绩均在[40，100]内）进行统计分析．按照成绩分数段[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频数分布表和频率分布直方图．(1)求n，x的值，并补充完整频率分布直方图：(2)老师对小明说，估计你在这次的测试中成绩中等，请写出小明这次测试成绩在哪个分数段内的可能性最大？(3)在选取的样本中，从低于60分的学生中随机抽取两名学生，请用列表法或树状图求这两名学生在同一成绩分数段的概率？参考答案：1．2【详解】试题分析：频数分布表中，频率之和等于1．则第6组的频率为：1-0.96=0.04；频数=样本容量×频率=50×0.04=2．点睛：本题主要考查的就是频率、频数与样本容量之间的关系，属于中等难度的题目．所有的频数之和等于样本容量，所有的频率之和等于1．很多题目会已知前面几组的频率，然后根据频率之和得出最后一组的频率，从而根据样本容量=频数÷频率可以求出样本容量．2．10【分析】根据各组的频率之和等于1，再根据第二、三、四、五、六组的频率，即可求出第一小组的频率，根据总人数=第一组的频数÷第一组的频率，最后根据第三组的频数=总人数×第三组的频率进行计算即可．【详解】解：∵第二、三、四、五、六组的频率分别为015．，025．，02．，015．，005．， ∵第一组的频率为10150250201500502-----=．．．．．．，∵第三组的频数为80202510÷⨯=．．．故答案为：10．【点睛】本题考查频率及频数的计算，用到的知识点是频率=频数÷总数，灵活运用有关公式是解决本题的关键．3．14【分析】根据频数直方图中大于300的各组频数进行计算即可.【详解】解：9+3+2=14（辆）故答案为：14【点睛】本题考查了频数分布直方图，根据直方图得出各组频数是解题的关键．4．59【分析】结合题意，根据频率的性质计算，即可得到答案．【详解】根据题意，总共有9个数字，其中数字“0”出现5次∵数字“0”出现的频率是：59故答案为：59． 【点睛】本题考查了频率的知识；解题的关键是熟练掌握频率的定义，从而完成求解．5．80%．【分析】根据频数分布直方图可得全班的总人数及成绩高于60分的学生，从而得出答案．【详解】∵全班的总人数为3+6+12+11+7+6＝45人，其中成绩高于60分的学生有12+11+7+6＝36人，∵成绩高于60分的学生占全班参赛人数的百分率是36100%80%45，故答案为80%． 【点睛】本题主要考查频数分布直方图，根据频数分布直方图明确各分组人数是解题的关键．6． 分组 频数【解析】略7．C【分析】根据频数与频率的计算公式,即可得解.【详解】根据题意，得跳绳次数x 在160 ≤x < 180的范围的学生占全班人数的百分比为13100%26%2326136⨯=++++ 故选：C.【点睛】此题主要考查了读频数分布表获取信息的能力．必须认真观察、分析、研究，才能作出正确的判断和解决问题．8．C【详解】分析：根据组数=（最大值﹣最小值）÷组距计算，注意小数部分要进位．详解：在样本数据中最大值与最小值的差为80，已知组距为9，那么由于809=889，故可以分成9组． 故选C ．点睛：本题考查的是组数的计算，属于基础题，只要根据组数的定义“数据分成的组的个数称为组数”来解即可．9．A【详解】根据题意，由频数分布表中各组的频率求出c,再由频数=总人数×频率可求出a 、b 的值. 解：由频数分布表中，各组的频数之和为样本容量，则c=1-0.05-0.15-0.35-0.15=0.3，根据题意，用150～155之间频率是0.15，而总人数为40人，a=40×0.15=6，b=40×0.3=12.“点睛”本题考查频率分别直方表的运用，以及数据的分析、处理的能力，注意结合题意，认真分析，查找数据时务必准确.10．D【分析】由80～100分钟占所抽查学生的17.5%，且由条形统计图可知有7人，可得抽查总人数，即可判断A 选项；通过总人数减去其他各组人数，得到60～80分钟的人数，根据中位数的定义（一组数据从小到大或从大到小排序后，最中间的数为中位数）即可判断B 选项；由图中数据可得每天超过1小时的人数，然后用学校总人数乘以每天超过1小时的人数占抽查人数的比例即可判断C选项；根据扇形统计图圆心角得计算方法：360︒乘以该组人数所占抽查总人数得比例即可判断D选项．【详解】解：80～100分钟占所抽查学生的17.5%，且由条形统计图可知有7人，∴抽查总人数为：74017.5%=，A选项正确；60～80分钟的人数为：40451678----=人，先对数据排序后可得：最中间的数在第20，21之间，459+=，91625+=，∴中位数落在60～80分钟这一组，故B选项正确；从图中可得，每天超过1小时的人数为：7815+=人，估算全校人数中每天超过1小时的人数为：1580030040⨯=人，故C选项正确；0～20分钟这一组有4人，扇形统计图中这一组的圆心角为：43603640︒⨯=︒，故D选项错误；故选：D．【点睛】题目主要考查通过条形统计图获取信息及估算满足条件的总人数，中位数，扇形统计图圆心角的计算等，理解题意，熟练掌握基础知识点是解题关键．11．A【分析】最合适的包装即顾客购买最多的包装，而顾客购买最多的包装质量即这组数据的众数，取所得范围的组中值即可．【详解】解：由图知这组数据的众数为1.5kg～2.5kg，取其组中值2kg，故选：A．【点睛】本题主要考查频数（率）分布直方图，解题的关键是根据最合适的包装即顾客购买最多的包装，并根据频数分布直方图得出具体的数据及众数的概念．12．D【分析】根据频率=频数÷总数，可以求得白色乒乓球的个数，从而得到黄色乒乓球个数.【详解】解：∵白色乒乓球的频率稳定在0.2左右∵白色乒乓球的个数=20×0.2=4个∵黄色乒乓球的个数=20-4=16个故选D.【点睛】本题主要考查了频率与频数的计算，解题的关键在于能够熟练掌握频率=频数÷总数.13．(1)填表见解析(2)画图见解析【分析】（1）通过调查，再把调查数据填入表格即可；（2）根据表格中的频数，画好条形图即可.(1)解：通过调查，填表如下：(2)解：画条形图如下：【点睛】本题考查的是频数分布表，频数直方图，掌握“频率=频数÷总数的计算方法；条形统计图的画法”是解本题的关键．14．(1)2；50(2)见解析(3)2280户【分析】（1）根据A、B两组户数直方图的高度比为1:5，即两组的频数的比是1:5，据此即可求得A组的频数；利用A和B两组的频数的和除以两组所占的百分比即可求得总数，即样本容量；（2）利用总数乘以百分比即可求得C组的频数，从而补全统计图；（3）利用总数3000乘以对应的百分比即可．（1）A组的频数是：10÷5=2调查样本的容量是：（2+10）÷（1－40%－28%－8%）=50故答案为：2；50．（2）A组的频数是：2C组的频数是：50×40%=20，D组的频数是：50×28%=14，E组的频数是：50×8%=4，补全直方图如图．（3）∵3000×（40%+28%+8%）=2280，答：估计月信息消费额不少于200元的户数是2280户．【点睛】本题考查频数分布直方图、频率分布表，解答本题的关键是明确题意，利用数形结合的思想解答．15．(1)206n x==，(2)[70，80）(3)1 3【分析】（1）用第一组的频数除以它的频率等到n的值，再用n的值分别减去其他组的频数即可得到x值，然后补全直方图即可．（2）根据中位数的意义即可求解．第 11 页 共 11 页 （3）在分数段[40，50）中的学生用A 表示，在分数段[50，60）内的学生用B 表示，画树状图展示所有可能的结果数，找出这两名学生在同一成绩分数段的结果数，然后根据概率公式求解．(1)n ＝1÷0.05＝20，x ＝20﹣1﹣2﹣5﹣4﹣2＝6；[70，80)这组的频率为620＝0.3； 频率分布直方图为：(2)样本的中位数在[70，80）中，所以小明这次测试成绩在[70，80)这个分数段内的可能性最大；(3)低于60分的有3个，在分数段[40，50）中的学生用A 表示，在分数段[50，60）内的学生用B 表示， 画树状图为：共有6种等可能的结果数，其中这两名学生在同一成绩分数段的结果数为2， 所以这两名学生在同一成绩分数段的概率为21=63．【点睛】本题考查了列表法与树状图法及概率公式、掌握统计图并理解，再结合题意是解答本题的关键．。

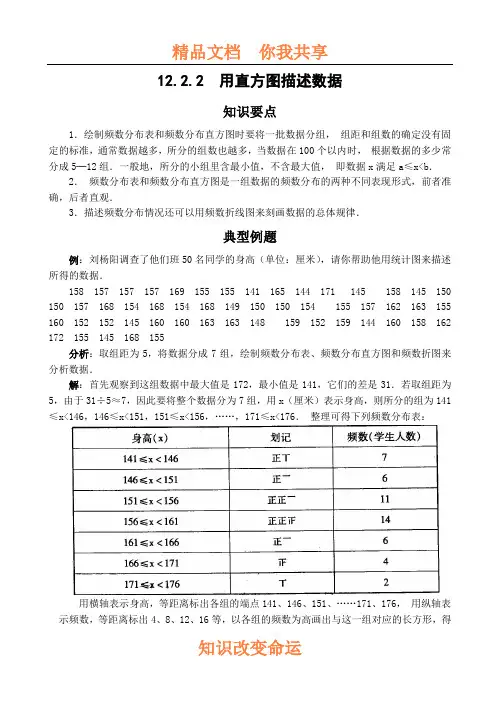
12.2.2 用直方图描述数据知识要点1．绘制频数分布表和频数分布直方图时要将一批数据分组，•组距和组数的确定没有固定的标准，通常数据越多，所分的组数也越多，当数据在100个以内时，•根据数据的多少常分成5─12组．一般地，所分的小组里含最小值，不含最大值，•即数据x满足a≤x<b．2．•频数分布表和频数分布直方图是一组数据的频数分布的两种不同表现形式，前者准确，后者直观．3．描述频数分布情况还可以用频数折线图来刻画数据的总体规律．典型例题例：刘杨阳调查了他们班50名同学的身高（单位：厘米），请你帮助他用统计图来描述所得的数据．158 157 157 157 169 155 155 141 165 144 171 •145 • •158 •145 150 150 157 168 154 168 154 168 149 150 150 154 • •155 •157 162 163 155 160 152 152 145 160 160 163 163 148 • •159 •152 159 144 160 158 162 172 155 145 168 155分析：取组距为5，将数据分成7组，绘制频数分布表、频数分布直方图和频数折图来分析数据．解：首先观察到这组数据中最大值是172，最小值是141，它们的差是31．若取组距为5，由于31÷5≈7，因此要将整个数据分为7组，用x（厘米）表示身高，则所分的组为141≤x<146，146≤x<151，151≤x<156，……，171≤x<176．•整理可得下列频数分布表：用横轴表示身高，等距离标出各组的端点141、146、151、……171、176，•用纵轴表示频数，等距离标出4、8、12、16等，以各组的频数为高画出与这一组对应的长方形，得到下面的频数分布直方图（如图1）取直方图中每一个长方形上边的中点，然后在直方图的左边取点（138.5，0），在直方图的右边取点（178.5，0），将这些点用线段依次连接起来，就得到频数折线图（如图2）（1）（2）同步练习一、选择题：1．考察50名学生的年龄，列频数分布表时，这些学生的年龄落在5个小组中，第一、二、三、五组的数据个数分别是2，8，15，5，则第四组的频率是（）A．20 B．0.4 C．0.6 D.302．有40个数据，其中最大值为35，最小值为15，若取组距为4，则应该分的组数是（） A．4 B．5 C．6 D．7二、填空题3．绘制频数折线图时，通常要求出各个小组两个端点的平均数，•这些平均数称为_________．4．利用频数分布直方图画频数折线图时，若组距为4，•第一个小组的范围是138≤x<142，最后一个小组的范围是154≤x<158．•则折线上最左边的点的坐标是_______，最右边的点的坐标是________．三、解答题5．某班同学参加环保知识竞赛，•将学生成绩（得分都是整数）进行整理后分成5组，绘成频数分布直方图（如图），•图中从左到右各小长方形的高的比为1：3：6：4：2，最后一组的频数为6，结合直方图提供的信息解答下列问题：（1）该班有多少名同学参赛？（2）成绩落在哪组数据范围内的人数最多？是多少？（3）求成绩在60分以上（含60分）的学生占全班参赛学生人数的百分率．（4）请你直接在直方图的基础上绘制频数折线图．60(每组含最低分数但不含最高分数)频数(学生人数)分数/分1009080705006．储蓄所太多必将增加银行支出，太少又难以满足顾客的需求．为此，•银行在某储蓄所抽样调查了50名顾客，他们的等待时间（进入银行到接受受理的时间间隔，单位：分）如下： 22 14 33 17 24 17 12 14 24 11 15 20 18 3 25 24 34 37 42 35 30 23 34 22 13 34 8 22 31 24 25 0 1 21 28 33 32 23 14 4 31 42 34 26 14 25 40 14 42 6（1）将数据适当分组，并绘制相应的频数分布直方图；（2）这50名顾客的平均等待时间是多少？根据这个数据，•你认为应该给银行提什么建议？答案:1．B 2．C 3．组中值 4．（136，0）；（160，0）5．①48人；②大于等于70分而小于80分的范围内的人数最多；③93.75%；④略6．①略（答案不唯一）；②平均等待的时间是22.74分．顾客平均等待的时间过长，应控制在12•分钟左右．为此，银行可以在高峰期增加办事人员，提高工作效率，加强业务训练，优化服务质量，同时可以适当的增加营业网点．。

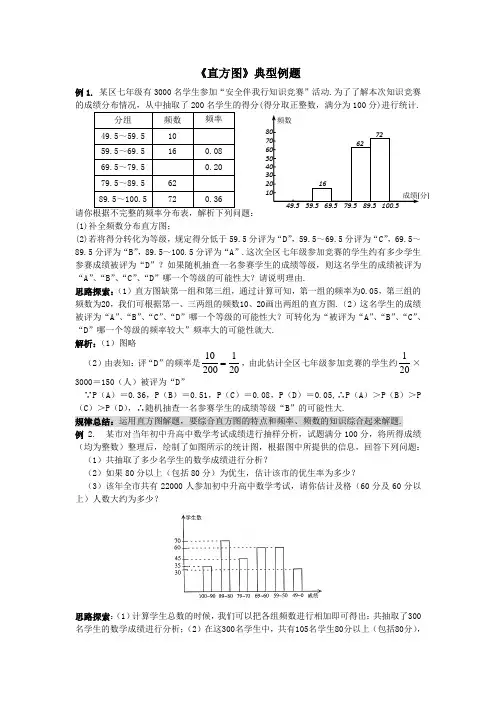
《直方图》典型例题例1. 某区七年级有3000名学生参加“安全伴我行知识竞赛”活动.为了了解本次知识竞赛的成绩分布情况，从中抽取了200名学生的得分(得分取正整数，满分为100分)进行统计.分组 频数 频率 49.5～59.5 10 59.5～69.5 16 0.08 69.5～79.5 0.20 79.5～89.5 62 89.5～100.5720.36请你根据不完整的频率分布表，解析下列问题： (1)补全频数分布直方图；(2)若将得分转化为等级，规定得分低于59.5分评为“D ”，59.5～69.5分评为“C ”，69.5～89.5分评为“B ”，89.5～100.5分评为“A ”.这次全区七年级参加竞赛的学生约有多少学生参赛成绩被评为“D ”？如果随机抽查一名参赛学生的成绩等级，则这名学生的成绩被评为“A ”、“B ”、“C ”、“D ”哪一个等级的可能性大？请说明理由. 思路探索：（1）直方图缺第一组和第三组，通过计算可知，第一组的频率为0.05，第三组的频数为20，我们可根据第一、三两组的频数10、20画出两组的直方图.（2）这名学生的成绩被评为“A ”、“B ”、“C ”、“D ”哪一个等级的可能性大？可转化为“被评为“A ”、“B ”、“C ”、“D ”哪一个等级的频率较大”频率大的可能性就大. 解析：（1）图略 （2）由表知：评“D ”的频率是10120020，由此估计全区七年级参加竞赛的学生约120×3000＝150（人）被评为“D ”∵P （A ）＝0.36，P （B ）＝0.51，P （C ）＝0.08，P （D ）＝0.05,∴P （A ）＞P （B ）＞P （C ）＞P （D ），∴随机抽查一名参赛学生的成绩等级“B ”的可能性大.规律总结：运用直方图解题，要综合直方图的特点和频率、频数的知识综合起来解题. 例 2. 某市对当年初中升高中数学考试成绩进行抽样分析，试题满分100分，将所得成绩（均为整数）整理后，绘制了如图所示的统计图，根据图中所提供的信息，回答下列问题： （1）共抽取了多少名学生的数学成绩进行分析？（2）如果80分以上（包括80分）为优生，估计该市的优生率为多少？（3）该年全市共有22000人参加初中升高中数学考试，请你估计及格（60分及60分以上）人数大约为多少？思路探索：（1）计算学生总数的时候，我们可以把各组频数进行相加即可得出：共抽取了300名学生的数学成绩进行分析；（2）在这300名学生中，共有105名学生80分以上（包括80分），20 10 30 40 50 60 70 80 166272频数成绩()49.5 59.5 69.5 79.5 89.5 100.5在样本里面的优生率为35％，根据样本估计总体可知，该市的优生率为大约是35％；（3）在这300个学生中，60分及60分以上人数为210人，频率为0.7, 22000×0.7＝15400（人），所以全市60分及60分以上人数估计为15400人.规律总结：利用样本估计总体的时候，只要样本的选取具有代表性和广泛性，根据样本的频率就可以估计总体的频率.。

直方图练习题直方图是一种用矩形表示数据分布的图表，它对于统计和分析数据的分布非常有用。

本文将通过一些练习题来帮助读者理解和应用直方图。

练习一：某班级的学生考试成绩如下：60, 75, 85, 95, 80, 70, 90, 85, 80, 75, 65, 70, 80, 90, 85, 75, 80, 90, 95, 80请绘制成绩的直方图。

解答一：首先，我们需要确定直方图的横轴和纵轴。

在这个例子中，横轴表示成绩的区间，纵轴表示对应区间内的学生人数。

接下来，我们需要确定每个区间的范围和宽度。

根据给出的成绩数据，我们可以选择区间为10分，从60到100。

因此，我们可以将成绩分为6个区间：60-69，70-79，80-89，90-99，100。

然后，我们可以计算每个区间内的学生人数。

在这个例子中，每个区间的人数为：2，5，7，4，1。

最后，我们可以按照上述计算结果绘制直方图。

每个区间的宽度可以根据实际需求进行调整，以保证直方图的整洁美观。

练习二：一家购物网站的用户对商品的评级如下：4, 3, 5, 4, 4, 2, 3, 5, 1, 4, 3, 2, 5, 4, 3请绘制评级的直方图。

解答二：同样地，我们需要确定直方图的横轴和纵轴。

在这个例子中，横轴表示评级的等级，纵轴表示对应等级的用户数量。

接下来，我们需要确定每个等级的范围和宽度。

根据给出的评级数据，我们可以选择等级为1到5。

因此，我们可以将评级分为5个等级：1，2，3，4，5。

然后，我们可以计算每个等级对应的用户数量。

在这个例子中，每个等级的用户数量为：1，2，4，5，2。

最后，我们可以按照上述计算结果绘制直方图。

每个等级的宽度可以根据实际需求进行调整，以保证直方图的整洁美观。

练习三：某城市一周七天的降雨量数据如下：10, 5, 12, 8, 15, 2, 0请绘制降雨量的直方图。

解答三：同样地，我们需要确定直方图的横轴和纵轴。

在这个例子中，横轴表示降雨量的区间，纵轴表示对应区间内的天数。

新人教版七年级数学下册《10.2直方图》练习题测试题难题课课练及答案这套新人教版七年级数学下册《10.2直方图》练习题测试题难题课课练及答案免费下载为绿色圃中小学教育网整理，所有试卷与教育部审定XX 新人教版初中教材大纲同步，本站试卷供大伙儿免费利用下载打印。

因为试卷复制时一些内容如图片之类无法显示，需要下载的教师、家长能够到本帖子底手下载WORD 编辑的DOC 附件利用！试卷内容预览：10、3 课题学习，从数据谈节水是“堂堂清”习命题人：蔡家沟中学岳淑芝 审题人：程国荣节水量/m3 1 1.5 2户数 20 120 60一、某小区居民开展节约用水活动，成效显著，对该小区200户家庭用水情形统计分析，3月份比2月份节约用水情形如下表所示。

请回答以下问题：（1）节水量为 的户数最多；（2）3月份平均每户节水 m3。

二、地球上的水资源散布情形如左图所示，淡水资源散布情形如右图所示。

由所给出的统计图可知人类能够利用的淡水资源仅占地球上水资源总量的 %。

3、为了了解某小区居民节约用水情形，随机抽查了该小区10户人家的日用水量，结果如下： 日用水量 10 13 14 17 18 户数 2 2 3 2 1 （1）这10户家庭的平均日用水量 吨。

（2）若是小区有500户家庭，依照上面的计算结果估量该小区居民每一个月共用 吨水。

4、某校数学小组了解到6个牛奶盒通过工艺处置能够制作成一个卷纸，为了解市民节约和环保意识，该课题小组调查了本市100户常常饮用牛奶的家庭对牛奶盒的处置方式，并制成如以下图统计图。

（1）这100户家庭中有多少户扔掉牛奶盒？（2）若是该市有1万户常常饮用牛奶的家庭，请估算扔掉牛奶盒的家庭有多少？（3）假设（2）中这1万户家庭每户一年平均饮用90盒牛奶，请估算一年扔掉的牛奶盒能够制成多少个卷纸？ 100户家庭对牛奶盒处置方式调查统计图 答案： 一、（1）1.5m3 (2)1.6 二、0.6 3、（1）14 （2）7000 4、（1）100×44%=44（户） 答：略 （2）44×100=4400（户） 答：略 （3）4400×90÷6=66000（个） 答：略这套新人教版七年级数学下册《10.2直方图》练习题测试题难题课课练及答案免费下载为绿色圃中小学教育网整理，所有试卷与教育部审定XX新人教版初中教材大纲同步，本站试卷供大伙儿免费利用下载打印。

初二数学频数分布表和频数分布直方图作业练习题（含答案）初二数学频数分布表和频数分布直方图作业练习题一．选择题（共8小题）1．如图是某班43名同学爱心捐款额的频数分布直方图（每组含前一个边界值，不含后一个边界值），则捐款人数最少的一组是( )A ．5~10元B ．10~15元C ．15~20元D ．20~25元2．如图是某组15名学生数学测试成绩统计图，则成绩高于或等于60分的人数是( )A ．4人B ．8人C ．10人D ．12人组号① ② ③ ④ ⑤频数 12 4 16 10则第3组的频数是( )A ．8B ．0.8C ．16D ．0.16 4．九年级体育测试某班跳绳成绩的频数分布表如下：次数100120x跳绳次数x 在160180xA ．6%B ．12%C ．26%D ．52%5．调查50名学生的年龄，列频数分布表时，这些学生的年龄落在5个小组中，第一、二、三、五组数据个数分别是2，8，15，5，则第四组的频数是( )A ．20B ．30C ．0.4D ．0.66．在1000个数据中，用适当的方法抽取50个作为样本进行统计，频数分布表中54.5~57.5这一组的频数是6，那么它的频率为( )A ．0.12B ．0.60C ．6D ．127．某班级的一次数学考试成绩统计图如图，则下列说法错误的是()A．得分在70~80分的人数最多B．该班的总人数为40C．人数最少的得分段的频数为2D．得分及格(60)…的有12人8．某校组织部分学参加安全知识竞赛，并将成绩整理后绘制成直方图，图中从左至右前四组的百分比分别是4%，12%，40%，28%，第五组的频数是8．则：①参加本次竞赛的学生共有100人；②第五组的百分比为16%；③成绩在7080-分的人数最多；④80分以上的学生有14名；其中正确的个数有()A．1个B．2个C．3个D．4个二．填空题（共6小题）9．若某校有学生4000名，从中随机抽取了40名学生，调查他们每天做作业的时间，结果如下表：每大做作业时间t（时)01t<?12t<?23t<?34t<?4t>人数316984则全校学生每天做作业超过3小时的人数约有．10．某校为了解七年级同学的体能情况，随机选取部分学生测试一分钟仰卧起坐的次数，并绘制了如图所示的直方图，学校七年级共有600人，则计该校一分钟仰卧起坐的次数不少于25次的有人．11．已知数据：25，21，23，25，29，27，28，25，27，30，22，26，25，24，26，28，26，25，24，27．若取组距为2，则列频数表时，应将数据分成的组数是．12．整理某个样本，其中最大值是24，最小值是2，取组距为3，则该样本可以分为组．13．为了更好的刻画数据的总体的规律，我们还可以在得到的频数分布直方图上，，得到图．14．频数分布折线图能直观地反映数据的．三．解答题（共2小题）15．某校为了了解初三年级1000名学生的身体健康情况，从该年级随机抽取了若干名学生，将他们按体重（均为整数，单位：)kg 分成五组(:39.5~46A ；:46.5~53.5B ；:53.560.5::60.5~67.5C D ；:67.5~74.5)E ，并依据统计数据绘制了如下两幅尚不完整的统计图．解答下列问题．（1）这次一共抽取了名学生，并补全频数直方图；（2）C 组学生的人数所占的百分比为；（3）在扇形统计图中D 组的圆心角是度；（4）请你估计该校初三年级体重超过60kg 的学生大约有多少名？16．为了解七年级学生的身体素质情况，体育老师对该年级部分学生进行了一分钟跳绳次数的测试，并把测试成绩绘制成如图所示的频数表和频数直方图（每组含前一个边界值，（2）求a ，b 的值，并把频数直方图补充完整．（3）若该年级共有320名学生，估计该年级学生一分钟跳绳次数不少于120次的人数．某校七年级部分学生一分钟跳绳次数测试的频数表组别（次)频数频率 80~1005 0.125 100~1208 0.2 120~140a 0.225 40~160l12 b 160~180 6 0.15。

直方图频数练习题直方图是一种用来表示数据分布特征的图表。

它将数据分成若干个等宽且互不重叠的区间，然后用长方形表示每个区间的频数或频率。

通过观察直方图，我们可以了解数据的分布情况，判断其是否呈现正态分布、偏态分布或其他特殊分布形态。

为了加深对直方图的理解和应用，以下是一些直方图频数练习题，希望能够帮助读者巩固所学知识，并提高解决实际问题的能力。

题目一：某班级有40名学生，他们的期末成绩如下表所示。

请根据这些数据绘制该班级期末成绩的直方图。

92, 74, 78, 88, 65, 90, 82, 92, 84, 73, 76, 79, 81, 84, 76, 70, 80, 82, 89, 95, 87, 88, 82, 84, 86, 95, 91, 78, 80, 79, 68, 92, 87, 89, 78, 90, 86, 76, 81,84解析：首先，将数据按照等宽区间（例如每10分为一个区间）进行划分。

然后，统计每个区间中的频数，即该分数区间中的学生个数。

最后，按照统计结果绘制直方图。

区间：60-69 70-79 80-89 90-99频数： 2 9 18 11绘制直方图示意：** * ** * * * *60-69 70-79 80-89 90-99（横坐标为分数区间，纵坐标为频数）题目二：某地区一周内的日降雨量如下表所示，请根据这些数据绘制该地区一周内日降雨量的直方图。

10, 13, 9, 6, 19, 7, 3解析：与题目一类似，我们先将数据按照等宽区间进行划分，然后统计每个区间的频数。

区间：0-4 5-9 10-14 15-19频数： 1 2 2 1绘制直方图示意：** ** *0-4 5-9 10-14 15-19（横坐标为降雨量区间，纵坐标为频数）通过解题练习，我们熟悉了直方图的绘制过程，并理解了直方图对于数据分布的可视化效果。

直方图不仅可以用于统计学和数据分析，还可以应用于各个领域，如市场调研、人口统计等。

初二数学频数分布表和频数分布直方图作业练习题一．选择题（共8小题）1．如图是某班43名同学爱心捐款额的频数分布直方图（每组含前一个边界值，不含后一个边界值），则捐款人数最少的一组是( )A ．5~10元B ．10~15元C ．15~20元D ．20~25元2．如图是某组15名学生数学测试成绩统计图，则成绩高于或等于60分的人数是( ) A ．4人 B ．8人 C ．10人 D ．12人组号 ① ② ③ ④ ⑤频数1241610则第3组的频数是( )A ．8B ．0.8C ．16D ．0.16 4．九年级体育测试某班跳绳成绩的频数分布表如下：次数100120x < 120140x < 140160x < 160180x < 180200x < 频数2326136跳绳次数x 在160180x <范围的学生占全班学生的( )A ．6%B ．12%C ．26%D ．52%5．调查50名学生的年龄，列频数分布表时，这些学生的年龄落在5个小组中，第一、二、三、五组数据个数分别是2，8，15，5，则第四组的频数是( )A ．20B ．30C ．0.4D ．0.6 6．在1000个数据中，用适当的方法抽取50个作为样本进行统计，频数分布表中54.5~57.5这一组的频数是6，那么它的频率为( ) A ．0.12B ．0.60C ．6D ．127．某班级的一次数学考试成绩统计图如图，则下列说法错误的是()A．得分在70~80分的人数最多B．该班的总人数为40C．人数最少的得分段的频数为2D．得分及格(60)的有12人8．某校组织部分学参加安全知识竞赛，并将成绩整理后绘制成直方图，图中从左至右前四组的百分比分别是4%，12%，40%，28%，第五组的频数是8．则：①参加本次竞赛的学生共有100人；②第五组的百分比为16%；③成绩在7080-分的人数最多；④80分以上的学生有14名；其中正确的个数有()A．1个B．2个C．3个D．4个二．填空题（共6小题）9．若某校有学生4000名，从中随机抽取了40名学生，调查他们每天做作业的时间，结果如下表：每大做作业时间t（时)01t<12t<23t<34t<4t>人数316984则全校学生每天做作业超过3小时的人数约有．10．某校为了解七年级同学的体能情况，随机选取部分学生测试一分钟仰卧起坐的次数，并绘制了如图所示的直方图，学校七年级共有600人，则计该校一分钟仰卧起坐的次数不少于25次的有人．11．已知数据：25，21，23，25，29，27，28，25，27，30，22，26，25，24，26，28，26，25，24，27．若取组距为2，则列频数表时，应将数据分成的组数是．12．整理某个样本，其中最大值是24，最小值是2，取组距为3，则该样本可以分为组．13．为了更好的刻画数据的总体的规律，我们还可以在得到的频数分布直方图上，，得到图．14．频数分布折线图能直观地反映数据的．三．解答题（共2小题）15．某校为了了解初三年级1000名学生的身体健康情况，从该年级随机抽取了若干名学生，将他们按体重（均为整数，单位：)kg 分成五组(:39.5~46A ；:46.5~53.5B ；:53.560.5::60.5~67.5C D ；:67.5~74.5)E ，并依据统计数据绘制了如下两幅尚不完整的统计图．解答下列问题．（1）这次一共抽取了 名学生，并补全频数直方图； （2）C 组学生的人数所占的百分比为 ； （3）在扇形统计图中D 组的圆心角是 度；（4）请你估计该校初三年级体重超过60kg 的学生大约有多少名？16．为了解七年级学生的身体素质情况，体育老师对该年级部分学生进行了一分钟跳绳次数的测试，并把测试成绩绘制成如图所示的频数表和频数直方图（每组含前一个边界值，不含后一个边界值）．（1）参加测试的学生有多少人？（2）求a ，b 的值，并把频数直方图补充完整．（3）若该年级共有320名学生，估计该年级学生一分钟跳绳次数不少于120次的人数． 某校七年级部分学生一分钟跳绳次数测试的频数表组别（次)频数 频率 80~100 5 0.125 100~120 8 0.2 120~140 a 0.225 40~160l 12 b 160~18060.15答案与解析一．选择题（共8小题）1．如图是某班43名同学爱心捐款额的频数分布直方图（每组含前一个边界值，不含后一个边界值），则捐款人数最少的一组是()A．5~10元B．10~15元C．15~20元D．20~25元【分析】根据直方图中的数据可以解答本题，本题得以解决．【解答】解：由直方图可得，捐款人数最少的一组是5~10元，只有5个人，故选：A．2．如图是某组15名学生数学测试成绩统计图，则成绩高于或等于60分的人数是() A．4人B．8人C．10人D．12人【分析】根据条形统计图数据计算即可．【解答】解：根据条形统计图可知成绩高于或等于60分的人数为8412+=（人)，故选：D．3．将50个数据分成五组，编成组号为①⑤的五个组，频数分布如下表：组号①②③④⑤频数1241610则第3组的频数是()A．8B．0.8C．16D．0.16【分析】根据频数的性质：一组数据中，各组的频数和等于总数，可以求出第③组的频数．根据频率、频数的关系：频率=频数÷数据总和，可以求出第③组的频率．【解答】解：根据统计表可知：第③组的频数是：5012416108----=， 故选：A ．4．九年级体育测试某班跳绳成绩的频数分布表如下：次数100120x < 120140x < 140160x < 160180x < 180200x <频数2326136跳绳次数x 在160180x <范围的学生占全班学生的( ) A ．6%B ．12%C ．26%D ．52%【分析】用在160180x <范围内的频数13除以总频数即可，135026%÷=， 【解答】解：1326%2326136=++++，故选：C ．5．调查50名学生的年龄，列频数分布表时，这些学生的年龄落在5个小组中，第一、二、三、五组数据个数分别是2，8，15，5，则第四组的频数是( ) A ．20 B ．30 C ．0.4 D ．0.6 【分析】由五个小组的频数总和等于50即可算出第四组的频数．【解答】解：第一、二、三、五组的数据个数分别是2，8，15，5，∴第四小组的频数是50(28155)20-+++=．故选：A ． 6．在1000个数据中，用适当的方法抽取50个作为样本进行统计，频数分布表中54.5~57.5这一组的频数是6，那么它的频率为( )A ．0.12B ．0.60C ．6D ．12 【分析】根据频率=频数÷样本总数解答即可．【解答】解：用样本估计总体：在频数分布表中，54.5~57.5这一组的频数是6， 那么估计总体数据落在54.5~57.5这一组的频率60.1250=， 故选：A ．7．某班级的一次数学考试成绩统计图如图，则下列说法错误的是( )A ．得分在70~80分的人数最多B ．该班的总人数为40C ．人数最少的得分段的频数为2D．得分及格(60)的有12人【分析】根据条形图各组频数逐一判断可得．【解答】解：A．得分在70~80分的人数最多，此选项正确；B．该班的总人数为412148240++++=（人)，此选项正确；C．人数最少的得分段的频数为2，此选项正确；D．得分及格(60)的有12148236+++=人，此选项错误；故选：D．8．某校组织部分学参加安全知识竞赛，并将成绩整理后绘制成直方图，图中从左至右前四组的百分比分别是4%，12%，40%，28%，第五组的频数是8．则：①参加本次竞赛的学生共有100人；②第五组的百分比为16%；③成绩在7080-分的人数最多；④80分以上的学生有14名；其中正确的个数有()A．1个B．2个C．3个D．4个【分析】根据条形统计图逐项分析即可．【解答】解：①参加本次竞赛的学生共有8(14%12%40%28%)50÷----=（人)，此项错误；②第五组的百分比为14%12%40%28%16%----=，此项正确；③成绩在7080-分的人数最多，此项正确；④80分以上的学生有50(28%16%)22⨯+=（名)，此项错误；故选：B．二．填空题（共6小题）9．若某校有学生4000名，从中随机抽取了40名学生，调查他们每天做作业的时间，结每大做作业时间t（时)01t<12t<23t<34t<4t>人数316984小时的人数约有1200人．【分析】用总人数乘以样本中做作业超过3小时的人数占被调查人数的比例．【解答】解：全校学生每天做作业超过3小时的人数约有844000120040+⨯=（人)， 故答案为：1200人．10．某校为了解七年级同学的体能情况，随机选取部分学生测试一分钟仰卧起坐的次数，并绘制了如图所示的直方图，学校七年级共有600人，则计该校一分钟仰卧起坐的次数不少于25次的有 340 人．【分析】用600乘以第3组和第4组的频率和可估计该校一分钟仰卧起坐的次数不少于25次的人数． 【解答】解：125600340310125+⨯=+++，所以估计该校一分钟仰卧起坐的次数不少于25次的有340人． 故答案为340．11．已知数据：25，21，23，25，29，27，28，25，27，30，22，26，25，24，26，28，26，25，24，27．若取组距为2，则列频数表时，应将数据分成的组数是 5 ． 【分析】求得极差，除以组距即可求得组数． 【解答】解：极差是：30219-=， 92 4.55÷=≈，则分成5组． 故答案是：5．12．整理某个样本，其中最大值是24，最小值是2，取组距为3，则该样本可以分为 8 组．【分析】求出最大值和最小值的差，然后除以组距，用进一法取整数值就是组数． 【解答】解：最大值与最小值的差是：24222-=， 则可以分成的组数是：2238÷≈（组)，故答案为：8．13．为了更好的刻画数据的总体的规律，我们还可以在得到的频数分布直方图上 取点 ， ，得到 图．【分析】根据画频数分布折线图的方法即可求解．【解答】解：为了更好的刻画数据的总体的规律，我们还可以在得到的频数分布直方图上取点，连线，得到频数分布折线图． 故答案为取点，连线，频数分布折线图．14．频数分布折线图能直观地反映数据的 频数分布的波动情况 ．【分析】利用折线图要与横轴相交，方法是在直方图的左右两边各延伸一个假想组，并将频数折线两端连接到假想组中点，它主要显示数据的变化趋势．【解答】解：频数分布折线图能直观地反映数据的频数分布的波动情况． 故答案为：频数分布的波动情况．三．解答题（共2小题）15．某校为了了解初三年级1000名学生的身体健康情况，从该年级随机抽取了若干名学生，将他们按体重（均为整数，单位：)kg 分成五组(:39.5~46A ；:46.5~53.5B ；:53.560.5::60.5~67.5C D -；:67.5~74.5)E ，并依据统计数据绘制了如下两幅尚不完整的统计图．解答下列问题．（1）这次一共抽取了 50 名学生，并补全频数直方图； （2）C 组学生的人数所占的百分比为 ； （3）在扇形统计图中D 组的圆心角是 度；（4）请你估计该校初三年级体重超过60kg 的学生大约有多少名？【分析】（1）从两个统计图可得，“A 组”的有4人，占调查人数的8%，可求出调查人数；进而求出“B 组”人数，补全频数分布直方图； （2）“C 组”的人数16人，占调查人数50人的百分比： （3）“D 组”人数占调查人数1050，因此圆心角占360的1050，可求出度数； （4）体重超过60kg 的人数占调查人数10850+，因此估计总体1000人的10850+是体重超过60kg ，可求出人数．【解答】解：（1）48%50÷=人，5041610812----=人，故答案为：50，补全频数直方图如图所示： （2）165032%÷=， 故答案为：32%； （3）103607250︒⨯=︒， 故答案为：72， （4）108100036050+⨯=名， 答：初三年级1000名学生中体重超过60kg 的有360人．16．为了解七年级学生的身体素质情况，体育老师对该年级部分学生进行了一分钟跳绳次数的测试，并把测试成绩绘制成如图所示的频数表和频数直方图（每组含前一个边界值，不含后一个边界值）．某校七年级部分学生一分钟跳绳次数测试的频数表频数频率组别（次)80~10050.125100~12080.2120~140a0.225140~16012b160~18060.15（1）参加测试的学生有多少人？（2）求a，b的值，并把频数直方图补充完整．（3）若该年级共有320名学生，估计该年级学生一分钟跳绳次数不少于120次的人数．【分析】（1）根据第二组的频数是8，频率为0.2，可求出参加测试的学生人数，（2）知道总数，依据频率可求出频数，已知频数可求出频率，（3）样本估计总体，样本中一分钟跳绳次数不少于120次所占的百分比为(0.2250.30.15)++，进而求出人数．【解答】解：（1）80.240÷=人，答：参加测试的学生有40人．（2）400.2259b=÷=，a=⨯=人，12400.3答：a、b的值分别为9，0.3，补全频数分布直方图如图所示：（3）320(0.2250.30.15)216⨯++=人，答：该年级320名学生中一分钟跳绳次数不少于120次的人数大约有216人．。

数据的描述-初中二年级数学试题练习、期中期末试卷、测验题、复习资料-初中数学试卷-试卷下载金禧中学2005－2006年度八年级数学第十二章《数据的描述》单元测试班级姓名座号评分一、选择题（每小题3分，共21分）1、为下列问题选择适当的统计图描述数据：⑴某小学为了清楚地表示学校男、女生各占全校学生人数的百分比，应绘制（）⑴反映某种股票的涨跌情况，应选择（）A、条形统计图B、折线统计图C、扇形统计图D、直方图2、在频数分布直方图中，小长方形的高（）A、与频数成正比B、是该组的频率C、是该组对应的频数D、是该组的组距3、某旅游团的所有30名游客按年龄分成3组，其中年龄在20～40岁组内有9名，那么这个小组的频率是（）A、3.3B、0.3C、0.9D、0.454、近年来国内生产总值年增长率的变化情况如下图所示，下列结论中不正确的是（）A、1995年－1999年，国内生产总值的年增长率逐年减小生产总值年增长率B、2000年国内生产总值的年增长率开始回升C、这7年中，每年的国内生产总值不断增长D、这7年中，每年的国内生产总值有增有减5、如图所示的世界人口扇形统计图中，关于中国部分的圆心角的度数为（）A、68°年份B、70°C、72°D、76°6、某一个容量为n的样本最大值是157，最小值是60，取组距为12，则可以分成（）A、10组B、9组C、8组D、7组二、填空题（每空2分，共60分）7、如右图是某学校图书馆各类藏书的统计图，其中期刊840册，根据图形回答下列问题：⑴该校图书馆目前藏书总数为册；⑴馆藏书中，最多的是类书；⑴类书，类书总数接近相等，占全部藏书的一半。

8、扇形统计图中，各扇形内标出的百分比等于此扇形的与的比。

9、已知数据35，31，33，35，37，39，35，38，40，39，36，34，35，37，36，32，34，35，36，34在列频数分布表时，如果取组距为2，那么应分成组。

第十章数据的收集、整理与描述10.2直方图1.为了绘制一批数据的频率分布直方图，首先要算岀这批数据的变化范用，数据的变化范国是指数据的A.最大值B.最小值C.最大值与最小值的差D.个数2.小杰调查了本班同学体重情况，画岀了频数分布直方图，那么下列结论不正确的是A.全班总人数为45人B.体重在50千克〜55千克的人数最多C.学生体重的众数是14D.体重在60千克〜65千克的人数占全班总人数的+3.如图是某班全体学生外岀时乘车.步行、骑车的人数分布直方图和扇形统计图（两图都不完整）.则下列结论中错误的是A.该班总人数为50C.步行人数为30D.乘车人数是骑车人数的2.5倍4.已知样本容量是40,在样本的频数分布直方图中各小矩形的髙之比依次为3:2:4:1,则第二小组的频数为_______ ，第四小组的频率为________5.某初一年级有500名同学，将他们的身高（单位：cm）数据绘制成频率分布直方图（如图），若要从身髙在［120,130），［130,140），［140,150］三组内的学生中，用分层抽样的方法选取30人参加一项活动,则从身髙在［130J40）内的学生中选取的人数为.6.李老师为了了解本班学生作息时间，调查班上50名学生上学路上所花的时间，他发现学生所花时间都少于50min,然后将调查数据整理，作出如下图所示的频数直方图的一部分.翩洋生人数）24…~ 13 •■■■ ————8——20 10 20 30 ^40 50 时间份钟）（1）补全频数直方图；（2）该班学生在路上花费的时间在哪个范羽内最多？（3）该班学生上学路上花费时间在30min以上（含30min）的人数占全班人数的百分比是多少?7・为创建“国家园林城市二某校举行了页'爱我黄石'‘为主题的图片制作比赛，评委会对200名同学的参赛作品打分发现，参赛者的成绩x均满足50SX100,并制作了频数分布直方图，如图.根据以上信息，解答下列问题：（1）请补全频数分布直方图；（2）若依据成绩.采取分层抽样的方法，从参赛同学中抽40人参加图片制作比赛总结大会，则从成绩80Sv<90的选手中应抽多少人？（3）比赛共设一.二.三等奖，若只有25%的参赛同学能拿到一等奖，则一等奖的分数线是多少？8・体冇老师对九年级（1）班学生"你最喜欢的体冇项目是什么（只写一项）？"的问题进行了调查，把所得 数据绘制成频数分布直方图（如图）.由图可知，最喜欢篮球的学生的人数是九年级（1）班学生最喜吹体育项目的频数分布直方图■频数（人）9.对赵中.安中最近的联考二的数学测试成绩（得分为整数）进行统计，将所有成绩由低到高分成五组,并绘制成如图所示的频数分布直方图，根据直方图提供的信息，在这次测试中，成绩为A 等（80分以上, 不含80分）的百分率为18H--15 12A. 24%C. 42% 10.某市内有一条主干路段，为了使行车安全同时也能增加车流呈，规左通过该路段的汽车时速不得低于40km/h,也不得超过70km/h,否则视为违规扣分.某天有1000辆汽车经过了该路段，经过雷达测速得 到这些汽车行驶时速的频率分布直方图如图所示，则违规扣分的汽车大约为 __________ 辆.A ・82U12o4B. 12 C ・16体育项目D ・20B. 40% D. 50%羽毛球乒乓球跳绳篮球 其它2420161284 09 6 3 0 50.5 60.5 70.5 80.5 90.5 100.530 40 50 <60 70 800 0320 012 OOH 0 005一|冊（ fan/h>11・江涛同学统计了他家10月份的长途电话明细淸单，按通话时间画出频数分布直方图.（1） ___________________________ 他家这个月一共打了次长途电话：（2） ______________________________ 通话时间不足10分钟的次：（3） __________________ 通话时间在_______________________ 分钟范围最多，通话时间在分钟范围最少.12.某校为了了解某个年级的学习情况，在这个年级抽取了50名学生.对某学科进行测试，将所得成绩（成绩均为整数）整理后，列出表格:分组50〜59分60~69 分70〜79分80〜89分90〜99分频率0.040.040」60340.42 <1）本次测试90分以上的人数有 ________ A：（包括90分）（2）________________________________________ 本次测试这50名学生成绩的及格率是: （60分以上为及格，包括60分）（3）这个年级此学科的学习情况如何？请在下列三个选项中，选一个填在题后的横线上A.好B. 一般C.不好13.（2018 •江西）某班组织了针对全班同学关于“你最喜欢的一项体冇活动”的问卷调查后，绘制出频数分布直方图，由图可知，下列结论正确的是（每组中只含最小分钟值，但不含杲大分钟值）A.最喜欢篮球的人数最多B.最喜欢羽毛球的人数是最喜欢乒乓球人数的两倍C.全班共有50名学生D.最喜欢田径的人数占总人数的10%14.（2018 •上海）某校学生自主建立了一个学习用品义卖平台，已知九年级200划学生义卖所得金额的频数分布直方图如图所示，那么20-30元这个小组的组频率是___________ .15.（2018 •贵阳）某班50名学生在2018年适应性考试中，数学成绩在100-110分这个分数段的频率为0.2,则该班在这个分数段的学生为____________ 人.16.（2018 •锦州）为了解同学们每月零花钱数额，校园小记者随机调查了本校部分学生，并根据调査结果绘制出如下不完整的统讣图表：学生每月零花钱频数直方图人数（频数）161412108642□60 120 150请根据以上图表，解答下列问题：（1）_____________________________ 这次被调查的人数共有人，＜/= •（2）计算并补全频数分布直方图：（3）请估计该校1500名学生中每月零花钱数额低于90元的人数.17.（2018 •贺州）某中学为了了解学生每周在校体冇锻炼时间，在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表，请根据图表信息解答下列问题：（1 ）表中的, b= ______________________ :（2）请将频数分布直方图补全；（3）若该校共有1200名学生，试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名？尺婷题参考笞帛1.【答案】C【解析】根据频率直方图的是将数据将参量的数值范国等分为若干区间，统讣该参呈在各个区间上出现的频率，并用矩形条的长度表示频率的大小.即按照数据的大小按序排列，故选C.2.【答案】C【解析】由频数直方图可以看出：全班总人数为8+10+14+8+5=45 （人），A正确：体重在50千克到55千克的人数最多，为14人：故众数在50千克到55千克之间.B正确，但C错误: 厲体重在60千克到65千克的人数为5人，则山全班总人数的5-45=1；D正确.9故选C.3.【答案】C【解析】由条形图中可知乘车的人有25人，骑车的人有10人，在扇形图中分析可知，乘车的占总数的50%,所以总数有25-50%=50 （人），所以骑车人数占总人数的20%：步行人数为0.3x50=15 （人）：乘车人数是骑车人数的2.5倍.故选C.4.【答案】8, 10%【解析】频数分布宜方图中，备个长方形的高之比依次为3： 2： 4： 1,则各组频数之比为3： 2：4：1, 据此即可求出第二小组的频数为40x_?_=8,第四小组的频率为_1_=0.1.故答案为：8： 0.1.3+2+4+1 3+2+4+15.【答案】10【解析】由已知中的频率分布直方图，根据各组矩形髙之和x组距=1,结合已知中频率分布直方图的组距为10,我们易求出身高在［120, 130）, ［130, 140）,（140, 150］的矩形高为0.1-（0.005+0.035+0.020+0.010）=0.030 , 0.020 , 0.010,故身高在［120, 130）, （130, 140） , ［140, 150］的频率为0.30, 0.20, 0.10；故分层抽样的方法选取30人参加一项活动，则从身髙在［130, 140）内的学生中选取的人数应为30x222 =10.故答案为：10.0.30+0.20+0.106.【解析】（1）花费时间在300<40范用内的频数为50-8-24-13-2=3,在宜方图上表示:| 0 10 20 30 40 50时间（井钟片（2）观察直方图可得：花费时间在10</<20范用内的人数最多：3+2（3）■路上花费时间在30min以上（含30min）的人数占全班人数的百分比是：—xl00% = 10%.40 x（3）依题意知获一等奖的人数为200x25%=50 （人）.则一等奖的分数线是80分.8.【答案】D【解析】由图可知，最喜欢篮球的学生的人数是20人，故选D.9.【答案】C【解析】总人数是：5+9+15+14+7=50,则成绩为A等（80分以上，不含80分）的百分率是：14+7------ xl00%=42%.故选C.5010.【答案】160【解析】如图，低于40km/力的频率为0.05,超过70km/〃的车辆的频率为0.11,有1000辆汽车经过了该路段，故违规扣分的车辆大约为1000X （0.05+0.11） =160 （辆），故答案为：160.11.【解析】（1）他家这月的长途电话次数约25+18+8+10+16=77次；（2）通话时间不足10分钟的次数为：25+18=43次;（3）通话时间在0~5分钟范最多，通话时间在10~15分钟范|1；1最少.12.【解析】（1）由题意可知：测试90分以上（包括90分）的人数为50x0.42=21人：（2）本食测试这50名「；叨:.成绩的及格率是03+°・16+0.34+0.42 =96%；1（3）由频数分布表可以看出该年级此学科的及格率比较髙，优秀人数比较多，成绩较好.故选A.13.【答案】C【解析】A、最喜欢足球的人数最多，此选项错误；B、最喜欢羽毛球的人数是最喜欢田径人数的两倍，此选项错误；C、全班学生总人数为12+20+8+4+6=50，此选项正确：4D、最H-XXIII径的人数占总人数X100%=8%,此选项祸故选C.14.【答案】0.25【解析】20・30元这个小组的组频率是50宁200=0.25,故答案为：0.25・15.【答案】10【解析】•・•频数=总数X频率，.••可得此分数段的人数为：50X0.2=10.故答案为：10.16.【解析】（1）这次被调查的人数共有64-0.15=40,则40=0.05；故答案为：40； 0.05；（2）补全频数直方图如下:40・16-12-6-2=4,学生每月零花钱频数直方图人数〈频数）817・【解析】（1）总人数=4^0.1=40, Zu/=4OXO.15=6. /?=—=0.2；40故答案为6, 0.2.（2）频数分布直方图如图所示：（3）由题意得，估计全校每周在校参加体冇锻炼时间至少有4小时的学生约为1200X （0.15+0.2+0.3）=780 （名）・。