巧移火柴棒1

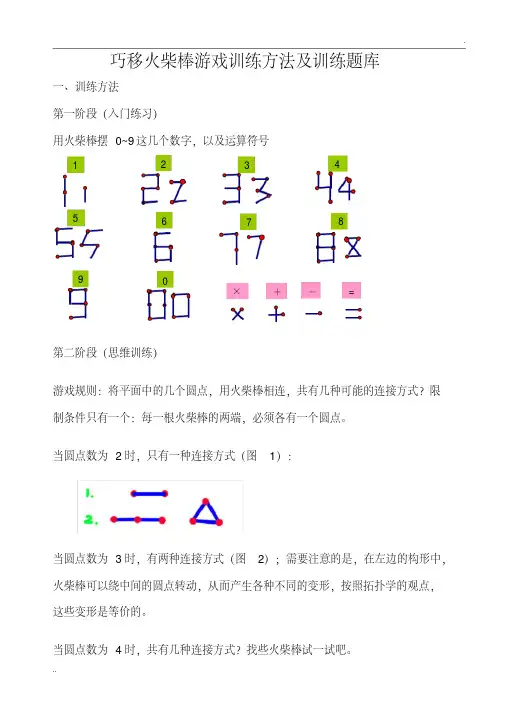
☆巧移火柴棒四年级第8讲第8讲巧移火柴棒一、种植园,1(根据数的特点，拿走或添上火柴棒，使它变成另一个数。

2(在给出的火柴棒组成的图形中，通过火柴棒的移动得到新的图形。

二、播种园,种子1:小马用火柴棒搭了算式，小唐见了忙叫到:“这个等式不成立呀～”小马不紧不慢地说:“这就是我要考大家的题目呀，只移动其中一根火柴棒，让这个算式成立～” 你会移动吗,分析:在这个算式中～左边的计算结果是20～比右边的结果多了20～我们可以让左边的两个加数的和减少10～让减数增加10～这样一共减少了20 ～算式就相等了。

解法一:可以这样移动:解法二:也可以这样想:从左边拿出多的一个10～放到右边:种子2:右面方格里的数字都是用火柴棒组成的。

请你移动其中的1根火柴，使每一横行和竖行里的数相加的和都相等。

分析:3个横行的数之和分别是10、16、10～3个竖行的数之和分别是8、18、10～相等的和是10～那么肯定要将第2行的前两个数进行调整。

,见右图,解:说明:用火柴棒拼成算式～要根据火柴棒组成的数的特点和算式的特点来做。

我们可以根据算式中给出的数的特点～从火柴棒排成的数拿走或添上火柴棒～变成另一个数～或改变一个运算符号～就可以使算式成立。

种子3:用火柴棒可以组成一些算式，也可以用火柴棒摆成各种图形。

如果拿掉或是移动火柴，还可以变成其他图形。

请你只移动3根火柴把3个三角19第8讲四年级形变成5个三角形。

分析:3个三角形用了9根火柴～要变成5个三角形～需要用到15根火柴～这样少了6根火柴。

因此～变成的三角形中一定要使6根火柴重复使用。

可以这样移动:解:三、成长园,1(移动两根火柴棒，使右面等式成立。

2(用4根火柴棒可以分别表示一些加减法运算符号，然后把这4根火柴棒放到数字1至9中间去，使最终的运算结果等于100。

1 2 3 4 5 6 7 8 9 = 100 3(右图是由4个小正方形组成的正方形。

现在要移动3根火柴，使它变成3个相等的正方形，应该怎样移动, 四、收获园,1(下面有火柴棒摆成的算式都错了，请你移动一根火柴棒，使等式成立。

三年级数学火柴游戏例题与方法例1 下面是一些错误的等式,你能只移动两根火柴就能使等式成立吗？【思路点睛】(1)变“4"为“2",变“7”为“1”,变“1”为“11”得（2）变“＋”为“－”，变“7”为“2”，变“4”为“2"得（3）变“＋”为“×”得(4）移“－"到“4”前作“1”，移“1”到等号的右边得【数学思考】火柴游戏要遵循以下规律：1．“拿来”：就是拿掉一根火柴，使得等式中的数减少或增大，或使算式中的运算符号有所改变。

如：变“4"为“＋”，变“7"为“1”，变“＋"为“－”，变“＝”为“－"，变“2”为“7”，去“－”，去“1”等；2．“添上":就是在算式中的数字或运算符号上添加1根火柴，使得算式发生变化；这与“拿去"正好相反。

如，变“1”为“7”等，还可以在数之伺加“一”，在数前，数后加“1"等；3．“移动”：就是把“拿去”与“添上”两个动作结合起来,使得算式中的火柴总数不增不减。

如,变“2”为“4”,变“＋”为“7”,变“1”为“一”，变“7'为“×"等。

例2 用10根火柴摆成头朝上的龙虾(如图2－1）,试移动3根火柴，使它变成头朝下的龙虾图2-1【思路点睛】为了方便起见,我们把火柴编号,如下图2－2所示。

要把龙虾的头变成朝下的，需要把下面的“头”拆掉，并摆出“尾”，还要在下面“摆”出“头”，这样一来，马上就可以找到移动办法(如图2-3所示)：图2—2 图2-33移动8的右边，1移动2的右边，9移动10的右边。

【数学思考】这道题很有启发性，在摆弄中渗透了几何知识，当然还有其他移法，如不向右移，而是向左移。

例3 如图15—4所示,用12根火柴摆成六边形，分别拿走3根，4根、5根，使它成为3个相同的三角形，应该怎样做?图3—4 图3—5【思路点睛】(1）如果拿走3根，那么12根火柴还剩9根，用9根火柴摆成3个相同的三角形,9÷3=3，必须是3根火柴摆1个三角形,也就是说，它们是没有公共边的。

移动一根火柴题解题技巧
1. 哎呀呀，一定要仔细观察呀！就像这道题“1+7=6”，你看看是不
是发现什么啦？咱就盯着这些火柴棍，好好想想移动哪根能改变等式呢！2. 要大胆去尝试呀！比如说“3-2=7”，难道就没办法了吗？别急别急，大胆地去挪动一根火柴，说不定就有惊喜出现呢！
3. 注意那些关键的数字呀！像“5+3=9”，是不是觉得有个数字很关键呀？对啦，就是 9 嘛，从它入手，也许就能找到解题的办法啦！
4. 学会换个角度思考嘛！看看“2+6=8”，咦，要是从不同的方向去看这
些火柴，会不会有新的思路呢，嘿嘿！
5. 别着急下结论呀！就如同“4=1+3”，也许第一眼觉得没什么可动的，
但是再仔细琢磨琢磨，说不定就有突破呢，对吧！
6. 多想想各种可能呀！类似“7-3=2”，不要轻易就放弃了，多想想有哪些火柴可以移动，会有不同的答案等你发现呢！
我的观点结论就是：掌握这些解题技巧，移动一根火柴题就会变得超级有趣又简单啦，大家快来试试呀！。

三年级数学火柴游戏例题与方法 例1下面是一些错误的等式，你能只移动两根火柴就能使等式成立⑵74+N 二耳N -Z + l -Z吗？ T - V【思路点睛】(1)变“4为“2；变“7为“ 1；变“ 1为“ 1T⑵变丄”为-；,变“ 7为“ 2；变“ 4为“ 2 ； 得 W 二二二Zxi-Z(4)移•”到“4前作“ 1,”移“1到等号的右边得 【数学思考】火柴游戏要遵循以下规律:1 .拿来”就是拿掉一根火柴，使得等式中的数减少或增大，或使算式中的运算符号有所改变。

女口：变“4为丄”变“7为“ 1；变丄为-；,变二”为-；,变“2为“7；去-；,去“ 1等；2.添上”就是在算式中的数字或运算符号上添加 1根火柴，使得1件二1件式发生变化；这与拿去”正好相反。

如，变“ 1为“7等，还可以在数之伺加一”在数前，数后加“ 1等;3.移动”就是把拿去”与添上”两个动作结合起来，使得算式中的火柴总数不增不减。

女口，变“2为“4；变丄”为“7；变“ 1为一” 变“7为“X等。

例2用10根火柴摆成头朝上的龙虾（如图2 - 1），试移动3根火柴,使它变成头朝下的龙虾/\・777 八图2-1【思路点睛】为了方便起见，我们把火柴编号，如下图 2 - 2所示。

要把龙虾的头变成朝下的，需要把下面的头”拆掉，并摆出尾”还要在下面摆”出头”这样一来，马上就可以找到移动办法（如图2-3八\/WV 八八八萨弋\/所示）：图2-2 图2-33移动8的右边，1移动2的右边，9移动10的右边【数学思考】 这道题很有启发性，在摆弄中渗透了几何知识，当然 还有其他移法，如不向右移，而是向左移。

例3如图15 — 4所示，用12根火柴摆成六边形，分别拿走3根, 4根、5根，使它成为3个相同的三角形，应该怎样图3-4 【思路点睛】(1)如果拿走3根，那么12根火柴还剩9根，用9 根火柴摆成3个相同的三角形，9+3=3 ,必须是3根火柴摆1个三 角形，也就是说，它们是没有公共边的。

三年级数学火柴游戏例题与方法例1 下面是一些错误的等式，你能只移动两根火柴就能使等式成立吗.【思路点睛】(1)变“4〞为“2〞，变“7〞为“1〞，变“1〞为“11〞得(2)变“＋〞为“－〞，变“7〞为“2〞，变“4〞为“2〞得(3)变“＋〞为“×〞得(4)移“－〞到“4〞前作“1〞，移“1〞到等号的右边得【数学思考】火柴游戏要遵循以下规律：1．“拿来〞：就是拿掉一根火柴，使得等式中的数减少或增大，或使算式中的运算符号有所改变。

如：变“4〞为“＋〞，变“7〞为“1〞，变“＋〞为“－〞，变“＝〞为“－〞，变“2〞为“7〞，去“－〞，去“1〞等；2．“添上〞：就是在算式中的数字或运算符号上添加1根火柴，使得算式发生变化；这与“拿去〞正好相反。

如，变“1〞为“7〞等，还可以在数之伺加“一〞，在数前，数后加“1〞等；3．“移动〞：就是把“拿去〞与“添上〞两个动作结合起来，使得算式中的火柴总数不增不减。

如，变“2〞为“4〞，变“＋〞为“7〞，变“1〞为“一〞，变“7’为“×〞等。

例2 用10根火柴摆成头朝上的龙虾(如图2－1)，试移动3根火柴，使它变成头朝下的龙虾图2-1【思路点睛】为了方便起见，我们把火柴编号，如以下图2－2所示。

要把龙虾的头变成朝下的，需要把下面的“头〞拆掉，并摆出“尾〞，还要在下面“摆〞出“头〞，这样一来，马上就可以找到移动方法(如图2-3所示)：图2-2 图2-33移动8的右边，1移动2的右边，9移动10的右边。

【数学思考】这道题很有启发性，在摆弄中渗透了几何知识，当然还有其他移法，如不向右移，而是向左移。

例3 如图15—4所示，用12根火柴摆成六边形，分别拿走3根，4根、5根，使它成为3个一样的三角形，应该怎样做?图3-4 图3-5【思路点睛】(1) 如果拿走3根，则12根火柴还剩9根，用9根火柴摆成3个一样的三角形，9÷3=3，必须是3根火柴摆1个三角形，也就是说，它们是没有公共边的。

三年级数学火柴游戏之迟辟智美创作例题与方法例1 下面是一些毛病的等式，你能只移动两根火柴就能使等式成立吗？【思路点睛】 (1)变“4”为“2”，变“7”为“1”，变“1”为“11”得(2)变“＋”为“－”，变“7”为“2”，变“4”为“2”得(3)变“＋”为“×”得(4)移“－”到“4”前作“1”，移“1”到等号的右边得【数学思考】火柴游戏要遵循以下规律：1．“拿来”：就是拿失落一根火柴，使得等式中的数减少或增年夜，或使算式中的运算符号有所改变.如：变“4”为“＋”，变“7”为“1”，变“＋”为“－”，变“＝”为“－”，变“2”为“7”，去“－”，去“1”等；2．“添上”：就是在算式中的数字或运算符号上添加1根火柴，使得算式发生变动；这与“拿去”正好相反.如，变“1”为“7”等，还可以在数之伺加“一”，在数前，数后加“1”等；3．“移动”：就是把“拿去”与“添上”两个举措结合起来，使得算式中的火柴总数不增不减.如，变“2”为“4”，变“＋”为“7”，变“1”为“一”，变“7’为“×”等.例2 用10根火柴摆成头朝上的龙虾(如图2－1)，试移动3根火柴，使它酿成头朝下的龙虾图2-1【思路点睛】为了方便起见，我们把火柴编号，如下图2－2所示.要把龙虾的头酿成朝下的，需要把下面的“头”拆失落，并摆出“尾”，还要在下面“摆”出“头”，这样一来，马上就可以找到移动法子(如图2-3所示)：图2-2 图2-33移动8的右边，1移动2的右边，9移动10的右边.【数学思考】这道题很有启发性，在玩弄中渗透了几何知识，固然还有其他移法，如不向右移，而是向左移.例3 如图15—4所示，用12根火柴摆成六边形，分别拿走3根，4根、5根，使它成为3个相同的三角形，应该怎样做?图3-4 图3-5【思路点睛】 (1) 如果拿走3根，那么12根火柴还剩9根，用9根火柴摆成3个相同的三角形，9÷3=3，必需是3根火柴摆1个三角形，也就是说，它们是没有公共边的.如图3－5所示.(2) 如果拿走4根，那么12根火柴还剩8根，用8根火柴摆成3个相同的三角形，8÷3=2……2，肯定有1根火柴要充任2个三角形的公共边，也就是说，摆出的3个相同三角形肯定在2个三角形连在一起.如图15－6所示.图2-6 图2-7(3) 同理拿走5根，还剩7根火柴，7÷3＝2……1，肯定有两根火柴要充任三角形的公共边，也就是说摆出的3个相同三角形肯定全都连在一起.如图2－7所示.例4 用16根火柴可以摆成四个年夜小相同的正方形(图2－8).试问如果用15根、14根、13根、12根火柴是否也可以分别成四个年夜小相同的正方形？【思路点睛】我们在图2－8的基础上思考.图2-8(1) 如果要减少一根火柴，用15根火柴摆成四个年夜小相同的正方形，那么只需让图2—8中的一个正方形与另一个正方形共同使用一根火柴就可以了.于是获得图2－9的①或②或③图2-9(2) 如果用14根火柴摆成四个年夜小相同的正方形；只需让图2－8中的两个正方形，具有2根共同使用的火柴就可以了，于是获得图2－10的①或②.图2-10(3) 如果用13根火柴摆成四个年夜小相同的正方形，只需让图2—8中的三个正方形具有3根共同使用的火柴就可以了，于是获得图2－11的①或②或③.图2-11(4) 如果用12根火柴摆成四个年夜小相同的正方形，只需让图2－8中的四个小正方形，具有4根共同使用的火柴就可以了.于是获得图2-12图2-12总结与提示用火柴可以摆成一些数字和运算符号，还可以摆成几何图形，通过移动火柴，可以进行算式的变动以及几何图形的变动，发生出许大都学游戏.这是年夜家喜欢的一项益智活动.英国著名数学家哈代曾专门研究过火柴游戏，我国著名数学家陈景润也喜欢火柴游戏.通过本章的学习，希望年夜家能自己设计一些有趣的火柴游戏.练习与思考1．移动一根火柴，使下列毛病的算式酿成正确的算式.2．要求你只能移动一根火柴，使下列算式成立，谜底都是61.3．下面每题只许移动一根火柴，使等式成立.4．只许移动一根火柴，使算式成立.5．请你在下面算式上再添上一根火柴，使等式成立.6．如图2-13所示，用火柴搭成的4个算式，请你移动一根火柴，使4个等式都成立.图2-137．用12根火柴可组成3个正方形，若用11根、10根火柴还可组成3个正方形吗？8．如图2-14是由12根火柴组成的，拿去2根使它留下2个正方形.图2-14家庭能力检测与提高训练1．如图2-15用4根火柴可摆出一个正方形，那么要摆出五个正方形(年夜小纷歧定相同)，最少需要根火柴.图2-152．如图2-16是用12根火柴摆成的图形，共含有五个正方形.要求只移动2根火柴，使新图形中呈现七个正方形.图2-163．如2-17图是用18根火柴拼成的有许多三角形组成的图形.你能否移去其中3根火柴获得7个相同的三角形？图2-17 图2-18 4．如图2-18是用16根火柴摆成的图形，其中有两个三角形.请你移动其中3根火柴，共摆成4个三角形，其中要有三个完全一样.5．移动两根火柴，使下列等式仍然成立.6．24根火柴可以摆成两个正方形(如图).请问如何把持可使：移动其中4根，使其酿成3个正方形.参考谜底：【练习与思考】1．(1) 4×2＋2×2÷2＝12或2×8-2×2=12 (2) 11+1=122．(1) 56＋5=61 (2) 69-8＝61(3) 98-37＝61 (4) 35＋26＝6l(重叠放在符号上)3．(1) 3+2＝5 (2)5-2＝3 (3)9-6=3 (4) 3+2＝5(5)8-2=6 (6)9+6＝154．15+2-17=0或5+12-7=10或15+2-7=105．16×6=96 6．将右下角的6移去一根到左上角5，使6酿成5，5酿成6.7．如图2-19图2-198．如图2-20图2-20 图2-21【家庭能力检测与提高训练】1．至少需要6根火柴（如图2-21） 2．运用分割法，如图2-22图2-22 图2-23 图2-24 3．能，如图2-23所示 4．如图2-24所示5．等号两端各移动一根火柴，使9酿成6，可获得等式.左右两端各移动一根火柴，使9酿成0有：左右两端各移动一根火柴，使9酿成5，使9酿成8得：6．移法请见图2-25所示.图2-25。

在数学的海洋中，火柴棒数学题犹如一颗颗璀璨的珍珠，闪耀着智慧的光芒。

它们不仅能帮助孩子们开拓思维，培养创造力，还能激发他们对数学的兴趣。

今天，我们就来一起走进一年级巧移火柴棒数学题的世界，领略它们的神奇魅力吧！一、巧妙的数字变换数字变换是火柴棒数学题中最常见的一种题型。

它要求孩子们通过移动或改变火柴棒的数量，使之变成另一个数字。

例如：1. 将数字“5”移动一根火柴棒，变成数字“7”。

2. 将数字“8”改变一根火柴棒的数量，变成数字“3”。

3. 将数字“9”移动一根火柴棒，变成数字“10”。

这些数字变换题看似简单，但实际上却蕴含着丰富的数学知识。

孩子们在解题的过程中，需要观察、思考、比较，才能找到正确的方法。

二、灵动的几何图形火柴棒数学题中，还经常会出现各种各样的几何图形。

这些图形可以是简单的线段、三角形、正方形，也可以是复杂的圆形、五角星、六边形等。

孩子们需要通过移动或改变火柴棒的数量，使之变成这些几何图形。

例如：1. 用火柴棒摆出一个小正方形，然后在它里面再摆出一个小正方形。

2. 用火柴棒摆出一个小三角形，然后在它的旁边再摆出一个小三角形。

3. 用火柴棒摆出一个五角星，然后在它的旁边再摆出一个五角星。

这些几何图形题不仅能锻炼孩子们的动手能力，还能培养他们的空间想象力。

三、神奇的排列组合火柴棒数学题中，还经常会出现排列组合的问题。

这些问题要求孩子们根据给定的条件，排列或组合出各种各样的图形或数字。

例如：1. 用3根火柴棒摆出多少个不同的三角形？2. 用6根火柴棒摆出多少个不同的正方形？3. 用8根火柴棒排列出多少个不同的数字？这些排列组合题不仅能锻炼孩子们的逻辑思维能力，还能培养他们的发散思维能力。

四、巧妙的加减乘除火柴棒数学题中，还经常会出现加减乘除的问题。

这些问题要求孩子们根据给定的数字或图形，进行加减乘除运算。

例如：1. 用火柴棒摆出数字“3”和数字“5”，然后算出它们的和。

2. 用火柴棒摆出数字“6”和数字“8”，然后算出它们的积。

巧移火柴棒答案2．“添上”：就是在算式中的数字或运算符号上添加1根火柴，使得算式发生变化；这与“拿去”正好相反。

如，变“1”为“7”等，还可以在数之伺加“一”，在数前，数后加“1”等；3．“移动”：就是把“拿去”与“添上”两个动作结合起来，使得算式中的火柴总数不增不减。

如，变“2”为“4”，变“＋”为“7”，变“1”为“一”，变“7’为“×”等。

例2 用10根火柴摆成头朝上的龙虾(如图2－1)，试移动3根火柴，使它变成头朝下的龙虾图2-1【思路点睛】为了方便起见，我们把火柴编号，如下图2－2所示。

要把龙虾的头变成朝下的，需要把下面的“头”拆掉，并摆出“尾”，还要在下面“摆”出“头”，这样一来，马上就可以找到移动办法(如图2-3所示)：图2-2 图2-33移动8的右边，1移动2的右边，9移动10的右边。

【数学思考】这道题很有启发性，在摆弄中渗透了几何知识，当然还有其他移法，如不向右移，而是向左移。

例3 如图15—4所示，用12根火柴摆成六边形，分别拿走3根，4根、5根，使它成为3个相同的三角形，应该怎样做?图3-4 图3-5【思路点睛】(1) 如果拿走3根，那么12根火柴还剩9根，用9根火柴摆成3个相同的三角形，9÷3=3，必须是3根火柴摆1个三角形，也就是说，它们是没有公共边的。

如图3－5所示。

(2) 如果拿走4根，那么12根火柴还剩8根，用8根火柴摆成3个相同的三角形，8÷3=2……2，必定有1根火柴要充当2个三角形的公共边，也就是说，摆出的3个相同三角形必定在2个三角形连在一起。

如图15－6所示。

图2-6 图2-7(3) 同理拿走5根，还剩7根火柴，7÷3＝2……1，必定有两根火柴要充当三角形的公共边，也就是说摆出的3个相同三角形必定全都连在一起。

如图2－7所示。

例4 用16根火柴可以摆成四个大小相同的正方形(图2－8)。

试问如果用15根、14根、13根、12根火柴是否也可以分别成四个大小相同的正方形？【思路点睛】我们在图2－8的基础上思考。

移动火柴题解题技巧
1. 嘿，拿到移动火柴题，先别急着动手呀！想想看，就像走迷宫一样，得先观察好整个局面呢！比如“4+7=1”，这明显不对呀，但别急，咱观
察观察，看怎么移动火柴能变得合理。

2. 然后呢，注意数字和符号的变化呀！每一根火柴的移动都可能带来大不同哦。

就好像蝴蝶效应，小小的改动可能引发巨大的变化呢，像“3+6=8”
这样的，稍微挪一下火柴可能结果就完全不一样啦。

3. 还有呀，大胆尝试各种可能。

别害怕错，难道还能比现在更错不成？试试把这个数字的火柴移到那个数字上，说不定就柳暗花明啦，比如“9-3=7”，咱多试试几种移动方法嘛。

4. 要学会联想呀！把题目和你熟悉的东西联系起来，哎呀，这就容易多啦。

好比“2+5=9”，你就联想下平时做加法的场景，说不定灵感就来咯。

5. 也别忘了和小伙伴一起讨论哦！两个人总比一个人想得周到吧。

“6+3=1”，和朋友一起讨论下怎么移火柴才能得出合理答案呢。

6. 嘿嘿，最后就是保持耐心啦，别一看见难题就打退堂鼓呀！就像爬山一样，一步一步慢慢来，总能登顶的。

就像“8-7=0”，耐心找找移动火柴的方法呀。

我的观点结论就是：掌握这些技巧，移动火柴题就能轻松拿下啦！。

移动火柴攻略1. 简介移动火柴（MatchMove）是一种智力益智游戏，玩家通过移动、翻转或组合火柴棒的方式，使得等式成立或图案变化。

这项游戏既能锻炼思维逻辑能力，又能发展创造力和空间想象力。

本文将为你介绍移动火柴的玩法、规则以及一些技巧和攻略。

2. 游戏规则移动火柴游戏通常由一些火柴棒和一些预设的图案或等式组成。

玩家需要根据规则，通过移动或翻转火柴，改变图案或等式的形式。

下面是一些常见的游戏规则：•移动火柴：玩家可以将火柴从一个位置移动到另一个位置，但是不能改变火柴原有的长度和形状。

•翻转火柴：玩家可以将火柴翻转，即将火柴的正面变成反面，反面变成正面。

但是需要注意的是，有些火柴棒的两面可能有不同的标识或颜色，翻转时需要选择正确的一面。

•组合火柴：玩家可以将多个火柴棒组合在一起，形成新的形状。

例如，可以用两根火柴棒组合成一个等腰三角形。

•禁止改变数量：玩家在移动或翻转火柴时，不能改变火柴的数量。

即使火柴棒不在正确的位置上，也不能添加或移除火柴。

3. 基本技巧在玩移动火柴游戏时，有一些基本的技巧可以帮助你更好地解决问题：•观察：首先，仔细观察图案或等式的现状，找出其中的规律和特点。

观察可能包括火柴的数量、方向、位置以及图案的对称性等。

•推理：通过观察，对图案或等式进行合理的推理。

根据已有的信息，预测需要移动的火柴棒的位置和数量。

•试错：如果一开始没有找到解决方法，可以采用试错的方式。

尝试移动一些火柴，观察结果是否符合要求。

如果不符合，再尝试其他方法。

4. 策略攻略除了基本的技巧外，还有一些策略可以帮助你更有效地玩移动火柴游戏：•交换思维：有时候，你需要改变思维的方式来解决问题。

例如，可以尝试从“增加”或“减少”火柴的角度考虑问题，而不是一直局限于“移动”火柴。

•充分利用预设条件：有些游戏中会给出一些固定的条件，例如等式的结果或图案的一部分。

这些条件可以提供一些线索，帮助你找出解决方法。

•分析并消除无效选项：在观察图案或等式时，分析可能的移动或翻转方式，并先尝试消除一些明显无效的选项。

巧移火柴棒答案-火柴数学题巧移火柴棒答案火柴数学题在我们的日常生活中，数学以各种有趣的形式存在着，其中火柴数学题就是一种既简单又充满挑战的智力游戏。

它通过巧妙地移动火柴棒来改变数字或图形的形状，从而达到特定的条件或得出正确的答案。

火柴数学题通常以简单的数字和图形为基础，例如用火柴棒摆出的数字 0 到 9，或者常见的几何图形如三角形、正方形等。

题目会给出一个初始的火柴棒排列，然后要求我们通过移动一定数量的火柴棒来实现某种变化，比如将一个等式变得成立，或者将一个错误的图形纠正为正确的。

让我们先来看一个简单的例子。

比如用火柴棒摆出数字“8”，如果要将其变成数字“0”，我们只需要移动两根火柴棒就可以实现。

具体的操作是将数字“8”上下两个封闭的部分打开，就得到了数字“0”。

再来看一个稍微复杂一点的例子。

题目给出用火柴棒摆成的等式“3＋ 5 ＝9”，很明显这个等式是错误的。

那么我们怎样通过移动火柴棒来使它成立呢？首先，我们观察到数字“9”需要的火柴棒数量比数字“8”多一根，而等式左边的“3”和“5”通过移动火柴棒有可能组合成数字“8”。

经过尝试，我们可以将数字“5”的一根火柴棒移动到数字“3”的左上角，这样数字“3”就变成了数字“9”，数字“5”就变成了数字“6”，等式变成了“9 ＋ 0 ＝9”，从而成立。

解决这类火柴数学题需要我们具备一定的观察能力和逻辑思维能力。

首先，我们要仔细观察题目中给出的初始状态，分析每个数字或图形的构成，找出可能的移动方案。

然后，我们要根据题目要求的目标，逐步尝试不同的移动方法，通过不断地调整和尝试，最终找到正确的答案。

在解决火柴数学题的过程中，我们还需要注意一些规则和限制。

比如，每次移动火柴棒都要保证火柴棒的数量不变，而且移动后的形状必须是合法的数字或图形。

此外，我们还要充分利用火柴棒的特点，比如火柴棒的长度、端点的位置等，来寻找最优的解决方案。

除了数字等式，火柴数学题还可以以图形的形式出现。