多重共线性案例分析

解决多重共线性实例天津市1974-1987年与粮食销售量有关的影响因素如下表。

建立粮食销售量模型。

年份 Y2X 3X 4X 5X 6X 1974 98.45 560.20 153.20 6.53 1.23 1.89 1975 100.70 603.11 190.00 9.12 1.30 2.03 … … … … … … … 1987 178.69 828.73 1094.67 23.53 11.68 23.37天津统计年鉴（1988）其中：Y 是粮食销售量（万吨）；2X 常住人口（万人）； 3X 人均收入（元）； 4X 肉类销售量（万吨）； 5X 蛋类销售量（万吨）； 6X 鱼虾销售量（万吨）； 一、初步模型及存在的问题多元线性回归模型估计结果如下：65432491445336782073670125305003X X X X X Y......ˆ-++++-=（2.119）(1.945)（2.130）(1.409）（-2.028） 970402.=R 5352.=F7205.ˆ=σ9731.=DW 方程中可决系数2R 和F 统计量很大，但t 统计量较小。

临界值30626140250.)(t .=-，所有参数估计值都不能通过显著性检验。

这是存在多重共线性的典型特征。

如果利用相关系数检验法，可以得到各解释变量之间的相关系数分别为8666023.=r 8823024.=r 8524025.=r 8213026.=r 9459034.=r 9648035.=r 9825036.=r 9405045.=r 9484046.=r 9820056.=r 可见任何两个解释变量之间都有很强的正线性相关关系。

因此样本存在严重的多重共线性。

二、模型的修正由以上结果表明，任何一个解释变量与被解释变量之间的关系都是显著的。

从经济意义角度来看，人口数和人均收入应该构成影响粮食销售量的主要因素，因此建模时常住人口数X和人均收入3X应作为基本解释2变量予以保留。

实验五 多重共线性‎检验实验时间： 姓名：学号： 成绩：【实验目的】1、掌握多元线‎性回归模型‎的估计、检验和预测‎；2、掌握多重共‎线性问题的‎检验方法3、掌握多重共‎线性问题的‎修正方法 【实验内容】1、数据的读取‎和编辑；2、多元回归模‎型的估计、检验、预测；3、多重共线性‎问题的检验‎4、多重共线性‎问题的修正‎ 【实验背景】为了评价报‎账最低工资‎（负收入税）政策的可行‎性，兰德公司进‎行了一项研‎究，以评价劳动‎供给（平均工作小‎时数）对小时工资‎提高的反应‎，词研究中的‎数据取自6‎000户男‎户主收入低‎于1500‎0美元的一‎个国民样本‎，这些数据分‎成39个人‎口组，并放在表1‎中，由于4个人‎口组中的某‎些变量确实‎，所以只给出‎了35个组‎的数据，用于分析的‎各个变量的‎定义如下：Y 表示该年‎度平均工作‎小时数；X1表示平‎均小时工资‎（美元）；X2表示配‎偶平均收入‎（美元）；X3表示其‎他家庭成员‎的平均收入‎（美元）；X4表示年‎均非劳动收‎入（美元）；X5表示平‎均家庭资产‎拥有量；X6表示被‎调查者的平‎均年龄；X7表示平‎均赡养人数‎；X 8表示平‎均受教育年‎限。

μ为随机干扰‎项，考虑一下回‎归模型：μβββββββββ+++++++++=87654321876543210X X X X X X X X Y （1） 将该年度平‎均工作小时‎数Y 对X 进‎行回归，并对模型进‎行简单分析‎； （2） 计算各变量‎之间的相关‎系数矩阵，利用相关系‎数法分析变‎量间是否具‎有多重共线‎性；（3） 利用逐步回‎归方法检验‎并修正回归‎模型，最后再对模‎型进行经济‎意义检验、统计检验。

表5观测组Y X1 X2 X3 X4 X5 X6 X7 X81 2157 2.905 1121 291 380 7250 38.5 2.34 10.52 2174 2.97 1128 301 398 7744 39.3 2.335 10.53 2062 2.35 1214 326 185 3068 40.1 2.851 8.94 2111 2.511 1203 49 117 1632 22.4 1.159 11.55 2134 2.791 1013 594 730 12710‎57.7 1.229 8.86 2185 3.04 1135 287 382 776 38.6 2.602 10.77 2210 3.222 1100 295 474 9338 39 2.187 1128 2105 2.495 1180 310 255 4730 39.9 2.616 9.39 2267 2.838 1298 252 431 8317 38.9 2.024 11.110 2205 2.356 885 264 373 6489 38.8 2.662 9.511 2121 2.922 1251 328 312 5907 39.8 2.287 10.312 2109 2.499 1207 347 271 5069 39.7 3.193 8.913 2108 2.796 1036 300 259 4614 38.2 2.4 9.214 2047 2.453 1213 397 139 1987 40.3 2.545 9.115 2174 3.582 1141 414 498 10239‎40 2.064 11.716 2067 2.909 1805 290 239 4439 39.1 2.301 10.517 2159 2.511 1075 289 308 5621 39.3 2.486 9.518 2257 2.516 1093 176 392 7293 37.9 2.042 10.119 1985 1.423 553 381 146 1866 40.6 3.833 6.620 2184 3.636 1091 291 560 11240‎39.1 2.328 11.621 2084 2.983 1327 331 296 5653 39.8 2.208 10.222 2051 2.573 1197 279 172 2806 40 2.362 9.123 2127 3.263 1226 314 408 8042 39.5 2.259 10.824 2102 3.234 1188 414 352 7557 39.8 2.019 10.725 2098 2.28 973 364 272 4400 40.6 2.661 8.426 2042 2.304 1085 328 140 1739 41.8 2.444 8.227 2181 2.912 1072 304 383 9340 39 2.337 10.228 2186 3.015 1122 30 352 7292 37.2 2.046 10.929 2188 3.01 990 366 374 7325 38.4 2.847 10.630 2077 1.901 350 209 95 1370 37.4 4.158 8.231 2196 3.009 947 294 342 6888 37.5 3.047 10.632 2093 1.899 342 311 120 1425 37.5 4.512 8.133 2173 2.959 1116 296 387 7625 39.2 2.342 10.534 2179 2.959 1116 296 387 7625 39.2 2.342 10.535 2200 2.98 1126 204 393 7885 39.2 2.341 10.6 【实验过程】一、利用Evi‎e ws软件‎建立年度平‎均工作小时‎数y的回归‎模型。

《多重共线性案例分析》实验报告表2由此可见，该模型，可决系数很高，F 检验值173.3525,明显显著。

但是当时,不仅、系数的t 检验不显著，而且系数的符号与预期的相反，这表明很可能存在严重的多重共线性。

9954.02=R 9897.02=R 05.0=α776.2)610()(025.02=-=-t k n t α2X 6X 6X②.计算各解释变量的相关系数，选择X2、X3、X4、X5、X6数据，点”view/correlations ”得相关系数矩阵表3由关系数矩阵可以看出：各解释变量相互之间的相关系数较高，证实确实存在严重多重共线性相。

4.消除多重共线性①采用逐步回归的办法，去检验和解决多重共线性问题。

分别作Y 对X2、X3、X4、X5、X6的一元回归 如下图所示变量 X2 X3 X4 X5 X6 参数估计值0.08429.0523 11.6673 34.3324 2014.146 t 统计量8.665913.1598 5.1967 6.4675 8.74870.90370.95580.77150.83940.9054表4 按的大小排序为：X3、X6、X2、X5、X4。

以X3为基础，顺次加入其他变量逐步回归。

首先加入X6回归结果为：t=(2.9086) (0.46214)2R 2R 631784.285850632.7639.4109ˆX X Y t ++-=957152.02=R1995 1375.7 62900 464.0 61.5 115.70 5.97 1996 1638.4 63900 534.1 70.5 118.58 6.49 1997 2112.7 64400 599.8 145.7 122.64 6.60 1998 2391.2 69450 607.0 197.0 127.85 6.64 1999 2831.9 71900 614.8 249.5 135.17 6.74 2000 3175.5 74400 678.6 226.6 140.27 6.87 2001 3522.4 78400 708.3 212.7 169.80 7.01 2002 3878.4 87800 739.7 209.1 176.52 7.19 2003 3442.3 87000 684.9 200.0 180.98 7.30表1：1994年—2003年中国游旅收入及相关数据表2：OLS 回归表3：关系数矩阵变量 X2 X3 X4 X5 X6 参数估计值0.08429.0523 11.6673 34.3324 2014.146 t 统计量8.665913.1598 5.1967 6.4675 8.74870.90370.95580.77150.83940.9054表4：Y 对X2、X3、X4、X5、X6的一元回归六、实验结果及分析1. 在参数估计模型和关系数矩阵中， ，可决系数很高，F 检验值173.3525,明显显著。

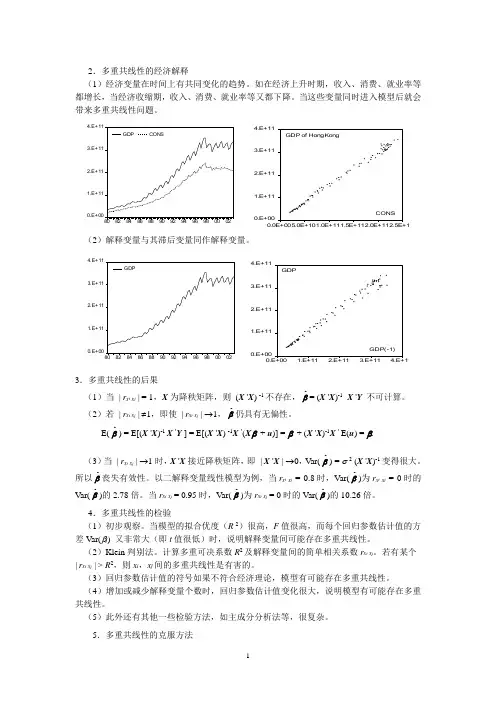
2．多重共线性的经济解释（1）经济变量在时间上有共同变化的趋势。

如在经济上升时期，收入、消费、就业率等都增长，当经济收缩期，收入、消费、就业率等又都下降。

当这些变量同时进入模型后就会带来多重共线性问题。

0.E+001.E+112.E+113.E+114.E+11808284868890929496980002GDPCONS0.E+001.E+112.E+113.E+114.E+110.0E+005.0E+101.0E+111.5E+112.0E+112.5E+11CONSGDP of HongKong（2）解释变量与其滞后变量同作解释变量。

0.E+001.E+112.E+113.E+114.E+11808284868890929496980002GDP0.E+001.E+112.E+113.E+114.E+110.E+001.E+112.E+113.E+114.E+11GDP(-1)GDP3．多重共线性的后果（1）当 | r x i x j | = 1，X 为降秩矩阵，则 (X 'X ) -1不存在，βˆ= (X 'X )-1 X 'Y 不可计算。

（2）若 | r x i x j | ≠1，即使 | r x i x j | →1，βˆ仍具有无偏性。

E(βˆ) = E[(X 'X )-1 X 'Y ] = E[(X 'X ) -1X '(X β + u )] = β + (X 'X )-1X ' E(u ) = β. （3）当 | r x i x j | →1时，X 'X 接近降秩矩阵，即 | X 'X | →0，V ar(βˆ) = σ 2 (X 'X )-1变得很大。

所以βˆ丧失有效性。

以二解释变量线性模型为例，当r x i x j = 0.8时，Var(βˆ)为r x i x j = 0时的Var(βˆ)的2.78倍。

计量经济学中多重共线性案例问题研究摘要：本论文主要通过案例来研究计量经济学中的多重共线性的问题，对案例进行EVIEWS分析,并利用诊断共线性的经验方法及修正共线性的经验方法和通过EVIEWS分析对案例中的多重共线性进行诊断与修正，以能够完成减弱多重共线性的目标。

关键字：多重共线性诊断共线性的经验方法修正共线性的经验方法经典的线性回归模型的假定之一是各解释变量X之间不存在多重共线性。

然而，在计量经济学中所说的多重共线性（mnlti-collinearity），不仅包含解释变量之间精确的线性关系，还包含解释变量之间近似的线性关系。

下面来通过研究国内生产总值的增加会影响财政收入的增加还是减少的案例对多重共线性进行研究。

一、研究的目的和要求国内生产总值GDP按照支出法的公式为：国内生产总值=消费+投资+政府购买支出+净出口，而财政收入的主要来源为各项税收收入如增值税等。

只有经济持续的增长，才能提供稳定的税收来源。

所以，影响财政收入的主要因素是税收收入。

但是，税收收入还影响着国内生产总值。

因此，为了中国未来经济的发展，需要定量的分析影响中国财政收入的因素。

二、模型设定及其估计经过研究与分析，影响财政收入的主要因素，除了税收收入以外，还有与一些其他因素有关。

为此，考虑的影响因素主要有财政支出CZZC/亿元用X2表示，国内生产总值GDP/亿元用X3表示，税收总额SSZE/亿元用X4表示。

各影响变量与财政收入之间呈现正相关。

因此设定了如下形式的计量经济模型来研究“国内生产总值的增加会减少财政收入吗”这个问题：Y t=β1+β2X2t+β3X3t+β4X4t+μt式中，Yt为第t年国内财政收入（亿元）；X2为财政支出（亿元）；X3为国内生产总值（亿元）；X4为税收总额（亿元）。

各解释变量前的回归系数预期都大于0.为估计模型参数，1985～2011年阶段财政收入的统计数据，如下表：运用EVIEWS软件，生成Y、X2、X3、X4数据，采用OLS方法估计模型参数，得到的回归结果如下图所示：该模型R²=0.999857，Rˉ²=0.999838，可决系数非常高，F的检验值为53488.54，明显很显著。

实验报告实验题目：多重共线性的研究指导老师：学生一：学生二：实验时间：2011年10月多重线性回归分析及其实验报告实验目的：为了更好地了解财政收入构成，需要定量地分析影响财政收入的因素模型设定及其估计：经分析，影响财政收入的主要因素，农业增加值X1，工业增加值X2，建筑业增加值X3，总人口X4，受灾面积X5.为此设定了如下形式的计量经济模型：Y=β1+β2X1+β3X2+β4X3+β5X4+β6X5+u0其中，Y为财政收入（元），X1农业增加值（元），X2为工业增加值(元)，X3为建筑业增加值（元），X4为总人口（万人），X5为受灾面积（千公顷）为估计模型参数，收集1978~2007年财政收入及其影响因素数据，如图：1978~2007年财政收入及其影响因素数据年份财政收入CS/亿元农业增加值NZ/亿元工业增加值GZ/亿元建筑业增加值JZZ/亿元总人口TPOP/万人受灾面积SZM/千公顷1978 1132.3 1027.5 1607 138.2 96259 50790 1979 1146.6 1270.2 1769.7 143.8 97542 39370 1980 1159.9 1371.4 1996.5 195.5 98705 44526 1981 1175.8 1559.5 2048.5 207.1 100072 39790 1982 1212.3 1777.4 2162.3 220.7 101654 33130 1983 1367 1978.5 2375.8 270.6 103008 34710 1984 1642.5 2316.1 2789 316.7 104357 31890 1985 2004.6 2564.3 3448.5 417.9 105851 44365 1986 2122 2788.7 3987.5 525.7 107507 47170 1987 2199.4 3233 4565.9 665.8 109300 42090 1988 2357.6 3865.4 5062 810 111026 50870 1989 2664.5 5062 8087.3 794 112704 46991 1990 2937.4 5342.3 10284.5 859.4 114333 384741991 3149.48 5866.8 14188 1015.1 115823 55472 1992 3483.48 6963.6 19480.5 1415 117171 51333 1993 4348.95 9572.7 19480.4 2266.5 118517 48829 1994 5218.1 12315.7 24950.7 2964.7 119850 55043 1995 6242.2 14015.8 29447.6 3728.8 121121 45821 1996 7407.99 14441.8 32921.4 4387.4 122389 46898 1997 8615.14 14917.6 34018.4 4985.8 123626 53429 1998 9875.95 14944.5 40036 5172.1 124761 59145 1999 11444.08 15871.8 43580.6 5522.3 125786 49981 2000 13395.23 16537 47431.6 5913.7 126743 54688 2001 16386.04 17381.8 54945.5 6465.5 127627 52215 2002 18903.64 21412.7 65210 7490.8 128453 47119 2003 21715.25 22420 76912.6 8694.3 129227 54506 2004 26396.47 21224 87632.4 8967.8 129988 37106 2005 31649.29 22420 89834.5 10133.8 130756 38818 2006 38760.2 24040.9 91310.9 11851.1 131448 41091 2007 51321.45 28095 107367.2 14014.1 132129 48992利用Eviews软件，生成Y、X1、X2、X3、X4、X5等数据，采用这些数据进行OLS回归，结果如下Dependent Variable: YMethod: Least SquaresDate: 10/24/11 Time: 22:49Sample: 1978 2007Included observations: 30Variable Coefficient Std. Error t-Statistic Prob.C -6734.394 11259.37 -0.598115 0.5554X1 -1.678611 0.328371 -5.111937 0.0000X2 0.071078 0.081171 0.875666 0.3899X3 5.699199 0.745591 7.643870 0.0000X4 0.101481 0.114244 0.888277 0.3832X5 -0.010922 0.057578 -0.189691 0.8511R-squared 0.983660 Mean dependent var 10047.83Adjusted R-squared 0.980255 S.D. dependent var 12585.61S.E. of regression 1768.473 Akaike info criterion 17.97048Sum squared resid 75059958 Schwarz criterion 18.25072Log likelihood -263.5572 F-statistic 288.9512Durbin-Watson stat 0.898668 Prob(F-statistic) 0.000000由此可见，该模型R2=0.983660，R2=0.980255可决系数很高，F检验值为288.9512，明显显著。

实验名称：多重共线性的检验与处理实验时间：2011.12.10实验要求：主要是学习多重共线性的检验与处理，主要是研究解释变量与其余解释变量之间有严重多重共线性的模型，分析变量之间的相关系数。

通过具体案例建立模型，然后估计参数，求出相关的数据。

再对模型进行检验，看数据之间是否存在多重共线性。

最后利用所求出的模型来进行修正。

实验内容：实例：我国钢材供应量分析通过分析我国改革开放以来（1978－1997）钢材供应量的历史资料，可以建立一个单一方程模型。

根据理论及对现实情况的认识，影响我国钢材供应量 Y（万吨）的主要因素有：原油产量X1（万吨），生铁产量X2（万吨），原煤产量X3（万吨），电力产量X4（亿千瓦小时），固定资产投资X5(亿元)，国内生产总值X6(亿元)，铁路运输量X7（万吨）。

（一）建立我国钢材供应量的计量经济模型：（二）估计模型参数，结果为：Dependent Variable: YMethod: Least SquaresDate: 11/02/09 Time: 16:09Sample: 1978 1997Included observations: 20Variable Coefficient Std. Error t-Statistic Prob.C 139.2362 718.2493 0.193855 0.8495X1 -0.051954 0.090753 -0.572483 0.5776X2 0.127532 0.132466 0.962751 0.3547X3 -24.29427 97.48792 -0.249203 0.8074X4 0.863283 0.186798 4.621475 0.0006X5 0.330914 0.105592 3.133889 0.0086X6 -0.070015 0.025490 -2.746755 0.0177X7 0.002305 0.019087 0.120780 0.9059R-squared 0.999222 Mean dependent var 5153.350Adjusted R-squared 0.998768 S.D. dependent var 2511.950S.E. of regression 88.17626 Akaike info criterion 12.08573Sum squared resid 93300.63 Schwarz criterion 12.48402Log likelihood -112.8573 F-statistic 2201.081Durbin-Watson stat 1.703427 Prob(F-statistic) 0.000000由此可见，该模型可绝系数很高，F检验值2201.081，明显显著。

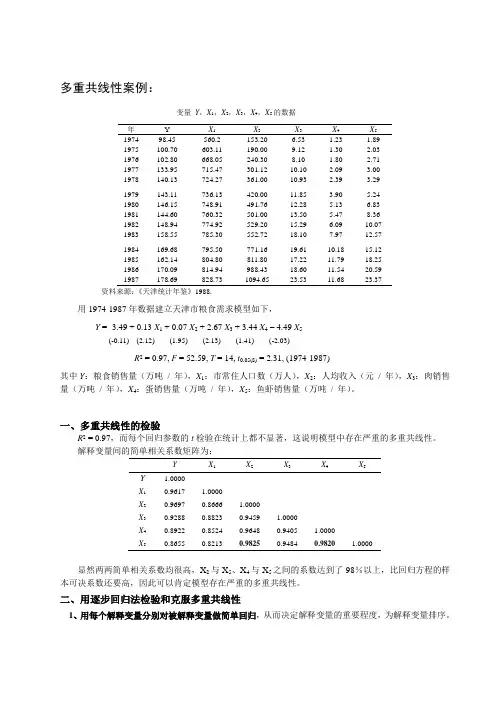
多重共线性案例：变量Y，X1，X2，X3，X4，X5的数据年Y X1X2X3X4X51974 98.45 560.2 153.20 6.53 1.23 1.891975 100.70 603.11 190.00 9.12 1.30 2.031976 102.80 668.05 240.30 8.10 1.80 2.711977 133.95 715.47 301.12 10.10 2.09 3.001978 140.13 724.27 361.00 10.93 2.39 3.291979 143.11 736.13 420.00 11.85 3.90 5.241980 146.15 748.91 491.76 12.28 5.13 6.831981 144.60 760.32 501.00 13.50 5.47 8.361982 148.94 774.92 529.20 15.29 6.09 10.071983 158.55 785.30 552.72 18.10 7.97 12.571984 169.68 795.50 771.16 19.61 10.18 15.121985 162.14 804.80 811.80 17.22 11.79 18.251986 170.09 814.94 988.43 18.60 11.54 20.591987 178.69 828.73 1094.65 23.53 11.68 23.37资料来源：《天津统计年鉴》1988.用1974-1987年数据建立天津市粮食需求模型如下，Y = -3.49 + 0.13 X1 + 0.07 X2 + 2.67 X3 + 3.44 X4– 4.49 X5(-0.11) (2.12) (1.95) (2.13) (1.41) (-2.03)R2 = 0.97, F = 52.59, T = 14, t0.05(8) = 2.31, (1974-1987)其中Y：粮食销售量（万吨/ 年），X1：市常住人口数（万人），X2：人均收入（元/ 年），X3：肉销售量（万吨/ 年），X4：蛋销售量（万吨/ 年），X5：鱼虾销售量（万吨/ 年）。

多重共线性分析案例例用1974-1987年数据建立天津市粮食需求模型如下：表1 变量y，x1，x2，x3，x4，x5的数据年y x1x2x3x4x51974 98.45 560.2 153.20 6.53 1.23 1.891975 100.70 603.11 190.00 9.12 1.30 2.031976 102.80 668.05 240.30 8.10 1.80 2.711977 133.95 715.47 301.12 10.10 2.09 3.001978 140.13 724.27 361.00 10.93 2.39 3.291979 143.11 736.13 420.00 11.85 3.90 5.241980 146.15 748.91 491.76 12.28 5.13 6.831981 144.60 760.32 501.00 13.50 5.47 8.361982 148.94 774.92 529.20 15.29 6.09 10.071983 158.55 785.30 552.72 18.10 7.97 12.571984 169.68 795.50 771.16 19.61 10.18 15.121985 162.14 804.80 811.80 17.22 11.79 18.251986 170.09 814.94 988.43 18.60 11.54 20.591987 178.69 828.73 1094.65 23.53 11.68 23.37资料来源：《天津统计年鉴》1988.设回归模型:Y＝β0＋β1X1＋β2X2＋β3X3＋β4X4＋β5X5+ε利用spss统计软件进行线性回归(点选Statistics选项框中Collinearity共线性诊断选项)，设显著性水平0.05，输出结果如下：从回归方程的P检验结果看出Sig＝0，整体通过显著性检验。

从输出结果看，在0.05的显著性水平下，βi的t统计量单独对因变量y都无显著性影响（P 值都大于0.05）。

实验五__多重共线性检验参考案例多重共线性检验是用来检验自变量之间是否存在高度相关性的一种方法。

在回归分析中，如果自变量之间存在高度相关性，会导致回归方程中的相关系数估计值不稳定，难以准确地解释自变量对因变量的影响。

因此，进行多重共线性检验是非常重要的。

下面将以一个案例来说明如何进行多重共线性检验。

假设我们想研究一些城市的房价与以下自变量相关性的影响：房屋面积、房间数量、距离市中心的距离。

我们采集了100个样本，并进行了回归分析。

首先，我们可以查看自变量之间的相关系数矩阵，以判断是否存在高度相关性。

下面是自变量之间的相关系数矩阵：房屋面积房间数量距离市中心的距离房屋面积10.80.2房间数量0.810.1距离市中心的距离0.20.11从相关系数矩阵可以看出，房屋面积和房间数量之间存在高度相关性，相关系数为0.8、这可能意味着两个自变量提供了类似的信息，在回归分析中可能会造成多重共线性的问题。

接下来，我们可以计算自变量的方差膨胀因子（VIF）来进一步检验多重共线性。

VIF是用来度量自变量之间相关度的指标，VIF值越大，说明自变量之间的共线性越强。

计算VIF的公式如下：VIF_i=1/(1-R_i^2)其中，VIF_i表示自变量i的VIF值，R_i^2表示通过其他自变量对自变量i进行回归分析得到的决定系数。

下面是计算三个自变量的VIF值：VIF_房屋面积=1/(1-0.8^2)=1.67VIF_房间数量=1/(1-0.8^2)=1.67VIF_距离市中心的距离=1/(1-0.1^2)=1.01从计算结果可以看出，三个自变量的VIF值都在可接受的范围内，说明它们之间并不存在严重的多重共线性问题。

最后，我们可以绘制自变量对因变量的散点图，以观察它们之间的关系。

如果自变量之间存在高度相关性，会导致散点图中观测点呈现出一种线性的形态。

综上所述，通过相关系数矩阵、VIF值以及散点图的分析，我们可以得出结论：在这个案例中，房屋面积、房间数量和距离市中心的距离之间不存在严重的多重共线性问题，可以继续进行回归分析。

计量经济学中多重共线性案例问题研究摘要：本论文主要通过案例来研究计量经济学中的多重共线性的问题，对案例进行EVIEWS分析,并利用诊断共线性的经验方法及修正共线性的经验方法和通过EVIEWS分析对案例中的多重共线性进行诊断与修正，以能够完成减弱多重共线性的目标。

关键字：多重共线性诊断共线性的经验方法修正共线性的经验方法经典的线性回归模型的假定之一是各解释变量X之间不存在多重共线性。

然而，在计量经济学中所说的多重共线性（mnlti-collinearity），不仅包含解释变量之间精确的线性关系，还包含解释变量之间近似的线性关系。

下面来通过研究国内生产总值的增加会影响财政收入的增加还是减少的案例对多重共线性进行研究。

一、研究的目的和要求国内生产总值GDP按照支出法的公式为：国内生产总值=消费+投资+政府购买支出+净出口，而财政收入的主要来源为各项税收收入如增值税等。

只有经济持续的增长，才能提供稳定的税收来源。

所以，影响财政收入的主要因素是税收收入。

但是，税收收入还影响着国内生产总值。

因此，为了中国未来经济的发展，需要定量的分析影响中国财政收入的因素。

二、模型设定及其估计经过研究与分析，影响财政收入的主要因素，除了税收收入以外，还有与一些其他因素有关。

为此，考虑的影响因素主要有财政支出CZZC/亿元用X2表示，国内生产总值GDP/亿元用X3表示，税收总额SSZE/亿元用X4表示。

各影响变量与财政收入之间呈现正相关。

因此设定了如下形式的计量经济模型来研究“国内生产总值的增加会减少财政收入吗”这个问题：Y t=β1+β2X2t+β3X3t+β4X4t+μt式中，Yt为第t年国内财政收入（亿元）；X2为财政支出（亿元）；X3为国内生产总值（亿元）；X4为税收总额（亿元）。

各解释变量前的回归系数预期都大于0.为估计模型参数，1985～2011年阶段财政收入的统计数据，如下表：运用EVIEWS软件，生成Y、X2、X3、X4数据，采用OLS方法估计模型参数，得到的回归结果如下图所示：该模型R²=0.999857，Rˉ²=0.999838，可决系数非常高，F的检验值为53488.54，明显很显著。

第10章 案例分析
一、研究的目的要求
近年来，中国旅游业一直保持高速发展，旅游业作为国民经济新的增长点，在整个社会经济发展中的作用日益显现。

中国的旅游业分为国内旅游和入境旅游两大市场，入境旅游外汇收入年均增长22.6%，与此同时国内旅游也迅速增长。

改革开放20多年来，特别是进入90年代后，中国的国内旅游收入年均增长14.4%，远高于同期GDP 9.76%的增长率。

为了规划中国未来旅游产业的发展，需要定量地分析影响中国旅游市场发展的主要因素。

二、模型设定及其估计
经分析，影响国内旅游市场收入的主要因素，除了国内旅游人数和旅游支出以外，还可能与相关基础设施有关。

为此，考虑的影响因素主要有国内旅游人数2X ，城镇居民人均旅游支出3X ，农村居民人均旅游支出4X ，并以公路里程5X 和铁路里程6X 作为相关基础设
施的代表。

为此设定了如下对数形式的计量经济模型： 23456123456t t t t t t t Y X X X X X u ββββββ=++++++
其中 ：t Y ——第t 年全国旅游收入
2X ——国内旅游人数 （万人）
3X ——城镇居民人均旅游支出 （元） 4X ——农村居民人均旅游支出 （元） 5X ——公路里程（万公里） 6X ——铁路里程（万公里）
为估计模型参数，收集旅游事业发展最快的1994—2003年的统计数据，如表4.2所示：
三、消除多重共线性
采用逐步回归的办法，去检验和解决多重共线性问题。

影响贵州省旅游业收入的分析-----多重共线性问题的处理案例一．问题的提出近年来，由于中国经济的稳定高速增长，人们的消费水平和收入水平逐步提高，可支配人均收入的增加使得人们有更多的机会和经济基础出门旅游。

因此旅游业的发展逐渐成为一个重要的产业，所以，有必要对影响旅游业发展的因素进行分析，抓住主要因素更好的发展旅游业。

贵州省地处西南，旅游线路和资源相当丰富。

但是，经济却处于欠发达状态，如何有效地开发利用旅游资源发展旅游产业将对贵州经济增长是值得深入研究的问题。

众所周知，推动贵州旅游业发展的因素众多，如交通运输条件的改善、信息技术的发展、居民收入水平的提高等。

2008年，贵州省旅游总收入创下了653.13亿元的好成绩，较2007年净增140亿元，增长27.50%，旅游总收入在全国的排名由18位上升至17位；接待总人数8190.23万人次，同比增长30.77%。

2009年，贵州省全年共接待游客1.043亿人次，同比增长27.46%，旅游总收入805.23亿元，同比增长23.29%，远远超过了预期的780亿和20%的增长率。

本文主要对五个方面的因素进行多重共线性的分析，剔除具有严重共线性的解释变量，改善计量模型。

并最终确定影响贵州旅游发展的重要因素。

二． 模型设定1. 旅游影响因素的选择影响旅游市场收入的主要因素，除了国内旅游人数和居民消费外还有很多，但是应该挑选在长期内具有较稳定的变动趋势的因素、剔除随机性较强的因素如：自然灾害的发生；国内外突发事件或重大活动，如2008年的凝冻灾害、农运会的举办等。

此外还可能与基础设施建设有关，由于发达的交通方便了人们出门旅游，而收入的增加提供了经济支持。

综合上述分析，我们选取五个解释变量如下：X1:国内旅游人数（万人次）； X2:城镇居民人均消费性支出（元）； X3:农村居民人均消费性支出（元）； X4:公路里程数（公里）； X5:铁路旅程（公里）； 2．模型形式的设计由于是根据实际数据进行实证分析，所以将被解释变量（Y ）与五个解释变量进行回归分析，形式为 γγγγγγββββββ55443322110XXXXX +++++=Y三． 数据的收集本文收集了贵州省从1984年-2007年的24组数据。