湖南省长郡中学2019届高三上学期第一次月考(开学考试)数学(文)试题+Word版含答案

湖南省长郡中学2019届高三第一次模拟考试数学（文）试题本试题卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共8页，23题（含选考题）。

全卷满分150分。

考试用时120分钟。

★祝考试顺利★注意事项：1、考试范围：高考范围。

2、答题前，请先将自己的姓名、准考证号用0.5毫米黑色签字笔填写在试题卷和答题卡上的相应位置，并将准考证号条形码粘贴在答题卡上的指定位置。

用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。

3、选择题的作答：每个小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

写在试题卷、草稿纸和答题卡上的非选择题答题区域的答案一律无效。

4、填空题和解答题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域的答案一律无效。

如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

5、选考题的作答：先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。

答案用0.5毫米黑色签字笔写在答题卡上对应的答题区域内，写在试题卷、草稿纸和答题卡上的非选修题答题区域的答案一律无效。

6、保持卡面清洁，不折叠，不破损，不得使用涂改液、胶带纸、修正带等。

7、考试结束后，请将本试题卷、答题卡、草稿纸一并依序排列上交。

第I 卷一、选择题(本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的)1.设,a R i ∈为虚数单位.若复数()21z a a i =-++是纯虚数，则复数32a ii--在复面上对应的点的坐标为 A. 18,55⎛⎫- ⎪⎝⎭B. 74,55⎛⎫-- ⎪⎝⎭C. 47,55⎛⎫-⎪⎝⎭D. 74,55⎛⎫-⎪⎝⎭2.已知集合(){}(){}2222log 34,3200A x y x x B x x mx m m ==--=-+<>，B A ⊆若，则实数m 的取值范围为A. ()4+∞，B. [)4+∞，C. ()2+∞，D. [)2+∞，3.回文数是指从左到右读与从右到左读都一样的正整数，如11，323，4334等.在所有小于150的三位回文数中任取两个数，则两个回文数的三位数字之和均大于3的概率为 A.16B.23C.310D.254. 已知O 为坐标原点，双曲线()222210,0x y a b a b-=>>的左、右焦点分别为12F F ，，若右支上有点M 满是221,cos 3OM OF MOF =∠=，则双曲线的离心率为5.长郡中学某次高三文数周测，张老师宣布这次考试的前五名是：邓清、武琳、三喜、建业、梅红，然后让五人分别猜彼此名次。

长郡中学2019届高三月考试卷（一）数学（理科）第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.1.设复数，则（）A. B. C. D.【答案】D【解析】【分析】根据复数除法运算，分子分母同时乘以分母的共轭复数，化简即可。

【详解】所以所以选D【点睛】本题考查了复数的除法运算，复数模的定义，属于基础题。

2.2.已知集合，，，则（）A. B. C. D.【答案】C【解析】集合，故，集合表示非负的偶数，故，故选C.3.3.若定义在上的偶函数满足且时，，则方程的零点个数是（）A. 个B. 个C. 个D. 个【答案】C【解析】【分析】根据函数的周期性和奇偶性，画出函数图像，根据函数图像的交点个数确定零点个数即可。

【详解】因为数满足，所以周期当时，，且为偶函数，所以函数图像如下图所示由图像可知，方程有四个零点所以选C【点睛】本题考查了函数的奇偶性和周期性，绝对值函数图像的画法和函数零点的概念，关键是根据函数解析式能够正确画出函数的图像，属于基础题。

4.4.计算的结果为（）A. B. C. D.【答案】B【解析】【分析】根据诱导公式，化简三角函数值；再根据正弦的差角公式合并即可得到解。

【详解】所以选B【点睛】本题考查了三角函数诱导公式、正弦差角公式的简单应用，属于基础题。

5.5.已知、、是双曲线上不同的三点，且、连线经过坐标原点，若直线、的斜率乘积，则该双曲线的离心率为（）A. B. C. D.【答案】C【解析】【分析】根据题意，设出A、B、P点的坐标，代入方程做差，得到；利用两条直线的斜率乘积关系，得到。

联立可以得到的关系式，进而求得离心率。

【详解】由题意，设则将A、P坐标代入双曲线方程，得两式相减得所以，即所以所以选C【点睛】本题考查了点与双曲线的关系，设而不求法是解决圆锥曲线问题常用方法，属于基础题。

6.6.某单位为了落实“绿水青山就是金山银山”理念，制定节能减排的目标，先调查了用电量（单位：千瓦·时）与气温（单位：℃）之间的关系，随机选取了天的用电量与当天气温，并制作了以下对照表：（单位：℃）（单位：千瓦·时）由表中数据得线性回归方程：，则由此估计：当某天气温为℃时，当天用电量约为（）A. 千瓦·时B. 千瓦·时C. 千瓦·时D. 千瓦·时【答案】A【解析】【分析】根据回归直线方程经过样本中心点，求得，代入回归直线可求得；代入回归方程后，可预报当气温为℃时，当天的用电量。

长郡中学2019届高三月考试卷（一）数学（文科）一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.1.已知集合，，则（）A. B. C. D.【答案】D【解析】【分析】根据集合的运算，求并集即为求满足两个集合的最大范围。

【详解】集合A为，集合B为所以并集所以选D【点睛】本题考查了集合的基本运算，属于基础题。

2.2.复数满足（为虚数单位），则复数的虚部为（）A. B. C. D.【答案】B【解析】【分析】根据复数的除法运算，分子分母同时乘以分母的共轭复数，进而化简即可得到复数的虚部。

【详解】所以复数z的虚部为-3所以选B【点睛】本题考查了复数的基本运算和基本概念，注意复数的虚部只有数字，不含虚数单位，属于基础题。

3.3.已知，则（）A. B. C. D.【答案】C【解析】分析：直接利用二倍角的余弦公式求解即可.详解：,故选C.点睛：本题主要考查二倍角的余弦公式，属于简单题.4.4.某家具厂的原材料费支出（单位：万元）与销售额（单位：万元）之间有如下数据，根据表中提供的全部数据，用最小二乘法得出与的线性回归方程为，则为（）A. B. C. D.【答案】A【解析】【分析】根据回归直线经过样本平均数中心点，求得平均值，代入即可求得b。

【详解】因为回归直线方程经过样本中心点，代入回归直线方程得所以选A【点睛】本题考查了回归直线的简单应用，注意回归直线会经过平均数中心点，而不是某个样本点，属于基础题。

5.5.已知向量，，则（）A. B. C. D.【答案】D【解析】由题意，所以答案A，B都不正确；又，且，所以答案C不正确，应选答案D。

6.6.执行如图所示的程序框图输出的结果是（）A. B. C. D.【答案】A【解析】【分析】根据程序框图循环结构运算，依次代入求解即可。

【详解】根据程序框图和循环结构算法原理，计算过程如下：所以选A【点睛】本题考查了程序框图的基本结构和运算，主要是掌握循环结构在何时退出循环结构，属于基础题。

长郡中学2019届高三月考试卷（一）数学（文科）（考试时间：120分钟，满分150分）注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

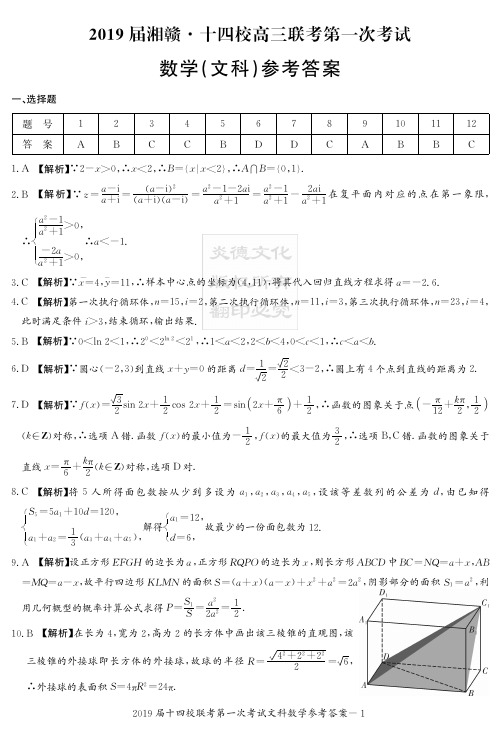
一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{|02}A x x =<<，{|1}B x x =≥，则AB =（ ）A ．{|01}x x <<B ．{|1}x x ≥C ．{|12}x x ≤<D ．{|0}x x > 2.复数z 满足(2)36z i i +=-（i 为虚数单位），则复数z 的虚部为（ ） A ．3 B ．3- C ．3i D ．3i -3.已知2sin 5α=，则cos2α=（ ） A ．725 B ．725- C ．1725D ．1725-4.某家具厂的原材料费支出x （单位：万元）与销售额y （单位：万元）之间有如下数据，根据表中提供的全部数据，用最小二乘法得出y 与x 的线性回归方程为8.5y x b =+，则b 为（ ）A ．7.5B ．10C ．12.5D ．17.5 5.已知向量(2,1)a =-，(1,3)b =-，则（ ）A ．//a bB ．a b ⊥C ．//()a a b -D ．()a a b ⊥- 6.执行如图所示的程序框图输出的结果是（ ）A ．8B ．6C ．5D ．3 7.已知曲线1C ：sin y x =，2C ：2sin 23y x π⎛⎫=+ ⎪⎝⎭，则下面结论正确的是（ ） A ．把1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移23π个单位长度，得到曲线2CB ．把1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移3π个单位长度，得到曲线2CC ．把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移23π个单位长度，得到曲线2CD ．把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移3π个单位长度，得到曲线2C8.曲线()2xf x x e =-在点(0,(0))f 处的切线方程是（ ） A ．210x y --= B ．10x y -+= C ．0x y -= D ．10x y --=9.平面α截球O 的球面所得圆的半径为1，球心O 到平面α，则此球的体积为（ ）A ．B ．CD ．10.已知()f x 是定义在R 上的偶函数，且在区间(,0]-∞上单调递增.若实数a 满足()(f a f >，则a 的取值范围是（ ）A ．(,-∞B ．)+∞C．( D．(,(2,)-∞+∞11.已知四棱锥S ABCD -的三视图如图所示，则围成四棱锥SABCD -的五个面中的最大面积是（ ）A ．3B ．6C ．8D ．1012.已知F 是抛物线C ：28y x =的焦点，M 是C 上一点，FM 的延长线交y 轴于点N .若M 为FN 的中点，则FN =（ ）A ．4B ．6C ．8D ．10二、填空题：本题共4小题，每小题5分，共20分.13.已知x ，y 满足020x y x y y -≥⎧⎪+≤⎨⎪≥⎩，则2z x y =+的最大值为 ．14.若点(1,1)P 为圆2260x y x +-=的弦MN 的中点，则弦MN 所在直线的方程为 ．15.在ABC ∆中，面积2221()4S a b c =+-，则角C 的大小为 ． 16.已知函数3()lg 92f x x x =+-在区间(,1)()n n n Z +∈上存在零点，则n = ．三、解答题：本大题共70分.解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必需作答.第22、23题为选考题，考生根据要求作答. （一）必考题：共60分.17.等比数列{}n a 中，已知12a =，416a =. （1）求数列{}n a 的通项公式；（2）若3a ，5a 分别为等差数列{}n b 的第3项和第5项，试求数列{}n b 的通项公式及前n 项和n S . 18.已知四棱锥P ABCD -中，底面ABCD是边长为2的正方形，PA PD ==CD PD ⊥，E 为CD的中点.（1）求证：PD ⊥平面PAB ； （2）求三棱锥P ABE -的体积.19.某家电公司销售部门共有200名销售员，每年部门对每名销售员都有1400万元的年度销售任务.已知这200名销售员去年完成的销售额都在区间[2,22]（单位：百万元）内，现将其分成5组，第1组、第2组、第3组、第4组、第5组对应的区间分别为[2,6)，[6,10)，[10,14)，[14,18)，[18,22]，并绘制出如下的频率分布直方图.（1）求a 的值，并计算完成年度任务的人数；（2）用分层抽样的方法从这200名销售员中抽取容量为25的样本，求这5组分别应抽取的人数； （3）现从（2）中完成年度任务的销售员中随机选取2名，奖励海南三亚三日游，求获得此奖励的2名销售员在同一组的概率.20.过椭圆C ：22221(0)x y a b a b+=>>的右焦点2F 的直线交椭圆于A ，B 两点，1F 为其左焦点，已知1AF B ∆的周长为3. （1）求椭圆C 的方程；（2）设P 为椭圆C 的下顶点，椭圆C 与直线y x m =+相交于不同的两点M 、N .当PM PN =时，求实数m 的值. 21.已知函数()xxa f x e e =-. （1）当1a =时，求函数()[()'()]F x x f x f x =-的最小值；（2）若()()g x f x =在[0,1]上单调递增，求实数a 的取值范围.（二）选考题：共10分.请考生在22、23题中任选一题作答，如果多做，则按所做的第一题记分.22.选修4-4：坐标系与参数方程在平面直角坐标系xOy 中，直线l 的参数方程为12x ty a t=+⎧⎨=-⎩（其中t 为参数）.在以坐标原点为极点，x 轴的正半轴为极轴的极坐标系中，圆C 的极坐标方程为4cos ρθ=. （1）分别写出直线l 的普通方程和圆C 的直角坐标方程； （2）若直线l 与圆C 相切，求实数a 的值. 23.选修4-5：不等式选讲 设函数()f x x a x a =++-. （1）当1a =时，解不等式()4f x ≥；（2）若()6f x ≥在x R ∈上恒成立，求a 的取值范围.长郡中学2019届高三月考试卷（一）数学（文科）参考答案一、选择题1-5: DBCAD 6-10: ABDAC 11、12：CB二、填空题13. 4 14. 210x y --= 15. 45︒ 16. 5三、解答题17.【解析】（1）设{}n a 的公比为q 由已知得3162q =，解得2q =，所以2n n a =.（2）由（1）得38a =，532a =，则38b =，532b =， 设{}n b 的公差为d ，则有1128432b d b d +=⎧⎨+=⎩，解得11612b d =-⎧⎨=⎩，从而1612(1)1228n b n n =-+-=-. 所以数列{}n b 的前n 项和2(161228)6222n n n S n n -+-==-.18.【解析】（1）∵底面ABCD 是正方形，∴//AB CD ，又CD PD ⊥， ∴AB PD ⊥，∵PA PD ==2AD =，∴222PA PD AD +=，∴PD PA ⊥，又PA AB A =，∴PD ⊥平面PAB .（2）∵AB AD ⊥，AB PD ⊥且ADPD D =，∴AB ⊥平面PAD ，又AB ⊂平面ABCD ，∴平面PAD ⊥平面ABCD ， 过P 作PO AD ⊥于O ，则PO ⊥平面ABCD ， ∴PO 为三棱锥P ABE -的高，∴13P ABE ABE V S PO -∆=⋅112122323=⨯⨯⨯⨯=. 19.【解析】（1）∵(0.020.080.092)41a +++⨯=，∴0.03a =， 完成年度任务的人数为2420048a ⨯⨯=. （2）第1组应抽取的人数为0.024252⨯⨯=， 第2组应抽取的人数为0.084258⨯⨯=， 第3组应抽取的人数为0.094259⨯⨯=， 第4组应抽取的人数为0.034253⨯⨯=， 第5组应抽取的人数为0.034253⨯⨯=.（3）在（2）中完成年度任务的销售员中，第4组有3人，记这3人分别为1A ，2A ，3A ；第5组有3人，记这3人分别为1B ，2B ，3B ；从这6人中随机选取2名，所有的基本事件为12A A ，13A A ，11A B ，12A B ，13A B ，23A A ，21A B ，22A B ，23A B ，31A B ，32A B ，33A B ，12B B ，13B B ，23B B ，共有15个基本事件.获得此奖励的2名销售员在同一组的基本事件有6个， 故所求概率为62155=. 20.【解析】（1）由椭圆定义知，4a =，a =3c e a ===得c =1b =， 所以椭圆C 的方程为2213x y +=. （2）由方程组2213y m x y ⎧=+⎪⎪⎨⎪+=⎪⎩2223(1)0x m ⇒++-=， 设11(,)M x y ，22(,)N x y ，MN 的中点为00(,)E x y，则12x x +=.∴12022x x x m +==-，02m y =，∴,22m E m ⎛⎫- ⎪ ⎪⎝⎭，由PM PN =得PE MN ⊥，又(0,1)P -，∴13PE k ⨯=-，∴1m =. 满足221224(1)0m m ∆=-->.综上1m =. 21.【解析】（1）2()x x F x e =-，2(1)'()0xx F x e -==，令'()0F x =，得1x =， 所以当1x <时，'()0F x <，()F x 单调递减，当1x >时，'()0F x >，()F x 单调递增， 所以当1x =时，()F x 取得最小值为2e-. （2）当0a ≤时，()0xxaf x e e =->，()()g x f x =， 若在[0,1]上单调递增，则'()0f x ≥恒成立，即：2max []xa e ≥-，1a ≥-，10a -≤≤；当0a >时，'()0xx a f x e e =+>，()xx a f x e e=-在[0,1]上是单调递增的， 又()()g x f x =在[0,1]上单调递增，所以()0f x ≥在[0,1]上恒成立.2min []x a e ≤，01a <≤.综上：11a -≤≤.22.【解析】（1）直线l 的直角坐标系方程是220x y a +--=， 圆C 的直角坐标方程是22(2)4x y -+=. （2）由（1）知圆心为(2,0)C ，半径2r =， 设圆心到直线的距离为d ，因为直线与圆相切，所以2d ===，解得2a =±23.【解析】（1）当1a =时，不等式()4114f x x x ≥⇔++-≥， 当1x >时，()24f x x =≥，解得2x ≥； 当11x -≤≤时，()24f x =≥，无解； 当1x <-时，()24f x x =-≥，解得2x ≤-， 综上所述，不等式的解集为(,2][2,)-∞-+∞. （2）()f x x a x a =++-()()2x a x a a ≥+--=， ∴26a ≥，解得3a ≥或3a ≤-， 即a 的取值范围是(,3][3,)-∞-+∞.21。

长郡中学2019届高三月考试卷（一）数学（文科）得分: _____________本试卷共8页。

时量120分钟。

满分150分。

一、选择题：本大题共12小题•每小题5分，共60分•在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合人=心|0<工<2},£=&|*$1},则AUB=A.{j?|0<.r<l}B.匕|工》1}C. {z| lMz<2}D. {広匕〉。

}★2•复数n满足之（2 + i） = 3 — 6i（i为虚数单位）•则复数之的虚部为A. 3B. -3C. 3iD. -3i3.已知sin a=-z~,则cos 2a=oA Z B—2 cH D—□* 25 •25 • 25•254.某家具厂的原材料费支H2、（单位:万元）与销售额y（单位：万元）之间有如下数据•根据表中提供的全部数据•用最小二乘法得出丿与乂的线性回归方程为$ = & 5久+〃・则〃为、厂 2 4 5 6 825 35 6() 55 75★5.已知向量a=（— 2,1）,〃=（一1,3）,则A. a//b B a丄bC. a//（a—h）D. a丄（a—b）★6.执行如图所示的程序框图输出的结果是7.已知曲线C. ：y=sin M2 ：y=sin（2«r+普），则下面结论正确的是A.把G上各点的横坐标缩短到原来的+倍，纵坐标不变，再把得到的曲线向左平移?个单位长度，得到曲线GB.把G上各点的横坐标缩短到原來的+倍，纵坐标不变，再把得到的曲线向左平移于个单位长度，得到曲线GC.把G上各点的横坐标伸氏到原来的2倍，纵坐标不变，再把得到的曲线向左平移警个单位长度，得到曲线D.把G上各点的横坐标伸长到原來的2倍，纵坐标不变，再把得到的曲线向左平移于个单位氏度，得到曲线G&曲线f（x） = 2x-^在点（0,/（（）））处的切线方程是A. 2工一y—l=0 $+1=0C.久一y=0 I）, y—1 = 09.平而a截球的球而所得恻的半径为1,球心（）到平而a的距离为施，则此球的体积为A. 4用兀B. 6箱兀C.用兀D. 4用冗10.已知*工）是定义在R上的偶函数，且在区间（一8,0］上单调递增.若实数a满足/"）＞/'（一施），则a的取值范围是A. （—OO,—血）B.（s/2 , +oo）C. （-72,72）D. （-OO,-V2）U（/2,+CXD）★ 11.已知四棱锥S-ABCI）的三视图如图所示，则围成四棱锥S-ABCI）的五个面中的最大面积是A. 3B. 6C. 8D. 1012.已知F是抛物线C：/=8^的焦点,M是C上一点,FM的延长线交y轴于点N.若M为FN的中点,则丨FN | =A. 4B. 6C. 8D. 10选择题答题卡二、填空题:本题共4小题・每小题5分.共2（）分.严一夕鼻0,13._________________________________________________ 已知小歹满足占+3<2,则之=2久+歹的最大值为___________________________ .★14•若点P（l,l）为圆云+ b _6工=0的弦MN的中点，则弦MN所在直线的方程为 _______ .15.在中，面积S=*（/ +圧一疋），则角（：的大小为 ______________ ・★16.已知函数/Cr） = lg卄号工一9在区间5」+l）（”WZ）上存在零点,则n= ________ .三、解答题:本大题共70分.解答应写出文字说明.证明过程或演算步骤.第17〜21题为必考题•每个试题考生都必需作答.第22.23题为选考题，考生根据要求作答.（一）必考题：共60分.17.（本小题满分12分）等比数列｛d”｝中，已知01=2,04=16.（T ）求数列仏”｝的通项公式；（II）若心心分别为等差数列血｝的第3项和第5项，试求数列仇｝的通项公式及前"项和S”・1& （本小题满分12分）已知四棱锥P-ABCI）中，底面ABCI）是边氏为2的正方形,PA = PD=V2, CD丄PD.E为CD的中点.（I ）求证:FD丄平而PAB；（|［）求三棱锥P-ABE的体积.PR某家电公司销售部门共有200名销售员•每年部门对每名销售员都有 1 400万元的年度销售任务.已知这200名销售员去年完成的销售额都在区间[2,22]（单位:百万元）内，现将其分成5组，第1组、第2组、第3 组、第4组、第5组对应的区间分别为[2,6）,[6,10）,口0,14）,[14,18）, [18,22],并绘制出如下的频率分布直方图.（丨）求“的值，并计算完成年度任务的人数；（U）用分层抽样的方法从这20（）名销售员中抽取容量为25的样本•求这5组分别应抽取的人数；（m）现从（H）中完成年度任务的销售员中随机选取2名，奖励海南三亚三II游，求获得此奖励的2名销售员在同一组的概率.过椭恻C：若+君=1（5>0）的右焦点R的直线交椭I员1于AJ3两点,只为其左焦点，已知△AR B的周长为4州,椭圆的离心率为普.（I）求椭圆0的方程；（II）设P为椭圆C的下顶点，椭圆C与直线歹=曾工+加相交于不同的两点M、N.当| PM| =| PN|时,求实数加的值.已知函数/（^） = e*-4.（I ）当a=l时,求函数F（;r）=jr［/（工）一/"（丁）］的最小值; （U）若gCr）=l*》）l在［0,1］上单调递增，求实数。

长郡中学2019届高三月考试卷（一）数学（理科）第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.1.设复数，则（）A. B. C. D.【答案】D【解析】【分析】根据复数除法运算，分子分母同时乘以分母的共轭复数，化简即可。

【详解】所以所以选D【点睛】本题考查了复数的除法运算，复数模的定义，属于基础题。

2.2.已知集合，，，则（）A. B. C. D.【答案】C【解析】集合，故，集合表示非负的偶数，故，故选C.3.3.若定义在上的偶函数满足且时，，则方程的零点个数是（）A. 个B. 个C. 个D. 个【答案】C【解析】【分析】根据函数的周期性和奇偶性，画出函数图像，根据函数图像的交点个数确定零点个数即可。

【详解】因为数满足，所以周期当时，，且为偶函数，所以函数图像如下图所示由图像可知，方程有四个零点所以选C【点睛】本题考查了函数的奇偶性和周期性，绝对值函数图像的画法和函数零点的概念，关键是根据函数解析式能够正确画出函数的图像，属于基础题。

4.4.计算的结果为（）A. B. C. D.【答案】B【解析】【分析】根据诱导公式，化简三角函数值；再根据正弦的差角公式合并即可得到解。

【详解】所以选B【点睛】本题考查了三角函数诱导公式、正弦差角公式的简单应用，属于基础题。

5.5.已知、、是双曲线上不同的三点，且、连线经过坐标原点，若直线、的斜率乘积，则该双曲线的离心率为（）A. B. C. D.【答案】C【解析】【分析】根据题意，设出A、B、P点的坐标，代入方程做差，得到；利用两条直线的斜率乘积关系，得到。

联立可以得到的关系式，进而求得离心率。

【详解】由题意，设则将A、P坐标代入双曲线方程，得两式相减得所以，即所以所以选C【点睛】本题考查了点与双曲线的关系，设而不求法是解决圆锥曲线问题常用方法，属于基础题。

6.6.某单位为了落实“绿水青山就是金山银山”理念，制定节能减排的目标，先调查了用电量（单位：千瓦·时）与气温（单位：℃）之间的关系，随机选取了天的用电量与当天气温，并制作了以下对照表：（单位：℃）（单位：千瓦·时）由表中数据得线性回归方程：，则由此估计：当某天气温为℃时，当天用电量约为（）A. 千瓦·时B. 千瓦·时C. 千瓦·时D. 千瓦·时【答案】A【解析】【分析】根据回归直线方程经过样本中心点，求得，代入回归直线可求得；代入回归方程后，可预报当气温为℃时，当天的用电量。