2013—2014学年度人教版九年级下《26.1.1~26.1.3二次函数》单元测试卷

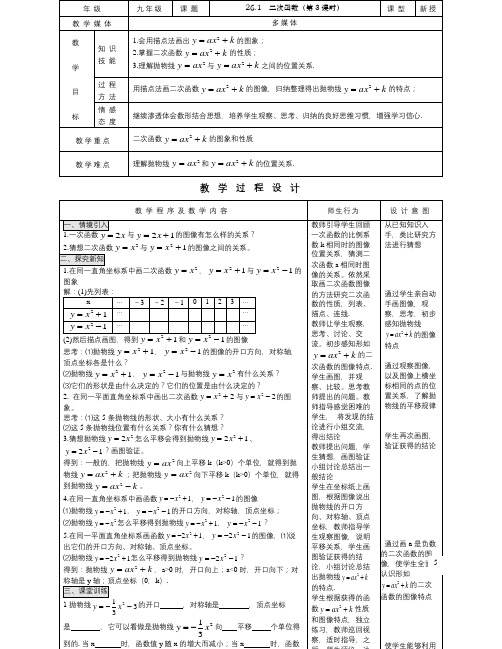
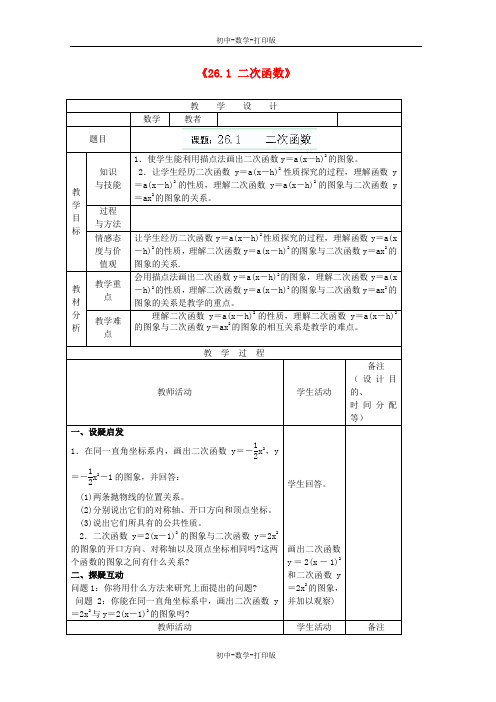
《26.1 二次函数》教 学 设 计数学教者题目教 学 目 标知识 与技能 1．使学生能利用描点法画出二次函数y ＝a(x —h)2的图象。

2．让学生经历二次函数y ＝a(x －h)2性质探究的过程，理解函数y＝a(x －h)2的性质，理解二次函数y ＝a(x －h)2的图象与二次函数y＝ax 2的图象的关系。

过程与方法情感态度与价值观 让学生经历二次函数y ＝a(x －h)2性质探究的过程，理解函数y ＝a(x－h)2的性质，理解二次函数y ＝a(x －h)2的图象与二次函数y ＝ax 2的图象的关系.教 材 分 析教学重点 会用描点法画出二次函数y ＝a(x －h)2的图象，理解二次函数y ＝a(x－h)2的性质，理解二次函数y ＝a(x －h)2的图象与二次函数y ＝ax 2的图象的关系是教学的重点。

教学难点理解二次函数y ＝a(x －h)2的性质，理解二次函数y ＝a(x －h)2的图象与二次函数y ＝ax 2的图象的相互关系是教学的难点。

教 学 过 程教师活动 学生活动备注 （设计目的、时间分配等）一、设疑启发1．在同一直角坐标系内，画出二次函数y ＝－12x 2，y＝－12x 2－1的图象，并回答：(1)两条抛物线的位置关系。

(2)分别说出它们的对称轴、开口方向和顶点坐标。

(3)说出它们所具有的公共性质。

2．二次函数y ＝2(x －1)2的图象与二次函数y ＝2x 2的图象的开口方向、对称轴以及顶点坐标相同吗?这两个函数的图象之间有什么关系? 二、探疑互动 问题1：你将用什么方法来研究上面提出的问题? 问题2：你能在同一直角坐标系中，画出二次函数y ＝2x 2与y ＝2(x －1)2的图象吗?学生回答。

画出二次函数y ＝2(x －1)2和二次函数y＝2x 2的图象，并加以观察)教师活动学生活动 备注。

各位老师：大家好！今天我说课的题目是：《26.1.1二次函数》。

我准备从如下几个方面展示：教材分析，教法、学法分析，教学程序设计，评价与反思。

一、教材分析（一）教材内容的地位和作用《二次函数》是初中数学教材九年级上册第二章第一节内容。

在此之前，我们学习了平面直角坐标系、认识了函数，学习反比例函数，以及一次函数，对函数已经有了一定的认识。

《二次函数》在初中数学学习中占据了非常重要的地位，是初中数学的核心内容，是学生体会数形结合思想的载体，华罗庚说过：数缺形时少直观，形缺数时难入微。

是对函数学习最好的注解。

（二）教学目标根据上述教材分析，考虑到学生已有的认知结构和心理特征，制定如下教学目标：知识与技能：经历二次函数定义的过程，掌握二次函数的一般式；学会用待定系数法求二次函数关系式。

数学思考：通过用函数表述数量关系的过程，体会模型的思想，建立应用意识。

问题解决：初步学会在具体的情境中从数学的角度发现问题和提出问题，并运用数学知识和方法解决简单的实际问题，增强应用意识。

情感与态度：使学生明白数学来源于生活，从一般情境中归纳出特点，激发学生探究数学问题的兴趣。

（三）教学重点、难点教学重点：二次函数的定义及其一般式，运用待定系数法求二次函数；教学难点：概括二次函数的模型。

二：教法、学法分析类比学习：变量与变量的关系的一种特殊形式共同点：变量与变量的关系，不同点：形式不同，()20=++≠y ax bx c a教法与学法可以以此为基础进行叙述。

由于本节课的内容是学生在学习了《一次函数》和《反比例函数》的基础上的加深，所以可以利用学生已有的知识在问题一、二中放手让学生先去探究探究两个问题中的变量之间的关系，在得到具体的关系式后，再引导学生观察关系式都有着什么样的特点，可以和一元二次方程比较认识，并最终得出二次函数的一般式及二次项系数的取值为什么不为零的道理。

（我改的）学生在我的鼓励引导下，克服思维定势，并通过小组讨论、合作交流等方式，增加学生的学习积极性和自信心，从而培养浓厚的学习兴趣。

第26章 二次函数二次函数y =ax 2的图象与性质1．关于抛物线y ＝12x 2，y ＝x 2，y ＝－x 2的共同性质：①都是开口向上；②都以点(0，0)为顶点；③都以y 轴为对称轴；④都关于x 轴对称．其中正确的个数是( ) A ．1 B ．2 C ．3 D ．42.已知抛物线y ＝ax 2()a >0经过A ()－2，y 1，B ()1，y 2两点，则下列关系式一定正确的是( )A ．y 1>0>y 2B ．y 2>0>y 1C ．y 1>y 2>0D ．y 2>y 1>03．在同一坐标系中画出下列函数的图象： (1)y ＝3x 2；(2)y ＝－13x 2.4．当物体自由下落时，下落的高度h (m)与下落时间t (s)之间的关系式是h ＝12gt 2(g 为定值，g 取9.8 m/s 2)，这表明h 是t 的函数．(1)当t ＝1、2、3时，求出物体的下落高度h ； (2)画出函数h ＝12gt 2的图象．5．已知a ≠0，在同一直角坐标系中，函数y ＝ax 与y ＝ax 2的图象有可能是( )A B C D6．[2018·株洲]已知二次函数y ＝ax 2的图象如图，则下列表示的点有可能在反比例函数y ＝a x的图象上的是( )A ．(－1，2)B ．(1，－2)C ．(2，3)D ．(2，－3)7．[2018·岳阳]在同一直角坐标系中，二次函数y ＝x 2与反比例函数y ＝1x(x >0)的图象如图所示，若两个函数图象上有三个不同的点A (x 1，m )、B (x 2，m )、C (x 3，m )，其中m 为常数，令ω＝x 1＋x 2＋x 3，则ω的值为( )A ．1B ．mC ．m2D.1m8．[2018·孝感]如图，抛物线y ＝ax 2与直线y ＝bx ＋c 的两个交点坐标分别为A (－2，4)、B (1，1)，则方程ax 2＝bx ＋c 的解是______________．9．已知直线y ＝kx ＋b 与抛物线y ＝ax 2(a ＞0)相交于A 、B 两点(点A 在点B 的左侧)，与y 轴正半轴相交于点C ，过点A 作AD ⊥x 轴，垂足为点D .若∠AOB ＝60°，AB ∥x 轴，AB ＝2，求a 的值．10．二次函数y ＝3x 2的图象如图所示，点O 为坐标原点，点A 在y 轴的正半轴上，点B ，C 在二次函数y ＝3x 2的图象上，四边形OBAC 为菱形，且∠OBA ＝120°，求菱形OBAC的面积．11．如图，平行于x 轴的直线AC 分别交函数y 1＝x 2(x ≥0)与y 2＝x 23(x ≥0)的图象于B 、C 两点，过点C 作y 轴的平行线交y 1的图象于点D ，直线DE ∥AC ，交y 2的图象于点E ，求DEAB的值．12．有一座抛物线形拱桥，正常水位时桥下水面宽度为20 m ，拱顶距离水面4 m. (1)在如图所示的直角坐标系中，求出该抛物线的解析式；(2)设正常水位时桥下的水深为 2 m ，为保证过往船只顺利航行，桥下水面的宽度不得小于18 m ，求水深超过多少米时就会影响过往船只在桥下的顺利航行．参考答案【分层作业】 1．B 2．C 3．解：列表：3(2)描点，连线，图略．4．解：(1)把t ＝1、2、3分别代入关系式h ＝12gt 2，可求得h 1＝12×9.8×12＝4.9(m)，h 2＝12×9.8×22＝19.6(m)， h 3＝12×9.8×32＝44.1(m)．(2)列表：答图在平面直角坐标系中描点，然后用光滑的曲线顺次连结各点，得到函数h ＝12gt 2的图象，如答图所示．5．C 6．C【解析】∵抛物线开口向上，∴a ＞0，∴点(2，3)可能在反比例函数y ＝ax的图象上． 7．D【解析】根据题意可得A ，B ，C 三点有两点在二次函数图象上，一点在反比例函数图象上．不妨设A ，B 两点在二次函数图象上，点C 在反比例函数图象上．∵二次函数y ＝x 2的对称轴是y 轴，∴x 1＋x 2＝0.∵点C 在反比例函数y ＝1x (x >0)上，∴x 3＝1m ，∴ω＝x 1＋x 2＋x 3＝1m .8．x 1＝－2，x 2＝1【解析】∵抛物线y ＝ax 2与直线y ＝bx ＋c 的两个交点坐标分别为A (－2，4)、B (1，1)，∴⎩⎪⎨⎪⎧y ＝ax 2，y ＝bx ＋c 的解为⎩⎪⎨⎪⎧x 1＝－2，y 1＝4， ⎩⎪⎨⎪⎧x 2＝1，y 2＝1， 即方程ax 2＝bx ＋c 的解是x 1＝－2，x 2＝1. 9． 解：∵AB ∥x 轴，∴点A 、B 关于y 轴对称． ∵AB ＝2，∴AC ＝BC ＝1. ∵∠AOB ＝60°， ∴OC ＝3，AD ＝ 3. 又∵点A 在第二象限， ∴点A 的坐标是(－1，3)． ∴3＝a ·(－1)2，解得a ＝ 3.10．答图解：连结BC 交OA 于点D ，如答图． ∵四边形OBAC 为菱形，∴BC ⊥O A. ∵∠OBA ＝120°，∴∠OBD ＝60°， ∴OD ＝3BD .设BD ＝t ，则OD ＝3t ，∴B (t ，3t )， 把B (t ，3t )代入y ＝3x 2，得3t ＝3t 2， 解得t 1＝0(舍去)，t 2＝1，∴BD ＝1，OD ＝ 3. ∴BC ＝2BD ＝2，OA ＝2OD ＝23， ∴菱形OBAC 的面积＝12×2×23＝2 3.11．解：设A 点坐标为(0，a )(a ＞0)， 则x 2＝a ，解得x ＝a ， ∴点B (a ，a )． 又∵x 23＝a ，则x ＝3a ，∴点C (3a ，a )． ∵CD ∥y 轴，∴点D 的横坐标与点C 的横坐标相同，为3a ， ∴y ＝(3a )2＝3a ，∴点D 的坐标为(3a ，3a )． ∵DE ∥AC ，∴点E 的纵坐标为3a ， ∴x 23＝3a ，∴x ＝3a ， ∴点E 的坐标为(3a ，3a )， ∴DE ＝3a －3a ，∴DEAB＝3a－3aa＝3－ 3.12．解：(1)设该抛物线的解析式是y＝ax2.结合图象，把(10，－4)代入，得100a＝－4,∴a＝－125，则该抛物线的解析式是y＝－125x2.(2)当x＝9 m时，则有y＝－125×81＝－3.24，4＋2－3.24＝2.76(m)，所以水深超过2.76 m时就会影响过往船只在桥下的顺利航行．。

九年级下册（新人教版）
26.1.1二次函数（教学设计）
教学设计思想：
本节内容可以安排一课时，在课堂中，先以现实生活中的实际问题为例，激起学生的求知欲与探索兴趣，然后利用与一次函数的类比、归纳得出二次函数的概念，教师出示巩固性练习，学生以多种形式完成。

通过这节课的学习要让学生充分理解二次函数的有关概念，能够表示简单的二次函数关系，在学习活动，体会通过探究得到发现的乐趣。

教学目标：
1．知识与技能：
结合具体情境体会二次函数的意义，理解二次函数的有关概念。

能够表示简单变量之间的二次函数关系。

2．过程与方法：
通过二次函数的有关概念的学习，体会由一次函数走向二次函数的归纳、类比思想，即为以后二次函数的图象和性质的学习打下基础；
3．情感、态度与价值观：
体会数学与人们生活的联系。

在探究二次函数的学习活动中，体会通过探究得到发现的乐趣。

教学重点：
结合具体情境体会二次函数的意义，理解二次函数的有关概念。

教学难点：
寻找、发现实际生活中的二次函数问题。

教学方法：
采取引导发现法，创设合理的问题情境，激发学生思维的积极性，充分体现学生的主体作用。

教学安排：
1课时。

教具准备：
投影仪。

课后反思：
这节课我从学生熟悉的问题入手，列出变量间的二次函数关系式，归纳二次函数的概念，通过例题的学习加深对二次函数的概念的理解。

在教学活动中积极组织学生参与和教师的有效指导，培养学生的合作意识和交流能力，帮助学生树立正确的人生观和价值观。

一、学习目标：知识目标：1．探索并归纳二次函数的定义；2．能够表示简单变量之间的二次函数关系．情感目标：1．把数学问题和实际问题相联系,从学生感兴趣的问题入手，能使学生积极参与数学学习活动，对数学有好奇心和求知欲；2．使学生初步体会数学与人类生活的密切联系及对人类历史发展的作用；3．通过学生之间互相交流合作，让学生学会与人合作，并能与他人交流思维的过程，培养大家的合作意识．数学思考：1．感悟新旧知识间的关系，让学生更深地体会数学中的类比思想方法；2．经历探索、分析和建立两个变量之间的二次函数关系的过程，进一步体验如何用数学的方法描述变量之间的数量关系．二、教学重点、难点：教学重点：1．经历探索和表示二次函数关系的过程，获得二次函数的定义。

2．能够表示简单变量之间的二次函数关系．教学难点：经历探索和表示二次函数关系的过程，获得用二次函数表示变量之间关系的体验．三、教学方法：教师引导——自主探究——合作交流。

四、教学过程：温故知新，引出课题。

师：对于“函数”这个词我们并不陌生，大家还记得我们学过哪些函数吗?生：学过正比例函数，一次函数，反比例函数．师：那函数的定义是什么，大家还记得吗?生：记得，在某个变化过程中，有两个变量x和y，如果给定一个x值，相应地就确定了一个y值，那么我们称y是x的函数，其中x是自变量，y是因变量．师：能把学过的函数回忆一下吗?生：可以。

一次函数y=kx+b （其中k、b是常数，且k≠0）正比例函数y＝kx （k是不为0的常数）k（k是不为0的常数）反比例函数y=x师：学习这些函数的时候，大家还记得我们从哪几个方面探究的吗?生：定义、函数的一般形式、函数的图像和性质、函数在实际问题中的应用、函数与方程与不等式的关系等。

师：很好，创设情境探究新知：问题1．设圆的半径长为x ，面积为y ，则y 关于x 的关系式为是什么？2．某工厂一种产品现在年产量是20件，计划今后两年增加产量，如果每年都比上一年的产量增加x 倍，那么两年后这种产品的产量y将随计划所定的x的值而确定，y与x之间的关系应怎样表示？这种产品的原产量是20件，一年后的产量是件，再经过一年后的产量是件，即两年后的产量为。